随着浅部煤炭资源的逐步枯竭,对深部煤炭资源的开采利用成为解决能源问题的重要途径。大量深埋回采巷道开挖后围岩发生剧烈的冒顶、片帮及底臌等变形破坏,严重影响了煤矿的安全高效生产。由于巷道两帮的煤体强度通常较顶底板岩层低,变形量显著而成为巷道围岩控制的重点和难点。长期以来,大量专家学者和现场技术人员对两帮煤体的变形破坏范围进行了深入研究。侯朝炯等[1]基于松散介质应力平衡理论研究了巷道煤帮与顶板界面上的应力分布规律及其极限平衡区宽度;郑桂荣等[2]根据煤巷两帮煤体的受力特点,通过简化煤帮应力分布曲线,建立了煤帮破裂区厚度的理论计算公式;李树清等[3]应用弹塑性极限平衡理论分析了锚注联合支护条件下的煤帮塑性区宽度;于远祥等[4]基于煤帮支承压力的双曲函数分布模型,提出了煤帮极限平衡区和破碎区的计算公式,并分析了煤帮极限平衡区宽度的主要影响因素;单仁亮等[5]指出巷道帮部的破坏主要由帮部薄弱体压剪破坏与交界面滑移破坏共同作用导致;刘德峰等[6]考虑工程扰动和岩体地质强度对煤帮岩体在变形过程中的影响,建立了非线性摩尔库伦准则,确定了煤帮滑移面正应力及其极限平衡区宽度;李延军[7]讨论了大跨度开切眼煤帮极限平衡区深入围岩的最大深度;黄庆享等[8]基于巷道底板极限平衡深度计算模型,得到了巷帮极限平衡区宽度与巷道底板破坏深度成线性增长关系的规律。
上述专家学者从不同角度对巷道帮部岩体的变形破坏规律进行了系统深入的分析,所得研究成果对确定合理的巷道开挖及支护方案具有重要参考价值。工程实际中,由于巷道帮部岩体的变形破坏与其应力应变状态密切相关,但从现有关于巷道帮部变形的研究中可以看出,基于岩体自身的应力应变极限条件来反演分析巷道帮部极限平衡区宽度的研究成果还较少。因此,笔者通过建立巷道煤帮在支撑压力作用下的力学分析模型,运用弹性理论,从分析煤帮岩体的应力应变入手,结合煤帮岩体的变形特征来反演分析煤帮的极限平衡区宽度,并基于工程实例对所得结论进行验证,为研究回采巷道两帮稳定性及其控制措施提供新的思路。
1 巷道帮部煤体受力变形分析
1.1 煤帮力学分析模型的建立
巷道开挖后,围岩应力发生重新分布并在其帮部形成支承压力。在无支护情况下,在垂直支承压力作用下帮部岩体将会依次出现破碎区、塑性区及弹性区3个区域,如图1所示[9]。

图1 巷道煤帮支承压力分布模型
Fig.1 Abutment pressure distribution model of the side-wall coal
为方便讨论,将巷道煤帮上方支承压力简化为直线分布形式,如图2所示。

图2 巷道煤帮支承压力简化模型
Fig.2 Abutment pressure reduction model of the side-wall coal
1.2 煤帮岩体变形计算原理
尽管巷道帮部岩体具有非连续、非均质且各向异性的物理力学特性,但由于开挖卸载所引起的巷道帮部岩体变形范围通常较小,且直线分布形式能基本反映煤帮上方支承压力的客观分布规律,不妨设巷道帮部岩体连续、均质且各向同性,支承压力按均匀荷载和线性荷载两种工况进行叠加。在煤帮一定范围内任取一单元体作为研究对象,根据半无限体在法向荷载作用下各应力分量的分析原理,分别计算各部分荷载作用下该单元体产生的各应力分量σx,σy及τxy,然后将各应力分量进行叠加即可求得煤帮内任一点的应力分量[10-11]。建立均匀分布荷载和线性分布荷载作用下巷道煤帮内任一点的受力模型如图3所示和图4所示。由弹性理论可知均匀分布荷载下煤帮岩体中任一点的应力分量分别为
(1)
(2)
(3)
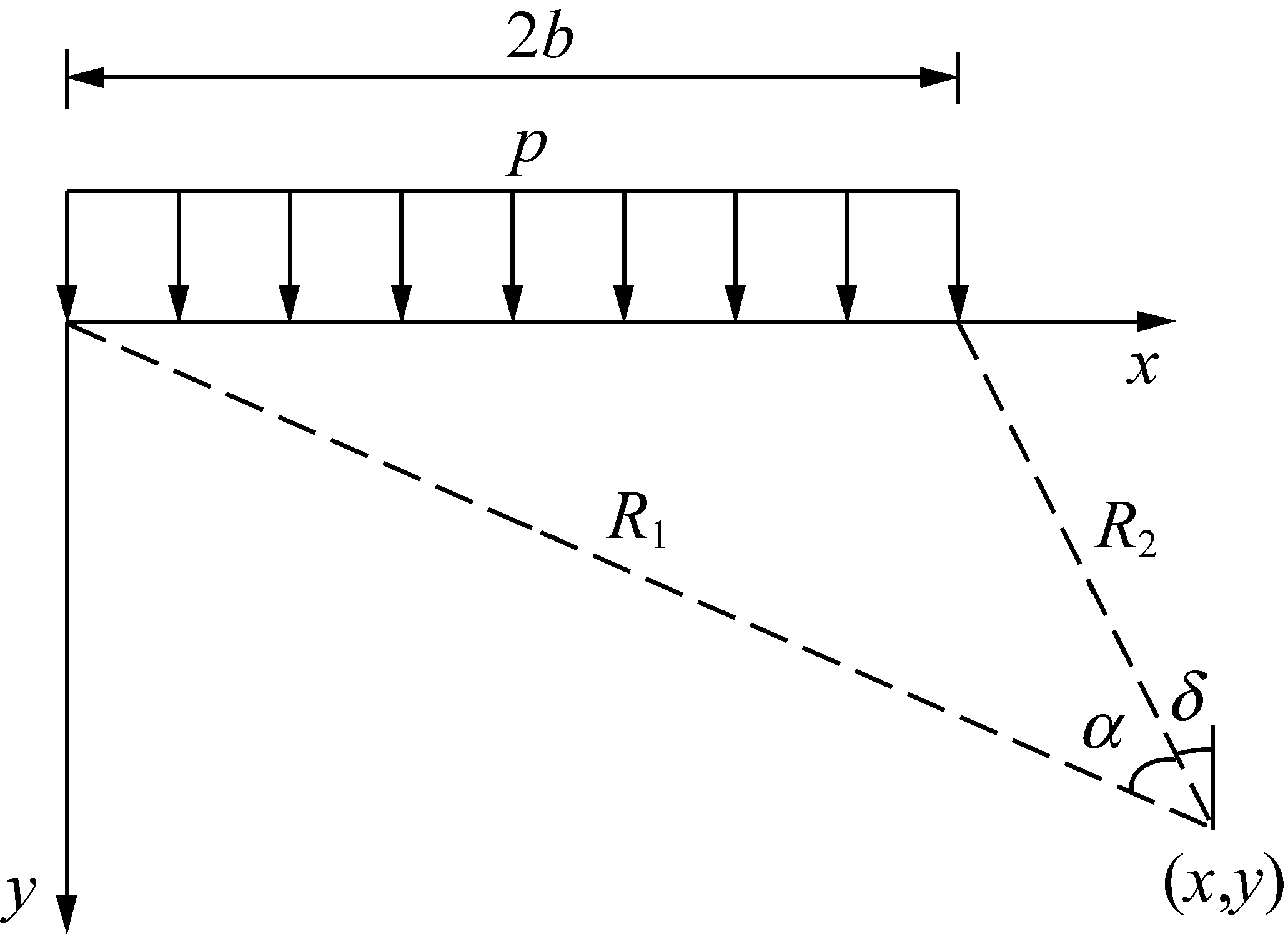
图3 均匀分布荷载
Fig.3 Uniformly distributed loading
同理,线性分布荷载下煤帮岩体中任一点的应力分量分别为
(4)
(5)
(6)

图4 线性分布荷载
Fig.4 Linear distributed loads
1.3 煤帮岩体应力分量的确定
将式(1)~(6)中的所有变量采用直角坐标值x和y表示。令峰值应力P1=kγH,P0=γH,按荷载分布形式,将图2所示巷道煤帮支承压力简化模型划分为3个部分,各部分应力分量计算如下:
(1)极限平衡区线性荷载
煤帮极限平衡区线性荷载计算模型如图5所示。由式(4)~(6)可得该区内任一点的应力分量为
(7)
(8)
(9)
(2)弹性区均布荷载
煤帮弹性区均布荷载计算模型如图6所示。由式(1)~(3)可得该区内任一点的应力分量为
(10)
(11)
(12)

图5 极限平衡区线性荷载计算模型
Fig.5 Calculation model of linear load in limit equilibrium zone

图6 弹性区均布荷载计算模型
Fig.6 Calculation model of uniformly distributed load in elastic zone
(3)弹性区线性荷载
煤帮弹性区线性荷载计算模型如图7所示。由式(4)~(6)可得该区内任一点的应力分量为
(13)
(14)
(15)

图7 弹性区线性荷载计算模型
Fig.7 Calculation model of linear load in elastic zone
1.4 煤帮岩体应力应变分析
通过确定煤帮岩体内任一点在各部分支承压力作用下的应力分量,由弹性力学理论可得该点的应力分量大小为
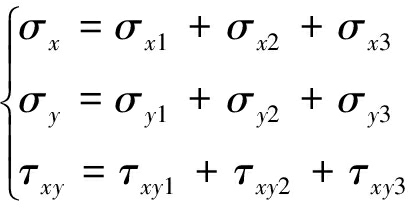
(16)
将巷道煤帮岩体简化为均质连续的弹性体,根据虎克定律可得煤帮岩体内任一点的应变分量为
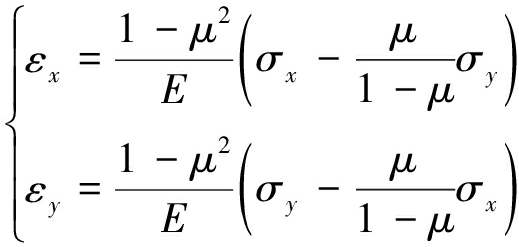
(17)
式中,E,μ分别为煤帮岩体的综合弹性模量和泊松比。
2 巷道煤帮极限平衡区宽度分析
2.1 支承压力下煤帮岩体柱条模型的建立
工程实际中,巷道开挖后,煤帮岩体在较大的竖向支承压力作用下向巷道内产生膨胀变形,进而导致煤帮岩体出现朝向巷道内的径向拉应变,该应变值随支承压力的增加而不断增大。对某一具体界面上的煤帮岩体而言,其在支承压力下的变形破坏具有明显的“压缩柱条”挠曲特征,如图8所示。
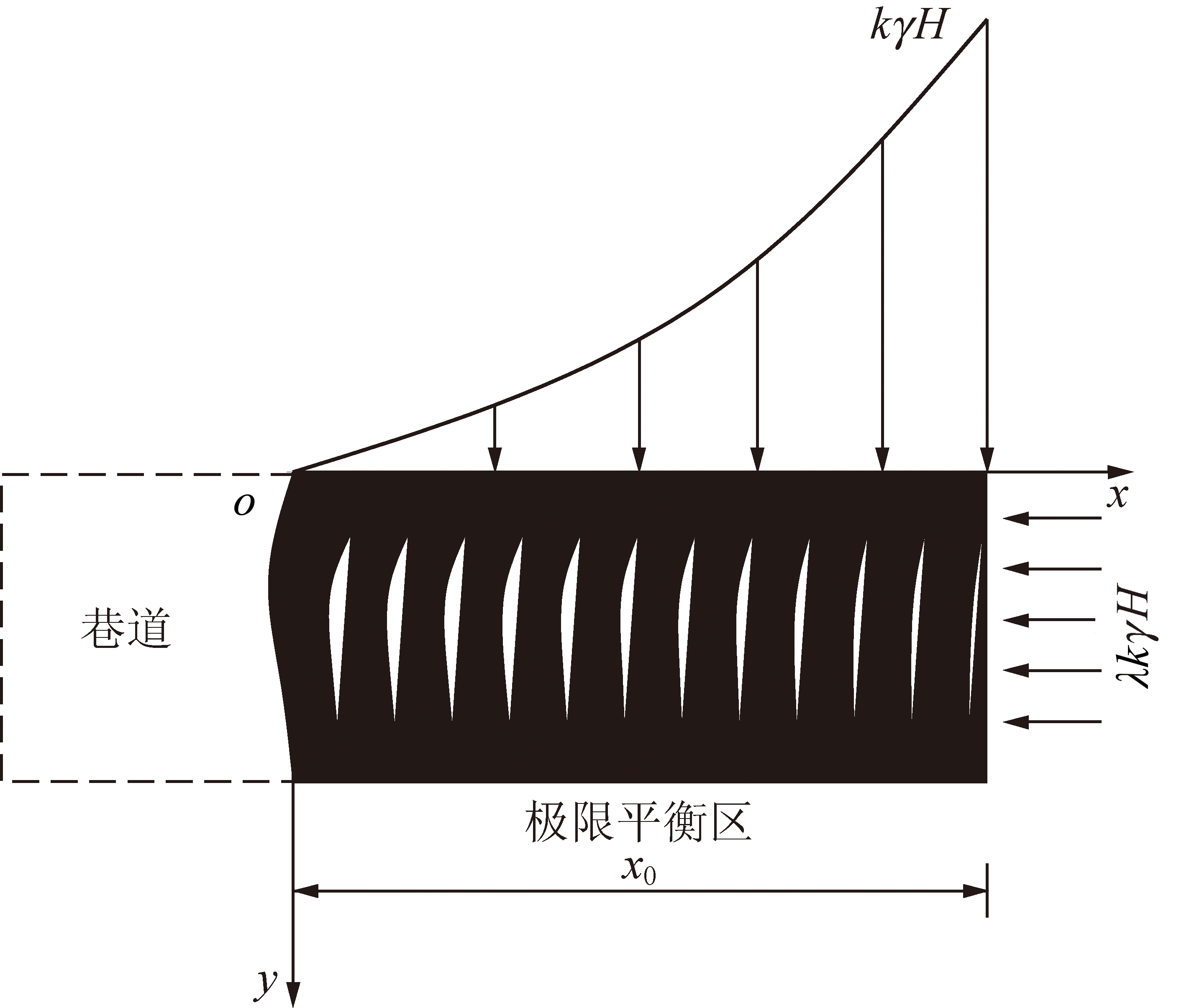
图8 煤帮岩体“压缩柱条”分析模型
Fig.8 Analysis model of “compression column”of coal wall rock mass
当煤帮弹塑性界面上的岩体在其上方支承压力作用下产生的径向拉应变达到其极限拉应变时,该界面上“压缩柱条”岩体将均处于挠曲断裂的临界状态。由于煤帮上方支承压力的连续分布,在由弹塑性界面至煤帮表面的不同界面上,“压缩柱条”岩体所发生的挠曲变形量逐渐增大,多个并列“压缩柱条”岩体的径向挠曲变形连续叠加并在煤帮表面产生“帮臌”,最终在煤帮一定深度范围内形成一个连续的极限平衡区[12-14]。
2.2 煤帮岩体挠曲断裂力学分析
以煤帮弹塑性界面岩体为研究对象,忽略该界面岩体自重及其在垂直方向上的压缩变形,建立支承压力下弹塑性界面岩体的的“压缩柱条”模型如图9所示。

图9 煤帮弹塑性界面岩体“压缩柱条”模型
Fig.9 Model of “compression column”for elastic plastic interface rock mass of coal wall
如图9(c)所示,取x截面以下部分为分离体,以x截面的形心为中心建立力矩平衡方程得:
(18)
式中,M为x截面形心的弯矩;Fp为煤壁所受垂直方向压力;w为煤壁挠度;M0为煤壁固定端力矩;h为巷道设计高度。
由材料力学理论[15]可知
M=-EIw″
(19)
式中,EI为煤壁的弯矩刚度。
由式(18)和(19)可得
(20)
令
(21)
则由式(20)和(21)可得
(22)
微分方程(22)的通解为
(23)
式中,c1和c2均为微分方程的通解系数。
由图9可知压缩柱条变形的边界条件为
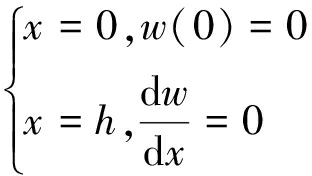
(24)
由式(23)和(24)可得
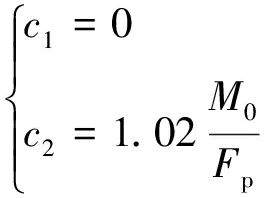
(25)
将式(23)代入式(21)得:
(26)
当![]() 时,挠度w取得最大值,此时有
时,挠度w取得最大值,此时有
(27)
式中,k∈Z。
解之得:
x=(-1.39k+0.65)h
(28)
考虑x≥0的实际情况,当k=0时,有
x=0.65h
(29)
式(29)表明,煤帮弹塑性界面上的“压缩柱条”岩体在支承压力作用下的水平挠曲变形曲线为正弦半波,其水平挠曲位移的最大值位于距离底板0.65h处。当该点岩体发生的水平拉应变达到其极限拉应变时,“压缩柱条”岩体将进入挠曲断裂临界状态,这与文献[8,16-17]的研究结果相吻合。
2.3 煤帮极限平衡区宽度计算
由上述分析可以看出,在煤帮弹塑性界面上发生最大水平挠曲位移的单元体位于(x0,0.35h),将其坐标(x0,0.35h)代入式(7),(8),(10),(11),(13)及(14)得该单元在各部分支承压力作用下的应力分量分别为
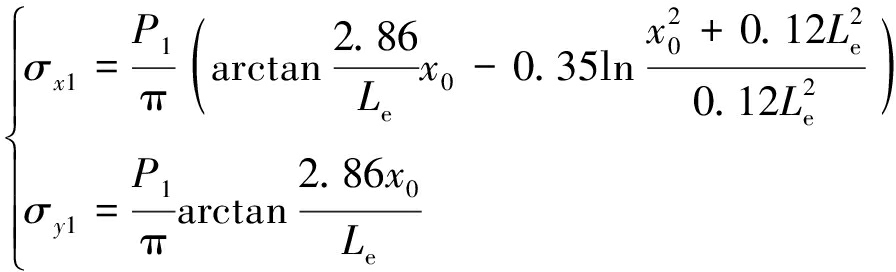
(30)
(31)
(32)
将式(30)~(32)代入式(16)得煤帮弹塑性界面上具有最大水平位移的单元岩体的应力分量为
(33)
(34)
对于峰值支承压力下的煤帮弹塑性界面而言,发生最大水平应变的单元煤体的水平拉应变将达到其极限拉应变,由式(17),(33)及(34)得
(35)
由式(35)可以看出,巷道煤帮极限平衡区宽度是一个关于煤帮岩体极限拉应变的隐函数,其大小不仅取决于煤体的极限拉应变、泊松比及弹性模量,而且与原岩应力大小及巷道开挖后发生重分布的峰值应力水平及煤帮弹性区宽度密切相关。
2.4 煤帮极限平衡区宽度影响因素分析
(1)极限平衡区宽度与岩体弹性模量的关系
参考文献[1]及[18-20]所述围岩物理力学参数,设某回采巷道埋深H=600 m,其上覆岩层容重γ=25 kN/m3,煤帮岩体的平均泊松比μ=0.3,极限拉应变εtmax=0.35×10-3,煤帮弹塑性界面上应力集中系数K=1.5,将上述参数代入式(35)可得
arctan(0.715x0)+0.585]×109
(36)
由式(36)可得煤帮极限平衡区宽度与岩体综合弹性模量的关系如图10所示。

图10 煤帮极限平衡区与岩体弹性模量的关系
Fig.10 Relationship between ultimate equilibrium zone of coal seam and elastic modulus of rock mass
(2)极限平衡区宽度与岩体极限拉应变的关系
当巷道煤帮相关参数分别为:H=600 m,γ=25 kN/m3,μ=0.3,K=1.5,E=3.4 GPa,由式(35)可得
11arctan(0.715x0)+0.6}×10-4
(37)
由式(37)可得煤帮极限平衡区宽度与岩体极限拉应变的关系如图11所示。
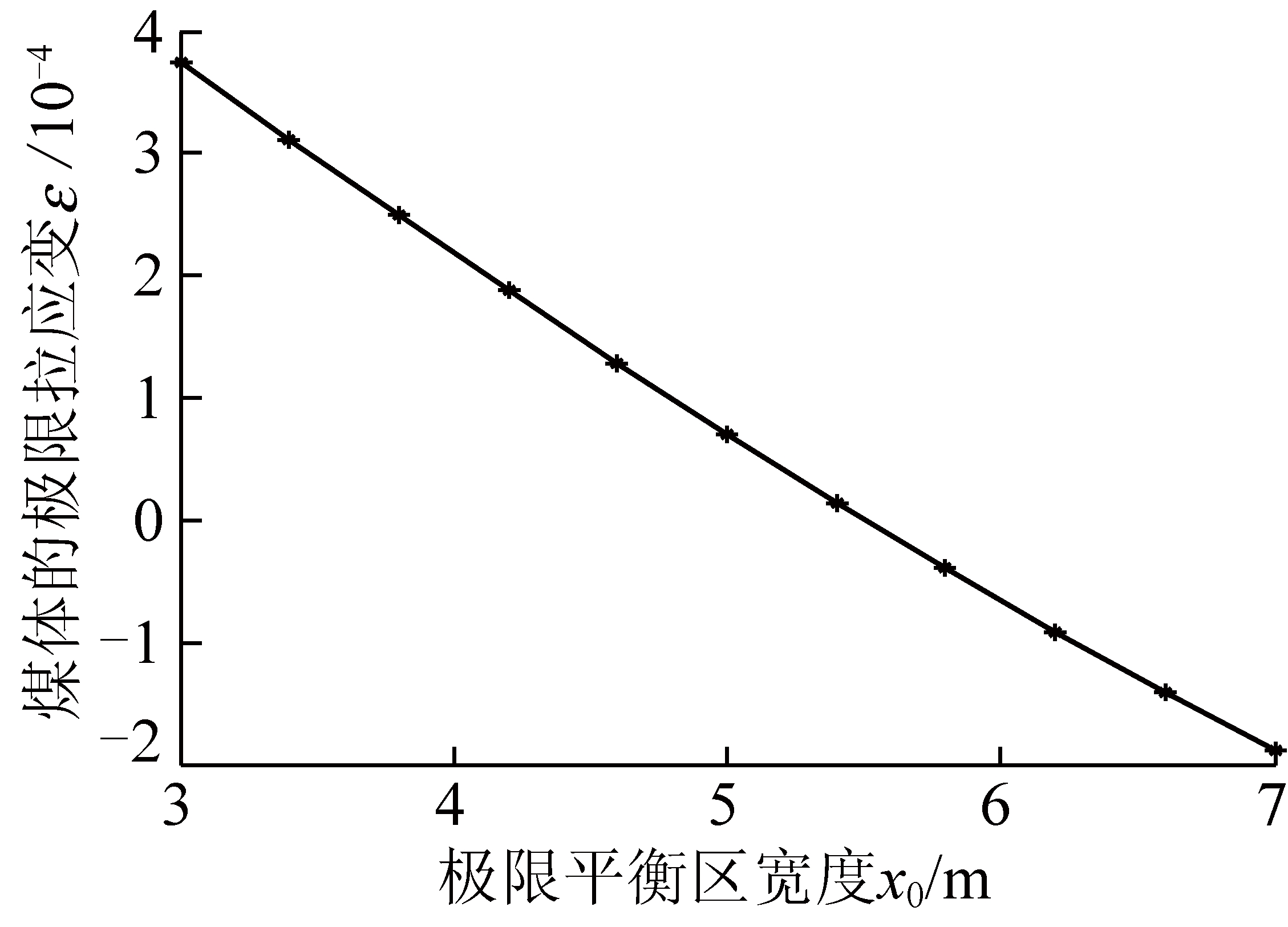
图11 煤帮极限平衡区与岩体极限拉应变的关系
Fig.11 Relationship between ultimate equilibrium zone of coal seam and ultimate tensile strain of rock mass
(3)极限平衡区宽度与巷道埋深的关系
同理,当巷道煤帮相关参数分别为:H=600 m,γ=25 kN/m3,εtmax=0.35×10-3,μ=0.3,K=1.5,E=3.4 GPa,由式(35)可得
13.7arctan(0.715x0)-0.75]
(38)
由式(38)可得煤帮极限平衡区宽度与巷道埋深的关系如图12所示。

图12 煤帮极限平衡区与巷道埋深的关系
Fig.12 Relation between limit equilibrium zone of coal side and roadway depth
3 巷道煤帮破裂区宽度计算
由文献[4]可知,回采巷道开挖后,煤帮处于二向受压状态,承载能力大幅度降低。与此同时,由于应力集中,煤帮受力急剧增加,当煤帮表面岩体所受压应力超过其极限强度时,表面岩体将由塑性状态进入破裂状态,形成如图1所示的破裂区,其宽度为
(39)
式中,系数β和B分别由下式确定:
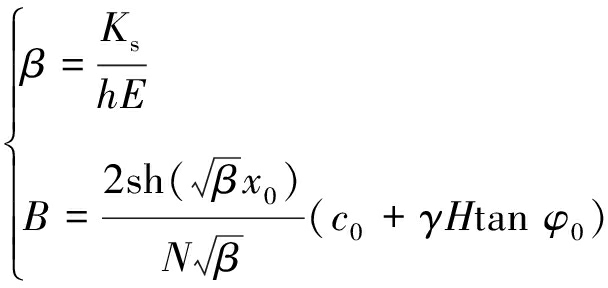
(40)
式中,c0,φ0及Ks分别为巷道煤帮与顶底板界面的黏聚力、内摩擦角及剪切刚度系数;N为煤帮弹塑性界面上所受的水平推力,其大小为
N=λkγHh
(41)
式中,λ为煤帮弹塑性界面上的侧压力系数。
此时,巷道煤帮塑性区宽度为
Lp=x0-Ls
(42)
4 算例分析
4.1 工程概况
陕西澄合百良煤矿4号主采煤层14501工作面运输巷设计为4 000 mm×4 600 mm的矩形断面,平均埋深为600 m,在运输巷350~450 m里程处,由于帮部煤体整体强度较低,尽管开挖初期对巷道围岩采取了高强度的锚杆(索)支护(图13),但仍然出现了严重帮臌和顶板下沉变形,两帮收敛速率高达40~45 mm/d,严重影响了后期回采工作的正常开展。

图13 14501工作面运输巷原支护方案
Fig.13 Original support scheme of the transport channel in 14501 working face
本文将根据上述理论公式确定14501工作面运输巷煤帮的极限平衡区及其破裂区,进而对巷道围岩的原支护参数进行优化。
4.2 14501工作面运输巷煤帮变形分析
(1)煤帮极限平衡区宽度分析
经现场测试和工程类比,百良矿巷道煤帮岩体各参数的取值见表1。
表1 煤帮各计算参数取值
Table 1 Value of calculating parameters of coal wall

参数γ/(kN·m-3)Ks/(GPa·m-1)c0/MPaφ0/(°)λkE/GPaμεtmax/10-3取值250.143.0270.751.53.40.150.35
在14501工作面运输巷350~450 m段开挖前后,煤帮上方原岩应力和支撑压力峰值大小分别为
P0=γH=25×103×600=1.5×107Pa
(43)
P1=1.5×25×103×600=2.25×107Pa
(44)
设煤帮弹性区宽度为巷道设计高度,将式(43)和(44)代入式(33)和(34)得
(45)
(46)
将表1中相关参数、式(45)及(46)代入式(35)并化简得
1.1arctan(0.715x0)+0.32
(47)
由式(47)即可解得14501运输巷350~450 m段煤帮的极限平衡区宽度为x0=3.2 m。
(2)煤帮破裂区宽度分析
将表1中相关参数代入式(40)和(41)可得
(48)
N=0.75×1.5×25×103×600×4=
6.75×107N
(49)
103×600tan 27°)=1.03
(50)
将式(50)代入式(39)得煤帮破裂区宽度为
(51)
上述计算表明,14501工作面运输巷350~450 m段巷道帮部锚杆未锚入塑性区,导致帮部岩体严重变形。在将帮部锚杆长度由2.2 m调整到2.8 m后,现场监测结果表明,巷道帮部岩体的收敛速率大大降低,顶底板稳定状态得以显著改善。
5 结 论
(1)本文以弹性理论为基础,将巷道帮部岩体简化为均质、连续的介质,通过建立支承压力下回采巷道煤帮的受力模型,推导了煤帮岩体的应力应变解析解公式,为客观反映煤帮岩体的变形破坏规律提供了理论依据。
(2)基于煤帮弹塑性界面岩体在支承压力下的压缩柱条模型,根据材料力学理论,建立了该界面岩体所产生的径向极限拉应变与煤帮极限平衡区宽度的理论公式,结果表明:极限平衡区宽度与煤帮岩体的弹性模量及其极限拉应变呈反相关,与巷道埋深呈正相关关系。
(3)工程实例分析表明,本文提出的相关理论公式具有一定的科学合理性,能够较好地阐述巷道帮部变形的力学原理,对深埋矿山巷道甚至其他地下硐室施工具有一定的参考价值。
[1] 侯朝炯,马念杰.煤层巷道两帮煤体应力和极限平衡区的探讨[J].煤炭学报,1989(4):21-29.
HOU Chaojiong,MA Nianjie.Stress in in-seam roadway sides and limit equilibrium Zone[J].Journal of China Coal Society,1989(4):21-29.
[2] 郑桂荣,杨万斌.煤巷煤体破裂区厚度的一种计算方法[J].煤炭学报,2003,28(1):37-40.
ZHENG Guirong,YANG Wanbin.A Calculation method of the failure zone width of side coal-wall of roadway in seams[J].Journal of China Coal Society,2003,28(1):37-40.
[3] 李树清,潘长良,王卫军.锚注联合支护煤巷两帮塑性区分析[J].湖南科技大学学报(自然科学版),2007,22(2):5-8.
LI Shuqing,PAN Changliang,WANG Weijun.Analysis of plastic region of sidewalls in coal drifts reinforced by association of rock bolt and grouting[J].Journal of Hunan University of Science & Technology(Natural Science Edition),2007,22(2):5-8.
[4] 于远祥,洪兴,陈方方.回采巷道煤体荷载传递机理及其极限平衡区的研究[J].煤炭学报,2012,37(10):1630-1636.
YU Yuanxiang,HONG Xing,CHEN Fangfang.Study on load transmission mechanism and limit equilibrium zone of coal-wall in roadway[J].Journal of China Coal Society,2012,37(10):1630-1636.
[5] 单仁亮,孔祥松,蔚振廷,等.煤巷强帮支护理论与应用[J].岩石力学与工程学报,2013,32(7):1304-1314.
SHAN Renliang,KONG Xiangsong,WEI Zhenting,et al.Theory and application of strong support for coal roadway sidewall[J].Chinese Journal of Rock Mechanics and Engineering,2013,32(7):1304-1314.
[6] 刘德峰,郭兵兵,刘长武,等.考虑工程扰动和地质条件的巷帮极限平衡区分析[J].煤炭学报,2017,42(3):597-603.
LIU Defeng,GUO Bingbing,LIU Changwu,et al.Analysis of limit equilibrium zone for roadway side wall considering engineering disturbance and geological condition[J].Journal of China Coal Society,2017,42(3):597-603.
[7] 李延军.松软煤层复合顶板条件下大跨度切眼支护技术研究[J].煤田地质与勘探,2018,46(4):147-153.
LI Yanjun.Support technology of large span open-off cut under compound roof in mining soft coal seam[J].Coal Geology & Exploration,2018,46(4):147-153.
[8] 黄庆享,郝高全.回采巷道底板破坏范围及其影响研究[J].西安科技大学学报,2018,38(1):51-58.
HUANG Qingxiang,HAO Gaoquan.Research on the floor failure range and its effects of entry[J].Journal of Xi’an University of Science and Technology,2018,38(1):51-58.
[9] 钱鸣高,石平五.矿山压力与岩层控制[M].徐州:中国矿业大学出版社,2003.
[10] 黄庆享,刘建浩.浅埋大采高工作面煤壁片帮的柱条模型分析[J].采矿与安全工程学报,2015,32(2):187-191.
HUANG Qingxiang,LIU Jianhao.Vertical slice model for coal wall spalling of large mining height longwall face in shallow seam[J].Journal of Mining & Safety Engineering,2015,32(2):187-191.
[9] 许国安,靖洪文,丁书学,等.沿空双巷窄煤柱应力与位移演化规律研究[J].采矿与安全工程学报,2010,27(2):160-165.
XU Guo’an,JING Hongwen,DING Shuxue,et al.Evolution rules of stress and displacement for narrow coal[J].Journal of Mining & Safety Engineering,2010,27(2):160-165.
[10] 王卫军,黄成光,侯朝炯,等.综放沿空掘巷底鼓的受力变形分析[J].煤炭学报,2002,27(1):26-30.
WANG Weijun,HUANG Chengguang,HOU Chaojiong,et al.Mechanical deformation analysis of floor strata of roadway driving along next goaf in fully mechanized sub-level caving face[J].Journal of China Coal Society,2002,27(1):26-30.
[11] 薛强.弹性力学[M].北京:北京大学出版社,2006.
[12] 顾金才,顾雷雨.深部开挖洞室围岩分层断裂破坏机制模型试验研究[J].岩石力学与工程学报,2008,27(3):433-438.
GU Jincai,GU Leiyu.Model test study on mechanism of layered fracture within surrounding rock of tunnels in deep stratum[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(3):433-438.
[13] 宫守才.煤帮塑性区弹塑性位移解[A].陕西省岩石力学与工程学会、陕西省土木建筑学会、陕西省煤炭学会.西部矿山建设工程理论与实践[C].陕西省岩石力学与工程学会、陕西省土木建筑学会、陕西省煤炭学会:陕西省煤炭学会,2009:6.
[14] 徐思朋,茅献彪,张东升.煤柱塑性区的弹粘塑性理论分析[J].辽宁工程技术大学学报,2006,25(2):194-196.
XU Sipeng,MAO Xianbiao,ZHANG Dongsheng.Study on pillar’s plastic zone based on elasto-visco-plastic theory[J].Journal of Liaoning Technical University,2006,25(2):194-196.
[15] 孙训方,方孝淑.材料力学(I)[M].北京:高等教育出版社,2009.
[16] 宁宇.大采高综采煤壁片帮冒顶机理与控制技术[J].煤炭学报,2009,34(1):50-52.
NING Yu.Mechanism and control technique of the rib spalling in fully mechanized mining face with great mining height[J].Journal of China Coal Society,2009,34(1):50-52.
[17] 尹希文,闫少宏,安宇.大采高综采面煤壁片帮特征分析与应用[J].采矿与安全工程学报,2008,25(2):222-225.
YIN Xiwen,YAN Shaohong,AN Yu.Characters of the rib spalling in fully mechanized caving face with great mining height[J].Journal of Mining & Safety Engineering,2008,25(2):50-52.
[18] 李世平.岩石力学简明教程[M].徐州:中国矿业大学出版社,1986.
[19] 沈明荣,陈建峰.岩体力学[M].上海:同济大学出版社,2006.
[20] 赵彦钵,吴瑞祥,李政林,等.极限拉应变准则在围岩松动圈模拟中的应用[J].地下空间与工程学报,2014,10(2):315-321.
ZHAO Yanbo,WU Ruixiang,LI Zhenglin,et al.Application of ultimate tensile strain criteria to simulate the loose zone of surrounding rock[J].Chinese Journal of Underground Space and Engineering,2014,10(2):315-321.
