对深埋巷道围岩进行理想弹塑性分析，主要包括强度准则的选取、平衡方程、几何方程、本构方程的建立以及边界条件的确定，其中强度准则、平衡方程和本构方程一直都是研究的重点。常用的岩石强度准则主要包括:Mohr-Coulomb(MC)准则[1],Drucker-Prager(DP)准则[2]、统一强度理论(UST)[3]和Mogi-Coulomb(MO)准则[4]。其中除MC准则之外，其余3种准则均可反映中间主应力效应的影响。

赵春风等[5]针对5种常用的可考虑中主应力效应的破坏准则，分别建立了各准则内摩擦角与中主应力系数之间的关系，探讨了各准则对中主应力的反映能力及其适用性;张常光等[6]建立了包含8种岩土常用强度准则的统一线性方程，探讨了围岩弹塑性分析的强度理论效应与塑性区位移的参数影响特性;潘继良等[7]归纳总结了4种常用岩石强度准则的平面应变统一屈服方程，引入强度参数软化模量和扩容系数，推导了考虑应变软化和扩容的巷道围岩应力场和位移场的封闭解析解;高召宁等[8]、范浩等[9]分别基于Mohr-Coulomb准则和统一强度理论，综合考虑围岩剪胀、中间主应力效应等影响因素，对受渗流影响的圆形巷道围岩应力场和位移场解析解进行了理论推导。可见，建立一个统一形式的屈服方程，对不同强度准则的计算结果进行对比分析，了解不同强度准则间的差异性和适用性，然后结合具体的工程背景选取合适的强度准则，具有重要的理论意义和工程应用价值。

对于岩土类材料，在剪切应力的作用下，由于岩土体内部颗粒的相互错动，往往会出现非线性的体积膨胀现象，称之为岩土类材料的剪胀特性[10-11]，这也使岩土材料的塑性变形与金属类材料具有本质的区别。大量研究表明[12-14]，岩土类材料塑性变形不遵守关联流动法则，传统塑性位势理论并不适应岩土材料的变形机制。

笔者在前人研究的基础上，首先对4种岩石材料常用强度准则进行归纳总结，得到平面应变条件下包含中主应力系数b(MC准则除外)的统一屈服方程;然后针对受地下水渗流影响的深埋巷道围岩，建立理想弹塑性模型，结合塑性位势理论和线性非关联流动法则得到与塑性势函数有关的剪胀系数表达式，同时考虑围岩塑性区内弹性应变不同的处理方式，推导了渗流作用下的深埋圆形巷道应力场和位移场解析解;新的解析解不仅可以灵活匹配不同的岩石强度准则，而且还能反映孔隙水压力、中间主应力效应和围岩剪胀特性;最后通过具体算例对不同强度准则的理论计算结果进行了对比，并对各影响因素进行了分析。

1 常用强度准则统一方程

岩土类材料的强度参数可通过黏聚力c和内摩擦角φ来反映。定义压应力为正，拉应力为负，假设主应力次序为σ1=σθ≥σ2=σz≥σ3=σr，其中σθ,σz,σr分别为巷道围岩切向、轴向和径向应力。

在岩土工程中，常采用中主应力系数b来反映3个主应力之间的关系[15]:

(1)

在假定的主应力次序下，0≤b≤1。

1.1 Mohr-Coulomb准则

大量的试验研究及工程实践表明，MC准则能够较好地描述岩土材料的屈服和破坏特性，表达式[1]为

σθ=MMCσr+NMC

(2)

其中，

1.2 Drucker-Prager系列准则

由于MC准则在三维应力空间的屈服面为不规则的六棱锥体表面，为了消除屈服面在锥顶和棱线上的奇异性，Drucker和Prager提出了内切于MC准则六棱锥的光滑圆锥形屈服面。根据DP准则与MC准则在π平面上的相对位置关系，又衍生出了DP系列准则[2,16]，表达式为

(3)

式中，参数αd和kd与黏聚力和内摩擦角有关，根据与MC准则的匹配关系，对应的表达式见表1;I1为应力张量第1不变量，I1=σθ+σz+σr;J2为应力偏张量第2不变量，J2=[(σθ-σz)2+(σz-σr)2+(σr-σθ)2]/6。

表1 DP系列准则计算参数[16]

Table 1 Calculated parameters of different DP yield criteria[16]

将式(1)代入式(3)，整理得到平面应变条件下包含中主应力系数b的DP系列准则表达式

σθ=MDPσr+NDP

(4)

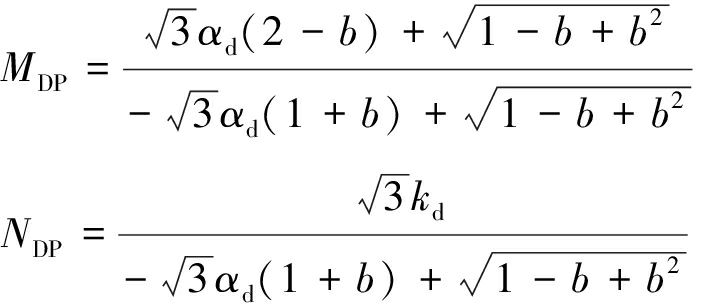
研究表明[17]，DP系列准则的参数αd为具有区间性的，若使中主应力系数b在[0，1]范围内任意取值，则αd需满足αd<0.288;当0.288≤αd<0.577时，只对部分中主应力系数b成立;当αd≥0.577时，DP系列准则不成立。

1.3 统一强度理论

俞茂宏提出的统一强度理论(Unified Strength Theory)不仅具有统一形式的数学表达式，而且可灵活适用于各种材料，表达式[3]为

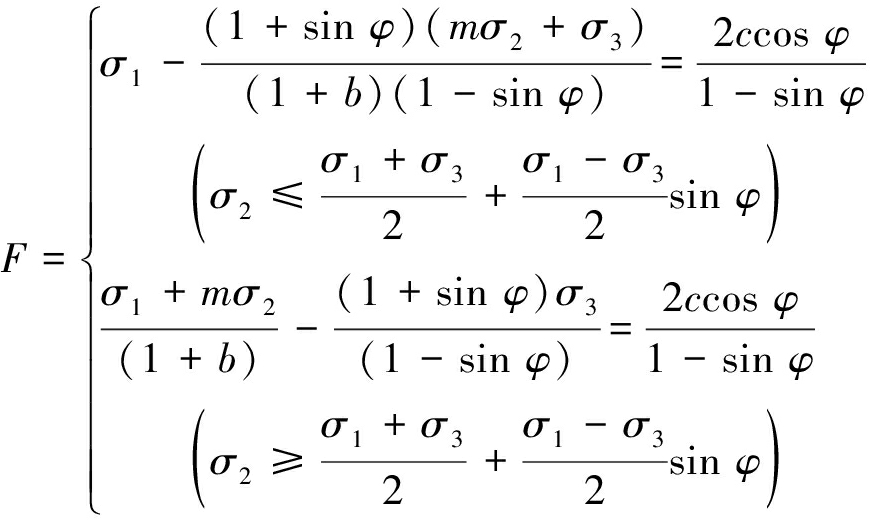
(5)

式中，m为反映中间主应力影响的权系数，0≤m≤1。当m=0时，退化为MC强度准则;m=1时，为双剪强度准则。

将式(1)代入式(5)，求得平面应变状态下含中主应力系数b的统一强度理论表达式

σθ=MUSTσr+NUST

(6)

其中，当b≤(1+sin φ)/2时，有

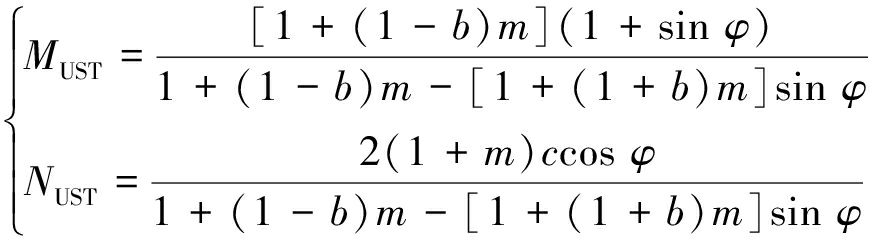
当b≥(1+sin φ)/2时，有

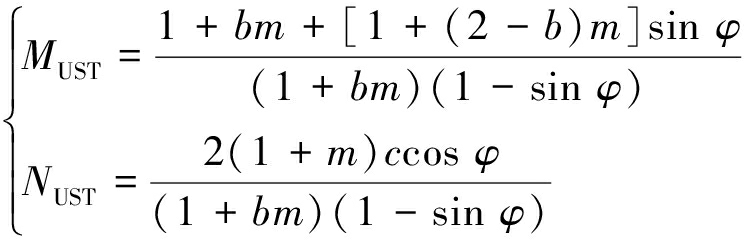
1.4 Mogi-Coulomb准则

Mogi通过大量不同岩性的岩石真三轴试验，以Mises准则为基础，提出了可考虑中间主应力影响的Mogi经验强度准则通式[18]:

τoct=f(σm，2)

(7)

其中，σm,2为最大和最小主应力的平均值，σm,2=(σθ+σr)/2;τoct=[(σθ-σz)2+(σz-σr)2+(σr-σθ)2]1/2/3，为八面体剪应力。

Al-Ajim等[19]将线性Mogi强度准则和Coulomb强度准则相结合，建立了以岩石抗剪强度参数表示的MO破坏准则[4,19]，表达式为

τoct=αmσm,2+km

(8)

式中，

将式(1)代入式(8)，求得平面应变状态下含中主应力系数b的MO准则表达式

σθ=MMOσr+NMO

(9)

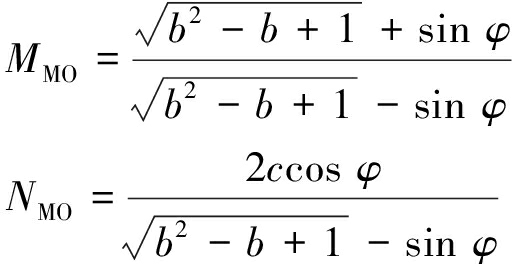
1.5 统一形式屈服方程

综合以上4种常用的岩石强度准则，得到平面应变状态下统一形式的屈服方程

f=σθ-Mσr-N=0

(10)

对于不同的强度准则，取不同参数M，N即可。从是否能够体现中间主应力效应的角度，将强度准则分为2类:一是不能够体现中间主应力效应的MC准则；二是能够体现中间主应力效应的DP系列准则、统一强度理论(UST)和MO准则。

2 渗流场计算

假设巷道无限长，围岩为各向同性的均质岩体，渗流水为单相不可压缩的牛顿液体，岩体内各向渗透系数相同，距离巷道足够远处水头为p0，巷道壁处水头为0，巷道支护力为pi，巷道半径小于内外水头差，流动属层流且符合Darcy定律，渗流方向以径向为主，忽略计算区域内水自重及岩土体自重的影响，将该问题简化为轴对称恒定渗流问题，建立的计算模型如图1所示。

渗流连续微分方程[8]:

(11)

其中，pw(r)为半径r处的孔隙水压力，MPa。若取pw(r)=0，即为不考虑渗流时的工况，属于本文的一个特例。

选取与原始渗流场外水压力p0相同的半径R0处为计算区域，计算区域外保持原始地应力场状态，初始地应力为σ0，巷道内半径为r0，塑性区半径为Rs，确定渗流场内外边界条件:

pw(r)r=r0=0，pw(r)r=R0=p0

(12)

求得孔隙水压力沿巷道径向分布规律为

(13)

令常数s=p0/(ln r0/R0)，式(13)简化为

(14)

3 巷道围岩弹塑性统一解

3.1 基本方程

考虑到岩石与松散体介质具有不同的孔隙特性，引入岩石等效孔隙水压力系数η对太沙基有效应力原理进行修正[20]。渗透水压力为体积力，不考虑渗透体积力中的浮力部分，建立的考虑渗流影响的平衡微分方程为

(15)

几何方程:

(16)

3.2 剪胀特性

研究表明[21]，岩土材料塑性变形不遵守关联流动法则，岩土材料所具有的剪胀特性，使得传统塑性位势理论并不适应岩土材料的变形机制。剪胀系数应该由塑性位势理论和非关联流动法则得到，但遗憾的是，目前多数研究都是直接代入与MC准则形式相同的塑性势函数下的剪胀系数计算公式χ=(1+sin ψ)/(1-sin ψ)，这是不合理的。

李学丰等[22]在连续介质力学理论框架下，把应变分配法则和材料特性联系起来，建立了与岩土材料特性相关的塑性位势理论，表达式为

(17)

式中，为塑性应变增量;dλ为塑性因子增量;g为塑性势函数;σij为应力张量;为组构张量的各向异性部分。

本文假定巷道围岩体各向同性，因此上式可以简化为

(18)

假设塑性势函数与屈服函数具有相同的形式，将屈服函数中的内摩擦角φ替换为剪胀角ψ(小于等于内摩擦角φ)，虽然没有物理意义，但能够反映材料的剪胀特性，定义塑性势函数g为

g=σθ-M*σr-N*

(19)

将式(19)代入式(18)求得塑性应变增量

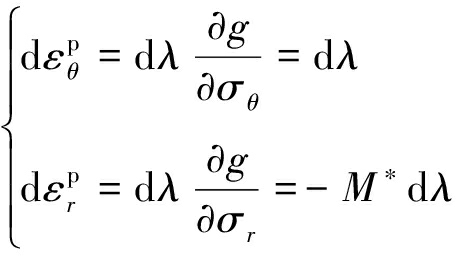
(20)

基于线性非关联流动法则，塑性应变增量满足关系式

(21)

联立式(20)和式(21)求得剪胀系数表达式

(22)

当ψ=φ时，非关联流动法则转变为关联流动法则;当ψ=0°时，材料不发生剪胀。

3.3 弹性区分析

根据广义胡克定律，平面应变问题本构方程为

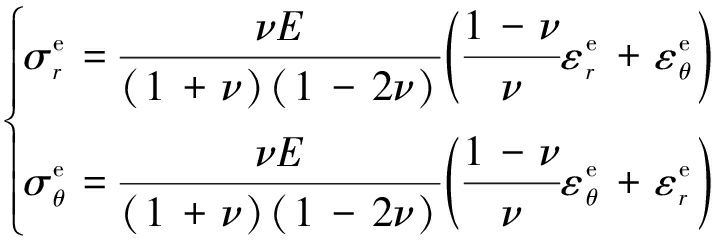
(23)

式中，E为弹性模量;ν为泊松比;分别为弹性区的径向应力与切向应力;分别为弹性区的径向应变与切向应变。

将几何方程(16)和本构方程(23)代入平衡微分方程(15)中，求得

(24)

式中，为一阶Lame常数。

对式(24)的积分进行求解，得到弹性区总位移表达式

(25)

将式(25)代入几何方程(16)，求得弹性区总应变表达式

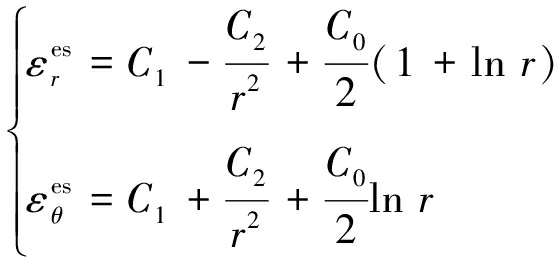
(26)

式中，分别为弹性区的总径向应变与总切向应变。

边界条件:

(27)

式中，σ0为初始地应力;为弹性区与塑性区交界处的径向应力。

由于在弹性区始终满足关系式

(28)

在弹塑性交界面r=Rs处，同时满足屈服方程(10)，联立式(28)求得

(29)

结合边界条件(27)，求得待定常数C1,C2的表达式分别为

(30)

代入本构方程(23)，求得弹性区应力场分布为

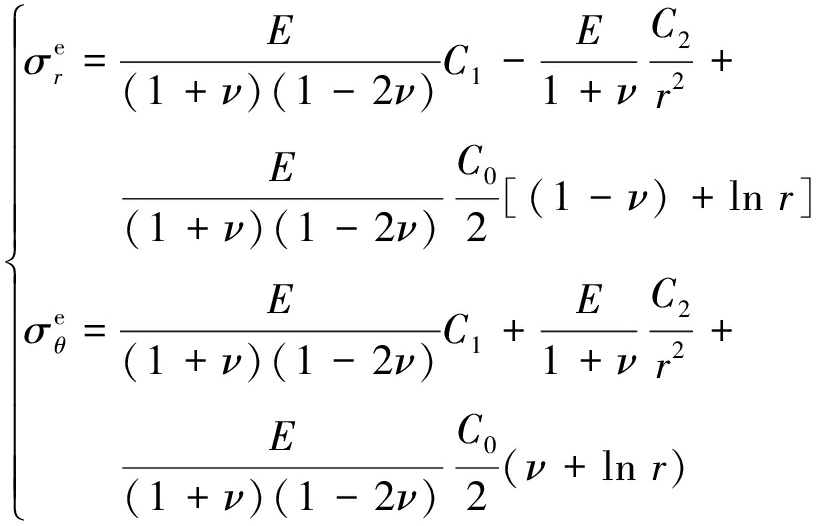
(31)

弹性区的实际位移应忽略巷道开挖前初始地应力引起的变形，因此弹性区的真实应变为

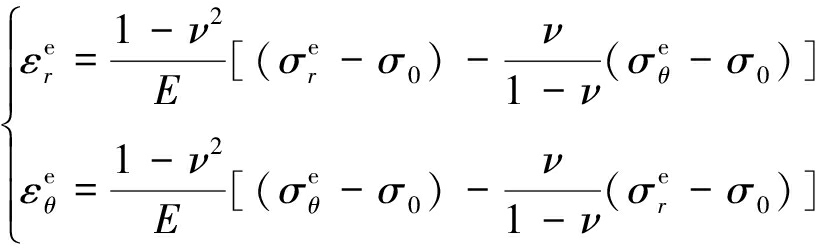
(32)

将式(32)代入几何方程(16)，即可求得弹性区的真实位移ue*。

3.4 塑性区分析

根据弹塑性理论，塑性区应变由弹性应变和塑性应变2部分构成[23]，即

(33)

式中，分别为塑性区的径向应变与切向应变;上标se表示塑性区内的弹性部分；sp表示塑性区内的塑性部分，令

(34)

结合式(21)和式(33)，得

(35)

代入几何方程(16)，有

(36)

结合弹塑性交界面处边界条件:r=Rs时，us=ue-p，积分得塑性区位移表达式

(37)

式中，us为塑性区位移;ue-p为弹塑性交界面处的径向位移;χ为剪胀系数。

对于巷道围岩塑性区中的弹性应变，目前常用的处理方式可分为以下2种:

方法(1):不考虑围岩塑性区内应力重分布的影响，视塑性区弹性应变为常数，其值为弹塑性交界面处弹性区的应变，即

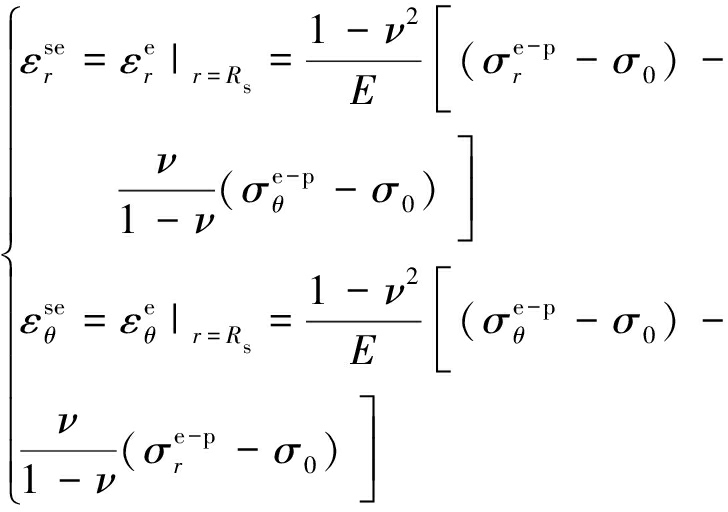
(38)

代入式(35)，求得方法(1)的f(r)表达式

(39)

式中，D1=1-ν-χν，D2=χ-ν-χν，D3=(1-2ν)(1+χ)。

把式(39)代入式(37)，求得方法(1)所得到的塑性区位移表达式

(40)

方法(2):考虑塑性区内应力重分布的影响，利用广义胡克定律计算塑性区内弹性应变，不考虑巷道开挖前地应力作用产生的位移，得到塑性区的弹性应变为

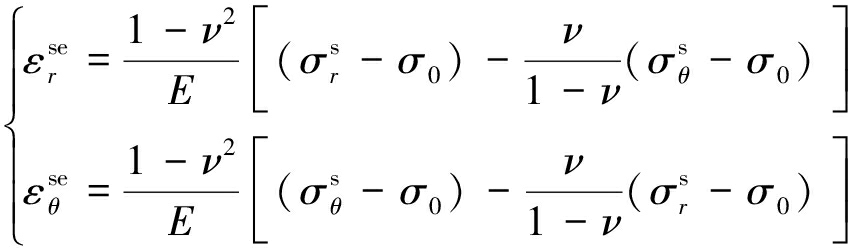
(41)

联立屈服方程(10)和平衡微分方程(15)，结合弹塑性交界面处的边界条件:r=Rs时，求得塑性区重分布应力为

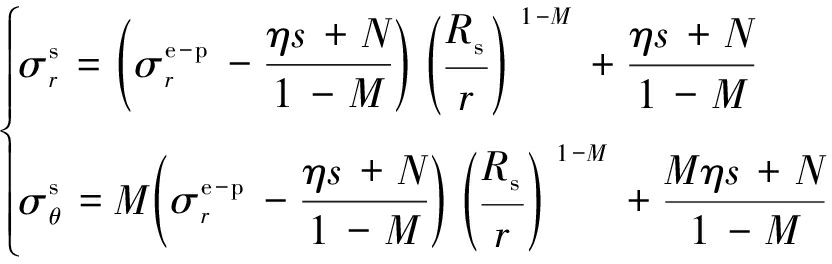
(42)

式中，分别为塑性区的径向应力与切向应力。

将式(42)代入式(41)，联立式(35)求得

(43)

代入式(37)求得方法(2)的塑性区位移表达式

(44)

把r=r0分别代入式(40)和式(44)即可得到2种计算方法所求出的巷道硐壁处位移。

3.5 塑性区半径

结合边界条件:r=r0时，可得

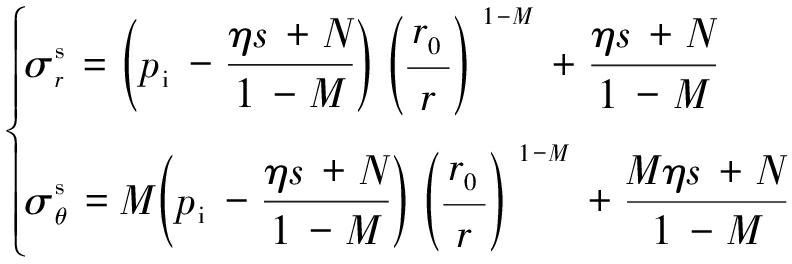
(45)

联立式(42)，求得塑性区半径Rs与巷道半径r0之比表达式为

(46)

4 算例分析

为了进一步探讨强度准则效应、中间主应力效应、围岩剪胀特性以及塑性区弹性应变对渗流巷道围岩的影响，下面选取一个算例进行分析。选取的深埋圆形巷道半径r0=3 m，从工程角度考虑，当应力变化不超过5%时，便可将其视为原岩应力[24]。因此，计算区域半径取R0=30r0=90 m，选取的巷道围岩力学参数见表2。

表2 巷道围岩力学参数

Table 2 Mechanical parameters of surrounding rock

4.1 强度准则效应

当中主应力系数b=0时，统一强度理论和MO准则退化为MC准则，此时只需要讨论MC准则和DP系列准则;当中主应力系数b≠0时，MC准则不再适用，取b=0.5讨论其余3种准则。4种常用岩石强度准则的巷道围岩应力分布规律如图2所示。为了方便讨论，统一强度理论(UST)的权系数m=0.5时记为UST1/2，m=1时记为UST1。

由图2(a)可以看出，在不考虑中间主应力效应的情况下，MC准则以及与MC准则相匹配的DP系列准则都具有明显不同的应力分布规律;不同的强度准则对应不同的塑性区半径，半径越小，峰值应力越大，在巷道硐壁处的切向应力越大;在σθ≥σz=σr条件下，DP1准则与MC准则精准匹配，围岩具有相同的应力分布规律;DP3准则在巷道硐壁处的切向应力最小，所对应的塑性区半径最大，说明DP3准则最容易低估巷道围岩的实际强度，原因在于DP3准则是MC准则的下限;DP2,DP4和DP5准则在巷道硐壁处的切向应力相差不大，DP2,DP5准则应力分布规律最为接近。

由图2(b)可以看出，对于考虑中间主应力效应的强度准则，UST1准则塑性区半径最小，在巷道硐壁处切向应力最大，径向应力与峰值应力也最大，说明UST1准则最容易高估中间主应力效应;MO准则塑性区半径最大，在巷道硐壁处的切向应力最小，径向应力与峰值应力也最小;DP1,UST1/2准则处于中间水平，且两者较为接近。

4.2 中间主应力效应

图3给出了不同强度准则下，不同中间主应力系数b所对应的塑性区位移分布。由图3可以看出，DP3,UST1/2和MO准则均存在明显的中间主应力效应，不同的b将得到不同的塑性区半径和位移;随着b的增大，塑性区半径和巷道硐壁处的位移均表现出先减小、后增大的变化规律，这说明中间主应力存在区间效应，也就是说，中间主应力σ2在从下限σ3逐渐过渡到上限σ1的过程中，围岩强度先是不断增加，达到某一峰值后又逐渐回落，这与目前的真三轴试验结果是一致的;DP3准则对这种区间效应的反映不是很明显，说明DP3准则并不能很好地反映中间主应力效应。

图3还可看出，考虑中间主应力效应(b=0.5)时的巷道硐壁处位移相较于不考虑(b=0)时，UST1/2准则和MO准则所对应的硐壁位移分别降低了63.5%和42.3%，而DP3准则在巷道硐壁处的位移下降幅度高达73.5%，这说明不考虑中间主应力效应的强度准则普遍偏于保守，在计算工程围岩稳定性时，不应忽视中间主应力效应对围岩强度造成的影响。

4.3 剪胀特性

巷道围岩的剪胀特性通过剪胀角ψ来体现，主要讨论相关联流动法则(ψ=φ)，非关联流动法则(ψ≠φ)和不考虑剪胀(ψ=0)3种情况，根据塑性位势理论求出相应的剪胀系数χ的值。在考虑中间主应力时b取0.5，塑性区弹性应变由方法(2)进行计算。

图4给出了不同强度准则下，不同剪胀角所对应的塑性区位移分布。由图4可以看出，剪胀系数不仅与剪胀角有关，还与强度准则有关，这是由于建立的塑性势函数与强度准则形式相同引起的;相同的强度准则下，不同剪胀角对应不同的塑性区位移分布，但塑性区半径保持不变;相关联流动法则过多地考虑了剪胀效应，特别是在巷道硐壁处的位移量，约为非关联流动法则的2.3倍;若不考虑剪胀，则塑性区位移最小，在巷道硐壁处的位移约为非关联流动法则的70%～80%，此时低估了巷道围岩的实际变形，不利于巷道的安全。因此，在实际计算过程中，应选取适合于岩石材料剪胀特性的非关联流动法则，建立塑性势函数，利用塑性位势理论计算其剪胀系数。

4.4 塑性区弹性应变

图5给出了不同强度准则下，采用2种计算方法分别得到的围岩塑性区位移分布。DP1准则、UST1/2准则和MO准则均考虑中间主应力(b取0.5)，剪胀角统一取ψ=10°。由图5可以看出，对于塑性区内的弹性应变，不同的处理方式将得到不同的位移分布，且差别较为明显;方法(1)没有考虑塑性区应力重分布的影响，所得到的位移普遍低于方法(2);方法(2)采用广义胡克定律，考虑了塑性区应力的重分布特征，所得到的塑性区弹性应变也更加符合实际;在巷道硐壁处，方法(2)所得到的位移是方法(1)的1.7～2.0倍，说明不考虑塑性区的应力重分布特征，会在一定程度上低估巷道围岩的真实变形。因此，在实际应用中，应该优先选用方法(2)。

5 结 论

(1)针对受渗流影响的深埋圆形巷道，综合考虑强度准则效应、渗流体积力、中间主应力效应、围岩的剪胀特性以及不同的塑性区弹性应变处理方式，推导了可反映多种常用强度准则的弹塑性统一解析解，新解不仅形式简洁，而且具有可比性和广泛的适用性。

(2)深埋巷道围岩存在明显的强度准则效应，不考虑中间主应力效应的MC准则和与之匹配的DP系列准则计算得到的塑性区范围更大，位移更明显;在考虑中间主应力效应时，MO准则得到的塑性区范围最大，UST1准则得到的塑性区范围最小，DP1准则和UST1/2准则处于中间水平;因此，应根据具体的工程需要选取合适的强度准则。

(3)中间主应力对围岩强度具有区间效应，适当提高中间主应力有利于提高围岩的强度;岩土材料的剪胀特性不仅与剪胀角有关，而且还与塑性势函数有关;采用相关联流动法则会低估围岩的强度，不考虑剪胀则会低估围岩的实际变形;因此，需采用考虑剪胀的非关联流动法则对围岩塑性区应变进行分析。

(4)对于巷道围岩塑性区内的弹性应变，不建议把它视为常数，应当考虑塑性区应力重分布的影响，采用广义胡克定律进行分析;不考虑塑性区应力重分布特征，会在一定程度上低估围岩的真实变形。

参考文献(References):

[1] 邓楚键,郑颖人,朱建凯.平面应变条件下M-C材料屈服时的中主应力公式[J].岩土力学,2008,29(2):310-314.

DENG Chujian,ZHENG Yingren,ZHU Jiankai.Formula of intermediate principal stress at failure for Mohr-Coulomb material in plane strain state[J].Rock and Soil Mechanics,2008,29(2):310-314.

[2] 张信贵,许胜才,严利娥,等.Drucker-Prager准则参数有效性及第二主应力对强度的影响分析[J].应用力学学报,2015,32(5):810-816,898.

ZHANG Xingui,XU Shengcai,YAN Li’e,et al.Validness analysis of parameters in Drucker-Prager criterion and effects of the second principal stress on strength[J].Chinese Journal of Applied Mechanics,2015,32(5):810-816,898.

[3] 俞茂宏.岩土类材料的统一强度理论及其应用[J].岩土工程学报,1994,16(2):1-10.

YU Maohong.Unified strength theory for geomaterials and its applications[J].Chinese Journal of Geotechnical Engineering,1994,16(2):1-10.

[4] 丁立钦,王志乔,吕建国,等.基于围岩本体Mogi-Coulomb强度准则的层理性岩层斜井井壁稳定模型[J].岩石力学与工程学报,2017,36(3):622-632.

DING Liqin,WANG Zhiqiao,LÜ Jianguo,et al.A model for inclined borehole stability in bedding rocks based on Mogi-Coulomb criterion of rock matrix[J].Chinese Journal of Rock Mechanics and Engineering,2017,36(3):622-632.

[5] 赵春风,杨砚宗,张常光,等.考虑中主应力的常用破坏准则适用性研究[J].岩石力学与工程学报,2011,30(2):327-334.

ZHAO Chunfeng,YANG Yanzong,ZHANG Changguang,et al.Investigation on applicability of common failure criteria considering intermediate principal stress[J].Chinese Journal of Rock Mechanics and Engineering,2011,30(2):327-334.

[6] 张常光,张成林,周菲,等.圆形隧道弹塑性分析的强度理论效应研究[J].岩土工程学报,2018,40(8):1449-1456.

ZHANG Changguang,ZHANG Chenglin,ZHOU Fei,et al.Effect of strength theory in elastic-plastic analysis of a circular tunnel[J].Chinese Journal of Geotechnical Engineering,2018,40(8):1449-1456.

[7] 潘继良,高召宁,任奋华.考虑应变软化和扩容的圆形巷道围岩强度准则效应[J].煤炭学报,2018,43(12):3293-3301.

PAN Jiliang,GAO Zhaoning,REN Fenhua.Effect of strength criteria on surrounding rock of circular roadway considering strain softening and dilatancy[J].Journal of China Coal Society,2018,43(12):3293-3301.

[8] 高召宁,孟祥瑞,付志亮.考虑渗流、应变软化和扩容的巷道围岩弹塑性分析[J].重庆大学学报,2014,37(1):96-101.

GAO Zhaoning,MENG Xiangrui,FU Zhiliang.Elasto-plastic analysis on surrounding rock of roadways based on seepage,strain softening and dilatancy[J].Journal of Chongqing University,2014,37(1):96-101.

[9] 范浩,刘万荣,付腾飞,等.考虑渗流剪胀和中间主应力的隧洞围岩稳定性分析[J].中国安全科学学报,2016,26(2):139-145.

FAN Hao,LIU Wanrong,FU Tengfei,et al.Stability analysis of surrounding rock of tunnel considering seepage,shear dilation and intermediate principal stress[J].China Safety Science Journal,2016,26(2):139-145.

[10] 曾开华,鞠海燕,盛国君,等.巷道围岩弹塑性解析解及工程应用[J].煤炭学报,2011,36(5):752-755.

ZENG Kaihua,JU Haiyan,SHENG Guojun,et al.Elastic-plastic analytical solutions for surrounding rocks of tunnels and its engineering applications[J].Journal of China Coal Society,2011,36(5):752-755.

[11] 邓楚键,郑颖人,王凯,等.有关岩土材料剪胀的讨论[J].岩土工程学报,2009,31(7):1110-1114.

DENG Chujian,ZHENG Yingren,WANG Kai,et al.Some discussion on the dilatancy of geotechnical materials[J].Chinese Journal of Geotechnical Engineering,2009,31(7):1110-1114.

[12] 杨强,冷旷代,张小寒,等.Drucker-Prager弹塑性本构关系积分:考虑非关联流动与各向同性硬化[J].工程力学,2012,29(8):165-171.

YANG Qiang,LENG Kuangdai,ZHANG Xiaohan,et al.An integration algorithm for Drucker-Prager elastic-plastic model with non-associated flow rule and isotropic hardening[J].Engineering Mechanics,2012,29(8):165-171.

[13] 孔位学,芮勇勤,董宝弟.岩土材料在非关联流动法则下剪胀角选取探讨[J].岩土力学,2009,30(11):3278-3282.

KONG Weixue,RUI Yongqin,DONG Baodi.Determination of dilatancy angle for geomaterials under non-associated flow rule[J].Rock and Soil Mechanics,2009,30(11):3278-3282.

[14] 陈梁,茅献彪,李明,等.基于Drucker-Prager准则的深部巷道破裂围岩弹塑性分析[J].煤炭学报,2017,42(2):484-491.

CHEN Liang,MAO Xianbiao,LI Ming,et al.Elastoplastic analysis of cracked surrounding rock in deep roadway based on Drucker-Prager criterion[J].Journal of China Coal Society,2017,42(2):484-491.

[15] 张小波,赵光明,孟祥瑞.基于Drucker-Prager屈服准则的圆形巷道围岩弹塑性分析[J].煤炭学报,2013,38(S1):30-37.

ZHANG Xiaobo,ZHAO Guangming,MENG Xiangrui.Elastoplastic analysis of surrounding rock on circular roadway based on Drucker-Prager yield criterion[J].Journal of China Coal Society,2013,38(S1):30-37.

[16] 邓楚键,何国杰,郑颖人.基于M-C准则的D-P系列准则在岩土工程中的应用研究[J].岩土工程学报,2006,28(6):735-739.

DENG Chujian,HE Guojie,ZHENG Yingren.Studies on Drucker-Prager yield criterions based on M-C yield criterion and application in geotechnical engineering[J].Chinese Journal of Geotechnical Engineering,2006,28(6):735-739.

[17] 刘金龙,栾茂田,许成顺,等.Drucker-Prager准则参数特性分析[J].岩石力学与工程学报,2006,25(S2):4009-4015.

LIU Jinlong,LUAN Maotian,XU Chengshun,et al.Study on parametric characters of Drucker-Prager Criterion[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(S2):4009-4015.

[18] MOGI K.Experimental rock mechanics[M].London:CRC Press,2007.

[19] AL-AJMI A M,ZIMMERMAN R W.Stability analysis of vertical boreholes using the Mogi-Coulomb failure criterion[J].International Journal of Rock Mechanics and Mining Sciences,2006,43(8):1200-1211.

[20] 李宗利,任青文,王亚红.考虑渗流场影响深埋圆形隧洞的弹塑性解[J].岩石力学与工程学报,2004,23(8):1291-1295.

LI Zongli,REN Qingwen,WANG Yahong.Elasto-plastic analytical solution of deep-buried circle tunnel considering fluid flow field[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(8):1291-1295.

[21] 刘志钦,余东明.考虑中间主应力和剪胀特性的深埋圆巷弹塑性应力位移解[J].工程力学,2012,29(8):289-296.

LIU Zhiqin,YU Dongming.Elastoplastic stress and displacement analytical solutions to deep-buried circular tunnels considering intermediate principal stress and dilatancy[J].Engineering Mechanics,2012,29(8):289-296.

[22] 李学丰,孔亮,黄茂松.岩土材料特性相关塑性位势理论[J].岩土工程学报,2013,35(9):1722-1729.

LI Xuefeng,KONG Liang,HUANG Maosong.Property-dependent plastic potential theory for geomaterials[J].Chinese Journal of Geotechnical Engineering,2013,35(9):1722-1729.

[23] 张常光,范文,赵均海.深埋圆形巷道围岩塑性区位移及特征曲线新解和参数分析[J].岩土力学,2016,37(1):12-24,32.

ZHANG Changguang,FAN Wen,ZHAO Junhai.New solutions of rock plastic displacement and ground response curve for a deep circular tunnel and parametric analysis[J].Rock and Soil Mechanics,2016,37(1):12-24,32.

[24] 谭学术,鲜学福.复合岩体力学理论及其应用[M].北京:煤炭工业出版社,1994.

Comparative analysis of different strength criteria for deep-buried rock roadway under seepage

PAN Jiliang1,2,3,GUO Qifeng1,2,3,REN Fenhua1,2,3,CAI Meifeng1,2,3

(1.School of Civil and Resource Engineering,University of Science and Technology Beijing,Beijing 100083,China; 2.Beijing Key Laboratory of Urban Underground Space Engineering,University of Science and Technology Beijing,Beijing 100083,China; 3.Key Laboratory of Ministry of Education for Efficient Mining and Safety of Metal Mines,University of Science and Technology Beijing,Beijing 100083,China)

Abstract:The selection of strength criterion will directly affect the stability evaluation and control of surrounding rock.In order to study the effect of strength criterion on the surrounding rock stability of deep-buried circular roadway considering seepage,under the plane strain condition,a unified yield equation was firstly summarized for four commonly used strength criteria of rock materials,such as Mohr-Coulomb (MC)criterion,Drucker-Prager (DP)criterion,Uniform strength Theory and Mogi-Coulomb (MO)criterion.Then,an ideal elastic-plastic model was established for the deep-buried circular roadway under the action of pore water pressure.With the considerations of seepage body force,intermediate principal stress effect,dilatancy and different elastic strains in the plastic zone,the unified analytical solutions of stress field,displacement field and radius of plastic zone of surrounding rock under seepage were deduced based on the elastic-plastic theory.Finally,some comparative analyses were conducted on the various influence factors of the new solutions by a specific example.It was found that the new solutions proposed not only have the form of conciseness,but also can flexibly match various commonly used rock strength criteria.The results of MC criterion and DP criteria without considering the effect of intermediate principal stress are relatively conservative.When considering the effect of intermediate principal stress,the circumcircle DP criterion and the uniform strength theory with a weight coefficient of 0.5 can be prioritized,and the unified strength theory with a weight coefficient of 1 should be chosen carefully.Intermediate principal stress has interval effect on surrounding rock strength.The strength criteria without considering the effect of intermediate principal stress are generally conservative.The dilatancy of geomaterial is not only related to the dilatancy angle of surrounding rock,but also related to the plastic potential function.The dilatancy does not change the radius of plastic zone,but it will affect the displacement distribution of plastic zone.The actual deformation of surrounding rock will be underestimated without the consideration of dilatancy.The effect of the stress redistribution in the plastic zone should be considered,and the generalized Hook’s law should be used for the analysis,instead of regarding the elastic strain in the plastic zone as a constant.

Key words:circular roadway;effect of strength criterion;intermediate principal stress;dilatancy;elastic strain in the plastic zone

中图分类号:TD322

文献标志码:A

文章编号:0253-9993(2019)11-3369-10

收稿日期:2018-11-18

修回日期:2019-02-22 责任编辑:常 琛

基金项目:国家自然科学基金资助项目(51774022);国家重点研发计划资助项目(2016YFC0600703，2018YFC0808403)

作者简介:潘继良(1994—)，男，安徽寿县人，博士研究生。E-mail:panjiliang2015@163.com

通讯作者:郭奇峰(1985—)，男，河南焦作人，讲师。E-mail:guoqifeng@ustb.edu.cn

潘继良，郭奇峰，任奋华,等.渗流作用下深埋岩石巷道不同强度准则对比分析[J].煤炭学报,2019,44(11):3369-3378.doi:10.13225/j.cnki.jccs.2018.1534

PAN Jiliang,GUO Qifeng,REN Fenhua,et al.Comparative analysis of different strength criteria for deep-buried rock roadway under seepage[J].Journal of China Coal Society,2019,44(11):3369-3378.doi:10.13225/j.cnki.jccs.2018.1534