在深部岩体工程中，如富水地层煤矿开采、核废料深层地质掩埋、天然气和石油开采等过程，裂隙岩石的渗流特性随应力状态的演变是影响工程安全的关键因素[1-2]。一方面，随着地下工程深度的不断增加，在高地应力与高渗水压力的共同作用下，裂隙岩石中的渗流不再是简单的线性Darcy流，而表现为非线性渗流。另一方面，裂隙岩石在天然地质状态或工程扰动下往往会经历复杂的应力历史，例如，不断变化的地应力状态和水压致裂等特殊施工工艺作用下导致岩体经历复杂的加、卸载过程。因此，考虑高地应力与高渗水压力下的非线性渗流以及应力过程和应力历史对裂隙岩石渗流特性的影响具有现实意义。
WITHERSPOON等[3]忽略裂隙中流体流动的惯性项，通过对Navier-Stokes方程进行简化提出了立方定律。然而，立方定律的适用条件过于严苛，也无法精确描述裂隙岩石非线性渗流特性。因此，国内外许多学者对裂隙岩石非线性渗流特性做出了研究。胡少华等[4]通过研究不同JRC(粗糙度系数)的单裂隙岩石的非线性渗流，提出了定量表征裂隙岩石非线性渗流发生条件的临界雷诺数Rec模型。尹乾等[5]基于人工裂隙网络，研究了不同侧压力系数下岩体裂隙网络的非线性渗流。刘日成等[6]通过制作裂隙网络试验模型，模拟流体在裂隙网络内的流动状态，研究了等效水力隙宽和水力梯度对岩体裂隙网络非线性渗流特性的影响。
深部岩体在高地应力和工程扰动的共同作用下往往处于峰后状态，针对峰后岩石的渗流特征，缪协兴等[7]研究峰后岩石非Darcy渗流系统的失稳和分岔，得出非Darcy流因子β<0是导致岩石产生渗流失稳的原因之一。程宜康等[8]通过开展峰后破碎砂岩非达西渗流试验，给出了砂岩渗透率随轴向应变的关系。张春会等[9]通过开展三轴压缩与渗流试验，获得不同围压下砂岩全过程应力-应变曲线、体积应变与渗透率关系曲线，并在FLAC下模拟了砂岩在不同围压下的应变软化行为和渗透率演化过程。孙明贵等[10]在石灰岩的应力-应变全过程中采用瞬态渗透法测定了试样非Darcy流渗流特性，研究得出试样无论在峰前还是峰后，渗流都不服从Darcy定律，并改进了非Darcy流渗透特性的测定方法。
许多学者考虑不同应力、渗透压力以及不同粗糙度等因素对岩石裂隙非线性渗流特性的影响，但其中多数研究是基于单调加载力学条件进行的。近年来，有一些学者开始考虑应力历史与裂隙渗流之间的关系。江宗斌等[11]通过开展加、卸载条件下岩石蠕变-渗流耦合试验，给出了渗透率与体积应变之间的关系。WANG等[12]分析沉积岩三轴压缩试验全应力-应变过程中的渗透性，得出渗透率在峰值强度之前随着荷载的增加而增加，在应变软化阶段中渗透率显著降低。胡大伟等[13]从平均应力和循环加卸载两方面对多孔红砂岩三轴试验下的渗透率进行了全过程分析。孙可明等[14]开展了加、卸载作用下不同粗糙度裂隙岩石的渗流试验，并将裂隙面扫描之后的三维形貌信息导入到ABAQUS软件，模拟不同荷载作用下的粗糙裂隙渗流。
综上所述，尽管许多学者关注了不同因素对裂隙岩石非线性渗流特性的影响，但是对峰后岩石的渗流特性研究较少，并且往往只考虑单轴加载的力学条件下的渗流特性。因此，考虑应力过程和应力历史对裂隙岩石渗流特性的影响具有现实意义。笔者开展峰后破裂砂岩和花岗岩加、卸载围压过程的渗流特性试验，研究水力梯度与渗流流量之间的非线性关系，同时对比围压加、卸载前后的裂隙渗流流量与裂隙渗透系数，分析围压加、卸载前后产生明显差异性的发生机制。试验成果可以为高地应力与高渗水压力下的应力过程和应力历史对岩石裂隙渗流特性的影响提供理论依据。
1 加卸载-渗流试验
1.1 试样制备
为研究不同岩性岩石加、卸载围压过程对峰后破裂岩石渗流特性的影响，本文选用花岗岩和砂岩作为试样，依照《工程岩体试验方法标准》和《水利水电工程岩石试验规程》所建议的方法，取芯加工成尺寸为φ50 mm×100 mm的标准岩石试样，如图1所示。
图1 砂岩和花岗岩试样
Fig.1 Sandstone and granite samples
1.2 试验系统
本文试验均在由中国科学院武汉岩土力学研究所与南昌大学合作研制的温度-应力-渗流多场耦合岩石三轴试验系统上进行，该系统主要由围压、轴压、孔隙压力自动伺服装置组成(图2)。该装置的围压最大可达100 MPa，轴向偏压最大可达500 MPa。系统采用高精密轴向LVDT、压力数据传感器、特制环向应变传感器、高性能数据集控装置等进行全自动数据采集，可以实时记录试验过程中轴向应力、侧向应力、位移、应变和孔隙压力值等数据，系统采用特制的水压加压装置，流量泵可以输出高达100 MPa的水压，可以满足开展渗流特性试验的各项要求。
1.3 试验步骤
根据相关试验标准和本文试验思路，设计花岗岩的渗流试验步骤如下:
(1)将标准试样与氟化橡胶套经热风机处理并且保证紧密贴合后放于多场耦合岩石三轴围压缸内(图3)。
(2)试样安装完毕后，首先采用应力控制方式并以0.05 MPa/s的速率施加围压至10 MPa后，然后再采用应力控制方式并以0.1 kN/s的速率施加轴压直至试样破坏，破坏后的试样如图4所示。由图4可知，花岗岩试样破裂后，产生了一条贯穿的粗糙剪切裂隙面，砂岩试样破裂后，形成了一条以贯穿剪切裂隙为主，并伴随有少量张拉裂隙的破裂形态。
(3)试样破坏后，采用应力控制方式并以0.05 MPa/s的速率施加第一级围压至5 MPa，待围压稳定后，根据围压大小选择施加第一级渗透压力，围压为5，10，15，20，25 MPa对应的第一级渗透压力分别为0.5，1，1，1，1 MPa。待渗流稳定后，测量该级渗透水力梯度下的渗流流量，然后根据试验过程中的实际情况施加下一级渗透压。
(4)完成5 MPa围压后，依次增加围压至10，15，20，25 MPa，并在每一级围压水平下测量各级渗透水力梯度下的渗流流量。
(5)完成25 MPa围压下的渗流试验后，依次逐级卸载围压至20，15，10，5 MPa，并在每一级围压水平下测量各级渗透水力梯度下的渗流流量。
完成以上步骤后，可以得到加、卸载围压情况下，渗流流量随着水力梯度变化的关系曲线。加、卸载围压过程对峰后破裂砂岩渗流特性试验与花岗岩试验的步骤一致，只是加、卸载过程中的各级围压水平不一样，砂岩按照1，3，5，7，9 MPa逐级增加围压，然后再按9，7，5，3，1 MPa逐级降低围压，各围压对应的第一级渗透压力分别为0.05，0.05，0.1，0.1，0.5 MPa。试验过程中的水温测得为25 ℃，此温度下水的密度与运动黏滞系数分别为ρ=0.997×103 kg/m3，υ=8.936 8×10-7 m2/s。
根据试验中记录的试样两端渗透压力差与过流流量测量试样渗透系数，试样渗透系数可由如下公式进行计算[15]:
(1)
式中，k为试样的渗透系数;Q为通过裂隙的渗流流量;L为试样长度;γw为流体的容重;A为试样的过流面积;
P为试样两端的渗透压力。由于式(1)中试样长度、流体的容重、试样的过流面积都是常量，因此过流流量与渗透压力的比值直接反映了裂隙渗透系数的变化。相对应的，该比值也与gradP-Q曲线斜率的倒数有着正相关关系。
图2 温度-应力-渗流多场耦合岩石三轴试验系统
Fig.2 Multi-field coupled rock triaxial test system of temperature-stress-seepage
图3 试样安装示意
Fig.3 Schematic diagram of sample installation
图4 试样三轴压缩破坏后
Fig.4 Sample after triaxial compression failure
2 gradP-Q关系曲线试验结果
图5和6分别给出了由试验得到的砂岩和花岗岩加、卸载围压过程中gradP-Q关系曲线,其中,gradP为水力梯度；Pc为围压。通过对图5和图6的gradP-Q曲线进行分析，可以将渗流流量随水力梯度的演化过程大致分为2个阶段，即:① 线性阶段，试验初期岩样的孔隙压力较小，岩样变形也较小，水流在裂隙中的渗流速率也较小，渗流近似为Darcy流;② 非线性阶段，随着水力梯度的不断增大，孔隙压力与静水压力越来越接近，试样变形慢慢增大，水流在裂隙中的渗流速率也随之增大，渗流逐渐转变为非Darcy流。
通过对峰后破裂砂岩和花岗岩水力梯度与渗流流量数据进行分析，发现水力梯度与渗流流量之间主体呈现出非线性关系，即在gradP-Q关系曲线中直观的表现为曲线凸向gradP轴(凹向Q轴)以及凸向Q轴(凹向gradP轴)的两种情形。对于第一种情况，随着水力梯度的不断增加，渗流流量的增长率不断降低，这是由惯性效应引起的附加压力耗损所致。对于第2种情况，随着水力梯度的不断增加，渗流流量的增长率不断升高，该现象可能由渗透失稳所致。
通过分析以上结果，本文确定采用二次函数Forchheimer公式来拟合水力梯度与渗流流量之间的关系。从图5和图6曲线中可以看出，砂岩围压加载过程中的gradP-Q关系曲线属于第1种非线性渗流情况，花岗岩围压加载过程中的gradP-Q关系曲线属于第2种非线性渗流情况，而砂岩与花岗岩围压卸载过程中的gradP-Q之间的关系变得复杂，可能是线性的，也可能是凸向gradP轴或凸向Q轴。但无论是哪种gradP-Q关系曲线，随着围压的增大，同一水力梯度水平下的渗流流量都在不断减小。由此可以印证，随着岩体赋存深度的不断增大，地应力的增大导致岩石裂隙网络更加的致密，从而降低了岩石裂隙面的渗流流量。
图5 砂岩加、卸载过程不同围压下水力梯度与渗流流量曲线
Fig.5 Curves of seepage flow and pressure gradient under different confining pressures during loading and unloading process of sandstone
图6 花岗岩加、卸载过程不同围压下水力梯度与渗流流量曲线
Fig.6 Curves of seepage flow and pressure gradient under different confining pressures during loading and unloading process of granite
3 非线性渗流理论分析
3.1 基于Forchheimer公式的非线性渗流分析
法国学者Forchheimer通过对试验数据进行统计学分析，提出了Forchheimer公式，该公式广泛的应用于裂隙介质中因水流惯性效应引起的非线性渗流特性[16-20]，其具体表达式为
grad P=aQ+bQ2
(2)
式中，a，b分别为线性项系数与非线性项系数，可通过试验数据拟合得到。
对图5和6中峰后破裂砂岩和花岗岩加、卸载围压过程的渗流试验数据进行Forchheimer公式拟合，将拟合所得参数值列于表1。
由表1可知，Forchheimer方程很好的拟合了渗流流量与水力梯度之间的关系，其拟合的相关系数很高。表中拟合所得的线性项系数a均为正值，而非线性项系数b有正值也有负值，结合图5，6分析可知，当gradP-Q关系曲线表现为曲线凸向gradP轴(凹向Q轴)时，即由惯性效应引起非线性渗流特性时，b值为正值。当gradP-Q关系曲线表现为曲线凸向Q轴(凹向gradP轴)时，即因渗透失稳引起非线性渗流时，b值为负值。
表1 破裂砂岩与花岗岩加、卸载围压过程中非线性渗流系数拟合值
Table 1 Fitting results of nonlinear seepage coefficients during the process of loading and unloading confining pressure of fractured sandstone and granite
岩性荷载方式Pc/MPaForchheimer公式a/1016b/1024R2破裂砂岩围压加载围压卸载10.05220.05100.9913830.30460.00230.9970250.48990.28080.9822970.85530.44680.9910890.90202.65320.9959471.6303-1.18870.9809350.94351.41990.9851830.8009-0.47590.9721610.24710.00330.98987花岗岩围压加载围压卸载51.9700-2.00690.97984102.6712-1.77630.98741153.8819-2.39520.99618204.7934-2.29770.99058255.6028-2.438040.99198206.4887-3.87190.98552157.6163-10.33800.99594105.3353-6.72320.9659453.1402-5.13880.93965
3.2 非线性影响因子
第2节已经提及，随着水力梯度的不断增大，水流在岩样裂隙中的渗流速率也逐渐增大，流体速度损失不再是由黏滞力决定，而是由惯性力起主导作用。此时，水力梯度和渗流流量之间的关系不再单纯的服从达西定律，而是呈现出非线性渗流关系。为了进一步量化裂隙岩石渗流的非线性程度，本文采用ZENG等[21]根据Forchheimer公式定义的非线性影响因子E，其表达式为
(3)
式中，bQ2为非线性压降;aQ2+bQ2为总压降。当非线性影响因子E大于某一个值时，非线性项造成的压降不可忽略。ZENG等[21]认为当E<0.1时，可以只考虑线性Darcy流的影响，但当E>0.1时，非线性项在渗流过程中的影响将不可忽略。
根据E=0.1这一划分线性流与非线性流的临界值，图7给出了破裂砂岩加载过程中非线性影响因子E随着渗透压力的变化关系。由图7可知，破裂砂岩的非线性影响因子E随着渗透压力的增大而逐渐增大，并且当试样处于较高的围压水平下，随着渗透压力的增大，非线性影响因子E渐渐趋于一个稳定值。这表明在比较高的水力梯度下，非线性项造成的压降不可以被忽略，即不能再简单的使用线性达西流来进行裂隙渗流分析。
图7 破裂砂岩加载围压过程中非线性影响因子E与渗透压力的关系
Fig.7 Relationships between nonlinear influence factor E and osmotic pressure during the process of loading confining pressure of fractured sandstone
4 加、卸载围压过程中的非线性渗流特性
由式(1)可知，渗流流量与渗透压力的比值Q/P可以反映裂隙渗透系数的变化情况，因此为了进一步分析破裂花岗岩和砂岩的非线性渗流特性，图8，9分别给出了峰后破裂花岗岩和砂岩加、卸载围压过程中Q/P随渗透压力的变化曲线。对比图8和图9可以看出在围压加载过程中，当处于同一级渗透压力水平下，随着围压的增加，裂隙面渗透性逐渐减小，且减小的速率是变化的。但当砂岩处于较高围压、较低渗透压力状态时，随着围压的增加，裂隙面的渗透性演化规律可能受到张拉裂隙的影响。例如，当砂岩渗透压力为0.5 MPa，围压从7 MPa加载到9 MPa时，裂隙面渗透性略微增大，结合砂岩破坏型式可知，在高围压加载过程中，砂岩剪切裂隙逐渐压缩闭合，而存在的少量张拉裂隙可能会逐渐扩展和连通，从而导致试样内部裂隙面渗透性的增大。而随着渗透压力的不断增大，试样内部剪切裂隙面重新张开，大大增加了裂隙面的过水能力，使得存在的少量张拉裂隙对试样渗透性的影响减弱，试样裂隙面渗透性的演化规律恢复正常。而在同一级围压水平下，随着渗透压力的增大，破裂花岗岩和砂岩的裂隙渗透性总体上呈现上升趋势。并且随着试样所受围压的逐步增加，花岗岩的裂隙渗透性随着渗透压力的增大而减缓了上升趋势，最终趋于水平，这说明了围压的增大可以有效减弱岩石非线性渗流的发展。在卸载过程中，由于试样裂隙面发生了不可逆的塑性变形，试样每级围压下裂隙面渗透性与渗透压力之间的关系变得更加复杂和无序，裂隙面渗透性的增大与减小不再单纯只由裂隙面所处的围压、渗透压力的大小而决定。
图8 破裂花岗岩加、卸载围压过程Q/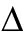
P与渗透压力的关系
Fig.8 Relationships between Q/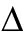P and osmotic pressure during the process of loading and unloading confining pressure of fractured granite
图9 破裂砂岩加、卸载围压过程Q/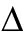P与渗透压力的关系
Fig.9 Relationships between Q/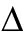P and osmotic pressure during the process of loading and unloading confining pressure of fractured sandstone
5 加、卸载围压过程试验结果对比分析
对比加、卸载围压过程中峰后破裂岩石裂隙渗流特性可知，不论是砂岩还是花岗岩，两种岩样在加载和卸载围压过程中的渗流特性都产生了较大的差异性。
图10 破裂砂岩加、卸载围压过程渗流流量对比
Fig.10 Comparison of seepage flow during the process of loading and unloading confining pressure of fractured sandstone
图11 破裂花岗岩加、卸载围压过程渗流流量对比
Fig.11 Comparison of seepage flow during the process of loading and unloading confining pressure of fractured granite
图10和图11给出了砂岩与花岗岩在不同围压水平下加载与卸载过程中同一渗透压力下的渗流流量。由图10，11可知，当围压卸载到与加载过程同一水平时，各级渗透压力下的渗流流量均大幅下降。例如，当砂岩围压卸载至1 MPa后，同一级渗透压力下的流量降幅达到47.6%～72.6%，而当花岗岩卸载至5 MPa后，同一级渗透压力下的流量降幅达到25%～50%。对比图8和9也可以看出卸载后的裂隙渗透系数都大大低于加载时的裂隙渗透系数。
在图5(b)中将围压从9 MPa卸荷至7 MPa，以及在图6(b)中将围压从25 MPa卸荷至20 MPa还可以看出，当试样从较高围压水平卸荷后，试验所测得的渗流流量在同等渗透压力的情况下不但没有增加反而降低了。结果都表明，即使卸荷后围压降低了，其结果只是使得岩样内部裂隙受到的法向应力减小了，此时，裂隙面受到的有效应力依然足够大，而相对于裂隙平面的法向变形或裂隙开度的减小却没有停止。另外，也可能由于在较高围压作用下裂隙面的局部应力足够大，从而导致裂隙面产生局部破坏，产生的碎屑物质堵塞了裂隙通道，进而使得裂隙的渗流开度进一步的减小。
在卸载围压过程中，当围压保持不变，水力梯度与渗流流量之间的关系变得非常复杂，gradP-Q曲线可能是线性的，也有可能是凸向Q轴或凸向gradP轴。究其原因，一方面是由于在初次加载过程中，岩石裂隙产生了不可逆的塑性变形，即使卸载了围压，裂隙面也存在较大的有效应力，使得裂隙开度较小。另一方面，随着逐渐增大的渗透压力，水压可以冲刷掉积聚的碎屑物质，使得裂隙面重新张开，进而大大的增加了岩样裂隙的流体过流能力。从而导致卸载过程的渗流特性相比于初次加荷的加载过程显得更加的复杂与无规律。
6 结 论
(1)在高水力梯度与高围压作用下，裂隙岩石渗流特性由线性Darcy流转变成非线性渗流，采用Forchheimer公式能够很好的对非线性渗流过程进行拟合分析，非线性影响因子E=0.1可以作为区分线性流与非线性流的临界点。
(2)在围压加载过程中，随着围压的增加，裂隙面的渗透性会逐渐减小。但在高围压作用下，虽然会一定程度的压缩闭合，但存在的少量张拉裂隙会逐渐扩展和连通，可能会引起峰后破裂岩石的渗透性发生改变。
(3)当峰后破裂岩石从较高围压水平卸荷后，且裂隙面渗透压力处于较低状态下时，其裂隙渗透性没有增加反而减小，表明裂隙面仍然存在较高的有效应力，法向变形的存在使得裂隙面的开度进一步减小。
(4)当围压卸载到与加载过程同一水平时，各级渗透压力下的渗流流量均大幅下降，表明裂隙面渗流能力的恢复存在明显的滞后效应。
[1] 杨天鸿，师文豪，李顺才，等.破碎岩体非线性渗流突水机理研究现状及发展趋势[J].煤炭学报，2016,41(7):1598-1609.
YANG Tianhong,SHI Wenhao,LI Shuncai,et al.State of the art and trends of water-inrush mechanism of nonlinear flow in fractured rock mass[J].Journal of China Coal Society,2016,41(7):1598-1609.
[2] ZHENG Jiangtao,JU Yang,ZHAO Xi.Influence of pore structures on the mechanical behavior of low-permeability sandstones:Numerical reconstruction and analysis[J].International Journal of Coal Science & Technology,2014,1(3):329-337.
[3] WITHERSPOON P A,WANG J S Y,IWAI K,et al.Validity of cubic law for fluid flow in a deformable rock fracture[J].Water Resources Research,1980,16(6):1016-1024.
[4] 胡少华,周佳庆,陈益峰,等.岩石粗糙裂隙非线性渗流特性试验研究[J].地下空间与工程学报,2017,13(1):48-56.
HU Shaohua，ZHOU Jiaqing，CHEN Yifeng,et al.Laboratory Researchon nonlinear flow behavior of rough fractures[J].Chinese Journal of underground Space and Engineering,2017,13(1):48-56.
[5] 尹乾,靖洪文,刘日成,等.不同侧压力系数下裂隙网络岩体非线性渗流特性[J].岩土力学,2019,40(2):1-9.
YIN Qian,JING Hongwen,LIU Richeng,et al.Nonlinear fluid flow behaviors in fracture networks subjected to various lateral pressure ratios[J].Rock and Soil Mechanics,2019,40(2):1-9.
[6] 刘日成,李博,蒋宇静,等.效水力隙宽和水力梯度对岩体裂隙网络非线性渗流特性的影响[J].岩土力学,2016,37(11):3165-3174.
LIU Richeng,LI Bo,JIANG Yujing,et al.Effects of equivalent hydraulic aperture and hydraulic gradient on nonlinear seepage properties of rock mass fracture networks[J].Rock and Soil Mechanics,2016,37(11):3165-3174.
[7] 缪协兴,陈占清,茅献彪,等.峰后岩石非Darcy渗流的分岔行为研究[J].力学学报,2003,35(6):22-29.
MIAO Xiexing,CHEN Zhangqing,MAO Xianbiao,et al.the bifurcation of non-darcy flow in post-failure rock[J].Theoretical and Applied Mechanics,2003,35(6):22-29.
[8] 程宜康,陈占清,缪协兴,等.峰后砂岩非Darcy流渗透特性的试验研究[J].岩石力学与工程学报,2004,23(12):2005-2009.
CHENG Yikang，CHEN Zhanqing，MIAO Xiexing，et al.Testing study on permeability of non-darcy flow in post-peak sandstone[J].Chinese Journal of Rock Mechanics and Engineering，2004,23(12):2005-2009.
[9] 张春会,赵全胜,王来贵,等.三轴压缩岩石应变软化及渗透率演化的试验和数值模拟[J].煤炭学报,2015,40(8):1774-1782.
ZHANG Chunhui,ZHAO Quansheng,WANG Laigui,et al.Test and numerical modeling on strain softening behavior and permeability evolution of rock under tri-axial compression[J].2015,40(8):1774-1782.
[10] 孙明贵,黄先伍,李天珍,等.石灰岩应力-应变全过程的非Darcy流渗透特性[J].岩石力学与工程学报,2006,25(3):484-491.
SUN Minggui，HUANG Xianwu，LI Tianzhen，et al.Seepage properties of non-darcy flow in complete failure process of limestone[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(3):484-491.
[11] 江宗斌,姜谙男,李宏,等.加卸载条件下石英岩蠕变-渗流耦合规律试验研究[J].岩土工程学报,2017,39(10):1832-1841.
JIANG Zongbin,JIANG Annan,LI Hong,et al.Creep-seepage coupling laws of quartzite under cyclic loading-unloading conditions[J].Chinese Journal of Geotechnical Engineering,2017,39(10):1832-1841.
[12] WANG J A,PARK H D.Fluid permeability of sedimentary rocks in a complete stress-strain process[J].Engineering Geology,2002,63(3):291-300.
[13] 胡大伟,周辉,潘鹏志,等.砂岩三轴循环加卸载条件下的渗透率研究[J].岩土力学,2010,31(9):2749-2754.
HU Dawei，ZHOU Hui,PAN Pengzhi,et al.Study of permeability of sandstone in triaxial cyclic stress tests[J].Rock and Soil Mechanics,2010,31(9):2749-2754.
[14] 孙可明,辛利伟,翟诚,等.考虑三维形貌特征粗糙裂隙加卸载渗流规律研究[J].岩土力学,2016,37(S2):161-166.
SUN Keming,XIN Liwei,ZHAI Cheng,et al.Seepage law of rough fracture during loading-unloading process considering 3D topography characteristics[J].Rock and Soil Mechanics,2016,37(S2):161-166.
[15] 杨金保,冯夏庭,潘鹏志.考虑应力历史的岩石单裂隙渗流特性试验研究[J].岩土力学,2013,34(6):1629-1635.
YANG Jinbao,FENG Xiating,PAN Pengzhi,Experimental study of permeability characteristics of single rock fracture considering stress history[J].Rock and Soil Mechanics,2013,34(6):1629-1635.
[16] MACINI P,MESINI E,VIOLA R.Laboratory measurements of non-Darcy flow coefficients in natural and artificial unconsolidated porous media[J].Journal of Petroleum Science & Engineering,2011,77(3):365-374.
[17] 熊峰,孙昊,姜清辉,等.粗糙岩石裂隙低速非线性渗流模型及试验验证[J].岩土力学,2018,39(9):3294-3302,3312.
XIONG Feng,SUN Hao,JIANG Qinghui,et al.Theoretical model and experimental verification on non-linear flow at low velocity through rough-walled rock fracture[J].Rock and Soil Mechanics,2018,39(9):3294-3302,3312.
[18] 师文豪,杨天鸿,刘洪磊,等.矿山岩体破坏突水非达西流模型及数值求解[J].岩石力学与工程学报,2016,35(3):446-455.
SHI Wenhao，YANG Tianhong,LIU Honglei，et al.Non-Darcy flow model and numerical simulation for water-inrush in fractured rock mass[J].Chinese Journal of Rock Mechanics and Engineering,2016,35(3):446-455.
[19] CHEN Y F,ZHOU J Q,HU S H,et al.Evaluation of Forchheimer equation coefficients for non-Darcy flow in deformable rough-walled fractures[J].Journal of Hydrology,2015,529:993-1006.
[20] NI X D,NIU Y L,WANG Y,et al.Non-darcy flow experiments of water seepage through rough-walled rock fractures[J].Geofluids,2018,2018:1-12.
[21] ZENG Z,GRIGG R.A criterion for non-darcy flow in porous media[J].Transport in Porous Media,2006,63(1):57-69.
