近年来，随着国家基础设施建设的大力发展和高新技术的不断应用，全国范围内交通工程建设呈现一派繁荣景象。隧道工程因其具有改善线形、克服高程或地形障碍、保护生态环境等优势，已成为交通工程建设中最重要的控制性工程之一。截至2018年底，中国隧道建设包括铁路隧道、公路隧道以及城市轨道交通隧道共计36 103 km，正在施工的各类隧道约20 000 km，计划修建的隧道约20 000 km[1]。目前，我国在隧道工程规模、工程质量与修建技术等方面已成为世界上发展最为迅速的国家。尽管隧道工程建设发展迅速，但在隧道修建过程中仍存在许多难题，其中，行业内公认的隧道建设难点之一是隧道掘进工作面前方的不良地质条件。由于修建隧道所处位置的地质情况较为复杂且地形起伏较大，在修建前期，限于现有的地质勘察技术手段，难以对工程区域内复杂地形地貌进行准确且全面地掌握，且隧道沿线出现的一些不良地质情况(如溶洞、断层与破碎带等)对后期的修建、维护与运营带来了巨大的安全隐患[2-4]。
随着国内外学者在地质探测领域的技术突破，使得无损探测技术发展迅速且广泛应用于实际工程。隧道施工超前地质预报方法有地质分析法、超前钻探法、地震反射波法、地质雷达法、瞬变电磁法、陆地声纳法、地震波层析成像法等，每种方法都有各自的优、缺点及适用范围[5-8]。地质雷达因其具有分辨率高、图像直观以及对施工干扰少等优点，被广泛应用于隧道短距离超前地质预报中(预测掘进工作面前方30 m左右)[9-10]。地质雷达信号特征分析是研究地质雷达电磁波在介质中传播规律的前提与基础，也是对地质雷达信号图谱特征进行定量解释的最有效手段。地质雷达信号分析方法普遍采用基于傅里叶理论的仪器自带分析软件，而傅里叶理论没有时频局部化分析能力，无法对隧道掘进工作面前方的地质情况进行精确定位。近年来，随着科学技术的不断进步，小波变换、S变换、复信号分析以及希尔伯特-黄变换等技术在地质雷达信号阈值去噪与特征提取等方面具备了良好的信号解译能力[11-15]。由于小波变换具有许多优良的特性，并且理论比较成熟，因而在工程领域应用最为广泛。然而，采用经典小波对地质雷达信号进行小波时频局部化分析时，选取何种尺度的小波基通常依赖于技术人员的经验，虽然由经验选取的小波基能够对地质雷达信号进行一般化处理，但是小波基天然无法准确选取的事实，阻碍了小波时频局部化分析技术在地质雷达信号处理中的应用。因此，如何利用最新的信号处理方法，构造与地质雷达信号特征相似度高的最优小波基，将是小波理论运用于地质雷达信号处理中亟需突破的难题。
笔者以此为切入点，在小波变换与奇异性检测原理的基础上，构造与地质雷达发射子波波形契合度高的小波基，然后将该小波基添加到MATLAB小波分析工具箱中，提出一种新的基于雷达小波基的小波变换时能密度法，将其应用于隧道空洞充填物地质雷达正演模拟与室内模型实验采集信号的定量识别与分析，以期为隧道短距离超前地质预报定量识别不良地质体提供技术支持。
1 识别分析方法
1.1 波形分析法
地质雷达超前地质预报的工作原理是利用地质雷达发射天线发射高频电磁波以脉冲的形式传播至隧道掘进工作面前方的岩土介质中，遇到溶洞、断层与破碎带等界面时会发生反射，反射波由地质雷达接收天线所接收，最后将在地质雷达主机显示器上获得时-距剖面图像。通过对地质雷达时-距剖面进行处理、分析与解释，达到对隧道掘进工作面前方的地质情况进行短距离超前地质预报的目的[8-10]。
地质雷达回波反射信号可以表示为
x(t)=A(t)cos[2πf0t+θ(t)]
(1)
式中，x(t)为地质雷达回波反射信号;A(t)为振幅函数;t为记录时间;f0为中心频率;θ(t)为相位函数。
地质雷达发射的脉冲电磁波遇到岩土层中存在2种不同介质的分界面时，由于相对介电常数的差异，将在界面上产生反射现象，其规律符合反射定律，产生的电磁波能量大小取决于反射系数Γ。
(2)
式中，ε1，ε2分别为分界面上、下介质的相对介电常数。由式(2)可知，隧道围岩与充填物的相对介电常数的差异，直接影响了地质雷达图像的振幅大小、频率高低与相位起伏，这为地质雷达信号特征解译提供了良好的理论基础。
1.2 小波变换模极大值法
小波变换模极大值法最突出的特征是选取信号的奇异点。信号奇异点与突变部分往往带有明显的个性化特征，它是一个信号区别于其他信号的重要特征之一。利用小波变换方法分析局部奇异性特征时，小波变换分解系数取决于信号在某一点相邻区域内的特征信号以及小波变换所选用的尺度。将任意信号f(t)的连续小波变换表示为Wf(a,b)[16]，若对b0的某一邻域内的任意一点b，有
|Wf(a0,b)|≤|Wf(a0,b0)|
(3)
则称(a0,b0)为f(t)在尺度a0上的小波变换模极大值点，|Wf(a0,b0)|为f(t)在尺度a0上的小波变换模极大值。
如果信号在某点或某区间内可微的次数越高，那么该信号越平滑，奇异性越弱。在数字信号处理中，常用李氏指数来表征信号的局部奇异性特征。信号f(t)在区间(t1,t2)上具有一致李氏指数α的充要条件为:存在常数k>0，使得对所有的t∈(t1,t2)，信号f(t)的小波变换Wf(a,b)满足如下不等式:
|Wf(a,b)|≤kaα
(4)
由式(3)～(4)可以得出，信号产生突变的特征点就是小波变换的模极大值点。由于不同尺度下的小波变换模极大值，具有突出不同时频局部特征信号的能力。因此，采用小波变换模极大值法对信号奇异性特征进行分析时，最重要的前提是选取一个最佳的尺度，在该尺度下才能最大限度显示信号的奇异性与突变成分。
1.3 小波基的构造与添加
小波基函数的选取在小波变换分析中具有不唯一性。采用不同小波基分析同一信号，所得结果也会各有差异。构造适合被分析信号特征选用的最优小波基，是目前小波分析中亟需解决的难题。从理论上讲，构造一个新的小波基的前提是只要满足小波基的允许条件。因此，可根据地质雷达发射子波f(t)=t2e-atsin ω0t的特点，其中，a为衰减系数；ω0为中心角频率，由发射子波来进行自适应波形匹配，构造与地质雷达发射子波波形相似度高的自适应雷达小波基，将该小波基添加到小波分析工具箱中，以期对地质雷达信号进行小波变换时作为小波基进行选用。
1.4 小波变换时能密度法
设信号f(t)连续小波变换系数的幅度平方在时间尺度平面上的加权积分与信号的能量成比例关系，则满足下列能量守恒关系[17-18]，即
(5)
式中，Cψ为小波基容许条件;R为实数。
由式(5)可知，小波变换幅度平方的积分同被分析信号的能量成正比。在分析与处理非平稳信号时，由于海森堡(Heisenberg)测不准原理的限制，在时-频相空间中某一点的瞬时能量密度无法得知。因此，在某一指定时刻瞬时频率的说法是不存在的。如果把|Wf(a,b)|2/Cψa2认为是时间-尺度平面上的能量密度函数，那么可将|Wf(a,b)|2ΔaΔb/Cψa2看作是以尺度a和时间b为中心、尺度间隔为Δa、时间间隔为Δb的能量。根据能量的概念，式(5)可以改写成
|f(t)|2dt=E(b)db
(6)
式中，
(7)
小波变换中，尺度因子a在某种意义上对应于频率。因此，式(7)表示信号所有频带的能量随时间b的分布情况，称为时能密度函数。
2 空洞充填物的正演模拟
2.1 时域有限差分法
地质雷达正演模拟是地质雷达图像解译的基础，解译人员要想对地质雷达信号进行清楚掌握与定量解释，就必须事先了解电磁波在隧道掘进工作面前方的传播规律与图谱特征。时域有限差分法以其具有存储空间小与计算效率高等优势，成为了地质雷达正演模拟的最主要方法[19-21]。
在无源场区域内，Maxwell方程的2个旋度可以表示为
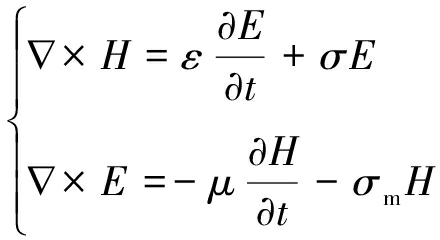
(8)
式中，H为磁场强度，A/m;E为电场强度，V/m;ε为媒质的介电常数;σ为电导率，S/m;t为时间s;μ为相对磁导率，H/m;σm为等效磁导率，w/m。
时域有限差分法利用二阶精度的中心差分形式，将Maxwell方程中的2个旋度由微分转成差分，电场与磁场在时间顺序上交替抽样，彼此相差半个时间步长。因此，二维电磁波的时域有限差分方程可以表示为
(9)
(10)
其中，
为电场与磁场在时间顺序上交替抽样，彼此相差半个时间步长,n为时间步;Ex为坐标轴x方向的电场强度;Ez为坐标轴z方向的电场强度;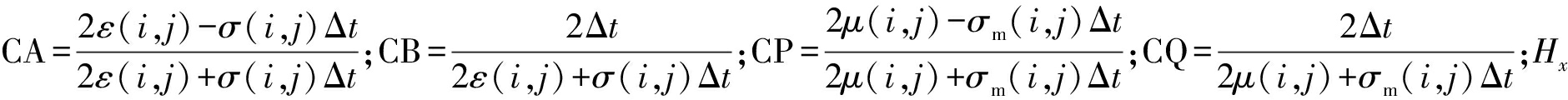
和Hy分别为x和y方向上的磁场强度;Δx和Δy分别为x和y方向上的空间步长;Δt为时间步长;(i,j)为节点坐标。
为了保证离散后时域有限差分方程组解的稳定收敛性，要求时间步长Δt和空间步长Δx与Δy满足以下关系式
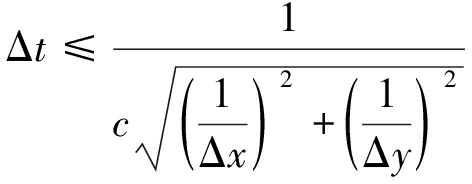
(11)
式中，c为电磁波在真空中的传播速度，c=3×108 m/s。
2.2 空洞充填物的正演模拟
假设隧道掘进工作面前方为半无限空间连续的均匀介质，电磁波反射与折射均在二维平面内进行。为了研究隧道空洞内充填不同介质的地质雷达正演模拟图像的反射特征，设计了如图1所示的隧道空洞充填物的地电模型。
图1 隧道空洞充填物的地电模型
Fig.1 Geoelectric model of tunnel cavity fillings
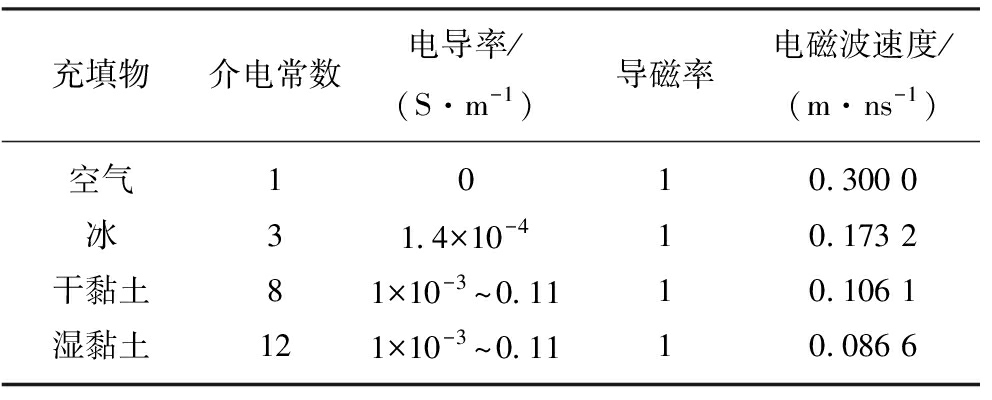
隧道掘进工作面前方空洞充填物的地电模型参数设置为:① 区域范围:12 m×20 m，左上角为坐标原点，横坐标为隧道掘进工作面水平距离，纵坐标为探测深度;② 目标体:长方形空洞，尺寸为2 m×1 m，空洞左侧与模拟区域边缘相距5 m，埋深为2 m;③ 围岩灰岩的相对介电常数为6，电导率为0.001 S/m，导磁率为1;④ 空洞充填物分别为空气、冰、干黏土与湿黏土。表1给出了隧道掘进工作面前方空洞内不同充填物的几何与物理参数。
表1 隧道空洞充填物的几何与物理参数
Table 1 Geometric and physical parameters of tunnel cavity fillings
充填物介电常数电导率/(S·m-1)导磁率电磁波速度/(m·ns-1)空气1010.3000冰31.4×10-410.1732干黏土81×10-3～0.1110.1061湿黏土121×10-3～0.1110.0866
2.3 地质雷达正演模拟特征分析
根据隧道超前地质预报实际检测所使用的参数，模拟时采用的中心频率为100 MHz，边界吸收条件为完全匹配层，激励源采用Ricker子波，网格的空间步长为0.05 m，采样步长为0.05 m，采样道数为227，总采样时间为200 ns。
由于隧道开挖过程中，特别是灰岩地区，隧道掘进工作面前方经常会遇到空洞，且空洞内含有不同的充填物。为了更好反映地质雷达正演模拟的实际情况，本次模拟将在空洞中分别填充空气(ε=1)、冰(ε=3且ε<6)、干黏土(ε=8且ε>6)与湿黏土(ε=12且ε>6)。采用100 MHz频率天线对如图1所示的地电模型空洞内充填不同介质进行正演模拟，得到正演模拟雷达响应图像，并将其减去完整灰岩的地质雷达正演模拟图像，结果如图2所示。处理过程中对每种工况进行标记，如“y1”对应充填物为空气，“y2”对应充填物为冰，“y3”对应充填物为干黏土，“y4”对应充填物为湿黏土。从图2可以看出:① 地质雷达电磁波遇到充填物空气、冰、干黏土与湿黏土等不同介质时，界面处均存在反射，空洞充填物与灰岩的相对介电常数差异较小时，电磁波回波信号的反射不明显;② 电磁波由空气进入灰岩，经灰岩再进入充填物，最后进入灰岩，各界面反射波依次被接收天线所接收。当空洞充填物的相对介电常数小于或大于灰岩的相对介电常数时，电磁波会在空洞充填物的第一或第二界面的界面处发生相位反相。而从图2所示的地质雷达时间剖面上无法识别电磁波遇到界面产生反射波的瞬时位置(究竟处于波峰还是波谷)。因此，需采用其他方法作进一步分析。
图2 隧道空洞充填物的地质雷达信号时间剖面
Fig.2 Time-sections of GPR signals with different tunnel cavity fillings
3 空洞充填物正演模拟的定量识别
3.1 波形分析法的定量识别
地质雷达正演模拟是研究高频电磁波在隧道掘进工作面前方传播规律的有效途径。在本次正演模拟中，当电磁波信号从灰岩传播到空洞充填物时，根据空洞充填物相对介电常数与灰岩的差异，电磁波将在空洞充填物上、下界面处发生反射，由反射系数可以推断反射波相位在界面处的正负，即反射波的波峰或波谷。根据波峰与波谷或波谷与波峰之间的时间差，利用公式
可以计算得到空洞充填物的厚度。从图2所示的地质雷达信号时间剖面中抽取最中间的一条信号，由此获得一条反映空洞充填物典型特征的单道信号，结果分别如图3所示。
由图3可知，根据空洞充填物与灰岩相对介电常数的关系，通过计算反射系数来确定反射界面位于反射波波峰还是波谷，从而得到电磁波在不同空洞充填物上的第一、二反射界面，分别如图3所示的a1，a2，b1，b2，c1，c2和d1，d2。依次计算不同空洞充填物单道信号两特征点的时间差，计算结果分别为11.21，11.21，19.23和23.59 ns。也就是说，空洞充填物的厚度分别为1.68，0.97，1.02和1.02 m。采用波形分析法识别不同空洞充填物的相对误差分别为68%，-3%，2%和2%，说明后三者的识别精度高。但须事先知道空洞充填物与灰岩相对介电常数的关系，即电磁波遇到异种界面时瞬时反射的位置究竟是反射波波峰还是波谷的位置。否则，难以准确确定反射界面在单道信号上的两特征点。
3.2 小波变换模极大值法的定量识别
小波变换模极大值法是一种经典小波去噪方法，信号模极大值点的位置对应于信号奇异点。从理论上讲，小波变换尺度选取得越小，模极大值点与信号奇异点的对应位置越准确，但小尺度下的小波变换系数易受噪声的干扰，产生伪奇异点。尺度较大时，可使噪声相对平滑，模极大值点位置易于寻找，但会使模极大值点位置产生一定的偏移。因此，在采用小波变换模极大值法识别信号的奇异点时，应选取适宜的尺度以避免小波变换所产生的交迭干扰。
大量试验与研究结果表明，离散小波变换选取合适小波基时，Daubechies系列小波基因其具有良好的紧支撑性、光滑性与近似对称性等优点被广泛应用于地质雷达信号的处理与分析中[22-25]。经过比较Daubechies系列小波变换模极大值法提取信号奇异点的效果后，选取Db4小波作为小波变换模极大值法提取地质雷达信号奇异点的小波基。通过分别对图3所示的地质雷达单道信号进行Db4小波变换模极大值法分析，得到如图4所示结果。
图3 隧道空洞充填物的地质雷达单道信号
Fig.3 Single-channel GPR signals of tunnel cavity fillings
图4 地质雷达单道信号Db4小波变换模值(a=10)
Fig.4 Db4 wavelet transform modulus maximum curves of GPR signals(a=10)
由图4可知，空洞不同充填物的第一、二反射界面在地质雷达正演模拟单道信号Db4小波变换模极大值曲线上的两特征点分别为a1，a2，b1，b2，c1，c2和d1，d2。两特征点的时间差分别为8.26,13.45，21.81和26.41 ns，即空洞充填物的厚度分别为1.24,1.16,1.16和1.14 m，则识别空洞充填物的相对误差分别为24%，16%，16%和14%，相对误差均大于10%。由此说明，小波分析工具箱中已有的小波基分析地质雷达信号误差较大，亟需构造新的小波基以提高地质雷达探测深度的准确率。
3.3 雷达小波变换模极大值法的定量识别
选择合适尺度的小波基是对地质雷达信号进行小波分析与处理的重要环节，其原因是不同小波基分析同一信号会产生不同的结果。在小波分析工具箱中拥有众多小波基可供挑选，但不能保证找到与地质雷达特征信号相吻合的小波基。因此，需构造与地质雷达特征信号相似度高的自适应雷达小波基，将其添加到小波分析工具箱中，以供进行小波变换时选用。
根据前文1.3节所列方法构造雷达小波基，对空洞不同充填物的地质雷达正演模拟单道信号进行雷达小波变换模极大值法分析，结果如图5所示。
图5 地质雷达单道信号雷达小波变换模值(a=10)
Fig.5 Radar wavelet transform modules maximum curves of GPR signals(a=10)
由图5可知，空洞不同充填物的上、下反射界面在地质雷达正演模拟单道信号雷达小波变换模极大值曲线上的两特征点分别为a1，a2，b1，b2，c1，c2和d1，d2。根据两特征点的时间差8.61，11.09,19.22和23.58 ns，可以得到空洞不同充填物的厚度分别为1.29，0.96，1.02和1.02 m，即识别结果的相对误差分别为29%，-4%，2%和2%。
3.4 小波变换时能密度法的定量识别
采用已构造的雷达小波基作为小波变换用的小波基，在MATLAB语言平台工作环境下编写小波变换时能密度分析程序，对空洞不同充填物的地质雷达正演模拟单道信号进行小波变换时能密度法分析，结果如图6所示。
由图6可知，空洞不同充填物的上、下反射界面在地质雷达正演模拟单道信号小波变换时能密度曲线上的两特征点分别为a1，a2，b1，b2，c1，c2和d1，d2。通过计算两特征点的时间间隔，结果依次为8.49，11.09，19.22和23.58 ns，即空洞充填物的厚度分别为1.27，0.96，1.02和1.02 m，由此可以说明识别结果的相对误差分别为29%，-4%，2%和2%。
为了比较波形分析法、Db4小波变换模极大值法、雷达小波变换模极大值法和小波变换时能密度法的识别效果，将不同方法得到的测量值与相对误差汇总于表2。
由表2可知，当空洞充填物为空气时，不同方法得到的识别结果相对误差都比较大，依据电磁波在空气中的传播速度0.3 m/ns，可以得到电磁波在空气中的波长为3 m。由于充填物的厚度仅为1 m，可能发生波形混叠，导致无法识别空洞充填物的第二界面;空洞充填物为冰、干黏土与湿黏土时，电磁波在相应介质中的波长分别为1.73，1.06与0.87 m。波形分析法、雷达小波变换模极大值法与小波变换时能密度法的识别效果均较好，但波形分析法需预先了解围岩前方的介质属性，通过计算电磁波在界面上反射系数的正负，才能确定空洞充填物第一、二反射界面在电磁波反射信号上的具体位置;通过对图5与图6的比较不难看出，小波变换时能密度法的分辨率要比雷达小波变换模极大值法的高，表明小波变换时能密度法具有更好突出地质雷达信号奇异点的位置，从而验证了将地质雷达发射子波作为地质雷达信号小波分析用的小波基是切实可行的，解决了适合地质雷达信号特征的小波基构造、添加与实现等问题，为分析地质雷达信号小波变换时选择小波基提出了一种新的方法。
图6 地质雷达单道信号小波变换时能密度曲线
Fig.6 Time-energy density analysis based on wavelet transform curves of GPR signals
表2 不同方法识别空洞充填物的测量值与相对误差
Table 2 Measurement values and relative errors of cavity fillings under different methods
空洞充填物波形分析法测量值相对误差/%Db4小波变换模极大值法测量值相对误差/%雷达小波变换模极大值法测量值相对误差/%小波变换时能密度法测量值相对误差/%空气1.68681.24241.29291.2727冰0.97-31.16160.96-40.96-4干黏土1.0221.16161.0221.022湿黏土1.0221.14141.0221.022
4 实验研究
4.1 方案设计
在众多研究方法中，室内模型实验是最直观与最可靠的研究手段之一。隧道空洞充填物模型实验中，模型尺寸与材料是影响室内模型实验结果好坏的重要因素。根据已有相关文献与资料，隧道模型尺寸相似比应尽量控制在15～30。采用地质雷达100 M天线对隧道掘进工作面前方地质情况进行短距离超前地质预报预测的探测深度一般为30 m，本次实验模型箱相似比(深度方向)取为20，即模型箱的高度为1.5 m。地质雷达电磁波在空气中的传播速度为0.3 m/ns，即波长为3 m。根据模型尺寸相似比可将空洞的尺寸设置为10～20 cm，本次实验空箱的尺寸取为10 cm，除去壁厚与加工误差，空箱的实际尺寸为9.25 cm。地质雷达用于识别隧道掘进工作面前方空洞位置的精确程度主要取决于电磁波的传播速度，即围岩的介电常数。因此，应优先选择与灰岩相对介电常数相同或相近的介质作为模型的实验材料。干砂的相对介电常数为4～6，与灰岩的介电常数较为接近，具有重复使用、试制材料垃圾少以及成本低等优点，本次模型背景材料选择干砂。为便于砂箱物理模型成型，砂箱四周采用混凝土围制而成，长、宽和高分别设置为4，3和1.5 m，以尽可能减少混凝土边界对地质雷达采集信号的干扰，具体如图7所示。砂箱中心埋设空箱模拟空洞，空洞充填物分别为空气、冰、干黏土与湿黏土的实物图如图8所示。
4.2 地质雷达信号的采集
由于空箱的实际尺寸为9.25 cm，在空洞充填物地质雷达检测的物理模型实验中，采用意大利RIS地质雷达，配以1 600 MHz天线。RIS地质雷达具有轻质便携、天线屏蔽效果好与抗干扰能力强等优点。主机技术参数如下:扫描速度4 761扫/s，脉冲重复频率400 kHz，采样点数128～8 192，A/D转换16 bit，叠加数1～32 768，分辨率5 psec，动态范围>160 dB，信噪比>160 dB。按照奈奎斯特采样定理，采样频率至少应为反射波最高频率的2倍，但在频率比仅仅为2时，雷达信号失真很明显。地质雷达在实际应用过程中，为了达到良好的探测效果，其采样频率应为天线主频的10倍以上，本次使用1 600 MHz天线所设采样频率为32 GHz。根据天线的中心频率，将实验记录时间设为16 ns和叠加次数为512。
图7 隧道空洞充填物的模型箱
Fig.7 Physical experiment box of tunnel cavity fillings
图8 隧道空洞不同充填物的实物
Fig.8 Physical drawings of different tunnel cavity fillings
依据空洞充填物埋设在模型中的具体位置已知，地质雷达检测时沿一条直线匀速前进。地质雷达数据采集过程中对每种工况进行标记，如“y5”对应充填物为空气，“y6”为冰，“y7”为干黏土，“y8”为湿黏土。采用地质雷达所携带的分析软件对采集的原始信号进行静校正、去直流点漂移、增益以及带通滤波等处理，得到空洞不同充填物的实测地质雷达信号时间剖面如图9所示。
图9 隧道空洞充填物的实测地质雷达信号时间剖面
Fig.9 Time-sections of measured GPR signals with different tunnel cavity fillings
由图9可知，地质雷达电磁波遇到空洞、冰、干黏土与湿黏土等介质时，界面处均存在反射，但不能显示具体的量值，尤其是空洞充填物的第一界面位于电磁波波形的波峰还是波谷无法得知。因此，需采用其他方法作进一步分析。
4.3 空洞充填物的定量识别
从如图9所示的隧道空洞充填物实测地质雷达信号时间剖面中抽取最中间的1条信号，获得1条反映空洞充填物典型特征的单道信号。采用前文已构造的雷达小波作为小波变换用的小波基，在MATLAB语言环境下运行小波变换时能密度法分析程序，对空洞不同充填物单道信号进行小波变换时能密度法分析，结果如图10所示。
从图10可以看出，空洞不同充填物的上、下反射界面在实测单道信号小波变换时能密度曲线上的两特征点分别为e1，e2，f1，f2，g1，g2与h1,h2。通过计算两特征点的时间间隔(分别0.908 4，1.065 0，1.911 0与2.412 1 ns)，可以得到空洞充填物的厚度分别为13.63，9.36，9.87与8.92 cm，则识别结果的相对误差为47.35%,1.19%，3.35%与-3.57%。尽管采用地质雷达1 600 MHz高频天线(探测深度浅、精度高)，但仍无法识别10 cm左右空洞，究其原因是电磁波在空气中的波长为18.75 cm，大于空洞的实际尺寸。采用小波变换时能密度法识别空洞充填物为冰、干黏土与湿黏土的精度高，相对误差均小于5%。由此表明，小波变换时能密度法能成功识别空洞充填物第一、二界面地质雷达反射信号奇异点的位置，为隧道施工现场超前地质预报图像定量识别提供技术支持。
图10 实测单道信号小波变换时能密度曲线
Fig.10 Time-energy density analysis based on wavelet transform curves of measured GPR signals
5 结 论
(1)波形分析法虽能有效识别空洞充填物的尺寸大小，但需通过计算反射系数的正或负值等先验知识来确定空洞充填物的界面特征点处于波峰还是波谷，由于空洞充填物的介电常数存在大于或小于围岩介电常数的情况，导致判断过程较繁琐，因此不适用于隧道超前地质预报精细化定量检测。
(2)尽管小波变换模极大值法容易得到信号突变的模极大值点，但选取不同小波基，可能会产生截然不同的结果。通过地质雷达正演模拟分析结果得知，小波变换模极大值法识别结果的误差约15%，误差相对较大，其原因是小波基的时频特征与被分析信号时频特征的相似性不高。
(3)在小波变换原理的基础上，从与地质雷达反射子波波形相匹配出发，成功构造了地质雷达小波基。雷达小波变换模极大值法与小波变换时能密度法的识别效果均较好，但小波变换时能密度法的分辨率更高，压制随机干扰的能力更强，更重要的是不需优选最优尺度。当空洞充填物的尺寸大于电磁波波长时，小波变换时能密度法识别结果的相对误差均小于5%。
[1] 严金秀.中国隧道工程技术发展40年[J].隧道建设(中英文)，2019，39(4):537-544.
YAN Jinxiu.Achievements and challenges of tunneling technology in China over past 40 years[J].Tunnel Construction,2019,39(4):537-544.
[2] 钱七虎.隧道工程建设地质预报及信息化技术的主要进展及发展方向[J].隧道建设，2017，37(3):251-263.
QIAN Qihu.Main developments and directions of geological prediction and informatized technology of tunnel construction[J].Tunnel Construction,2017,37(3):251-263.
[3] 程久龙，李飞，彭苏萍，等.矿井巷道地球物理方法超前探测研究进展与展望[J].煤炭学报，2014，39(8):1742-1750.
CHENG Jiulong,LI Fei,PENG Suping,et al.Research progress and development direction on advanced detection in mine roadway working face using geophysical methods[J].Journal of China Coal Society,2014,39(8):1742-1750.
[4] ZHANG Kai,TANNANT D D,ZHENG Wenbo,et al.Prediction of karst for tunnelling using fuzzy assessment combined with geological investigations[J].Tunnelling and Underground Space Technology,2018,80:64-77.
[5] 李术才，刘斌，孙怀凤，等.隧道施工超前地质预报研究现状及发展趋势[J].岩石力学与工程学报，2014，33(6):1090-1113.
LI Shucai,LIU Bin,SUN Huaifeng,et al.State of art and trends of advanced geological prediction in tunnel construction[J].Chinese Journal of Rock Mechanics and Engineering,2014,33(6):1090-1113.
[6] LI Shucai,LIU Bin,XU Xinji,et al.An overview of ahead geological prospecting in tunneling[J].Tunnelling and Underground Space Technology,2017,63:69-94.
[7] 李天斌，孟陆波，朱劲,等.隧道超前地质预报综合分析方法[J].岩石力学与工程学报，2009，28(12):2429-2436.
LI Tianbin,MENG Lubo,ZHU Jin,et al.Comprehensive analysis method for advanced forecast of geology in tunnels[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(12):2429-2436.
[8] LAI W W L,DÉROBERT X,ANNAN P.A review of ground penetrating radar application in civil engineering:A 30-year journey from locating and testing to imaging and diagnosis[J].NDT & E International,2018,96:58-78.
[9] 刘新荣，刘永权，杨忠平，等.基于地质雷达的综合超前预报技术[J].岩土力学，2015，37(S2):51-56.
LIU Xingrong,LIU Yongquan,YANG Zhongping,et al.Synthetic advanced geological prediction technology for tunnels based on GPR[J].Rock and Soil Mechanics,2015,37(S2):51-56.
[10] 宋劲，王磊.探地雷达探测采煤工作面隐伏钻杆研究[J].煤炭学报，2014，39(3):537-542.
SONG Jin,WANG Lei.Study on the high precision detection of buried drill pipe by ground penetrating radar in the coal face[J].Journal of China Coal Society,2014,39(3):537-542.
[11] ZHANG W Y,HAO T,CHANG Y,et al.Time-frequency analysis of enhanced GPR detection of RF tagged buried plastic pipes[J].NDT and E International,2017,(92):88-96.
[12] 刘宗辉，刘毛毛，周东，等.基于探地雷达属性分析的典型岩溶不良地质识别方法[J].岩土力学，2019，40(8):3282-3290.
LIU Zonghui,LIU Maomao,ZHOU Dong,et al.Recognition method of typical anomalies in karst tunnel construction based on ground penetrating radar attribute analysis[J].Rock and Soil Mechanics,2019,40(8):3282-3290.
[13] 李尧，李术才，刘斌，等.钻孔雷达探测地下不良地质体的正演模拟及其复信号分析[J].岩土力学，2017，38(1):300-308.
LI Yao,LI Shucai,LIU Bin,et al.Forward simulation and complex signal analysis of borehole radar detection for underground adverse geological bodies[J].Rock and Soil Mechanics,2017,38(1):300-308.
[14] 凌同华，张胜，李升冉.地质雷达隧道超前地质预报检测信号的HHT分析法[J].岩石力学与工程学报，2012，31(7):1422-1428.
LING Tonghua,ZHANG Sheng,LI Shengran.Hilbert-huang transform method for detection signal of tunnel geological prediction using ground penetrating radar[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(7):1422-1428.
[15] 周辉林，田茂，熊俊志.探地雷达回波信号的特征提取和分类[J].电波科学学报，2006，21(4):586-589.
ZHOU Huilin,TIAN Mao,XIONG Junzhi.Feature extraction and classification of ground penetrating radar echo signals[J].Chinese Journal of Radio Science,2006,21(4):586-589.
[16] 于生宝，郑建波，高明亮，等.基于小波变换模极大值法和阈值法的CSAMT静态校正[J].地球物理学报，2017，60(1):360-368.
YU Shengbao,ZHENG Jianbo,GAO Mingliang,et al.CSAMT static correction method based on wavelet transform modulus maxima and thresholds[J].Chinese Journal of Geophysics,2017,60(1):360-368.
[17] 张胜，凌同华，刘浩然，等.模式自适应小波时能密度法及其在微差爆破振动信号分析中的应用[J].煤炭学报，2014，39(10):2007-2013.
ZHANG Sheng,LING Tonghua,LIU Haoran,et al.Pattern adapted wavelet time-energy density method and its application in millisecond blast vibration signal analysis[J].Journal of China Coal Society,2014,39(10):2007-2013.
[18] CHENG Junsheng,YU Dejie,YANG Yu.Time-energy density analysis based on wavelet transform[J].NDT & E International,2005,38(7):569-572.
[19] 邓国文，王齐仁，廖建平，等.隧道不良地质现象的探地雷达正演模拟与超前探测[J].物探与化探，2015，39(3):651-656.
DENG Guowen,WANG Qiren,LIAO Jianping,et al.Forward modeling and advanced detection of radar in adverse geological phenomena tunnel[J].Geophysical & geochemical exploration,2015,39(3):651-656.
[20] 刘伟，周斌，甘伏平，等.隧道超前预报中不同性质充填溶洞地质雷达正演实验研究[J].现代隧道技术，2014，51(1):153-158.
LIU Wei,ZHOU Bin,GAN Fuping,et al.GPR forward simulation of filled karst caves in advance geological prediction for tunnels[J].Modern Tunneling Technology,2014,51(1):153-158.
[21] 钟声，王川婴，吴立新，等.点状不良地质体钻孔雷达响应特征——围岩及充填效应正演分析[J].岩土力学，2012，33(4):1191-1195.
ZHONG Sheng,WANG Chuanying,WU Lixin,et al.Borehole radar response characteristics of point unfavorable geo-bodies:Forward simulation of its surrounding rock and filling condition[J].Rock and Soil Mechanics,2012,33(4):1191-1195.
[22] LIU Haoran,LING Tonghua,LI Diyuan,et al.A quantitative analysis method for GPR signals based on optimal biorthogonal wavelet[J].Journal of Central South University,2018,25(4):879-891.
[23] MOHANA M A,ABBAS A M,GOMAA M L,et al.Discrimination between landmine and mine-like targets using wavelets and spectral analysis[J].NRIAG Journal of Astronomy and Geophysics,2013,2(1):54-66.
[24] 黄航如，程志平，王小龙，等.小波分析在地质雷达反射目标提取的应用[J].工程地球物理学报，2012，9(1):99-102.
HUANG Hangru,CHENG Zhiping,WANG Xiaolong,et al.The application of wavelet analysis to GPR reflective target extract[J].Chinese Journal of Engineering Geophysics,2012,9(1):99-102.
[25] 师学明，张剑，刘梦花，等.小波变换在地质雷达干扰波压制中的应用[J].工程地球物理学报，2008，5(3):279-286.
SHI Xueming,ZHANG Jian,LIU Menghua,et al.Application of wavelet transform in de-nosing ground penetrating radar data[J].Chinese Journal of Engineering Geophysics,2008,5(3):279-286.
