采动影响下,上覆岩层原始平衡状态改变,应力重新分布。围岩中逐渐形成裂隙网络,并随着采动进程不断扩展演化。采动裂隙的扩展演化规律对评价采动围岩渗透性、预测采空区地表沉降及分析评价采动岩体的安全性及稳定性具有重要影响[1-3]。钱鸣高等[4]提出了采动裂隙发展两阶段特征,揭示了煤矿长壁开采条件下裂隙O形圈分布特性。李树刚等[5]讨论了关键层在裂隙网络分布形式上的作用,指出采动过程中张开裂隙和离层裂隙最终会相互贯通,在上覆岩层中形成椭抛带分布。李树刚等[6]通过相似模型试验描述了综采条件下离层裂隙的分布特征,推导了关键层破断前后离层裂隙当量面积理论解和不同分区空隙渗流特性。分形几何理论为定量描述复杂物体和不规则自然现象提供了强有力的工具[7]。近年来,许多学者将分形理论和物理模型相结合,在定量描述采动裂隙扩展演化规律方面取得了重要进展[3,8-10]。
确定裂隙岩体的渗透特性是地质科学和岩土工程领域的重要课题,并在资源开采、地下水资源开发与保护、核废料处置和二氧化碳存储等方面得到广泛应用[11-12]。裂隙网络的渗透特性主要取决于宏观层面的裂隙特性(空间分布、密度、连通性等)和微观层面的裂隙特性(长度、宽度、方向性、粗糙度等)。然而由于地下岩体的隐蔽性和岩体裂隙网络的复杂性,准确定量描述裂隙网络的裂隙特性非常困难。众多研究表明[13-15],岩体中的裂隙网络具有分形特征。近年来,许多学者借助分形理论在裂隙网络渗流特性研究方面取得了丰硕成果[16-21]。
笔者应用大尺度相似模型试验研究了不同荷载、岩层性质及开采速度等影响下上覆岩层周期性垮落及采动裂隙的形成和分布形态。应用分形理论,得到了采动裂隙随开采进程及在开采工作面不同分区内的分形变化规律。在此基础上推导了裂隙岩体的分形渗流关系式,得到了渗透系数随开采进程及裂隙扩展的关联性演化规律。
1 物理模型试验
1.1 地质条件
根据地勘报告,所研究矿区地层分布及其物理力学参数见表1。
本文物理模型试验较精细地模拟了上述地质条件。
1.2 模型相似比
根据相似理论,模型和原型应在几何条件、边界条件、荷载及运动条件等方面满足一定的相似条件。相似材料的各种力学参数(如容重、强度、变形参数及水力特性参数等)应和原型的参数之间满足一定的相似比。根据流固耦合理论[22],相似模型试验中各参数的相似比详见表2。
1.3 物理模型试验
大型水岩耦合模型试验台架长8 m,宽1.8 m,高4 m。外围框架由槽钢和工字钢组成,正立面为钢化玻璃,两侧面及背面均为整体钢板与框架焊接而成。模型背面相应高度设置开采槽,用于模拟煤层的开采;两侧面分别设置进水口、出水口及相应流量、水压调节、测量装置。
如图1所示,在试验台架内部自下而上依次浇筑21层相似材料,分别模拟不同性质的岩层,其中5号煤层和2号煤层的底层浇筑深度(底板埋深)分别为2.25 m和0.5 m,层厚均为0.05 m。每个煤层分别设置3个尺寸相同的工作面,工作面净长度2.1 m,煤柱宽度为0.3 m,用以研究不同埋深及开采速度等条件下上覆岩层的位移、应力变化及采动裂隙的扩展演化规律,工作面参数见表3。
表1 地层参数
Table 1 Site stratigraphy and physical prosperities

编号地层厚度/m单轴抗压强度/MPa密度/(kg·m-3)1风积沙、黄土3002 0002泥岩1534.862 3043细砂岩、粉砂岩1050.002 5504泥岩2025.222 2045细砂岩、粉砂岩105.262 1336泥岩1525.222 20472号煤层520.071 2338泥岩1534.862 3049细砂岩、粉砂岩205.262 13310泥岩1534.862 30411中粗粒砂岩2050.002 55012泥岩2025.222 20413细砂岩、粉砂岩105.262 13314泥岩1025.222 20415中粗粒砂岩2050.002 55016泥岩2025.222 20417中粗粒砂岩205.262 133185号煤层520.071 23319泥岩1534.862 30420中粗粒砂岩1550.002 55021泥岩1034.862 30422中粗粒砂岩1050.002 550
表2 相似参数
Table 2 Similarity ratios

相似指标相似比Rγ,Rμ,Rε,Rφ1Pk,Pt10RL,Rδ,Rc,Rσ,Rσt,Rσc,RE100
注:γ为容重;L为几何长度;δ为位移;ε为应变;E为弹性模量;σ为应力;σt为抗拉强度;σc为抗压强度;c为黏聚力;φ为内摩擦角;μ为泊松比;k为渗透系数;t为时间。

图1 物理相似模型剖面示意
Fig.1 Cross-section of the physical simulation model
表3 工作面参数
Table 3 Mining face parameters

工作面煤层尺寸(长×高)/cm煤层埋深/cm开采速率/(cm·min-1)间歇/min开挖顺序2-1210×51004.33012-2210×51004.33022-3210×51002.01535-1210×52751.2545-2210×52752.0555-3210×52751.056
2 采动裂隙扩展演化规律
2.1 采动过程描述
通过模型试验,可以直观的观测到开采过程中上覆岩体的变形、垮落和采动裂隙扩展演化过程。以5-3工作面为例进行说明。当开采距离达到30 m,直接顶发生首次垮落,垮落范围30 m,裂隙扩展高度5 m。而后,当开采距离从30 m推进到80 m过程中,直接顶先后4次垮落,平均垮落范围为10 m,垮落高度为5 m。当开采长度推进到85 m时,基本顶首次垮塌,塌落长度85 m,塌落高度10 m。在持续开采过程中,基本顶在120 m和180 m先后垮塌,每次基本顶垮塌周期内伴随着直接顶的连续垮落(平均垮落长度为5~15 m)和数次基本顶部分垮塌。根据该采区采动过程实际监测结果,直接顶首次来压步距在80~95 m,周期来压步距18~40 m,可见试验模拟结果与现场实测结果基本吻合。总体上随着开采过程推进,采动裂隙不断产生,并在高度和长度范围内不断扩展。当工作面开采完成之后,裂隙网络布满整个工作面长度范围,裂隙网络发育高度约为60 m。开采过程的详细描述见表4。
2.2 采动裂隙分形演化规律
本文中,分形维数计算采用“覆盖法”(数方格法)。用一定边长的方格覆盖裂隙网络,计算覆盖全部裂隙网络所需的方格数量,按比例放大或者缩小方格尺寸,依次计算覆盖裂隙网络所需的方格数量。这样就得到一组方格边长r和数量N一一对应的数据。如果裂隙网络具有分形特性,方格的边长r和数量N符合
N(r)=r-D
(1)
其中,D为分形维数。将N(r)和1/r分别取对数在双对数坐标中将得到一条直线,其斜率就是D,对二维图形0<D<2。就裂隙网络图而言,分形维数反映了裂隙网络与垮落岩体之间的占比关系,D增大说明裂隙占比提高。
表4 开采进程描述
Table 4 Description of the mining process

开采进尺/m垮落高度/m垮落长度/m垮落描述30530直接顶垮落50520直接顶垮落60510直接顶垮落70510直接顶垮落80510直接顶垮落851080基本顶垮塌(整体)90510直接顶垮落9555直接顶垮落1101030基本顶垮塌(部分)11555直接顶垮落12020120基本顶垮塌(整体)12555直接顶垮落1351010直接顶垮落14055直接顶垮落1452025基本顶垮塌(部分)1503050基本顶垮塌(部分)155510直接顶垮落1651020基本顶垮塌(部分)175510直接顶垮落18060180基本顶垮塌(整体)18555直接顶垮落19055直接顶垮落19555直接顶垮落210515直接顶垮落
利用式(1)对不同开采进尺下的裂隙网络图进行分维计算,可以得到分形维数与开采进尺的关系曲线(图2),曲线有以下特点:① 曲线可以分为几个台阶形折线,包含平台段和下降段;② 下降段对应开采引起的基本顶垮塌处;③ 平台段各点对应直接顶垮落点;④ 平台段对应折线段可近似拟合为直线,各段斜率基本一致。

图2 分形维数与开采进尺关系曲线
Fig.2 Evolution of the fractal dimension of crack network with mining length
从以上特点可知,分形维数的变化可以很好地描述采动岩体的周期性垮落和岩体裂隙的扩展演化规律。下降段对应基本顶垮塌处,基本顶大面积垮塌造成裂隙网络沿水平及竖向的大面积扩展以及垮落区裂隙压实闭合,裂隙相对垮落岩体占比减小。平直段对应直接顶小面积垮落,裂隙网络不断向前扩展,对应分形维数缓慢增加。
为了分析不同开采速率对上覆岩层破坏和裂隙扩展演化规律的影响,5-1工作面和5-3工作面分别以不同开采速率进行模拟开采。图3为不同开采速率条件下分形维数与开采进度关系曲线。由图3可知,5-1工作面开采速度较快,其分形维数比5-3工作面整体偏高。同时,5-1工作面和5-3工作面曲线形式类似,均有上升段和下降段组成,但是不同的是5-3工作面上升段数较5-1工作面多,说明5-3工作面直接顶垮落间距更短,在垮落区其裂隙发育程度更高,这一特点与2个工作面最终采动裂隙网络图相符(图4)。

图3 不同工作面分形维数与开采进尺关系曲线
Fig.3 Relationship between the fractal dimension with mining length with different mining footage

图4 最终采动裂隙网络
Fig.4 Final crack network
2.3 分区分形维数演化规律
随着开采工作面向前推进,不同分区的裂隙如何形成和扩展是本文研究的重点内容之一。本文将工作面采空区(以5-1工作面为例)横向分为7个区,竖向分为6个区(表5,6),不同分区的分形维数随开采进度变化关系曲线如图5~7所示。
表5 水平分区
Table 5 Horizontal zone description

分区H1H2H3H4H5H6H7开采进尺/m 0~3030~6060~9090~120120~150150~180180~210
表6 竖向分区
Table 6 Vertical zone description

分区V1V2V3V4V5V6竖向高度/m 0~1010~2020~3030~4040~5050~60

图5 5-1工作面水平分区分形曲线
Fig.5 Evolution of the fractal dimension of crack network in different horizontal zones(minging face 5-1)

图6 不同开采进尺条件下竖向分区分形曲线
Fig.6 Evolution of the fractal dimension of crack network in different vertical zone

图7 竖向分区分形柱状图及比率曲线
Fig.7 Ratio of the fractal dimension of crack network in different vertical zones
图5为水平分区分形维数随开采距离推进的演化规律。曲线表明,水平分区的分形演化规律与图2总体分形演化规律相同。对应不同平台段的分形曲线(90,120,150,190 m),随着开采进尺增加,总体分形维数下降;对应同一平台段(如150,180,190,210 m),随着开采进尺增加,D随之缓慢增大。总体上水平分区H3和H6的D值相对较低,H1,H4和H7的D值相对较高,这说明采动裂隙扩展演化在空间分布上大体上呈“W”形。
图6为竖向分区分形演化关系曲线。竖向分形演化规律与水平分形演化规律基本形同。总体上对应不同平台段,随着开采进尺增加,分形维数下降;对应同一平台段,随着开采进尺增加,分形维数缓慢增加。对应某一具体开采进尺分形曲线,随着竖向分区向上扩展分形维数随之减小,但在最后分区处,即V7处分形维数有跃升现象,类似的规律如图7所示。由图7可知,总体上随着裂隙逐渐向上扩展,D随之逐渐减小,即冒落区较裂隙区分形维数大,裂隙发育程度高。在裂隙带和弯曲带交接部位分形维数跃升,造成该现象的原因是在交接部位生成了离层裂隙,对分形维数增大效果显著。
3 裂隙岩体渗透性的分形模型
3.1 裂隙岩体分形特性
研究表明[7],分形介质表面完整块体分布服从幂次分布
N(A>a)∝a-D/2
(2)
其中,N为面积A大于常数a的完整块体总数。在此基础上,用amax表示最大完整块体的面积[22],得到:
![]()
(3)
裂隙宽度e和裂隙长度l的关系[23-26]可以表示为
e=βln
(4)
其中,β为比例系数,该系数与围岩的力学性质参数有关,其取值区间为[0.001,0.100][24,27];n为反映裂隙特性的常数,其取值为0.5~2.0[24,26],当n=1时,表明裂隙宽度和裂隙长度服从线性分布,裂隙网络具有自相似性和分形特征[23,26,28]。则式(4)可以写为
e=βl
(5)
许多研究表明裂隙长度分布满足分形规律[26,29-33],因此式(3)可以类推用以描述裂隙介质中裂隙面积分布,即
![]()
(6)
其中,emax和lmax分别为宽度最大宽度和最大长度;Df为裂隙长度的分形维数。式(5),(6)化简后得到
![]()
(7)
对于二维问题0<Df<2,对于三维问题0<Df<3。
由于裂隙网络中裂隙数量众多,可以将式(7)视作连续可微分方程,将式(7)对l求微分可得
![]()
(8)
式(8)表示长度在[l,l+dl]之间的裂隙数量,负号表示N随l增加而减少。
孔隙率和分形维数的关系[27,34-35]可以表示为
![]()
(9)
式中,φ为裂隙网络的孔隙率;lmin和lmax分别为裂隙长度的最小值和最大值;dE为欧式维数,对于二维问题dE=2,对于三维问题dE=3。
根据孔隙率的定义,可得
![]()
(10)
式中,A为计算截面的面积;Af为计算截面的孔隙面积。
![]()
(11)
由式(9),(11)可得
![]()
(12)
将式(12)代入式(10),可得
![]()
(13)
3.2 裂隙岩体分形渗流方程
在三维空间中,裂隙的方向由走向和倾角确定,如图8所示。图中x轴和y轴分别为水平面两坐标方向,取x轴对应N向,y轴对应E向;α为走向线与y轴夹角;θ为裂隙平面与水平面夹角(倾角);Lft为考虑裂隙粗糙度情况下流体在裂隙中的渗流长度;Lf为裂隙渗流方向的直线长度;L0为Lf投影到x轴方向的直线长度;Jf为水力梯度对裂隙的切向分量;Jn为水力梯度对裂隙的法向分量。

图8 三维裂隙渗流示意
Fig.8 Fracture seepage in space
通常裂隙岩体中裂隙数量众多,逐一确定裂隙的走向和倾角是不可能的。研究表明[25,36-38]在一定区域内众多裂隙的方向性并不完全一致,但通常都表现出一种倾向性。因此可以将研究区域裂隙岩体中裂隙走向和倾角的统计平均值作为计算值。
假设流体在裂隙中的流动可以用立方定律描述[24,39-40],即
![]()
(14)
式中,q(l)为单个裂隙流量;μ为动力黏滞系数; Lft为考虑裂隙粗糙度情况下流体在裂隙中的渗流长度;ΔP为裂隙两端的压力差。
由于裂隙表面粗糙不平,裂隙中流体渗流路径为曲线,导致渗流路径加长,有效过流能力降低,如图8所示。通常情况下Lft>裂隙渗流方向的直线长度Lf,只有当裂隙为理想平板模型情况下Lft=Lf,Lft和Lf关系[28,41-42]可以表示为
![]()
(15)
其中,DT为流线的分形维数。DT反映了流线的非线性程度,当DT=1,流线为直线,Lft=Lf。
将式(5)和(15)代入式(14),可得
![]()
(16)
将水力梯度分解为沿裂隙法向和切向2个分量,如图8所示。只有切向方向水力梯度产生渗流流量,即
![]()
(17)
假设裂隙面法向方向与各个坐标轴的夹角分别为α1,α2和α3,其法向方向向量可表示为
nn=cos α1i+cos α2j+cos α3k
(18)
同时,将水力梯度矢量沿裂隙面法向和切向进行分解,得到

(19)
在计算截面上对裂隙渗流量沿裂隙长度进行积分,可得到总体渗流量
Q=-![]() q(l)dN(l)
q(l)dN(l)
(20)
由式(8),(17),(19)和式(20),并考虑到裂隙法向面方向余弦与大地坐标走向和倾角关系,可得


(21)
考虑到lmin远小于lmax,1<DT<2,1<Df<2,(lmin/lmax)3+DT-Df远小于1,将式(21)简化为
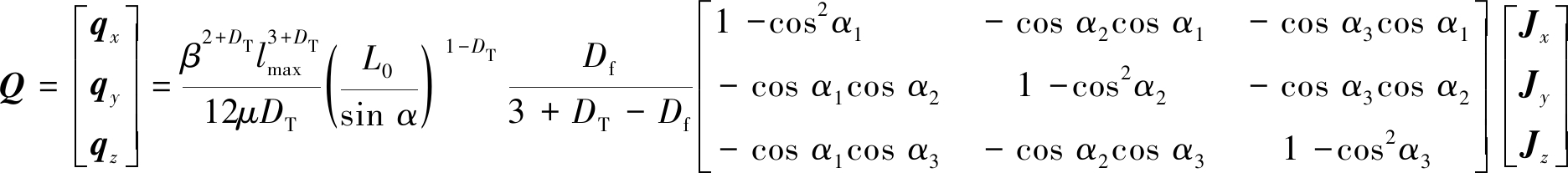
(22)
由图8可知,裂隙法向面方向余弦与大地坐标走向和倾角关系如下

(23)
由于
![]()
(24)
将式(13),(22),(23)代入式(24),可得

(25)
4 试验验证与分析
4.1 注水试验
为了得到裂隙岩体在不同裂隙发育区域的渗透参数,在模拟开挖完成之后,在物理模型上进行了现场注水试验。为了和裂隙扩展演化情况进行对比,将工作面划分7个水平分区和6个竖向分区,分区情况见表5,6。为了减小边界效应和注水孔之间的相互影响,注水孔采用梅花形布设在水平分区的中间位置,如图9所示。

图9 注水试验点位平面布置
Fig.9 Layout of water injection test
注水试验孔施工采用台架式水钻,成孔直径约90 mm。施工时先在模型顶部平面按照图9所示对注水试验点位进行定位,然后进行钻孔施工。注水试验采用由上至下分层注水测试的方法,从而得到采动工作面内不同平面位置、不同标高岩层的渗透参数。注水试验剖面如图10所示。

图10 注水试验示意
Fig.10 Profile of water injection test
4.2 试验结果及分析
注水试验完成后,采用TS-C1201多功能钻孔成像分析仪对注水孔内部孔壁情况进行观测和拍照,注水孔内部裂隙情况如图11所示。将ZS3-6号钻孔55~65,65~75,225~235和235~245 cm段裂隙图像进行数字处理,得到裂隙展开图,如图12所示。对裂隙展开图进行分形维数计算,依据式(25)进行渗透系数计算并和模型试验实际注水测试结果进行对比,如图13所示。可以看到,理论计算数值和注水试验实测数值基本一致。
应用式(25)和采动裂隙网络的分形演化规律可以得到开采过程中渗透系数随裂隙网络扩展的关联性演化规律。
图14为5-1工作面水平分区渗透系数随开采距离推进的演化规律。曲线表明,水平分区的渗透系数演化规律与分形演化规律基本相同。对应不同平台段的分形曲线(如90,120,150,190 m),随着开采进尺增加,渗透系数下降;对应同一平台段(如150,180,190和210 m),随着开采进尺增加,渗透系数缓慢增加。总体上中间分区(3区、4区)渗透系数相对较低,两端分区(1区、7区)渗透系数相对较高,采动裂隙渗透系数在横向分布上大体上呈“V”形。
图15为竖向分区渗透系数演化曲线。总体上随着竖向分区增高,渗透系数逐渐减小,但在最高分区处渗透系数有跃升现象,这与图6,7所示具有一致性。在裂隙带和弯曲带结合部位离层裂隙发育,导致渗透系数显著增大。

图11 ZS3-6内视图
Fig.11 Inside view of drill hole ZS3-6

图12 ZS3-6裂隙展开图
Fig.12 Fracture spread sketch of drill hole ZS3-6

图13 注水试验与理论计算结果对比
Fig.13 Comparison chart of water injection test

图14 5-1工作面水平分区渗透系数曲线
Fig.14 Evolution of permeability of crack network in different horizontal zones(mining face 5-1)

图15 5-1工作面竖向分区渗透系数曲线
Fig.15 Evolution of permeability of crack network in different vertical zones(mining face 5-1)
5 结 论
(1)分形维数能很好地描述采动岩体的周期性垮落和岩体裂隙的扩展演化规律。分形维数与开采距离关系曲线为台阶状折线,包含若干平台段和下降段。下降段对应基本顶大面积垮塌处,裂隙网络沿水平及竖向的大面积扩展以及垮落区裂隙压实闭合,分形维数显著减小;平直段对应直接顶小面积垮落,裂隙网络不断向前扩展,对应分形维数缓慢增加。
(2)开采速度对裂隙扩展分形演化规律有一定的影响。总体上讲,开采速度快分形维数相对较高;开采速度较慢则直接顶垮落周期较短,垮落带裂隙发育程度更高。
(3)水平分区和竖向分区裂隙演化特征具有自相似性。对应不同平台段的分形曲线,随着开采进尺增加,总体分形维数下降;对应同一平台段分形曲线,随着开采进尺增加,总体分形维数缓慢增加。总体上水平分区H3和H6分形维数相对较低,H1,H4,H7分形维数相对较高,采动裂隙扩展演化在水平分布上大体上呈“W”形;竖向分区随着垮落高度增加分形维数逐渐减小,在裂隙带和弯曲带交接部位分形维数跃升。
(4)渗透系数演化规律与分形演化规律基本相同。采动裂隙渗透系数在横向分布上大体上呈“V”形分布,总体上中间分区渗透系数相对较低,两端分区渗透系数相对较高。随着竖向分区增高,渗透系数逐渐减小,在裂隙带和弯曲带结合部位离层裂隙发育,导致渗透系数显著增大。
[1] 刘天泉.矿山岩体采动影响与控制工程学及其应用[J].煤炭学报,1995,20(1):1-5.
LIU Tianquan.Influence of mining activities on mine rock mass and control engineering[J].Journal of China Coal Society,1995,20(1):1-5.
[2] 于广明,谢和平,周宏伟,等.结构化岩体采动裂隙分布规律与分形性实验研究[J].实验力学,1998,13(2):145-154.
YU Guangming,XIE Heping,ZHOU Hongwei,et al.Distribution law of cracks in structured rock mass and its experimental investigation[J].Journal of Experimental Mechanics,1998,13(2):145-154.
[3] YU Guangming,XIE Heping,ZHAO Jianfeng,et al.Fractal evolution of a crack network in overburden rock stratum[J].Discrete Dynamics in Nature & Society,2000,5(1):47-52.
[4] 钱鸣高,许家林.覆岩采动裂隙分布的“O”形圈特征研究[J].煤炭学报,1998,23(5):466-469.
QIAN Minggao,XU Jialin.Study on the “O-shape” circle distribution characteristics of mining-induced fractures in the overlaying strata[J].Journal of China Coal Society,1998,23(5):466-469.
[5] 李树刚,石平五,钱鸣高.覆岩采动裂隙椭抛带动态分布特征研究[J].矿山压力与顶板管理,1999,Z1(3-4):44-46.
LI Shugang,SHI Pingwu,QIAN Minggao.Study on the dynamic distribution characteristic of fissures elliptic paraboloid zone in the mining overlying strata[J].Mine pressure and Roof Management,1999,Z1(3-4):44-46.
[6] 李树刚,钱鸣高,石平五.综放开采覆岩离层裂隙变化及空隙渗流特性研究[J].岩石力学与工程学报,2000,19(5):604-607.
LI Shugang,QIAN Minggao,SHI Pingwu.Study on bed-separated fissures of overlying stratum and interstice permeability in fully-mechanized top coal caving[J].Chinese Journal of Rock Mechanics and Engineering,2000,19(5):604-607.
[7] MANDELBROT Benoit.The fractal geometry of nature[M].San Francisco:W.H.Freeman,1982.
[8] 王志国,周宏伟,谢和平.深部开采上覆岩层采动裂隙网络演化的分形特征研究[J].岩土力学,2009,30(8):2403-2408.
WANG Zhiguo,ZHOU Hongwei,XIE Heping.Research on fractal characterization of mined crack network evolution in overburden rock stratum under deep mining[J].Rock and Soil Mechanics,2009,30(8):2403-2408.
[9] WEI Xiujun,GAO Mingzhong,LÜ Youchang,et al.Evolution of a mining induced fracture network in the overburden strata of an inclined coal seam[J].International Journal of Mining Science and Technology,2012,22(6):779-783.
[10] 李宏艳,王维华,齐庆新,等.基于分形理论的采动裂隙时空演化规律研究[J].煤炭学报,2014,39(6):1023-1030.
LI Hongyan,WANG Weihua,QI Qingxin,et al.Study on fissure development rule of overlying strata influenced by mining based on fractal theory[J].Journal of China Coal Society,2014,39(6):1023-1030.
[11] MIN Kibok,JING Lanru,STEPHANSSON Ove.Determining the equivalent permeability tensor for fractured rock masses using a stochastic REV approach:Method and application to the field data from Sellafield,UK[J].Hydrogeology Journal,2004,12(5):497-510.
[12] JAFARI Alireza,BABADAGLI Tayfun.Equivalent fracture network permeability of multilayer-complex naturally fractured reservoirs[J].Transport in Porous Media,2012,91(1):339-362.
[13] BARTON Christopher,LARSEN Eric.Fractal geometry of two-dimensional fracture networks at yucca mountain,southwestern Nevada[A].Proceedings of the International Symposium on Fundamentals of Rock Joints[C].Bjorkliden,Sweden,1985:77-84.
[14] LA Pointe Paul.A method to characterize fracture density and connectivity through fractal geometry[J].International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts,1988,25(6):421-429.
[15] HATTON CG,MAIN Ian,MEREDITH Philip.Non-universal of fracture length and opening displacement[J].Nature,1994,367(6459):160-162.
[16] JEAN-RAYNALD Dreuzy,DAVY Philippe,OLIVIER Bour.Hydraulic properties of two-dimensional random fracture networks following a power law length distribution:1.Effective connectivity[J].Water Resources Research,2001,37(8):2065-2078.
[17] JEAN-RAYNALD Dreuzy,DAVY Philippe,OLIVIER Bour.Hydraulic properties of two-dimensional random fracture networks following power law distributions of length and aperture[J].Water Resources Research,2002,38(12):1276-1284.
[18] JAFARI Alireza,BABADAGLI Tayfun.A sensitivity analysis for effective parameters on fracture network permeability[A].SPE Western Regional and Pacific Section AAPG Joint Meeting.Society of Petroleum Engineers[C].Bakersfield,CA,2008.
[19] ROSSEN William,GU Yongan,Lake LW.Connectivity and Permeability in Fracture Networks Obeying Power-Law Statistics[A].SPE Permian Basin Oil and Gas Recovery Conference[C].Midland,TX,2000:2226-2232.
[20] JAFARI Alireza,BABADAGLI Tayfun.Estimation of equivalent fracture network permeability using fractal and statistical network properties[J].Journal of Petroleum Science & Engineering,2012,92-93:110-123.
[21] JAFARI Alireza,BABADAGLI Tayfun.Effective fracture network permeability of geothermal reservoirs[J].Geothermics,2011,40(40):25-38.
[22] 张恩铭.水岩耦合模型实验相似材料特性研究[D].北京:清华大学,2015.
ZHANG Enming.Research on the properties of water-rock coupling similar material[D].Beijing:Tsinghua University,2015.
[23] SCHULTZ Richard,SOLIVA Roger,FOSSEN Haakon,et al.Dependence of displacement-length scaling relations for fractures and deformation bands on the volumetric changes across them[J].Journal of Structural Geology,2008,30(11):1405-1411.
[24] KLIMCZAK Christian,SCHULTZ Richard,Parashar Rishi,et al.Cubic law with aperture-length correlation:Implications for network scale fluid flow[J].Hydrogeology Journal,2010,18(4):851-862.
[25] MIAO Tongjun,YU Boming,DUAN Yonggang,et al.A fractal analysis of permeability for fractured rocks[J].International Journal of Heat & Mass Transfer,2015,81(81):75-80.
[26] Torabi Anita,Berg Silje Støren.Scaling of fault attributes:A review[J].Marine and Petroleum Geology,2011,28(8):1444-1460.
[27] MIAO Tongjun,YANG Shanshan,LONG Zhangcai,et al.Fractal analysis of permeability of dual-porosity media embedded with random fractures[J].International Journal of Heat & Mass Transfer,2015,88:814-821.
[28] LIU Richeng,JIANG Yujing,LI Bo,et al.A fractal model for characterizing fluid flow in fractured rock masses based on randomly distributed rock fracture networks[J].Computers & Geotechnics,2015,65:45-55.
[29] CHANG Jincai,YORTSOS Yanis C.Pressure-transient analysis of fractal reservoirs[J].Spe Reservoir Evaluation & Engineering,1990,5(1):31-38.
[30] WATANABE Katsumi,TAKAHASHI Hiroki.Fractal Geometry ch-aracterization of geothermal reservoir fracture networks[J].Journal of Geophysical Research Atmospheres,1995,100(B1):521-528.
[31] BONNET E,BOUR Olivier,ODLING Noelle,et al.Scaling of fracture systems in geological media[J].Reviews of Geophysics,2001,3(39):347-383.
[32] ANDRADE Jr José S,OLIVEIRA Erneson,MOREIRA Andre,et al.Fracturing the optimal paths[J].Physical Review Letters,2009,103(22):225503.
[33] MUHAMMAD Sahimi.Flow phenomena in rocks:From continuum models to fractals,percolation,cellular automata,and simulated annealing[J].Reviews of Modern Physics,1993,4(65):1393-1534.
[34] YU Boming,LI Jianhua.Some fractal characters of porous media[J].Fractals,2001,9(3):365-372.
[35] YU Boming.Analysis of flow in fractal porous media[J].Applied Mechanics Reviews,2008,61:050801.
[36] KHAMFOROUSH Mehrdad,SHAMS Kayghobad,THOVERT Jean-Francois,et al.Permeability and percolation of anisotropic three-dimensional fracture networks[J].Physical Review E Statistical Nonlinear & Soft Matter Physics,2008,77(2):463-470.
[37] ADLER Pierre,THOVERT Jean-Francois.Fractures and Fracture Networks[M].Amsterdam:Kluwer,1999.
[38] MASSART Benoit,PAILLET Marie,HENRION Vincent,et al.Fracture Characterization and Stochastic Modeling of the Granitic Basement in the HDR Soultz Project (France)[A].Proceedings World Geothermal Congress[C].Indonesia:IGA,2010:1-7.
[39] NEUZIL Christopher,TRACY James.Flow through fractures[J].Water Resources Research,1981,17(1):191-199.
[40] BEAR Jacob.Dynamics of Fluids in Porous Media[M].New York:Elsevier,1972.
[41] YU Boming,LEE James,CAO Hanqiang.A fractal in-plane permeability model for fabrics[J].Polymer Composites,2002,23(2):201-221.
[42] YU Boming,CHENG Ping.A fractal permeability model for bi-dispersed porous media[J].International Journal of Heat & Mass Transfer,2002,45(14):2983-2993.
