
移动阅读
金解放1,2,王 杰1,郭钟群1,梁 晨1,袁 伟1,吴 越3,张 睿1,王熙博1
(1.江西理工大学 建筑与测绘工程学院,江西 赣州 341000; 2.江西省环境岩土与工程灾害控制重点实验室,江西 赣州 341000; 3.江西理工大学 资源与环境工程学院,江西 赣州 341000)
摘 要:围压可以改变岩石内部微观结构,导致波阻抗发生变化,进而影响应力波在岩石中的透反射能力。为探索围压对岩石应力波传播特性的影响,通过一维应力波理论推导,得到了岩石应力波透射系数和反射系数随波阻抗值的变化关系。用红砂岩制备短试件和长试件,基于动静组合加载实验系统进行不同围压下的应力波传播试验,分析岩石的纵波波速、波阻抗、反射系数和透射系数与围压的关系。根据岩石波阻抗与围压的经验模型,结合理论分析所得的透射系数与波阻抗的关系,得到不同围压下透射系数的理论值,并与相应的试验值进行对比,证明理论分析结果的正确性。综合分析了岩石的纵波波速、波阻抗、透射系数和反射系数与围压的关系,得到围压对红砂岩应力波传播衰减特性的影响规律。结果表明,岩石短试件和长试件的纵波波速及波阻抗与围压之间均具有正向相关性。随着围压的增加,短试件反射系数的绝对值逐渐减小,透射系数逐渐增大,长试件的透射系数逐渐减小,透射系数和反射系数均与围压呈二次函数关系。纵波波速、波阻抗、透射系数及反射系数与围压的关系都表明,增大围压有利于应力波穿过岩石,减小其幅值的衰减。
关键词:应力波传播;围压;波阻抗;透反射系数;纵波波速
中图分类号:TD315
文献标志码:A
文章编号:0253-9993(2019)02-0435-10
收稿日期:2018-05-04
修回日期:2018-11-26
责任编辑:郭晓炜
基金项目:国家自然科学基金资助项目(51664017);江西理工大学清江青年英才支持计划资助项目(JXUSTQJBJ2017007);江西省教育厅科学技术研究资助项目(GJJ160616)
作者简介:金解放(1977—),男,河南杞县人,教授,博士。E-mail:jjf_chang@126.com
金解放,王杰,郭钟群,等.围压对红砂岩应力波传播特性的影响[J].煤炭学报,2019,44(2):435-444.doi:10.13225/j.cnki.jccs.2018.0603
JIN Jiefang,WANG Jie,GUO Zhongqun,et al.Influence of confining pressure on stress wave propagation character-istics in red sandstone[J].Journal of China Coal Society,2019,44(2):435-444.doi:10.13225/j.cnki.jccs.2018.0603
JIN Jiefang1,2,WANG Jie1,GUO Zhongqun1,LIANG Chen1,YUAN Wei1,WU Yue3,ZHANG Rui1,WANG Xibo1
(1.School of Architectural and Surveying Engineering,Jiangxi University of Science and Technology,Ganzhou 341000,China; 2.Jiangxi Provincial Key Laboratory of Environmental Geotechnology and Engineering Disaster Control,Ganzhou 341000,China; 3.School of Resources and Environmental Engineering,Jiangxi University of Science and Technology,Ganzhou 341000,China)
Abstract:Confining pressure has a great effect on the internal microstructure of the rock,and results in a change in wave impedance,which affects the propagation attenuation laws of the stress wave in the porous rock subjected to high stress.In order to investigate the effect of confining pressure on the characteristics of stress wave propagation in rock,the relationships between both reflection coefficient and transmission coefficient with the wave impedance of rock were established based on one dimensional stress wave theory.Then the short and long rock specimens were made of red sandstone,and the experiments of stress wave propagation in specimens under different confining pressures were carried out based on the modified Split Hopkinson Pressure Bar (SHPB).Also,the experimental longitudinal wave velocities,wave impedances,reflection coefficients and transmission coefficients of rock under different confining pressures were analyzed.Based on the empirical relationship between wave impedance and confining pressure,and the theoretical relationship between wave impedance and transmission coefficient,the theoretical transmission coefficients under different confining pressures were obtained and compared with experimental values.The comparison shows that the differences between theoretical and experiment values were very small,and verifies the theoretical analysis of transmission and reflection coefficients are valid.The influence laws of confining pressure on the stress wave propagation along red sandstone were obtained by the comprehensive analysis of longitudinal wave velocity,wave impedance,transmitted and reflected coefficients of rock under different confining pressures.The results show that both the longitudinal wave velocity and wave impedance of rock specimen increase with the increase in confining pressure.With the increase of confining pressure,the transmission coefficient of short specimen increases,and the absolute value of reflection coefficient decreases,the transmission coefficient of long specimen,however,decreases gradually.The variation trends of both the reflection coefficient and trans-mission coefficient with confining pressure can be fitted with quadratic function.All of the above variation tendencies show that the increase of confining pressure decreases the attenuation of its amplitude.
Key words:stress wave propagation;transmission and reflection coefficient;confining pressure;wave impedance;longitudinal wave velocity
岩石(体)中应力波的传播衰减规律一直是地球物理、防护工程、交通工程以及矿山工程等领域的重点研究问题之一。深部岩体工程在爆破开挖及运营过程中,由于原岩应力的二次分布以及构造应力的复杂性,围岩体承受的地应力值随空间和时间的变化而变化。研究具有不同地应力环境下岩石(体)中应力波传播衰减特性,对深部工程岩体爆破开挖过程中围岩及邻近建(构)筑物稳定性分析具有重要的理论指导意义。
岩石属于天然孔隙材料,在静载荷作用过程中,岩石的变形依次有孔隙压密、短暂弹性变形、损伤演化、峰后宏观失效等阶段。在上述变形过程中,岩石孔隙度及孔隙形状始终在变化,导致其声波波速等物理力学参数具有应力相关性[1]。由于围压对岩石侧向位移的限制作用,随围压的增加,岩石的强度逐渐增大,其变形会出现脆-延转化、流变及扩容等特性[2-4]。有关静应力对纵波波速的影响已取得较为丰硕的研究成果,并建立了许多经验模型关系[5-9]。岩石的纵波波速和密度具有良好的正相关性[10-11],二者的乘积为岩石的波阻抗值,波阻抗是表征岩石应力波透射和反射能力的基本物理量。
针对深部工程岩体爆破开挖过程中的高应力问题,众多学者开展了动静组合作用下岩石动态力学特性研究,取得了较为系统的理论和试验成果。研究表明,静应力的大小及作用方式对岩石动态强度、变形特性、能量耗散、抵抗疲劳冲击性能、破坏类型及机理都有较大的影响[12-17]。白羽等[18]通过数值模拟研究双孔爆破裂纹演化规律,结果表明,裂纹演化过程与地应力密切相关,裂纹主要向最大地应力方向扩展,扩展半径和裂区面积随初始地应力的增大逐渐减小,地应力明显抑制了爆破致裂。范勇等[19]的研究表明,深部岩体隧洞爆破开挖,洞壁围岩受到爆破荷载和地应力瞬态卸荷两者耦合作用,其中爆破荷载以张拉破坏为主,而地应力瞬态卸荷以围岩的压剪破坏为主。具有高地应力的岩体在开挖卸荷以后应力会重新分布,造成岩体强度弱化,不稳定块体增加及地下水渗流条件改善,为深部工程岩体非爆连续化开采提供了有利条件[20-22]。
静应力影响岩石(体)应力波传播特性方面的研究较少,刘少虹等[23]基于霍布金逊压杆对煤岩组合体进行动静加载试验,研究了应力波振幅和静载荷对煤岩组合应力波传播特性的影响。结果表明,随着静载荷的增加,动载荷能耗先增大后减小。李新平等[24]通过模型实验研究了深部高应力对工程岩体应力波传播衰减的影响。结果表明,高地应力下,节理岩体中爆炸应力波衰减由岩石材料和节理两部分引起;随着围压的增加,应力波在节理处的透射能力增强,岩石材料自身对应力波衰减起主导作用,节理导致的衰减越来越小。金解放等[25]利用动静组合加载实验装置,对红砂岩试件进行不同轴压下的应力波传播试验,通过纵波波速、振幅随空间、时间以及轴向静应力的衰减系数,研究了轴向静应力对应力波传播衰减的影响。FAN L F等[26]通过理论分析,研究了原岩应力对节理岩体应力波传播衰减的影响,结果表明,随着原岩应力的增加,应力波透射系数、能量透射系数和有效波速越来越大,且上述影响规律与应力波幅值和频率有关。上述研究对深部高应力下工程岩体安全高效爆破开挖具有重要的理论和实际意义,而对围压影响岩石应力波传播衰减特性鲜有研究。
为探索围压对岩石应力波传播衰减规律的影响,基于一维应力波理论,分析不同波阻抗环境下应力波的多次透反射过程,针对霍布金逊压杆(Split Hopkinson Pressure Bar,SHPB)装置的实际,建立了透射系数和反射系数与波阻抗的理论关系。分别应用红砂岩长试件和短试件进行不同围压下的应力波传播试验,得到不同围压工况下岩石的纵波波速、反射系数和透射系数,并与理论结果进行对比,研究得到围压对岩石应力波传播衰减特性的影响。研究结果有助于分析深部工程岩体爆破开挖应力波的传播规律以及邻近结构稳定性分析。
岩体应力波透反射系数的大小取决于岩体的波阻抗值,在进行岩体损伤检测和围岩稳定性分析时,常通过测试岩体应力波透反射系数反演波阻抗值,进而得到岩体的纵波波速、密度等基本物理参数。因此有必要从理论上探讨透反射系数与波阻抗值之间的定量关系。为系统分析围压对岩石应力波传播特性的影响,基于SHPB装置中入射杆-岩石试件-透射杆的组成关系,并借助围压有助于提高岩石试件纵波波速C和密度ρ的结论,分析岩石试件波阻抗ρC的变化对岩石试件透反射系数的影响,从理论角度分析围压对岩石应力波传播的影响。
理论分析模型如图1所示,图中杆1和杆3的材料相同,其波阻抗为ρ1C1,杆2为具有围压的岩石试件,其波阻抗为ρ2C2,长度为Ls,杆1,2和3的横截面面积相同,J1和J2分别表示杆1和2以及杆2和3的交界面。根据一维应力波理论,应力波σI(t)由入射杆进入岩石试件时,由于二者波阻抗不同,在界面J1处产生反射波σR1(t)和透射波![]() 应力波
应力波![]() 在试件与透射杆的界面J2处产生反射波
在试件与透射杆的界面J2处产生反射波![]() 和透射波σT1(t)。如此往复,应力波会在界面J1和J2处分别产生多次透反射,如图1所示,σRi(t)和σTi(t)分别表示第i次的反射和透射应力波。
和透射波σT1(t)。如此往复,应力波会在界面J1和J2处分别产生多次透反射,如图1所示,σRi(t)和σTi(t)分别表示第i次的反射和透射应力波。

图1 应力波在不同介质界面上的透反射过程
Fig.1 Transmission and reflection of stress wave at interfaces of different media
假设入射应力脉冲为σI(t)=f (t),延续时间为τ,入射波到达界面J1的时刻为0,则有
(1)
根据一维应力波理论[27],入射波σI(t)第1次经过界面J1时,反射波和透射波分别为
σR(t)=λfI(t)(2)
![]() (3)
(3)
λ=(ρ2C2-ρ1C1)/(ρ2C2+ρ1C1)(4)
式中,λ为应力波在波阻抗不同界面处的反射系数。
同理,应力波![]() 在界面J2处的反射波和透射波分别为
在界面J2处的反射波和透射波分别为
(5)
![]() (6)
(6)
反射波![]() 又在界面J1处产生透反射,如此往复,界面J1处的反射波σR(t)应为多次反射波的叠加而成,界面J2处的透射波σT(t)应为多次透射波的叠加而成,分别为
又在界面J1处产生透反射,如此往复,界面J1处的反射波σR(t)应为多次反射波的叠加而成,界面J2处的透射波σT(t)应为多次透射波的叠加而成,分别为
σR(t)=σR1(t)+σR2(t)+σR3(t)+…=λf(t)+
![]() (7)
(7)
σT(t)=σT1(t)+σT2(t)+σT3(t)+…=
![]() (8)
(8)
若入射脉冲f(t)为矩形波,在延续时间τ内,任何时刻的脉冲值相等,式(7),(8)中f(t)=f(t-Ls/Cs)=f(t-2Ls/Cs)=f(t-3Ls/Cs)=f(t-4Ls/Cs)=…。而当f(t)为半正弦和三角形脉冲时,在其延续时间内,脉冲值随时在变化,多次反射波σR2(t),σR3(t),…的幅值与一次反射波的幅值没有重合在一起。同理,多次透射波的幅值也不会与一次透射波幅值重叠,即f(t)≠f(t-Ls/Cs)≠f(t-2Ls/Cs)≠f(t-3Ls/Cs)≠f(t-4Ls/Cs)≠…。因此当通过反射波和透射波与入射波幅值之比研究应力波的传播特性时,若入射波是非矩形波时,式(7),(8)中不应考虑多次透射波和反射波的影响,即应力波的反射系数Rt和透射系数Tt分别为
(9)
![]() (10)
(10)
根据式(9)和(10),反射系数Rt和透射系数Tt与波阻抗比值ρ2C2/(ρ1C1)的关系如图2,3所示。

图2 反射系数Rt与波阻抗之比ρ2C2/(ρ1C1)的关系
Fig.2 Reflection coefficient Rt under different wave impedance ratio ρ2C2/(ρ1C1)

图3 透射系数Tt与波阻抗之比ρ2C2/(ρ1C1)的关系
Fig.3 Transmission coefficient Ttunder different wave impedance ratio ρ2C2/(ρ1C1)
由图2可以看出,当波阻抗比值小于1时,反射系数Rt为负值,表示反射波和入射波方向相反。随ρ2C2/(ρ1C1)值增加,反射系数Rt的绝对值逐渐减小,表示反射波幅值越来越小。当波阻抗比值ρ2C2/(ρ1C1)大于1时,反射系数Rt为正值,表示反射波与入射波方向相同,随波阻抗比值的增加,反射系数Rt逐渐增大,表示反射波幅值越来越大。ρ2C2/(ρ1C1)值越靠近1,反射波幅值越小。
由图3可以看出,当波阻抗比值小于1时,透射系数Tt随着ρ2C2/(ρ1C1)的增大逐渐增大,但增大趋势越来越小。当波阻抗比值ρ2C2/(ρ1C1)>1时,透射系数Tt随波阻抗比值的增大逐渐减小。当波阻抗比值等于1时,即岩石试件与入射杆和透射杆的波阻抗相同,应力波的衰减系数为1,表示应力波不会发生透反射,可以无衰减地通过试件。
试件选用赣州红砂岩制成,其均质性较好且孔隙度较大。其纵波波速为2 390 m/s,单轴抗压强度为52 MPa,密度为2.53 g/cm3,孔隙度为5.22%。在研究围压对岩石应力波传播特性的影响时,基于动静组合加载实验系统,可以用两种长径比的试件进行试验:一是短试件,图1中的杆1和杆3分别是加载实验系统中弹性入射杆和透射杆,杆2为岩石试件,其尺寸为φ50 mm×100 mm。二是利用长试件,图1中的杆1,2和3为同一岩石试件,仅是在杆2部分施加围压,其尺寸为φ50 mm×1 500 mm。试件的加工制作严格按照相关标准,将其两端面研磨抛光,保证其不平行度和不垂直度均小于0.02 mm。

图4 试件尺寸及应变片位置示意
Fig.4 Diagrams of specimen size and strain gauge position
应变片尺寸为2 mm×1 mm,电阻为120 ± 0.1 Ω,为最大限度消除偏心压缩对试验应力波信号的影响,每一测点处纵向轴对称粘贴2个应变片。对于φ50 mm×1 500 mm的长试件,两组应变片都粘贴在岩石试件上,第1组应变片粘贴在距离试件入射端200 mm处,第2组应变片粘贴在距离试件末端1 000 mm处。对于尺寸为φ50 mm×100 mm短试件,两组应变片分别粘贴在入射杆和透射杆上,入射杆应变片距离短试件900 mm,透射杆应变片距离短试件600 mm,如图4所示。
采用基于SHPB的动静组合加载实验系统,其动力冲击系统与围压系统相对独立,可以在施加动载前对试件施加围压。围压装置外部总长度为284 mm,内部施压长度为100 mm,孔径为φ50 mm。入射杆、透射杆及异型冲头的材质均为40 Cr高强度合金钢,纵波波速为5 400 m/s,密度为7.81 g/cm3,波阻抗的大小为413 MPa/s。异型冲头选用纺锤形,以实现半正弦波加载并消除PC振荡。将岩石试件在两端面均匀涂抹黄油后水平放置在动静组合加载试验设备入射杆和透射杆之间,最大限度保证入射杆、试件和透射杆轴向重合,以试件φ50 mm×1 500 mm为例,如图5所示。
试验过程中轴压为0 MPa,围压设置10个等级,分别为0,4,8,12,16,20,24,28,32和36 MPa。10个等级的围压分别对不同试件进行试验,长、短两类试件的数量均为30个,每种围压工况使用3个试件,每个试件冲击1次。为了使不同工况下的试验结果具有可比性,两种尺寸的试件在所有围压工况下的试验,最大限度保证弹性入射杆上的入射波幅值相等。实现方法是固定冲击气压值以及冲头在枪膛中的起始位置,保证冲头以相同冲击速率撞击入射杆。冲头的冲击速率由激光测速仪测定。

图5 具有围压作用的岩石应力波传播试验示意
Fig.5 Schematic of stress wave propagation experiment along rock specimen under confining pressure
通过试验可以测得长试件和短试件在不同围压情况下的应力波数据,图6和7仅给出各自3种围压下的应力波时程曲线。由图6和7可以看出,当试件的长径比相同时,随围压的增加,应力波形状一致。对短试件,由于两组应变片都在弹性杆上,且距界面J1和J2的距离较大,能得到完整的反射波和透射波。对长试件,两组应变片都粘贴在岩石试件上,且应变片1距界面J1的距离仅有100 mm,J1处的反射波与入射波叠加,致使图7中没有明显的反射波,但无论如何图7中的入射波和透射波是图4(b)所示工况下岩石应力波真实表现,不影响用透射系数来表征其应力波传播特性。
表1给出了不同围压情况下应变片1和应变片2处应力波幅值和起跳点对应的时间,其中εIA和εTA分别为入射波和透射波的幅值;t1和t2分别为入射波和透射波起跳点对应的时间;εRA表示短试件时反射波的幅值。纵波波速Cp、透射系数αT和反射系数αR的计算方法在后文介绍。
纵波波速是表征应力波传播特性的一个重要参数,也能很好地反映材料孔隙度和损伤度的大小。当岩石中的应力波属于弹性波的范围时,应力波的传播速度可以认为与纵波波速一致。根据不同围压等级情况下应力波-时间数据,由式(11),(12)可以分别计算出长试件和短试件在不同围压工况下的纵波波速值
长试件:![]() (11)
(11)
短试件:![]() (12)
(12)
其中,C0为岩石纵波波速;C1为弹性杆纵波波速;l1为试件围压作用的有效长度,本文中长试件和短试件都为100 mm;t1和t2分别见表1;l2为图4(b)所示的测点1和2的间距减去l1,其值为200 mm;l3为图4(a)所示的测点1和2间弹性杆的长度,其值为1 500 mm。
计算得到的纵波波速值见表1,纵波波速与围压的关系如图8所示。由图8可以看出,随围压的增加,岩石纵波波速逐渐增加,这与采用静载试验方法得到的其他岩性的结果一致[5-6],纵波波速Cp与围压σc之间具有较好的二次函数关系,长试件和短试件的经验模型关系分别如下
表1 试验数据
Table 1 Test data

注:纵波波速Cp单位为(m·s-1)。

图6 不同围压下短试件中的应力波(φ50 mm×100 mm)
Fig.6 Stress waves of short rock specimen under different confining pressure

图7 不同围压下长试件中的应力波(φ50 mm×1 500 mm)
Fig.7 Stress waves of long rock specimen under different confining pressure

图8 不同围压情况下岩石的纵波波速
Fig.8 Relationships between confining pressure and longitudinal wave velocity
(13)
![]() (14)
(14)
式(13)和(14)的相关性系数分别为0.988 76和0.981 38。根据纵波波速与岩石孔隙度或损伤度的定性关系,由图8的结果可以推测,随着围压的增加,岩石的初始孔隙逐渐被压密,密度逐渐增加,即围压有助于岩石孔隙的压密及密度的增加。岩石的波速与密度之间具有正向相关性。根据上述经验模型,在工程实际中,可以通过监测纵波波速,反演工程岩体围压大小的变化,以及围岩体的稳定性。
由图8还可以发现,长试件和短试件纵波波速相差较小,利用图中所示的两个拟合关系,计算出的纵波波速值相差在2%之内。这表明,采用长试件和短试件,都可以测得岩石在不同围压下的纵波波速值。
已有研究表明[10-11,28],岩石的纵波波速与密度间具有良好的正相关关系。GARDNER[10]和朱广生[11]的研究都认为,岩石的密度与纵波波速间具有幂函数关系,前者是基于盐水饱和岩石试验值及野外资料统计得出的结果;后者是针对砂岩和泥岩并通过全波声波测井和密度测井建立的经验模型,其函数关系为
(15)
岩石波阻抗Z等于密度ρ和纵波波速Cp的乘积,应用式(14)中纵波波速和围压的经验关系,以及式(15)的关系,可以得到不同围压情况下岩石的波阻抗值,如图9所示。

图9 围压与波阻抗的关系
Fig.9 Relationship between confining pressure and wave impedance
由图9可以看出,随着围压的增大,波阻抗值逐渐增大。岩石的初始孔隙和微裂隙在围压作用下逐渐被压密,增大了岩石的密度和纵波波速,而波阻抗是密度与纵波波速的乘积,因此波阻抗值会随围压增大而增大。由式(14),(15)直接得到的关系式比较复杂,不便于应用。将图9中波阻抗与围压的关系进行拟合,由拟合结果可以看出,围压区段岩石的波阻抗与围压间具有良好的二次函数关系。实际应用中,根据波阻抗与围压的经验模型关系,可以利用其中的某些参数反演另外一些参数,比如利用波阻抗反演围岩体的围压大小。
为定量分析围压对应力波传播衰减的影响,且与第1节的理论分析结果对应,本文分别应用透射系数Te和反射系数Re表征应力波幅值的衰减比例。当应用图4(a)所示短试件的试验数据时,忽略弹性杆中应力波的衰减,利用图6所示的入射波、反射波和透射波幅值,通过下式可以分别计算反射系数Re和透射系数Te:
Re=εRA/εIA,Te=εTA/εIA(16)
式中,εIA,εRA和εTA分别表示入射波、反射波和透射波的幅值。
当应用图4(b)所示长试件进行试验时,由于测点1处的应变片离围压界面较近,不能测得反射波,因此不能得到反射系数Re,只能得到透射系数Te。测点1和测点2到围压边界还各有100 mm的距离,岩石试件在这两段的轴压和围压都为0。当计算应力波的透射系数时,应剔除这两段对透射系数的影响。本文与文献[22]都是使用红砂岩进行研究,文献[22]考虑了不同轴压下红砂岩的衰减特性。根据文献[22]的研究结果,使用长试件试验时的透射系数Te的计算方法如下:
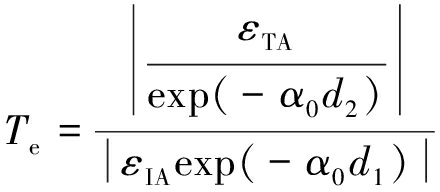
(17)
其中,d1为图4(b)中应变片1距围压右侧界面的距离,其值为100 mm;d2为图4(b)中应变片2距围压左侧界面的距离,其值为100 mm;α0为无轴压无围压时红砂岩的空间衰减系数,其值为0.727 3 m-1[25]。
利用式(16),(17),可以计算得到短试件在不同围压工况下的反射系数和透射系数,以及长试件的透射系数,见表1。根据表1的计算结果,不同围压情况下的透反射系数如图10所示。

图10 不同工况下岩石的反射系数Re和透射系数Te
Fig.10 Reflection coefficient Re and transmission Te coefficient of rock under different confining pressure
由图10(a)可以看出,当试件的尺寸为φ50 mm×100 mm时,应力波反射系数Re始终为负值,随着围压的增加,反射系数Re的绝对值逐渐减小,二者间呈二次函数关系。这是由于随着围压的增大,岩石内部孔隙和微裂隙逐渐被压密,增大了岩石的密度,缩小了岩石试件与入射杆的波阻抗差距,被反射的应力波逐渐减少。反射系数Re随围压的变化趋势与图2所示的理论结果趋势一致,证明前文理论分析的正确性。
由图10(b)可以看出,随着围压的增加,短试件得到的透射系数都为正值,且越来越大,二者也满足二次函数关系。当围压增大时,岩石被压实挤密,导致密度增大,短试件的波阻抗增大并且与入射杆、透射杆的波阻抗差距不断减小,发生透射的应力波逐渐增大。这表明,增加围压有助于提高岩石的波阻抗,使应力波穿过岩石的比例越来越大,从而增强岩石应力波的穿透能力,减小其衰减率。此种情况下图3中的ρ2C2表示岩石试件的波阻抗,ρ1C1表示弹性杆的波阻抗。根据图9的关系,ρ2C2/(ρ1C1)的值随着围压的增加而增大。图3中的透射系数位于增大区域内,其值越来越大。证明理论结果和试验结果具有一致性。
由图10(c)可以看出,当试件的尺寸为φ50 mm×1 500 mm时,随围压值的增加,应力波透射系数Te值逐渐减小。由于围压区段岩石密度会随着围压的增大而增大,使其波阻抗与相邻区段岩石的波阻抗差距越来越大,导致发生透射的应力波逐渐减小。此种情况下图3中的ρ2C2表示有围压段试件的波阻抗,ρ1C1表示无围压段试件的波阻抗。结合图9的结果,具有围压段岩石试件的波阻抗ρ2C2大于无围压时ρ1C1的值,随着围压的增加,ρ2C2/(ρ1C1)的值越来越大。这也意味着,随围压的增加,图3中的透射系数位于减小区域内,其值越来越小。这也能证明理论结果和试验结果具有一致性。
关于图10所示的围压对岩石透反射系数的影响规律,笔者认为其主要是由于围压改变岩石波阻抗引起的,其原因如下:围压与岩石纵波波速是正相关的,岩石的纵波波速与密度间也是正相关的[10-11,25],进而可得岩石波阻抗随围压增加而增加。波阻抗是反映岩石材料应力波传播特性的重要力学参数,波阻抗越大,越有利于应力波传播,透射系数增加,反射系数减小。在实际应用中,可以根据工程场地的地应力条件预测围岩的应力波透反射能力,为爆破方案设计提供理论参考依据。
利用图9中围压和波阻抗的经验关系,结合式(10)透射系数的理论模型,可以得到不同围压下透射系数的理论值。为了对比理论分析与试验结果,将短试件在不同围压下透射系数的理论及试验值显示在图11中。应用式(18)定义的差值百分比δ衡量试验与理论值的偏离程度:
(18)
式中,Te和Tt分别为试验方法和理论方法得到的透射系数。
由图11可以看出,随着围压的增加,透射系数的理论和试验值都逐渐增加,二者的变化趋势相同。在整个围压变化过程中,透射系数的理论和试验值大小没有完全重合,这主要是因为前文理论分析中,仅考虑了应力波在两分界面J1和J2处的透反射引起的幅值衰减,并没有考虑两分界面之间岩石材料本身造成的物理衰减;且由式(7),(8)到式(9),(10)过程中,仅考虑了一次透反射过程,没有考虑多次透反射过程对反射系数和透射系数的影响;此外,试验数据也具有一定的离散性,因此理论分析与试验结果得到的透射系数值必然存在一定差异。然而只要二者随围压的变化趋势一致,即可得到不同围压工况下岩石应力波幅值的衰减规律。且二者的差值百分比在7.2%以内,差别较小。这表明理论分析与试验结果的吻合度较高,结合不同围压下岩石波阻抗的变化关系,应用本文第1节的理论分析结果,可以研究不同围压工况下岩石应力波的衰减规律。

图11 不同围压下短试件透射系数的理论和试验值对比
Fig.11 Theoretical and experimental transmission coefficients
and their deviation
(1)理论研究结果表明,ρ2C2/(ρ1C1)<1时,反射系数Rt为负值,随ρ2C2/(ρ1C1)值逐渐增加,反射系数Rt的绝对值逐渐减小,表示反射波幅值越来越小。当波阻抗比值ρ2C2/(ρ1C1)>1时,反射系数Rt为正值,随波阻抗比值ρ2C2/(ρ1C1)的增加,反射系数Rt逐渐增大,表示反射波幅值越来越大。随着ρ2C2/(ρ1C1)值逐渐增加,透射系数Tt值始终为正值,其值先增加后减小。
(2)试验结果表明,随着围压的增加,岩石纵波波速和波阻抗都逐渐增加,二者与围压都满足二次函数关系。短试件和长试件所得结果相差较小。
(3)在本文设置围压范围,短试件的反射系数都为负值,随围压的增加,反射系数和透射系数都逐渐增大。长试件的透射系数随围压的增加而逐渐减小。增加围压有助于提高岩石应力波的穿透性,减小其衰减率。反射系数与透射系数都与围压呈二次函数关系。
(4)试验和理论所得不同围压下岩石的透射系数吻合度较高,证明理论结果的正确性。
本文仅对岩石试件施加了围压作用,关于围压和轴压共同作用下岩石的应力波传播特性,有待进一步研究。
参考文献
[1] AMOS NUR.Effects of stress on velocity anisotropy in rock with cracks[J].Journal of Geophysical Research,1971,76(8):2022-2034.
[2] WEI Yujie,LALLIT ANAND.On micro-cracking,inelastic dilatancy,and the brittle-ductile transition in compact rocks:A micro-mechanical study[J].International Journal of Solids and Structures,2008,45(10):2785-2798.
[3] ZONG Yijiang,HAN Lijun,WEI Jianjun,et al.Mechanical and damage evolution properties of sandstone under triaxial compression[J].International Journal of Mining Science and Technology,2016,26(4):601-607.
[4] YANG Chunhe,DAEMEN J J K,YIN Jianhua.Experimental investigation of creep behavior of salt rock[J].International Journal of Rock Mechanics and Mining Sciences,1999,36(2):233-242.
[5] 嵇少丞,王茜,DENIS MARCOTTE,等.苏鲁超高压变质岩中地震波速随围压的变化规律[J].地质学报,2006,80(12):1807-1812.
JI Shaocheng,WANG Qian,DENIS MARCOTTE,et al.Pressure-dependence of P-Wave velocities in Sulu UHP metamorphic rocks[J].Acta Geologica Sinica,2006,80(12):1807-1812.
[6] 李阿伟,孙东生,王红才.致密砂岩波速各向异性及弹性参数随围压变化规律的实验研究[J].地球物理学进展,2014,29(2):754-760.
LI Awei,SUN Dongsheng,WANG Hongcai.Seismic anisotropy and elastic parameter of tight sandstone with confining pressure[J].Progress in Geophysics,2014,29(2):754-760.
[7] AMOS NUR.Effects of stress on velocity anisotropy in rock with cracks[J].Journal of Geophysical Research,1971,76(8):2022-2034.
[8] 巩思园,窦林名,徐晓菊,等.冲击倾向煤岩纵波波速与应力关系试验研[J].采矿与安全工程学报,2012,29(1):67-71.
GONG Siyuan,DOU Linming,XU Xiaoju,et al.Experimental study on the correlation between stress and P-wave velocity for burst tendency coal-rock samples[J].Journal of Mining & Safety Engineering,2012,29(1):67-71.
[9] 尹帅,丁文龙,孙圆辉,等.不同围压条件下含气致密砂岩孔裂隙形态演化试验研究[J].石油物探,2016,55(3):326-332.
YIN Shuai,DING Wenlong,SUN Yuanhui,et al.Experimental study on pore fracture morphology evolution of gas-bearing tight sandstone under different confining pressure[J].Geophysical Prospecting for Petroleum,2016,55(3):326-332.
[10] GARDNER G H F,GARDNER L W,GREGORY A R.Formation velocity and density-the diagnostic basics for stratigraphic traps[J].Geophysics,1974,39(6):770-780.
[11] 朱广生,桂志先,熊新斌,等.密度与纵横波速度关系[J].地球物理学报,1995,38(S1):260-264.
ZHU Guangsheng,GUI Zhixian,XIONG Xinbin,et al.Relationships between density and P-wave,S-wave velocities[J].Chinese Journal of Geophysics,1995,38(S1):260-264.
[12] 金解放,李夕兵,殷志强,等.轴压和循环冲击次数对砂岩动态力学特性的影响[J].煤炭学报,2012,37(6):923-930.
JIN Jiefang,LI Xibing,YIN Zhiqiang,et al.Effects of axial pressure and number of cyclic impacts on dynamic mechanical characteristics of sandstone[J].Journal of China Coal Society,2012,37(6):923-930.
[13] 金解放,李夕兵,钟海兵,等.三维静载与循环冲击组合作用下砂岩动态力学特性研究[J].岩石力学与工程学报,2013,32(7):1358-1372.
JIN Jiefang,LI Xibing,ZHONG Haibing,et al.Study of dynamic mechanical characteristic of sandstone subjected to three-dimensional coupled static-cyclic impact loadings[J].Chinese Journal of Rock Mechanics and Engineering,2013,32(7):1358-1372.
[14] 吕晓聪,许金余,葛洪海,等.围压对砂岩动态冲击力学性能的影响[J].岩石力学与工程学报,2010,29(1):193-201.
LÜ Xiaocong,XU Jinyu,GE Honghai,et al.Effects of confining pressure on mechanical behaviors of sandstone under dynamic impact loads[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(1):193-201.
[15] LI Xibing,TAO Ming,WU Chengqing,et al.Spalling strength of rock under different static pre-confining pressures[J].International Journal of Impact Engineering,2017,99:69-74.
[16] 李夕兵,宫凤强,ZHAO J,等.一维动静组合加载下岩石冲击破坏试验研究[J].岩石力学与工程学报,2010,29(2):251-260.
LI Xibing,GONG Fengqiang,ZHAO J,et al.Test study of impact failure of rock subjected to one-dimensional coupled static and dynamic loads[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(2):251-260.
[17] 尤业超,李二兵,谭跃虎,等.基于能量耗散原理的盐岩动力特性及破坏特征分析[J].岩石力学与工程学报,2017,36(4):843-851.
YOU Yechao,LI Erbing,TAN Yuehu,et al.Analysis on dynamic properties and failure characteristics of salt rock based on energy dissipation principle[J].Chinese Journal of Rock Mechanics and Engineering,2017,36(4):843-851.
[18] 白羽,朱万成,魏晨慧,等.不同地应力条件下双孔爆破的数值模拟[J].岩土力学,2013,34(S1):466-471.
BAI Yu,ZHU Wancheng,WEI ChenHui,et al.Numerical simulation on two-hole blasting under different in-situ stress conditions[J].Rock and Soil Mechanics,2013,34(S1):466-471.
[19] 范勇,江璐,卢文波,等.圆形隧洞爆破荷载与瞬态卸荷作用围岩应变能效应研究[J].岩石力学与工程学报,2017,36(8):1855-1866.
FAN Yong,JIANG Lu,LU Wenbo,et al.Strain energy characteristics of surrounding rock under blasting load and transient release of geostress during excavation of circular tunnel[J].Chinese Journal of Rock Mechanics and Engineering,2017,36(8):1855-1866.
[20] 李夕兵,姚金蕊,杜坤.高地应力硬岩矿山诱导致裂非爆连续开采初探——以开阳磷矿为例[J].岩石力学与工程学报,2013,32(6):1101-1111.
LI Xibing,YAO Jinrui,DU Kun.Preliminary study for induced fracture and non-explosive continuous mining in high-geostress hard rock mine-a case study of Kaiyang phosphate mine[J].Chinese Journal of Rock Mechanics and Engineering,2013,32(6):1101-1111.
[21] DOU Linming,MU Zonglong,LI Zhenlei,et al.Research progress of monitoring,forecasting,and prevention of rockburst in underground coal mining in China[J].International Journal of Coal Science & Technology,2014,1(3):278-288.
[22] XU Jialin,XUAN Dayang,HE Changchun.Innovative backfilling longwall panel layout for better subsidence control effect-separating adjacent subcritical panels with pillars[J].International Journal of Coal Science & Technology,2014,1(3):297-305.
[23] 刘少虹,毛德兵,齐庆新,等.动静加载下组合煤岩的应力波传播机制与能量耗散[J].煤炭学报,2014,39(S1):15-22.
LIU Shaohong,MAO Debing,QI Qingxin,et al.Under static loading stress wave propagation mechanism and energy dissipation in compound coal-rock[J].Journal of China Coal Society,2014,39(S1):15-22.
[24] 李新平,赵航,罗忆,等.深部裂隙岩体中弹性波传播与衰减规律试验研究[J].岩石力学与工程学报,2015,34(11):2319-2326.
LI Xinping,ZHAO Hang,LUO Yi,et al.Experimental study of propagation and attenuation of elastic wave in deep rock mass with joints[J].Chinese Journal of Rock Mechanics and Engineering,2015,34(11):2319-2326.
[25] 金解放,程昀,昌晓旭,等.轴向静载对红砂岩中应力波传播特性的影响试验研究[J].岩石力学与工程学报,2017,36(8):1939-1950.
JIN Jiefang,CHENG Yun,CHANG Xiaoxu,et al.Experimental study on stress wave propagation characteristics in red sandstone under axial static stress[J].Chinese Journal of Rock Mechanics and Engineering,2017,36(8):1939-1950.
[26] FAN L F,SUN H Y.Seismic wave propagation through an in-situ stressed rock mass[J].Journal of Applied Geophysics,2015,121:13-20.
[27] 王礼立.应力波基础[M].北京:国防工业出版社,2005.
[28] 孟召平,张吉昌,JOACHIM Tiedemann.煤系岩石物理力学参数与声波速度之间的关系[J].地球物理学报,2006,49(5):1505-1510.
MENG Zhaoping,ZHANG Jichang,JOACHIM Tiedemann.Relationship between physical and mechanical parameters and acoustic wave velocity of coal measures rocks[J].Chinese Journal of Geophysics,2006,49(5):1505-1510.