移动阅读
尹光志1,2，马 波1,2，刘 超1,2，李铭辉1,2，鲁 俊1,2，尹思禹1,2
(1.重庆大学 煤矿灾害动力学与控制国家重点实验室，重庆 400030; 2.重庆大学 资源及环境科学学院，重庆 400030)
摘 要:为了更准确地认识真三轴应力条件下加卸荷速率对岩石力学特性与能量特征的影响规律，利用自主研发的“多功能真三轴流固耦合试验系统”开展了砂岩真三轴加卸荷力学特性试验，实现了最小主应力方向上的单面卸荷，模拟实际围岩应力演化过程。试验结果表明：随着卸荷速率的增大，砂岩破坏时的最大主应力、最大主应变、最小主应变和体积应变均减小、中间主应变增大，扩容起始点提前，岩样破坏模式逐渐由剪切破坏转为张拉破裂，且张性裂纹多集中于卸荷面附近。加载速率的增大，砂岩破坏时的最大主应力、最大主应变、最小主应变和体积应变增大，扩容起始点滞后，岩样破坏模式逐渐由张剪破坏转向剪切破坏，产生非贯通性裂纹。引入应变偏应力柔量分析不同加卸荷速率下砂岩变形规律，最小主应变和体积应变的偏应力敏感性与卸荷速率呈正相关，最大主应变的偏应力敏感性与加载速率呈正相关。此外，岩石在峰值应力前能量演化有明显的阶段性，峰前吸收的能量大多以可释放弹性应变能的形式存储，耗散能在峰后超过弹性应变能。耗散能比例Ud/U随着最大主应变的增加呈现出先增后降再增的趋势，峰值应力时Ud/U随着卸荷速率的增大而减小，随着加载速率的增大而增大。达到峰值应力时，岩石吸收的总能量U、弹性应变能Ue、耗散能Ud和相应的应变能增量与时间间隔的比值u均随着卸荷速率的增大而减小，随着加荷速率的增大而增大。
关键词:真三轴应力;加卸荷速率;力学特性;能量特征
中图分类号:TD313
文献标志码:A
文章编号:0253-9993(2019)02-0454-09
收稿日期:2018-04-03
修回日期:2018-05-07
责任编辑:常 琛
基金项目:国家自然科学基金资助项目(51434003,51374256);国家科技重大专项资助项目(2016ZX05044002)
作者简介:尹光志(1962—)，男，四川西昌人，教授，博士生导师。E-mail:gzyin@cqu.edu.cn
移动阅读
尹光志，马波，刘超，等.真三轴应力条件下加卸荷速率对砂岩力学特性与能量特征的影响[J].煤炭学报,2019,44(2):454-462.doi:10.13225/j.cnki.jccs.2018.0438
YIN Guangzhi，MA Bo，LIU Chao，et al.Effect of loading and unloading rates on mechanical properties and energy characteristics of sandstone under true triaxial stress[J].Journal of China Coal Society,2019,44(2):454-462.doi:10.13225/j.cnki.jccs.2018.0438
YIN Guangzhi1,2，MA Bo1,2，LIU Chao1,2，LI Minghui1,2，LU Jun1,2，YIN Siyu1,2
(1.State Key Laboratory of Coal Mine Disaster Dynamics and Control,Chongqing University,Chongqing 400030,China; 2.College of Resources and Environmental Sciences,Chongqing University,Chongqing 400030,China)
Abstract:In order to understand exactly the effect of loading and unloading rates on the mechanical properties and energy characteristics of rock under true triaxial stress conditions,a self-developed true triaxial fluid-solid coupling experiment system was applied to investigate the mechanical properties of sandstone under different true triaxial loading-unloading stress paths.During the tests one-side platen was unloaded in the direction of the minimum principal stress to simulate the actual stress evolution of surrounding rock.The results indicate that with the increase of the unloading rates,the maximum principal stress,the maximum principal strain,the minimum principal strain and the volume strain of the sandstone at peak strength are all decreased,the intermediate principal strain is increased,and the volume expansion point is advanced.The failure mode of rock sample gradually changes from shear to tensile,and the tensile cracks are mostly concentrated near the unloading surface.As the loading rate increases,the maximum principal stress,the maximum principal strain,the minimum principal strain and the volume strain increase when the sandstone fails.The volume expansion point gradually lags,and the fracture pattern of rock sample changes from tension-shear to shear,and the non-penetrating crack appears.By introducing a description variable presented as strain-deviatoric stress compliance,the deformation laws of sandstone specimens under the different loading and unloading rates were analyzed.The deviatoric stress sensitivity of the minimum principal strain and the volume strain is positively correlated with the unloading rates.The deviatoric stress sensitivity of the maximum principal strain is positively correlated with the loading rates.Additionally,the energy evolution of rock before peak stress can be divided into obvious different stages,and the energy absorbed before the peak is mostly stored in the form of the elastic strain energy,and the dissipated energy exceeds the elastic strain energy after the peak.The dissipated energy ratio Ud/U tends to increase first,then decrease,and finally increase again with the increase of the maximum principal strain.The rates of Ud/U at peak strength decrease with the increase of unloading rates and increase with the increase of loading rates.When approaching the peak stress,the absorbed total energy U,the elastic strain energy Ue,the dissipated energy Ud and the corresponding ratios of strain energy increments to time intervals decrease with the increase of unloading rates and increase with the increase of loading rates.
Key words:true triaxial stress;loading and unloading rates;mechanical property;energy characteristics
近年来，矿井开采、水利工程、硐室开挖以及地质钻探等地下工程正逐步向深部延伸[1]。随着埋深的增加，地下工程的地质环境更加复杂，这些内外环境作用特点可概括为“三高一扰动”[2]。由于地质构造作用，地层中岩石常处于三向不等压状态(σ1>σ2>σ3)。因此，常规岩石力学试验(σ1>σ2=σ3)无法研究真实应力状态下的岩石力学特性。此外，由于地下工程开挖的扰动作用，围岩应力场重新分布，具体表现为围岩的切向应力升高，径向应力降低[3]。地下工程施工中常通过减慢开挖速率，减小开挖进尺来降低岩体失稳发生的风险，其本质是调整开挖引起的围岩应力加卸荷速率的大小，以降低岩体失稳与岩爆发生的可能性[4]。可见，岩体的力学特性和能量特征与加卸荷速率有密切关系。因此，采用真三轴加卸荷试验模拟地下硐室开挖过程中的围岩应力路径，可更真实地反映地下岩体的实际情况，得出更为符合实际的结果。
目前，已有大量学者研究了加卸荷速率对岩石力学性质的影响。黄润秋等[5]对大理岩在不同卸荷速率下的力学特性进行了试验研究，指出卸荷速率对锦屏大理岩的变形特征、断裂特征和强度特征有较显著的影响。谢和平等[6-7]利用常规三轴加卸载试验进行了3种不同开采方式(不同加卸荷速率比)下原煤力学特性研究，结果表明不同开采方式下煤岩力学特性有显著差异。邱士利等[8]进行了不同卸荷速率下的三轴卸围压试验，对大理岩的变形破裂特征、体积扩容特征以及强度变化规律进行了较详细地研究。何满潮等[4]基于真三轴岩爆试验系统，对北山花岗岩进行三向六面加荷，然后单面以4种不同速率突然卸载的试验方法来进行研究，找到了卸载速率对岩爆的影响机制。从能量角度开展岩石破坏研究方面。LIU等[9]以能量耗散为桥梁定义了损伤变量，计算了泥砂岩和粉砂岩在循环加卸载条件下的损伤演化方程。张黎明、许国安、从宇等[10-12]分析了单轴试验、常规三轴试验和加卸载试验条件下岩石破坏过程的能量转化特征，探讨应力路径对能量演化的影响规律。吕有厂等[13]得出恒定轴压、卸载围压试验过程中煤岩的能量耗散与卸围压速率有关，且含瓦斯煤岩的能量耗散随着卸围压速率的增大而减小。苏国韶等[14-15]利用自主研发的真三轴岩爆试验系统，进行了不同加荷、卸荷速率下的单面临空试验，探讨不同支护力失效、不同失效时机及不同失效速率对岩爆破坏特征的影响。
以上研究成果对于正确认识加卸荷条件下岩石力学特性与能量特征具有重要的意义，但由于实验设备条件的限制，前人大多是基于常规三轴试验所进行的岩石加卸荷研究，鲜有最小主应力方向上单面变速率卸荷试验报道。鉴于此，本文利用自主研发的多功能真三轴流固耦合试验系统研究了单面卸荷条件下不同加荷、卸荷速率对砂岩力学特性与能量特征的影响。研究成果可为制定硐室的开挖与支护方案，预测围岩的稳定性提供借鉴。
试验采用自主研发的“多功能真三轴流固耦合试验系统”[16]进行，如图1所示。该装置由框架式机架、真三轴压力室、加荷系统、内密封渗流系统、数据测量与采集系统及声发射测试系统等组成。可实现多种复杂应力路径下(单向、双向、三向应力状态下)岩石力学特性与渗透规律试验研究。
图1 多功能真三轴流固耦合试验系统
Fig.1 True triaxial fluid-solid coupling experiment system
试验所用砂岩取自重庆市北碚地区，视密度为2 260 kg/m3，泊松比ν =0.17，平均单轴抗压强度为σc=61 MPa。其主要矿物成分为长石和石英，该砂岩均质度好，离散性较小，呈灰青色，表面无明显节理、裂隙。用切割机将岩石切割成100 mm×100 mm×100 mm的正方体试件，然后利用磨床进行精加工，保证其端面不平行度和不垂直度均小于0.05 mm。
为研究不同加荷、卸荷速率下的砂岩力学特性及能量特征，进行了恒定加荷速率变卸荷速率和恒定卸荷速率变加荷速率两组试验，分别称为A组和B组。具体试验条件见表1。每个速率水平试验独立重复3次，以降低试验结果的离散性。试验步骤如下:
(1)初始应力加荷阶段。以力控制方式(2 kN/s)同步加荷三向应力至静水压应力σ1=σ2=σ3=40 MPa。保持最小主应力σ3(Z向)不变，以2 kN/s的速率同步增加最大主应力σ1(Y向)和中间主应力σ2(X向)到60 MPa。保持σ1,σ2不变，增加σ1到80 MPa。
(2)加卸荷阶段。以位移控制方式增加σ1，同时以力控制方式单面卸σ3，并保持卸荷面对面加荷压头的位移不变，直至砂岩试样破坏，停止试验。加卸荷应力路径如图2所示。
表1 不同加卸荷速率试验方案
Table 1 Experimental schemes of different loading and unloading rates
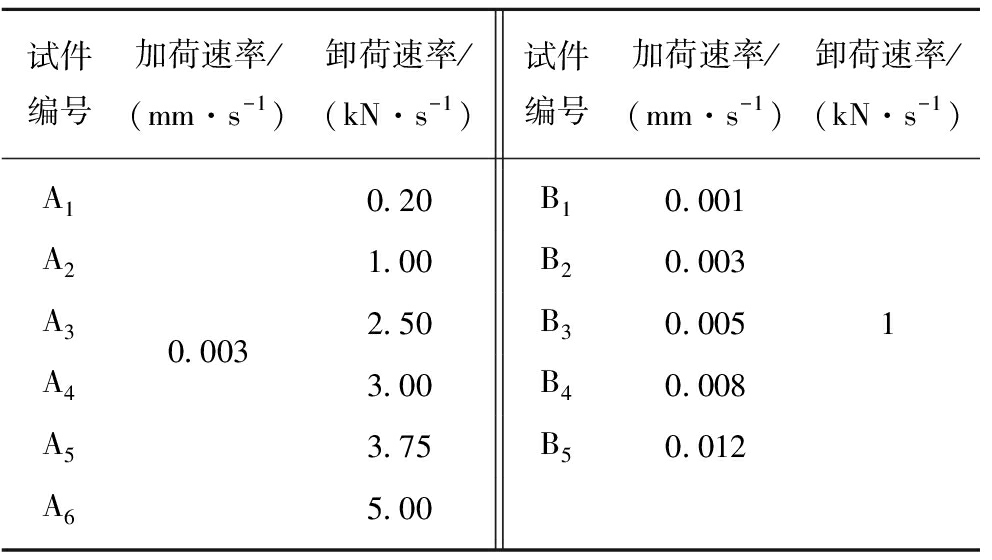
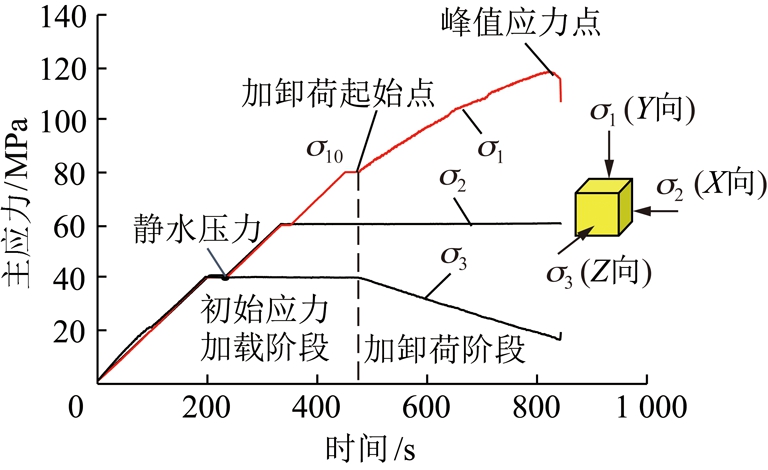
图2 加卸荷应力路径
Fig.2 Paths of stress loading and unloading
以加卸荷起始点应变作为应变测量的参考基点，不同卸荷速率下岩样加卸荷阶段应力-应变曲线如图3所示。
图3 不同卸荷速率下砂岩应力-应变曲线
Fig.3 Stress-strain curves of sandstone specimens under different unloading rates
由图3可见，岩石在不同卸荷速率条件下应变与峰值应力呈一致性规律。同一加荷速率条件下，随着卸荷速率增加，最大主应变随着最大主应力的增加逐渐变缓，砂岩破坏时的峰值应力降低，对应的最大主应变也随之减小。究其原因，在同一位移加荷速率条件下，Y向应变随时间增加的幅度大致相同，卸荷速率越快，Z向力急剧减小，使得砂岩的承载变形能力降低，导致其峰值应力减小。因此，岩石破坏时Y方向应变也较小。与此相反，在最小主应力方向上，随着卸荷速率的增加，Z向力急剧减小，使得岩石发生破坏时Z向膨胀量逐渐增大。中间主应力在加卸荷过程中保持不变，由于泊松效应，Y向压缩作用导致X向和Z向膨胀，Z向卸荷面作为主要的膨胀面，X向膨胀量随着卸荷速率的增大逐渐减小，且X向膨胀量小于Z向膨胀量。此外，不同卸荷速率下岩石破坏时均发生扩容现象，但扩容的起点不一样。卸荷速率较低时，岩石在加卸荷初期阶段逐渐被压缩，接近峰值应力时，岩石出现扩容现象，表现出明显的应变硬化特征。卸荷速率较高时，岩石在加卸荷初始阶段即发生扩容现象，接近峰值应力时，扩容速率加快，扩容量增大，岩石的承载能力迅速降低，表现出明显的脆性破坏特征。此时，Z向卸荷作用对岩石的扩容起主导作用。
砂岩在不同卸荷速率条件下的破坏形态如图4所示，本文以卸荷速率0.2,1和3.75 kN/s时的试验结果为例，以说明不同卸荷速率下砂岩宏观破坏形态上的差异。可以看出，砂岩的破坏面均沿着垂直最小主应力方向发育形成，但裂纹发育程度与破坏模式有明显的差异。卸荷速率为0.2 kN/s时，砂岩主要是以宏观剪切面的贯通形成而失稳破坏，裂纹发育较为充分。1 kN/s和3.75 kN/s卸荷速率下砂岩在σ1和σ2方向加荷面上形成多条近垂直于卸荷方向的张拉裂纹，且裂纹多集中于卸荷面附近，远离卸荷面的裂纹则呈现出张剪复合特征，最终劈裂形成岩石板块。不同卸荷速率下的砂岩破坏时裂纹的成分有差别，高卸荷速率有利于张性裂纹的形成，导致砂岩产生的宏观破坏形态有所差异。表2为不同卸荷速率下砂岩的特征力学参数。
不同加荷速率下岩样应力-应变曲线如图5所示。可见，砂岩在不同加荷速率条件下变形过程基本一致。随着加荷速率的增加，砂岩破坏时的峰值应力明显增大，相应的最大主应变也随之增大。同一卸荷速率条件下，加荷速率越大，岩石内部的裂隙发育时间相对缩短，裂纹扩展滞后于载荷的增加，试件在破坏时Y向能承受更大的压缩作用，峰值应力也增加到更高的水平。随着加荷速率的增加，岩石发生破坏时Z向膨胀量减小。此外，加荷速率为0.001 mm/s时，岩石在加卸荷初始阶段即发生扩容，无明显的扩容起始点;加荷速率较高时，加卸荷初始阶段岩石逐渐被压缩，进入屈服阶段后发生扩容，扩容点随着加荷速率的增大逐渐滞后，岩石发生破坏时，扩容特征越不明显。此时，Y向的压缩作用对岩石的扩容占主导作用。
图4 不同卸荷速率下砂岩破坏形态
Fig.4 Failure modes of sandstone specimens under different unloading rates
表2 不同卸荷速率下砂岩特征力学参数
Table 2 Mechanical parameters of sandstone specimens under different unloading rates
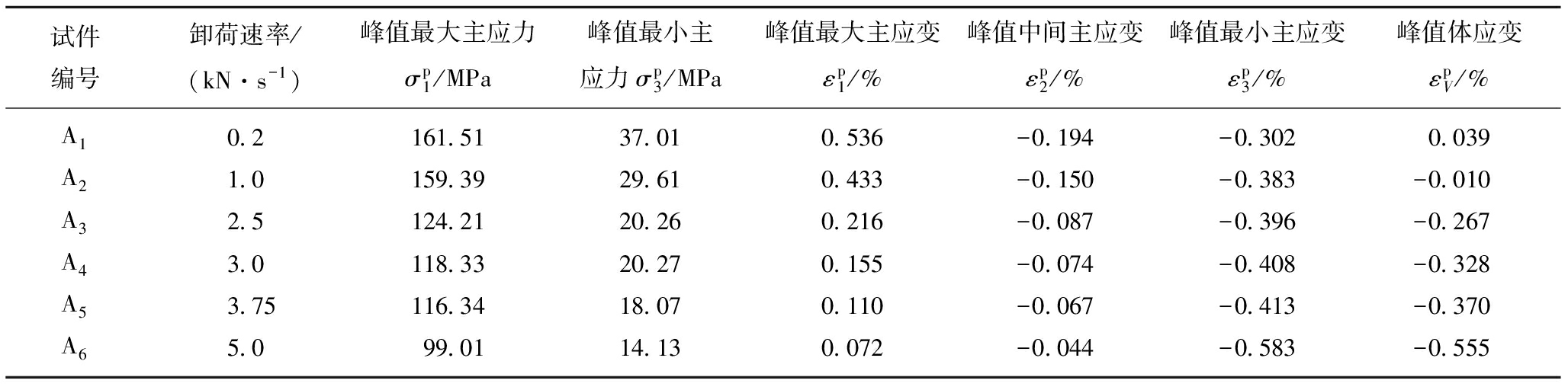
图5 不同加荷速率下砂岩应力-应变曲线
Fig.5 Stress-strain curves of sandstone specimens under different loading rates
不同加荷速率下砂岩的破坏形态如图6所示。本文以加荷速率0.001,0.003和0.008 mm/s时的试验结果为例，以说明不同加荷速率下砂岩在宏观破坏形态上的差异。不同加荷速率下砂岩的破坏面均沿着垂直最小主应力方向形成，但裂纹的发育程度与破坏形式有明显的差异。加荷速率为0.001和0.003 mm/s时，砂岩主要以张剪破坏为主，在卸荷面附近伴有张拉裂纹产生，而远离卸荷面的裂纹则呈张剪复合特征，0.008 mm/s加荷速率下的砂岩主要发生剪切破坏。加荷速率越大时，恒定的最小主应力卸荷速率引起的对砂岩强度与变形影响效果变得不明显，也就是卸荷面效应减弱，砂岩以产生剪切裂纹为主。表3为不同加荷速率下砂岩的特征力学参数。
加卸荷条件下，随着σ1增大和σ3减小引起的砂岩破坏，实质上是偏应力q增大导致其发生破坏。偏应力计算公式如下:
(1)
为了分析砂岩加卸荷过程中偏应力对应变的影响效果，本文提出了一个新的变量——应变偏应力柔量
是指加卸荷起始点和峰值应力点之间因σ1增大和σ3减小而引起的应变增量Δεi的绝对值与偏应力增量Δq之比，可表示为
(2)
式中,Δεi(i=1，2，3，V)分别表示最大主应变、中间主应变、最小主应变和体积应变增量。
应变偏应力柔量
是表示加卸荷过程中增加单位偏应力时对应各应变增量变化快慢的物理量，能更好地反映加卸荷过程中偏应力变化对变形的影响效应，也可以表征岩石内部结构对应力状态变化过程的响应速度
越大，单位偏应力增量下某方向变形响应越敏感。图7给出了各主应变和体积应变偏应力柔量与加卸荷速率的关系。可以看出，A组与B组的试验结果有较为明显的差异。A组岩样随着卸荷速率的增加，砂岩破坏时广义剪应力增量Δq逐渐减小，
和
呈增大趋势，
和
则呈减小趋势，且变化较缓。A组砂岩的最小主应变主导体应变的变化趋势，因此和的变化趋势与大小都较为接近。5 kN/s时的最小主应变偏应力柔量是0.2和1 kN/s时的3.0～4.0倍，说明高卸荷速率下最小主应变和体积应变的偏应力敏感性升高，而最大主应变和中间主应变的偏应力敏感性降低。B组岩样随着加荷速率的增大，砂岩破坏时广义剪应力增量Δq逐渐增大，和呈减小趋势，逐渐增大，而在一定范围内小幅度波动。B组砂岩的最大主应变主导体应变的变化趋势，最大主应变随加荷速率的增加对偏应力的敏感性升高，但变化幅度不大，0.012 mm/s时的最大主应变偏应力柔量是0.001和0.003 mm/s时的1.5～2.0倍，和的变化幅度相对较大。对比图7(a)和(b)均有
说明此试验条件下加卸荷速率对中间主应变的影响要小于对最小主应变的影响，即最小主应变在加卸荷过程中相对更敏感。
图6 不同加荷速率下砂岩破坏形态
Fig.6 Failure modes of sandstone specimens under different loading rates
表3 不同加荷速率下砂岩特征力学参数
Table 3 Mechanical parameters of sandstone specimens under different loading rates
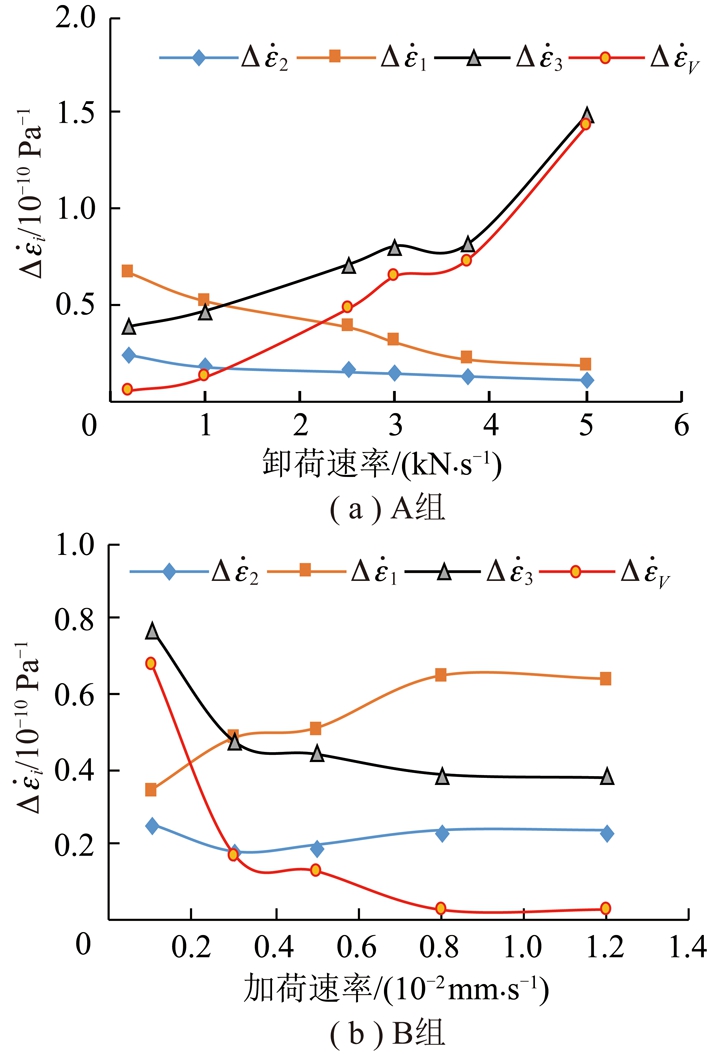
图7 砂岩破坏时应变偏应力柔量与加卸荷速率关系
Fig.7 Relationships between strain-deviatoric stress compliance and loading or unloading rates when sandstone failure
对于砂岩真三轴加卸荷试验，将其视为一个封闭系统，在试验过程中系统与外界没有热交换，外力做的功即为试件吸收的总能量U。总能量U分两部分组成，即单位体积所储存的可释放弹性应变能Ue和用于形成岩样内部损伤以及塑性变形的耗散能Ud。其中[17]:
U=Ue+Ud(3)
U=
σ1dε1+
σ2dε2+
σ3dε3+U0(4)
(5)
为了简化计算，将初始应力加荷阶段中静水压力做的功视为恒定值，全部以可释放弹性应变能的形式存储起来。式中:U 0为初始应力加荷阶段静水压力对岩石所做的功，因此[18]:
(6)
其中，
为平均卸荷弹性模量，
为平均泊松比。一般取初始应力加荷阶段弹性模量E0和ν [19]，并假定加卸荷过程中弹性常数保持不变。将静水压峰值点
作为能量计算的参考点。初始应力加荷阶段，三向应力对岩样做正功;加卸荷应力阶段，最大主应力对岩样做正功，最小主应力方向，卸荷面上的应力对岩样做负功，卸荷面对面上的应力不做功(位置保持不动)。本文对岩样的能量分析均为单位体积能量。
本文仅分析岩石峰前加卸荷能量特征。岩石在受力过程中，从微破裂出现、扩展直至贯通整个过程中都伴随着能量的转化。岩石在孔隙、裂隙压密阶段(oa)以及进入线弹性阶段(ab)所吸收的能量大都以可释放弹性应变能的形式存储，耗散能很小;进入微破裂稳定发展阶段(bc)，弹性应变能增速变缓，耗散能开始增加;岩石屈服后(c点)，弹性应变能基本不变，耗散能增加明显，但此时弹性应变能仍大于耗散能，微破裂不断发展;至峰值应力时(d点)，弹性应变能达到最大值，而后，弹性应变能逐渐释放，耗散能急剧增大，裂纹贯通，岩石发生破坏。A组与B组加卸荷试验过程的能量变化曲线规律相似，图8为试样B1加卸荷过程的能量变化曲线。
图8 砂岩试样B1应力和应变能与应变的关系曲线
Fig.8 Variation of stress and strain energy with strain for sandstone specimen B1
砂岩破坏过程中伴随着能量耗散，耗散能量主要用于岩石内部裂纹的萌生与扩展，是引起岩石损伤的原因。本文定义耗散能比例为岩石变形破坏过程中累积耗散能Ud与岩石吸收的总能量U的比值。以A组为例，图9为A组试样耗散能比例随最大主应变变化的关系曲线。由图9可以看出，岩石的耗散能比例随最大主应变的增加呈现出先增大后减小，然后再变大的规律，大致分为3段。oa段处于压密变形阶段，耗散能量用于岩石原生裂隙的压密与颗粒之间的咬合，耗散能比例逐渐增大。ab段处于弹性变形阶段，这个阶段的能量耗散较少，主要以可释放弹性应变能的形式存储，耗散能比例逐渐降低。bd段为微破裂稳定发展阶段至峰值应力阶段，裂纹逐渐扩展，耗散能比例随应变增加稳定增长，岩石内部损伤加剧。随着卸荷速率的增加，裂隙的传播和应力的转移不充分，大量的弹性能以颗粒弹射、小块剥离的形式释放，岩石在破坏时所释放的能量越大。因此，砂岩破坏时可释放弹性应变能占总能量的比例越高。
图9 A组砂岩耗散能比例与应变关系曲线
Fig.9 Variation of proportion of dissipated energy to total energy with strain for group A sandstone specimens
从初期弹性应变能的集聚到后期释放，在这个过程中必然存在一个最大值，即峰值应力点处对应的弹性应变能，称为储能极限
定义加卸荷起始点至峰值应力点之间的应变能增量ΔU与该段时间Δt之比为加卸荷过程中应变能转化速率u [20]，即
(7)
图10为岩样峰值应力处应变能和应变能转化速率与加卸荷速率的关系曲线。卸荷速率越大，岩石在峰值应力点处吸收的总能量U、弹性应变能Ue和耗散能Ud越小。相反，随着加荷速率增大，岩石在峰值应力点处的U，Ue和Ud越大。究其原因，随着卸荷速率增大，岩石发生破坏时峰值应力越小，故峰值弹性应变能越小;最大主应变越小，压头对试样输入的能量越少，即U也越小。同理，加荷速率越大，岩石破坏时峰值应力越大，对应的弹性应变能Ue越大，最大主应力对试件输入的能量也越多，岩石主要发生剪切破坏，剪切裂纹的产生需要消耗大量能量，导致岩石的耗散能比例也越高。由图10还可以看出，应变能转化速率与应变能随着加卸荷速率的增大变化趋势较为一致。峰前卸荷速率越大，U，Ue和Ud的转化速率越低。峰前加荷速率越大，U，Ue和Ud的转化速率越大。在地下硐室开挖过程中减慢开挖速率(卸荷速率)，有利于提高岩体的承载能力，控制围岩的变形量，提高围岩的稳定性;另一方面，可以有效地降低岩石破坏时释放的能量，保障施工人员的生命安全与降低财产设备的损失。
图10 砂岩峰值时应变能-加卸荷速率和加卸荷速率-应变能转化率关系曲线
Fig.10 Variation of strain energy and conversion rates with loading or unloading rates for sandstone at peak strength
(1)真三轴加卸荷应力条件下，随着卸荷速率的增大，砂岩破坏时的最大主应力、最大主应变和最小主应变均减小，扩容特征逐渐明显，扩容量增大。岩样破坏模式逐渐由剪切破坏转为张拉破裂，且张性裂纹多集中于卸荷面附近;随着加荷速率的增大，砂岩破坏时的最大主应力、最大主应变和最小主应变均增大，扩容点逐渐滞后，扩容量减小。岩样在低加荷速率下主要以张剪破坏为主，在高加荷速率下以产生剪切裂纹为主。
(2)引入应变偏应力柔量分析真三轴加卸荷过程中砂岩的变形规律。随着卸荷速率的增大，和
呈增大趋势，和则呈减小趋势，且变化较缓，最小主应变和体积应变的偏应力敏感性升高，而最大主应变和中间主应变的偏应力敏感性降低;随着加荷速率的增大，和呈减小趋势，逐渐增大，最大主应变的偏应力敏感性升高，但变化幅度不大，和的变化幅度相对较大;最小主应变在加卸荷过程中较中间主应变相对更敏感。
(3)岩样在峰值应力前能量演化过程可大致分为4个阶段，与峰前应力-应变曲线对应较好。峰前耗散能比例随最大主应变的增加呈现出先增后降再增的趋势，且岩石破坏时的耗散能比例随卸荷速率的增大而减小。
(4)岩样在峰值应力点处吸收的总能量U、弹性应变能Ue和耗散能Ud随卸荷速率的增大而减小，相应的应变能转化速率也越小。随着加荷速率的增大则相反。加卸荷速率对岩石的力学特性与能量演化特征影响表现出明显的差异性。
参考文献
[1] 谢和平,周宏伟,薛东杰,等.煤炭深部开采与极限开采深度的研究与思考[J].煤炭学报,2012,37(4):535-542.
XIE Heping,ZHOU Hongwei,XUE Dongjie,et al.Research and consideration on deep coal mining and critical mining depth[J].Journal of China Coal Society,2012,37(4):535-542.
[2] 何满潮,钱七虎.深部岩体力学基础[M].北京:科学出版社,2010.
[3] 哈秋舲.岩石边坡工程与卸荷非线性岩石(体)力学[J].岩石力学与工程学报,1997,16(4):386-391.
HA Qiuling.Rock slope engineering and unloading nonlinear rock mass mechanics[J].Chinese Journal of Rock Mechanics and Engineering,1997,16(4):386-391.
[4] 何满潮,赵菲,杜帅,等.不同卸载速率下岩爆破坏特征试验分析[J].岩土力学,2014,35(10):2737-2747,2793.
HE Manchao,ZHAO Fei,DU Shuai,et al.Rockburst characteristics based on experimental tests under different unloading rates[J].Rock and Soil Mechanics,2014,35(10):2737-2747,2793.
[5] 黄润秋,黄达.高地应力条件下卸荷速率对锦屏大理岩力学特性影响规律试验研究[J].岩石力学与工程学报,2010,29(1):21-33.
HUANG Runqiu,HUANG Da.Experimental research on affection laws of unloading rates on mechanical properties of Jinping marble under high geostress[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(1):21-33.
[6] 谢和平,周宏伟,刘建锋,等.不同开采条件下采动力学行为研究[J].煤炭学报,2011,36(7):1067-1074.
XIE Heping,ZHOU Hongwei,LIU Jianfeng,et al.Mining-induced mechanical behavior in coal seams under different mining layouts[J].Journal of China Coal Society,2011,36(7):1067-1074.
[7] 谢和平,张泽天,高峰,等.不同开采方式下煤岩应力场-裂隙场-渗流场行为研究[J].煤炭学报,2016,41(10):2405-2417.
XIE Heping,ZHANG Zetian,GAO Feng,et al.Stress-frature-seepage field behavior of coal under different mining layouts[J].Journal of China Coal Society,2016,41(10):2405-2417.
[8] 邱士利,冯夏庭,张传庆,等.不同卸围压速率下深埋大理岩卸荷力学特性试验研究[J].岩石力学与工程学报,2010,29(9):1807-1817.
QIU Shili,FENG Xiating,ZHANG Chuanqing,et al.Experimental research on mechanical properties of deep-buried marble under different unloading rates of confining pressures[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(9):1807-1817.
[9] LIU X S,NING J G,TAN Y L,et al.Damage constitutive model based on energy dissipation for intact rock subjected to cyclic loading[J].International Journal of Rock Mechanics & Mining Sciences,2016,85:27-32.
[10] 张黎明,高速,王在泉,等.大理岩加卸荷破坏过程的能量演化特征分析[J].岩石力学与工程学报,2013,32(8):1572-1578.
ZHANG Liming,GAO Su,WANG Zaiquan,et al.Analysis of marble failure energy evolution under loading and unloading conditions[J].Chinese Journal of Rock Mechanics and Engineering,2013,32(8):1572-1578.
[11] 许国安,牛双建,靖洪文,等.砂岩加卸载条件下能耗特征试验研究[J].岩土力学,2011,32(12):3611-3617.
XU Guoan,NIU Shuangjian,JING Hongwen,et al.Experimental study of energy features of sandstone under loading and unloading[J].Rock and Soil Mechanics,2011,32(12):3611-3617.
[12] 丛宇,王在泉,郑颖人,等.不同卸荷路径下大理岩破坏过程能量演化规律[J].中南大学学报(自然科学版),2016,47(9):3140-3147.
CONG Yu,WANG Zaiquan,ZHENG Yingren,et al.Energy evolution principle of fracture propagation of marble with different unloading stress paths[J].Journal of Central South University (Science and Technology),2016,47(9):3140-3147.
[13] 吕有厂,秦虎.含瓦斯煤岩卸围压力学特性及能量耗散分析[J].煤炭学报,2012,37(9):1505-1510.
LÜ Youchang，QIN Hu.Investigation into mechanical responses and energy dissipation properties of coal containing methane to confinement unloading[J].Journal of China Coal Society,2012,37(9):1505-1510.
[14] 苏国韶,陈智勇,蒋剑青,等.不同加载速率下岩爆碎块耗能特征试验研究[J].岩土工程学报,2016,38(8):1481-1489.
SU Guoshao,CHEN Zhiyong,JIANG Jianqing,et al.Experimental study on energy dissipating characteristics of rockburst fragments under different loading rates[J].Chinese Journal of Geotechnical Engineering,2016,38(8):1481-1489.
[15] 苏国韶,莫金海,陈智勇,等.支护失效对岩爆弹射破坏影响的真三轴试验研究[J].岩土力学,2017,38(5):1243-1250.
SU Guoshao,MO Jinhai,CHEN Zhiyong,et al.True triaxial test study of the influence of support failure on rockburst ejection[J].Rock and Soil Mechanics,2017,38(5):1243-1250.
[16] 尹光志,李铭辉,许江,等.多功能真三轴流固耦合试验系统的研制与应用[J].岩石力学与工程学报,2015,34(12):2436-2445.
YIN Guangzhi,LI Minghui,XU Jiang,et al.A new multi-functional true triaxial fluid-solid coupling experiment system and its applications[J].Chinese Journal of Rock Mechanics and Engineering,2015,34(12):2436-2445.
[17] 谢和平,鞠杨,黎立云,等.岩体变形破坏过程的能量机制[J].岩石力学与工程学报,2008,27(9):1729-1740.
XIE Heping,JU Yang,LI Liyun,et al.Energy mechanism of deformation and failure of rock masses[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(9):1729-1740.
[18] 李天斌,陈子全,陈国庆,等.不同含水率作用下砂岩的能量机制研究[J].岩土力学,2015,36(S2):229-236.
LI Tianbin,CHEN Ziquan,CHEN Guoqing,et al.An experimental study of energy mechanism of sandstone with different moisture contents[J].Rock and Soil Mechanics,2015,36(S2):229-236.
[19] 黄达,黄润秋,张永兴.粗晶大理岩单轴压缩力学特性的静态加载速率效应及能量机制试验研究[J].岩石力学与工程学报,2012,31(2):245-255.
HUANG Da,HUANG Runqiu,ZHANG Yongxing.Experimental investigations on static loading rate effects on mechanical properties and energy mechanism of coarse crystal grain marble under uniaxial compression[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(2):245-255.
[20] HUANG D,LI Y R.Conversion of strain energy in triaxial unloading tests on marble[J].International Journal of Rock Mechanics & Mining Sciences,2014,66(1):160-168.