
移动阅读
杨 阳,李 明,秦大同,胡明辉,米玉泉
(重庆大学 机械传动国家重点实验室,重庆 400044)
摘 要:为解决采煤机截割部摇臂箱体变形导致传动系统失效的问题,提出了由多台电动机、耦合轮系和行星轮系构成的机电短程截割传动系统。耦合轮系汇集多台电机的动力,其动态性能影响系统的承载能力和使用寿命。分析了引起耦合轮系输入转速波动且不一致的原因,在输入转速波动且相位差恒定的情况下,通过仿真研究了输入转速不一致对耦合轮系动态特性的影响规律。机电短程传动系统中的制造装配误差、多台电机转速响应的差异等因素可使耦合轮系输入转速波动且不一致。输入转速波动且不一致使耦合轮系的动态啮合力出现低频波动,且各个传动路线中的动态啮合力的相位不同;随输入转速不一致程度的增加,动态啮合力波动幅度增加。动态啮合力的低频波动使得作用在主动齿轮上的载荷出现低频波动,影响主动齿轮的切向和径向振动加速度;输入转速不一致程度由0增加至0.005时,切向振动加速度增大11.89 m/s2,径向振动加速度增大7.07 m/s2,输入转速不一致对切向振动加速度的影响更大。进行了机电短程传动系统的动态特性实验,耦合轮系存在输入转速波动且不一致的现象,测得的耦合轮系输入轴振动加速度的时域特征与仿真结果的相近,振动加速度幅值谱的主要频率成分与仿真结果的相似,验证了仿真结果的合理性。
关键词:采煤机;机电短程截割传动系统;输入转速不一致;输入转速波动;动态特性
中图分类号:TD421.6
文献标志码:A
文章编号:0253-9993(2019)02-0628-11
收稿日期:2018-04-09
修回日期:2018-08-08
责任编辑:郭晓炜
基金项目:国家重点基础研究发展计划资助项目(2014CB046304)
作者简介:杨 阳(1958—),男,四川成都人,教授,博士。E-mail:yangyang@cqu.edu.cn
杨阳,李明,秦大同,等.输入转速不一致对机电短程截割传动耦合轮系动态特性的影响[J].煤炭学报,2019,44(2):628-638.doi:10.13225/j.cnki.jccs.2018.0459
YANG Yang,LI Ming,QIN Datong,et al.Effect of inconsistent input speed on dynamics of torque coupled gear set in electromechanical short-range cutting transmission of shearer[J].Journal of China Coal Society,2019,44(2):628-638.doi:10.13225/j.cnki.jccs.2018.0459
YANG Yang,LI Ming,QIN Datong,HU Minghui,MI Yuquan
(State Key Laboratory of Mechanical Transmissions,Chongqing University,Chongqing 400044,China)
Abstract:A compacted cutting powertrain consisting of multiple motors,a torque coupled gear train and a planetary gear train was proposed to avoid the influence of longwall shearers’ ranging arm deformation.Dynamic behavior of the torque coupled gear train affects the load carrying capacity and service life of the powertrain.Causes of inconsistent fluctuant input speeds in the torque coupled gear train were analyzed.Effects of the inconsistent input speeds on the dynamic behavior of the gear train were studied through simulating.Manufacturing and assembly errors in the powertrain and different responses from multiple motors can cause inconsistent fluctuant input speeds.Inconsistent fluctuant input speeds make the dynamic meshing forces in the torque coupled gear train to fluctuate.The phase of the dynamic meshing force of each transmission path is different from each other.The inconsistent input speeds also affect the pinion vibration acceleration in the torque coupled gear train.When the inconsistent degree of input speeds increases from 0 to 0.005,the tangential and radial vibration accelerations increase by 11.89 and 7.07 m/s2,respectively.The inconsistent input speeds have a greater impact on the tangential vibration acceleration.Some dynamic behaviors of the torque coupled gear train were verified by an experiment.There exist inconsistent fluctuant input speeds in the gear train.Features of the input shaft vibration acceleration acquired by the experiment are similar with those acquired by simulation in the time and frequency domains.
Key words:longwall shearer;electromechanical short-range cutting transmission;inconsistent input speed;input speed fluctuation;dynamic behavior
滚筒式采煤机是综采成套装备的重要组成部分,广泛应用于大型煤矿[1-2]。滚筒式采煤机截割部的摇臂与传动系统相互耦合,摇臂的变形会降低传动系统的承载能力、加速系统的失效。为提高截割部传动系统的承载能力和可靠性,提出了机电短程传动系统[3],由多台电机、耦合轮系和行星轮系构成。其中,耦合轮系是由N个主动齿轮和1个被动齿轮构成的定轴轮系,每个传动路线传递1/N的转矩,这使得机电短程传动系统具有紧凑的结构。可将机电短程传动系统布置于滚筒内部,避免摇臂箱体变形对传动系统的影响。但滚筒式采煤机可能工作于重载突变工况,而且,在机电短程传动系统中,耦合轮系的多个输入存在不一致的现象。这些因素可能使耦合轮系的动态性能恶化,影响机电短程传动系统的承载能力和使用寿命。因此有必要研究耦合轮系的动态特性。
SHU等[4-5]研究了脉冲负载的幅值、电机故障对机电短程传动系统动态特性和电机同步特性的影响。ZHANG等[6]研究了脉冲负载对耦合轮系输入齿轮和输出齿圈平移振动的影响。LI等[7-10]研究了输入转矩不一致、输入转速恒定且不一致、静态传递误差、齿隙、齿轮惯量、啮合刚度与阻尼、电机转子惯量、负载大小、主动齿轮数量对输出转速的影响;以及静态传递误差、齿隙、被动齿轮惯量、负载大小、齿面摩擦系数对齿轮平移振动速度的影响。SUN等[11]研究了负载波动对耦合轮系振动的影响。ZHANG等[12]研究了时变啮合刚度的频率、幅值和相位对耦合轮系稳定性的影响。WEI等[13-14]在负载稳定工况研究了耦合轮系齿轮的振动,以及轮系的均载性能。文献[15-19]研究了影响耦合轮系均载性能的因素。
耦合轮系输入转速不一致时,各个传动路线的状态不同。目前,在输入转速不一致对耦合轮系动态特性影响的研究方面,仅分析了输入转速不一致对输出转速的作用,而且各个输入转速为恒定值。然而,耦合轮系的输入转速波动且相位不同时,也将出现输入转速不一致现象,这种形式的输入转速不一致对轮系动态特性的影响尚未得到研究。
笔者以采煤机截割部机电短程传动系统为研究对象,分析了引起耦合轮系输入转速波动且不一致的原因;在输入转速波动且相位差恒定的情况下,研究了输入转速不一致对轮系动态特性的影响规律;通过实验验证了轮系的部分动态特性。为通过多电机同步控制提高机电短程截割传动系统的性能奠定基础。
基于MG300/700-WD型采煤机参数设计的机电短程传动系统如图1所示,动力源包括3台电机,传动系统包括两级减速器。第1级减速器为耦合轮系,由3个均布的主动齿轮和一个被动齿轮构成,有3个传动路线,耦合3台电机的动力。第2级减速器为行星轮系,采用3个行星轮,以行星架为输出元件。

图1 机电短程截割传动系统结构
Fig.1 Structure of short-range cutting transmission
1—电机;2—耦合轮系;3—行星轮系
耦合轮系和行星轮系各有3个传动路线,每个传动路线承担1/3的负载,可显著减小传动系统的体积,便于将其布置于滚筒内部。此外,动力源包含3台电机,每台电机的功率较小,电机转子的转动惯量较小,在调速过程中响应速度快。
使用三相异步电机,并且采用了直接转矩控制(Direct Torque Control,DTC)调节电机转速。DTC电机系统的结构如图2所示,系统包括整流器、逆变器、电机、DTC单元和转速控制器。

图2 DTC电机系统的结构示意
Fig.2 Schematic of DTC motor system
DTC电机具有调速功能,转速控制器根据电机实际转速n和目标转速n*之间的转速差产生目标电磁转矩![]() 单元根据目标电磁转矩
单元根据目标电磁转矩![]() 目标磁链
目标磁链![]() 母线电压Ub和电机定子电流iab,控制逆变器的开关状态,调节电机的输入电压,进而改变电机的定子磁链和电磁转矩,使电机实际转速跟踪目标转速。使用Simulink模型库中的DTC电机模型。
母线电压Ub和电机定子电流iab,控制逆变器的开关状态,调节电机的输入电压,进而改变电机的定子磁链和电磁转矩,使电机实际转速跟踪目标转速。使用Simulink模型库中的DTC电机模型。
采用建立在旋转正交坐标系(dq坐标系)中的电机动态模型,电机在dq坐标系中的动态等效电路如图3所示。
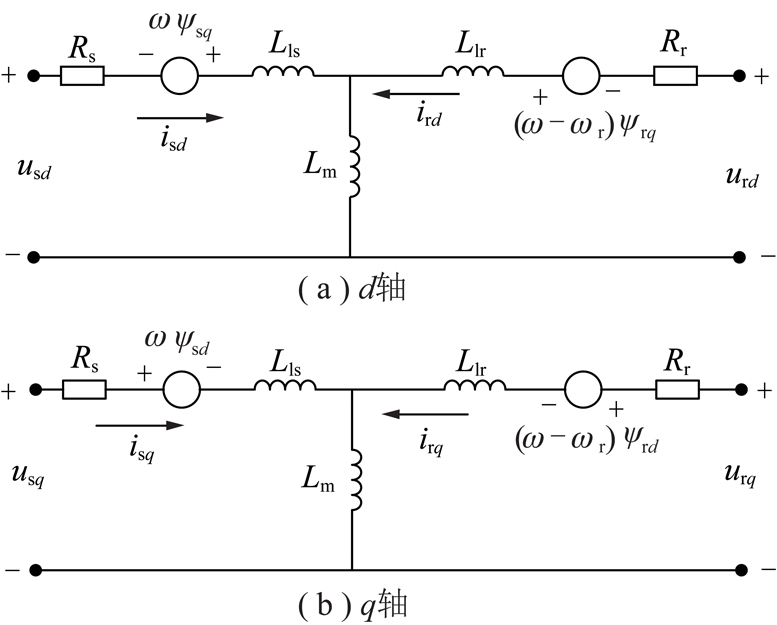
图3 电机的动态等效电路
Fig.3 Dynamic equivalent circuit of motor
在dq坐标系中,电动机的动态模型为

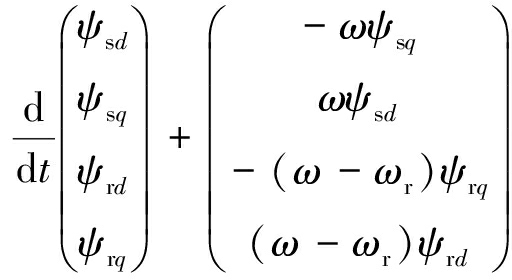 (1)
(1)
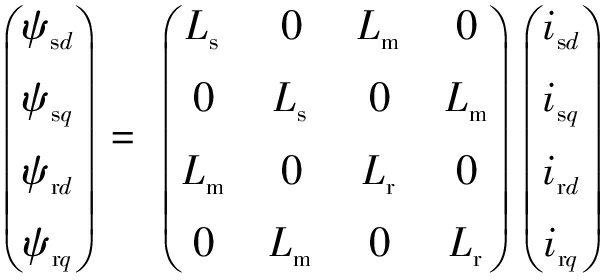 (2)
(2)
式中,Ls=Lls+Lm,Lr=Llr+Lm。
电机的电磁转矩为
Tm=1.5np(ψsdisq-ψsqisd)(3)
式中,usd,usq,urd和urq分别为d轴定子电压、q轴定子电压、d轴转子电压和q轴转子电压;Rs和Rr分别为定子和转子电阻;isd,isq,ird和irq分别为d轴定子电流、q轴定子电流、d轴转子电流和q轴转子电流;ψsd,ψsq,ψrd和ψrq分别为d轴定子磁链、q轴定子磁链、d轴转子磁链和q轴转子磁链;ω为dq坐标系相对于定子的旋转角速度;ωr为电角速度;Ls和Lr分别为定子和转子等效两相绕组的自感;Lm为定子与转子同轴等效绕组间的互感;Lls和Llr分别为定子和转子漏感;np为极对数。
文中研究采煤机截割部机电短程传动系统耦合轮系的动态特性,因此建立耦合轮系的平移扭转模型,将行星轮系及其之后的部件简化为等效转动惯量。耦合轮系输入输出轴的动力学模型如图4所示,轮系的动力学模型如图5所示。
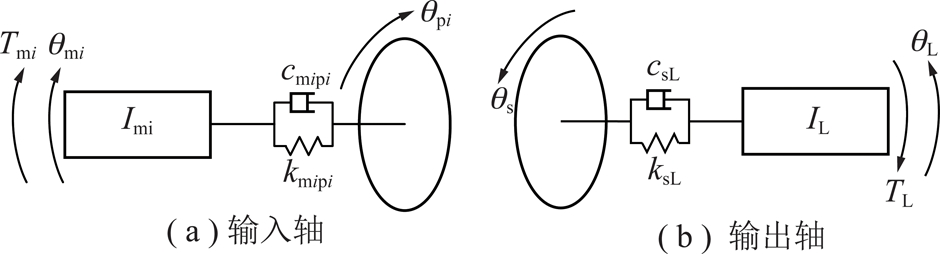
图4 耦合轮系输入输出轴的动力学模型
Fig.4 Dynamic models of input and output shafts of torque coupled gear train
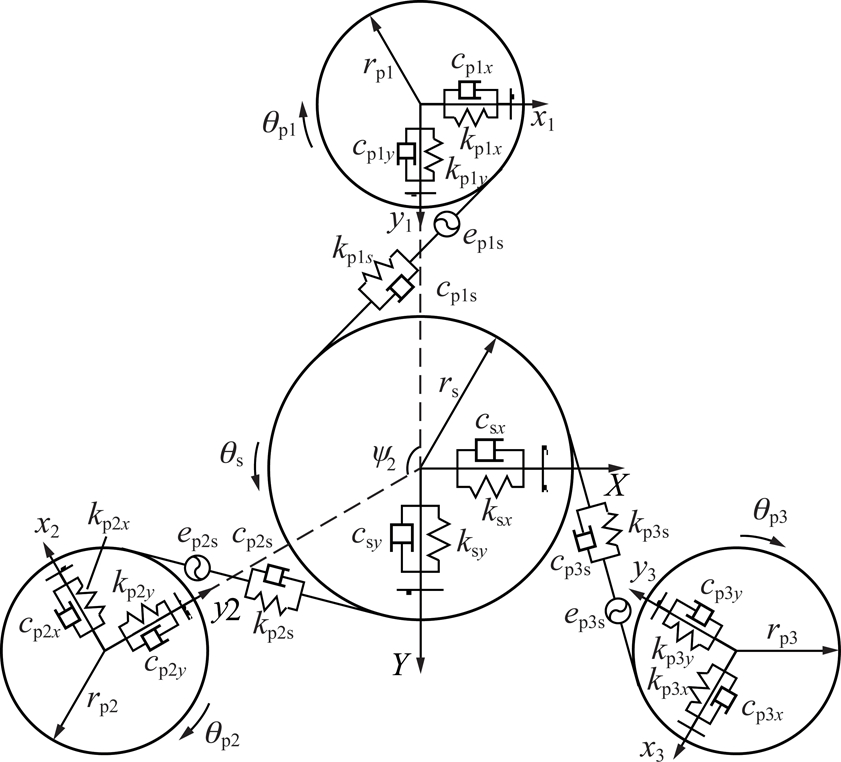
图5 耦合轮系的动力学模型
Fig.5 Dynamic model of torque coupled gear train
传动系统的数学模型为

(4)
式中,Fpis为耦合轮系的主动齿轮i(i=1,2,3)与被动齿轮之间的动态啮合力,其表达式为
(5)
式中,δpis为耦合轮系的主动齿轮i与被动齿轮之间的动态传递误差,其表达式为
δpis=rpiθpi-rsθs-xpicos α+xscos(α+ψi)+
ypisin α-yssin(α+ψi)-epis(6)
式中,rpi和rs分别为主动齿轮i和被动齿轮的基圆半径;θmi,θpi,θs和θL分别为电机i的转子、主动齿轮i、被动齿轮和等效构件的角位移;xpi和ypi分别为主动齿轮i在x和y向的振动位移;xs和ys分别为被动齿轮在x和y向的振动位移;α为啮合角,ψi为主动齿轮i的位置角;ψi=(i-1)×120°;epis为静态传递误差;kpis和cpis分别为主动齿轮i和被动齿轮间的啮合刚度和阻尼;kmipi和cmipi分别为输入轴i的扭转刚度和阻尼;kpix和cpix分别为主动齿轮i在x向的支撑刚度和阻尼;kpiy和cpiy分别为主动齿轮i在y向的支撑刚度和阻尼;ksL和csL分别为输出轴的扭转刚度和阻尼;ksx和csx分别为被动齿轮在x向的支撑刚度和阻尼;ksy和csy分别为被动齿轮在y向的支撑刚度和阻尼;Tmi为作用在电机i的转子上的驱动转矩;TL为作用在等效构件上的负载转矩;Imi,Ipi,Is和IL分别为电机i的转子、主动齿轮i、被动齿轮和等效构件的转动惯量;mpi和ms分别为主动齿轮i和被动齿轮的质量。
时变啮合刚度取为傅里叶级数形式[16]:
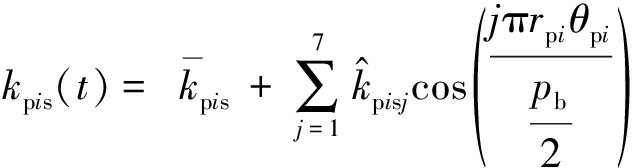
(7)
式中,![]() 为时变啮合刚度的均值;
为时变啮合刚度的均值;![]() 为时变啮合刚度傅里叶级数周期项的幅值;pb为主动齿轮的基圆齿距。
为时变啮合刚度傅里叶级数周期项的幅值;pb为主动齿轮的基圆齿距。
啮合阻尼[14]为
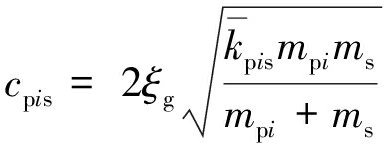
(8)
式中,ξg为阻尼比。
静态传递误差取为傅里叶级数形式[20]:
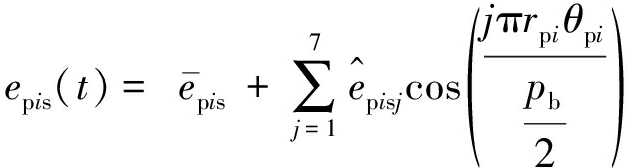
(9)
式中,![]() 为静态传递误差的均值;
为静态传递误差的均值;![]() 为静态传递误差傅里叶级数周期项的幅值。
为静态传递误差傅里叶级数周期项的幅值。
机电短程传动系统的主要参数见表1。
表1 动力传动系统的主要参数
Table 1 Parameters of short-range cutting transmission

在机电短程传动系统的动力学模型(式(1)~(4))中,isd,isq,ird,irq,θmi,θpi,θs,θL,xpi,ypi,xs和ys为待求解的未知函数。在模型中,未知函数及其导数均为一次项,动力学模型为线性微分方程组。传动系统动力学模型(式(4))中的动态啮合力Fpis含有时变啮合刚度,时变啮合刚度(式(7))是齿轮角位移的周期函数,其数值随时间变化,这使得机电短程传动系统的动力学模型为线性时变微分方程组。变步长Dormand-Prince算法是一种显式龙格库塔算法,具有较好的精度[21]。因此,采用变步长Dormand-Prince算法求解系统的动力学模型。在求解线性时变动力学模型的过程中,首先在当前时间步实时计算时变啮合刚度的取值,再将啮合刚度用于计算此时间步微分方程组的系数和未知函数的值。
齿轮的偏心误差等因素会引起齿轮转速波动,当耦合轮系3个主动齿轮偏心误差的相位不同时,3个输入转速间将出现相位差,使耦合轮系的输入转速波动且不一致。随误差幅值的增加,齿轮转速波动的幅度将增加。
电机的制造装配误差,会使机电短程传动系统中各台电机的电阻、互感、漏感等参数不一致;而且,在实际运行中,系统中每台电机的输入电压不是理想的交流电。这些因素影响电机的动态特性,使各台电机的转速响应存在差异。
转速响应不同的多台电机,与耦合轮系耦合后,会出现转速波动且不一致。在耦合轮系无误差的情况下,当各台电机转速响应不一致时,耦合轮系的输入转速如图6所示。在3.5 s时,电机转速出现变化的趋势,且各转速变化的趋势不同。由于耦合轮系中的主动齿轮和被动齿轮间存在啮合刚度,因此转速出现波动,且相位不同。
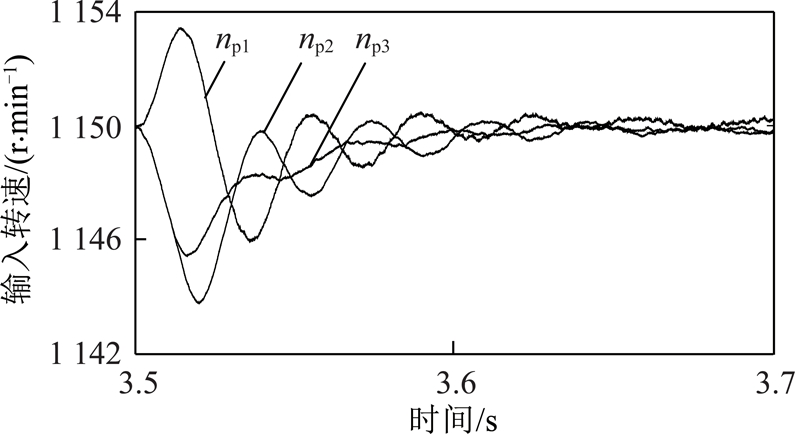
图6 电机转速响应不一致对输入转速的影响
Fig.6 Effect of inconsistent response from multiple motors on input speed
多种因素共同导致了耦合轮系的输入转速波动且不一致,而且在实际中,无法完全避免这些因素。耦合轮系的输入转速将存在波动,而且不一致。通过多电机同步控制,可以改变转速的同步误差。因此,有必要将输入转速不一致作为一个因素,分析其对耦合轮系动态特性的影响。
在负载突变工况下,分析输入转速波动且不一致对耦合轮系动态特性的影响规律。在1.3 s时,负载转矩TL由8 936.2 N·m突变至12 383.0 N·m[22]。
采用第1节所建立的动力学模型,设置电机的目标转速为恒定值,在耦合轮系的输入轴上施加短暂的转矩扰动,使输入转速波动,出现不一致现象,以分析其对轮系动态特性的影响。输入转速不一致程度Ds定义为
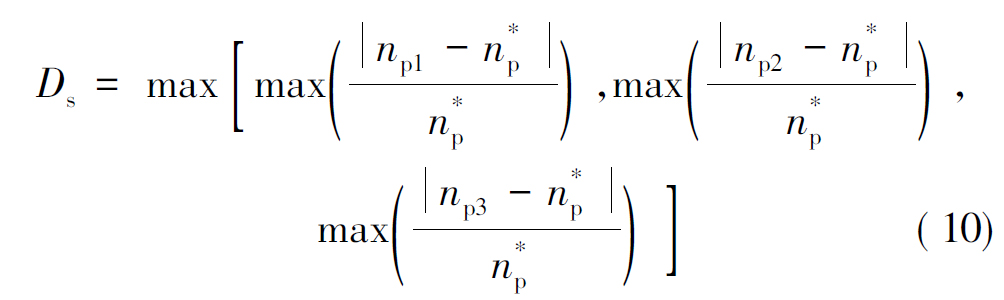
式中,![]() 为耦合轮系3个输入转速的均值,r/min。
为耦合轮系3个输入转速的均值,r/min。
当输入转速不一致程度Ds=0.004 7时,耦合轮系的输入转速如图7所示。图8为输入转速np3的频谱,输入转速不一致程度Ds分别为0,0.000 9,0.002 7和0.004 7。输入转速一致时,输入转速np3的频率成分主要有:负载突变引起的频率成分(fs=76.3 Hz)和啮频(fm=306.1 Hz)。输入转速不一致时,输入转速np3的频谱中出现频率成分fr=27.8 Hz。因此,图7中的输入转速np3存在低频波动。输入转速np1和np2的特点与输入转速np3的类似,图7中输入转速np2的波动幅度略大于输入转速np3。输入转速不一致时,耦合轮系3个输入转速的趋势一致,但是呈现波动形式且相位不同,3个输入之间存在转速差。输入转速低频波动的幅值增加时,3个转速之间的差值增加,输入转速不一致程度增加。

图7 耦合轮系的输入转速
Fig.7 Input speeds of torque coupled gear train

图8 输入转速np3的频谱
Fig.8 Spectra of input speed np3
输入转速不一致程度Ds=0.004 7时,耦合轮系的输出转速如图9所示。图10为输出转速的频谱,输入转速不一致程度Ds分别为0,0.002 7和0.004 7。

图9 耦合轮系的输出转速
Fig.9 Output speed of torque coupled gear train

图10 输出转速的频谱
Fig.10 Spectra of output speed
在图10中,输出转速的频率成分主要有:负载突变引起的频率成分(fs=76.3 Hz)、啮频(fm=306.1 Hz)和啮频的倍频(2fm=612.5 Hz,3fm=918.9 Hz)。随输入转速不一致程度的变化,输出转速各频率成分的幅值无明显变化。输入转速不一致时,输入转速存在低频波动(fr=27.8 Hz),但是输出转速未产生这种形式的波动。
当输入转速不一致程度Ds=0.004 7时,耦合轮系的动态啮合力如图11所示。图12为轮系传动路线3的动态啮合力Fp3s的频谱,输入转速不一致程度Ds分别为0,0.000 9,0.002 7和0.004 7。

图11 动态啮合力
Fig.11 Dynamic meshing force

图12 动态啮合力Fp3s的频谱
Fig.12 Spectra of dynamic meshing force Fp3s
输入转速一致时,动态啮合力Fp3s的频率成分主要有:负载突变引起的频率(fs=76.3 Hz)、啮频(fm=306.1 Hz)和啮频的倍频(2fm=612.5 Hz)。输入转速不一致时,动态啮合力Fp3s的频谱中出现低频成分(fr=27.8 Hz),其频率与输入转速低频波动的频率相同;而且,随输入转速不一致程度的增加,fr频率成分的幅值增加。由图11也可得,输入转速不一致时,传动路线3的动态啮合力Fp3s存在低频波动。动态啮合力Fp1s和Fp2s的特点与Fp3s的类似。这种低频波动使动态啮合力的波动程度增加,轮齿的受力情况恶化。在图11中,动态啮合力低频成分(fr=27.8 Hz)的相位不同,其相位关系与3个输入转速的相位关系相同。
输入转速不一致时,输入转速低频波动(fr=27.8 Hz)且相位不同,而输出转速无低频波动。齿轮角位移为转速的积分,因此主动齿轮角位移低频波动且相位不同,被动齿轮角位移无低频波动。动态传递误差为齿轮角位移的函数,因此动态传递误差低频波动且相位不同,进而导致动态啮合力低频波动且相位不同。齿轮转速影响齿轮角位移、动态传递误差和动态啮合力,因此,当输入转速不一致程度增加时,动态啮合力低频波动的幅度增加。
图13为输入转速一致和输入转速不一致(Ds=0.004 7)时主动齿轮3的切向振动加速度。图14为主动齿轮3切向振动加速度的频谱,输入转速不一致程度Ds分别为0,0.000 9,0.002 7和0.004 7。图14中,输入转速一致时,主动齿轮3切向振动加速度频谱中的主要频率成分有:负载突变引起的频率成分(fs=76.3 Hz)、啮频(fm=306.1 Hz)和啮频的倍频(2fm=612.5 Hz,3fm=918.9 Hz);输入转速不一致时,切向振动加速度的频谱中出现低频成分(fr=27.8 Hz),与输入转速中低频成分的频率相同。随输入转速不一致程度的增加,这种低频成分的幅值逐渐增加,其它频率成分的幅值无明显变化。这种低频波动使切向振动加速度的波动增加,如图13所示。

图13 主动齿轮3的切向振动加速度
Fig.13 Tangential vibration acceleration of pinion 3

图14 主动齿轮3切向振动加速度的频谱
Fig.14 Spectra of tangential vibration acceleration of pinion 3
图15为输入转速一致和输入转速不一致(Ds=0.004 7)时主动齿轮3的径向振动加速度,图16为主动齿轮3径向振动加速度的频谱。主动齿轮3径向振动加速度频谱的特征和切向振动加速度频谱的特征类似。输入转速不一致导致低频波动,使主动齿轮3径向振动加速度的波动幅度增加,如图15所示。

图15 主动齿轮3的径向振动加速度
Fig.15 Radial vibration acceleration of pinion 3

图16 主动齿轮3径向振动加速度的频谱
Fig.16 Spectra of radial acceleration of pinion 3
图17为主动齿轮3振动加速度最大值与输入转速不一致程度的关系。随输入转速不一致程度Ds的增加,切向振动加速度由24.13 m/s2增加至36.02 m/s2,增大11.89 m/s2;径向振动加速度由17.66 m/s2增加至24.73 m/s2,增大7.07 m/s2。在某个Ds下,切向振动加速度的最大值大于径向振动加速度的最大值。而且,随Ds的增加,切向振动加速度的增幅大于径向振动加速度的增幅。因此,输入转速不一致对切向振动加速度的影响更大。主动齿轮1和2的平移振动加速度的特点与主动齿轮3类似。

图17 振动加速度最大值与输入转速不一致程度的关系
Fig.17 Relationship between maximum vibration acceleration and inconsistent input speed
输入转速不一致时,主动齿轮和被动齿轮间的动态啮合力低频波动(fr=27.8 Hz)。由于作用在主动齿轮上的载荷存在低频波动,因此主动齿轮的振动加速度出现低频波动。随着输入转速不一致程度的增加,动态啮合力低频波动的幅值增加,这导致主动齿轮振动加速度低频成分的幅值逐渐增加,动态啮合力和振动加速度低频成分的幅值见表2。
表2 动态啮合力和振动加速度低频成分的幅值
Table 2 Low-frequency component amplitude of dynamic meshing force and vibration acceleration

机电短程传动系统的多个电机相互独立,通过多电机同步控制,可以减小各个电机之间的转速差,即减小耦合轮系输入转速不一致程度。研究结果表明:随着输入转速不一致程度Ds的减小,耦合轮系的动态啮合力波动幅度减小,主动齿轮振动加速度的波动幅度减小,轮系的动态性能提高。因此,在系统运行过程中,可以通过多电机转速同步控制减小输入转速不一致程度Ds,提高耦合轮系的动态性能。
机电短程传动系统的实验台架如图18所示,主要由驱动电机、耦合轮系、行星轮系、飞轮、升速箱和测功机组成。在耦合轮系输入轴上布置转速转矩传感器,并在输入轴3的轴承座上布置PCB 352C03型振动加速度传感器,如图19所示。两个振动加速度传感器分别测量耦合轮系输入轴3在竖直和水平方向的振动加速度。使用QuantumX数据采集系统采集转速转矩传感器的数据,使用SC305-VTP/3P92-B型数据采集箱采集振动加速度传感器的数据。

图18 机电短程截割传动系统实验台架
Fig.18 Short-range cutting transmission test bench

图19 实验台架中安装的传感器
Fig.19 Sensors in the test bench
实验台架中,机电短程传动系统的主要参数见表3。
在实验台架上进行负载突变工况的实验,在第25.3 s,作用在飞轮上的负载转矩由8 500 N·m突变增加至11 500 N·m。图20为测得的耦合轮系的输入转速,3个输入转速呈现波动形式,输入转速np1和np2的相位相反,输入转速np2和np3的相位相近,3个输入转速波动且相位不同,输入转速不一致,输入转速不一致程度约为0.005 3。实验中耦合轮系输入转速(图20)的特征与仿真中输入转速(图7)的特征相似。
表3 实验台架动力传动系统的参数
Table 3 Parameters of powertrain in test bench


图20 实验中耦合轮系的输入转速
Fig.20 Measured speeds of torque coupled gear train
实验测得的振动加速度,是主动齿轮3输入轴在水平和竖直方向的振动加速度ah和av,为方便与仿真结果进行对比,将其投影至切向(x方向)和径向(y方向),投影关系如图21所示。

图21 振动加速度的投影关系
Fig.21 Projection relationship of acceleration
切向和径向的振动加速度ax和ay为
(11)
图22和图23分别为主动齿轮3在切向的振动加速度及其频谱,图24和图25分别为主动齿轮3在径向的振动加速度及其频谱。

图22 主动齿轮3输入轴在切向的振动加速度
Fig.22 Tangential acceleration of input shaft 3
仿真和实验获得的主动齿轮3振动加速度的最大值见表4。其中,S1阶段指负载突变前的阶段,S2阶段指负载突变引起的瞬态过程,S3阶段指负载突变后响应趋于稳定之后的阶段。

图23 主动齿轮3输入轴切向振动加速度的频谱
Fig.23 Spectrum of tangential vibration acceleration of input shaft 3

图24 主动齿轮3输入轴在径向的振动加速度
Fig.24 Radial vibration acceleration of input shaft 3
表4中,仿真与实验结果有相似的趋势,负载突变后振动加速度的最大值大于负载突变前振动加速度的最大值,切向振动加速度的最大值大于径向振动加速度的最大值。然而,仿真与实验结果之间存在误差。造成这些误差的可能原因有:齿轮传动系统建模中,考虑了影响扭转和平移运动的主要因素,忽略了一些制造装配误差、齿轮-箱体耦合等因素,使得模型与实际传动系统的特性存在差异;通过经验公式计算获得的刚度、阻尼等参数值,与实际值之间存在误差[23-24]。此外,表4中,S2阶段的误差大于S1和S3阶段的误差。可能的原因是:在仿真分析中,负载突变呈阶跃形式,负载增加过程耗时0 s;在实验中,负载突变呈斜坡形式,负载增加过程耗时0.2 s。仿真分析中,负载突变对系统的冲击更大。
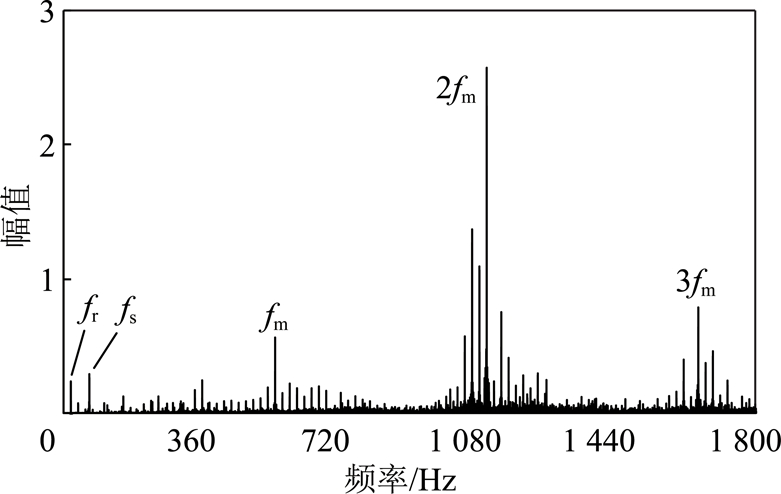
图25 主动齿轮3输入轴径向振动加速度的频谱
Fig.25 Spectrum of radial vibration acceleration of input shaft 3
表4 振动加速度最大值的仿真与实验结果
Table 4 Simulation and experimental results of maximum vibration acceleration
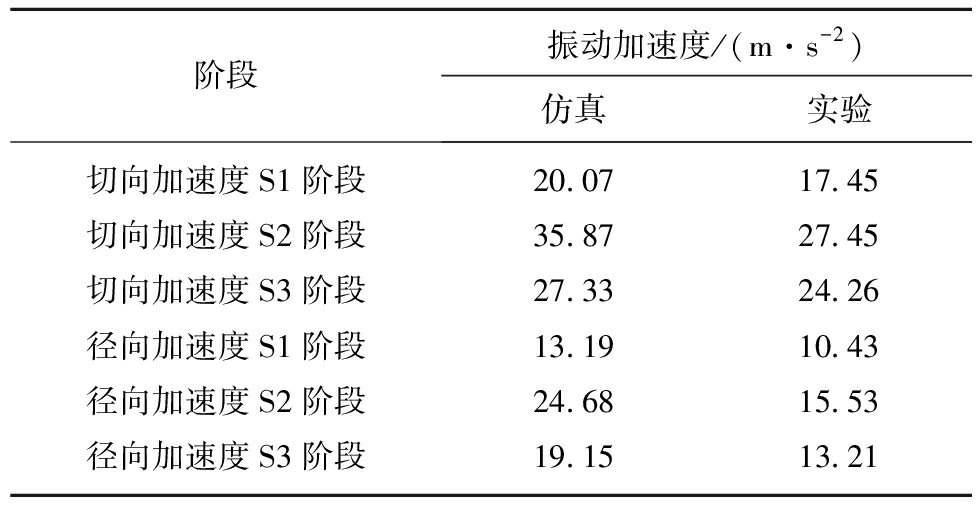
图23和图25中,主动齿轮3振动加速度频谱中的主要频率成分有:耦合轮系输入轴的转频(fr=18.9 Hz)、负载突变引起的频率(fs=82.7 Hz)、耦合轮系啮频(fm=548.6 Hz)和啮频的倍频(2fm=1 097.5 Hz,3fm=1 645.9 Hz)。实验测得的振动加速度主要频率成分和仿真结果的相似。由于仿真和实验所使用的耦合轮系齿轮的齿数不同,因此仿真和实验所得的耦合轮系的啮频的数值不同。
(1)耦合轮系的输入转速不一致时,3个输入转速的趋势一致,存在低频波动,它们的相位不同。但是,输入转速不一致并不影响轮系的输出转速,输出转速无低频波动。
(2)齿轮转速影响角位移、动态传递误差和动态啮合力。因此,当输入转速波动且不一致时,耦合轮系的动态啮合力出现低频波动,这种低频波动使动态啮合力的波动程度增大,轮齿的受力情况恶化;3个动态啮合力低频成分的相位不同,3个传动路线不均载;随着输入转速不一致程度的增加,动态啮合力的波动幅度逐渐增加。
(3)耦合轮系输入转速波动且不一致时,轮系的动态啮合力存在低频波动,作用在主动齿轮上的载荷低频波动。这使得主动齿轮的切向和径向振动加速度出现低频波动,使振动加速度的波动幅度增大。
(4)在机电短程传动系统的实验台架上进行动态特性实验。实验表明:耦合轮系存在输入转速波动且不一致的现象;测得的主动齿轮输入轴振动加速度在时域和频域的特征与仿真结果的特征相似。验证了仿真结果的正确性。
研究结果为通过多电机同步控制提高耦合轮系的动态性能提供了依据。在机电短程传动系统的运行过程中,可通过多电机转速同步控制减小输入转速不一致程度,提高耦合轮系的动态性能。进而可以提高采煤机截割部机电短程传动系统的承载能力和使用寿命。
参考文献
[1] WANG Jinhua.Development and prospect on fully mechanized mining in Chinese coal mines[J].International Journal of Coal Science & Technology,2014,1(3):153-260.
[2] WANG Jinhua,YU Bin,KANG Hongpu,et al.Key technologies and equipment for a fully mechanized top-coal caving operation with a large mining height at ultra-thick coal seams[J].International Journal of Coal Science & Technology,2015,2(2):97-161.
[3] 孙冬野,李明,舒锐志,等.采煤机截割部动力传动装置[P].中国专利:ZL 2014 1 0728258.3,2016-08-17.
[4] SHU Ruizhi,WEI Jing,QIN Datong,et al.Influence of motor fault on synchronization and dynamic characteristics of a multi-motor driving system[J].Journal of Advanced Mechanical Design,Systems,and Manufacturing,2018,12(1):1-23.
[5] WEI Jing,SHU Ruizhi,QIN Datong,et al.Study of synchronization characteristics of a multi-source driving transmission system under an impact load[J].International Journal of Precision Engineering and Manufacturing,2016,17(9):1157-1174.
[6] ZHANG Hao,WANG Meiling,HAN Qingkai,et al.Dynamic behaviors of the cutterhead driving system in tunneling boring machine with impact[J].Proceedings of the Institution of Mechanical Engineers,Part C:Journal of Mechanical Engineering Science,2016,230(14):2427-2437.
[7] LI Xianhong,YU Haibin,WANG Jin,et al.Dynamic modeling and analysis of shield TBM cutterhead driving system[J].Journal of Dynamic Systems,Measurement,and Control,2010,132(4):1-14.
[8] LI Xianhong,YU Haibin,YUAN Mingzhe,et al.Study on the linear dynamic model of shield TBM cutterhead driving system[A].IECON 2011-37th Annual Conference on IEEE Industrial Electronics Society[C].Melbourne:IEEE,2011:3864-3871.
[9] LI Xianhong,YU Haibin,ZENG Peng,et al.Dynamic two-dimensional nonlinear vibration modeling and analysis for shield TBM cutterhead driving system[J].Transactions of the Canadian Society for Mechanical Engineering,2014,38(4):417-463.
[10] LI Xianhong,YU Haibin,YUAN Mingzhe,et al.Research on dynamic models and performances of shield tunnel boring machine cutterhead driving system[J].Advances in Mechanical Engineering,2013,5:1-29.
[11] SUN Wei,MA Honghui,SONG Xueguan,et al.Modeling and dynamic analysis of cutterhead driving system in tunnel boring machine[J].Shock and Vibration,2017(2017):1-12.
[12] ZHANG K Z,YU H D,ZENG X X,et al.Numerical simulation of instability conditions in multiple pinion drives[J].Proceedings of the Institution of Mechanical Engineers,Part C:Journal of Mechanical Engineering Science,2011,225(6):1319-1327.
[13] WEI Jing,SUN Qinchao,SUN Wei,et al.Load sharing characteristic of multiple pinions driving in tunneling boring machine[J].Chinese Journal of Mechanical Engineering,2013,26(3):532-540.
[14] WEI Jing,SUN Qinchao,SUN Wei,et al.Dynamic analysis and load-sharing characteristic of multiple pinion drives in tunnel boring machine[J].Journal of Mechanical Science and Technology,2013,27(5):1385-1392.
[15] LI Ming,YANG Yang,HU Minghui,et al.Influence of motor control characteristics on load sharing behavior of torque coupling gear set[J].Journal of Vibro Engineering,2016,18(7):4539-4549.
[16] YANG Yang,LI Ming,HU Minghui,et al.Influence of controllable parameters on load sharing behavior of torque coupling gear set[J].Mechanism and Machine Theory,2018,121:286-298.
[17] SHU Ruizhi,LIU Zhenjun,LIU Changzhao,et al.Load sharing characteristic analysis of short driving system in the long-wall shearer[J].Journal of Vibro Engineering,2015,17(7):3572-3585.
[18] YU Haidong,EBERHARD Peter,ZHAO Yong,et al.Sharing behavior of load transmission on gear pair systems actuated by parallel arrangements of multiple pinions[J].Mechanism and Machine Theory,2013,65:58-70.
[19] 袁镭,余海东,丁晟,等.基于几何耦合模型的多齿轮系统载荷均匀性分析[J].上海交通大学学报,2013,47(5):687-691.
YUAN Lei,YU Haidong,DING Sheng,et al.Analysis on load-sharing behavior of multiple gear system with geometric coupled model[J].Journal of Shanghai Jiaotong University,2013,47(5):687-691.
[20] KAHRAMAN Ahmet.Load sharing characteristics of planetary transmissions[J].Mechanism and Machine Theory,1994,29(8):1151-1165.
[21] ASHINO R,NAGASE M,VAILLANCOURT R.Behind and beyond the matlab ODE suite[J].Computers and Mathematics with Applications,2000,40(4):491-512.
[22] 葛帅帅,秦大同,胡明辉.突变工况下滚筒式采煤机调速控制策略研究[J].煤炭学报,2015,40(11):2569-2578.
GE Shuaishuai,QIN Datong,HU Minghui.Research on drum shearer speed control strategies under impact conditions[J].Journal of China Coal Society,2015,40(11):2569-2578.
[23] 崔亚辉,刘占生,叶建槐.齿轮—转子耦合系统的动态响应及齿侧间隙对振幅跳跃特性的影响[J].机械工程学报,2009,45(7):7-15.
CUI Yahui,LIU Zhansheng,YE Jianhuai.Dynamic response of geared rotor system and the effect of clearance on jump characteristics of amplitude[J].Journal of Mechanical Engineering,2009,45(7):7-15.
[24] 翟洪飞,朱才朝,宋朝省,等.大功率风电齿轮箱系统耦合动态特性研究[J].振动与冲击,2017,36(8):97-104.
ZHAI Hongfei,ZHU Caichao,SONG Chaosheng,et al.Dynamic characteristics of a high-power wind turbine gearbox coupled system[J].Journal of Vibration and Shock,2017,36(8):97-104.