移动阅读
刘旭南1，赵丽娟1，黄 凯2，罗贵恒1
(1.辽宁工程技术大学 机械工程学院，辽宁 阜新 123000; 2.昆山佰奥智能装备股份有限公司，江苏 昆山 215311)
摘 要:随着中厚煤层不断开采完毕，薄煤层开采比重将不断加大，其安全、高效开采日显重要，但由于开采空间有限、条件恶劣，采煤机易出现设计结构不合理、工作状态不稳定、可靠性差等问题。以MG2*100/455-BWD新型薄煤层采煤机截割部为工程对象，采用Pro/E，ANSYS，ADAMS建立了该采煤机的刚柔耦合虚拟样机模型，基于破煤理论建立了采煤机螺旋滚筒的力学模型，通过MATLAB编制了相关程序解决了刚柔耦合虚拟样机模型载荷添加的问题;通过虚拟仿真获取了关键零件输出轴、壳体、行星架的Von Mises应力分布及最大应力节点应力值的时域信息，以30组不同牵引速度仿真模型的仿真结果建立了各关键零件的最大应力分布函数;以应力-强度干涉可靠性理论为基础，结合各关键零件的最大应力分布函数及所用材料强度分布函数，在考虑载荷作用次数情况下，建立各关键零件在随机载荷多次作用下的可靠度计算模型。经分析计算得到输出轴、行星架、壳体的可靠度分别为0.978，0.536及0.614，研究发现:行星架与壳体存在应力集中现象，应力最大位置分别位于行星架腹板与花键轴相交处及壳体惰轮轴孔后侧与行星减速器承载部分相交处。在对薄弱零件改进后，行星架、壳体的可靠度分别达到0.969 0和0.997 4，满足使用要求。该方法可有效缩短产品设计周期，提高采煤机关键零件的设计质量及可靠性。
关键词:应力-强度干涉理论;截割部;采煤机;可靠性
移动阅读
刘旭南，赵丽娟，黄凯,等.基于应力-强度干涉理论的采煤机截割部关键零件可靠性分析[J].煤炭学报,2019,44(3):964-972.doi:10.13225/j.cnki.jccs.2018.0505
LIU Xunan,ZHAO Lijuan,HUANG Kai,et al.Reliability analysis on the key parts of the cutting unit of shearer based on stress-strength interference theory[J].Journal of China Coal Society,2019,44(3):964-972.doi:10.13225/j.cnki.jccs.2018.0505
中图分类号:TD421.6
文献标志码:A
文章编号:0253-9993(2019)03-0964-09
收稿日期:2018
0415
修回日期:20190115
责任编辑:郭晓炜
基金项目:国家自然科学基金资助项目(51674134);辽宁省自然科学基金资助项目(20170540420);辽宁省虚拟仿真实验教学中心资助项目
作者简介:刘旭南(1985—)，男，辽宁开原人，讲师。E-mail:yuwuknan@163.com
LIU Xunan1,ZHAO Lijuan1,HUANG Kai2,LUO Guiheng1
(1.College of Mechanical Engineering,Liaoning Technical University,Fuxin 123000,China; 2.Kunshan Topa Intelligent Equipment Co.,Ltd.,Kunshan 215311,China)
Abstract:With the completion of medium-thick seam mining gradually,the proportion of thin seam mining will continue to increase,and its safe and efficient mining is becoming increasingly important.Due to the limitation of mining space and harsh conditions,the shearer is prone to the problems of unreasonable structure design,instability and poor reliability.Taking new thin coal seam shearer of MG2*100/455-BWD cutting parts as an investigation target,the rigid flexible coupling virtual prototype model of the shearer was established by Pro/E,ANSYS and ADAMS.The mechanical model of shearer spiral drum was established based on coal breaking theory.The problem of load addition of rigid-flexible coupling virtual prototype model was solved by programming with MATLAB.The maximum stress nodes’ time-domain information and Von Mises stress distribution of output shaft,shell and planetary carrier were obtained by virtual simulation.Based on the simulation results of 30 sets simulation models for different hauling speeds,the maximum stress distribution function of each key part was established.Based on the reliability theory of stress-strength interference,combined with the maximum stress distribution function of each key part and the strength distribution function of the material used,the reliability calculation model of each key part under multiple random loads was established considering the cycle of loads.The reliabilities of output shaft,planet carrier and shell were cal-culated as 0.978,0.536 and 0.614 respectively.The results show that the stress concentration phenomena exist on planetary carrier and shell.The maximum stress locates at the intersection of web and spline shaft of planetary carrier,and at the intersection of backside of idler shaft hole and outside of planetary reducer of the shell,respectively.After the improvement of the weak parts,the reliability of the planet carrier and shell are 0.969 and 0.9974 respectively,which can meet the operation requirement.This method can effectively shorten the product design cycle and improve the design quality and reliability of the key parts of shearer.
Key words:stress-strength interference theory;cutting unit;shearer;reliability
我国薄煤层分布广泛，储量丰富，目前已探明可采储量可达到67亿t，约占全国煤炭储量的1/5，有些地区的薄煤层储量可达到煤炭储量的72%以上。但由于开采空间狭小，使得采煤机尺寸、电机功率得到了极大的制约，采煤机易出现设计结构不合理、可靠性差等问题。
大量学者采用相关理论对采煤机可靠性问题进行研究:2009年，贺声阳[1]以可靠性理论为基础建立了整机系统的可靠性数学模型，研究大功率电牵引采煤机整机系统的可靠性，分析获得采煤机薄弱环节;2011年，陈鹏[2]运用全寿命周期理论研究了滚筒采煤机寿命的可靠性，从管理学的角度出发深入研究了滚筒采煤机的可靠性;2015年，张义民等[3]应用MATLAB软件对MG300/700-WD型采煤机摇臂传动系统进行了非线性动力学特性分析，得到了系统危险部位的应力谱，分析了摇臂传动系统的可靠性及可靠性灵敏度，对系统可靠性的影响大小与系统结构参数的关系进行了分析;同年，周笛等[4]基于3自由度齿轮集中质量模型，对采煤机牵引部进行了整体动力学建模，研究变速重载工况下系统的振动响应，获得了牵引部各位置的动态接触应力，得到了系统功能函数的概率分布函数和概率密度函数，对牵引部传动系统在载荷多次作用下的动态可靠性进行了分析研究;2016年，赵津[5]以国内某大型煤矿集团公司数年来收集的多台进口采煤机的故障数据为基础，建立了采煤机在不同状态下的可靠性模型，统计辨识采煤机在运行时的可靠性临界状态，分析研究了采煤机在多数可靠性状态下的停留时间和可靠度分布情况;同年，张义民等[6]基于BP神经网络非线性映射功能，模拟获得了疲劳寿命和随机参数之间的关系表达式，以最大可能点摄动法对行星机构进行可靠设计，最终依据对行星轮与太阳轮进行的可靠性灵敏度设计，获得各个参数均值和方差对结构可靠性的影响情况。
以上学者很好的将可靠性理论应用在采煤机以及行星齿轮的可靠性分析上，若能以虚拟样机为平台，建立采煤机截割部的刚柔耦合模型，通过仿真获取关键零件的应力信息，并应用可靠性理论建立应力-强度干涉模型，进而分析、推导、计算零件在指定工况下的可靠性，将为采煤机关键零件可靠性分析提供一种便捷方法，该方法将缩短产品设计周期、节约劳动成本、提高产品质量，对提高采煤机设计质量具有较高的理论意义和应用价值。
零件强度和所受应力的相对大小决定着零件的失效与否，若使零件能够在载荷作用下完成正常工作，必须满足
S-s>0
(1)
式中，S为零件的强度，MPa;s为零件所承受的最大应力，MPa。
而实际情况下应力和强度的大小符合一定的统计概率分布。如图1所示，h(s)和f(S)分别为应力和强度的概率密度函数，阴影部位表明存在应力值大于零件强度的可能性，零件有可能会失效，即为传统的应力-强度干涉模型。
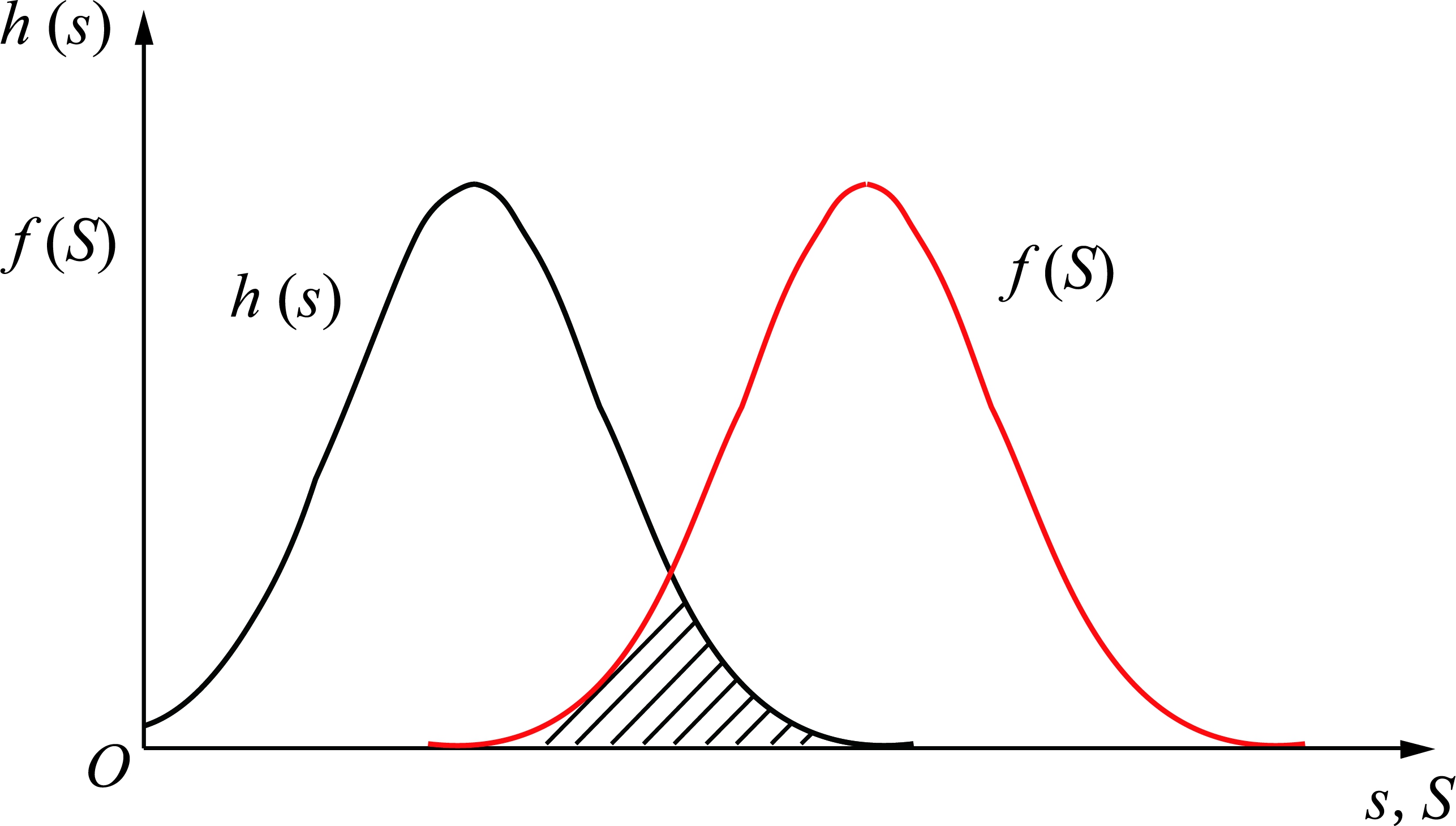
图1 应力-强度干涉模型
Fig.1 Stress-strength interference (SSI) model
当应力s与强度S的概率密度函数分别为h(s)，f(S)时，可靠度R则可表示[7]为
R=
h(s)
f(S)dSds=f(S)
h(s)dsdS
(2)
式(2)表述为计算在寿命周期内产品只承受一次载荷情况下的可靠度计算公式。而对于有些工作时间过长和载荷作用次数较多的产品应用公式时，应以随机载荷作用下的统计学意义为基础，运用顺序统计理论得到等效载荷分布情况，进而得到随机载荷多次作用下的可靠性模型。
在随机载荷多次作用情况下服役的零件，在载荷作用下不发生失效的概率大小即为零件的可靠度。设零件所承受的最大应力的累积分布函数与概率密度函数分别为H(s)，h(s)，选取m个载荷样本(s1,s2,…,sm)中等效载荷(载荷样本中最大载荷值)作为随机变量X。根据以上分析与顺序统计量相关知识可得可靠性等效载荷X在载荷作用m次时的累积分布函数FX(x)为
FX(x)=[H(x)]m
(3)
概率密度函数fX(x)为
fX(x)=m[H(x)]m-1h(x)
(4)
设零件所受载荷s的累积分布函数与概率密度函数分别为H(s)和h(s)，强度S的概率密度函数为f(S)，当载荷s作用m次时，应用载荷-强度干涉模型以及由式(3)和式(4)分别得到s作用m次时等效载荷X累积分布函数FX(x)与概率密度函数fX(x)，可获得随机载荷多次作用下的零件可靠度计算模型[7]:
R(m)=fX(x)f(S)dSdx=
m[H(x)]m-1h(x)
f(S)dSdx
(5)
根据式(5)采用Monte-Carlo法，只需构建零件应力与强度的概率密度函数，输入载荷作用次数，便可对零件的可靠度进行求解，其程序框图如图2所示。其中，h为指针记录载荷作用次数;i为模拟的不可靠次数;j为随机载荷作用的次数的过程变量。
图2 可靠度求解程序框图
Fig.2 Reliability solution block diagram
采煤机滚筒受力主要包括:螺旋滚筒装煤反力、截齿截割阻力、牵引阻力、侧向阻力，此外在截割煤壁时对采煤机滚筒会产生一个附加的轴向力，其中截割阻力Zj,牵引阻力Yj及侧向阻力Xj如图3所示，计算如式(6)～(8)所示。
(6)
Yj=0.6Zj-100δcmSaKδ(60f′-1)
(7)
(8)
式中，Zj为截齿的截割阻力，N;Yj为截齿的牵引阻力，N;Xj为截齿的侧向阻力，
为煤层非地压影响区的平均截割阻抗，N/mm;bp为截齿工作部分计算宽度，cm;hmax为截齿的最大切削厚度，cm;θ为截齿所处位置角度，(°);tcp为截齿的切削宽度，cm;β为截齿在牵引方向上的偏转角，(°);δcm为煤的单向抗压强度，MPa;Sa为截齿磨损面在截割平面上的投影面积，cm2;Kψ，Kz，Ky，Kφ，KC，Kot，f′，Kδ分别为煤的脆性系数、外露自由表面系数、截角影响系数、前刀面形状影响系数、排列方式系数、地压对工作面煤壁影响系数、截割阻抗系数、矿体体积系数;截齿的排列方式为顺序式时，C1，C2和C3分别取1.40，0.30，0.15，交叉式时，C1，C2和C3分别取1.00，0.22，0.10。
图3 滚筒受力简图
Fig.3 Force diagram of drum
装煤反力RS为
(9)
式中，Dsr为有效直径，m;Dg为筒毂直径，m;δ为叶片的宽度，m;Z为螺旋叶片的头数;L为螺旋叶片的导程，m;α为截割角度，(°);B为滚筒截深，m;WZ为原煤被推移时的阻力系数;Ψ为滚筒充满系数;γs为松散煤容重，N/m3。
附加轴向力Xq
(10)
式中，L2为后滑靴中心到前滚筒煤壁侧端面距离，m;L1为导向滑靴间的距离，m;α0为采煤机切入煤壁时的最大旋转角度，(°);Ry为正常采煤时滚筒受到的牵引方向的阻力，N;K2为截割力增加系数。
由图3可将截齿的截割阻力及牵引阻力按坐标系进行分解，则:
每条截线上X向合力:
(11)
每条截线上Y向合力:
(12)
每条截线上Z向合力:
(13)
式中，i为第i条截线;j为任意一条截线上的第j把截齿;n为任意一条截线上总截齿数;Xij，Yij，Zij分别为第i截线，第j把截齿的侧向力、牵引阻力、截割阻力。
将所有力转化到截割机构质心三向力及三相力矩分别为
(14)
(15)
(16)
式中，N为总截线条数。
对于采煤机还需考虑滚筒的附加轴向力Xq，则
(17)
375RSDcos γ
(18)
375RSDcos γ
(19)
(20)
式中，γ为叶片与煤的摩擦角，(°);di为第i条截线距离质心的距离，mm;Mx，My为截割头截齿受力转化到质心点后X，Y向的力矩。
根据式(7)～(20)，采用MATLAB软件便可编制程序计算滚筒质心处PCM所受载荷[8-11]，根据井下实际工况设置滚筒转速、牵引速度、煤的坚固系数分别为71 r/min，4 m/min，3，通过程序计算得到的载荷曲线如图4所示。
图4 载荷曲线
Fig.4 Load curves
使用三维实体建模软件Pro/E对采煤机截割部的各个零件进行数字化建模及装配，并将其导入到ADAMS中;采用ANSYS对输出轴、壳体、行星架进行网格划分生成中性文件，并通过Rigid to Flex命令完成相关柔性件的替换。按采煤机截割部各结构之间的运动关系添加约束，按赫兹接触理论完成齿轮间接触的添加。采用单位阶跃函数定义电机转速，在滚筒质心处添加一广义力并将计算好的载荷曲线(图4)添加到该广义力上，最终建立的截割部的刚柔耦合模型如图5所示。
图5 采煤机截割部刚柔耦合模型
Fig.5 Rigid-flex coupled model of shearer cutting unit
进入ADAMS/Postprocessor，选择Von Mises stress，将时间调整到最值时刻，观察最值时刻零件的应力分布情况[12-14]，如图6所示。
经过ADAMS分析得出输出轴的最大应力出现在与方头连接的花键槽根部;行星架应力较大位置主要集中在行星架的腹板与花键的连接处;壳体应力较大位置在后端盖与电机、行星部分联接螺栓处，最大应力点位于壳体惰轮轴后侧与行星减速器承载部分相交处。
将输出轴、行星架以及壳体的最大应力节点编号27116，24448，10905输入到对应柔性体的Nodal plot对话框中，调整后处理为plot模式，找到相应的节点便可显示应力最大节点处的应力时域曲线，如图7所示，并记录相应最大应力值638.074 8，897.160 2以及379.008 1 MPa，由参考文献[15-16]可知3个零件的应力分别为:631.521，837.801以及309.267 MPa，这与本仿真结果相一致，证明了刚柔耦合仿真计算关键零件应力的可靠性。
由于其受滚筒的截割功率、截齿伸出齿座的长度，牵引力和牵引功率等因素的制约，一般取变异系数0.05[17]，即牵引速度为vq～N(4,0.22)，在不同牵引速度下对采煤机截割部刚柔耦合模型进行30组仿真，并记录截割部各关键零件的最大应力信息(表1)，进而为关键零件应力分布奠定基础。
图6 关键零件最值时刻应力云图
Fig.6 Max von mises stress of key parts
图7 关键零件节点应力时域曲线
Fig.7 Time domain curves of node stress of key parts
表1 各工况下应力值
Table 1 Stress values under each condition
3.2.1 输出轴可靠性分析
截割部输出轴采用的材料为42CrMo,根据采煤机工作条件，在80 ℃时对该材料强度数据进行分析，其分散性符合正态分布[18]，强度均值为950 MPa，若变异系数为0.05，则标标准差为47.5 MPa，即
由表1所列数据，假设输出轴所承受最大应力服从正态分布，并设检验显著水平α=0.05，在MATLAB软件中，进行K-S假设检验即柯尔莫诺夫—斯米尔诺夫检验，通过程序运行得到h=0,表示不能拒绝零假设，说明所提出的假设“应力数据样本服从正态分布”是合理的。其拟合结果如图8所示。
图8 输出轴K-S拟合检验
Fig.8 K-S fitting test of output shaft
根据其检验结果得到输出轴最大应力值服从正态分布，其均值为636.878 3 MPa，标准差为33.043 4 MPa，即
通过载荷s概率密度函数和强度S概率密度函数得到载荷作用m次条件下的等效载荷X的概率密度函数如下:
根据在随机载荷多次作用下的可靠度计算模型可得到可靠度表达式为
以截割部输出轴所受载荷作用500次为基础，根据图2计算程序得到输出轴可靠度R=0.978，由此可见截割部输出轴满足采煤机的使用要求。
3.2.2 行星架可靠性分析
采煤机行星架材料与输出轴相同，因此其材料强度数据分布与输出轴一致。
行星架最大应力分布为:s～N(916.619 8,53.625 72)，其K-S假设检验后拟合结果如图9所示。
图9 行星架K-S拟合检验
Fig.9 K-S fitting test of planet carrier
行星架载荷概率密度函数
则随机载荷多次作用下的可靠度表达式:
Monte-Carlo计算后可得R=0.536，行星架明显强度不足，要使采煤机正常工作，需对行星架进行进一步改进。根据截割部行星架模型和其对应应力云图分析，在行星架腹板与花键轴相交处存在应力集中，应力集中原因为此处导角过小，为减小应力集中导角增大2 mm，改进结构如图10所示。
图10 行星架结构对比
Fig.10 Comparison of the structure of the planetary carriers
将模型更改后使用ANSYS柔性化替代原柔性件，再根据不同的牵引速度进行动力学仿真，得到最值应力曲线和应力云图如图11所示，由图11可知经改进后的行星架在薄弱处的应力值明显减小。
图11 改进后行星架应力曲线及云图
Fig.11 Stress curve and contour plot of improved planet carrier
统计不同牵引速度下的最值应力数据得改进后行星架的最大应力的分布为:s′～N(667.36,34.72)，根据动态可靠性模型得R=0.969，其应力特性得到改善满足使用要求。
3.2.3 壳体可靠性分析
壳体为整体铸造件，采用的材料为ZG30Mn2，根据其物理性能、力学性能和强度数据统计分析可得出壳体材料的强度符合均值为390 MPa，标准差为20.28 MPa的正态分布。按如上方法统计壳体在不同牵引速度下的最值应力值数据得到其应力分布符合s～N(381.728 7,13.155 42)，其K-S假设检验如图12所示。
图12 壳体K-S拟合检验
Fig.12 K-S fitting test of the shell
根据等效载荷方程和载荷多次作用下可靠性模型得可靠度R=0.614。其可靠度较低，同样达不到采煤机的实际工作要求，因此有必要对壳体应力值过大的部位进行结构改进。
根据壳体模型和应力云图分析，壳体惰轮轴后侧与行星减速器承载部分相交处存在应力集中，因此需对此处结构进行改进，改进方法为在应力集中处添加凸台结构如图13所示。
图13 结构改进前后对比
Fig.13 Comparison of the structure of the shell
同样将改进后壳体模型使用ANSYS柔性化后替换原柔性件，加载仿真得到其在不同牵引速度下的最大应力值，最值时刻应力曲线和应力云图14所示。
图14 改进后壳体应力曲线及云图
Fig.14 Stress curve and contour plot of improved shell
图中原应力集中处经改进后消失。统计改进后不同牵引速度下壳体的最大应力值数据，其应力分布为s′～N(146.27,11.582)。据载荷多次作用可靠性模型得R=0.997 4，可达到使用要求。
(1)采用MATLAB，Pro/E，ANSYS及ADAMS软件构建了该采煤机截割部的刚柔耦合虚拟样机模型，通过仿真发现输出轴、行星架以及截割部壳体的最大应力位置及最大应力值。
(2)通过30组仿真结果建立了输出轴、行星架、截割部壳体最大值的概率密度函数。
(3)考虑载荷作用次数和应力情况的影响，对采煤机截割部进行可靠性分析。通过应力、材料强度的分布以及建立好的零件可靠性模型，使用Monte Carlo仿真计算出了采煤机截割部输出轴、行星架壳体在载荷作用下的可靠度分别为0.978，0.536，0.614。并对可靠性低的行星架和壳体进行相应的改进，使得两者的可靠度达到0.969，0.997 4，保证了其安全可靠的工作。
参考文献
[1] 贺声阳.大功率电牵引采煤机整机系统可靠性研究[D].太原:太原理工大学，2009.
HE Shengyang.Research on reliability of high-power electric traction shearer whole system[D].Taiyuan:Taiyuan University of Technology,2009.
[2] 陈鹏.基于全寿命周期理论的滚筒采煤机可靠性工程技术研究[D].太原:太原理工大学,2011.
CHEN Peng.Research on reliability engineering technology of drum shearer based on life cycle theory[D].Taiyuan:Taiyuan University of Technology,2011.
[3] 张义民,黄婧,朱丽莎,等.采煤机摇臂传动系统可靠性稳健优化设计[J].煤炭学报,2015,40(11):2540-2545.
ZHANG Yimin,HUANG Jing,ZHU Lisha,et al.Reliability-based robust optimization design of the transmission system of a shearer ranging arm[J].Journal of China Coal Society,2015,40(11):2540-2545.
[4] 周笛,张旭方,杨周,等.采煤机牵引部传动系统动态可靠性分析[J].煤炭学报,2015,40(11):2546-2551.
ZHOU Di,ZHANG Xufang,YANG Zhou,et al.Vibration reliability analysis on tractive transmission system of shearer[J].Journal of China Coal Society,2015,40(11):2546-2551.
[5] 赵津.采煤机潜在故障预测和可靠性分析[D].太原:太原理工大学,2016.
ZHAO Jin.The potential failure prediction and reliability analysis of drum shearer[D].Taiyuan:Taiyuan University of Technology,2016.
[6] 张义民,王婷,黄婧.采煤机摇臂系统行星轮系疲劳可靠性灵敏度设计[J].东北大学学报自然科学版,2016,37(10):1426-1431.
ZHANG Yimin,WANG Ting,HUANG Jing.Fatigue reliability-based sensitivity design of planet gear for shearer rocker arm system[J].Journal of Northeastern University (Natural Science),2016,37(10):1426-1431.
[7] 王正,谢里阳,李兵.随机载荷作用下的零件动态可靠性模型[J].机械工程学报,2007,43(12):20-25.
WANG Zheng,XIE Liyang,LI Bing.Time-dependent reliability model of component under random load[J].Chinese Journal of Mechanical Engineering,2007,43(12):20-25.
[8] 赵丽娟,刘旭南,刘鹏.截齿排列方式对采煤机工作性能的影响[J].机械科学与技术,2014,33(12):1838-1844.
ZHAO Lijuan,LIU Xunan,LIU Peng.Picks arrangement mode’s influence on shearer’s working performance[J].Mechanical Science and Technology for Aerospace Engineering,2014,33(12):1838-1844.
[9] 刘旭南,赵丽娟,冯认金,等.薄煤层采煤机运动学参数最佳匹配问题研究[J].机械科学与技术,2017,36(11):1701-1707.
LIU Xunan,ZHAO Lijuan,FENG Renjin,et al.The research on kinematic parameter optimum matching of thin coal seam shearer[J].Mechanical Science and Technology for Aerospace Engineering,2017,36(11):1701-1707.
[10] 赵丽娟,董萌萌.含硫化铁结核薄煤层采煤机工作机构载荷问题[J].煤炭学报,2009,34(6):840-844.
ZHAO Lijuan,DONG Mengmeng.Load problems of working mechanism of the shearer in containing pyrites and thin coal seam[J].Journal of China Coal Society,2009,34(6):840-844.
[11] 刘旭南.采煤机、掘进机动力学仿真及控制中若干关键技术研究[M].沈阳:辽宁科学技术出版社,2017.
[12] 赵丽娟,马永志.基于多体动力学的采煤机截割部可靠性研究[J].煤炭学报,2009,34(9):1271-1275.
ZHAO Lijuan,MA Yongzhi.Reliability research on shearer cutting unit based on multi-body dynamics[J].Journal of China Coal Society,2009,34(9):1271-1275.
[13] 赵丽娟,刘旭南,马联伟.基于经济截割的采煤机运动学参数优化研究[J].煤炭学报,2013,38(8):1490-1495.
ZHAO Lijuan,LIU Xunan,MA Lianwei.Optimization research on shearer’s kinematic parameters based on economical cutting[J].Journal of China Coal Society,2013,38(8):1490-1495.
[14] 赵丽娟,田震.薄煤层采煤机截割部动态特性仿真研究[J].机械科学与技术,2014,33(9):1329-1334.
ZHAO Lijuan,TIAN Zhen.Simulation on dynamic characteristics of cutting unit for thin seam shearer[J].Mechanical Science and Technology for Aerospace Engineering,2014,33(9):1329-1334.
[15] 赵丽娟,李佳,田震,等.新型薄煤层采煤机截割部建模与仿真研究[J].机械传动,2013,37(1):47-50.
ZHAO Lijuan,LI Jia,TIAN Zhen,et al.Reliability analysis of a new shearer cuting unit in shin coal seam[J].Journal of Mechanical Transmission,2013,37(1):47-50.
[16] 李佳.新型薄煤层采煤机截割部可靠性研究[D].阜新:辽宁工程技术大学,2013.
LI Jia.Reliability Study of new shearer cutting unit working in thin coal seam[D].Fuxin:Liaoning Technical University,2013.
[17] 王丹玉,王启佳,孙维.采煤机牵引速度的分析与选择[J].煤矿机械,2012,33(10):201-203.
WANG Danyu,WANG Qijia,SUN Wei.Analysis and selection of shearer haulage speed[J].Coal Mine Machinery,2012,33(10):201-203.
[18] 曾波.某航空发动机涡轮叶片动态可靠性建模与分析[D].成都:电子科技大学,2013.
ZENG Bo.Dynamic Reliability modeling and analysis of an aero-engine turbine blade[D].Chengdu:University of Electronic Science and Technology of China,2013.