![]() 刘阳辉1,2,洪泽群1,2,韩延广3
刘阳辉1,2,洪泽群1,2,韩延广3
(1.同济大学 地下建筑与工程系,上海 200092; 2.同济大学 岩土及地下工程教育部重点实验室,上海 200092; 3.上海市隧道股份有限公司,上海 200232)
摘 要:在人工地层冻结工程中,平均温度是评价冻土帷幕状态,进行冻土帷幕力学性能分析的基本参数,本文研究单排管冻结形成的冻土帷幕的平均温度计算。基于单排管冻结稳态温度场解析解,直接对温度场表达式进行积分运算,运用分部积分法和积分中值定理,得到了单排管冻结平均温度计算公式,根据工程中的实际参数取值进行了公式的简化。考虑到温度场解析解在冻结管区域的不适用,采用相同的积分策略求解冻结管区域对平均温度计算的影响,进行了平均温度计算公式的修正。使用ANSYS进行了单排管冻结的热学稳态数值模拟与平均温度计算公式的结果进行比对,考察管间距l=0.4,0.6,0.8,1.0,1.2,1.4 m,相对厚度ξ/l=0.5,0.6,0.7,0.8,1.0,1.5共6种冻结发展状态,根据试验报告进行土质参数取值,冻结参数为工程中常用取值。对比计算结果显示,公式计算与数值计算的结果较为吻合。当相对厚度大于0.5时,随着冻土厚度的发展(相对厚度的增大),理论计算结果与数值计算结果的差值迅速减小到0.5 ℃以内,当相对厚度大于0.6时,差值小于0.2 ℃,当相对厚度为1及以上时,差值小于0.1 ℃。通过数值模拟验证了平均温度计算公式的准确性,也说明公式简化和修正的合理性,公式计算的误差满足工程应用的要求。
关键词:人工地层冻结法;单排管冻结;稳态温度场解析解;平均温度;数值模拟
中图分类号:TU752
文献标志码:A
文章编号:0253-9993(2019)04-1092-06
收稿日期:2018![]() 05
05![]() 27
27
修回日期:2018![]() 09
09![]() 18
18
责任编辑:常 琛
基金项目:国家自然科学基金资助项目(51478340)
作者简介:胡向东(1961—2018),男,浙江衢州人,副教授,博士生导师。Tel:021-65988771,E-mail:anton.geotech@tongji.edu.cn
通讯作者:刘阳辉(1993—),男,福建龙岩人,硕士研究生。Tel:021-65985249,E-mail:liuyanghui@tongji.edu.cn
HU Xiangdong1,2,LIU Yanghui1,2,HONG Zequn1,2,HAN Yanguang3
(1.Department of Geotechnical Engineering,Tongji University,Shanghai 200092,China; 2.Key Laboratory of Geotechnical and Underground Engineering of the Ministry of Education,Tongji University,Shanghai 200092,China; 3.Shanghai Tunnel Engineering Co.,Ltd.,Shanghai 200232,China)
Abstract:In the artificial ground freezing project,the average temperature is the basic parameter for evaluating the frozen soil curtain state and the mechanical analysis of the frozen soil curtain.The average temperature calculation of the frozen soil curtain formed by the single-row pipe freezing is studied in this paper.Based on the analytical solution of the steady-state temperature field of a single-row pipe freezing,the integral calculation of the temperature is directly performed.Using the partial integral method and the integral median theorem,the calculation formula of the average temperature of the single-row tube freezing is obtained,and the formula is simplified according to the actual parameter values in the project.Considering that the temperature field analytical solution is not applicable in the frozen pipe area,the same integral strategy is used to solve the influence of the frozen pipe area on the average temperature calculation,and the average temperature calculation formula is corrected.The results of the average temperature calculation formula were compared with the results of the thermal steady-state numerical simulation of the single-row pipe freezing using ANSYS.The pipe spacing l=0.4,0.6,0.8,1.0,1.2,1.4 m,and there are six kinds of frozen development states with relative thickness ξ/l=0.5,0.6,0.7,0.8,1.0 and 1.5.The values of soil parameters are taken according to the test report and the freezing parameters are commonly used in engineering.The comparison calculation results show that the formula calculation is in good agreement with the numerical calculation results.When the relative thickness is over more than 0.5,the difference between the formula calculation result and the numerical calculation result is rapidly reduced to within 0.5 ℃ with the development of the frozen soil thickness (relative thickness increase).When the relative thickness is greater than 0.6,the difference between the results is less than 0.2 ℃.When the relative thickness is 1 or greater,the difference is less than 0.1 ℃.The accuracy of the average temperature calculation formula is verified by numerical simulation,and the rationality of the formula simplification and correction is also explained.The error calculated by the formula satisfies the requirements of engineering application.
Key words:artificial ground freezing;single row-piped freezing;analytical solution of steady-state temperature field;average temperature;numerical simulation
胡向东,刘阳辉,洪泽群,等.直线形单排管冻土帷幕平均温度计算[J].煤炭学报,2019,44(4):1092-1097.doi:10.13225/j.cnki.jccs.2018.0709
HU Xiangdong,LIU Yanghui,HONG Zequn,et al.Calculation of average temperature of frozen soil wall by single row-piped freezing[J].Journal of China Coal Society,2019,44(4):1092-1097.doi:10.13225/j.cnki.jccs.2018.0709
在人工地层冻结技术运用过程中,需要对冻土结构进行力学分析计算,此时通常假设冻土为均质介质,选用冻土帷幕平均温度所对应的物理力学参数作为均质假定下冻土结构材料参数。因此冻土帷幕的平均温度不仅仅是冻结效果的重要判据,也是确定冻土力学参数,进行冻土帷幕承载力评估的重要依据。
目前常用的平均温度求解方法有:积分法、等效截面法、经验公式法。积分法是利用已有的温度场解析公式,对冻土区域进行积分求解,直接求得平均温度。由于温度场的解析公式较为复杂,积分求解的难度较大,目前这一方法的研究较少。等效截面法是以冻结壁某一横截面的平均温度来代表整体冻结壁的平均温度,诸如笔者所提出的利用等效三角形法、等效梯形法、等效抛物弓或梯形-抛物弓叠合得到的特征截面处的平均温度来代替帷幕的平均温度[1-4]。单排管冻结平均温度等效计算的基础是巴霍尔金的温度场解析公式,因此计算准确性得到保证,但截面的选取和计算过程较为繁琐。经验法求解冻土帷幕的平均温度也是一种可行办法。陈文豹、汤志斌基于大量实测数据,给出了计算平均温度的“成冰公式”[5],但该公式过于保守,适用性较差[6],汪仁和等学者根据数值计算结果拟合出平均温度的计算公式[7],笔者根据等效截面计算公式形式也给出了平均温度的经验公式[8]。
目前,直线排管冻结温度场解析解主要有巴霍尔金单排、双排[9]和笔者的三排管稳态温度场解析解[10],这些解有较高的准确性[11-12]。本文将以笔者采用边界分离法得到的单排管冻结稳态温度场解析解为基础[13-14],采用积分法推导平均温度的直接计算公式。
单排管冻结的模型如图1所示。在单排管的管间距相等,冻结管表面温度相等情况下,笔者利用边界分离法得到稳态温度场解析公式(1)[14]:

(1)
式中,T(x,y)为任意点(x,y)的温度,℃;Tf为冻结管外表面温度,℃;ξ 为冻土帷幕厚度之半,m;l为相邻冻结管间距,m;r0为冻结管外半径,m。

图1 单排管冻结模型
Fig.1 Model of single row-piped freezing
式(1)按照工程实际参数近似处理可以简化成巴霍尔金的单排管冻结温度场解析公式。
由图1所示,根据模型的对称性,冻土帷幕的平均温度tcp为T(x,y)在给定区域(-l/2<x<l/2,0<y<ξ)的平均值,即
(2)
把式(1)代入式(2),得到单排管冻结平均温度的计算式。
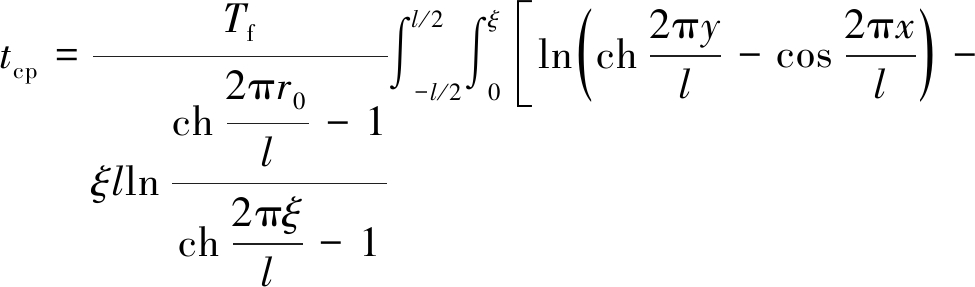
![]()
(3)
式(3)主要问题是积分
(4)
利用贝塞特求和公式[15],得
(5)
对式(5)的积分部分进行分部积分,得到积分结果为
再次运用贝塞特求和公式,得
上式积分项在积分区间(-l/2<x<l/2)是连续函数,使用积分中值定理,并代入式(6),最终得到式(4)的积分结果,即
![]()
(6)
其中,X为区间(-l/2,l/2)内的某个实数。
将式(6)代入式(3),得到单排管冻结冻土帷幕平均温度为
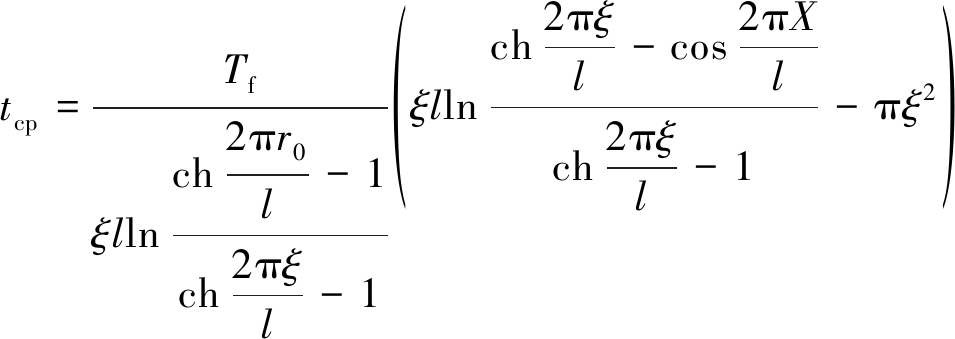
(7)
考虑到土层的冻结温度T0的单排管冻结平均计算公式为

T0
(8)
在冻结后期,有πξ/l >1,所以ch(2πξ/l)远大于cos(2πX/l),得ch(2πξ/l)-cos(2πX/l)≈ch(2πξ/l)-1,式(8)可简化为
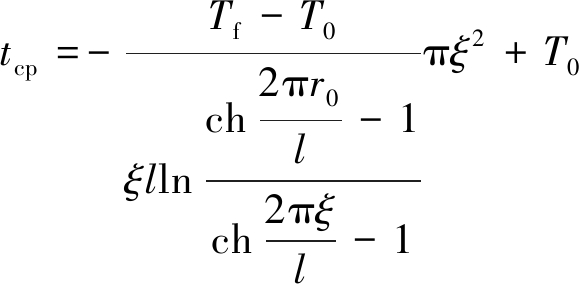
(9)
在上述推导过程,积分区域包含了冻结管部分,实际土层的平均温度的计算不应包含上述区域。同时,由于T(x,y)在冻结管圆心(0,0)处的取值趋于无穷,无法确定冻结管处的温度对积分结果的影响。因此需要对式(9)进行修正,减小偏差。
由于曲线积分较为困难,修正将采用已有积分策略对矩形区域(-r0<x<r0,0<y<r0)进行温度积分,整理得到修正后的平均温度表达式(11):
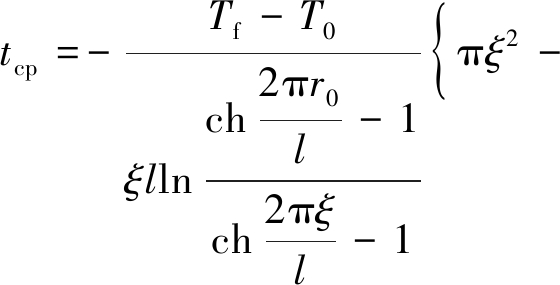
![]()
(10)
上述修正是对矩形区域(-r0<x<r0,0<y<r0)的区域进行温度积分,此时又有新的误差来源(矩形区域与冻结管的差集)。第3节将对此部分产生的误差的影响进行分析。
本文推导的平均温度计算公式是基于单排管冻结的稳态解析解,并根据实际工程对一些参数进行了简化,因此需要对解析公式的准确性进行研究。本文ANSYS进行热学数值计算,来研究公式的准确性和精度,确定计算公式的适用范围,即ξ/l满足什么条件时,理论计算较为精确。
考虑到单排管冻结布管形式的对称性,计算选取1/4区域,如图2所示。土性参数选取根据《上海地区人工冻土物理力学性能试验及其应用技术研究报告》[16],主要参数的取值初始温度为-20 ℃;冻土导热系数为172 W/(m·K);未冻土导热系数为122 W/(m·K);比热容为1.65 kJ/(kg·℃)。冻结参数根据常见情况,取Tf=-30 ℃,T0=0 ℃,r0=0.054 m,选用管间距l=0.4,0.6,0.8,1.0,1.2,1.4 m,考虑ξ/l=0.5,0.6,0.7,0.8,1.0,1.5共6种冻结发展状态。图3为l=1.0 m,ξ/l=0.8计算结果的温度云图。理论计算采用式(11),计算结果见表1,其中绝对误差为理论计算与数值计算结果的差值。

图2 计算模型
Fig.2 Calculation model

图3 l=1.0 m,ξ/l=0.8的温度云图
Fig.3 Contour plot of calculation results
将修正公式和数值计算的结果进行比较,如图4所示。
根据计算结果及对比,得到以下结论。
(1)理论计算结果与数值计算结果较为吻合。所完成的算例中,平均温度的误差小于0.5 ℃,随着冻土厚度的发展,理论计算结果与数值计算结果的差值逐渐减小。
(2)针对第2节提出得矩形修正区域与冻结管的差集,在常见布管参数条件下,该区域对计算结果的影响是有限的。这片区域的土体温度约为-30 ℃,面积约为0.001 3 m2。取最不利情况(冻土区域最小),l=0.4 m,ξ=0.2 m计算。这片区域造成的误差约为0.47 ℃,随着冻土厚度的发展,误差逐渐减小。同时,这块区域对理论计算的影响是提高平均温度,使计算结果偏向安全。因此采用矩形区域进行修正是可行的。
表1 计算结果
Table 1 Calculation results


图4 结果对比
Fig.4 Calculation results
(1)基于单排管冻结稳态温度场解析解,本文采用积分法推导出冻土帷幕平均温度的直接计算公式,并对在冻结管附近的计算进行了修正。
(2)根据算例,随着冻土厚度的发展(相对厚度的增大),理论计算结果与数值计算结果的差值迅速减小到0.5 ℃以内,当相对厚度大于0.6时,对比计算结果的差值小于0.2 ℃。当相对厚度为1及以上时,差值小于0.1 ℃。通过数值模拟验证了平均温度计算公式的准确性,也说明公式简化和修正的合理性,公式计算的误差满足工程应用的要求。
参考文献:
[1] 胡向东.直线形单排管冻土帷幕平均温度计算方法[J].冰川冻土,2010,32(4):778-785.
HU Xiangdong.Average temperature calculation for the straight single-row-pipe frozen soil wall[J].Journal of Glaciology and Geocryology,2010,32(4):778-785.
[2] HU Xiangdong.Average temperature model of double-row-pipe frozen soil wall by equivalent trapezoid method[A].The Second International Symposium on Computational Mechanics (ISCM II) and The Twelfth International Conference on the Enhancement and Promotion of Computational Methods in Engineering and Science (EPMESCXII)[C].Hong Kong Macau,2009:1333-1338.
[3] 胡向东,赵飞,佘思源,等.直线双排管冻结壁平均温度的等效抛物弓形模型[J].煤炭学报,2012,37(1):28-32.
HU Xiangdong,ZHAO Fei,SHE Siyuan,et al.Equivalent parabolic arch method of average temperature calculation for straight double-row-pipe frozen soil wall[J].Journal of China Coal Society,2012,37(1):28-32.
[4] 胡向东,任辉.三排管冻结梯形-抛物弓叠合等效温度场模型和平均温度[J].煤炭学报,2014,39(1):78-83.
HU Xiangdong,REN Hui.A trapezoidal-parabolic arch superimposed equivalent temperature field model and its average temperature for-mula for triple-row-pipe freezing[J].Journal of China Coal Society,2014,39(1):78-83.
[5] 陈文豹,汤志斌.潘集矿区冻结壁平均温度及冻结孔布置圈径的探讨[J].煤炭学报,1982(1):46-52.
CHEN Wenbao,TANG Zhibin.The average temperature in ice wall and the diameter of frozen circle in Panji Coal Field[J].Journal of China Coal Society,1982(1):46-52.
[6] 何挺秀,胡向东.冻土帷幕平均温度“成冰”公式的适应性研究[J].低温建筑技术,2009,31(5):77-81.
HE Tingxiu,HU Xiangdong.Study on adaptability of “CHENG-BING” formula for average temperature of frozen soil wall[J].Low Temperature Architecture Technology,2009,31(5):77-81.
[7] 汪仁和,曹荣斌.双排管冻结下冻结壁温度场形成特征的数值分析[J].冰川冻土,2002,24(2):181-185.
WANG Renhe,CAO Rongbin.FEM analysis of transient freezing temperature field of frozen multi-wall tube[J].Journal of Glaciology and Geocryology,2002,24(2):181-185.
[8] 胡向东,郭晓东.直线排管冻结冻土帷幕平均温度通用公式[J].煤炭学报,2016,41(4):850-857.
HU Xiangdong,GUO Xiaodong.Unified formula for average temperature of frozen soil wall by row-piped freezing[J].Journal of China Coal Society,2016,41(4):850-857.
[9] Бахолдин Б В.Выбор оптимального режима замораживания грунтов в строительных целях[M].Москва:Госстройиздат,1963.
[10] 胡向东,汪洋.三排管冻结温度场的势函数叠加法解析解[J].岩石力学与工程学报,2012,31(5):1071-1080.
HU Xiangdong,WANG Yang.Analytical solution of three-row-piped frozen temperature field by means of superposition of potential[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(5):1071-1080.
[11] 胡向东,白楠,余锋.单排管冻结温度场ТРУПАК和БАХОЛДИН公式的适用性[J].同济大学学报(自然科学版),2008,36(7):906-910.
HU Xiangdong,BAI Nan,YU Feng.Analysis of trupak and bakholdin formulas for temperature field of single-row-pipe frozen soil wall[J].Journal of Tongji University(Natural Science),2008,36(7):906-910.
[12] 胡向东,赵俊杰.人工冻结温度场巴霍尔金模型准确性研究[J].地下空间与工程学报,2010,6(1):96-101.
HU Xiangdong,ZHAO Junjie.Research on precision of Bakholdin model for temperature field of artificial ground freezing[J].Chinese Journal of Underground Space and Engineering,2010,6(1):96-101.
[13] HU Xiangdong,HAN Yanguang.Analytical solution to steady-state temperature field of asymmetric frozen soil wall by single-row-pipe freezing[A].International Conference on Advances in Physics and Engineering Mathematics[C].2013.
[14] 韩延广.人工地层冻结稳态温度场边界分离解析方法及新解答[D].上海:同济大学,2015:41.
HAN Yanguang.Boundary separation method for static temperature field of artificial ground freezing and new analytical solutions[D].Shanghai:Tongji University,2015:41.
[15] WILLIAM H.Reservoir engineering and conformal mapping of oil and gas fields[M].Tulsa:The Petroleum Publishing Company,1979:115-118.
[16] 上海地区人工冻土物理力学性能试验及应用技术研究报告[R].上海:上海申通轨道交通研究咨询有限公司,2010.
Research report on physical and mechanical properties test and application technology of artificial frozen soil in Shanghai[R].Shanghai:Shanghai Shentong Rail Transit Research & Consultancy Co.,Ltd.,2010.