1016 李立功，张晓雨，李 超，张润旭，康天合
(太原理工大学 原位改性采矿省部共建教育部重点实验室，山西 太原 030024)
摘 要:渗透率是影响煤层气开发的关键参数之一，采用测井方法可以较为全面的获取储层渗透率，但测井方法求取的渗透率的准确度主要依赖于建立孔隙结构与渗透率关系计算模型。目前渗透率计算模型大都是基于平均孔径所建立的，忽略了孔隙分布特征对渗透率的影响。对于孔隙分布较为均匀的常规储层而言，孔隙分布对渗透率的影响不大，但对于孔隙结构复杂的低渗透煤层而言，孔隙分布对渗透率(尤其是气体渗透率)的影响不容忽视。采用上海纽迈公司生产的MesoMR23-060H-I型核磁共振仪及太原理工大学自主研发的气体渗透率测试仪对山西西山煤田古交区块8号煤孔径分布特征与气体渗透率的关系进行研究，建立了考虑孔径分布的气体渗透率计算模型;比较新模型、基于平均孔径模型所计算的气体渗透率与实测气体渗透率的差异;以孔径分布符合高斯分布为例，研究了孔隙分布特征对气体渗透率的影响。研究结果表明:在考虑孔径分布的影响后，考虑孔径分布气体渗透率计算模型计算结果与实测值符合度较基于平均孔径计算结果符合度更好;当孔隙分布满足高斯分布时，孔隙率、气体压力和分布期望相同的低渗透煤样，标准差越大，孔隙结构越复杂，气体渗透率越大，与基于平均孔径所计算的气体渗透率差异越大，当标准差从0.05增加到0.18时考虑孔径分布计算的气体渗透率由3.97×10-15m2变为4.2×10-15m2，变化幅度达10.7%，考虑孔径分布模型与基于平均孔径模型计算气体渗透率结果的差异率由0.97%变为11.78%;孔隙率、气体压力和标准差相同的低渗透煤样，分布期望值越大，气体渗透率越大，与基于平均孔径所计算的气测渗透率差异越小，当期望由0.35变为0.55时，考虑孔径分布计算的气体渗透率由2.18×10-15m2变为4.86×10-15m2，变化幅度达123%;在计算孔隙结构较为复杂的低渗透煤储层渗透率时，新模型可以更为准确的计算低渗透煤储层气体渗透率。
关键词:低渗透煤储层;孔径分布;气体渗透率;高斯分布
中图分类号:P618.11
文献标志码:A
文章编号:0253-9993(2019)04-1161-08
收稿日期:20181016
修回日期:20190328
责任编辑:韩晋平
基金项目:国家自然科学基金资助项目(U1810102)
作者简介:李立功(1986—)，男，山西大同人，博士研究生。E-mail:13453157358@163.com
通讯作者:康天合(1959—)，男，山西运城人，教授，博士。E-mail:kangtianhe@163.com
LI Ligong,ZHANG Xiaoyu,LI Chao,ZHANG Runxu,KANG Tianhe
(Key Laboratory of In-situ Property-improving Mining of Ministry of Education,Taiyuan University of Technology,Taiyuan 030024,China)
Abstract:Permeability is one of the key parameters affecting the development of coal-bed gas.The logging method can be used to obtain the reservoir permeability comprehensively,however,the accuracy of the logging method mainly depends on the computation model of the relationship between pore size and permeability.At present,computation models for gas permeability are mostly based on the assumption that the pore size is the same,ignoring the influence of the distribution of pore size.For conventional reservoirs with uniform pore distribution,the error of permeability between predicated value and the measured value can be ignored.However,for low permeability reservoirs with complex pore sizes,the distribution of pore size has tremendous influence on permeability,especially gas permeability,the error is very large that cannot be ignored.The relationship between the distribution characteristics of pore size and gas permeability of No.8 coal seam in the Gujiao coalmine of Shanxi Xishan Coal Mining Group was studied by MesoMR23-060H-I,NMR spectrometer manufactured by Shanghai Newmai Company,and the device of gas perme-ability developed by Taiyuan University of Technology independently.Then the computation model of gas permeability considering pore size distribution was established.The difference of gas permeability between measured values,calculated by the new model and calculated by the traditional models was compared.Taking the Gaussian distribution of pore size as an example,the effect of distribution of pore size on gas permeability was studied.The results indicated that the calculated results by the new model was in more agreement for the measured gas permeability than that of the traditional models.Assume that the coal samples obtained from low permeability coal seam with same porosity,gas pressure and distribution expectation,and the pore size satisfied the Gaussian distribution,when the standard deviation was larger,the pore structure was more complicated,the gas permeability was larger,and the difference of gas permeability was larger compared with computation models.When the standard deviation increased from 0.05 to 0.18,the gas permeability calculated with pore size distribution was changed from 3.97×10-15m2 to 4.2×10-15m2,with an increase of 10.7%,and the difference changed from 0.97% to 11.78% compared with computation models.Assuming that coal samples were obtained from low permeability coal seam with same porosity and standard deviation,and the pore size satisfied the Gaussian distribution,when distribution expectation was larger,the gas permeability was larger,the gas permeability calculated by the new model is less different from traditional models.When the expectation changed from 0.35 to 0.55,the gas permeability calculated with pore size distribution was changed from 2.18×10-15m2 to 4.86×10-15m2,with an increase of 123%.When calculating the permeability of low permeability coal seams with complex pore size,the new model can calculate the gas permeability more accurately.
Key words:low permeability coal seam;distribution of pore size;gas permeability;Gaussian distribution
移动阅读
李立功，张晓雨，李超，等.考虑孔径分布的低渗透煤层气体渗透率计算模型[J].煤炭学报,2019,44(4):1161-1168.doi:10.13225/j.cnki.jccs.2018.1379
LI Ligong,ZHANG Xiaoyu,LI Chao,et al.A computation model for gas permeability in low permeability coal seam considering the distribution of pore size[J].Journal of China Coal Society,2019,44(4):1161-1168.doi:10.13225/j.cnki.jccs.2018.1379
渗透率在油气田开发中起着十分重要的作用。井的数量、井间距的确定和储层改造方式的选取等都离不开渗透率的准确获取[1]。目前，获得储层渗透率的途径主要有岩芯实验室测量渗透率[2-3]、地震解释渗透率[4]、电缆地层测试渗透率[5]、钻杆地层测试渗透率[6]以及测井解释渗透率等方法。但前几种方法相对于测井解释获取渗透率，其成本较高，且受到各种限制。因此，在地层评价中常常利用测井数据来获取连续的地层渗透率资料[7-8]。核磁共振测井技术[9-10]为基于测量信号直接反映储层孔隙度分布的测量方法，不仅能够测量孔隙度的大小，还能够识别不同孔隙直径所对应的孔隙度，最终得到不同孔隙类型及分布状况，然后通过孔隙与渗透率的关系，建立测井渗透率模型，进而获取储层渗透率。采用测井方法可以较为全面的获取储层渗透率，但测井方法求取的渗透率的准确度主要依赖于建立孔隙结构与渗透率关系计算模型。因此，研究储层孔隙结构与渗透率之间的关系，建立孔隙结构与渗透率关系模型是测井方法准确获取渗透率的关键。目前常用的渗透率模型大都是基于平均孔隙半径所建立的，如KLINKENBERG[11]、BESKOK和KARNIADAKIS[12]、COATES[13]、JAVADPOUR[14]、CIVAN[15]、ZIARANI[16]、李立功[17]等依据岩石的宏观孔隙率或者将岩石孔隙等效为n个半径相同的毛细管，并基于不同假设条件下的微管模型提出了气体渗透率计算公式。CAO[18]、BANAVAR[19]、LATOUR[20]、BERNAB
Y[21]、韩玉娇[22]等在研究低渗透储层渗透率时发现采用平均孔径计算的渗透率与实测值有较大差异，对于常规储层而言，其孔喉相对均匀，采用平均孔喉半径来研究储层渗透率准确度较好，但对于孔隙结构较为复杂的低渗透储层而言，孔喉分布与常规储层有明显的区别，孔隙结构较常规储层复杂的多，呈现强烈的非均质性特征，采用平均孔径来计算储层渗透率，忽略了储层孔隙分布特征这一关键因素，其计算结果与储层真实渗透率可能存在较大差距。
鉴于此，笔者针对我国山西地区低渗透煤层孔隙结构复杂的特点，提出利用核磁测井T2频谱测得的孔隙分布资料，建立考虑孔径分布特征的低渗透煤储层气体渗透率计算模型，使用实验室试验数据验证模型计算结果的准确性;以孔径分布符合高斯分布为例，分析孔隙分布特征对低渗透煤储层渗透率的影响，比较新模型与基于平均孔径计算渗透率的差异，分析新模型的适用性。
为了便于描述，对模型做如下假设:① 低渗透煤储层孔隙可以等效为不同孔径的微管，且各管之间不连通，微管长度为l=τL，其中τ为微管迂曲度;L为试件长度，如图1所示;② 微管不可压缩，即不考虑孔隙压力变化引起的孔隙半径变化;③ 不考虑气体吸附、解吸引起的孔隙半径变化。
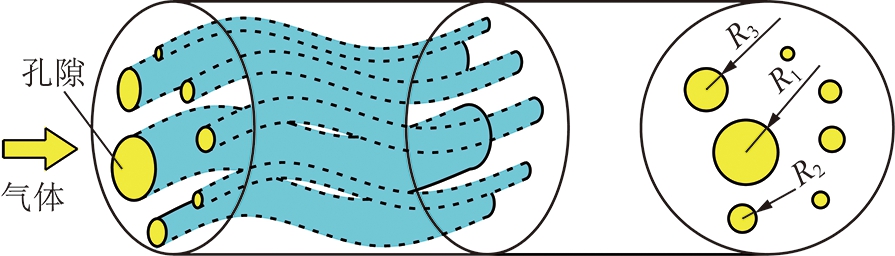
图1 低渗透煤储层等效孔隙示意
Fig.1 Equivalent pores of low permeability coal reservoir
依据Klinkenberg给出在时间t内单个微管在半径r0到r0+dr区域流过的气体体积[11]为
(1)
式中，μ为气体黏度，Pa·s;p为压力，MPa;c为比例因子，一般取0.9，无量纲;λ为平均分子自由程，m。
通过整个微管横截面积的体积为
(2)
根据气体状态方程，单位时间内微管中压力p与气体物质的量n的关系为
(3)
式中，R为普氏气体常数，J/(mol·K);T为温度，K;n为物质的量，mol。
将式(3)代入式(2)，整个毛细管长度上压力与物质的量的关系为
(4)
(5)
式中，p为毛细管内气体平均压力;p1为进口压力，MPa;p2为出口压力，MPa。
将式(5)代入式(4)得
(6)
理想气体平均分子自由程λ的计算公式[23-24]为
(7)
将式(5)代入式(7)得
(8)
其中，M为气体分子的质量,g/mol。将式(8)代入(6)得半径为r0的单个微管在进口压力p1出口压力p2时的气体流量Qg为
(9)
将储层孔隙等效为n1个孔径为r1,n2个孔径为r2，…，nn个孔径为rn的几何体，假设半径为ri的孔，其分布频率为f(ri)，则ni可表示为
(10)
其中，φ为储层孔隙率。通过ni个半径为ri孔的总流量Qg(ri)为
(11)
通过储层的总流量Qg可表示为
(12)
对于气体在多孔介质中流动，其流量可表示为
(13)
由式(12)，(13)得考虑孔径分布的气体渗透率计算表达式为
(14)
采用山西西山煤田古交区块8号低渗透煤样孔径分布及气体渗透率测试数据进行实例验证。核磁共振测井作为目前惟一能够表征储层孔隙结构的测井方法，具有快速、无损害、可重复等优点，能够实现致密岩石微米-纳米级孔隙的高精度测量[25-26]。因此，本试验孔径分布测试采用核磁共振T2谱获取。试验使用仪器为上海纽迈公司生产的MesoMR23-060H-I型核磁共振仪，共振频率为21.68 MHz，射频脉冲频率21.68 MHz。将现场取回煤样制成φ25 mm ×60 mm 的规格制成圆柱形煤样，将煤样放在干燥箱中干燥12 h以上，将干燥过后的煤样放入核磁共振仪中采集样品的T2频谱，将采集的T2频谱通过式(15)获取孔径分布[27-28]:
(15)
式中，Fs称为几何形状因子，对球状孔隙，Fs=3;对柱状管道，Fs=2;ρ2为岩石的横向表面弛豫强度，μm/ms。
不同煤样核磁共振孔径分布如图2所示。
图2 山西地区低渗透煤样核磁共振孔径分布
Fig.2 NMR pore size distribution of low permeability coal samples in Shanxi area
基于平均孔径计算气体渗透率计算采用Klinkenberg给出的气体渗透率式(KLINKENBERG L J，1941):
(16)
式中，
为平均孔隙半径，m，其表达式为
为滑脱系数，MPa，其表达式为
(17)
考虑孔径分布气体渗透率计算依据式(14)。
实验室测试气体渗透率采用太原理工大学原位改性采矿省部共建教育部重点实验室自主研发的三轴渗透仪对所取试样进行测试。测试气体为氮气，实验室实测与计算所取平均孔隙压力
入口压力p1=1.9 MPa，出口气体压力为大气压p2=0.1 MPa。
考虑孔径分布新模型计算的气体渗透率、基于平均孔径计算的气体渗透率及实验测得的气体渗透率结果如图3所示。计算结果表明，考虑孔径分布计算的气体渗透率与实验测得的气体渗透率具有较好的匹配性，且考虑孔径分布所计算的气体渗透率结果较基于平均孔径所计算的气体渗透率结果更为准确。由图3看出考虑孔径分布气体渗透率模型计算气体渗透率总略大于实测值而基于平均孔径计算的气体渗透率模型总小于实测值。这是因为在实测中采用氮气作为测试气体进行试验，虽然煤样对氮气的吸附性较小，但仍有一定吸附性，吸附氮气后试验膨胀孔隙半径减小，气体渗透率减小，而建立考虑孔径分布的气体渗透率模型时忽略了气体吸附引起的孔径变化，导致其计算的气体渗透率略大于实测值;实际试样各种孔径均存在，而基于平均孔径计算时取孔径的平均值，根据式(16)中滑脱系数与孔隙半径呈反比例关系(图4)，因此
基于平均孔径计算的滑脱系数小于实际值，由此导致基于平均孔径计算的气体渗透率小于实测值。
图3 试验数据、模型计算数据及平均半径计算渗透率比较
Fig.3 Comparison of test data,model calculation data and average radius calculation permeability
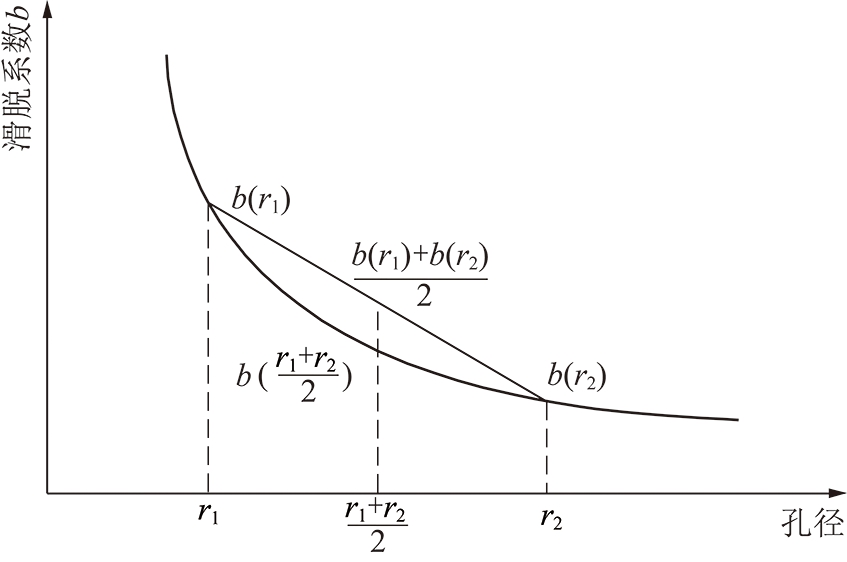
图4 滑脱系数随孔径变化关系示意
Fig.4 Schematic diagram of the relationship between slip factor and pore diameter
为了方便计算，假设孔径与孔径分布频率满足高斯函数，则低渗透煤储层孔径分布频率可表示为
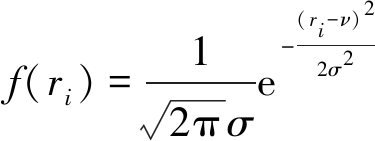
(18)
3.1.1 影响规律
假设孔隙率φ=12%不变，期望ν=0.5，标准差σ=0.05,0.07,0.10,0.13和0.18时，孔径分布如图5所示。
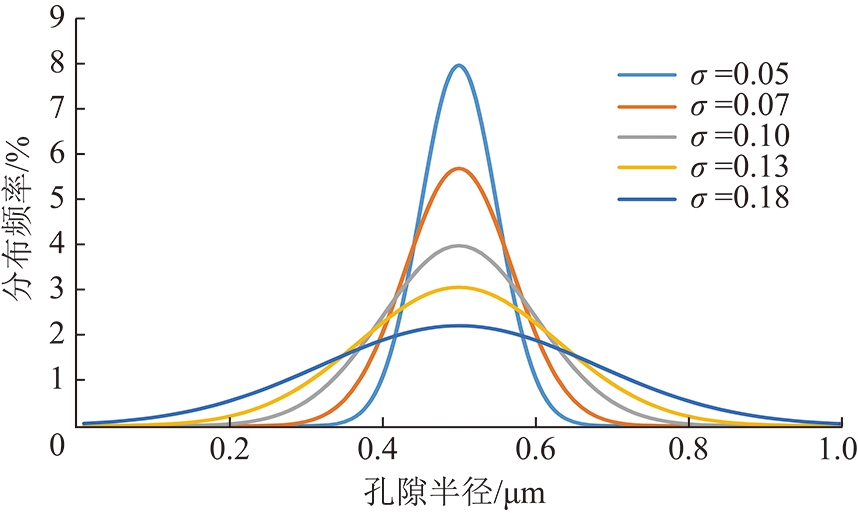
图5 期望为0.5时不同标准差下的孔径分布
Fig.5 Pore diameter distribution diagram for different standard deviations under the expectation is 0.5
图6为孔隙率φ=12%、ν=0.5、平均气体压力为1 MPa下考虑孔径分布与基于平均孔径计算渗透率随标准差变化图。可以看出在孔隙率、期望和孔隙压力一定时随着标准差的增加，气体渗透率逐渐增大，即在φ,ν和
一定时，孔径分布越分散，气体渗透率越大;孔隙分布越集中气体渗透率越小。气体渗透率从σ=0.05时的3.79×10-15m2增加到σ=0.18时的4.2×10-15m2，增加幅度达10.7%。基于平均孔径所计算的渗透率由于其平均孔径及孔隙率不产生变化，其计算的渗透率结果不随标准差σ变化而变化。
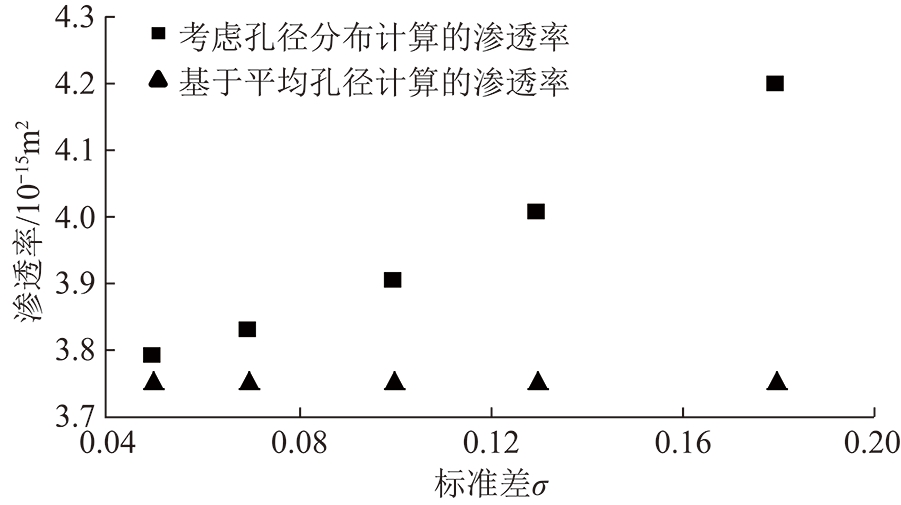
图6 考虑孔径分布与基于平均孔径计算渗透率随标准差变化
Fig.6 Considering the pore size distribution and the variation of calculated permeability with standard deviation based on average pore size
图7为不同标准差下新模型计算结果与基于平均孔径计算结果差异随标准差变化关系。可以看出随标准差的增加考虑孔径分布与基于平均孔径气体渗透率计算模型计算的气体渗透率差异逐渐增大，即在孔隙分布符合高斯分布时，低渗透煤样的孔隙越集中两者差异越小，孔隙分布越分散其差异越大。两者差异由σ=0.05时的0.97%增加到σ=0.18时的11.78%。从考虑孔径分布模型与基于平均孔径模型计算气体渗透率结果的差异可以看出，在研究孔隙较为均匀的常规储层时，即标准差σ较小时，基于平均孔径方法计算的渗透率往往误差较小，采用平均孔径计算气体渗透率基本能满足预测需要，但对于孔隙分布较为复杂的低渗透煤储层而言，即σ较大时，孔隙越复杂(σ越大)其计算结果准确度越差，此时孔径分布特征对渗透率的影响不容忽视，在计算低渗透煤储层气体渗透率时基于平均孔径计算气体渗透率已不能准确获取渗透率值，必须考虑孔隙分布特征对渗透率的影响。
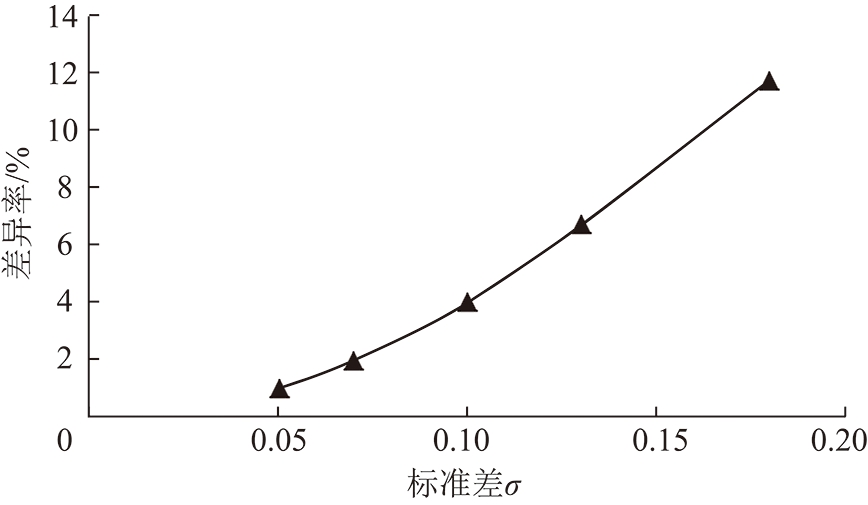
图7 考虑孔径分布模型计算与基于平均孔径模型计算的
气体渗透率差异率随标准差变化关系
Fig.7 Relationship between the gas permeability calculated by the new model and the difference of gas permeability calculated based on average pore diameter varies with standard deviation
3.1.2 影响机理分析
对于半径为r、长度为l的单个微管而言，其在进口压力为p1，出口压力p2(p1>p2)时通过单管的流量Qg(r)可将式(9)表示为
(19)
对Q(r)求二阶导为
(20)
由于p1>p2，r>0，所以Q″(r)>0，根据二阶倒数的性质可知
Qg(r+dr)+Qg(r-dr)<2Qg(r)
(21)
因此，在计算气体渗透率时考虑孔径分布计算的渗透率略大于基于平均孔径所计算的渗透率。在孔隙率和平均孔径相同时，σ越大，偏离平均孔径孔隙所占的比例越大，考虑孔隙分布和基于平均孔径所计算的渗透率差异越大，基于平均孔径所计算的渗透率误差越大。
图8为期望ν=0.35,0.40,0.45,0.50和0.55时及标准差σ=0.15时孔径的高斯分布图。图9为气体渗透率随期望ν变化关系图(p=1 MPa;φ=12%;σ=0.15)。由图9可以看出在孔径分布符合高斯分布时，当低渗透煤样的孔隙率、标准差σ及压力一定，随期望ν的增大，气体渗透率逐渐增大，气体渗透率从ν=0.35时的2.18×10-15增加到ν=0.55时的4.86×10-15，增加幅度达到123%。图10为新模型与基于平均孔径计算气体渗透率差异随期望ν的变化关系，由图10可以看出，在孔隙率和标准差相同时，随着期望ν的增加，2者的差异逐渐减小，当ν=0.35时，2者的差异达到17%，而当ν=0.55时，2者的差异仅为7%。即在孔隙率和孔径分布相同时，储层越致密(平均孔径越小)新模型与基于平均孔径计算的渗透率差异越大。因此，在预测孔径相对较小的低渗透煤储层气体渗透率时，必须考虑孔径分布特征对气体渗透率的影响。
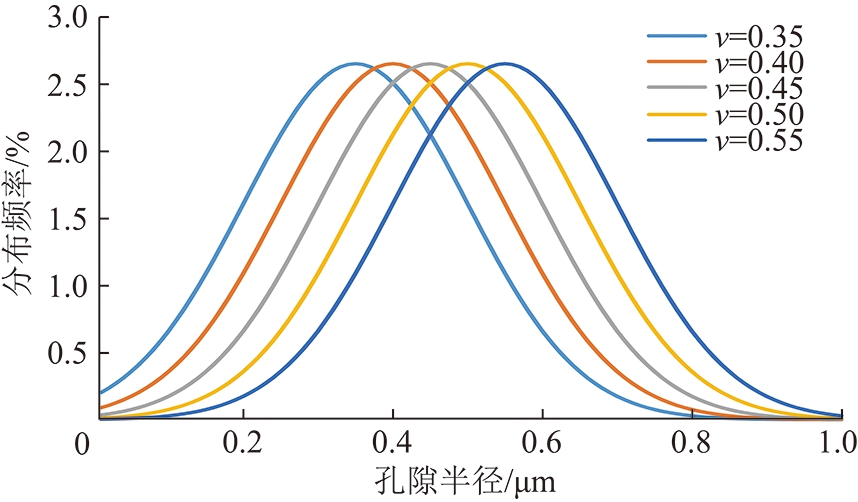
图8 不同期望ν下的孔径高斯分布
Fig.8 Pore diameter of gaussian distribution under the different expectations ν
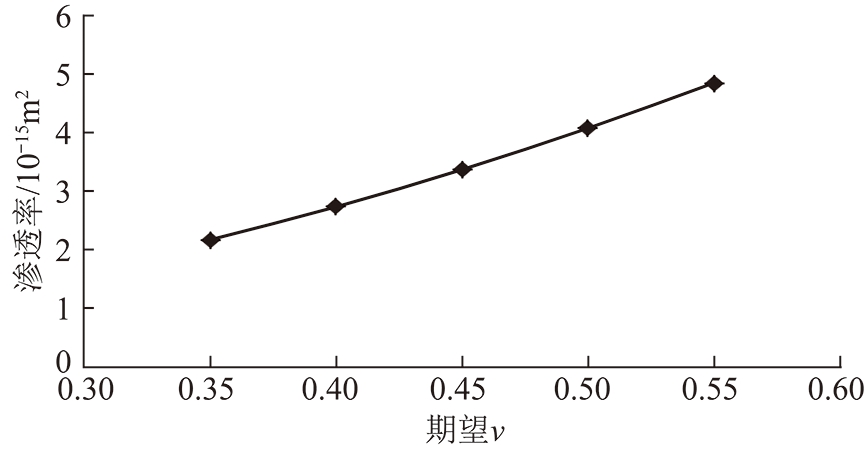
图9 气体渗透率随期望变化关系
Fig.9 Relationship between gas permeability and expectations
图10 考虑孔径分布与基于平均孔径计算气体渗透率差异率随期望变化
Fig.10 Difference between the new model and the calculated gas permeability based on average pore diameter varies with expectation
图11 考虑孔径分布与基于平均孔径计算气体渗透率随压力变化
Fig.11 Change of gas permeability with pressure based on average pore diameter under the considers of the pore diameter distribution
图11为孔径分布为标准差σ=0.1，ν=0.5时考虑孔径分布与基于平均孔径时气体渗透率计算结果。由图11 可以看出，随着压力的降低，气体渗透率急剧增加，压力越低渗透率增加幅度越大，这是由于气体滑脱效应的存在，压力越低，气体滑脱效应越明显，渗透率增加越快。两种方式计算的渗透率在压力大于1 MPa时，两者差异不明显，并且渗透率随压力减小变化均不大。考虑孔径分布计算的渗透率在压力小于1 MPa后，渗透率变化模型，呈快速增加趋势;基于平均孔径计算的渗透率在压力小于0.2 MPa后才呈现快速增加趋势。这是由于孔径越小，滑脱效应引起的渗透率变化量对压力的变化越敏感，考虑孔径分布渗透率计算模型考虑了小于平均孔径滑脱效应对渗透率的影响。
图12为考虑孔径分布与基于平均孔径计算渗透率随压力变化的差异。由图12可以看出，随着压力的降低，两者差异越来越明显，呈增大趋势。这是由于小于平均孔径孔在低压时，滑脱效应的增量随孔径变化的非线性关系，使得考虑孔隙分布计算的渗透率与基于平均孔径计算的渗透率差异逐渐增大。
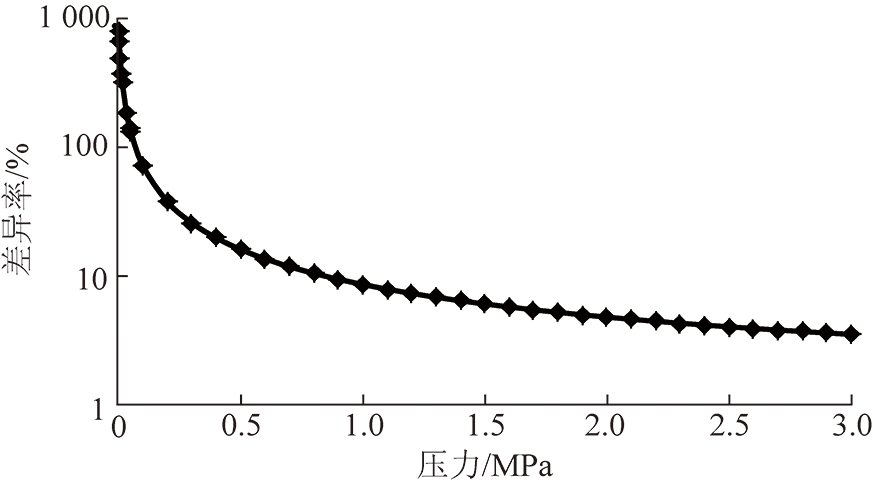
图12 考虑孔径分布与基于平均孔径计算渗透率差异随压力变化
Fig.12 Calculated permeability difference with pressure based on average pore diameter under the considers of the pore diameter distribution
(1)对于低渗透煤储层而言，考虑孔径分布特征的气体渗透率计算结果较基于平均孔径的气体渗透率计算结果与实测数据吻合度更好，计算结果更为精确。
(2)对于孔径较小、孔隙分布复杂的低渗透煤储层而言，采用理论计算的方法计算气体渗透率时孔径分布特征对气体渗透率的影响不可忽略。
(3)在孔隙率和期望ν一定时，σ越大，低渗透煤储层的气测渗透率越大，与基于平均孔径计算的气体渗透率差异越大，当σ=0.18时两者计算结果差异可达11.78%;在孔隙率和标准差σ一定时，ν值越大，气体渗透率越大，与基于平均孔径计算的气体渗透率差异越小;在孔隙率相同时，压力越低考虑孔径分布与基于平均孔径计算的气体渗透率差异越大。针对孔隙分布复杂的低渗透煤储层，计算气体渗透率时，新模型较基于平均孔径模型更为准确。
参考文献:
[1] 孙建孟,闫国亮.渗透率模型研究进展[J].测井技术,2012,36(4):329-335.
SUN Jianmeng,YAN Guoliang.Review on absolute permeability model[J].Well Logging Technology,2012,36(4):329-335.
[2] WANG H L,XU W Y,CAI M,et al.An experimental study on the slippage effect of gas flow in a compact rock[J].Transport in Porous Media,2016,112(1):117-137.
[3] JONES F O,OWENS W W.A laboratory study of low permeability gas sands[J].Society of Petroleum Engineers,1980,32(9):1-10.
[4] YANG Ruizhao,ZHAO Zhengguang,PENG Weijun,et al.Integrated application of 3D seismic and microseismic data in the development of tight gas reservoirs[J].Applied Geophysics,2013,10(2):157-169.
[5] 关富佳,李相方,李菊花,等.考虑各向异性的电缆地层测试产能预测方法[J].中国石油大学学报(自然科学版),2009,33(4):93-97.
GUAN Fujia,LI Xiangfang,LI Juhua,et al.Deliverability prediction method of wireline formation testing considering permeability anisotropy[J].Journal of China University of Petroleum,2009,33(4):93-97.
[6] 任国富,马建国.随钻地层测试技术及其应用[J].测井技术,2005,29(4):385-387.
REN Guofu,MA Jianguo.A technique of formation pressure testing while drilling and its application[J].Well Logging Technology,2005,29(4):385-387.
[7] 贾文玉,闫安宇.渗透率的理论计算方法[J].测井技术,2000,24(3):216-219.
JIA Wenyu,YAN Anyu.Theoretical calculation method of permeability[J].Well Logging Technology,2000,24(3):216-219.
[8] 罗万静.渗透率的常用确定方法及其相互关系[J].西部探矿工程,2006(1):63-64.
LUO Wanjing.Common methods for determining permeability and their relationship[J].West-China Exploration Engineering,2006(1):63-64.
[9] 王忠东,汪浩,李能根,等.核磁共振岩芯基础实验分析[J].测井技术,2001,25(3):170-174.
WANG Zhongdong,WANG Hao,LI Nenggen,et al.Analysis of core NMR data from laboratory measurements[J].Well Logging Technology,2001,25(3):170-174
[10] 常文会,赵永刚,华新军.用核磁共振测井技术评价储层渗透率特性[J].测井技术,2005,29(6):528-530.
CHANG Wenhui,ZHAO Yonggang,HUA Xinjun.On reservoir permeability evaluation with NMR technology[J].Well Logging Technology,2005,29(6):528-530.
[11] KLINKENBERG L J.The permeability of porous media to liquids and gases[J].Socar Proceedings,1941,2(2):200-213.
[12] BESKOK A,KARNIADAKIS G E.A model for flows in channels,pipes and ducts at micro and nano scales[J].Microscale Thermophysical Engineering,1999,3(1):43-77.
[13] COATES G R,MILLER M N,BOUTON J.Nuclear magnetic resonance detection of geologic structures[J].Magnetic Resonance Imaging,1995,13(8):2559.
[14] JAVADPOUR F.Nanopores and apparent permeability of gas flow in mudrocks(shales and siltstone)[J].Journal of Canadian Petroleum Technology,2009,48(8):16-21.
[15] CIVAN F.Effective correlation of apparent gas permeability in tight porous media[J].Transport in Porous Media,2010,82(2):375-384.
[16] ZIARANI A S,AGUILERA R.Knudsen’s permeability correction for tight porous media[J].Transport in Porous Media,2012,91(1):239-260.
[17] 李立功,康天合,李彦斌.考虑动态克林伯格系数的煤储层渗透率预测模型[J].地球物理学报,2018,61(1):304-310.
LI Ligong,KANG Tianhe,LI Yanbin.Prediction model of permeability in coal reservoirs considering the dynamic Klinkenberg coefficient[J].Chinese J.Geophys,2018,61(1):304-310.
[18] CAO R,WANG Y,CHENG L,et al.A new model for determining the effective permeability of tight formation[J].Transport in Porous Media,2016,112(1):21-37.
[19] BERNAB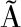
Y,BRUDERER C.Effect of the variance of pore size distribution on the transport properties of heterogeneous networks[J].Journal of Geophysical Research Solid Earth,1998,103(B1):513-525.
[20] LATOUR L L,KLEINBERG R L,MITRA P P,et al.Pore-size distributions and tortuosity in heterogeneous porous media[J].Journal of Magnetic Resonance,1995,112(1):83-91.
[21] BANAVAR J R,JOHNSON D L.Characteristic pore sizes and tran-sport in porous media[J].Physical Review B,1987,35(13):7283-7286.
[22] 韩玉娇,周灿灿,范宜仁,等.基于孔径组分的核磁共振测井渗透率计算新方法——以中东A油田生物碎屑灰岩储集层为例[J].石油勘探与开发,2018,45(1):170-178.
HAN Yujiao,ZHOU Cancan,FAN Yiren,et al.A new permeability calculation method using nuclear magnetic resonance logging based on pore sizes:A case study of bioclastic limestone reservoirs in the A oilfield of the Mid-East[J].Petroleum Exploration and Development,2018,45(1):170-178.
[23] CIVAN F,RAI C S,SONDERGELD C H.Shale-gas permeability and diffusivity inferred by improved formulation of relevant retention and transport mechanisms[J].Transport in Porous Media,2011,86(3):925-944.
[24] 吴克柳,李相方,陈掌星,等.页岩气复杂孔裂隙真实气体传输机理和数学模型[J].中国科学:技术科学,2016,46(8):851-863.
WU Keliu,LI Xiangfang,CHEN Zhangxing,et al.Real gas transport mechanism and mathematical model through complex nanopores and microfractures in shale gas reservoirs[J].Sci.Sin.Tech.,2016,46(8):851-863.
[25] 代全齐,罗群,张晨,等.基于核磁共振新参数的致密油砂岩储层孔隙结构特征———以鄂尔多斯盆地延长组7段为例[J].石油学报,2016,37(7):887-897.
DAI Quanqi,LUO Qun,ZHANG Chen,et.al.Pore structure characteristics of tight-oil sandstone reservoir based on a new parameter measured by NMR experiment:A case study of seventh member in Yanchang formation,Ordos basin[J].Acta Petrolei Sinica,2016,37(7):887-897.
[26] 白松涛,程道解,万金彬,等.砂岩岩石核磁共振T2谱定量表征[J].石油学报,2016,37(3):382-391.
BAI Songtao,CHEN Daojie,WAN Jinbin,et al.Quantitative characterization of sandstone NMR T2 spectrump[J].Acta Petrolei Sinica,2016,37(3):382-391.
[27] 何雨丹,毛志强,肖立志,等.核磁共振T2 分布评价岩石孔径分布的改进方法[J].地球物理学报,2005,48(2):373-378.
HE Yudan,MAO Zhiqiang,XIAO Lizhi,et al.An improved method of using NMR T2 distribution to evaluate pore size distribution[J].Chinese J.Geophys,2005,48(2):373-378.
[28] 李军,金武军,王亮,等.页岩气岩芯核磁共振T2与孔径尺寸定量关系[J].测井技术,2016,40(4):460-464.
LI Jun,JIN Wujun,WANG Liang,et al.Quantitative relationship between NMR T2 and pore size of shale gas reservoir from core experiment[J].Well Logging Technology,2016,40(4):460-464.