汪金花,郭云飞,郭立稳,张 博,吴 兵
(华北理工大学 矿业工程学院,河北 唐山 063210)
摘 要:针对井下生产管理、灾后避险以及定点搜救的高精度定位需求,提出一种标签识别与地磁匹配组合定位的GRPM方法。GRPM方法是从井下物联网的智能化角度,设计的一种高精度、自主、新型的井下定位方法。结合井下实际地磁测量时噪声干扰较大,地磁异常场空间分布不明显、缓变或特征相似情况下的地磁匹配定位精度低的问题,建立了一种地磁空间向量积的最优估计匹配模型MPMD,也称为磁特征参量联合距离匹配算法。试验选取了模拟矿井的2个水平巷道H-11和H-21,通过对2个巷道地磁数据的均值、标准差、粗糙度和信息熵的统计分析,评价出H-11为地磁定位弱适配区,H-21为强适配区。在H-11和H-21巷道内开展了MSD,MAD,MPMD算法匹配定位的对比试验,分析了3种算法在地磁变化、噪声扰动下的地磁匹配的精度和抗噪性能。结果表明:在地磁特征丰富的H-21强适配区,3种算法的总体匹配概率都达到了95%以上,但MPMD定位精度高于MSD,MAD算法,基本上保持在一个网格间格内;在地磁特征贫乏的H-11弱适配区,MPMD算法能够较好的处理模糊匹配多值问题,不易出现虚定位。在H-21强适配区开展了算法性能测试,当噪声为200 nT时,MSD和MAD匹配有少量虚定位,MPMD算法匹配结果基本无误差,效果很好;在噪声400 nT和600 nT抗噪性能试验中,MSD和MAD匹配出现大量虚定位,MPMD算法有少量虚定位,总体匹配概率也达到了89%,表现出较强的鲁棒性。MPMD算法是一种有效高精度地磁匹配方法,在准确度、精度和鲁棒性方面确实具有明显优势,但匹配过程耗时较多,需要从搜索策略上进一步优化。
关键词:井下地磁定位;GRPM定位;匹配算法;MPMD匹配;射频识别;鲁棒性
中图分类号:TD76
文献标志码:A
文章编号:0253-9993(2019)04-1274-09
收稿日期:2018![]() 06
06![]() 15
15
修回日期:2019![]() 01
01![]() 01
01
责任编辑:郭晓炜
基金项目:国家自然科学基金面上资助项目(51374089);河北省自然科学基金资助项目(E2018209345);河北省博士研究生创新资助项目(CXZZBS2017123)
作者简介:汪金花(1974—),女,新疆伊宁人,教授,博士研究生。E-mail:jinhua66688@126.com
通讯作者:郭立稳(1964—),男,河北石家庄人,教授,博士生导师。E-mail:guoliwen64@163.com
WANG Jinhua,GUO Yunfei,GUO Liwen,ZHANG Bo,WU Bing
(College of Mining Engineering,North China University of Science and Technology,Tangshan 063210,China)
Abstract:Experimental research and theoretical analysis of MPMD matching algorithm based on the GRPM underground positioningHigh-precision positioning service is important for the underground production management,the intelligent escape and the emergency search.A novel method named GRPM was proposed in this paper,which is the combination of the radio frequency identification and the geomagnetic matching.GRPM is the positioning method with a high precision,autonomous,and suitable for the mine Internet of Things.The MPMD algorithm based on GRPM is a matching model for the optimal estimation of the joint distance of two-dimensional magnetic parameters,which can solve the problem of low accuracy of geomagnetic matching because the spatial distribution of geomagnetic anomaly field is not obvious,slowly changing or similar.Two horizontal roadways named H-11 and H-21 in simulated mine were selected in the study.The suitability of geomagnetic positioning in the H-21 roadway is good and in the H-11 roadway is poor,which were obtained through the statistical analysis of the mean,standard deviation,roughness and information entropy of their geomagnetic data.The geomagnetic matching studies with MSD,MAD,and MPMD algorithms in the H-11 and H-21 roadways were carried out to compare the positioning accuracy and anti-noise performance of the three algorithms under the conditions of geomagnetic variation and noise disturbance.The study results show that the matching probability of the three matching algorithms all reached more than 95% in the roadway H-21 with abundant geomagnetic features,the matching accuracy of MPMD is higher than that of MSD and MAD,its matching error keep within a grid.MPMD algorithm is better than MSD and MAD algorithm in dealing with the problem of fuzzy matching value in H-11 roadway with poor geomagnetic features,and its matching results show few false locations.The algorithm performance was tested in the H-21 roadway,there is a small amount of false location in the MSD and MAD matching under the 200 nT measurement noise,and the matching result of MPMD is nearly error-free.There are a lot of virtual localization in the matching result of MSD and MAD under the 400 nT or 600 nT measurement noise,and MPMD has a few false locations,and the matching probability still reaches 89%.MPMD matching algorithm is an effective and high-precision geomagnetic matching method,which has obvious advantages in accuracy and robustness.However,its matching process is more computational and time-consuming than other algorithms,which needs further optimization in the search strategy.
Key words:underground magnetic positioning;GRPM positioning;matching algorithm;MPMD matching;radio frequency identification;robustness
汪金花,郭云飞,郭立稳,等.基于GRPM井下定位的MPMD匹配算法的试验研究[J].煤炭学报,2019,44(4):1274-1282.doi:10.13225/j.cnki.jccs.2018.0793
WANG Jinhua,GUO Yunfei,GUO Liwen,et al.Experimental research of MPMD matching algorithm based on the GRPM underground positioning[J].Journal of China Coal Society,2019,44(4):1274-1282.doi:10.13225/j.cnki.jccs.2018.0793
井下高精度自主定位是井下物联网智能化生产管理、灾后避险以及定点搜救的关键技术。目前井下有RFID,Zigbee,TOA,UWB等多种定位技术和相关产品。其中RFID技术已应用于矿山井下安全管理,有KJ728型、KJ536型、KJ133型等井下定位系统。这类定位系统可以实时查询井下人员的分布地点,运动轨迹等信息,但是实际应用时存在定位盲区,定位精度取决于读卡器硬件分布的密度,精度较低约10 m。现有的矿井Zigbee,TOA,UWB技术在一定程度上弥补了RFID高精度定位的空白,能达到米级或亚米级,但是与井下物联网应用、智能机器人定位要求的厘米级精度还有较大的差距,而且其定位过程主要依赖井下通讯系统、网络和供电,如果井下出现供电中止或信号中断情况,定位系统则不能正常工作[1-5]。GRPM[6](Geomagnetic and RFID Combined Positioning Method),是地磁匹配与标签识别技术组合的一种定位方法,主要针对现有井下定位方法的局限性,从井下物联网的高精度定位和自主导航的需要出发探索的一种新型井下定位方法。这种定位方法是以地磁匹配作为基础理论,在现有井下定位方法基础上,只需要在移动设备或井下人员身上增加一个装置,就能实现精度较高的自主定位。并且在井下供电中止或信号中断情况,仍然能够实现人员自主定位。GRPM定位技术的研究内容涉及井下地磁分布特征、射频识别、地磁探测、地磁相关匹配、组合导航和搜索策略等多个技术问题,其中井下地磁匹配算法研究是井下GRPM定位的关键核心技术之一。
国内外关于地磁匹配算法研究已经取得了一些成果,大部分是关于舰艇导航、无人机定位、卫星定轨的相关研究。如武汉大学测绘学院赵建虎等针对惯导定位INS积累误差及TERCOM匹配算法的机理缺陷,运用Hausdorff距离算法改进了匹配准则,提高了水下地磁匹配导航精度[7]。国防科学技术大学吕云霄等研究了FFT频域相关地磁匹配算法,减少了地磁信号测量误差对地磁匹配定位精度的影响[8]。第二炮兵工程大学贾磊等在MAD算法基础上引入RANSAC鲁棒算法与粗精匹配结合的分层搜索策略,提高了水下地磁导航的单一特征量地磁匹配的定位精度[9]。国防科技大学刘颖等提出了一种改进的基于等值线约束的相关匹配算法,能够有效消除无人机导航系统的初始位置误差并能限制匹配过程中惯性导航系统的积累误差[10]。石志勇等提出了地磁信息熵和地磁差异熵综合的匹配算法,提高了MAD算法抗测量误差干扰的能力[11]。郭庆等提出了地磁匹配双等值线算法,增加了地磁场数据在缓变区域匹配精度[12]。朱占龙针对惯性、地磁匹配组合导航模型,提出了适用于地磁匹配的人工鱼群搜索寻优算法[13]。关于地磁定位技术的民用还处于起步阶段,相关匹配算法理论研究较少。西安电子科技大学薛程[14]运用了粒子滤波算法、东华理工大学郑梦含[15]利用自适应粒子滤波算法开展了室内地磁定位搜索策略的实验研究。笔者运用MAD,Hausdorff算法开展了井下地磁定位的基础试验,分析了这类算法匹配结果的精度[16]。这些研究主要是MSD,MAD,Hausdorff等一维批处理相关算法的应用或改进,没有本质的突破性研究,难以满足GRPM定位技术要求[17-18]。
井下实际地磁的测量结果是井下空间点位的地磁异常场和周边环境磁场的叠加效应。不仅空间分布有一定独特性,而且空间统计特征明显,能够满足地磁定位的需要,但是地磁测量时噪声干扰较大,常规MSD,MAD,Hausdorf算法的匹配概率较低,需要一种适合井下地磁空域特点的地磁匹配算法来解决GRPM技术中地磁精确定位的难题。本文在GRPM定位技术架构的基础上,提出了一种二维磁特征参量联合距离的相关度匹配模型MPMD[19](Multi-Parameter Matching Model of Least Magnetic Distance),是一种匹配精度高且抗噪性能好的算法。文中通过井下不同区域、高噪声情况下不同算法地磁匹配的定位试验和精度对比,测试了MPMD算法的适应性和鲁棒性。
地磁场是地球固有的矢量场之一,由主地磁场、磁化地壳岩石产生磁场和干扰磁场3部分组成,其地磁强度会随空间和时间变化而变化。根据现代地磁理论,局部地区地磁定位主要依据地磁异常场。异常是相对而言的,对于大尺度地壳异常场,是把地核主磁场作为正常场;对于小区域异常场,一般是将地核主磁场加上大尺度异常场作为背景稳定场。井下空间范围属于小区域,因此其地磁定位主要依靠是地磁异常场的变化情况。
井下巷道内实际测量地磁数据是地磁异常场、周围环境各类磁场源的叠加。由于井下巷道内区域内会有钢筋支护、通风设备等,它们产生的磁场会叠加在巷道原有的基础地磁场上,这也大大增加了井下地磁空间分布的独特性。通常情况下,井下实测地磁数据主要包含了地磁异常场、地磁测量误差、载体干扰场等,即
Bi=g(xi,yi,t)+ei+mi
(1)
其中,Bi为磁力仪测得磁场强度;g(xi,yi,t)为空间点(xi,yi)处t时刻的异常磁场,虽然其数值会有“月变”、“日变”的周期波动,但是仍然是一个相对固定的基数;ei为随机常值和一个高斯白噪声组合误差,包含地磁模型误差、日变误差,大小从50~500 nT变化很大,是影响地磁匹配算法匹配精度的主要原因;mi为磁力仪载体的干扰场,井下人员在巷道内行走速度较慢,平均在5 m/s以下,对地磁测量影响很小,通常在匹配中可以忽略不计。
井下工程范围一般不超几十平方公里,区域变化尺度较小。并且井下巷道是线状结构,每种巷道因功能不同,其支护措施、布设装置都会不同。这些诸多变化的因素形成井下巷道地磁空间分布独特的特点。
(1)井下地磁异常场空间分布复杂。有些巷道地磁特征明显丰富,地磁数值统计结果的标准场、粗糙度、信息熵数值大,空间地磁分布的独特性明显,适配性很强。而有些巷道几十米长度内的磁异常只围绕着几百至几千纳特变动,地磁数值随着空间变化的波动较小,地磁匹配定位的适配性弱。图1为长约160 m某巷道的磁总场空间三维分布图,其空间磁总场变化的最大差值为2 000 nT,空间分布变化较小。另外在一些特殊的巷道,受到周围环境或设备的磁场影响较大,可能两个空间点相距仅仅几米,实际测量地磁值会陡增到上万纳特。

图1 井下地磁总场三维分布
Fig.1 Underground geomagnetic field 3D map
(2)部分巷道区域磁剖面存在较多特征相似区。如图2所示的巷道中线的磁剖面,存在多处相似剖面段,其中,m1,m2,m3为3段地磁序列。当匹配步长取3时,m1,m2,m3地磁序列相似;当匹配步长取4时,m1和m3地磁序列相似。这类巷道地磁定位时易发生模糊匹配,虚定位的概率大,属于地磁匹配弱适配区。

图2 井下巷道地磁总场剖面
Fig.2 Underground tunnel geomagnetic field profile
(3)井下实际测量地磁噪声总体数值较大,高达几百纳特。由于井下地磁测量会受到日变、作业面采掘、机电设施工作状态等因素影响,地磁匹配过程中测量的地磁数值与基准数据相比具有一定的差值。小的数值波动会有几十纳特,大的噪声甚至达到几百纳特,这些扰动会直接影响地磁匹配的精确度。特别是在地磁特征缓变区内,较大的噪声干扰有可能会淹没巷道实际地磁微小的变化,直接导致虚定位。这种地磁强噪声需要借助一种抗干扰的地磁匹配数学模型来减弱其对匹配结果影响。
根据井下地磁异常场空间变化复杂和扰动噪声大的特点,架构了一种标签识别技术与地磁匹配技术组合定位的GRPM方法。GRPM方法是从井下物联网技术的智能化角度,设计一种高精度、自主、新型的井下定位方法,该定位方法过程包含电子标签识别的粗略定位和地磁匹配的精确定位2个步骤。其定位原理是:① 井下人员随身携带GRPM定位装置,定位装置的辐射场激活所在巷道的电子标签,获取所在巷道位置信息,完成粗略定位。粗略定位后可以将井下人员的位置圈定在一个或两个巷道范围以内,粗定位的精度主要与电子标签分布密度、有效识别距离有关。② 井下人员在巷道内行走时,GRPM定位装置可以实时测量人员通行路径的地磁值,构成行走路径的地磁序列,通过路径地磁序列和基准图的匹配计算,可以求解出人员所在的精确位置。
如图3所示,井下人员随身携带GRPM定位装置,定位装置内装有读卡器、地磁传感器等;井下巷道端口或连接处装有电子标签。当井下人员行走在巷道中,定位装置辐射场可激活周边的电子标签,通过主动射频识别技术获取标签内的电子信息,作为地磁匹配的初始位置;同时地磁传感器连续接收所经过路径地磁数据,形成匹配地磁数据。通过与基准数据库进行相关匹配计算后,可以解算出井下人员精确位置。

图3 井下GRPM定位机理示意
Fig.3 GRPM Underground positioning mechanism diagram
GRPM方法是一种兼容型的定位算法,既可以与现有井下定位系统并行使用,也可以单独发挥定位导航作用。井下人员运用GRPM技术定位后,实时记录并存贮行走的精确路径信息。当井下通信网络正常时,信息可以通过井下通讯系统发送到系统监控中心,经过数据格式转换后,与其他类型的井下定位系统的定位数据进行互补,实现信息共享。当井下通讯网络供电中止、信号中断或不稳定时,井下人员通过GRPM技术可以单独、自主定位,并结合装置的可视化界面,查询自己当前的位置信息、周边的避险设施信息及最优路径。
GRPM实际定位精度会受到多种因素的综合影响,如井下巷道地磁空间分布适配性、装置内部的地磁传感器灵敏程度、实际测量地磁噪声大小、匹配算法的适应性等。文中仅从井下地磁特征匹配算法模型角度来阐述GRPM定位的关键技术。
地磁匹配本质上是一个数据关联问题。其关联算法是实测地磁轨迹与地磁基准图中匹配关联计算。目前大部分地磁定位的匹配算法采用的是TERCOM相关算法,该算法是指数据积累一段时间后,用测量地磁序列与基准图的相关计算实现定位的方法。TERCOM匹配一般是以磁总场作为参数进行计算,属于一维相关匹配。MPMD匹配算法是在TERCOM相关算法基础上进行了改进,从原来一维相关匹配拓展为二维相关性匹配。
由于地球空间任一点都对应相应的磁总场,X,Y,Z三轴磁分量等特征量。同一点的特征量与地理位置的相关程度不相同,每个特征量在一定空间范围内的变化幅度也不相同。MPMD算法依据同一点的多维地磁向量之间变化的差异性,建立了一种空间向量积的最优估计的匹配模型,也称为磁特征参量联合距离匹配算法。其数学描述为

(2)
其中,H(x,y,v,…)为所在巷道电子标签信息;G为识别后圈定匹配不确定域,是GRPM定位装置识别巷道的电子标签后获取的;(i,j)为运动物体S的匹配初始位置;S(i,j)为起点(i,j)的待匹配运动轨迹,由多个磁特征点顺序组成;RS(i,j)为待匹配轨迹的磁总场基准序列;RM为测量的磁总场序列;M为X,Y,Z三轴磁分量中适配性最好的分量;MS(i,j)为待匹配轨迹的M分量的地磁基准序列;MM为测量的M分量地磁序列;D(i,j)为磁总场的测量序列与基准序列的欧氏距离;L为匹配步长;cos θ(i,j)为M地磁分量的测量序列与基准序列匹配的夹角余弦;C(i,j)为匹配夹角余弦与欧氏距离的积;![]() 为最优估计,估计原则是:相关度越大,磁特征参量联合等价权距离C(i,j)越小;MS(a,b)为最优匹配结果所对应的地磁序列;(a,b)为MPMD最优匹配结果的起点。匹配结果通常需要2~3次估计后的递推检核、纠偏或补偿后才能确定。
为最优估计,估计原则是:相关度越大,磁特征参量联合等价权距离C(i,j)越小;MS(a,b)为最优匹配结果所对应的地磁序列;(a,b)为MPMD最优匹配结果的起点。匹配结果通常需要2~3次估计后的递推检核、纠偏或补偿后才能确定。
前期地磁试验表明:磁总场特征明显,是MPMD地磁匹配主要参量。由于水平磁分量易受磁暴影响,角度类磁特征量在小区域内变化较小,一般不考虑。因此MPMD公式的M分量是从X,Y,Z三轴磁分量中优选出来的。具体过程是根据巷道地X,Y,Z三轴磁分量的标准差、信息熵、粗糙度等指标大小,选取其中空间分布独特性强、适配性最好的分量作为式(2)中的M分量参与匹配计算。
井下环境复杂,匹配算法结果受到影响因素也较多。为了测试匹配算法精确度和抗噪性能,文中仅考虑在相同环境下,对不同匹配算法地磁匹配的定位精度、抗噪性能进行对比分析。试验选取了试验模拟矿井的2个走向分布不同的H-11和H-21水平巷道作为试验区域,长约150 m,宽约4 m。井下地磁测量采用便携式FVM-400磁通门磁力仪,其量程达到100 000 nT,分辨率达到了1 nT。测量噪声方差50 nT2,测量随机常值误差为10~30 nT。按照0.5 m间隔采集了点位的磁总场和三轴分量的地磁数据,经过粗差剔除、去噪后,建立了巷道多维向量的地磁基准数据。对地磁数据磁总场MR和三轴磁分量MX,MY,MZ进行适配性评价,计算H-11与H-21巷道4个特征量的特征指标,见表1。
表1 H-11与H-21巷道磁向量分布特征指标
Table 1 Magnetic vector distribution characteristics about H-11 and H-21 tunnel

从表1特征指标结果看出,H-11巷道磁向量特征指标数值比较接近,空间分布特征不明显,对比后选取MR和MZ为MPMD匹配向量。H-21巷道地磁标准差较大达到20以上,粗糙度接近30,空间分布特征明显,选取MR和MX作为MPMD匹配向量。

图4 H-11巷道中轴线磁数据MR,MZ等值线
Fig.4 H-11 tunnel magnetic contour about MR,MZ
图4,5是优选后的磁特征向量的等值线图,可以看出H-11磁数据MR,MZ地磁特征变化不明显,地磁变化缓慢,存在较大面积特征相似区,适配性较差,是模糊匹配多发区;H-21磁数据MR,MX等值线图对应空间差异明显,具有一定独特性,适配性较好。
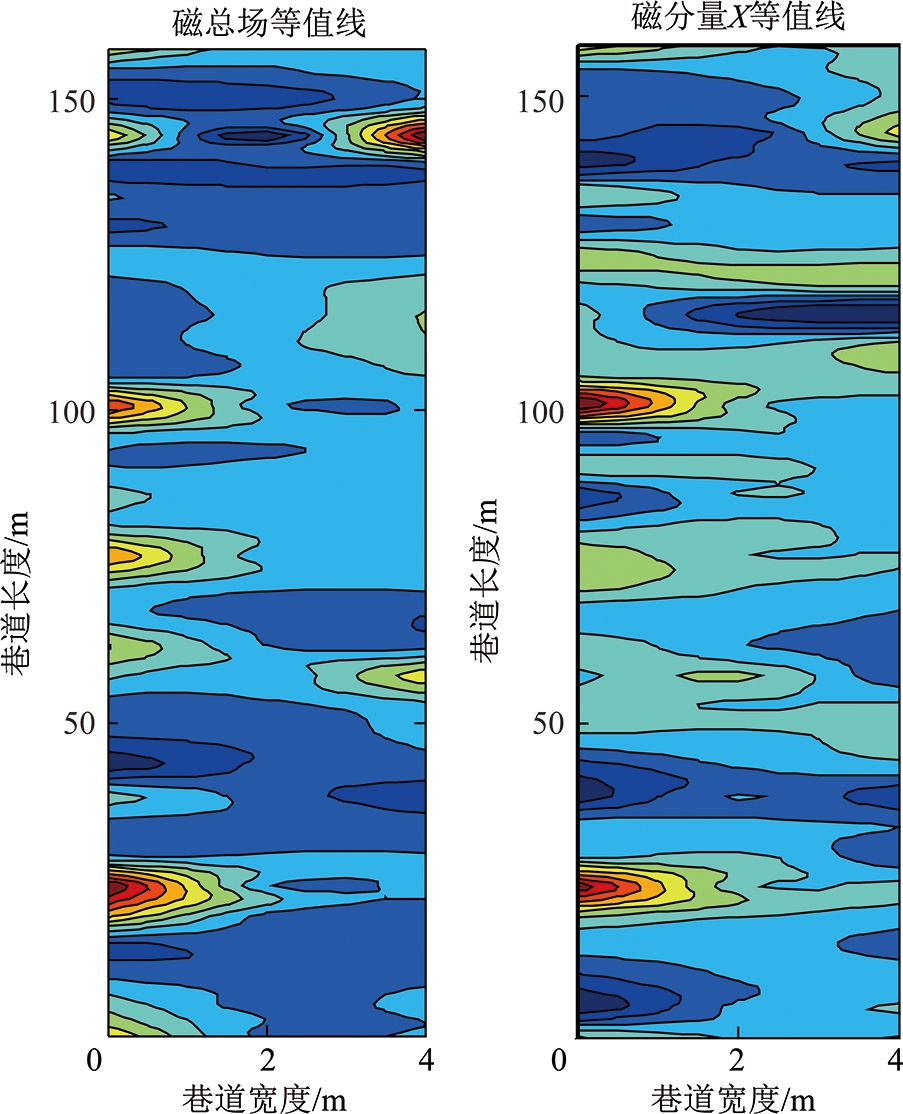
图5 H-21巷道中轴线磁数据MR,MX等值线
Fig.5 H-21 tunnel magnetic contour about MR,MX
(1)试验方案。在井下H-11巷道、H-21巷道内分别采用MSD,MAD,MPMD算法进行了地磁定位试验,验证相同条件下3种算法的匹配精度。在H-21巷道内,分别在200,400,600 nT 噪声下测试MPMD算法地磁定位的精度和鲁棒性,开展MPMD算法适应性测试和抗噪声性能测试。
(2)试验参数。匹配结果会受到采样频率、匹配步长、地磁测量噪声等因素的综合影响,需要设定试验参数。由于井下人员在不同情况下的平均行进速度是不一样的[20],但是最大行进速度不会超过3 m/s见表2,设定试验地磁采样周期为0.5 s,匹配步长为3个采样点,长度约1.5 m,虚定位阈值为5 m,选取匹配概率、匹配误差、匹配时间作为精度评定的指标。地磁图边缘不足一个匹配长度部分自动忽略。
表2 同等路径下井下人员的行进速度
Table 2 Travel speed of underground personnel under the same pathm/s

MSD,MAD,MPMD匹配算法在H-11,H-21匹配误差数据,见表3。在H-11地磁特征贫乏的弱适配区,3种算法匹配误差都较大,总体上MPMD算法相比MSD,MAD算法,匹配精度和匹配概率都有所提高。在地磁特征丰富的H-21适配区,3种算法的匹配概率达到了95%以上,但MPMD定位精度较高,基本上保持在一个网格间格以内。2个区域内MPMD匹配计算量较大,计算耗时增加了近2倍。
表3 不同算法匹配定位的误差数据
Table 3 Matching error data the for different algorithms


图6 巷道 H-11和H-21真实轨迹与估计轨迹对比
Fig.6 Comparison between the true trace and the estimated trace about H-11 tunnel and H-21 tunnel
图6是井下水平巷道H-11和H-21的 MSD,MAD,MPMD匹配定位轨迹对比图。由图6可知,在地磁特征贫乏的H-11区域,MPMD估计 轨迹与真实轨迹稳合度最高,虚定位次数少,较好处理了模糊匹配多值问题。在地磁特征丰富的H-21区域,3种算法的匹配轨迹稳合度都较好。
图7~9是H-21巷道在不同噪声下3种方法的匹配结果误差曲线,横坐标“匹配次数”是指匹配当前点在匹配序列中的排序。

图7 测量噪声200 nT时匹配误差曲线
Fig.7 Matching error curve in the 200 nT measurement noise

图8 测量噪声400 nT时匹配误差曲线
Fig.8 Matching error curve in the 400 nT measurement noise

图9 测量噪声600 nT时匹配误差曲线
Fig.9 Matching error curve in the 600 nT measurement noise
通常情况下,磁力仪测量白噪声大约在50 nT,由于周围环境测量噪声约100 nT内波动。图7加入噪声幅值为200 nT时的3种算法匹配误差曲线。可以看出当噪声为200 nT时,MSD和MAD匹配有少量虚定位,MPMD算法匹配结果基本无误差,效果很好;当测量噪声达到400 nT和600 nT时(图8,9),MSD和MAD匹配出现大量虚定位,模糊匹配概率大大增加,定位精度较低。MPMD算法只有少量虚定位,总体匹配效果较好。
考虑到井下环境复杂,如果出现异常干扰情况下,MPMD抗噪性能是否会出现匹配不收敛情况?因此开展了600 nT高噪声干扰测试。图10是噪声600 nT时,MSD,MAD,MPMD三种匹配定位轨迹对比,可以看出:MSD,MAD 匹配结果不收敛,出现大量虚定位。MPMD匹配并未出现明显发散现象,虚定位次数较少,在大多数情况MPMD估计轨迹收敛于真实轨迹,稳合度最好。

图10 噪声600 nT真实轨迹与估计轨迹对比
Fig.10 Comparison between true trace and estimated trace in the 600 nT measurement noise
当噪声600 nT时,MSD,MAD,MPMD匹配结果的分析数据见表4,分别从匹配概率、匹配误差和匹配时长对比分析了3种匹配算法的抗噪性能。
表4 测量噪声600 nT时定位误差数据
Table 4 Positioning error data in the 600 nT measu-rement noise

从表4中可以得出:MSD,MAD 平均匹配误差已经达到了几十米,说明MSD,MAD 匹配在高噪声干扰情况下,匹配结果不收敛。MPMD在高噪声干扰情况下的平均匹配误差控制在5 m以下,具有收敛性,总体概率达到了89%,抗噪性能较好。MPMD在匹配概率、匹配精度上明显优于MSD和MAD匹配算法,但是匹配耗时较多,接近MSD,MAD匹配时长的2倍。综合分析MSD,MAD属于TERCOM匹配的一维相关匹配,约束条件也是单一约束条件的最优估计,当在强噪声扰动条件下,约束作用不明显,故出现匹配发散现象。MPMD匹配优化后二维相关性匹配,即同一个结果的估计同时存在2个约束条件进行数学解算,因此抗干扰性能强,匹配耗时较长。
(1)GRPM以地磁定位技术为基础的、新型的井下定位方法,主要适用于井下灾后无电、无网络的自主定位。MPMD匹配模型是在GRPM实际应用基础上,针对井下地磁空间分布特征不明显、缓变或特征相似情况下一维匹配结果精度不高的问题,提出的一种二维相关匹配模型,是基于空间向量积的最优估计的匹配算法。
(2)在MSD,MAD和MPMD匹配定位对比试验中,在地磁特征丰富适配区,3种算法的匹配精度都较高;在地磁特征贫乏的弱适配区,MPMD算法优于MSD,MAD算法,能够较好处理模糊匹配多值问题,定位精度基本上保持在一个网格间格以内。在算法抗噪性能测试试验中,当噪声为200 nT时,MSD和MAD匹配有少量虚定位,MPMD算法匹配结果基本无误差,效果很好;在400 nT和600 nT高噪声时匹配试验中,MSD和MAD匹配出现大量虚定位,MPMD算法有少量虚定位,匹配概率达到了89%,匹配误差控制在5 m以下,未出现算法不收敛情况,总体匹配的鲁棒性较强。
(3)试验结果总体表明MPMD比MSD,MAD一维匹配算法在准确度、精度和鲁棒性方面确实有明显优势,但匹配过程耗时较多,接近MSD,MAD匹配时长2倍,需要从匹配搜索策略等方面进一步优化,才能符合井下快速定位的要求。
参考文献:
[1] 韩东升,杨维,刘洋,等.煤矿井下基于RSSI的加权质心定位算法[J].煤炭学报,2013,38(3):522-527.
HAN Dongsheng,YANG Wei,LIU Yang,et al.A weighted centroid localization algorithm based on received signal strength indication for underground coal mine[J].Journal of China Coal Society,2013,38(3):522-527.
[2] 田丰,秦涛,刘华艳,等.煤矿井下线性无线传感器网络节点定位算法[J].煤炭学报,2010,35(10):1760-1764.
TIAN Feng,QIN Tao,LIU Huayan,et al.Nodes localization algorithm for linear wireless sensor network in underground coal mine[J].Journal of China Coal Society,2010,35(10):1760-1764.
[3] 冯庆奇,王宇,汤建勋,等.激光捷联惯导系统的矿山井下定位技术研究[J].西部探矿工程,2010,22(5):118-120.
FENG Qingqi,WANG Yu,TANG Jianxun,et al.Research on mine location technology of laser strapdown inertial navigation system[J].West-China Exploration Engineering,2010,22(5):118-120.
[4] 张鹤丹.基于WiFi技术的井下人员定位系统研究[D].西安:西安建筑科技大学,2013.
ZHANG Hedan.Study on underground personnel positioning system based on WIFI communication technology[D].Xi’an:Xi’an University of Architecture and Technology,2013.
[5] 郭京京.基于RFID与ZIGBEE技术的井下作业定位系统的研究[D].成都:成都理工大学,2014.
GUO Jingjing.Research of underground mine positioning system based on technology of RFID and ZIGBEE[D].Chengdu:Chengdu University of Technology,2014.
[6] 汪金花.地磁与RFID射频结合井下定位方法[P].中国专利:ZL 2016 1 0401387.0,2016-07-22.
WANG Jinhua.The undergroud positioning method based on the geomagnetic and RFID[P].China Patent:201610401387.0,2016-07-22.
[7] 赵建虎,王胜平,王爱学.一种改进型TERCOM水下地磁匹配导航算法[J].武汉大学学报(信息科学版),2009,34(11):1320-1323.
ZHAO Jianhu,WANG Shengping,WANG Aixue.An improved TERCOM algorithm for underwater geomagnetic matching navigation[J].Geomatics and Information Science of Wuhan University,2009,34(11):1320-1323.
[8] 吕云霄,陈庆作,张维娜,等.基于地磁信号特征的频域相关地磁匹便配算法[J].中国惯性技术学报,2010,18(5):580-584.
LÜ Yunxiao,CHEN Qingzuo,ZHANG Weina,et al.Frequency-domain correlation matching algorithm based on characteristic of geomagnetic signal[J].Journal of Chinese Inertial Technology,2010,18(5):580-584.
[9] 贾磊,王跃钢,单斌,等.基于增强型MAD单特征量地磁匹配导航算法[J].现代防御技术,2012,40(1):90-94.
JIA Lei,WANG Yuegang,SHAN Bin,et al.Simulation of single element geomagnetic matching navigation based on intensified MAD[J].Modern Defence Technology,2012,40(1):90-94.
[10] 刘颖,吴美平,胡小平,等.基于等值线约束的地磁匹配方法[J].空间科学学报,2007,27(6):505-511.
LIU Ying,WU Meiping,HU Xiaoping,et al.Contour constraint based geomagnetic matching method[J].Chinese Journal of Space Science,2007,27(6):505-511.
[11] 石志勇,许杨,王毅,等.基于熵的地磁匹配定位算法[J].火力与指挥控制,2010,35(10):8-10.
SHI Zhiyong,XU Yang,WANG Yi,et al.Algorithm of geomagnetic matching localization based on entropy[J].Fire Control & Command Control,2010,35(10):8-10.
[12] 郭庆,魏瑞轩,胡明朗,等.地磁匹配双等值线算法仿真研究[J].系统仿真学报,2010,22(7):1576-1579.
GUO Qing,WEI Ruixuan,HU Minglang,et al.Research on dual iterative contour point algorithm for geomagnetic matching[J].Journal of System Simulation,2010,22(7):1576-1579.
[13] 朱占龙.惯性/地磁匹配组合导航相关技术研究[D].南京:东南大学,2015.
ZHU Zhanlong.Research on related technologies of INS/Geomagnetic matching integrated navigation[D].Nanjing:Southeast University,2015.
[14] 薛程.地磁室内定位导航系统的研究与实现[D].西安:电子科技大学,2017.
XUE Cheng.Research and implementation on Geomagentic indoor positioning and navigation system[D].Xi’an:School of Computer Science & Engineering,2017.
[15] 郑梦含.基于地磁敏感度的室内定位算法的研究[D].南昌:东华理工大学,2017.
ZHENG Menghan.Research on scientivity-based Algorithm for indoor geomagnetic localization[D].Nanchang:East China University of Technology,2017.
[16] 汪金花,李卫强,张亚静,等.基于地磁导航定位的井下避险系统的构建[J].矿业安全与环保,2016,43(2):33-36.
WANG Jinhua,LI Weiqiang,ZHANG Yajing,et al.Build of underground refuge system based on geomagnetic navigation and positioning[J].Mining Safety & Environmental Protection,2016,43(2):33-36.
[17] 张文杰.基于RFID和地磁场联合的室内定位技术研究[D].南京:南京邮电大学,2015.
ZHANG Wenjie.Research on hybrid indoor positioning with RFID and magnetic field[D].Nanjing:Najing University of Posts and Telecommunications,2015.
[18] 李鑫,程德福,周志坚.一种基于地磁总场梯度的匹配定位算法[J].传感技术学报,2017,30(12):1869-1875.
LI Xin,CHENG Defu,ZHOU Zhijian.A matching algorithm based on the gradient of the total geomagnetic [J].Chinese Journal of Sensors and Actuators,2017,30(12):1869-1875.
[19] 基于磁特征参量联合距离的井下定位方法[P].中国专利:CN 107504965 A,2017-08-15.
Undergroud positioning method based on parameter matching model of Least magnetic distance[P].China Patent:CN 107504965 A,2017-08-15.
[20] 汪金花,张亚静,李玉萍.井下最优避险路GIS网络分析数学建模与算法实现[J].煤炭学报,2014,39(S2):411-415.
WANG Jinhua,ZHANG Yajing,LI Yuping.Mathematical modeling and algorithm’s research of optimal hedge underground route’s GIS network analysis[J].Journal of China Coal Society,2014,39(S2):411-415.