
移动阅读
目前我国已有大部分矿井进入千米以下开采深度。随着开采深度增加,深部岩体所赋存的地质条件复杂,其地应力场的分布特征与浅部岩体存在显著的差异性。初始地应力是影响岩体围岩稳定的重要因素,地应力或原岩应力即储存在岩体中未受扰动的应力,它不仅是影响岩体力学行为的主要控制因素,同时也是引起岩体变形和破坏的力源之一。国际岩石力学学会推荐的主要地应力测量方法[1]:定性估计法、套孔解除法、水压致裂法、定量估计法4种方法。套孔解除法中以澳大利亚CSIRO型空心包体应变计测量方法应用最为普遍,应变计由环氧树脂胶胶结在试验钻孔内壁上,待胶固化后再套钻钻取含有应变计的小钻孔,钻取过程中不断采集解除应变[2-3]。
近些年众多机构对空心包体应变计结构、选材、制作工艺、温度补偿、围压试验和计算方法等多个方面进行了研究改进。李远等[4-5]提出了一种基于双温度补偿方法消除测量过程中温度对采集精度的影响,并且研发了一款数字化断电续采型无导线空心包体应变计。闫振雄等[6]采用线性参数的最小二乘拟合方法对地应力分量计算公式进行了推导,得出了地应力分量的改进算法及其标准误差的计算公式。董诚、王连婕等[7]空心包体三轴地应力测量系统的升级改造,研制了一套小型化、自动化的新型地应力测量系统,在某煤矿地应力测量中得到应用。王衍森和吴振业[8]推导出空心包体应变计在一定的布片方式下应变测值间的内在关系式,并由此提出了应变测值的直接检验法及应变计的最佳布片方式。刘少伟等[9]设计了一种使用 DS18B20 作为敏感元件的测温电路系统,经实验室试验校核并在煤矿现场进行了应用。中国地质科学院地质力学研究所彭华等[10]研发出一种无线数字CSIRO空心包体,但在深部地层原始应力的测量过程中,并没有考虑岩体非线性对其计算结果带来的影响。
在岩体非线性研究领域DUNCAN和CHANG[11]在1970年提出了一种非线性材料模型,且1972年KULHAWY和DUNCAN[12]对模型进行了修正。该模型采用双曲线应力-应变关系,并将其作为隧道变形分析的非线性弹性模型。席道瑛等[13-14]引入一种滞后非线性弹性材料的宏观模型——Preisach-Mayergoyz 模型(PM模型)。孔志鹏等[15]提出一种岩石材料非线性三参数强度准则,待定系数A,B,C 可通过简单的试验确定且具有明确的物理意义。
因此由岩体线弹性假设为前提的当前地应力测量理论在深部岩体地应力测量中将产生较大偏差,基于对深部地应力场与浅部地应力场分布特征的差异性的基本认识,深入探索随深度增加地应力场从由线性岩层向非线性岩层过渡的发展规律和原位特征[19]。在现有地应力测量理论基础上发展基于岩体非线性特征的测量理论,并在此理论指导下考虑深部岩体高应力下应力-应变非线性规律,发展适合深部岩体地应力测量的新理论、新方法。本文在研发了适用于多尺寸解除岩芯的高压双轴加载系统基础上,三山岛金矿埋深800 m的解除岩芯进行了双轴加卸载试验,处理试验数据后,提出了一种变形模量与平均应力的双曲线模型,推导了双轴加卸载试验中的变形与平均应力之间的非线性关系。将整个解除过程分成多个阶段,每个阶段的变形模量计算参数与解除岩芯所受应力状态有关,且符合推导的应力与应变的非线性关系公式,各个阶段叠加计算出最大水平主应力。
蔡美峰[16]提出了将双轴加卸载试验中卸载应变数据的用于计算岩体的力学参数弹性模量和泊松比。锦屏水电站[17]和玲珑金矿[18]深部岩体地应力测量结果表明双轴试验的径向压力大约需要加载到60 MPa,才能模拟现场的原位应力的大小。传统的双轴加载试验设备最大围压不能满足深部岩体解除岩芯的高压双轴试验。因此对传统的设备进行改造,设计并制造了一种能够进行高围压测试的双轴加载装置如图1所示。

图1 高压双轴试验仪器
Fig.1 High pressure biaxial test equipments
双轴加卸载试验具体过程为:径向围压采用手动压力泵逐步地加载,最初数值为零即不受力状态,每2 MPa为一个梯度,保持压力状态,连续记录3次3组应变片12个应变片数据,最大压力加载到16 MPa,然后按同样的方式进行卸载试验,加卸载试验数据如图2所示。
双轴加载试验数据用于确定解除岩芯的计算参数弹性模量和泊松比。解除岩芯放置在橡胶皮套增压室内。手动压力泵配有压力表用于测量当前的压力。在实验中解除岩芯样本处于平面应力状态,假设整个加载过程为线性弹性,弹性模量计算公式如下:
(1)
泊松比ν 计算公式如下:
ν=-εa/εθ
(2)
式中,εa为3组应变花轴向应变平均值;εθ为3组应变花环向应变平均值(压缩应力为正);σr为径向压力(压缩应力为正);R 和 r分别为解除岩芯外半径和小孔半径。
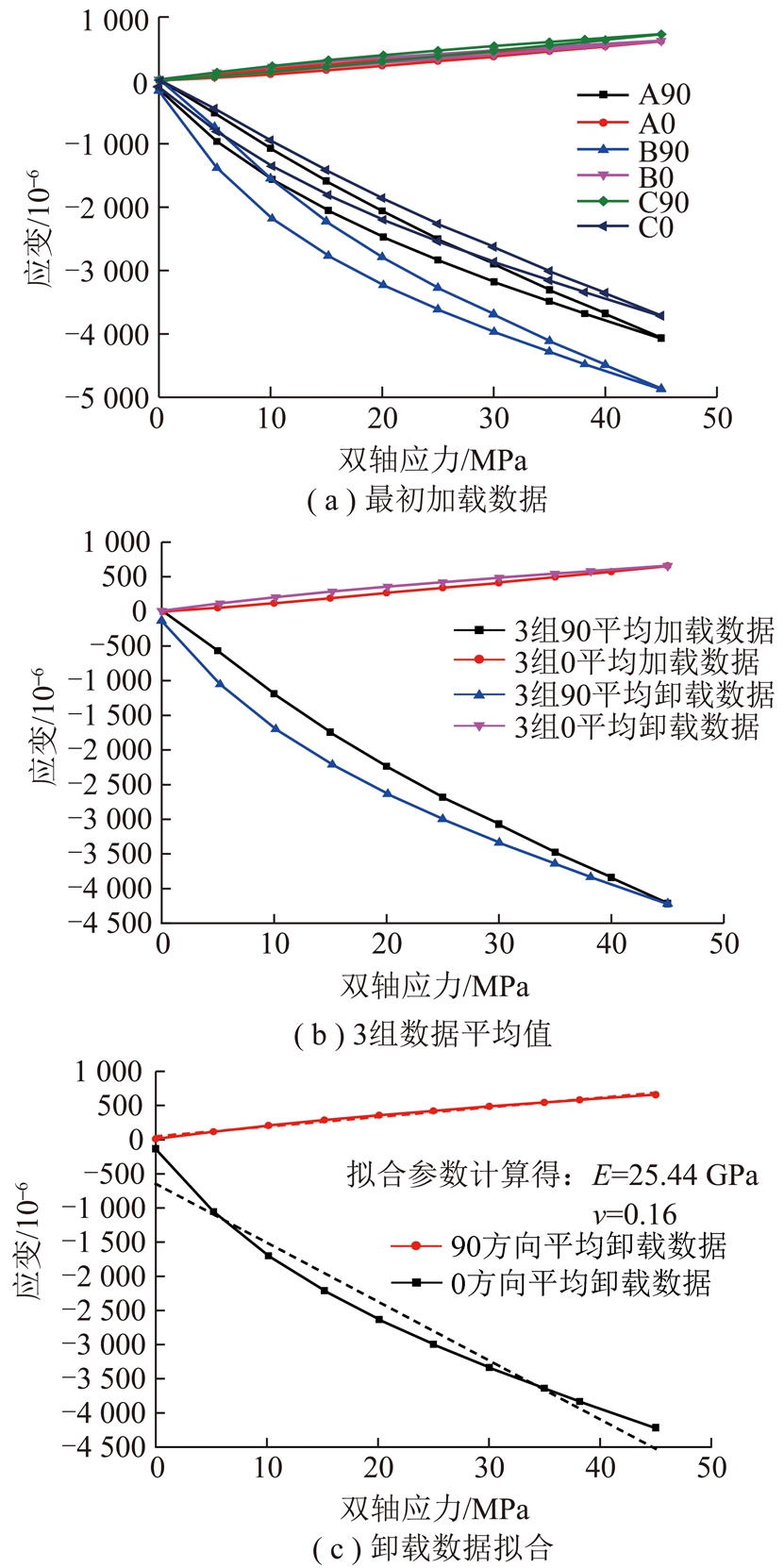
图2 双轴加卸载试验应力应变数据
Fig.2 Biaxial loading-unloading test stress vs strain
对原始卸载数据进行处理后,计算出每5 MPa范围内的弹性模量E和泊松比ν,在根据式(3)和(4)计算对应的体积模量K和剪切模量G值(表1)。双轴加卸载试验中岩芯的平均应力在不断变化,因此应力-应变曲线每阶段的最大值就算出对应的平均应力值,如式(5)所示:
K=E/[3(1-2ν)]
(3)
G=E/[2(1+ν)]
(4)
P=2σr/3
(5)
将体积模量和平均应力以及剪切模量与平均应力的关系选取双曲线模型拟合,拟合公式见式(6)和(7),图3和4相关系数分别为0.989和0.997,因此所应用的双曲线模型可以很好地用来表达变形模量和平均应力的关系(表2)。
表1 试验参数计算值
Table 1 Test parameters calculated value

平均应力/MPa体积模量K/GPa剪切模量G/GPa27.7221.76017.0724.3820.63015.5621.6719.77015.5518.3418.17014.0615.0315.72013.0511.7613.20011.338.4410.9409.625.128.0157.641.735.5805.75
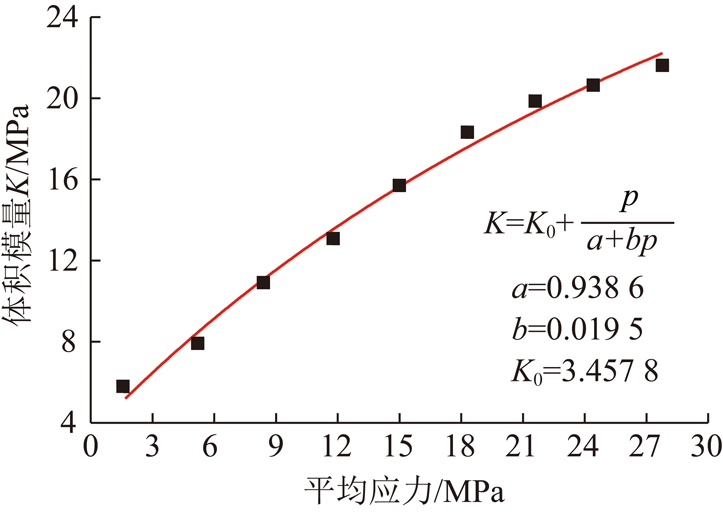
图3 体积模量与平均应力拟合
Fig.3 Fitting curve of bulk modulus vs the mean stress

图4 剪切模量与平均应力拟合
Fig.4 Fitting curve of shear modulus vs the mean stress
表2 非线性拟合参数
Table 2 Nonlinear fitting parameters

abK0cdG00.938 60.019 53.457 81.2790.033 34.306 8
(6)
![]()
(7)
式中,p为平均应力;K0 和 G0 为初始的体积模量和剪切模量,即当 p=0,K 和 G的值;参数 a,b,c,d 按以下定义:
(8)
![]()
(9)
![]()
(10)
![]()
(11)
解除岩芯双轴加载试验中,径向应力与CSIRO中平均径向应变在一定压力范围,非线性关系可以应用分段线性分析。则式(1)和(2)用增量形式改写成以下形式:
(12)
![]()
(13)
式中,E和ν分别为杨氏模量和泊松比;Δσr为径向压力增量式(压缩应力为正);R 和 r分别为解除岩芯外半径和小孔半径;Δεθ 和 Δεa分别为3组应变花环向应变和轴向应变的平均值增量式。
将式(12)和(13)代入式(3)和(4)得

(14)
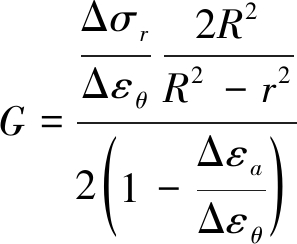
(15)
在双轴加载试验中,平均应力和径向应力的关系:
(16)
将式(16)代入式(14)和(15)化简得
(17)
![]()
(18)
将拟合公式(6)和(7)代入式(17)和(18)化简得
(19)
![]()
(20)
对式(19)和(20)两边积分得
![]()
(21)
![]()
(22)
图5应变与应力关系图中,由线性拟合和非线性拟合结果分析可得,随着平均应力不断增大,所提出的非线性关系公式更适合应力与应变的关系。
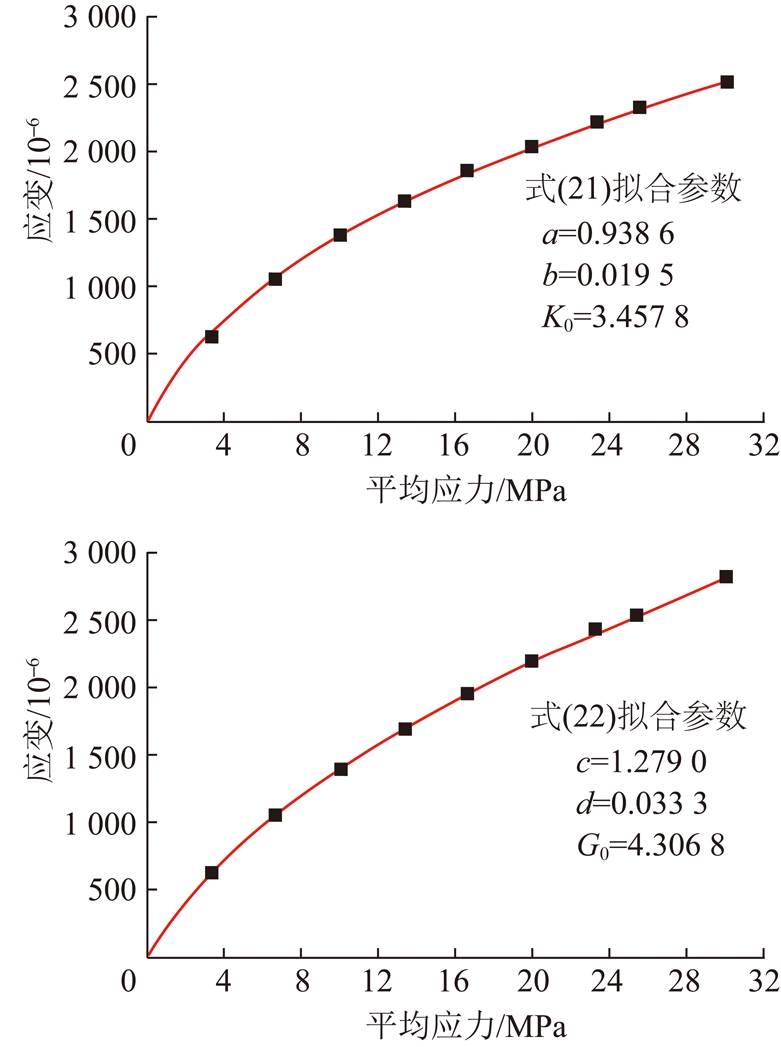
图5 应变与应力之间关系
Fig.5 Relationship between strain and stress
孔壁应变片为平面应力状态如图6所示,只有σθ,σz,τrθ三个应力分量,每个电阻应变花的4支应变片所测应变值为εθ,εz,ε45,ε-45即(ε135)和它们的关系式为
(23)
![]()
(24)
![]()
(25)
将6个应力分量σx,σy,σz,τxy,τxz,τyz替换极坐标中σθ,σz,τrθ三个应力分量,公式变为
cos 2θ-2τxysin 2θ]-νσz}
(26)
![]()
(27)
![]()
(28)
![]()
(29)
其中,εθ,εz,γzθ分别为空心包体应变计所测环向应变,轴向应变和剪切应变值。

图6 应变片受力状态示意
Fig.6 Stress state of strain gauge
3组应变片成120°胶粘与小孔内壁,应变花顺时针顺序为A-B-C。以A组应变片为例,1片为环向应变片记为A90;2片为轴向应变片记为A0;3和4片分别与钻孔轴线成±45°,记为A45,A135。如图7所示。

图7 空心包体应变计应变花粘贴位置
Fig.7 Hollow inclusion strain gauge location
如图8中CSIRO解除过程中各个通道应变中所标注,装有空心包体应变计的小孔在岩芯从开始解除到解除完成的过程中,钻机以恒定的推力及恒定转速进行钻取,保证解除数据的稳定性,间隔1 min进行一次应变数据采集,应变片从开始变化到最后稳定总共持续了8 min。因此解除全过程分成8个阶段(表3),每个阶段的微应变增量见表4,每个阶段微应变相加得最后的总应变值。

图8 CSIRO解除过程中各个通道应变
Fig.8 Each channel strain of CSIRO
表3 3组应变片的计算参数
Table 3 Calculation parameters of three groups of strain gauge
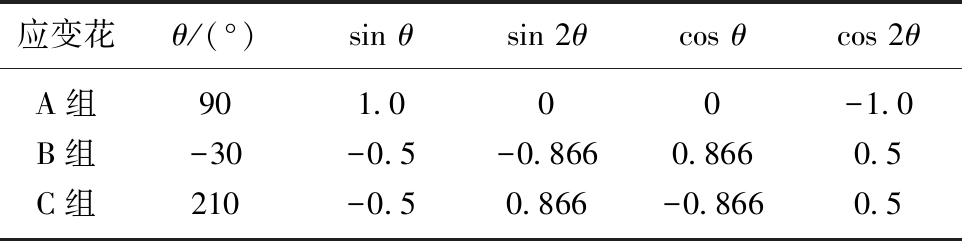
应变花θ/(°)sin θsin 2θcos θcos 2θA组901.000-1.0B组-30-0.5-0.8660.8660.5C组210-0.50.866-0.8660.5
3组应变花的12支应变片可以获得12个方程,但只有6个未知数,属于超定方程组,利用最小二乘法计算6个应力分量。
表4 空心包体应变计解除过程应变增量
Table 4 Strain increment of the hollow inclusion strain gauge during the unloading process 10-6

解除阶段A135A90A45A0B135B90B45B0C135C90C45C0Δ8126933979422917848166116Δ7762211051971405129030546145199Δ6372352027220223672194201326229137Δ54529831524299323322408266368248176Δ413122033024271427172173215415220113Δ322837044689372960413164830754252177Δ2179507246711 1749301 2891501 004847319130Δ19116123910376275318359245238116219∑8i=1Δi7991 8821 9214382 8003 3332 6661 9163 0703 4901 4951 267
(30)
其中,m代表有m个等式;n代表有n个未知数β,且m>n;将其进行向量化后为

(31)
引入残差平方和函数S
S(β)=‖Xβ-y‖2
(32)
当![]() 时,S(β)取最小值,记作:
时,S(β)取最小值,记作:
(33)
通过对S(β)进行微分求最值,可以得到
(34)
如果矩阵XTX非奇异则β有惟一解:
(35)
应用最小二乘算法优化,将基于双温度补偿算法的完全补偿修正应变值表代入原岩应力计算公式中,计算出原岩应力6个分量见表5。通过坐标公式的转换得到最大水平应力分量,最小水平应力分量以及第二主应力分量的大小、方向和倾角。
表5 最小二乘法应力数值求解
Table 5 Stress values of the least squares method

σx/MPaσy/MPaσz/MPaτxy/MPaτyz/MPaτzx/MPaσ1大小/MPa方向/(°)倾角/(°)σ2大小/MPa方向/(°)倾角/(°)σ3大小/MPa方向/(°)倾角/(°)49.16 33.84 31.66 -0.35 4.83 -8.86 53.11312835.912106125.622085
![]()
(36)
![]()
(37)
γθz=τyzcos θ-τzxsin θ/G
(38)
K=K0+p/b+ap
(39)
G=G0+p/d+cp
(40)
P=(σx+σy+σz)/3
(41)
其中,K0,a,b,G0,c,d通过高围压率定试验数据拟合获得。3组应变花测量结果共得到12个方程,可以求解出原岩应力的6个分量。其中体积模量K和剪切模量G是关于原岩应力的函数。在解除过程的8个阶段中,每个阶段都适用式(36)~(41),且所求阶段的平均应力取值为前几个阶段的增量和。每个阶段的增量计算公式为
[(Δσyi-Δσxi)cos 2θ-2Δτ(xy)isin 2θ]-
![]()
(42)
![]()
(43)
Δγ(θz)i=(Δτ(yz)icos θ-Δτ(zx)isin θ)/Gi
(44)
Ki=K0+Pi/b+aPi
(45)
Gi=G0+Pi/d+cPi
(46)

(47)
Δσzn,Δτ(xy)n,Δτ(xz)n,Δτ(yz)n)
(48)
其中,i为当前阶段数值,当i为第1阶段时其应力状态为σx0,σy0,σz0均为0,平均应力受力P为0,即岩芯已经完全解除,解除岩芯处于不受力的状态,K和G为初始值K0,G0,参数a,b,c,d分别由高压双轴加载试验数据拟合获得,每个阶段根据最小二乘法计算出其6个应力分量(表6)。
通过坐标公式的转换得到最大水平应力分量,最小水平应力分量以及第二主应力分量的大小、方向和倾角见表7。
表6 各个阶段计算参数及应力分量计算值
Table 6 Calculation parameters and stress components in each stage
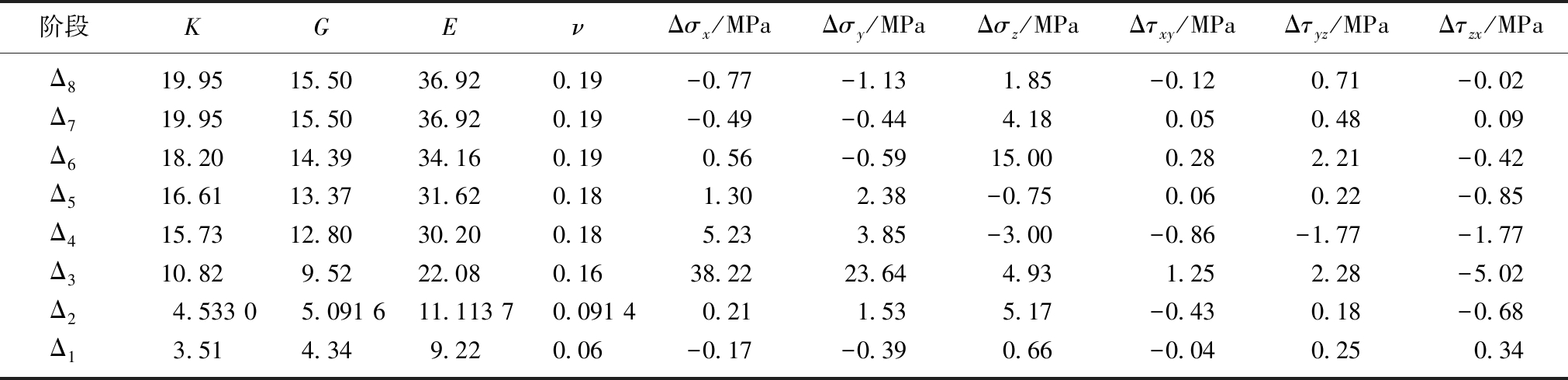
阶段KGEνΔσx/MPaΔσy/MPaΔσz/MPaΔτxy/MPaΔτyz/MPaΔτzx/MPaΔ819.95 15.50 36.92 0.19 -0.77 -1.13 1.85 -0.12 0.71 -0.02 Δ719.95 15.50 36.92 0.19 -0.49 -0.44 4.18 0.05 0.48 0.09 Δ618.20 14.39 34.16 0.19 0.56 -0.59 15.00 0.28 2.21 -0.42 Δ516.61 13.37 31.62 0.18 1.30 2.38 -0.75 0.06 0.22 -0.85 Δ415.73 12.80 30.20 0.18 5.23 3.85 -3.00 -0.86 -1.77 -1.77 Δ310.82 9.52 22.08 0.16 38.22 23.64 4.93 1.25 2.28 -5.02 Δ24.533 0 5.091 6 11.113 7 0.091 4 0.21 1.53 5.17 -0.43 0.18 -0.68 Δ13.51 4.34 9.22 0.06 -0.17 -0.39 0.66 -0.04 0.25 0.34
表7 考虑解除路径的应力计算值
Table 7 Calculated stress value of the relief path is considered

σx/MPaσy/MPaσz/MPaτxy/MPaτyz/MPaτzx/MPaσ1大小/MPa方向/(°)倾角/(°)σ2大小/MPa方向/(°)倾角/(°)σ3大小/MPa方向/(°)倾角/(°)44.1028.8528.060.204.56-8.3247.78311531.352145821.862066
(1)研发一套高压双轴加载试验仪器,该仪器具有高压加载性能、且能适用多种直接的解除岩芯、进行长期加载试验等优点。
(2)对三山岛金矿埋深800 m原位空心包体应变计地应力测量解除岩芯进行了双轴加卸载试验,处理试验数据后提出了平均应力与体积模量和剪切模量的非线性双曲线模型,模型拟合曲线与数据之间的确定系数分别为0.989和0.997,推导了双轴加卸载数据中平均应力与应变的非线性关系即式(19)和(20)。
(3)对12组解除数据应用最小二乘法进行应力计算,考虑了解除过程中,岩芯的计算参数与岩芯解除过程中受力状态相关,将整个解除应变按应变片采集的时间间隔进行分段,分段应用最小二乘法计算地应力值,结果表明根据解除路径确定每个阶段的变形模量计算的最大主应力数值要小于通过线性拟合双轴卸载试验数据求出弹性模量和泊松比的地应力计算值。
[1] SJÖBERG J,CHRISTIANSSON R,HUDSON J A.ISRM suggested methods for rock stress estimation-part 2:Overcoring methods[J].International Journal of Rock Mechanics and Mining Sciences,2003,40(7-8):999-1010.
[2] ZANG A,STEPHANSSON O,HEIDBACH O,et al.World stress map database as a resource for rock mechanics and rock engineering[J].Geotechnical and Geological Engineering,2012,30(3):625-646.doi:10,1007/s10706-012-9505-6.
[3] 蔡美峰.岩石力学与工程[M].北京:科学出版社,2013.
[4] 李远,乔兰,孙歆硕.关于影响空心包体应变计地应力测量精度若干因素的讨论[J].岩石力学与工程学报,2006,25(10):2140-2144.
LI Yuan,QIAO Lan,SUN Xinshuo.Analyses of some factors affecting precision in in-situ stress measurement with method of CSIRO cells[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(10):2140-2144.
[5] 李远,王卓.基于双温度补偿的瞬接续采型空心包体地应力测试技术研究[J].岩石力学与工程学报,2017,36(6):1479-1487.
LI Yuan,WANG Zhuo.Development of CSIRO cell with the compromised application of instantaneous datalogging,no-power data-connection and twin temperature compensation techniques[J].Chinese Journal of Rock Mechanics and Engineering,2017,36(6):1479-1487.
[6] 闫振雄,郭奇峰,王培涛.空心包体应变计地应力分量计算方法及应用[J].岩土力学,2018,39(2):725-721.
YAN Zhenxiong,GUO Qifeng,WANG Peitao.Calculation and application of in-situ stress components in hollow inclusion measurement[J].Rock and Soil Mechanics,2018,39(2):725-721.
[7] 董诚,王连婕,孙东生,等.空心包体三轴地应力测量系统的升级改造[J].实验技术与管理,2009,26(1):51-55.
DONG Cheng,WANG Lianjie,SUN Dongsheng,et al.The upgrading and improvement of hollow inclusion triaxial strain gauge for geostress measurement[J].Experimental Technology and Management,2009,26(1):51-55.
[8] 王衍森,吴振业.地应力测量应变值检验及应变计最佳布片方式[J].岩土工程学报,1999,21(1):53-55.
WANG Yansen,WU Zhenye.Direct method to verify virgin stress measurement and the optimum rosette arrangement style of hollow inclusion cell[J].Chinese Journal of Geotechnical Engineering,1999,21(1):53-55.
[9] 刘少伟,樊克松,尚鹏翔.空心包体应力计温度补偿元件的设计及应用[J].煤田地质与勘探,2014,42(6):105-109.
LIU Shaowei,FAN Kesong,SHANG Pengxiang.Design and application of temperature compensating element of hollow inclusion stress gauge[J].Coal Geology & Exploration,2014,42(6):105-109.
[10] 白金朋,彭华,马秀敏,等.深孔空心包体法地应力测量仪及其应用实例[J].岩石力学与工程学报,2013,32(5):902-908.
BAI Jnpeng,PENG Hua,MA Xiumin,et al.Hollow inclusion strain gauge geostress measuring instrument in deep borehole and its application example[J].Chinese Journal of Rock Mechanics and Engineering,2013,32(5):902-908.
[11] DUNCAN J M,CHANG C Y.Nonlinear analysis of stress and strain in soils[J].Journal of the Soil Mechanics and Foundations Division,1970,96(3):1629-1653.
[12] KULHAWY F H,DUNCAN J M.Stresses and movements in Oroville dam[J].Journal of the Soil Mechanics and Foundations Division,1972,98(1):653-655.
[13] 席道瑛,王鑫,陈运平.描写岩石非线性弹性滞后和记忆的宏观模型[J].岩石力学与工程学报,2005,24(20):2212-2219.
XI Daoying,WANG Xin,CHEN Yunping.Macroscopic model of hysteresis and memory for the description of rock nonlinear elastic[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(20):2212-2219.
[14] 席道瑛,陈运平,陶月赞.岩石的非线性弹性滞后特征[J].岩石力学与工程学报,2006,25(6):1083-1096.
XI Daoying,CHEN Yunping,TAO Yuezan.Nonlinear elastic hysteric characteristics of rocks[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(6):1083-1096.
[15] 孔志鹏,孙海霞,陈四利.岩石材料的一种非线性三参数强度准则及应用[J].岩土力学学报,2017,38(12):3524-3531.
KONG Zhipeng,SUN Haixia,CHEN Sili.A nonlinear tri-parameter strength criterion for rock materials and its application[J].Rock and Soil Mechanics,2017,38(12):3524-3531.
[16] 蔡美峰.地应力测量中温度补偿方法的研究[J].岩石力学与工程学报,1991,10(3):227-235.
CAI Meifeng.Studies of temperature compensation techniques in rock stress measurements[J].Chinese Journal of Rock Mechanics and Engineering,1991,10(3):227-235.
[17] 葛修润,侯明勋.钻孔局部壁面应力解除法(BWSRM)的原理及其在锦屏二级水电站工程中的初步应用[J].中国科学,2012,42(4):359-368.
GE Xiurun,HOU Mingxun.Principle of in-situ 3D rock stress measurement with borehole wall stress relief method and its preliminary applications to determination of in-situ rock stress orientation and magnitude in jinping hydropower station[J].Science China Technological Sciences,2012,42(4):359-368.
[18] 蔡美峰,刘卫东,李远.玲珑金矿深部地应力测量及矿区地应力场分布规律[J].岩石力学与工程学报,2010,29(2):227-233.
CAI Meifeng,LIU Weidong,LI Yuan.In-situ stress measurement at deep position of linglong gold mine and distribution law of in-situ stress field in mine area[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(2):227-233.
[19] FANG Shulin,ZHANG Jian.In-situ measure to internal stress of shotcrete layer in soft-rock roadway[J].International Journal of Coal Science & Technology,2014,1(3):321-328.