
移动阅读
地应力是岩土工程围岩变形及破坏的根本作用力,矿山地质灾害的诱因也大多与开采时围岩和矿体发生应力场的重分布有关,灾害的发生都伴随着应力场的突变[1-4]。因此,准确获取工程区域地应力场分布和状态是地下岩石工程,特别是深部开采中需重点把握的因素。
现场实测是获得初始地应力场数据最直接的方法,但是受到成本高、时间长、施工困难等因素制约,限制了大规模开展[4]。如何根据稀少样本地应力测量数据准确的进行地应力场的反演分析是现今地应力场研究的重点。许多学者对地应力场的反分析提出了多种理论方法。陈章华等[5]通过采用偏最小二乘法对乌鞘岭隧道岭脊地段地应力进行反演分析,得到较为精确的拟合结果。张乐文等[6]基于甘孜州江边水电站引水隧洞地区进行地质建模,并采用FLAC3D进行正计算得到足够多的学习样本数据,表明RBF神经网络在大样本数据下具有良好的拟合精度。叶智峰等[7]将极限学习机应用于地应力场的反演中,解决了神经网络收敛速度慢、拟合过度等缺点,为地应力场反演提供了新的思路。裴启涛等[8]将软件 FLAC3D和3DEC相结合,在整体连续的大范围内进行一次反演、局部非连续的小范围内2次精确反演的方法,大幅度的提高了复杂工程区地应力反演精度,为实际工程提供借鉴。高谦等[9]以金川矿区为工程背景,采用了正交数值分析算法,建立起地应力场和影响因素直接的函数关系,该方法可为复杂地应力场反演和工程稳定性分析提供一条途径。张风威等[10]采用多元线性回归法和粒子群—神经网络智能反演方法对兰州水源地工程输水隧洞进行地应力场重构,经对比分析,得出智能反演方法计算量小、精度高、效果好。然而,上述地应力场反演的精度都依赖多测点数据,且在数值模拟计算中边界条件采用线性、均匀原理进行组合施加,这实际上是对工程区域地应力场的一种线性简化,在工程地质较为复杂以及实测点较少的情况下,反演精确性会受到影响[11]。因此,如何在稀少样本测点数据情况下,提高复杂地质体地应力场反演精度至关重要。
笔者以ABAQUS为正分析计算平台,将Group Modeling of Data Handing(GMDH)神经网络算法应用于地应力场反演计算中,基于Matlab编写GMDH神经网络算法程序,实现了在稀少样本测点数据的情况下准确拟合出满足实际情况的非线性边界载荷函数表达式,从而提高了区域地应力场的反演计算精度。最后用两个算例对GMDH神经网络算法进行验证:① 构建二维复杂地质条件下的急倾斜地层地质模型;② 杏山铁矿区域地质构造及地形地貌特征十分复杂,且存在大型断层构造,露天开采转地下开采所产生的次生应力场会使原地应力场受到一定程度的扰动[11-12],鉴于此,建立起覆存含隐伏断层构造的杏山铁矿区域地质模型。
在地应力场反演工作中,通常需要在现场钻孔进行地应力测量,但受到成本昂贵的限制,现场钻孔数量往往很少。然而,研究的工程区域规模大、埋藏深、局部地质构造错综复杂,地应力场总体样本数据众多、维度庞大,而实测数据样本量显得十分稀少。因此,基于稀少样本测点数据,进行地应力场反演与重构显得尤为重要。
稀少样本地应力数据规模小,维度大,采用传统的学习算法进行样本数据分析,结果往往相关性小、离散性高。笔者采用GMDH神经网络算法,根据稀少样本数据特征类型,首先按照关联性进行特征计算;然后根据关联结果进行特征排序;最后设定阙值获取相关程度高的子数据集合。
设稀少样本数据集D容量为n,特征维度为m,样本数据采用aij,i∈1∶n,j∈1∶m,各数据特征采用c1,c2,…,ck,…,cm表示,c为数据特征的值域,其关联度I(aij,ck)计算公式为
(1)
其中,F为GMDH神经网络算法的拟合函数;I(aij,ck)为数据特征关联度,I(aij,ck)值越大,表示数据类型与特征之间的关联程度就越高,根据式(1)计算结果从高到底排序,并进一步筛选子数据集,其阙值Q′为
Q′=0.65min(I(aij,ck))+0.65min(I(aij,ck))
(2)
将I(aij,ck)和Q′进行对比,若I(aij,ck)<Q′,则说明这个特征与数据类型有较高的关联度,这时将该数据添加至子数据集;若I(aij,ck)≥Q′,则说明这个特征与数据类型离散度较大,将其剔除。
地应力场在长期的地质演变进程中,不断地受到来自于地壳内部作用和外部环境作用的影响,使地应力场呈现出时空复杂性特征[12]。但对于某一地质年代而言,地应力场可视为不考虑时间因素的相对稳定场[13]。大量研究和工程实践表明,地应力是如下变量的函数[14-15]:
σ=F(x,y,z,E,μ,ΔG,ΔH,T,W,Q)
(3)
式中,σ为地应力值;x,y,z为测点空间位置的坐标;E,μ为岩体的弹性模量、泊松比;ΔG为自重因素;ΔH为地质构造因素;T,W分别表示温度场、渗流场;Q为灰色因素,即影响研究区域地应力场其他无法确定的因素。
在地应力场反演过程中,x,y,z可以通过实际测量获得;E,μ可通过材料试验获得,故都可认为是已知量。ΔG,ΔH可视为主要未知量,其中ΔG的主要影响因素由重力G决定,ΔH的主要影响因素大致可以分为:① 横向挤压构造应力场Δh;② 纵向挤压构造应力场Δv;③ 水平向剪切构造应力场Δhh;④ 竖直向剪切构造应力场Δvv。此外,T,W,Q对地应力场影响较小,一般情况下可忽略不计。
σ=F(ΔG,ΔH,Δv,Δhh,Δvv)
(4)
因此,在ABAQUS数值模型分别单独施加重力G和构造应力场对应的边界条件Hh,Hv,Hhh,Hvv进行计算,其中Hh是在模型横向(x轴)施加的法向应力边界条件、Hv是在模型纵向(y轴)施加的法向应力边界条件、Hhh是在模型侧边界面施加平行于x-y平面的剪切应力边界条件、Hvv是在模型侧边界面施加平行于x-z平面施加的剪切应力边界条件,经计算获得的基本应力场分量依次为σG,σH,σv,σhh,σvv。

(5)
σ=g(K)·F(σG,σH,σv,σhh,σvv)T
(6)
g(K)=(g(kG),g(kh),g(kv),g(khh),g(kvv))
(7)
σ为初始地应力场的拟合值。一般情况下,在地应力场的反演计算中,测点处地应力值是由各个影响因素产生的应力场进行线性叠加形成的,而实际的地应力场分布具有显著的非线性特征,各影响因素不是单纯的线性叠加,因此,笔者充分利用GMDH神经网络算法的非线性拟合功能,并将常系数变为非线性泛函系数g(K),如式(7)所示,并以此来表征地应力场各个影响因素之间的非线性关系,实现复杂地质条件下地应力场的非线性反演计算。
传统的神经网络优化算法,网络结构固定,各层的神经元数量固定,因此需要大量的样本数据对神经网络进行训练,以获得较高的反演精度。这对于稀少样本测点数据的工程现场,一般神经网络算法的使用就受到了很大的限制。GMDH神经网络以结构的灵活性,通过不断调整网络的层数和各层神经元的数量,在稀少样本数据反演方面具有明显的优势。另外,GMDH神经网络算法高度的非线性拟合函数可充分挖掘输出值与输入值之间的关系,拟合出的非线性边界荷载函数式,一方面可模拟地应力复杂演化过程;另一方面,可充分考虑出工程区域内非线性、非连续的地质构造对地应力量值和方向的影响。
1.3.1 GMDH神经网络算法的概念
GMDH神经网络算法是在自组织控制原理的基础上,提出的一种有效的神经网络算法,又称多项式网络综合算法[16-17]。它无需规定网络结构,具有高度的非线性拟合功能,能自动选择出最佳的网络模型。对于有噪音的稀少样本数据建模、预测等方面优势十分明显,已经成为人们对非线性问题研究的有力工具[18-19]。
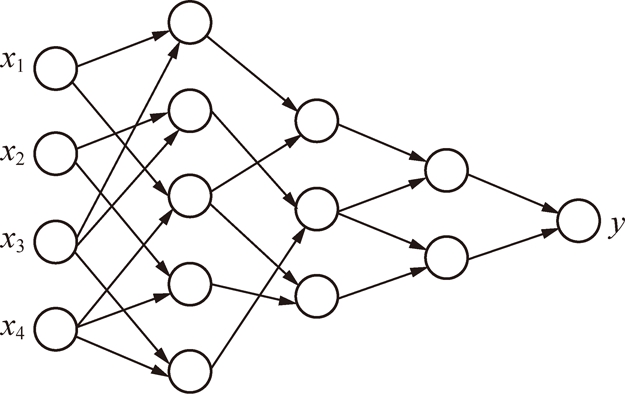
图1 GMDH神经网络结构模型
Fig.1 Structural model of GMDH neural network
在复杂区域地应力场反演中,基于现场实测点的地应力数据资料,分析了区域内地应力场方向变化特征及量值随深度的分布规律,得出了GMDH网络算法的非线性拟合函数,如式(8)所示。假定输入量![]() 为输出量,由网络将各个输入量两两交叉组合形成活动的神经元,,并进行每个神经元非线性函数的拟合(以i和j分量为例);再通过设定阙值将误差较大的神经元剔除,未被剔除神经元的拟合值作为下一代神经元的输入量,反复进行活动神经元的产生与选择,直到满足拟合精度要求为止[20-21]。
为输出量,由网络将各个输入量两两交叉组合形成活动的神经元,,并进行每个神经元非线性函数的拟合(以i和j分量为例);再通过设定阙值将误差较大的神经元剔除,未被剔除神经元的拟合值作为下一代神经元的输入量,反复进行活动神经元的产生与选择,直到满足拟合精度要求为止[20-21]。
(8)

式中,X为输入量;W为拟合系数矩阵,其中wkk,k∈i,j(i,j分别为指标索引,![]()
GMDH神经网络的训练实际上就是在数学层面上的有约束预测优化问题,该算法采用Widrow-Hoff学习规则,设约束函数为![]() 进下迭代寻优:当ek≤ε时,迭代终止,拟合系数取Wk;否则,利用样本数据进行系数调整:
进下迭代寻优:当ek≤ε时,迭代终止,拟合系数取Wk;否则,利用样本数据进行系数调整:![]() 当ek+1≤ε时,系数取Wk+1。其中,ε为阈值,
当ek+1≤ε时,系数取Wk+1。其中,ε为阈值,![]() 为拟合输出量,yk为目标输出量。
为拟合输出量,yk为目标输出量。
1.3.2 GMDH网络算法反演模型的建立
在对研究区域进行地应力场反演分析中,关键是建立起该区域的神经网络反演模型,即建立起边界条件和对应地质模型在实测点位置处应力计算值之间的非线性映射关系。笔者在此充分借助于该算法的全局寻优和可以任意逼近的特点来建立映射:
(ΔG,ΔH,Δv,Δhh,Δvv)T=F-1(σ)
(9)
式(9)是式(4)的逆函数,即是GMDH神经网络算法的初始应力场反演分析映射关系模型,其中σ为ABAQUS正计算出的应力张量表达形式,即σ=[σ1,σ2,σ3,τ12,τ23,τ31]。
按照算法实现流程(图2),构建GMDH神经网络算法,过程描述如下:
(1)根据工程现场地质资料,建立三维地质模型,在ABAQUS软件中将计算模型上施加几组边界条件进行正分析计算,获得稀少样本地应力数据,稀少样本数据N如式(10)所示。其中,i为施加的边界条件组序号,i∈[1,n],n为组数;j为在模型上选取的测点序号,j∈[1,m],m为测点总数。

(10)
(2)结合稀少样本的数据结构特征(式(10)),确定GMDH神经网络算法的初始模型。即岩体自重以及地质构造运动等边界条件作为输出量,测点处应力分量值作为输入量的网络初始化模型结构。
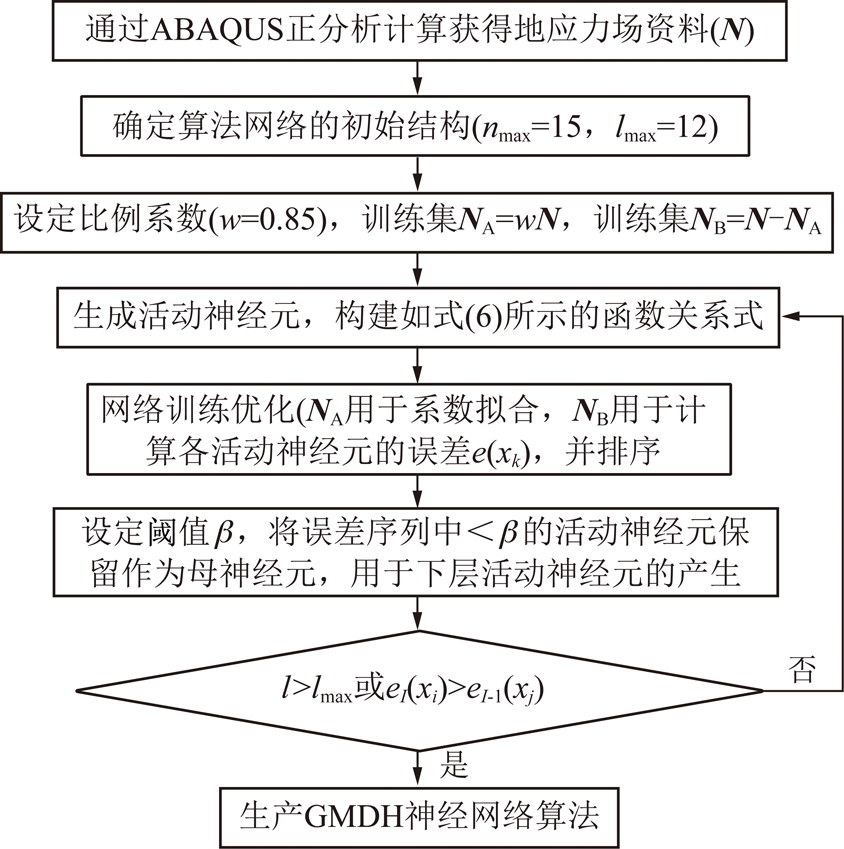
图2 GMDH神经网络算法流程
Fig.2 Flow chart of GMDH neural network algorithm

图3 稀少样本数据的分组流程
Fig.3 Flow chart of limited sample data for grouping
(3)采用随机抽取的方法将稀少样本数据N分为训练集NA和检验集NB(式(11),(12))。具体流程如图3所示。训练集用于网络中神经元的训练和非线性方程系数的拟合,检验集用于对网络模型计算均方差和筛选活动神经元。
(11)
N=[N1,N2,…,Ni,…,Nn]
(12)
其中,![]() 为自由指标[22]。fr(N)函数是自定义的算法程序,用于在稀少样本数据矩阵N随机抽取比例系数为w的列向量,形成子样本数据矩阵NA和NB。
为自由指标[22]。fr(N)函数是自定义的算法程序,用于在稀少样本数据矩阵N随机抽取比例系数为w的列向量,形成子样本数据矩阵NA和NB。
(4)网络训练。运用GMDH神经网络算法对稀少样本测点数据进行训练学习,建立起待反演的边界条件与地质模型内相应测点处的地应力计算值之间的GMDH网络算法模型,给定阈值,调整拟合系数Wk,并循环迭代直到满足精度要求。
(5)将实测应力值分量输入已优化的GMDH神经网络算法模型中,输出量即为反演出的最优化边界条件(符合实际情况的非线性边界荷载表达式)。
(6)将最优化边界载荷表达式施加在已建立的ABAQUS三维地质模型上进行正分析计算,获得工程区域中的三维地应力场分布。
因此,当区域工程现场的地质条件、地质构造非常复杂时,GMDH神经网络算法能够充分挖掘稀少样本数据的潜在特征,引入的非线性泛函系数能够表示地应力场中各个影响因素之间的非线性叠加关系,拟合出的非线性边界条件函数表达式能充分考虑地应力场随埋深的非线性特征及局部地质构造处地应力场的非连续性特点,使反演结果更加合理。
构建一个复杂地质条件下的二维急倾斜地层地质模型。如图4所示,区域内包含两岩层及两煤层,且各层材质均匀,材料参数见表1,模型埋深350 m,长度350 m。在模型的左边界施加0~3.5 MPa非均匀变化的压应力载荷条件,模型的下边界水平及竖向约束,右边界水平约束,产生一个应力场,并在模型中随机选择15,12,9,6个位置点的应力值作为“现场实测应力”(表2)。

图4 假定二维急倾斜地层
Fig.4 Assumed two-dimensional steeply inclined layer
表1 岩体力学参数
Table 1 Mechanical parameters of rock mass

为了比较GMDH神经网络算法和BP神经网络算法在地应力测点样本量不同情况下的反演精度,分别取15个、12个、9个及6个测点进行反演计算(选点情况见表3)。通过ABAQUS有限元软件对该二维煤层模型进行正分析计算,即在模型左侧边界面分别施加4组不同应力边界条件,获得不同边界条件下的地应力场分布情况。随后,选取各组边界条件下测点位置处的应力分量值,与对应模型边界条件构成训练样本,分别代入GMDH神经网络算法和BP神经网络算法进行训练与优化。将“实测应力”作为输入量,分别代入到两种已优化的神经网络算法中,输出值为对应的边界条件,最后,施加边界条件获得“实测点”处各应力分量反演值,并与“实测值”进行对比(对比结果如图5所示)。
表2 “实测应力”分量
Table 2 “Measured stress” components MPa
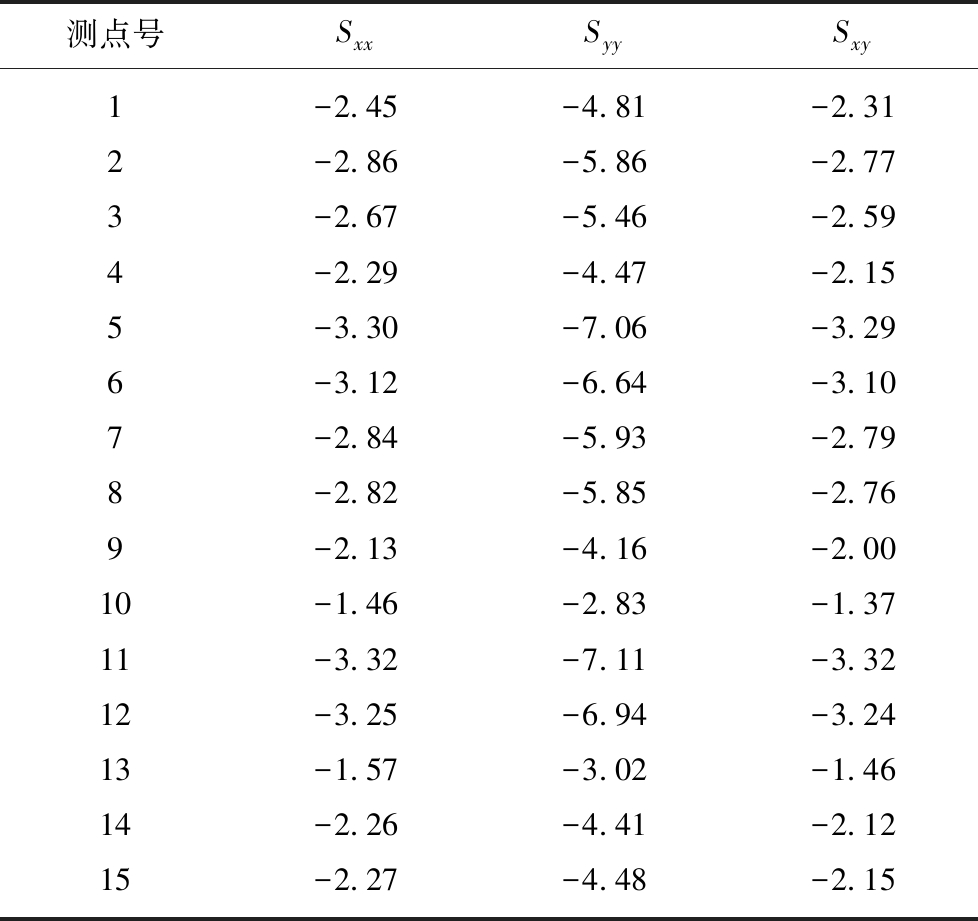
测点号SxxSyySxy1-2.45-4.81-2.312-2.86-5.86-2.773-2.67-5.46-2.594-2.29-4.47-2.155-3.30-7.06-3.296-3.12-6.64-3.107-2.84-5.93-2.798-2.82-5.85-2.769-2.13-4.16-2.0010-1.46-2.83-1.3711-3.32-7.11-3.3212-3.25-6.94-3.2413-1.57-3.02-1.4614-2.26-4.41-2.1215-2.27-4.48-2.15
表3 各样本选点序号
Table 3 Number of selected points for each sample

样本量测点编号15个1,2,3,4,5,6,7,8,9,10,11,12,13,14,1512个1,2,4,5,6,8,9,11,12,13,14,159个2,4,5,8,9,11,12,14,156个2,5,8,9,11,14

图5 反演精度对比
Fig.5 Contrast of inversion accuracy
由图5可以看出,当模型实测点数为15个时,两种神经网络算法在测点处应力反演精度高,其中GMDH神经网络算法反演精度为90%,而BP神经网络算法反演精度为86%,GMDH神经网络算法反演精度高于BP神经网络算法;当模型实测点数为12个时,GMDH神经网络算法反演精度为89%,而BP神经网络算法反演精度为84%,表明GMDH神经网络算法反演精度高于BP神经网络算法;当模型实测点数为9个时,GMDH神经网络算法反演精度为87%,而BP神经网络算法反演精度为80%,GMDH神经网络算法反演精度明显高于BP神经网络算法;在测点数量仅为6个时,GMDH神经网络算法保持了较高反演精度,其量值为84%,而BP神经网络算法反演精度仅为76%,且有3处应力分量的反演误差高于20%,从而说明GMDH神经网络反演误差受测点数量影响较小,反演精度整体高于BP神经网络算法。
如图6所示,通过对比两种神经网络算法的反演精度与测点样本量的关系曲线图可知:GMDH神经网络算法反演精度整体高于BP神经网络算法反演精度,特别是在稀少样本测点数据的条件下,GMDH神经网络算法反演精度显著高于GMDH神经网络算法;两种算法在测点数量大于9个的情况下,其反演精度相对较高,量值均大于80%。当测点数量<9个时,BP神经网络算法的精度大幅度降低。因此,GMDH神经网络算法在稀少样本地应力场反演计算中具有一定的优势。
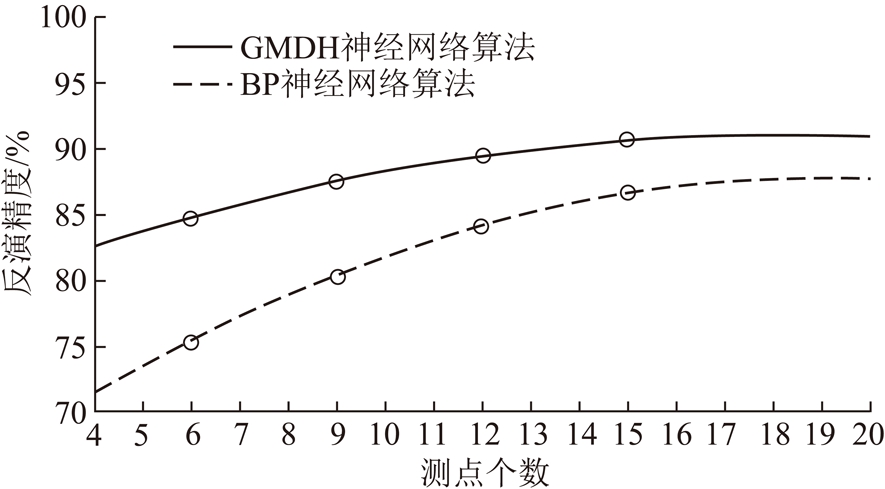
图6 反演精度与测点数量的关系曲线
Fig.6 Relation curves of inversion accuracy and the number of measured points
杏山铁矿地处河北省迁安市,位于迁安铁矿区南部,属于燕山支脉南麓,低山丘陵地貌。区域内地势为西北、西南高、东南低。矿床主体呈向斜构造,被F9断层南北向切割[23]。露天采场如图7所示,最高标高为305 m,最低标高为-33 m,矿体倾角约在50°~60°,平均厚度约30 m。现采区露天开采结束,正转入地下开采,根据实际矿体深度、存在方式及开采条件等因素,采用两期开挖方式:即-330 m以上为一期开采范围,-330 m以下的深部矿体为二期开采范围。

图7 实际矿区
Fig.7 Actual diagram of mine area
采用空心包体应力解除法在杏山铁矿进行两期地应力测试,共8个点[24]。为便于地应力场的反演计算,根据弹性理论,将实测地应力的主应力表示形式转换成正应力分量的表示形式[25](表4)。限于篇幅,不对转换过程进行描述。
表4 实测点地应力分量
Table 4 In-situ stress components at measured points MPa
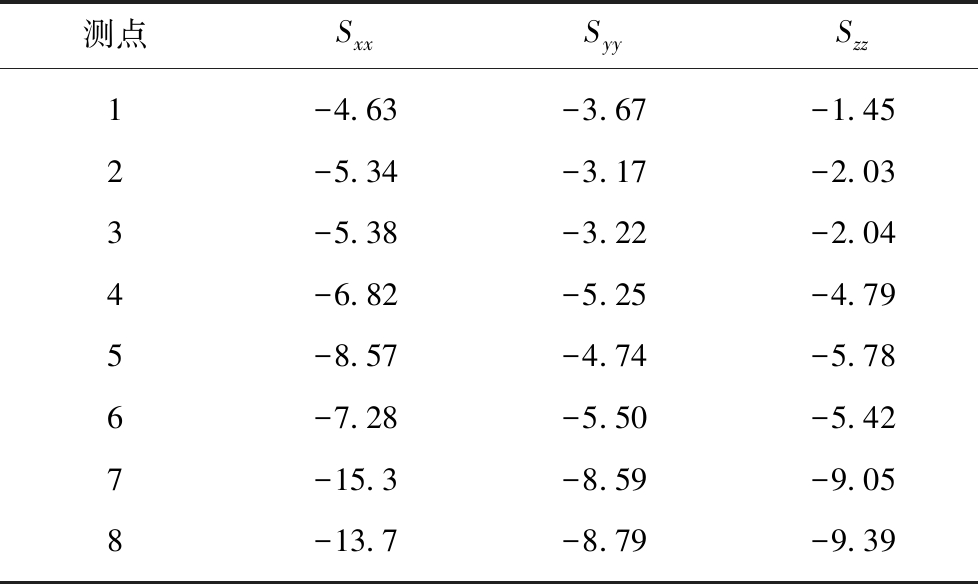
测点SxxSyySzz1-4.63-3.67-1.452-5.34-3.17-2.033-5.38-3.22-2.044-6.82-5.25-4.795-8.57-4.74-5.786-7.28-5.50-5.427-15.3-8.59-9.058-13.7-8.79-9.39
根据杏山铁矿地质剖面图等资料,结合工程地应力实测点空间位置,确定出模型范围(如图8所示)。模型原点坐标选为(503 100,4 422 300,0),Y方向沿正北向,x,y,z轴的计算范围分别是503100~504100,4422300~4423300,-340~330 m。

图8 矿区平面
Fig.8 Plane diagram of mine area
基于ABAQUS有限元软件建立杏山铁矿数值模型(图9),进行网格划分与参数定义,网格类型为C3D4四面体单元,共划分82 981个节点,451 935个单元。断层的处理采用弱化断层区域材料属性的方法,岩体力学参数取值见表5[26]。

图9 三维数值模型
Fig.9 3-D numerical model
表5 岩体力学参数
Table 5 Mechanical parameters of rock mass
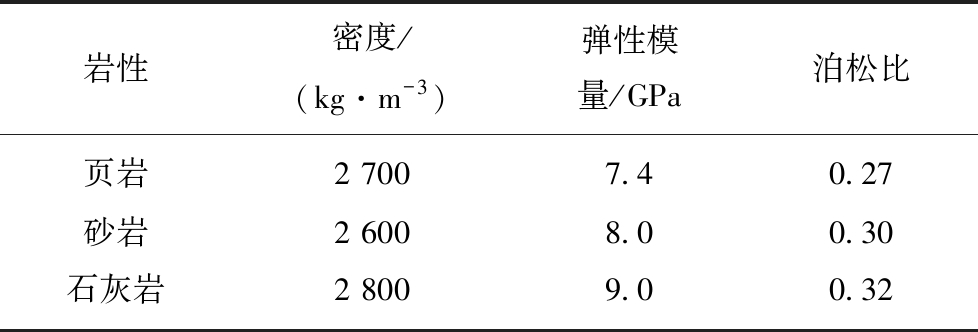
岩性密度/(kg·m-3)弹性模量/GPa泊松比页岩2 7007.40.27砂岩2 6008.00.30石灰岩2 8009.00.32
计算时,首先根据本地区地质资料,获得符合实际地应力场分布的边界条件形式,以提高反演精度,本矿区模型的边界条件形式是沿深部方向的非线性边界载荷函数(式(13))。随后,在数值模型上施加如图10所示的4组边界载荷(依次是Hx,Hy,Hxz,Hyz),得到各工况下数值模型测点处的应力值,将各组边界工况组合数据及对应的计算模型上测点处应力值分别作为训练样本的输出向量和输入向量,对GMDH神经网络算法进行优化。当计算精度达到90%以上,网络训练完毕。然后,将杏山铁矿实测地应力资料作为输入量代入已优化的GMDH神经网络中进行计算,得到拟合后的边界载荷表达式(式(14),(15))。最后,将上述边界条件施加在模型上进行地应力场重构计算,获得测点处应力反演值。另外,为了对比GMDH神经网络算法的反演精度,同样对杏山铁矿区采用BP神经网络算法进行地应力场的计算,得到测点处地应力的反演值,2种算法的反演精度对比见表6,地应力场分布如图11,12所示。
(13)

(14)

(15)
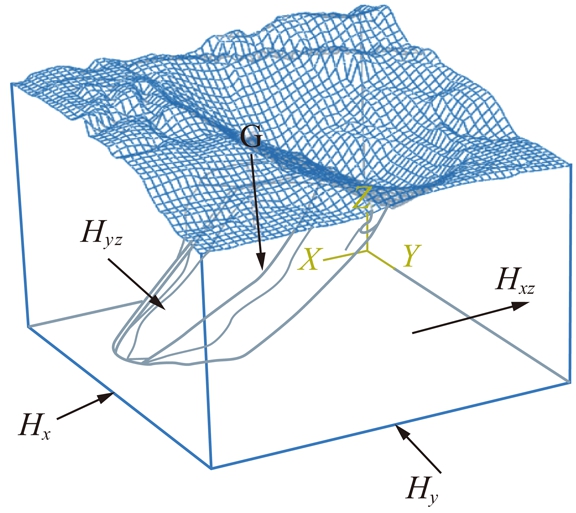
图10 矿区边界条件示意
Fig.10 A schematic diagram of the boundary condition of the mine area
表6 2种神经网络算法反演结果对比
Table 6 Comparison of the inversion results by the two neural network methods

测点GMDH/MPaSxxSyySzz误差/%SxxSyySzzBPSxxSyySzz误差/%SxxSyySzz1-4.69-3.60-2.121.182.8846.30-4.56-2.36-0.651.4310.8055.192-5.82-2.89-1.728.938.7915.71-5.44-2.21-1.401.8830.4931.353-5.91-3.10-2.029.783.741.15-5.56-2.46-1.773.2823.4913.334-6.97-5.01-4.472.284.656.66-6.71-4.59-4.241.5912.6911.545-7.26-5.26-5.1515.3110.7610.79-6.91-4.74-5.0919.340.1511.956-6.93-4.97-5.604.869.603.19-6.58-4.46-5.539.5815.871.987-14.70-8.87-10.604.083.2216.82-14.3-8.52-10.46.360.9315.108-13.00-9.10-7.894.823.4715.96-12.7-8.74-7.757.180.5517.41

图11 GMDH算法和BP算法反演矿体区域最大主应力云图
Fig.11 Maximum principal stress contour by GMDH method and BP method

图12 GMDH算法和BP算法反演典型剖面最大主应力云图(y=2 800 m)
Fig.12 Typical section of maximum principal stress contour by GMDH method and BP method (y=2 800 m)
表6给出了实测地应力与两种神经网络算法反演值对比情况,整体看来:BP神经网络算法反演应力值与实测应力值的相关系数为0.97,标准差为3.36 MPa;而GMDH神经网络算法反演应力值与实测应力值的相关系数为0.98,标准差为3.23 MPa。两种神经网络算法得出的应力值均与实测值相近,但GMDH神经网络算法计算精度更高,且效果更佳明显。
另外,BP神经网络算法得到反演值的相对误差较大,有3处测点应力分量误差高于30%,最大误差量为55.19%,发生在测点1的Z轴应力分量上。而GMDH神经网络算法反演误差相对小,除了测点1的Z轴应力分量误差为46.30%,其他测点的误差都在16%以内。说明该网络的反演精度明显高于BP神经网络。然而,上述两种反演算法计算出测点1竖直应力分量误差都较大,数值为46.30%和55.19%,究其原因可能一方面与矿区开采年代久远,表层岩体受到较为严重的侵蚀风化作用,导致浅部局部区域应力释放;另一方面,反映了地应力场受到多因素制约,而在本计算中主要考虑了自重和构造作用的影响,而忽略了其他因素。整体看来:GMDH神经网络算法在半数以上测点的预测精度都在5%以内,可见该神经网络算法在稀少样本测点数据的反演计算中具有较高的可靠性。
图11(a)为GMDH神经网络算法反演矿体区域最大主应力云图;图11(b)BP神经网络算法反演矿体区域的最大主应力云图;图12(a)为GMDH神经网络算法反演下矿区典型剖面(y=2 800 m)最大主应力云图;图12(b)为BP神经网络算法反演的矿区典型剖面(y=2 800 m)最大主应力云图。
由图11(a)可知,GMDH神经网络反演出的矿体区域地应力场有明显的分带、分层现象,最大主应力由上至下逐渐增大,其量值在4.71~19.24 MPa,属于高等应力水平。另外,深部矿层最大主应力受到自重应力场的作用,呈明显的分层现象;浅部矿层受到一定的地形和风化作用等因素影响,呈明显的分带现象,以构造应力场控制为主。
由图11(b)可知,BP神经网络算法反演出的矿体区域初始地应力场分层、分带现象并不明显,最大主应力值为18.74 MPa,绝大部分区域应力值在5.41~13.74 MPa,隶属于高等应力水平。但值得注意的是:矿体上部少数区域出现拉应力区,最大值达到1.25 MPa,由于矿体深埋于地下,实际并不会出现受拉区。因此,BP神经网络算法反演出的矿区地应力场与实际情况不符合,从而说明GMDH神经网络算法反演结果更加真实。
由图12(a)可知:GMDH神经网络算法重构出的地应力场沿深度方向呈递增趋势。一方面:深部岩层最大主应力以自重应力场为主,最大值为18.59 MPa,矿体应力值与周边岩体相比,呈增加趋势,出现应力集中区,在该矿区作业时应予以重视。而在断层位置出现应力释放;另一方面:浅部岩层受地形和风化作用的因素影响,以构造应力场控制为主,分层分带现象明显。地表少许区域出现应力集中现象,量值约为6.95 MPa。出现这类情况是因为铁矿一期开挖之后,地表出现较大的矿坑,受到矿坑高度差及坡体上部岩石自重作用影响所致。
由图12(b)可知,BP神经网络算法重构出的地应力场与GMDH神经网络算法重构出的地应力场基本一致,其最大主应力量值为19.84 MPa,隶属于高等应力水平。但相对GMDH神经网格构建的地应力场而言,BP神经网格构建的地应力场在深部分层、浅部分区及断层处应力释放现象并不明显。此外,在矿坑顶部区域受到拉应力作用,最大拉应力高到4.89 MPa,这与实际地应力场分布规律不符合。因此,验证了GMDH神经网络网络重构出的地应力场分布更加符合实际。
(1)GMDH神经网络算法在稀少样本测点数据预测方面相比其他网络神经算法具有显著的优越性。其根本原因:其一:在于网络训练过程中不断地进行学习集的筛选,将噪音数据删除,从而保证了网络的泛化能力。在个别测量数据含有较大误差的情况下,仍可以保证计算精度;其二,该神经网络仅仅设定了网络的最大层数和每层最大神经元的数量,并没有给定网络结构,从而最大程度上减少人为因素对神经网络的干扰,避免过拟合情况的发生。
(2)根据工程现场有限测点资料,建立起非线性边界载荷拟合函数,该函数为沿深度的2次方项、2次根号项、及常数项的叠加形式。该函数式能够考虑区域内地应力场方向变化及量值随深度的分布规律,从而使地应力场反演结果更加合理。
(3)研究发现,GMDH神经网络算法反演精度高于BP神经网络算法反演精度。在算例1中,当样本数量小于9个时,BP神经网络算法的反演精度大幅度降低。在算例2中,GMDH神经网络算法反演精度同样高于BP神经网络算法,但少数测点处应力分量反演精度仍较低,引起误差的原因可能是测点数据存在误差、数值模型概化、以及局部强烈的地质构造作用等因素所致。
(4)研究结果表明:在地层均匀,不存在非连续地质构造的区域内,GMDH神经网络算法比BP神经网络算法在稀少样本测点数据的情况下反演精度高;而在非连续构造覆存的区域,GMDH神经网络算法反演精度明显高于BP神经网络算法的反演精度。
在地应力场反演工作中,除了研究在稀少样本测点数量情况下如何反演高精度的地应力场,还需进一步对不同地质区域内最优测点数量及选点位置进行计算与分析、考虑不同尺度下岩体力学参数和非连续性特征的差异对地应力场分布的影响。另外,针对离散稀少样本应力测点数据的反演计算,单一算法出现鲁棒性差等问题,还需进一步研究多种算法相结合共同反演地应力场,克服单一方法存在的局限性,从而进一步提高反演精度。
[1] 张社荣,胡安奎,王超,等.基于SLR-ANN的地应力场三维智能反演方法研究[J].岩土力学,2017,38(9):2737-2745.
ZHANG Sherong,HU Ankui,WANG Chao,et al.Three-dimensional intelligent inversion method for in-situ stress field based on SLR-ANN algorithm[J].Rock and Soil Mechanics,2017,38(9):2737-2745.
[2] LI Qingfeng,ZHU Quanqu.Control technology and coordination deformation mechanism of rise entry group with high ground stress[J].International Journal of Mining Science and Technology,2012,22(3):429-435.
[3] 程远平,张晓磊,王亮.地应力对瓦斯压力及突出灾害的控制作用研究[J].采矿与安全工程学报,2013,30(3):408-414.
CHENG Yuanping,ZHANG Xiaolei,WANG Liang.Controlling effect of ground stress on gas pressure and outburst disaster[J].Journal of Mining & Safety Engineering,2013,30(3):408-414.
[4] 袁海平,王金安,蔡美峰.复杂地应力场几何跨尺度反演与重构方法研究[J].采矿与安全工程学报,2011,28(4):589-595.
YUAN Haiping,WANG Jinan,CAI Meifeng.Geometric cross-scale back-analysis and reconstruction method for complicated geo-stress field[J].Journal of Mining & Safety Engineering,2011,28(4):589-595.
[5] 陈章华,陈磊,纪洪广.基于偏最小二乘法的地应力场拟合[J].北京科技大学学报,2013,35(1):1-7.
CHEN Zhanghua,CHEN Lei,JI Hongguang.Geo-stress field fitting based on the partial least square method[J].Journal of University of Science and Technology Beijing,2013,35(1):1-7.
[6] 张乐文,张德永,邱道宏.径向基函数神经网络在地应力场反演中的应用[J].岩土力学学报,2012,33(3):799-804.
ZHANG Lewen,ZHANG Deyong,QIU Daohong.Application of radial basis function neural network to geostress field back analysis[J].Rock and Soil Mechanics,2012,33(3):799-804.
[7] 叶智峰,曹青.极限学习机在初始地应力场反演中的应用[J].水电能源科学,2016,34(6):158-160,157.
YE Zhifeng,CAO Qing.Application of extreme learning machine in back analysis of initial geostress field[J].Water Resources and Power,2016,34(6):158-160,157.
[8] 裴启涛,丁秀丽,卢波,等.考虑地应力分布形式的坝址区初始应力场二次反演方法[J].岩土力学,2016,37(10):2961-2970.
PEI Qitao,DING Xiuli,LU Bo,et al.Two-stage back analysis method of initial geostress field in dam areas considering distribution characteristics of geostress[J].Rock and Soil Mechanics,2016,37(10):2961-2970.
[9] 杨志强,高谦,翟淑花,等.复杂工程地质体地应力场智能反演[J].哈尔滨工业大学学报,2016,48(4):154-160.
YANG Zhiqiang,GAO Qian,ZHAI Shuhua,et al.Intelligent inversion method of in-situ stress field for a complicated engineering geological body[J].Journal of Harbin Institute of Technology,2016,48(4):154-160.
[10] 杨风威,房敬年,杨继华,等.兰州水源地工程超长输水隧洞初始地应力反演研究[J].水电能源科学,2018,36(8):94-97,73.
YANG Fengwei,FANG Jingnian,YANG Jihua,et al.initial geostress inversion of ultralong water transport tunnel in water source area of Lanzhou[J].Water Resources and Power,2018,36(8):94-97,73.
[11] 史佳欢.露天转地下开采上覆岩体变形机理及其灾害预测[D].北京:北方工业大学,2015:4.
SHI Jiahuan.Deformation mechanism and disaster analysis of overlying rock in mining with transition from pit to underground[D].Beijing:North China University of Technology,2015:4.
[12] 孙世国,苗子臻,龚之淇,等.杏山铁矿冲击地压预测的优化GM(1,1)模型[J].金属矿山,2017(1):165-168.
SUN Shiguo,MIAO Zizhen,Gong Zhiqi,et al.Optimized GM(1,1) model for prediction of rock burst in Xingshan Tron Mine[J].Metal Mine,2017(1):165-168.
[13] 戴荣,李仲奎.三维地应力场BP反分析的改进[J].岩石力学与工程学报,2005,24(1):83-88.
DAI Rong,LI Zhongkui.Modified BP back analysis of 3D in-situ stresses[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(1):83-88.
[14] 王金安,李飞.复杂地应力场反演优化算法及研究最新进展[J].中国矿业大学学报,2015,44(2):189-205.
WANG Jinan,LI Fei.Review of inverse optimal algorithm of in-situ stress field and new achievement[J].Journal of China University of Mining and Technology,2015,44(2):189-205.
[15] 穆成林,裴向军,路军富.基于多层次灰色理论围岩稳定性评价研究[J].地下空间与工程学报,2016,12(1):220-226.
MU Chenglin,PEI Xiangjun,LU Junfu.Study on evaluation of surrounding rock stability based on muti-hierarchy gray theory[J].Chinese Journal of Underground Space and Engineering,2016,12(1):220-226.
[16] 朱兵,贺昌政,肖进.基于GMDH方法的四川民用汽车保有量预测研究[J].现代管理科学,2006(6):20-21.
ZHU Bing,HE Changzheng,XIAO Jin.Study on the prediction of Sichuan civil automobile ownership based on GMDH method[J].Modern management science,2006(6):20-21.
[17] 徐玲.基于GMDH神经网络的轮胎硫化温度预测[J].橡胶工业,2013,60(5):301-304.
XU Ling.Tire vulanization temperature prediction based on gmdh neural network[J].Rubber Industry,2013,60(5):301-304.
[18] 李牡丹,王印松.基于灰色GMDH网络组合模型的风速预测[J].可再生能源,2017,35(4):522-527.
LI Mudan,WANG Yinsong.Wind speed prediction based on grey GMDH network combined model[J].Renewable Energy Resources,2017,35(4):522-527.
[19] 顾洁,李雪亮,牛新生,等.基于GMDH的中长期电力负荷组合预测模型[J].电力科学与技术学报,2012,27(1):54-58.
GU Jie,LI Xueliang,NIU Xinsheng,et al.Study on combination forecasting model for mid-long term power load based on GMDH[J].Jounal of Eiectric Power Science and Technology,2012,27(1):54-58.
[20] PHAM D T,LIU X.Modelling and prediction using GMDH networks of Adalines with nonlinear preprocessors[J].International Journal of Systems Science,1994,25(11):1743-1759.
[21] 崔霞,高建华.基于GMDH神经网络的组合预测模型[J].小型微型计算机系统,2016,37(6):1164-1167.
CUI Xia,CAO Jianhua.Combined prediction model based on gmdh neuro network[J].Journal of Chinese Computer Systems,2016,37(6):1164-1167.
[22] 黄克智,薛明德,陆明万.张量分析(第2版)[M].北京:清华大学出版社,2003.
[23] 邱海涛,黄正均,任奋华.杏山铁矿露天转地下开采边坡变形分析[J].矿冶,2011,20(2):1-4,9.
QIU Haitao,HUANG Zhengjun,REN Fenhua.Deformation analysis of the slope during the process from open-pit to underground mining in Xingshan iron mine[J].Mining & Metallurgy,2011,20(2):1-4,9.
[24] 王金安,黄琨,张然.高陡复杂露天矿边坡地应力场分区非线性反演分析[J].岩土力学,2013,34(S2):214-221.
WANG Jinan,HUANG Kun,ZHANG Ran.Sub-regional nonlinear in-situ stress inversion analysis of complex high steep slope of open pit[J].Rock and Soil Mechanics,2013,34(S2):214-221.
[25] 朱权洁,王胜开,田昭军,等.MATLAB在复杂地质区域地应力场反演中的应用[J].工业安全与环保,2017,43(7):24-28.
ZHU Quanjie,WANG Shengkai,TIAN Zhaojun,et al.Application of MATLAB in the in-situ stress inverse analysis[J].Industrial Safety and Environmental Protection,2017,43(7):24-28.
[26] 张龙飞,许英霞,高孝敏,等.冀东杏山沉沉积变质型铁矿床富铁矿成因探讨[J].地质与斟探,2015,51(3):405-413.
ZHANG Longfei,XU Yingxia,GAO Xiaomin,et al.Genesis of high-grade ores in the Xingshan sedimentary metamorphic iron deposit of eastern Hebei Province[J].Geology and Exploration 2015,51(3):405-413.