
移动阅读
随着我国经济的飞速发展,浅部资源逐渐开采殆尽,千米级深部资源开采已成为常态,未来我国资源开发将逐步进入1 000~2 000 m的深度,发展深地科学,开发深地资源[1],是我国乃至世界范围内的研究热点。同时由于传统地面空间面临着大气污染、自然灾害、宇宙辐射等问题,深地空间具有恒温恒湿、隔音隔震、天然抗自然灾害等优点,开发利用深地空间,成为构建城市可持续发展、支撑国家核心战略的重要组成部分[2]。当前,深部资源开采、城市地下空间利用、深埋交通长隧等重大工程,均涉及到深部地下工程围岩长期稳定性与时效性的关键问题。例如,中国首个极深地下实验室——“锦屏地下实验室(CJPL)”,是目前世界上岩石覆盖最深(2 400 m)的地下实验室。围岩由大理岩构成,其天然放射性低,为我国自主开展暗物质探测及其它低本底环境实验研究奠定了良好基础。实验室埋深大、地应力高,II期将开挖形成4硐8室的高边墙、大跨度的地下硐室群,其长期稳定性研究至关重要。
岩石的蠕变特性对保障深部地下工程运营期长期稳定具有重要影响[3-5],是深部地下工程围岩长期稳定性研究的核心与关键问题之一。蠕变是指材料在应力恒定条件下,应变随着时间推进而不断增长的现象。目前基于各种室内及现场蠕变试验,岩石材料的蠕变特性及本构模型研究日益丰富和完善,但是国内外学者对岩石蠕变特性的研究主要集中在软岩方面,硬岩的蠕变特性研究相对较少[6]。其中WANG[7]对某地片麻岩进行三轴蠕变压缩试验,将硬岩或中硬岩的岩石蠕变变形全过程划分为3类;ZHANG[8]对硬脆性花岗岩进行三轴卸荷蠕变试验,得到侧向比轴向更容易发生蠕变行为的结论;CHEN[9]对甘肃北山预选区450~550 m深度的花岗岩进行不同温度及应力状态下的蠕变特性试验,发现温度对蠕变破坏变形影响并不明显;YANG[6]对锦屏一级水电站坝基坚硬大理岩和绿片岩进行三轴压缩蠕变试验,探讨了围压与粒径对岩石轴向及侧向变形特性的影响规律;XU[10]对大理岩进行不同应力水平下的蠕变试验并辅以声发射测试,得出岩石在低蠕变应力水平作用下,承载能力增强,高蠕变应力作用下岩体会发生蠕变破坏;YAN[11]采用恒轴压分级卸围压的应力路径对锦屏二级水电站地下引水隧洞大理岩开展了室内三轴压缩蠕变试验,研究结果表明应力差是决定试样蠕变量的主要因素。
蠕变模型的研究是岩石蠕变力学理论研究的重要组成部分,也是当前岩石力学研究中的难点和热点,目前岩石蠕变的模型主要集中在经验模型和元件组合模型的研究上。经验模型是在蠕变试验的基础上建立的函数关系式,主要有幂函数和对数函数模型,元件组合模型是由几种简单的元件单独或者进行串并联组合而成,来描述岩石的弹性、黏弹性等力学特征,比较常见的如Maxwell模型、Kelvin模型、Bingham模型、Burgers模型、理想黏塑性体、西原模型等。而经验模型难以反映岩石内部机理及特征,元件组合模型的组合元件是线性的,无法描述岩石流变的非线性特征,因此广大学者开始采用各种新的方法和理论,以期对岩石蠕变的非线性特征进行准确的描述。分数阶时间导数[12]实际上是微分-积分卷积算子,其定义中的积分项充分地体现了系统函数发展的历史依赖性,在进行蠕变建模时具有天然的优势,因此基于分数阶导数的蠕变模型逐渐兴起。CHEN[13]将分数阶微积分关系运用到人工冻土蠕变计算中,发现分数阶导数蠕变模型能很好地模拟人工冻土的蠕变规律;ZHOU[14]根据岩石进入加速蠕变阶段时细微观尺度上的裂纹演化,提出了变系数Abel黏壶,并建立基于分数阶导数的盐岩蠕变模型;WU[15]对周的蠕变模型进行了2点改进,① 用Abel黏壶代替模型中的黏弹性体;② 认为2个Abel黏壶的求导阶数不一样,建立了形式更加简单的蠕变模型。
本文围绕锦屏地下实验室深埋大理岩蠕变特征开展研究,在2 400 m埋深取样工作的基础上,开展基础力学参数测试并设计分级加载蠕变试验,探索深部大理岩轴向与环向蠕变变形规律,同时对大理岩长期强度进行探讨,并改进了基于分数阶导数的大理岩黏弹塑性损伤蠕变模型,采用该模型对试验数据进行拟合,论证了运用该模型对大理岩蠕变行为进行描述的可行性。研究成果可为深部地下工程长期稳定性评估,深部地下空间利用,深部资源开发等提供试验和理论基础。
根据《水电水利岩石力学试验规程》(DL/T 5368—2007),将锦屏地下实验室大理岩切割、打磨,加工成φ50 mm×100 mm的标准圆柱体试样,并保证所加工试样两端面的平行度、平整度以及圆柱面的光滑度均满足试验要求。如图1所示,该大理岩试样均呈浅灰色,表面光滑,没有明显裂隙,其密度为2 820 kg/m3,弹性模量40 GPa,泊松比0.18,单轴抗压强度178 MPa。

图1 锦屏深埋大理岩岩样示意
Fig.1 Schematic view of deep buried marble samples
制样所用大理岩均为白山组大理岩,主要矿物为白云石、方解石,白云石含量在70%以上,方解石含量约为10%~30%,此外含有少量的石英矿物。大理岩自然断口电镜扫描结果如图2所示,为粒状变晶结构,块状构造,镶嵌状分布,多数相邻颗粒之间相交面角120°,形成三边镶嵌的平衡结构。内部结构致密,但仍存在部分裂隙、孔洞等初始微缺陷,这些缺陷的存在影响着岩石的宏观力学性能。

图2 自然断口微观结构
Fig.2 Microstructure of natural fracture
试验采用四川大学MTS815 Flex Test GT岩石力学试验系统,开展加载和应力变形数据的采集工作。MTS815 Flex Test GT岩石力学试验系统为全数字计算机自动控制系统,轴向荷载0~4 600 kN,轴向位移±50 mm。三轴轴向、环向变形量程分别为-2.5~5.0 mm,-2.5~8.0 mm,其控制精度为0.5%RO。
为确定分级加载蠕变试验需施加的各级应力,并初步了解不同围压下大理岩的变形行为,首先开展围压为13,27,40,53,64 MPa的三轴压缩试验。以3 MPa/min加载至设定围压,然后采用轴向荷载控制,以50 kN/min加载至100 kN,其后转为环向位移控制,加载速率为0.05 mm/min,直到试样破坏。加载试验装置示例如图3所示。

图3 三轴试验示例
Fig.3 Schematic view of triaxial tests
试样的轴向应力-应变关系如图4所示。图4中标出了64 MPa围压下大理岩轴向应力-应变曲线的各个阶段,加载初期,试样中原有微裂隙在荷载作用下逐渐闭合,此时为压密阶段,随着应力的增加,应变增量逐渐减小;试样压密后,裂隙面之间的摩擦力抑制变形的发展,试样进入弹性变形阶段,应力-应变曲线近似为一条直线;此后随着应力的增加,试样内开始出现新的微破裂并不断发展,变形主要为塑性变形,试样进入屈服阶段,应变增量逐渐增大;随着应力的进一步增加,裂纹大量产生并迅速扩展贯通,试样最终破坏。CJPL深部大理岩在峰值应力附近的应变曲线与围压的关系十分密切:13,27 MPa围压下,应力应变曲线达到峰值应力后快速跌落;40,53,64 MPa围压下,峰值应力附近的应变曲线呈现明显的平台段。具体地,应力水平为95%~100%时,各围压下的轴向应变增量分别为0.10%,0.07%,0.65%,0.56%,0.86%。可看出,随着围压的增大,总体而言峰值应力区的平台段呈增大趋势,这表明CJPL深部大理岩变形行为随着围压的增大具有由脆性向延性转化的特征。张春生[3]和汪斌[16]均对锦屏二级水电站大理岩进行了不同围压条件下的压缩试验,试验结果所揭示出的大理岩在不同围压下表现出的变形特性与本文结果具有较好的一致性。

图4 不同围压下大理岩轴向应力-应变曲线
Fig.4 Axial stress-strain curves of marble samples under different confining pressures

图5 大理岩强度与围压的关系
Fig.5 Relationship between strength and confining pressure
由图4可知,高围压下试样的强度和变形更大,明显区别于低围压试样。前文40 MPa围压下大理岩峰值应力附近的应变曲线开始出现平台段,表现出明显的延性特征,而在27 MPa围压时,应力应变曲线达到峰值应力后快速跌落,呈现出明显的脆性特征,由此推测大理岩脆-延转化点位于27~40 MPa,因此为更好的探索高低围压下大理岩蠕变力学特性,选取围压5,64 MPa分别代表低围压和高围压2种工况,开展分级加载蠕变试验。由图5的线性关系可以得到各围压下大理岩的预估强度值,按照该预估强度值的百分比确定分级加载荷载。具体地,以大理岩预估强度值的55%作为第一级应力水平,此后每级增加10%,每级加载24 h,直至试样破坏。围压5 MPa试样在向第6级加载的过程中破坏,围压64 MPa试样在第5级稳压状态时发生破坏。每级应力加载数值见表1。
表1 蠕变试验方案
Table 1 Creep test scheme

围压/MPa(σ1-σ3)/MPa123456511213315317419421564217257296335375
大理岩蠕变全过程轴向及环向变形如图6所示(本文试样变形均以向内压缩为正)。由图6可知,每增加一级轴向应力,试样产生一定量值的瞬时变形,经短暂的初始蠕变阶段,蠕变速率逐渐衰减至某一定值,试样进入稳态蠕变阶段,此时蠕变速率基本恒定。当轴向应力增加到较高应力水平时,随着时间的延长岩石内部裂隙大量产生并迅速扩展贯通,蠕变速率呈加速增长,试样由稳态蠕变阶段进入加速蠕变阶段,变形迅速增加,直至破坏。

图6 大理岩蠕变全过程曲线
Fig.6 Whole process creep curves of marble
蠕变试验大理岩破坏时的应力、变形与三轴试验结论类似,高围压下大理岩的强度和破坏时的变形均显著增加。围压5 MPa时,试样在向第6级加载的过程中破坏,破坏应力为209 MPa,破坏时轴向和环向应变分别为0.61%,-0.35%。围压64 MPa时,试样在第5级破坏,破坏应力为375 MPa,约为围压5 MPa时破坏应力的1.79倍,破坏时轴向和环向应变分别为2.11%~1.87%,分别约为围压5 MPa时的3.46倍和5.34倍。
由图7可知,应力水平对大理岩的蠕变变形有着重要的影响,随着应力水平的增加,大理岩各级蠕变应变占总变形的比值逐渐增大,表明高应力水平下,大理岩更容易发生蠕变变形。相同围压条件时,大理岩环向蠕变变形占比随着应力水平的增加幅度越大,表明随应力水平的增加大理岩的环向蠕变变形增加更快。为进一步分析大理岩蠕变过程中环向蠕变与轴向蠕变的变化关系,现给出大理岩各级蠕变变形量值,见表2。同时,根据大理岩各级轴向和环向蠕变变形,可得到各级体积蠕变变形:
εV=ε1+2ε3
(1)
式中,ε1为轴向应变;ε3为环向应变;εV为体积应变。

图7 蠕变应变与总应变的比值随应力百分比变化关系
Fig.7 Relationship between the ratio of creep strain to total strain and the percentage of stress
表2 大理岩蠕变变形量
Table 2 Creep deformation of marble %

应力百分比围压5 MPa轴向应变环向应变体积应变围压64 MPa轴向应变环向应变体积应变550.003 6-0.001 00.001 60.010 6-0.002 80.005 0650.004 3-0.004 0-0.003 70.022 3-0.013 3-0.004 3750.008 4-0.010 7-0.013 00.043 5-0.033 5-0.023 5850.018 3-0.030 2-0.042 10.109 4-0.117 6-0.125 8950.041 7-0.066 8-0.099 1
由表2可知,在低应力水平时,环向蠕变变形量值小于轴向蠕变变形,随着应力水平的增加,环向蠕变变形量值逐渐超过轴向蠕变变形量,表明低应力水平大理岩轴向蠕变变形更加明显,高应力水平环向蠕变变形更为显著。围压64 MPa时,大理岩轴向、环向蠕变变形量值均高于围压5 MPa,这说明高围压下大理岩更容易发生蠕变变形。
大理岩蠕变过程中的体积随着应力水平的增加由向内压缩转为向外膨胀。低应力水平时,体积蠕变变形量为正值,表明此时大理岩体积随着时间的延长向内压缩,高应力水平时体积蠕变变形量为负值,表明大理岩体积随着时间的增加向外膨胀。且应力水平越高,蠕变过程中的体积变形量越大,表明大理岩蠕变过程中的扩容现象在高应力水平时更加明显。同时对比不同围压下的各级体积蠕变变形量,发现高围压下大理岩体积蠕变变形量值均大于低围压。例如,试样破坏时,64 MPa围压条件下的体积蠕变变形为5 MPa围压下的16.3倍。上述分析表明高围压下大理岩蠕变过程中和破坏时的扩容现象均更加显著。
图8为蠕变试验各级加载过程中变形模量随应力百分比变化关系,围压5 MPa 和64 MPa蠕变试验加载过程中的变形模量变化既有相同的趋势又有明显的差异。整体上,试样的变形模量均是先增加后减小。这是由于试样内部存在原始微裂纹,低应力水平时,试样在外荷载条件下原始裂纹逐渐闭合,变形模量增大,随着应力水平的增加,新裂纹的产生和发展导致试样劣化,变形模量减小。高围压与低围压相比,峰值变形模量与初始变形模量之间的增加幅度更小。具体地,64 MPa围压下试样变形模量增加的幅值为1.8 GPa,小于5 MPa围压下的3.6 GPa。这是由于高围压试样受围压作用,已经部分压密,故在此后的加载过程中,试样压密的效果不如低围压试样明显。另一方面,高围压与低围压相比,峰值变形模量与试样破坏时变形模量之间的减小幅度更大。具体地,围压64 MPa下试样变形模量减小幅值为9.4 GPa,约为峰值变形模量的22%,围压5 MPa下试样减小幅值仅为1.8 GPa,约为峰值变形模量的4%,远小于围压64 MPa试样。说明高围压试样在破坏前裂纹的产生和扩展更为剧烈,岩石劣化程度更大。
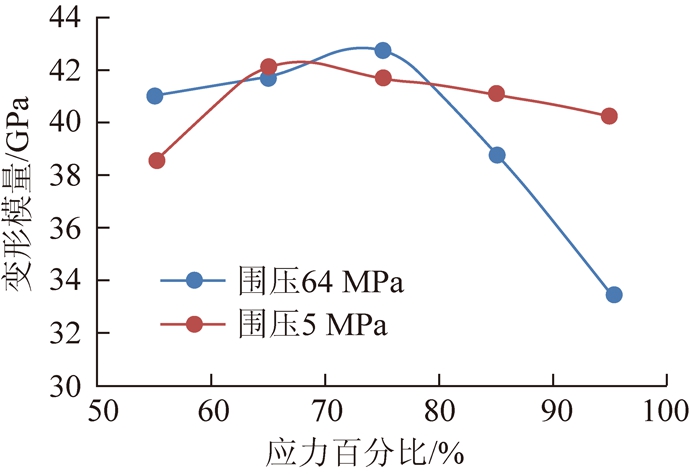
图8 变形模量随应力百分比变化关系
Fig.8 Relationship between deformation modulus and the percentage of stress
如图9所示,无论是高围压还是低围压,大理岩稳态蠕变速率随偏应力的增加而增加,且增加幅度逐渐变大,这表明高应力条件下大理岩更易发生蠕变变形。围压5,64 MPa的蠕变试样,破坏前一级环向稳态蠕变速率较上一级增幅分别为355%,274%,大于轴向稳态蠕变速率增幅228%,172%,表明试样破坏前环向变形比轴向反应剧烈。

图9 大理岩稳态蠕变速率随偏应力变化关系
Fig.9 Relationship between creep rate and deviator stress
从图9中曲线变化趋势来看,当偏应力相同时,围压越大的试样蠕变速率越小。并且根据前文所述,围压越大时,试样破坏时的变形更大且扩容现象明显。这可为解释深部围岩变形难以收敛,易发生时效大变形破坏提供机理上的解译。由于深部复杂的地质条件和赋存环境特征,使得深部与浅部岩体的力学行为具有较大的差异性。随着深度的增加,岩石赋存环境应力水平逐渐提高,大理岩破坏时的变形随之增大,变形行为逐渐由脆性向延性转化。当外荷载条件相同时,浅部围岩蠕变速率大,但破坏时的变形小,故破坏突然,成块状碎裂,破坏方式为典型的脆性劈裂破坏;深部围岩由于赋存环境应力水平较高,蠕变率小,但破坏时能够发生更大的变形,故变形难以收敛,随着时间的延长,可能会发生大变形破坏。因此,在深部工程设计和施工时,需要考虑围岩的长时力学响应,以避免发生时效大变形破坏。
岩石的长期强度是指岩石在长期荷载作用下抵御破坏的强度值。长期强度的试验取值方法有很多,比较常用的有体积膨胀法[17]、等时应力-应变曲线法等[18]。本文采用等时应力-应变曲线法对大理岩长期强度进行探讨。等时应力-应变曲线是指在一组不同应力水平的蠕变曲线中,相等时间所对应的蠕变变形与应力的关系曲线[19],曲线拐点对应应力即为长期强度。如图10所示,各图中轴向等时应力-应变曲线拐点应力分别为170,290 MPa,即5,64 MPa围压下,CJPL深部大理岩长期强度分别为170,290 MPa,是对应围压三轴抗压强度的82%,73%。

图10 轴向等时应力-应变曲线
Fig.10 Axial isochronous stress-strain curve
周宏伟[14]和吴斐[15]的模型虽均针对盐岩,但前文所述大理岩在高围压下变形行为具有延性特征,与软岩的变形性质类似,因此本文通过对上述两种模型的研究,建立了适用于大理岩的分数阶蠕变模型。
本文在周宏伟教授的分数阶模型上做了一点改进,以Abel黏壶代替该模型中的黏弹性元件,表征初始蠕变和稳态蠕变阶段。Abel黏壶的本构关系[14]为
σ=ηdγε(t)/dtγ(0≤γ≤1)
(2)
式中,η为黏性系数;γ为求导阶数。理想弹性体的应力-应变呈线性关系,满足胡克定律,当式(2)中γ=0时,即为理想弹性体的本构关系。牛顿流体的应力与应变呈一阶导数关系,当式(2)中γ=1时,即为牛顿流体的本构关系。由此可以推断Abel黏壶可以用来模拟介于理想弹性体和牛顿流体之间的中间材料。
由前文的分析可知,大理岩蠕变过程一般分为3个阶段,即:初始蠕变、稳态蠕变、加速蠕变。本文所改进的模型由3部分串联而成(图11)。① 号胡克体表征加载所产生的瞬时变形,② 号Abel黏壶表征初始蠕变和稳态蠕变,③ 号变系数Abel黏壶与④ 号塑性元件并联构成分数阶黏塑性体表征非线性加速蠕变。变系数Abel黏壶的本构关系可参考文献[14]。

图11 蠕变模型示意
Fig.11 Sketch map of creep model
由前文的分析可知,大理岩蠕变过程一般分为3个阶段,即:初始蠕变、稳态蠕变、加速蠕变。本文所改进的模型由3部分串联而成(图10)。胡克体表征加载所产生的瞬时变形,Abel黏壶表征初始蠕变和稳态蠕变,变系数Abel黏壶与塑性元件并联构成分数阶黏塑性体表征非线性加速蠕变。
改进后的模型形式更加简单合理,参数较少,同时保留了变系数Abel黏壶,考虑了岩石加速蠕变过程中的损伤演化,实现了对整个蠕变过程的模拟。
模型的本构关系为
(3)
![]()
(4)
式中,E0为弹性模量;![]() 为黏性系数;γ为求导阶次;α为与大理岩性质相关的系数;σs为屈服应力。
为黏性系数;γ为求导阶次;α为与大理岩性质相关的系数;σs为屈服应力。
引入Mittag-Leffler函数:
(z,β∈ ;R(α)﹥0)
;R(α)﹥0)
(5)
当σ≥σs,模型本构方程可表示为
(6)
采用基于分数阶导数的黏弹塑性损伤蠕变模型并运用最小二乘法分别对σ﹤σs和σ≥σs两种条件下的蠕变进行拟合分析,拟合结果见表3,4,试验数据与拟合曲线如图12所示。西原模型广泛应用于描述岩石材料的蠕变性能,现同时用西原模型与本文模型对试验数据进行拟合,并对其拟合效果进行对比分析,体现本文模型的优势。西原模型的本构关系[20]为
(7)
![]()
(8)
由图12可见,整体而言,分数阶导数蠕变模型与试验数据吻合良好,相关系数R更接近于1,表明分数阶导数模型的拟合效果更好。从蠕变的各阶段进行分析,对于初始蠕变阶段,西原模型拟合曲线距试验数据有部分偏离,例如图12(a)西原模型的起始点对应应变约为0.642 5%,高于试验数据,而分数阶模型能够很好的反应初始蠕变阶段的非线性渐变过程;对于稳态蠕变阶段,两种模型均能反映大理岩蠕变变形趋于稳定,但西原模型反映的稳态蠕变率与试验数据有较小偏差,图12(a)中西原模型稳态蠕变阶段的斜率稍小于试验数据,图12(b)西原模型稳态蠕变阶段的斜率稍大于试验数据,而分数阶导数蠕变模型反映的蠕变率基本与试验数据相同;对于加速蠕变阶段,西原模型最终趋于一条直线,不能反映大理岩的非线性加速蠕变特征,而分数阶导数模型则较好的反映了大理岩的非线性加速蠕变特征。
表3 基于蠕变试验的参数拟合结果(σ﹤σs)
Table 3 Parameters determined by fitting analysis based on creep tests of salt rock(σ﹤σs)

偏应力/MPaE0/GPaE1/GPaγηγ1/(GPa·hγ)γR西原模型40.201 62411 91010.976 8分数阶模型40.841 8440.200.997 6
表4 基于蠕变试验的参数拟合结果(σ≥σs)
Table 4 Parameters determined by fitting analysis based on creep tests of salt rock(σ≥σs)

偏应力/MPaE0/GPaE1/GPaηγ1/(GPa·hγ)ηγ2/(GPa·hγ)γα/h-1R西原模型25.104 7191 39481.45100.981 2分数阶模型25.423945500.490.550.994 3

图12 拟合结果与试验数据对比
Fig.12 Comparison of fitting results with experimental data
综上所述,本文改进的基于分数阶导数的大理岩黏弹塑性损伤蠕变模型不仅形式简单,参数物理意义明确,同时能够较好的反映大理岩的全过程蠕变特征,尤其是能对大理岩蠕变过程中的非线性特征进行良好的描述。
(1)低围压下,CJPL深部大理岩脆性特征明显,随着围压的升高,试样的塑性特征逐渐增强,其变形行为具有由脆性向延性转化的趋势。
(2)在低应力水平时,大理岩轴向蠕变现象较环向更加显著,在高应力水平时,环向蠕变现象更加明显。相同外荷载条件下,深部围岩蠕变率小,但较浅部围岩能够发生更大的变形,故深部围岩变形难以收敛,随着时间的延长,可能会逐渐发生大变形破坏。
(3)采用等时应力-应变曲线法确定大理岩长期强度,围压为5,64 MPa时,CJPL深部大理岩长期强度分别为170,290 MPa,分别为相应围压三轴强度的82%,73%。
(4)基于分数阶导数,改进了大理岩黏弹塑性蠕变损伤模型,该模型具有形式简单,参数物理意义明确,且能对非线性加速蠕变阶段进行很好的描述的特点。并分别对σ﹤σs和σ≥σs两种条件下的应变进行拟合,拟合效果良好,表明该模型能够很好的描述CJPL深部大理岩的蠕变变形过程。
[1] 谢和平,高峰,鞠杨,等.深地科学领域的若干颠覆性技术构想和研究方向[J].工程科学与技术,2017,49(1):1-8.
XIE Heping,GAO Feng,JU Yang,et al.Novel ideal and disruptive technologies for the exploration and research of deep earth[J].Advanced Engineering Sciences,2017,49(1):1-8.
[2] 谢和平,高明忠,张茹,等.地下生态城市与深地生态圈战略构想及其关键技术展望[J].岩石力学与工程学报,2017,36(6):1301-1313.
XIE Heping,GAO Mingzhong,ZHANG Ru,et al.The subversive idea and its key technical prospect on underground ecological city and ecosytem[J].Chinese Journal of Rock Mechanics and Engineering,2017,36(6):1301-1313.
[3] 张春生,陈详荣,侯靖,等.锦屏二级水电站深埋大理岩力学特性研究[J].岩石力学与工程学报,2010,29(10):1999-2009.
ZHANG Chunsheng,CHEN Xiangrong,HOU Jing,et al.Study of mechanical behavior of deep-buried marble at Jinping II hydropower station[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(10):1999-2009.
[4] 王来贵,赵娜,何峰,等.岩石蠕变损伤模型极其稳定性分析[J].煤炭学报,2009,34(1):64-68.
WANG Laigui,ZHAO Na,HE Feng,et al.Rock creep damage model and its stability analysis[J].Journal of China Coal Society,2009,34(1):64-68.
[5] 孙钧.岩石流变力学及其工程应用研究的若干进展[J].岩石力学与工程学报,2007,26(6):1081-1106.
SUN Jun.Rock rheological mechanics and its advance in engineering applications[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(6):1081-1106.
[6] 杨圣奇,徐卫亚,谢守益,等.饱和状态下硬岩三轴流变变形与破裂机制研究[J].岩土工程学报,2006,28(8):962-969.
YANG Shengqi,XU Weiya,XIE Shouyi,et al.Studies on triaxial rheological deformation and failure mechanismof hard rock in saturated state[J].Chinese Journal of Geotechnical Engineering,2006,28(8):962-969.
[7] 王芝银,艾传志,唐明明.不同应力下岩石蠕变全过程[J].煤炭学报,2009,34(2):169-174.
WANG Zhiyin,AI Chuanzhi,TANG Mingming.Complete process of rock creep in different stress states[J].Journal of China Coal Society,2009,34(2):169-174.
[8] 张龙云,张强勇,李术才,等.硬脆性岩石卸荷流变试验及长期强度研究[J].煤炭学报,2015,40(10):2399-2407.
ZHANG Longyun,ZHANG Qiangyong,LI Shucai,et al.Unloading rheological tests of hard brittle rock and its long-term strength analysis[J].Journal of China Coal Society,2015,40(10):2399-2407.
[9] 陈亮,刘建峰,王春萍,等.不同温度及应力状态下北山花岗岩蠕变特征研究[J].岩石力学与工程学报,2015,34(6):1228-1235.
CHEN Liang,LIU Jianfeng,WANG Chunping,et al.Creeping behavior of Beishan granite under different temperatures and stress conditions[J].Chinese Journal of Rock Mechanics and Engineering,2015,34(6):1228-1235.
[10] 徐子杰,齐庆新,李宏艳,等.不同应力水平下大理岩蠕变损伤声发射特性[J].煤炭学报,2014,39(S1):70-74.
XU Zijie,QI Qingxin,LI Hongyan,et al.Marble creep damage and acoustic emission characteristics under different stress levels[J].Journal of China Coal Society,2014,39(S1):70-74.
[11] 闫子舰,夏才初,李宏哲,等.分级卸荷条件下锦屏大理岩流变规律研究[J].岩石力学与工程学报,2008,27(10):2153-2159.
YAN Zijian,XIE Caichu,LI Hongzhe,et al.Study on rheological rules of marble in Jinping hydropower station under condition of step unloading[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(10):2153-2159.
[12] 陈文,孙洪广,李西成.力学与工程问题的分数阶导数建模[M].北京:科学出版社,2010.
[13] 陈军浩,姚兆明,徐颖,等.人工冻土蠕变特性粒子群分数阶导数模型[J].煤炭学报,2013,38(10):1763-1768.
CHEN Junhao,YAO Zhaoming,XU Ying,et al.Particel swarm fractional order derivative model of artificial frozen soil creep properties[J].Journal of China Coal Society,2013,38(10):1763-1768.
[14] 周宏伟,王春萍,段志强,等.基于分数阶导数的盐岩流变本构模型[J].中国科学:物理学 力学 天文学,2012(3):310-318.
ZHOU Hongwei,WANG Chunping,DUAN Zhiqiang,et al.The rheological constitutive model of salt rock based on fractional derivative[J].Scientia Sinica Physica,Mechanica & Astronomica,2012(3):310-318.
[15] 吴斐,谢和平,刘建锋,等.分数阶黏弹塑性蠕变模型试验研究[J].岩石力学与工程学报,2014,33(5):964-970.
WU Fei,XIE Heping,LIU Jianfeng,et al.Experimental study of fractional viscoelastic-plastic creep madel[J].Chinese Journal of Rock Mechanics and Engineering,2014,33(5):964-970.
[16] 汪斌,朱杰兵,邬爱清,等.锦屏大理岩加、卸载应力路径下力学性质试验研究[J].岩石力学与工程学报,2008,27(10):2138-2145.
WANG Bin,ZHU Jiebing,WU Aiqing,et al.Experimental study on mechanical properties of Jinping marble under loading and unloading stress paths[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(10):2138-2145.
[17] MARTIN C D,CHANDLER N A.The progressive fracture of Lac du Bonnet granite[A].International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts[C].Pergamon,1994,31(6):643-659.
[18] 张强勇,杨文东,陈芳,等.硬脆性岩石的流变长期强度及细观破裂机制分析研究[J].岩土工程学报,2011,33(12):1910-1918.
ZHANG Qiangyong,YANG Wendong,CHEN Fang,et al.Long-term strength and microscopic failure mechanism of hard brittle rocks[J].Chinese Journal of Geotechnical Engineering,2011,33(12):1910-1918.
[19] 沈明荣,谌洪菊.红砂岩长期强度特性的试验研究[J].岩土力学,2011,32(11):3301-3305.
SHEN Mingrong,CHEN Hongju.Testing study of long-term strength characteristics of red sandstone[J].Rock and Soil Mechanics,2011,32(11):3301-3305.
[20] 杨逾,李盈,周小科.基于西原加速模型的煤岩蠕变试验研究[J].煤炭学报,2014,36(11):2190-2194.
YANG Yu,LI Ying,ZHOU Xiaoke.Study on the coal creep test based on the improved Nishihara model[J].Journal of China Coal Society,2014,36(11):2190-2194.