
移动阅读
在深部煤层开采中,往往面临着高地应力、高地温、高渗透压环境,且会改变采空区围岩及其前方煤体的应力应变状态,造成强烈的开采扰动,致使煤体内部产生损伤[1-2]。此时,煤体中的原生裂隙和采动裂隙分布状态都会随应力状态发生改变,从而瓦斯在煤体中的运移规律也随之改变[3]。鉴于深部不是深度,强调的是一种应力状态[4-5],研究对应应力状态下深部煤体细观损伤演化规律及破坏特征,可以为深部煤层安全开采提供一定的理论依据。
岩石损伤是一个动态过程,CT作为一种非侵入性、非破坏性的成像技术,能够表征岩样内部结构特征,是描述岩石破裂损伤的一种常见且可靠的技术手段[6]。早期,国外学者KAWAKATA等[7]通过CT扫描技术对三轴压缩下的花岗岩断裂特征展开了观察,但是扫描时试件处于卸载状态;国内学者杨更社等[8]通过CT扫描分析了单轴压缩下的损伤扩展规律。随后,葛修润、仵彦卿和任建喜等[9-11]通过CT动态试验基于CT数定义的损伤因子研究了煤岩单轴和三轴压缩下的细观损伤演化规律和损伤本构方程。尽管如此,受实验设备、技术条件等因素的限制,在三维复杂应力状态下通过CT扫描实验进行实时损伤的精确监测仍相对困难。目前,单轴压缩过程中的高精度工业CT实时扫描实验技术已经相对成熟[12-13],然而,三轴应力加载状态下的高精度工业CT实时扫描实验设备正在研发之中。
煤体的宏观力学性质及损伤破坏与其细观材料组分的分布及力学性质密切相关,通过考虑材料的真实结构尽可能准确地建立数值模型已成为数值模拟与计算发展的一种趋势[14]。而CT技术的发展为三维数值模型的准确建立提供了一种可行方法。赵毅鑫、王刚、岳中琦等[12,15-17]通过岩石细观结构的重构建立了反映真实结构的数值模型,并进行了相关的数值模拟研究。而FLAC3D软件常常应用于岩土工程中宏细观材料相关力学行为及损伤演化的数值模拟研究[12,18-21]。因此,尝试通过准确的FLAC3D数值建模实现非均质煤体三维受力状态下实时损伤演化和破裂特征的模拟,不失为一种有效的研究手段。
笔者基于高分辨率工业CT实时成像系统对深部煤样进行了扫描,通过MIMICS软件对非均质深部煤体内部结构进行了三维数字化建模,最后对数字煤样进行了合理的三维网格划分并确定了各个材料单元组分的本构模型和单元属性。在此基础上,开展了单轴压缩的数值模拟,分析了单轴压缩过程中损伤演化规律,并与单轴压缩的CT扫描实验结果进行了对比分析,确定了数值模拟的准确性。进一步,通过数值模拟研究了三轴压缩过程中的损伤演化规律及破坏机理。
实验煤块(尺寸约为400 mm× 300 mm×200 mm)取自河南平煤12矿己15-17220采煤工作面。根据钻孔资料和己15煤层分析,该采煤工作面平均埋深约为900 m,平均煤层厚度约为3.3 m,平均煤层倾角约为 17°,原始瓦斯含量14.5 m3/t,瓦斯压力2.7 MPa。煤体为粉末状焦煤,平均密度约为1.45 t/m3,煤质松软,呈脆性。煤块在运输过程中使用防震防水泡沫小心密闭封装,并立即送往实验室进行加工钻孔取样。一是避免煤块因碰撞而发生破裂损伤,二是避免煤块被氧化或产生水分流失。在煤块取芯过程中,为避免取样的离散性和保证取样的成功率,煤样均取自同一煤块,用钻机钻取煤芯时均沿着平行于节理的方向,且尽可能避免肉眼可见的缺陷。按照国际岩石力学委员会(ISRM)建议方法,对煤样两端进行切割并抛光,将煤样加工成直径为25 mm、高分别为25和50 mm的2种圆柱体试件。其中,高为25 mm的试件用于压汞实验,高为50 mm的试件用于单轴和三轴压缩实验以及CT扫描实验。
1.2.1 压汞实验(MIP)
MIP是用于测试岩石内部孔隙和微裂隙尺寸及分布的最常用方法之一[13]。为了获取本文深部煤体的内部孔隙结构的尺寸及分布特征,取尺寸近似为φ25 mm × 25 mm的3个圆柱体煤样进行压汞实验。实验仪器采用美国Auto Pore Ⅳ9505压汞仪。试验前先将煤样中自由水分烘干,同时防止因烘烤而产生裂缝。然后,利用普通渗透仪(AP608)测得各个煤样的气测(氮气)孔隙度和渗透率。最后,进行压汞实验,记录进汞与退汞曲线。测试过程严格按照我国石油天然气行业标准《岩心常规分析方法》和《岩石毛管压力曲线的测定》执行。实验煤样的物理几何参数以及压汞实验结果见表1。
1.2.2 单轴和三轴压缩实验
选取4个直径为25 mm的标准圆柱体煤样分别进行单轴压缩实验以及围压分别为12.5,17.5和21.5 MPa的三轴压缩实验,计算得到煤样的弹性模量、泊松比、单轴抗压强度、黏聚力和内摩擦角等力学参数,见表2。其中,单轴抗压强度可以为单轴压缩的CT扫描实验扫描应力的选取提供参考依据,其他力学参数可以供数值模拟模型中不同组分力学属性的赋值提供理论参考值。
表1 煤样压汞法测量结果
Table 1 Results of mercury intrusion method for the coal samples

煤样编号直径/cm高度/cm密度/(g·cm-3)孔隙度/%孔喉半径/μm最大平均中值孔喉分布峰位/μm峰值/%汞饱和度/%最大最终剩余均质系数结构系数仪器最大退出效率/%排驱压力/MPaM12.4852.4491.3905.7702.8140.3330.0070.00611.30969.49220.0650.11830.77271.1260.261M22.4522.4381.4705.5802.8130.3650.0120.00610.91082.27128.7610.13012.75365.0410.261M32.4612.4141.5305.7705.3320.9450.0160.00611.98690.87730.6900.17719.18566.2300.138
表2 煤样的基本力学参数
Table 2 Basic mechanical parameters of coal samples

煤层编号单轴抗压强度σc/MPa弹性模量E/GPa泊松比μ黏聚力c/MPa内摩擦角φ/(°)己15-3103016.384.700.382.8434.95
注:表中值均为平均值。
实验设备采用中国矿业大学(北京)煤炭资源与安全开采国家重点实验室的ACTIS300-320/225CT/DR高分辨率工业CT实时成像系统,配上自制研发的单轴加载设备(图1(a))对一个圆柱形煤样(直径为25 mm,高为50 mm)进行了单轴压缩过程中的CT扫描实验。实验过程中对不同应力状态下的煤样分别进行全高扫描。CT扫描轴向应力根据煤体的单轴抗压强度确定,并结合煤样单轴压缩的应力应变曲线和实验过程中裂隙的扩展情况进行适当调整。本次实验整个加载过程通过应力控制,具体步骤为:① 加载前(0 MPa)进行第1次扫描;② 鉴于初始压密阶段没有宏细观裂缝形成,通过CT扫描无法检测到损伤,第2次CT扫描应力近似取30%的单轴抗压强度3 MPa;③ 在此之后每隔1 MPa进行一次CT扫描,直至试件完全破坏。最终对煤样进行CT扫描时轴向应力的近似取值依次为0,3.0,4.0,4.5,5.0,6.0,7.0,8.0,9.0,10.0 MPa,其轴向应力、应变分别通过图1(a)中的应力传感器和位移记录仪测得。实验过程中加载到4.0 MPa时,CT扫描检测到煤样局部已经产生微细观裂缝,因此加密了扫描间距,但是CT扫描发现4.5,5.0 MPa下的裂隙相对4.0 MPa下的裂隙基本没有变化,因此5.0 MPa之后仍然间隔1 MPa进行一次CT扫描。

图1 煤样单轴压缩的CT扫描系统
Fig.1 Experimental system for CT scanning of coal sample under uniaxial compression
CT扫描过程中的电流和电压的选择很重要,这直接影响到CT扫描图像的质量。在本研究中,根据CT检测器的性能以及长期实验经验,对于φ25 mm × 25 mm的圆柱体煤样最佳扫描源电压为105 kV,电流为300 μA。每个应力下都对煤样进行全高扫描,扫描间距为0.05 mm,切片厚度为0.05 mm,CT图像分辨率为750像素×750像素,视场为35 mm×35 mm,单个像素尺寸为46 μm。CT扫描原理及CT切片示意图分别如图1(b)和1(c)所示。
压汞实验结果表明煤样孔隙度的范围为5.58%~5.77%,煤中最大孔隙直径约为10 μm,平均孔喉半径不足1 μm,且孔喉分布的峰位在6 nm左右,说明加载前煤样中绝大数为纳米级的微观孔隙,不存在细观大孔隙或微裂隙。而CT图像中单个像素的尺寸约为46 μm,说明从CT扫描图像中无法识别煤样中的孔隙和微裂隙。初始煤样CT切片及煤基质-煤杂质二值化图像如图2所示。
图2(a)表明初始煤样的CT扫描图中不存在灰度值接近于0的黑色像素点,即初始煤样中不存在尺寸大于CT扫描精度的宏细观裂隙。因此,根据像素灰度值大致可以将CT图像分为两大部分:一部分是颜色偏暗灰色的像素集合,另一部分是颜色呈灰白色的像素集合。由于CT图像像素灰度值反映的是该处物质的密度大小,则灰白色部分表示密度较高的煤杂质,暗灰色部分表示物质密度较低的煤基质。根据文献[22]的阈值分割方法将CT图像进行二值化得到如图2(b)所示的由煤基质和煤杂质两部分组成的二值化图像。然后将1 000张二值化图像通过MIMICS重构得到二值化的三维圆柱体煤样(图3),其中绿色部分代表煤杂质,黑色部分代表煤基质。这样,我们建立数值软件与MIMICS的接口,就可以得到包含煤基质和煤杂质两个组别的数值几何模型。

图2 0 MPa下煤样CT切片
Fig.2 CT slices of coal sample under the stress of 0 MPa

图3 0 MPa下CT重构的圆柱体煤样
Fig.3 Cylindrical coal sample reconstructed by CT at 0 MPa
通常,FLAC3D中的网格划分得越密越均匀,其计算结果越精确。但是,网格过于密集会大大降低计算速度,处理器的配置需求也更高。如果采用MIMICS中自动划分的四面体网格,那么将会产生百万个网格单元,而且在2种组分的接触面上很容易出现网格畸形点,单元尺寸也不均匀。本文先建立一个和煤样同等尺寸的各向同性圆柱体几何模型,并进行了较为均匀的六面体网格划分,单元的数量控制在十万个左右。然后将重构的煤基质的几何体导入FLAC3D中,保持三维几何与自建圆柱体几何重合,通过设置几何体覆盖到的网格单元为煤基质组、剩余的单元为煤杂质组来实现单元分组。覆盖原则为:若六面体单元的几何中心被导入的煤基质几何体所覆盖,则认为该单元属于煤基质组。
网格尺寸不均匀往往导致数值计算结果不精确或不收敛。本文采用了一种六面体网格划分方法,避免了FLAC3D中圆柱体外环绕放射性网格划分不均匀的现象。其中,高度方向很容易保证均匀,圆形横截面上通过内置边长为0.466r的正八边形将圆等分成12个面积相等的四边形,如图4(a)所示四边形OABC,BEDC和AFEB组成了1/4圆。然后,将每个四边形均匀地划分成网格数量相等的四边形网格,如图4(b)所示。最终划分的四边形网格的最大面积与最小面积之比约为2。

图4 圆柱横截面网格划分示意
Fig.4 Schematic diagram of grid division of cylindrical cross section
按照上述方法成功的实现了基于CT三维重构煤样的数值几何模型的建立,且保证了网格单元的连续性、均匀性及计算的可实现性。
基于CT扫描及图像处理技术,对直径为25 mm、高为50 mm的标准圆柱体煤样进行了三维几何重构,导入到FLAC3D软件中建立了区分煤基质和煤杂质的数值计算模型,如图5所示。其中,蓝色组表示煤基质,单元数量为59 989个;绿色组表示煤杂质,单元数量为36 011个,数值模型中节点总数量为100 521个。

图5 基于mimics重构几何体的三维煤体结构的数值模型
Fig.5 Numerical model of three-dimensional “real coal” based on reconstruction geometry by Mimics
数值模拟材料本构模型的选取和参数的确定对于数值模拟的准确性具有至关重要的作用。由于孔隙尺寸较小,其结构无法通过CT扫描获取,同时数值软件中网格单元的尺寸精确不到孔隙的尺度,在本文的细观数值模型中,煤体简化成由煤基质和煤杂质(矿物夹杂物)2种组分组成,并通过CT将二者完全区分开来。MAHABADI、王桂华等[23-25]研究表明煤基质和煤杂质(材料)的弹性模量、泊松比、抗压强度等力学参数可以通过岩屑显微硬度试验估算,其中文献[25]通过大量实验得到了材料的各个力学参数与其岩屑显微硬度之间的经验关系式。然而,ZHAO等[12,23]的研究也指出该方法在描述地质材料力学性质的过程中存在很多不可避免的误差和难度,包括样品很难在微米尺度上绝对抛光、显微技术测定单一颗粒的不确定性以及颗粒间属性测量的难度等,从而使测量结果具有很大的不确定性。因此,参考实验测得的煤样力学参数及谢和平[18]和ZHAO[12]的实验数据给出了煤基质和煤杂质基本力学参数的近似值(表3)。
表3 数值模拟的物理力学参数
Table 3 Physical and mechanical parameters of numerical simulation

组分密度/(g·cm-3)弹性模量/GPa泊松比抗拉强度/MPa黏聚力初始值/MPa摩擦角初始值/(°)煤基质1.32.370.350.231.1335.0煤杂质1.816.000.181.116.4534.6
数值模拟过程中将2种材料组分均看成是各向同性的,但是由于2种材料在煤样中分布是不均匀的,因此煤样整体表现出各向异性。ZHAO等[12]在模拟中认为煤杂质为理想的弹塑性材料,选择了摩尔库伦准则作为其本构模型;认为煤基质为弹塑性材料,选择了应变软化模型作为其本构模型。实际上煤杂质不可能为理想弹塑性材料,其峰后阶段强度会降低,将煤杂质同样考虑成一般弹塑性材料更合理。因此,笔者选择应变软化模型作为煤基质和煤杂质的本构模型,认为2种材料均为一般弹塑性材料,峰后阶段强度会有所下降,但破坏后仍具有一定的残余强度。在FLAC3D应变软化模型中,当加载到屈服阶段时,材料的基本力学参数(黏聚力、内摩擦角、剪胀角)会随着塑性剪切变形的产生而减小,即煤样表现出软化性质[12,21]。文中通过自定义的分段线性函数对各个参数的软化过程进行描述,煤基质和煤杂质各个参数的软化曲线分别如图6所示。其中,剪胀角的值随围压变化而不同,笔者按照文献[21]的建议近似取值。图6中剪胀角仅为单轴压缩条件下的剪胀角变化曲线。
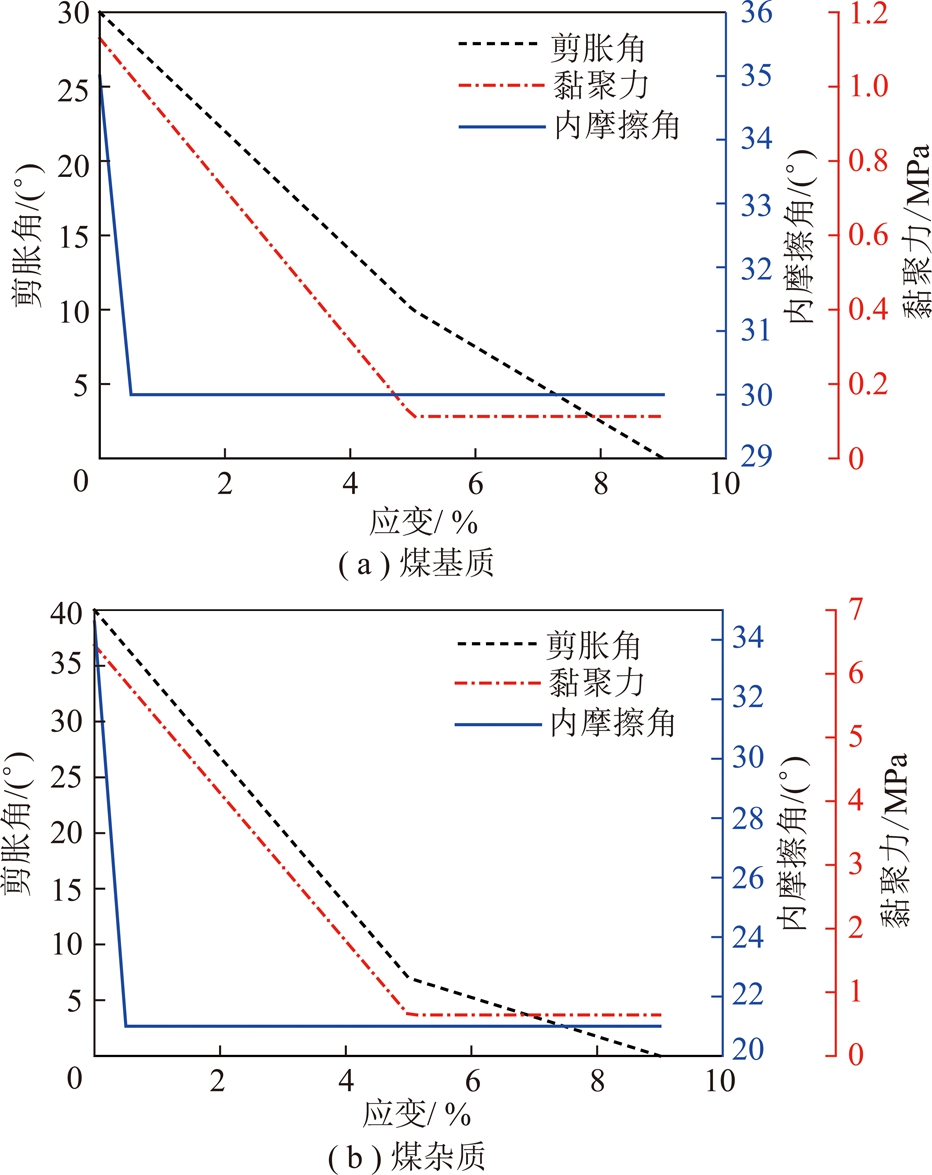
图 6 应变软化模型中剪胀角、内摩擦角和黏聚力随塑性剪切应变的变化规律
Fig.6 Variation of dilatancy angle,friction angle and cohesion with plastic shear strain applied in the strain-softening model
在FLAC3D模拟深部煤体损伤的过程中,采用一端固定,一端位移加载的方式,加载速率采用1.0×10-8 m/step,数值模拟加载状况及边界条件如图7所示。通常学者在绘制应力-应变曲线时会选择某一个单元或节点的相关结果进行求解,考虑到重构煤样的非均质性,若仅仅采用某一个单元的数据反映整个煤样加载过程中的应力-应变曲线会存在较大误差。因此,本文数值模拟在计算轴向应力、应变时采用某一横截面或者环向截面上所有节点的数据结果进行求解。式(1)~(3)分别给出了轴向应力σ、轴向应变ε1和环向应变ε2的计算方法:
(1)
式中,n为端面B上节点数;Fi为端面B上节点i所受的Z方向上的不平衡力;A为煤样横截面面积。
(2)
式中,m为端面A上节点数;sj为端面A上节点j的Z方向上的位移;H为煤样高度。
(3)
其中,N为试件中部截面最外侧单位宽度圆环上的节点数;skx,sky分别为圆环上节点k在X,Y方向上的位移;R为煤样的半径。为了简化计算,计算环向应变时假设圆环上节点在横截面内的合位移方向指向圆心。
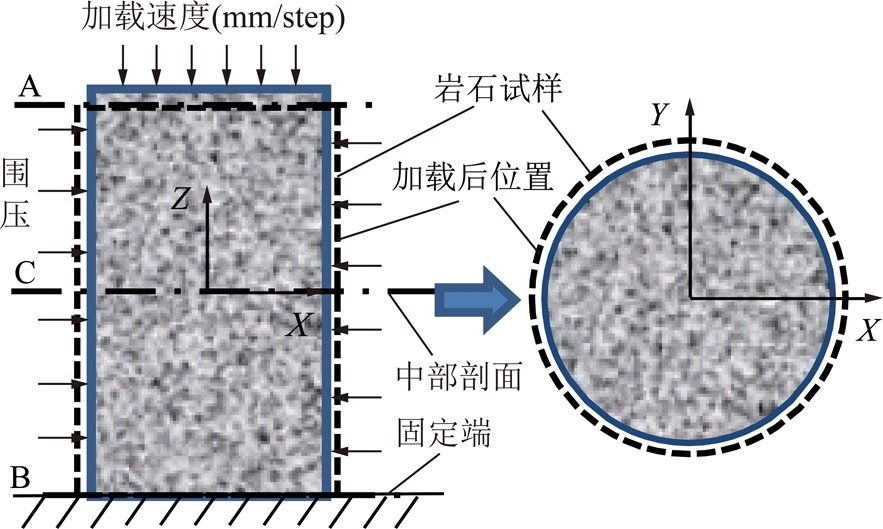
图7 数值模拟加载及边界条件示意
Fig.7 Diagram of loading and boundary condition in the numerical model
ZHOU等[13]已经通过单轴压缩的CT扫描实验对单轴压缩过程中煤体损伤演化规律进行了研究,并将单轴压缩的损伤演化过程分为了4个阶段:① 孔隙压密阶段(<0.3σc),此阶段认为是零损伤;② 新裂隙产生阶段((0.3 ~ 0.4)σc),即局部开始产生损伤;③ 主裂缝的稳定发展阶段((0.4 ~ 0.9)σc),即局部损伤逐渐稳定扩展贯通产生更大的损伤;④ 损伤加速产生和扩展阶段((0.9 ~ 1.0)σc),此时煤样产生破裂。其实验得到的单轴压缩的应力-应变曲线及不同应力水平下煤样中部CT切片如图8所示。由图8可以看出在单轴压缩的过程中,煤样逐渐破裂,产生的裂隙平行于或垂直于煤体2种材料的分界面,且两条主裂隙间也近似相互垂直。煤样破坏前后的图像如图9所示,可以看出煤样实验前不存在肉眼可见的宏细观裂缝,其最终发生脆性劈裂破坏,形成多条近似平行于轴向的竖直裂缝,直至完全破碎。

图8 煤样单轴压缩全应力-应变曲线及不同应力状况下的CT切片图像(煤样中心位置处)[11]
Fig.8 Stress-strain curve with the CT images of the center cross section of the coal sample at the different stress levels during the static uniaxial compression test[11]

图9 煤样图像
Fig.9 Images of coal sample
为了定量分析煤样单轴压缩过程中损伤演化规律,基于细观统计损伤力学的思想,参照文献[26]基于医用CT数定义损伤变量的方法,本文给出了基于工业CT图像灰度值的损伤变量D定义:
(4)
其中,T0m为煤样初始无损伤状态灰度值的平均值,本文取为试件压密后(即各个扫描应力下平均灰度值的最大值)的平均灰度值,认为在此之前的过程为无损阶段,损伤变量均等于0;Ti为某一应力状态下煤样发生损伤时灰度值的平均值;Tfm为煤样最终破坏时灰度值的平均值,该值取为各个扫描应力下煤样平均灰度值的最小值,认为此时煤样完全发生破坏,失去承载能力,损伤变量等于1。
根据式(4)计算得到的单轴压缩过程中煤样上部、中部、下部以及整个煤样的损伤变量与轴向应变关系曲线如图10所示。由图10可知,整个煤样单轴压缩的损伤过程大致可以细分为4个阶段:阶段I((0.3~0.4)σc),局部损伤开始产生阶段,此阶段损伤有一个快速增长的短暂过程;阶段II((0.4~0.5)σc),损伤线性稳定增长阶段,此阶段损伤的增长是一个线性增长过程;阶段III((0.5~0.9)σc),损伤非线性稳定增长阶段,此阶段损伤的增长是一个非线性增长过程,且增长速度逐渐增大;阶段IV((0.9~1.0)σc),损伤加速产生阶段,此时损伤呈指数型增长趋势,煤样迅速破裂,直至完全破坏。此损伤过程与文献[13]中图8显示的裂隙损伤扩展过程基本一致,说明本文基于CT图像灰度值定义的损伤变量能够定量的表征损伤演化过程。

图10 单轴压缩过程中煤样损伤变量与轴向应变关系曲线
Fig.10 Relation between damage variable and axial strain under uniaxial compression of coal sample
图10还表明煤样局部(上部、中部和下部)损伤演化规律与煤样整体损伤演化规律不尽相同。煤样上部损伤演化过程不存在损伤非线性稳定增长阶段,在整个损伤稳定增长阶段中损伤呈线性增长;煤样中部、下部损伤演化规律与整体损伤演化规律基本一致。在整个损伤演化过程中,煤样中部损伤最为严重,上部次之,说明煤样局部损伤程度存在一定的差异。从图10中煤样各个局部的损伤演化结果(阶段I和II)中定性分析可以得到主体损伤应该是从煤样中上部逐渐向下部发展的一个过程。
综上,基于CT图像灰度值定义的损伤变量可以定性和定量分析煤样整体及各个局部的损伤演化规律。
通常,加载过程中裂隙(断裂)的产生、扩展及贯通情况无法通过FLAC3D软件直接模拟得到,但是其损伤破坏通常出现在塑性变形较大或者剪切应变率较大的位置区域,也即塑性破坏区和最大剪切应变率区的变化规律在一定程度上可以间接反映损伤的演化规律。笔者基于CT重构对加载前煤样的内部结构进行了可视化,并将几何模型导入FLAC3D软件中,进行了单轴压缩的数值模拟,将数值模拟的应力-应变曲线及实验得到的应力-应变曲线绘制于图11中,结果表明数值模拟和实验的应力-应变曲线具有较好的一致性。

图11 单轴压缩的应力-应变曲线
Fig.11 Stress-strain curves under uniaxial compression
为了研究数值模拟和实验得到的损伤演化规律是否具有一致性,单轴压缩数值模拟的应力-应变曲线以及不同应力水平下试件中部横截面内的剪切应变率和塑性破坏区分布云图分别如图12所示。由图12可以明显看出随着轴向应力的逐渐增加,剪切应变率区域逐渐增大扩张,直至贯通,试件最终破坏时其最大剪切应变率区域及塑性区都近似平行或垂直于煤基质和煤杂质的交界面(层理面),且两个损伤发生的主区域面间相互垂直。其中,0~3 MPa基本无损伤产生;3~9 MPa为局部损伤的产生、扩展和连通阶段,在此阶段损伤稳定发展;9~10 MPa损伤急剧增长,煤样完全破坏。尽管数值模拟得到的损伤具体位置和实验得到的裂隙具体位置不完全相同,但是二者得到的裂隙整体形态以及随应力的演化规律基本吻合。上述结果表明,建立煤样结构的数值模型进行煤样加载过程中损伤演化的模拟是准确可靠的。说明本文网格划分及数值几何模型的建立方法提高了数值模拟的准确性,为后文进行三轴压缩的精确模拟提供了理论基础。
除上述结果外,从图12(b)中还可以看出单轴压缩煤样的破坏过程主要是一个拉伸破坏的过程,当应力达到屈服强度(约7 MPa)时才会逐渐发生剪切破坏。发生剪切破坏的原因可能是当试件由于非均质导致试件变形破坏后轴向应力的方向偏离了试件的几何中心,这样试件两端也会因为摩擦力而产生横向剪切力。可见,非均质试件在单轴压缩屈服应力前主要发生拉伸破坏,在屈服应力后由于非均匀的变形而产生剪切变形破坏。这些破坏机理通过实验并不能明显获得,然而通过本文的数值模拟结果可以很清楚直观地得到。因此,数值模拟对于非均质煤样损伤破坏的形式和机理研究具有优势。

图12 单轴压缩实验数值模拟的应力-应变曲线以及不同应力水平下试件中部横截面内的最大剪切应变率和塑性区分布云图
Fig.12 Stress-strain curves of numerical simulation for uniaxial compression experiment and distribution of failed (plastic) elements and shear strain rate in the center cross-section of the sample before the peak stress at various axial stress levels
上节对重构非均质深部煤样单轴压缩实验展开了数值模拟研究,并且其结果与实验结果能够很好地吻合。实际工程中深部煤体往往处于较高的三向应力状态下,受实验技术限制三轴压缩条件下煤体损伤演化规律很难通过细观实验得到。因此,对本文重构的非均质深部煤样进行不同三轴应力状态下的数值模拟,可以定性研究得到不同应力下煤体的细观损伤演化规律和破坏特征,为深部煤层安全开采提供理论依据。本节则采用同样的几何模型和单元属性,通过施加环向应力进行不同围压下三轴压缩的数值模拟。模拟时,先将试件加载至静水压力状态,然后以1.0×10-8 m/step的速度进行位移加载。
对CT三维重构的同一非均质煤样在5,10,15,20和25 MPa五种不同围压下进行三轴压缩数值模拟,其轴向应变、环向应变及体积应变与轴向偏应力的关系曲线如图13所示。图13结果表明,峰值强度、扩容点应力均随围压的增加而逐渐增大,且扩容点应力之前煤体处于线弹性阶段,弹性模量基本保持不变,峰前阶段围压越大煤样延性越好。峰后阶段围压越大,煤样破坏后的残余强度也越大。以上结果很好地符合了一般理论结果。
根据变形及破坏特征,蔡明等[27]将岩石三轴压缩的破坏过程细分成6个阶段:① 裂隙闭合;② 线弹性变形,裂隙初始形成;③ 裂隙稳定生长并局部贯通;④ 裂隙加速生长并全面贯通;⑤ 破坏;⑥ 峰后应变软化。数值模拟中,大孔隙、裂隙闭合阶段实际相当于将试件加载至静水压力的过程,此过程可以认为是零损伤过程,因此本文从静水压力后开始分析损伤演化规律。

图13 不同围压条件下三轴压缩数值模拟的应力-应变曲线
Fig.13 Stress-strain curves of numerical simulation of triaxial compression under different confining pressure
以5 MPa围压下的三轴压缩数值模拟结果为例,图14(a)和(b)分别给出了其应力-应变曲线及不同应力条件下塑性破坏区和最大剪切应变率的分布云图。

图14 三轴压缩数值模拟的应力-应变曲线以及不同损伤演化阶段下试件内的塑性区和最大剪切应变率分布云图
Fig.14 Stress-strain curves of numerical simulation for triaxial compression and distribution of failed (plastic) elements and maximum shear strain rate of the sample at different damage evolution stages
从图14中可以看出,AB段,即线弹性变形阶段,应力应变很小很均匀,基本没有损伤产生,主要表现为孔隙的进一步压缩和局部微裂隙的产生,且二者处于一个动态平衡过程;BC段因应力集中开始产生损伤,此时裂隙的产生占主导,且保持一个稳定增长的趋势,其破坏表现为近似轴向的局部剪切破坏。CD阶段应力集中现象加剧,裂隙加速形成、扩展和连通,出现明显的塑性变形,破坏形式与BC阶段基本相同。D点开始出现破坏,到E点煤样发生宏观破坏,DE阶段为一个逐渐破坏的过程。EF阶段为应变软化阶段,煤样中产生了明显的剪切破坏面,应力迅速减小。FG段为残余应力阶段,煤样仍然具有一定的强度,另一共轭剪切面开始逐渐形成。结果表明,本文基于CT重构的煤样三轴压缩的数值模拟得到的损伤演化定性表征结果与文献[27]提出的损伤演化的6个阶段能够较好的吻合。
图15给出了同一重构煤样在5种不同围压条件下最终破坏的塑性区分布云图以及破裂角与围压之间的拟合关系式。可以看出煤样主要发生了单剪破坏,且剪切面的位置基本相同,但是剪切面的倾角有所不同。当围压较低时(5 MPa),破裂角较大,约为60°,随着围压的增大,破裂角缓慢减小,当围压增加至25 MPa时,破裂角减小为56°,二者之间具有明显的负线性相关性。从单轴压缩到围压逐渐增大的过程中,试件从以拉伸破坏为主的破坏形式逐渐向以剪切破坏为主的破坏形式转变。通常,在进行三轴压缩的数值模拟时,采用的数值模型为完全各向同性的均质材料,且试件最终的破坏形式一般为X型双剪破坏,即形成一对共轭剪切面[20]。但是,进行三轴压缩的实验时,试件往往会发生类似本文数值模拟发生的单剪切破坏。说明采用本文基于CT三维重构的非均质煤样的数值模型得到的模拟结果更加真实准确,更接近于实验结果。其实,由于三轴压缩等实验为破坏性试验,同一试件一般只能进行某一种应力状态下的相关试验,欲得到破裂角与围压的关系往往需要展开大量的实验,且还需要考虑试件差异性的影响。因此,采用本文的数值研究方法既能够保证模拟结果的准确性,同时又能够弥补实验过程中因煤样离散性带来的误差。

图15 不同围压条件下试件最终破坏的塑性区及破裂角
Fig.15 Distribution of failed (plastic) elements and rupture angle of the sample under different confining pressure
值得注意的是,虽然FLAC3D能够通过塑性区和最大剪切应变率分布特征定性反映损伤演化过程,但其在模拟损伤演化本质问题上具有局限性,因此,通过细观试验进行三轴压缩条件下损伤演化的定量分析是未来研究的重点方向。本文的数值模拟主要是在网格划分、三维几何模型建立、材料参数的选取以及应力应变的计算方法上做出了相关优化和改进;当然,通过嵌入基于实验得到的损伤本构方程并设定合理的损伤判别准则进行损伤演化规律的模拟验证也值得研究。
(1)在单轴压缩的CT实时扫描实验的基础上,基于CT图像灰度值定义的损伤变量可以定性和定量分析煤样整体及各个局部的损伤演化规律。基于煤样三维重构结构的单轴压缩数值模拟结果与CT实时扫描实验结果能够很好地符合,表明本文网格的合理划分、几何模型的准确建立以及材料参数的准确选取可以大大提高数值模拟的准确性。
(2)单轴压缩的CT实时扫描实验的定量分析结果和数值模拟的定性分析结果一致表明,峰值应力前煤样损伤依次经历了零损伤阶段、局部损伤产生阶段、损伤线性和非线性稳定增长阶段和损伤加速增长阶段,试件最终破坏时其破坏面近似平行或垂直于煤基质和煤杂质的层理面,且损伤发生的两个主破坏面相互垂直。整个过程中煤样主要发生拉伸破坏,屈服应力后由于煤样的不均匀变形才发生剪切破坏。
(3)三轴压缩数值模拟得到的静水压力之后的损伤演化特征与经典的岩石损伤演化的6个阶段能够很好的吻合。数值模拟结果表明,煤样主要发生剪切破坏,形成单剪切破坏面,且随着围压的增大,破裂角逐渐缓慢减小,二者之间近似呈负线性相关。本文数值模拟方法能够消除实验样品差异性带来的影响,且能够直观准确地描述三轴压缩过程中的损伤演化规律。
[1] 谢和平,高峰,鞠杨.深部岩体力学研究与探索[J].岩石力学与工程学报,2015,34(11):2161-2178.
XIE Heping,GAO Feng,JU Yang.Research and development of rock mechanics in deep ground engineering[J].Chinese Journal of Rock Mechanics and Engineering,2015,34(11):2161-2178.
[2] XUE J H,WANG H P,ZHOU W,et al.Experimental research on overlying strata movement and fracture evolution in pillarless stress-relief mining[J].International Journal of Coal Science & Technology,2015,2(1):38-45.
[3] ZHANG R,AI T,LI H G,et al.3D reconstruction method and connectivity rules of fracture networks generated under different mining layouts[J].International Journal of Mining Science and Technology,2013,23(6):863-871.
[4] 谢和平,周宏伟,薛东杰,等.煤炭深部开采与极限开采深度的研究与思考[J].煤炭学报,2012,37(4):535-542.
XIE Heping,ZHOU Hongwei,XUE Dongjie,et al.Research and consideration on deep coal mining and critical mining depth[J].Journal of China Coal Society,2013,37(4):535-542.
[5] 谢和平,高峰,鞠杨,等.深部开采的定量界定与分析[J].煤炭学报,2015,40(1):1-10.
XIE Heping,GAO Feng,JU Yang,et al.Quantitative definition and investigation of deep mining[J].Journal of China Coal Society,2015,40(1):1-10.
[6] HOU P,JU Y,GAO F,et al.Simulation and visualization of the displacement between CO2 and formation fluids at pore-scale levels and its application to the recovery of shale gas[J].International Journal of Coal Science & Technology,2016,3(4):351-369.
[7] KAWAKATA H,CHO A,YANAGIDANI T,et al.The observations of faulting in westerly granite under triaxial compression by X-ray CT scan[J].International Journal of Rock Mechanics and Mining Sciences,1997,34(3-4):151-162.
[8] 杨更社,谢定义,张长庆,等.岩石损伤扩展力学特性的CT分析[J].岩石力学与工程学报,1999,18(3):250-254.
YANG Gengshe,XIE Dingyi,ZHANG Changqing,et al.CT analysis on damage mechanic characteristics of propagation of rock[J].Chinese Journal of Rock Mechanics and Engineering,1999,18(3):250-254.
[9] 葛修润,任建喜,蒲毅彬,等.煤岩三轴细观损伤演化规律的CT动态试验[J].岩石力学与工程学报,1999,18(5):497-502.
GE Xiurun,REN Jianxi,PU Yibin,et al.A real-in-time CT triaxial testing study of meso-damage evolution law of coal[J].Chinese Journal of Rock Mechanics and Engineering,1999,18(5):497-502.
[10] 仵彦卿,丁卫华,蒲毅彬,等.压缩条件下岩石密度损伤增量的CT动态观测[J].自然科学进展,2000,10(9):830-835.
WU Yanqing,DING Weihua,PU Yibin,et al.Dynamic observation of density damage increment for rock under compression conditions by CT technology[J].Process in Nature Science,2000,10(9):830-835.
[11] 任建喜,葛修润.单轴压缩岩石损伤演化细观机理及其本构模型研究[J].岩石力学与工程学报,2001,20(4):425-431.
REN Jianxi,GE Xiurun.Study of rock meso-damage evolution law and its constitutive model under uniaxial compression loading[J].Chinese Journal of Rock Mechanics and Engineering,2001,20(4):425-431.
[12] ZHAO Y X,LIU S M,ZHAO G F,et al.Failure mechanisms in coal:Dependence on strain rate and microstructure[J].Journal of Geophysical Research:Solid Earth,2014,119(9):6924-6935.
[13] ZHOU H W,ZHONG J C,REN W G,et al.Characterization of pore-fracture networks and their evolution at various measurement scales in coal samples using X-ray μCT and a fractal method[J].International Journal of Coal Geology,2018,189:35-49
[14] 于庆磊,杨天鸿,唐世斌,等.基于CT的准脆性材料三维结构重建及应用研究[J].工程力学,2015,32(11):51-62.
YU Qinglei,YANG Tianhong,TANG Shibin,et al.The 3D reconstruction method for quasi-brittle material structure and application[J].Engineering Mechanics,2015,32(11):51-62.
[15] 王刚,杨鑫祥,张孝强,等.基于CT三维重建的煤层气非达西渗流数值模拟[J].煤炭学报,2016,41(4):931-940.
WANG Gang,YANG Xinxiang,ZHANG Xiaoqiang,et al.Numerical simulation on non-Darcy seepage of CBM by means of 3D reconstruction based on computed tomography[J].Journal of China Coal Society,2016,41(4):931-940.
[16] 岳中琦.岩土细观介质空间分布数字表述和相关力学数值分析的方法、应用和进展[J].岩石力学与工程学报,2006,25(5):875-888.
YUE Zhongqi.Digital representation of meso-geomaterial spatial distribution and associated numerical analysis of geomechanics:Methods,applications and developments[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(5):875-888.
[17] 陈永强,郑小平,姚振汉.三维非均匀脆性材料破坏过程的数值模拟[J].力学学报,2002,34(3):351-361.
CHEN Yongqiang,ZHENG Xiaoping,YAO Zhenhan.Numerical simulation of failure process in 3-D heterogeneous brittle material[J].Acta Mechanica Sinica,2002,34(3):351-361.
[18] 谢和平,周宏伟,王金安,等.FLAC在煤矿开采沉陷预测中的应用及对比分析[J].岩石力学与工程学报,1999,18(4):29-33.
XIE Heping,ZHOU Hongwei,WANG Jin’an,et al.Application of FLAC to predict ground surface displacements due to coal extraction and its comparative analysis[J].Chinese Journal of Rock Mechanics and Engineering,1999,18(4):29-33.
[19] TAN X.Hydro-mechanical coupled behavior of brittle rocks:Laboratory experiments and numerical simulations[D].Freiberg:Geotechnical Institute of TU Bergakademie Freiberg,2013.
[20] 郭依宝,周宏伟,荣腾龙,等.采动应力路径下深部煤体扰动特征研究[J].煤炭学报,2018,43(11):3072-3079.
GUO Yibao,ZHOU Hongwei,RONG Tenglong,et al.Study on the disturbance characteristics of deep coal mass under the mining stress path[J].Journal of China Coal Society,2018,43(11):3072-3079.
[21] 赵星光,蔡明,蔡美峰.岩石剪胀角模型与验证[J].岩石力学与工程学报,2010,29(5):970-981.
ZHAO Xingguang,CAI Ming,CAI Meifeng.A rock dilation angle model and its verification[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(5):970-981.
[22] 钟江城,周宏伟,任伟光,等.基于CT 图像灰度分布的含杂质煤体三值化方法[J].力学与实践,2018,40(2):140-147.
ZHONG Jiangcheng,ZHOU Hongwei,REN Weiguang,et al.A three-value-segmentation method of coal containing inclusion based on gray distribution of computed tomography image[J].Mechanics in Engineering,2018,40(2):140-147.
[23] MAHABADI O K,RANDALL N X,ZONG Z,et al.A novel approach for micro-scale characterization and modeling of geomaterials incorporating actual material heterogeneity[J].Geophysical Research Letters,2012,39(1):1303.
[24] RANDALL N X,VANDAMME M,UlM F J.Nanoindentation analysis as a two-dimensional tool for mapping the mechanical properties of complex surfaces[J].Journal of Materials Research,2009,24(3):679-690.
[25] 王桂华,程远方,梁何生.岩屑显微硬度法确定地层力学参数[J].石油钻探技术,2003,31(3):7-9.
WANG Guihua,CHENG Yuanfang,LIANG Hesheng.A new method to determine the formation mechanical properties with cuttings microhardness[J].Petroleum Drilling Techniques,2003,31(3):7-9.
[26] 田威,党发宁,陈厚群.单轴压缩条件下混凝土细观损伤演化机理的CT试验研究[J].实验力学,2011,26(1):54-60.
TIAN Wei,DANG Faning,CHEN Houqun.Experimental study of concrete meso-damage evolution mechanism based on uniaxial compression CT method[J].Experiment Mechanics,2011,26(1):54-60.
[27] 蔡明,赵星光,KAISER P K.论完整岩体的现场强度[J].岩石力学与工程学报,2014,33(1):1-13.
CAI Ming,ZHAO Xingguang,KAISER P K.On field strength of massive rocks[J].Chinese Journal of Rock Mechanics and Engineering,2014,33(1):1-13.