大地震是地球岩石圈中局部区域突然发生、波及地表并造成巨大破坏力的一种自然现象,如汶川(Ms8.0)、尼泊尔(Ms8.1)与印尼苏门答腊(Ms9.3)地震,给人类造成极大的生命财产损失[1-3]。地震发生的机理一直是人类极其关注的重大科学难题和热点问题。迄今为止,对于地震发生的宏观物理过程有了比较明确的认识,但是其力学机制尚不清楚。
人类对地震的认识,经历了漫长的过程。LAWSON依据1906年的旧金山地震现象提出地震是由于断裂的大断层突然错动引起岩层振动产生的[4],其后的弹性回跳假说,以及丰富与完善了弹性回跳假说的黏滑说详尽论述了地震的成因和地震能量来源[5-7];力偶震源理论为地震震源的确定提供了理论基础[8];板块构造学说的提出解释了世界地震活动分布的规律[9]。这些成就为人们对地震的认识打下了良好的基础,很好的阐述了发生地震的宏观物理过程:板块运动→地壳断裂→弹性能释放→能量传播→地震。然而,关于地震形成的具体力学机制至今仍然是个未解之谜,仍无法科学地阐明怎样在地壳的实际环境中导致应力在地震震源区集中以及瞬时破裂的孕育与发生的微观物理过程[10-12],对于地震机理的解释主要是现象表述,缺乏合理的理论论证。
乔建永、马念杰、马骥[13-14]等基于动力系统结构稳定性理论中的Leau-Fatou花瓣定理逆定理和蝶形破坏理论,提出的X型共轭剪切破裂-地震复合模型,是具有明确物理意义的地震力学模型;应用纯粹的数学力学推导得到共轭剪切破裂长度的数学表达式、地震能量计算方法及其数学表达式,计算结果与真实存在的X型共轭剪切破裂长度以及有史以来地震发生时释放的所有能量级别高度吻合[15-17]。
笔者首先对X型共轭剪切破裂-地震复合模型进行简单介绍,然后深入分析随岩体应力状态改变,共轭剪切破裂扩展与地震能量变化特征,定量阐明共轭剪切破裂-地震发生及其演化的物理过程,合理论述了地震发生的力学机理,并提出了地震发生应具备的必要条件。
1 X型共轭剪切破裂-地震复合模型简介
地震发生的力学本质是地壳局部岩体结构瞬态失稳破坏的非线性动力学问题,研究地震震源区岩体的破坏与物理过程是揭示地震发生机理的基础和关键。采用文献[13]建立的X型共轭剪切破裂-地震复合模型(图1),由规则圆形软弱异性体中心点向外扩展的长度为X型共轭剪切破裂长度Rmax,其数学表达式为
![]()
(1)
其中,a为规则圆形软弱异性体半径;r,θ分别为极坐标下的塑性破坏区边界半径和角度,θ∈[0,π];Px(t),Pz(t)分别为软弱异性体周围岩体受到的水平主应力和垂直主应力,是时间t的函数;C,φ为岩体的黏聚力与内摩擦角;q为软弱异性体自身产生的反作用力。复合模型描述的地震能量是软弱异性体及其周围岩体构成的空间闭区域(一般取软弱异性体半径的5倍以上),由于触发事件的动载作用,导致该区域弹性能改变。地震释放能量Wm可通过式(2)求出,即
Wm=β(Uep-U′ep)
(2)
其中,β为震动能因子,0<β<1,文中如未特殊说明,β统一取值为0.5;Uep为地震发生前软弱异性体及其周围岩体构成的空间闭区域的弹性能,该区域分为未破坏弹性区的弹性能与已发生塑性破坏区域的仍离散为弹性单元体计算的弹性能;U′ep为地震发生时该区域的弹性能,由于形成了新的塑性破坏,该区域的弹性能发生了变化(具体计算公式见文献[13])。由式(1),(2)可知,在整个空间闭区域中,当软弱异性体和周围岩体的弹性模量E、泊松比μ、黏聚力C、内摩擦角φ,以及软弱异性体的反作用力q都为确定值,可定量计算随应力状态改变,X型共轭剪切破裂扩展长度与地震发生释放能量大小的变化关系。如图1所示,给定Px=2 160 MPa,Pz=360 MPa,a=5 m,C=30 MPa,φ=48°,q=180 MPa,计算得到X型共轭剪切破裂尺寸Rmax=27.85 m。

图1 X型共轭剪切破裂-地震复合模型
Fig.1 X-shaped conjugate fracture-seismic composite model
2 共轭剪切破裂—地震的“仿蝶存亡”规律
2.1 不同应力状态下,X型共轭剪切破裂的变化特征
水平构造应力场在中国乃至全球绝大部分地区的地壳应力环境中占主导地位,水平向应力的作用(大小与方向)对地震孕育、发生是主要的[18-20]。延用文献[13]中的确定参数,认为软弱异性体半径a=10 m,埋深h=15 km,纵向长度L=10 km,符合平面应变模型的力学条件[21];软弱异性体周围岩体为弹塑性、均质、各向同性的,泊松比μ=0.25,弹性模量E=50 GPa,黏聚力C=24 MPa,内摩擦角φ=46°;软弱异性体上覆岩层容重γ=27 kN/m3,假设Pz(t)随时间t保持恒定不变,即Pz=γh≡405 MPa;基于X型共轭剪切破裂-地震复合模型,应用控制变量法,通过改变水平主应力Px(t),式(1)可计算得到共轭剪切破裂长度Rmax的变化特征(图2)。
不同应力条件下,以软弱异性体围岩塑性破坏形态为核心可将X型共轭剪切破裂形成、演化过程划分为孕育期、生长期与剧变期。图2(a)是X型共轭剪切破裂尺寸Rmax随水平应力Px的变化曲线,随着水平主应力Px的变化,塑性区极值半径Rmax在曲线的两侧出现了指数型急剧增长的现象。图2(a)中I为共轭破裂形成前的孕育期;II为共轭破裂的平稳生长期;III为共轭破裂的剧变扩展期。具体地,假设Pz=Px=405 MPa为等压应力状态,随着水平应力Px逐渐增大,软弱异性体周围岩体受到强烈的挤压作用,在此阶段X型共轭剪切破裂形成与演化的3个时期以x坐标轴上的3个特征点为界进行划分的(图2(a)),这3个特征点被分别定义为X型共轭破裂的形成特征点A(Px/Pz=3),Rmax-Px曲线斜率为1(与x轴夹角为45°)的X型共轭剪切破裂生长拐点B、曲线斜率与x轴夹角趋近90°时的正无穷点C(图2(b),(c))。当405 MPa<Px≤729 MPa时,X型共轭破裂并未形成,软弱异性体周围岩体发生塑性破坏,在Px=1 013 MPa时,塑性破坏形态成椭圆形(图2(b));当Px=1 215 MPa时,形成蝶形塑性破坏(图2(b)),软弱异性体周围岩体的破坏呈现出由量变到质变的过程,该过程主要是X型共轭剪切破裂的孕育期。在此期间,水平应力Px增加了810 MPa,软弱异性体周围岩体的Rmax由0增大到16.35 m(图2(b)),从图2(a)中特征点A开始到特征点B是X型共轭剪切破裂的生长期,也是地震发生的孕震期。在此阶段,水平应力Px由1 215 MPa增加到2 525 MPa,X型共轭剪切破裂尺寸Rmax由16.35 m增加到141.85 m(图2(a)),形成一定程度的扩展,且扩展速度较为平稳;从特征点B开始,随着水平应力Px的增加,X型共轭剪切破裂尺寸Rmax成指数型迅速增大,直至达到渐近线Px=2 599 MPa时,Rmax达到无穷大(图2(a)),这一时期X型共轭剪切破裂进入剧变期,很容易随着水平应力Px的增加而剧烈扩展。当Px>2 599 MPa时,X型共轭剪切破裂尺寸Rmax直接达到地表,X型共轭剪切破裂的尺寸无法扩展。

图2 水平应力Px与破裂尺寸Rmax的变化关系
Fig.2 Relationship between horizontal stress Px,fracture’s radius Rmax
2.2 共轭剪切破裂动态扩展与地震活动规律
为了准确描述X型共轭剪切破裂动态破裂过程中地震的变化规律。以ΔPx=1 MPa/s为水平应力增量,绘制破裂尺寸动态扩展长度ΔR、地震震级随水平应力Px的变化关系曲线,如图3所示。两曲线具有几乎一致的特征,即在曲线左侧随水平主应力Px的减小,形成了垂直高偏应力场,使得ΔR与地震震级呈负指数增长趋势;水平主应力Px增大形成的水平高偏应力场,使得曲线的右侧呈正指数型增长。受软弱异性体围岩近似蝴蝶状塑性破坏区的启发(图2(b),(c)),我们用自然界中蝴蝶的4个发育阶段(卵化期、虫化期、化蛹期、羽化期)来形象地比拟破裂动态扩展与地震发生的规律[22]。以Px=Pz=405 MPa的等压原岩应力状态为中心,随着水平主应力逐渐增大,在Px=405~671 MPa为软弱异性体围岩塑性破坏的“卵化期”。此阶段能量积累,无地震发生;当Px=671~1 308 MPa时,围岩塑性破坏进入“虫化期”,地震虽频繁发生,但都是无感地震,里氏震级均小于4级;软弱异性体围岩塑性破坏的“卵化期”和“虫化期”统一起来是破裂动态发育阶段地震的弱震期,这个阶段我们几乎无法感受到地震的发生;从Px=1 308 ~2 583 MPa为软弱异性体围岩塑性破坏的“化蛹期”,此阶段主要发生中等强度地震,里氏震级变化在4~6级内,属于可破坏型地震,破坏轻重主要与震源深度、震中距、震源围岩应力状态等多种因素有关,是地震发生的中强震期;当2 583 MPa<Px≤2 598 MPa时,破裂扩展与地震级别曲线几乎与横坐标x轴垂直,此阶段为软弱异性体围岩塑性破坏的“羽化期”,这一阶段X型共轭剪切破裂急剧扩展,地震能也急剧增加,引发一系列大级别地震(里氏震级均>6级),是引发地震的强震期;当Px>2 598 MPa后,X型共轭剪切破裂尺寸Rmax直接达到地表,X型共轭剪切破裂的尺寸无法扩展,软弱异性体周围岩体中残余的地震能很小,随着形成断层的错动逐渐释放,产生的地震级别也不会很大。
同样的,随着水平主应力Px减小,破裂动态尺寸和地震级别的变化趋势也存在着“卵化期、虫化期、化蛹期和最后的羽化成蝶期”。我们以雌雄性别区分不同受力状态下伴随共轭剪切破裂发育的地震震级,即Px>405 MPa发育为雄蝶,发生地震级别高,能量大;Px<405 MPa为雌蝶,地震级别低,能量小。以上分析表明,随水平向主应力变化,共轭剪切破裂扩展与地震发生间存在“仿蝶存亡”的特征规律,即以蝴蝶的生长发育过程将地震发生的不同时期通过数学力学的语言进行了全新定义。需要指出,一般地质力学条件下,共轭剪切破裂扩展及其地震活动的“仿蝶存亡”规律同样存在,而且会得出与本文给出的完全相同的结论。
3 X型共轭剪切破裂-地震产生的力学机理及其物理过程
如图4所示,结合文献[13]的研究成果,阐明了X型共轭剪切破裂-地震产生的力学机理及其物理过程,具体表述为(图4):构造应力场变化剧烈的区域附近极易形成垂直、水平与剪切高偏应力场;在这种应力环境中地下软弱异性体周围岩体存在着性态极不稳定的蝶形破坏区,它的扩展将形成以软弱异性体为中心的显性或隐性X型共轭剪切破裂;蝶形破坏区周围集聚了巨大震源能量,在共轭剪切破裂尺寸扩展时以波的形式传播出去,在一定范围内引发地震。蝶形破坏区半径和震源能量对软弱异性体(形状,尺寸)、周围岩体应力环境和岩体物理力学性质的变化具有高度敏感依赖性,每当受到同向触发事件的突然加(减)载作用时,蝶叶就发生一次突然扩展,并伴随地震能的瞬时向外传播,发生一次相应级别的地震。

图3 水平应力增量为1 MPa/s,破裂动态扩展与地震震级的变化关系
Fig.3 Relationship between fracture dynamic expansion and seismic magnitude,when the horizontal stress increment is 1 MPa/s

图4 地震发生的力学机理与物理过程
Fig.4 Mechanical mechanism and physical process of earthquake
4 共轭剪切破裂-地震发生的必要条件
综合共轭剪切破裂扩展尺寸与地震释放能量的理论计算结果,将地震发生的必要条件归纳为软弱异性体存在条件,软弱异性体周围岩体的强度条件,地质构造剧烈变化形成的应力条件与引发地震的应力触发条件(图5)。
软弱异性体存在条件:软弱异性体存在是蝶形塑性破坏出现的基本条件,如果没有蝶形塑性破坏,就不会形成X型共轭剪切破裂,也不会产生岩体的瞬间破坏和能量释放。这里的软弱异性体是广义的概念,真实地壳岩体是非均质的,一定存在着强度较低、具有一定尺寸、任意形态特征,可能充斥有气态、液态物质的软弱岩体、破碎固体和熔融岩浆等,例如地下深处岩浆及其有关气体、固体碎屑在高温高压作用下从地壳中喷出,在地面冷却堆积形成的火山体或未出露地表被坚硬岩层堆覆凝固后形成的岩浆岩,美国黄石火山的地震波层析和地震成像技术显示,地下深处4~14 km存在8 km厚的岩浆体,在20~45 km深处也发现了巨型岩浆体[23-24];德国KTB大陆超深钻探资料显示,地下深处9~12 km存在许多构造与破碎带,充满着如地下水等高温高压的流体[25]。
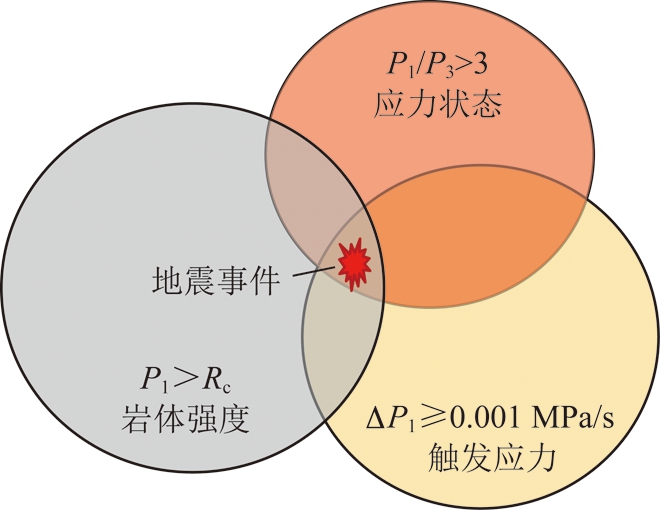
图5 共轭剪切破裂-地震的必要条件示意
Fig.5 Necessary conditions for conjugate fracture-seism
软弱异性体周围岩体的强度条件:只有软弱异性体围岩最大主应力P1大于岩体的单向抗压极限强度Rc,即P1>Rc,软弱异性体周围岩体才会出现塑性破坏,并释放能量,存在引发地震的可能。
地质构造剧烈变化形成的应力条件:软弱异性体周围原岩应力状态的最大与最小主应力比值较大且满足P1/P3>3时会出现蝶形塑性破坏[13,26](文中主应力Px与Pz分别为软弱异性体围岩区域最大与最小主应力P1,P3方向在水平与垂直时的情况,如果主应力方向发生改变则不再表示水平与垂直方向的应力),其为X型共轭剪切破裂形成的标志,同时具备了对于周围岩体应力环境的敏感依赖性条件。自然界中真实地壳岩体中具备P1>Rc的原岩应力环境比比皆是,但是达到P1/P3>3的情况相对较少,所以每年发生的有感地震不会很多。该条件主要表述了平面状态下软弱异性体围岩区域最大与最小主应力之间的关系。
引发地震的应力触发条件:如图5所示,软弱异性体周围岩体所受原岩应力状态为P1/P3>3,且同时满足岩体破坏的强度条件P1>Rc,软弱异性体周围岩体就会形成一定范围的X型共轭破坏,但是否发生地震还要取决于X型共轭剪切破裂每次扩展过程时间的长短。如果X型共轭剪切破裂的扩展每次量值很小,即软弱异性体周围岩体地应力场发生均匀变化,结合文献[13]的表格5中数据可知,位于地质构造应力场剧烈显现的区域及其附近水平主应力每年增加1 MPa(或每年减小1 MPa),其附近每秒变化量ΔP1=3.17×10-8 MPa/s,这种情况下共轭剪切破裂是在长时间内形成的,则围岩中的能量将慢慢释放,每次释放的能量不足以引发地震;只有在每秒变化量ΔP1恰好满足X型共轭剪切破裂产生突然的大范围扩展时,才会引发地震,ΔP1≥10-3 MPa/s作为引发地震的应力触发条件(结合文献[13]中表5数据分析得到),是地震发生的必要条件。基于以上分析,似乎只要探明软弱异性体及其周围岩体的强度、应力环境,就可以通过式(1),(2)计算得到地震活动的时期,多大应力触发条件下形成确切的地震级别等一系列有关于地震预测的讨论。
5 结 论
(1)阐明了地震发生的力学机理与物理过程,以及X型共轭剪切破裂形成的物理过程,具体表述为:构造应力场变化剧烈的区域地壳岩体中会形成水平、垂直与剪切高偏应力场,地层深处存在比周围岩体强度低的软弱异性体,如软弱岩体、破碎固体和融化岩浆等,软弱异性体周围岩体会形成蝶形塑性破坏区,是X型共轭剪切破裂生成的标志,即蝶形区域蝶叶的扩展在地壳岩体中形成了显性或隐性X型共轭剪切破裂。蝶形破坏区周围集聚了巨大能量,每当受到同向触发事件的突然加(减)载作用时,蝶叶就发生一次突然扩展,并伴随地震能的瞬时向外传播,发生一次相应级别的地震。
(2)X型共轭剪切破裂的孕育期、生长期与剧变期,描述了破裂在不同应力状态下的形态特征;共轭剪切破裂-地震的“仿蝶存亡”规律,即伴随共轭剪切破裂动态发育过程中地震的变化规律,重构了已有的地震发生时期体系。
(3)共轭剪切破裂-地震发生的必要条件主要包括软弱异性体条件(软弱岩体、破碎固体和融化岩浆等),软弱异性体周围岩体的强度条件(P1>Rc),地质构造剧烈变化形成的应力条件(P1/P3>3)与引发地震的应力触发条件(ΔP1≥0.001 MPa/s),以上条件同时具备一定会促使地壳中软弱异性体围岩突然的蝶形扩展,同时发生相应级别的地震。
[1] 雷建设,赵大鹏,徐锡伟,等.龙门山断裂带深部结构与2008年汶川地震发震机理[J].科学通报,2018,63(19):1906-1916.
LEI Jianshe,ZHAO Dapeng,XU Xiwei,et al.Deep structure of the Longmenshan fault zone and mechanism of the 2008 Wenchuan earthquake[J].Chinese Science Bulletin,2018,63(19):1906-1916.
[2] 滕吉文,马学英,张雪梅,等.2015年尼泊尔Ms8.1大地震孕育的深层过程与发生的动力学响应[J].地球物理学报,2017,60(1):123-141.
TENG Jiwen,MA Xueying,ZHANG Xuemei,et al.Deep processes and dynamic responses of the generation and occurrence of the 2015 Nepal Ms8.1 earthquake[J].Journal of Geophysics,2017,60(1):123-141.
[3] SHETH A,SNIGDHA S,JAISWA A,et al.Effects of the December 2004 Indian Ocean Tsunami on the Indian Mainland[J].Earthquake Spectra,2006,22(S3):S435-S473.
[4] LAWSON A C.The California Earthquake of April 18,1906.Report of the state earthquake investigation commission,Parts 1 and 2[M].Washington:Carnegie Institution of Washington,Publication,1908.
[5] REID H F.The mechanics of the earthquake,v.2 of The California Earthquake of April 18,1906:Report of the State Earthquake Investigation Commission[M].Washington:Carnegie Institution of Washington Publication,1910.
[6] BRACE W F,BYERLEE J D.Stick slip as a mechanism for earthquakes[J].Science,1966,153:990-992.
[7] 刘力强.弹性回跳模型:从经典走向未来[J].地震地质,2014,36(3):825-832.
LIU Liqiang.Elastic rebound model:From the classic to the future[J].Seismology and Geology,2014,36(3):825-832.
[8] NAKANO H.Note on the nature of forces which give rise to the earthquake motions[J].Seismol Bull Centr Meteorol Obs,Tokyo,1923,1:92-120.
[9] LE Pichon X,FRANCHETEAU J,BONNIN J.Plate tectonics developments in geotectonics 6[J].Likevier,Amsterdam,1973.
[10] 黄福明.地震预报研究的现状与动态[J].国际地震动态,1990,(2):4-9.
HUANG Fuming.Current status and developments of earthquake prediction research[J].Recent Developments in World Seismology,1990,(2):4-9.
[11] 黄福明.断层力学概论[M].北京:地震出版社,2013:303-305.
[12] 杜建国,仵柯田,孙凤霞.地震成因综述[J].地学前缘,2018,25(4):255-267.
DU Jianguo,WU Ketian,SUN Fengxia.Earthquake generation:A review[J].Earth Science Frontiers,2018,25(4):255-267.
[13] 乔建永,马念杰,马骥,等.基于动力系统结构稳定性的共轭剪切破裂-地震复合模型[J].煤炭学报,2019,44(6):1637-1646.
QIAO Jianyong,MA Nianjie,MA Ji,et al.Conjugate fault-seismic composite model based on structural stability of dynamic system[J].Jouranl of China Coal Society,2019,44(6):1637-1646.
[14] 赵志强,马念杰,刘洪涛,等.巷道蝶形破坏理论及其应用前景[J].中国矿业大学学报,2018,47(5):969-978.
ZHAO Zhiqiang,MA Nianjie,LIU Hongtao,et al.A butterfly failure theory of rock mass around roadway and its application prospect[J].China University of Mining and Technology,2018,47(5):969-978.
[15] 陈颙,史培军.自然灾害[M].北京:北京师范大学出版社,2007.
[16] 赵晓燕,于仁宝.地震概论[M].北京:清华大学出版社,2013.
[17] 杨瑞东,盛学庸,魏晓,等.基于Google Earth影像分析区域性大型“X”共轭节理系统对宏观岩溶作用的控制[J].地质论评,2009,55(2):173-180.
YANG Ruidong,SHENG Xueyong,WEI Xiao,et al.The control of regional large “X” conjugate joint system on Karstification from Google Earth image[J].Geological Review,2009,55(2):173-180.
[18] 罗灼礼.震源应力场、形变场和倾斜场[J].地震学报,1980(2):61-77.
LUO Zhuoli.Stress deformation and tilt fields of the earthquake sources[J].Acta Seismologica Sinica,1980(2):61-77.
[19] HEIDBACH O,TINGAY M,BARTH A,et al.Global crustal stress pattern based on the World Stress Map database release 2008[J].Tectonophysics,2010,482(1-4):3-15.
[20] ZANG A,STEPHANSSON O.Stress field of the earth’s crust[M].Berlin:Springer Netherlands,2010.
[21] WESTERGAARD H M.Theory of elasticity and plasticity[M].Cambridge:Harvard University Press,1952.
[22] 吕至坚,陈建仁.蝴蝶生活史图鉴[M].台湾:晨星出版有限公司,2014.
[23] FARRELL J,SMITH R B,HUSEN S,et al.Tomography from 26 years of seismicity revealing that the spatial extent of the Yellowstone crustal magma reservoir extends well beyond the Yellowstone caldera[J].Geophys Resarch Letters,2014,41:3068-3073.
[24] HUANG H H,LIN F C,SCHMANDT B,et al.The Yellowstone magmatic system from the mantle plume to the upper crust[J].Science,2015,348(6236):773-776.
[25] EMMERMANN R,LAUTERJUNG J.The German continental deep drilling program KTB:Overview and major results[J].Journal of Geophysical Research:Solid Earth,1997,102(B8):18179-18201.
[26] 郭晓菲,马念杰,赵希栋,等.圆形巷道围岩塑性区的一般形态及其判定准则[J].煤炭学报,2016,41(8):1871-1877.
GUO Xiaofei,MA Nianjie,ZHAO Xidong,et al.General shapes and criterion for surrounding rock mass plastic zone of round roadway[J].Journal of China Coal Society,2016,41(8):1871-1877.
