神东矿区煤炭储量丰富,煤层赋存稳定、开采条件优越。近年来,随开采强度增大,开采深度和范围也随之增加,神东矿区逐渐出现了强矿压、矿震、严重底臌等在深部开采中常出现的现象[1-3]。高强度开采同样加快了地表裂缝的形成,导致对水资源和生态环境的破坏加剧[4]。因此,有必要研究神东矿区不同赋存深度沉积岩物理力学参数随深度的变化特征,为分析神东矿区上覆岩层裂隙场形成机理和地下水库选址等提供基础参数。
不同赋存深度的岩石强度特性、破坏特征和孔隙度等均会存在差异。以往众多学者就赋存深度对岩石的物理力学性质开展过研究。如国外的HALLEY等[5]发现佛罗里达州南部高孔隙度新生代碳酸盐岩的孔隙度随赋存深度的增加而减小。BROWN[6]对密西西比系麦迪逊群碳酸盐的孔隙度进行研究,发现孔隙度是随赋存深度变化的函数。EHRENBERG等[7-8]以不同地质时期的油气储层为研究对象,分析了赋存深度对油气储层孔隙度的影响,得出孔隙度随赋存深度的增加而减少的变化规律。在国内,周宏伟等[9]对大台煤矿不同赋存深度下的玄武岩进行单轴、三轴及巴西劈裂试验研究,得出了玄武岩基本物理力学参数及变形破坏特征随赋存深度的变化规律。姜晨光等[10]通过力学试验得出了花岗岩的基本力学参数随赋存深度加深而增大,并给出相关数学模型。满轲等[11-13]对不同赋存深度玄武岩和花岗岩的拉伸特性及动态拉伸特性展开研究,发现花岗岩样品的动态拉伸强度并不随着赋存深度单调增大。汪虎等[14]对不同深度页岩储层单轴压缩下的力学参数展开分析,并研究了页岩储层力学参数的各向异性特征。李鹏波等[15]分析了煤层上覆岩层力学性质与赋存深度之间的变化规律。林斌等[16]研究了淮南矿区煤系地层中赋存深度对岩石力学参数的影响。仵彦卿、谢向东等[17-18]分析了不同赋存深度岩石的孔隙率和弹性模量变化特征。李化敏、李回贵等[19-20]对神东矿区补连塔煤矿、大柳塔煤矿及布尔台煤矿进行单轴压缩、三轴压缩和巴西劈裂试验,分析了不同沉积时期岩石的物理力学参数变化特征。
综上所述,国内外学者对不同赋存深度“硬岩”(如花岗岩、玄武岩等)研究较多,但对赋存深度对煤系地层沉积岩的断裂韧度和抗拉强度影响研究则鲜有报道。因此,笔者以神东矿区布尔台煤矿三盘区地质钻孔所钻取的不同赋存深度沉积岩岩芯为研究对象,通过巴西劈裂试验,获得了赋存深度对沉积岩抗拉强度及断裂韧度影响规律;基于不同赋存深度岩芯巴西劈裂过程中声发射数据,分析了试样破坏过程损伤和参数RA值演化特征,辨识了破坏前兆,为神东矿区中深部开采的工程地质力学特性分析提供了参考。
1 试验概述
1.1 试样制备
试验岩样取自神东矿区布尔台煤矿三盘区的BK212地质钻孔,钻孔深度达596.7 m。从钻孔岩芯中依次选取埋深为9.1,16.1,95.4,114.6,222.0,469.0,509.7,553.5,587.5,596.7 m的10组岩芯;根据国际岩石力学学会(ISRM)推荐方法,将10组岩芯分别加工成标准巴西圆盘试样(φ50 mm × 25 mm),每组3~4个样品,其中中粗砂岩因岩芯较短只有2个样品。试样两端面垂直于圆盘轴向,最大偏差不超过0.25°;端面的不平整度不大于0.1 mm。岩样的物理参数详见表1。
1.2 试验设备
试验采用WDW-100E万能试验机和美国物理声学公司的PCI-Express 8声发射监测系统,设备布置如图1所示。万能试验机的最大载荷为100 kN,加载速率为0.005~500 mm/min。声发射监测系统能实时记录并分析材料内部产生的声发射波形及相关参数。
表1 岩样的物理力学参数
Table 1 Physical and mechanical parameters of rock samples

岩性岩样编号赋存深度/m直径/mm高度/mm密度/(g·m-3)破坏载荷/kN抗拉强度/MPa断裂韧度/(MPa·m1/2)Pmin/kN比值k0119.148.6226.172.090.250.130.040.222.98粗砂岩10129.148.5425.542.090.300.150.060.272.770139.148.0326.022.070.500.250.100.492.620149.148.4125.561.970.520.260.090.452.8902116.149.2326.552.263.041.550.030.1845.67砂质泥岩102216.149.2226.222.313.201.630.030.1653.4002316.149.5526.372.384.592.340.020.12103.0402416.149.1426.062.573.011.530.020.0899.80中粗砂岩03195.448.0825.662.050.590.300.130.572.3803295.448.2025.862.090.380.190.110.371.69111114.648.7225.902.160.910.460.220.892.11含砾粗砂岩112114.648.8826.102.050.430.220.080.412.71113114.648.2825.642.110.490.250.090.452.75211222.048.8025.462.040.350.180.070.332.63粗砂岩2212222.048.6625.551.950.240.120.050.242.56213222.048.6525.371.950.470.240.090.452.60411469.049.2626.172.203.281.670.281.395.94粉砂岩1413469.049.3725.872.243.301.680.311.595.37414469.049.2225.512.131.620.830.321.612.57511509.748.5825.662.464.082.080.180.8811.47粉砂岩2512509.749.6326.122.472.271.160.381.963.03516509.749.4726.062.404.802.450.050.2745.61517509.749.3526.222.382.281.160.080.4114.51531553.549.4426.012.354.022.050.070.3529.65细砂岩1532553.549.9725.722.413.021.540.211.067.38534553.549.7726.422.412.811.430.261.375.43542587.549.1825.982.393.681.880.201.039.54细砂岩2543587.548.9026.642.274.262.170.030.1482.29545587.549.3025.502.294.212.150.673.363.20551596.749.5725.602.354.652.370.542.714.41砂质泥岩2552596.749.3126.232.314.582.330.462.365.21553596.749.1726.152.344.762.430.582.964.10554596.749.2626.032.354.692.390.562.853.94

图1 试验设备布置
Fig.1 Layout of the test equipment
1.3 试验方案
对已加工岩样进行劈裂试验,采用位移控制进行加载,加载速率为0.2 mm/min;并同步对试验加载过程中的声发射信号进行采集和存储。经过反复测定环境噪音,最终将信号门槛值设定为40 dB,采样率为1 MHz。利用耦合剂和胶带将传感器按照设计位置(图2)粘贴在岩样表面,保证两者充分接触且不脱落;并在加载前进行断铅试验,确保试验中能够获取大量有效的声发射数据。试验前,先对声发射系统和试验机系统进行计时同步,并同步开始记录,确保2个系统采集数据在时间上一致。然后开始对岩样进行加载,声发射系统采集岩样内部产生的声发射信号,直至岩样发生破坏,停止加载和数据采集,并对相关数据进行存储。试验结束后对储存的声发射信号数据进行处理,汇总不同岩样加载过程中4个通道的声发射能量、上升时间及幅值等数据为后续分析提供准备。

图2 巴西劈裂加载示意及实物
Fig.2 Splitting loading of Brazil test
2 试验结果与分析
2.1 不同赋存深度岩样巴西劈裂破坏特征
巴西劈裂法是国际岩石力学学会标准推荐的测定岩石抗拉强度方法[21-22],抗拉强度σt的计算公式为:![]() 其中P为最大载荷;D,t分别为试样的直径和厚度,各岩样计算结果详见表1。将试验结果与李化敏等[23]测得结果进行比对,结果基本一致。由于试验岩样较多,图3仅展示不同赋存深度典型岩样的应力-应变曲线,不难发现不同岩样抗拉强度和破坏应变差异较大,其中粉砂岩516的抗拉强度最大,为2.45 MPa;粗砂岩212的抗拉强度最小,为0.12 MPa,约为粉砂岩516的1/20;细砂岩545的破坏应变最大,为1.21×10-2,砂质泥岩021的破坏应变最小,为7.01×10-3,约为细砂岩545的1/2。
其中P为最大载荷;D,t分别为试样的直径和厚度,各岩样计算结果详见表1。将试验结果与李化敏等[23]测得结果进行比对,结果基本一致。由于试验岩样较多,图3仅展示不同赋存深度典型岩样的应力-应变曲线,不难发现不同岩样抗拉强度和破坏应变差异较大,其中粉砂岩516的抗拉强度最大,为2.45 MPa;粗砂岩212的抗拉强度最小,为0.12 MPa,约为粉砂岩516的1/20;细砂岩545的破坏应变最大,为1.21×10-2,砂质泥岩021的破坏应变最小,为7.01×10-3,约为细砂岩545的1/2。
图3中应力-应变曲线主要存在2种不同形式,根据其曲线特征可将10种沉积岩样品分为2大类:第1类主要为赋存深度-300 m以深的岩样,包含砂质泥岩021、粉砂岩413、粉砂岩516、细砂岩531、细砂岩545和砂质泥岩551,该类岩样表现出明显的脆性特征,峰后应力突降,破坏突然;第2类主要为赋存深度-300 m以浅的岩样,包括粗砂岩012、中粗砂岩032、含砾粗砂岩111和粗砂岩212,这些岩样在峰后阶段未发生突然破坏失稳,而是内部裂纹继续扩展贯通,应力随变形量增加缓慢下降,岩样逐渐失稳破坏,表现出一定的“延性”特征。

图3 不同赋存深度典型岩样巴西劈裂应力-应变曲线
Fig.3 Stress-strain curves of typical rock samples at different depths
图4为不同赋存深度典型岩样巴西劈裂破坏形态,可以看出岩样基本沿着直径方向劈裂成对称的两部分,部分岩样裂缝未经过圆盘中心,主要因岩样内部存在节理弱面。赋存-300 m以浅岩样破裂面多呈弧状,即破坏为张-剪混合型破坏,在达到峰值强度后破裂面两侧由于剪切摩擦产生相对滑动;而赋存-300 m以深岩样破裂面较浅部岩样更为平直,且达到峰值强度后立即发生破坏,破裂面两侧未出现相对滑动。
2.2 不同赋存深度岩样抗拉强度分布
图5为不同岩样抗拉强度随赋存深度的分布情况。赋存深度较浅的岩样抗拉强度较低(除砂质泥岩1外,其内部以钙质胶结为主,局部泥质胶结),赋存深度-300 m以浅的岩样抗拉强度基本在0.5 MPa以下。根据地质资料可知,该组岩样主要为泥质胶结,局部钙质胶结,厚层状;成分以石英、长石为主,云母次之,含暗色矿物;分选差、磨圆次棱角状;内部颗粒较大,存在空隙等微结构较多,因此在应力较小时易产生较大变形,且在峰后阶段表现出一定的“延性”,即达到峰值强度后不会立即发生破坏失稳,应力缓慢下降,变形量继续增加。赋存深度-300 m以深的岩样抗拉强度基本在1 MPa以上,该组岩样主要为泥质胶结,部分夹薄层粉砂岩或中砂岩,含大量植物茎叶化石碎片,夹薄层煤线;颗粒直径小,内部空隙等微结构少,因此抗拉强度相对较大。由图3可知,该组岩样峰后应力迅速降低,变形量增幅较小。

图4 不同赋存深度岩样劈裂破坏形态
Fig.4 Failure patterns of rock samples at different depths

图5 不同赋存深度岩样抗拉强度分布
Fig.5 Distribution of tensile strength of rock samples at different depths
总体而言,所测试岩样的抗拉强度随赋存深度增加而增大;对本实验所采用的不同赋存深度岩样(除砂质泥岩1外)的抗拉强度均值进行非线性拟合,可得抗拉强度σt与赋存深度H间呈幂函数关系,其表达式为:σt=a+b×|H-161.07|2.86,其中,a,b为拟合参数,分别等于0.18 MPa和1.15×10-8 MPa/m2.86,拟合参数单位由量纲分析确定。
2.3 不同赋存深度岩样断裂韧度分布
上述巴西劈裂试验采用弧形加载方式,弧形接触面圆心角约为20°,因此可根据王启智、张盛等[24-26]研究得出的平台巴西圆盘断裂韧度公式进行计算:![]() 其中,Pmin为紧接在最大载荷后的最小载荷;R,t分别为试样的半径和厚度,计算结果详见表1。
其中,Pmin为紧接在最大载荷后的最小载荷;R,t分别为试样的半径和厚度,计算结果详见表1。
图6为岩样I型断裂韧度随赋存深度的变化规律。赋存深度较浅的岩样断裂韧度较低,赋存深度-300 m以浅岩样断裂韧度多在0.15 MPa·m1/2以下,主要因该组岩样多为泥质胶结,内部颗粒较大,非均质性强,因此抗拉剪能力弱,断裂韧度较小;赋存深度-300 m以深岩样断裂韧度多大于0.15 MPa·m1/2。岩样断裂韧度总体上随赋存深度增加而增大(除粗砂岩2、砂质泥岩1和粉砂岩1外);对不同赋存深度岩样断裂韧度均值进行拟合,可得岩样I型断裂韧度KⅠC与赋存深度H间呈幂函数关系:![]() 其中,c,d均为拟合参数,分别等于4 432.47(MPa·m1/2)-3.63和7.41 (MPa-3.63·m-5.63/2)。
其中,c,d均为拟合参数,分别等于4 432.47(MPa·m1/2)-3.63和7.41 (MPa-3.63·m-5.63/2)。

图6 不同赋存深度岩样断裂韧度分布规律
Fig.6 Distribution of fracture toughness of rock samples at different depths
2.4 不同赋存深度岩样抗拉强度与断裂韧度关系特征
图7为所测试岩样抗拉强度和断裂韧度随赋存深度变化图。总体上,岩样抗拉强度、断裂韧度与赋存深度的关系可表示为
7KⅠC+8σt=55.9-8.3ln(H+659.38)
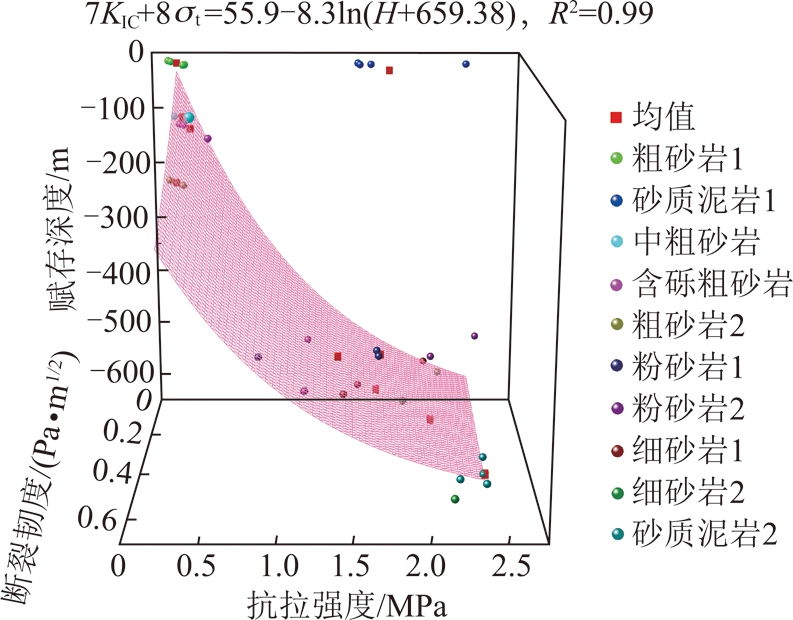
图7 不同赋存深度岩样抗拉强度和断裂韧度分布规律
Fig.7 Distribution of fracture toughness and tensile strength of rock samples at different depths
WHITTAKER,ZHANG,WANG等[27-29]分别分析了岩石和黏土材料I型断裂韧度与拉伸强度之间的关系,发现两者之间存在一定的线性关系。因此对不同赋存深度岩样抗拉强度与I型断裂韧度的比值(k)进行计算,结果详见表1。不难发现:在-300 m以浅(除砂质泥岩1外),k值为2~3,-400 m左右岩样k值为3~6,相对较接近文献[28]中比例系数6.88;-500 m以深岩样(除砂质泥岩2外)相对离散。
图8为不同岩样抗拉强度与I型断裂韧度比值k随赋存深度的变化规律。不难发现:赋存深度-300 m以浅岩样(除砂质泥岩1外)k值小于3,赋存深度-300 m以深岩样k值多大于3,对不同赋存深度岩样k值均值进行拟合,得到以下关系:k=13.04-1.72ln(H+597.00),需要指出因砂质泥岩2及粉砂岩2比值k的离散性造成了图8中曲线的拟合度相对不高。

图8 不同赋存深度岩样抗拉强度与断裂韧度比值k分布
Fig.8 Distribution of the ratio k of tensile strength and fracture toughness of rock samples at different depths
2.5 不同赋存深度岩样的声发射RA值及损伤演化特征
岩石在破坏变形过程中的声发射反映了其内部裂纹萌生、扩展和贯通破坏的演化过程,许多学者用声发射参数来定量描述岩石变形破坏过程中损伤变量的演化特征[30-32]。深入分析不同赋存深度岩样破坏形式及前兆将有利于认识样品抗拉强度与I型断裂韧度随深度的变化规律。本文采用声发射累积能量定义损伤变量D,即D=Ed/E0,其中,Ed为加载过程中某时刻声发射累积能量;E0为样品破坏停止采集时刻的声发射累积能量。同时,采用声发射RA值(上升时间/幅值)判定不同深度岩样在变形破坏过程中的主要形式,以往监测研究发现RA值较低时对应破坏形式为张拉破坏,RA值较高时对应破坏形式为剪切破坏[33-34]。
根据RA值演化规律对不同岩样劈裂破坏过程中的破坏特征及损伤演化特征分析结果详见表2。10种岩样的破坏形式均为张-剪混合型破坏,张拉破坏会贯穿整个破坏过程,而剪切破坏发生时间不同:赋存深度-300 m以浅岩样剪切破坏和损伤陡升发生在峰后阶段,而赋存深度-300 m以深岩样则发生在峰前阶段。
图9为不同赋存深度岩样的声发射RA值、损伤、应力与时间关系图。不难发现:赋存深度-300 m以深岩样峰后阶段较短,达到峰值强度后立即破坏,应力迅速下降;赋存深度-300 m以浅岩样达到峰值强度后并未完全失去承载力,随着应力缓慢下降变形继续增加,直至岩样完全破坏。结合岩石劈裂破坏过程中的损伤曲线,将峰值强度前损伤-时间曲线斜率最大处所对应的时刻确定为岩石破坏前兆点[35]。表2亦给出了测试岩样劈裂破坏前兆点,如粗砂岩012的破坏前兆点对应的应力强度为峰值强度的89.5%,砂质泥岩021为99.3%,中粗砂岩032为65.6%,含砾粗砂岩111为73.0%,粗砂岩212为72.3%,粉砂岩413为98.5%,粉砂岩516为97.7%,细砂岩531为97.0%,细砂岩545为99.3%,砂质泥岩551为92.1%。可以看出,赋存深度-300 m以深岩样破坏前兆点基本在峰值强度的92%以上;而赋存深度-300 m以浅岩样(除中粗砂岩外)则为峰值强度的70%~90%。从赋存深度看,赋存深度越深的沉积岩预警时间越短,失稳破坏越迅速剧烈。
需要指出,本文所获得的结果均基于神东布尔台煤矿BK212钻孔岩芯实验,部分岩样因内部结构的复杂性造成了部分结果的离散性,因此后期仍有必要通过更多岩芯测试数据对所得规律进行验证。

图9 不同赋存深度岩样损伤、RA值、应力与时间的关系
Fig.9 Relationship curves of time with damage,RA value and stress for rocks at different depths
表2 不同赋存深度岩样破坏形式、损伤特征及破坏前兆点
Table 2 Failure modes,damage characteristics and failure precursors of rock samples at different depths

岩性试件编号赋存深度/m不同阶段岩样破坏形式及损伤特征峰前阶段峰后阶段破坏前兆点的应力强度百分比/%粗砂岩10129.1张拉破坏,损伤缓慢增加以张拉破坏为主,损伤台阶上升;222 s出现剪切破坏,损伤出现陡升89.5砂质泥岩102116.1张-剪混合破坏,损伤线性增加张-剪混合破坏,损伤线性增加99.3中粗砂岩03295.4张拉破坏,损伤台阶上升以张拉破坏为主,损伤台阶上升;150,200和250 s出现剪切破坏,损伤出现陡升65.6含砾粗砂岩111114.6张拉破坏,损伤台阶上升以张拉破坏为主,损伤台阶上升;120 s出现剪切破坏,损伤出现陡升73.0粗砂岩2212222.0张拉破坏,损伤台阶上升以张拉破坏为主,损伤台阶上升;124 s和139 s出现剪切破坏,损伤出现陡升72.3粉砂岩1413469.0以张拉破坏为主,损伤台阶上升;138 s出现剪切破坏,损伤陡升张拉破坏,损伤台阶上升98.5粉砂岩2516509.7以张拉破坏为主,损伤台阶上升;142 s出现剪切破坏,损伤陡升张拉破坏,损伤台阶上升97.7细砂岩1531553.5以张拉破坏为主,损伤台阶上升;89 s和125 s出现剪切破坏,损伤陡升张拉破坏,损伤台阶上升97.0细砂岩2545587.5张-剪混合破坏,损伤台阶上升;179 s出现剪切破坏,损伤陡升张拉破坏,损伤台阶上升99.3砂质泥岩2551596.7以张拉破坏为主,损伤台阶上升;51 s出现剪切破坏,损伤陡升张拉破坏,损伤台阶上升92.1
3 结 论
(1)神东矿区不同赋存深度岩样抗拉强度和I型断裂韧度不同,-300 m以浅岩样分别在0.5 MPa和0.15 MPa·m1/2以下,而-300 m以深岩样则分别在1.0 MPa和0.15 MPa·m1/2以上;总体而言,岩样的抗拉强度和I型断裂韧度随着赋存深度的增加而增大,且均与赋存深度呈幂函数关系。
(2)不同赋存深度岩样抗拉强度与I型断裂韧度的比值k不同,在-300 m以浅岩样,k值为2~3,-400 m左右k值为3~6,-500 m以下相对离散;k值随赋存深度的增加而增大,且与赋存深度呈对数函数关系。
(3)不同赋存深度岩样在峰值强度前均会出现破坏前兆点,由浅到深其破坏前兆点对应的应力强度分别为峰值强度89.5%,99.3%,65.6%,73.0%,72.3%,98.5%,97.7%,97.0%,99.3%和92.1%;-300 m以浅岩样(除中粗砂岩外)破坏前兆点基本在70%~90%峰值强度内出现,而-300 m以深岩样的破坏前兆点多在92%峰值强度以后出现。因此,神东矿区沉积岩样随赋存深度增加岩样破坏预警时间减少。
致谢 感谢国家能源集团神东煤炭集团地质勘查测量公司王尔林副总工程师等在现场岩芯获取等方面所给予的指导和帮助。
[1] 杨登峰,陈忠辉,洪钦锋,等.浅埋煤层开采顶板切落压架灾害的突变分析[J].采矿与安全工程学报,2016,33(1):122-127.
YANG Dengfeng,CHEN Zhonghui,HONG Qinfeng,et al.Catastrophic analysis of support crushing disasters while roof cutting in shallow seam mining[J].Journal of Mining & Safety Engineering,2016,33(1):122-127.
[2] 973 计划(2013CB227900)“西部煤炭高强度开采下地质灾害防治与环境保护基础研究”项目组.西部煤炭高强度开采下地质灾害防治理论与方法研究进展[J].煤炭学报,2017,42(2):267-275.
Research Group of National Key Basic Research Program of China (2013CB227900)(Basic Study on Geological Hazard Prevention and Environmental Protection in High Intensity Mining of Western Coal Area).Theory and method research of geological disaster prevention on high-intensity coal exloitation in the west areas[J].Journal of China Coal Society,2017,42(2):267-275.
[3] 范钢伟,张东升,马立强.神东矿区浅埋煤层开采覆岩移动与裂隙分布特征[J].中国矿业大学学报,2011,40(2):196-201.
FAN Gangwei,ZHANG Dongsheng,MA Liqiang.Overburden movement and fracture distribution induced by longwall mining of the shallow coal seam in the Shendong coalfield[J].Journal of China University of Mining & Technology,2011,40(2):196-201.
[4] 顾大钊,颜永国,张勇,等.煤矿地下水库煤柱动力响应与稳定性分析[J].煤炭学报,2016,41(7):1589-1597.
GU Dazhao,YAN Yongguo,ZHANG Yong,et al.Experimental study and numerical simulation for dynamic response of coal pillars in coal mine underground reservoir[J].Journal of China Coal Society,2016,41(7):1589-1597.
[5] HALLEY R,SCHMOKER J W.High porosity cenozoic carbonate rocks of south Florida:Progressive loss of porosity with depth[J].AAPG Bulletin,1983,67(2):191-200.
[6] BROWN A.Porosity variation in carbonates as a function of depth:Mississippian madison group,Williston Basin//Kupecz J A,Gluyas J,Bloch S.Reservoir quality prediction in sandstones and carbonates[J].AAPG Memoir,1997,69:29-46.
[7] EHRENBERG S N,NADEAU P H.Sandstone vs.carbonate petroleum reservoirs:A global perspective on porosity-depth and porosity-permeability relationships[J].AAPG Bulletin,2005,89(4):435-445.
[8] EHRENBERG S N,NADEAU P H,STEEN Ø.Petroleum reservoir porosity versus depth:Influence of geological age[J].AAPG Bulletin,2009,93(10):1281-1296.
[9] 周宏伟,谢和平,左建平,等.赋存深度对岩石力学参数影响的实验研究[J].科学通报,2010,55(34):3276-3284.
ZHOU Hongwei,XIE Heping,ZUO Jianping,et al.Experimental study of the effect of depth on mechanical parameters of rock[J].Chinese Science Bulletin,2010,55(34):3276-3284.
[10] 姜晨光,姜祖彬,刘华,等.花岗岩岩石力学参数与岩体赋存深度关系的研究[J].石材,2004(7):4-6.
JIANG Chenguang,JIANG Zubin,LIU Hua,et al.Study on relation between the rock mechanical parameters of the granite and its covered depth[J].Stone,2004(7):4-6.
[11] 满轲.赋存深度对岩石动态断裂韧性的影响[J].金属矿山,2011,40(3):19-21.
MAN Ke.Depth effect on dynamic fracture toughness of rock[J].Metal Mine,2011,40(3):19-21.
[12] 满轲,刘晓丽,宫凤强,等.不同赋存深度新疆天湖花岗岩的动态拉伸力学特性研究[J].工程力学,2018,35(3):200-209.
MAN Ke,LIU Xiaoli,GONG Fengqiang,et al.Research on dynamic tension property of granite at different depth in tianhu area of Xinjiang autonomous region[J].Engineering Mechanics,2018,35(3):200-209.
[13] 满轲,周宏伟.不同赋存深度岩石的动态断裂韧性与拉伸强度研究[J].岩石力学与工程学报,2010,29(8):1657-1663.
MAN Ke,ZHOU Hongwei.Research on dynamic fracture toughness and tensile strength of rock at different depths[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(8):1657-1663.
[14] 汪虎,郭印同,王磊,等.不同深度页岩储层力学各向异性的试验研究[J].岩土力学,2017,38(9):2496-2506.
WANG Hu,GUO Yintong,WANG Lei,et al.An experimental study on mechanical anisotropy of shale reservoirs at different depths[J].Rock and Soil Mechanics,2017,38(9):2496-2506.
[15] 李鹏波,王金安.煤层上覆岩层力学性质随赋存深度变化试验[J].哈尔滨工业大学学报,2015,47(12):98-101.
LI Pengbo,WANG Jin’an.Experimental on mechanical properties of overlying strata rock changed with the occurrence depth[J].Journal of Harbin Institute of Technology,2015,47(12):98-101.
[16] 林斌,徐冬.深部岩石力学参数随赋存深度变化规律研究[J].安徽理工大学学报(自然科学版),2017,37(6):52-59.
LIN Bin,XU Dong.Study on the law of mechanical parameters of rock in deep coal bearing strata[J].Journal of Anhui University of Science and Technology(Natural Science),2017,37(6):52-59.
[17] 仵彦卿.岩石孔隙率随地层深度变化规律研究[J].西安理工大学学报,2000,16(1):6-8.
WU Yanqing.Research on the law of porosity of rock with depth[J].Journal of Xi’an University of Technology,2000,16(1):6-8.
[18] 谢向东.岩体弹性模量沿地层埋深变化规律研究[J].襄樊学院学报,2010,31(11):9-12.
XIE Xiangdong.Changing laws of the Young Modulus of rock body along stratigraphic depth[J].Journal of Xiangfan University,2010,31(11):9-12.
[19] 李化敏,李回贵,宋桂军,等.神东矿区煤系地层岩石物理力学性质[J].煤炭学报,2016,41(11):2661-2671.
LI Huamin,LI Huigui,SONG Guijun,et al.Physical and mechanical properties of the coal-bearing strata rock in Shendong coal field[J].Journal of China Coal Society,2016,41(11):2661-2671.
[20] LI Huigui,LI Huamin.Mechanical properties and acoustic emission characteristics of thick hard roof sandstone in Shendong coal field[J].International Journal of Coal Science & Technology,2017,4(2):147-158.
[21] ULUSAY R.The ISRM suggested methods for rock characterization,testing and monitoring:2007-2014[M].Cham:Springer International Publishing,2015:47-48.
[22] ISRM.Suggested methods for determining tensile strength of rock materials[J].International Journal of Rock Mechanics & Mining Science & Geomechanics Abstracts,1978,15(15):99-103.
[23] 李化敏,李回贵,Syd S.Peng,等.神东矿区岩石物理力学性质[M].北京:科学出版社,2018:118-122.
[24] 王启智,贾学明.用平台巴西圆盘试样确定脆性岩石的弹性模量、拉伸强度和断裂韧度——第1部分:解析和数值结果[J].岩石力学与工程学报,2002,21(9):1285-1289.
WANG Qizhi,JIA Xueming.Determination of elastic modulus,tensile strength and fracture toughness of brittle rocks by using flattened Brazilian disk specimen——part I:Analytical and numerical results[J].Chinese Journal of Rock Mechanics and Engineering,2002,21(9):1285-1289.
[25] 王启智,吴礼舟.用平台巴西圆盘试样确定脆性岩石的弹性模量、拉伸强度和断裂韧度——第2部分:试验结果[J].岩石力学与工程学报,2004,23(2):199-204.
WANG Qizhi,WU Lizhou.Determination of elastic modulus,tensile strength and fracture toughness of brittle rocks by using flattened Brazilian disk specimen——part II:Experimental results[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(2):199-204.
[26] 张盛,王启智.用5种圆盘试件的劈裂试验确定岩石断裂韧度[J].岩土力学,2009,30(1):12-18.
ZHANG Sheng,WANG Qizhi.Determination of rock fracture toughness by split test using five types of disc specimens[J].Rock and Soil Mechanics,2009,30(1):12-18.
[27] WHITTAKER B N,SINGH R N,SUN G.Rock fracture mechanics principles,design and applications[M].Amsterdam Elsevier,1992.
[28] ZHANG Z X.An empirical relation between mode I fracture toughness and the tensile strength of rock[J].International Journal of Rock Mechanics & Mining Sciences,2002,39(3):401-406.
[29] WANG Junjie,ZHU Jungao,CHIU C F,et al.Experimental study on fracture toughness and tensile strength of a clay[J].Engineering Geology,2007,94(1):65-75.
[30] 李术才,许新骥,刘征宇,等.单轴压缩条件下砂岩破坏全过程电阻率与声发射响应特征及损伤演化[J].岩石力学与工程学报,2014,33(1):14-23.
LI Shucai,XU Xinji,LIU Zhengyu,et al.Electrical resistivity and acoustic emission response characteristics and damage evolution of sandstone during whole process of uniaxial compression[J].Chinese Journal of Rock Mechanics and Engineering,2014,33(1):14-23.
[31] 刘保县,黄敬林,王泽云,等.单轴压缩煤岩损伤演化及声发射特性研究[J].岩石力学与工程学报,2009,28(S1):3234-3238.
LIU Baoxian,HUANG Jinglin,WANG Zeyun,et al.Study on damage evolution and acoustic emission character of coal-rock under uniaxial compression[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(S1):3234-3238.
[32] 夏冬,杨天鸿,徐涛,等.浸水时间对饱水岩石损伤破坏过程中声发射特征影响的试验[J].煤炭学报,2015,40(S2):337-345.
XIA Dong,YANG Tianhong,XU Tao,et al.Experimental study on AE properties during the damage process of watersaturated rock specimens based on time effect[J].Journal of China Coal Society,2015,40(S2):337-345.
[33] AGGELIS D G.Classification of cracking mode in concrete by acoustic emission parameters[J].Mechanics Research Communications,2011,38(3):153-157.
[34] SHIOTANI T.Evaluation of long-term stability for rock slope by means of acoustic emission technique[J].NDT & E International,2006,39(3):217-228.
[35] 张晖辉,尹祥础,梁乃刚,等.模拟引潮力作用下岩石破坏前兆的试验研究——加卸载响应比(LURR)理论和能量加速释放(AER)[J].岩石力学与工程学报,2005,24(17):3172-3179.
ZHANG Huihui,YIN Xiangchu,LIANG Naigang,et al.Experimental study of rock failure precursor using simulated tide stress-load/unload response ratio (LURR) and accelerating energy release (AER)[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(17):3172-3179.
