积水采空区对于煤矿井下采掘生产危害极大,必须进行治理。山西由于历史原因存在大量使用巷道穿采技术的小煤窑,遗留下大量巷道尺度的采空区,这些采空区往往与含水层连通,极易引发掘进工作面水害事故[1-3]。在我国煤矿井下,采空区井下超前探测目前以钻探为主,物探为辅。而采空巷道规模远小于一般采空区,正常布设的超前探放水钻孔密度很难对其进行覆盖,常规的物探超前探测技术也难以对这一尺度的异常体进行准确定位,更勿论对其形态、规模等参数做出精确解释[4-7]。考虑到钻孔孔内空间距离地质异常体很近,我可以利用它远离巷道、靠近地质异常这一特性,在巷道孔口处发射瞬变电磁信号,在钻孔孔内逐点接收,探测钻孔径向可能存在的小规模地质异常,并对其做出较为准确的地质解释,保障煤矿的安全生产。
利用钻孔进行瞬变电磁工作,以地-井装置研究最多,该装置属于二维工作装置,随收发距改变数据特征差异很大,对资料的处理解释带来了很大困难,所以热点研究方向主要集中在数据特征的总结:① 孔中信号的响应特征。通过物理模拟和多种数值模拟手段总结全空间条件下简单异常体(球体或板体)不同参数情况下的特征关系曲线及符号变化规律[8-10]。② 导电介质对信号的影响规律。通过理论推导和数值模拟研究围岩背景场或覆盖层对孔中瞬变电磁信号的影响,以及导电覆盖层下多个目标体的信号响应[11-14]。与正演工作相比,地-井瞬变电磁处理解释方面的研究工作开展很少,很难满足实际需求,具体可分为两类:① 从观测数据直接解释。根据正演研究得出的数据特征和规律,提出一些异常体定性或半定量解释方法,如通过多测道曲线变化判断异常体的大致方位和利用三分量信号矢量交汇定位异常体中心位置[15-16]。② 近似反演方法。通过一定的前提假设对地质情况进行简化,提出一些反演方法,如需要假定介质关于钻孔柱对称且源为磁偶极源的局部非线性近似快速反演和基于导电薄板等效涡流的异常反演方法[17-18]。在隧道或巷道中开展孔中瞬变电磁工作的相关资料更少,最早是国外VELLA L(1997)将地-井装置移至金属矿巷道中探测黄铁矿[19],之后国内王世睿(2016)研究了隧道10 m深钻孔中的瞬变电磁信号特性,提出根据发射线框改变产生的异常变化可定性解释隧道掘进工作面前方异常体方位[20]。孙怀凤等通过物理模拟试验证明了孔中瞬变电磁信号可用于判断隧道掘进工作面前方是否存在异常构造[21]。笔者(2017)研究了煤矿井下孔中动源定接收装置的超前探测技术,利用钻孔提高了常规井下瞬变电磁超前探测精度[22]。陈丁(2018)通过在全空间一维背景上增加三维异常体的积分方程数值模拟研究了煤矿巷道垂直孔中瞬变电磁特性[23]。
总体来看,尽管理论上巷道-钻孔/地-井瞬变电磁接收装置更加靠近异常,能通过地层压制电磁干扰,应该比矿井、地面方法有更优的异常反映和解释精度,但由于在于定源动接收情况下,孔中瞬变电磁其实是一组二维装置,尚缺乏好的反演成像技术,实际资料处理精度反而远落后于常规方法,仅能作为补充手段。所以必须另辟蹊径,避开收发距带给扩散场的复杂影响,采用数学办法将其转换为虚拟波场,针对特征简单的波场记录进行高效精准的拟地震反演。
瞬变电磁拟地震处理的基础是LEE等(1989)建立的电磁扩散方程与虚拟波动方程之间的数学关系[24],研究热点主要集中在:① 波场反变换。目前实现方法有全时段预条件正则化算法和分段奇异值分解法[25-28]。正则化法能基本还原波场特征,抗干扰能力强,但展宽效应和受正则化约束类型影响均较大;奇异值分解结果展宽效应小,但抗噪能力弱,结果稳定性差。② 波场分辨率增强。该研究主要为提高波场反变换效果,包括不同层位波幅的能量均衡、消除展宽效应的反褶积和压制噪音的相干叠加等方法[29-30]。此举虽能提高分辨率,但也必然损失部分有用信息。③ 虚拟波场速度分析、反演及成像。笔者之前通过等效导电平面法和声波全波形反演方法实现了中心回线装置数据的初始速度建模、速度分析和拟电阻率反演[31-32]。成像方面国外用电磁波旅行时实现了虚拟波场层析成像[33],国内则是对中心回线装置数据进行了Kirchhoff积分偏移成像[34-35]。
笔者将对井下巷道-钻孔定源动接收装置数据进行特征分析,通过基于相关叠加的滑动时窗波场反变换算法将二维瞬变电磁数据转换为虚拟波场数据,并研究其动校正技术,最终利用笔者以前完成的全波形反演方法实现巷道-钻孔数据的拟地震反演成像,精细解释钻孔径向存在的小规模地质异常,为井下准确探测积水采空巷道提供技术支撑。
1 方法原理
1.1 工作装置
笔者提出的工作装置如图1所示,在孔口巷道处布设一多匝小线框发射源,线框边长不大于2 m,接收使用磁探头。将发射线圈固定放置在孔口,法线指向钻孔延伸方向,之后沿钻孔按一定点距(如2 m)向孔中推送接收探头并逐点进行二次场测量,直至孔底。对于单个钻孔可观测三分量数据,通过垂直(Z)分量数据进行反演成像,水平(X,Y)分量对异常体中心进行定位;对于多个钻孔,可以通过对不同钻孔的垂直分量反演成像结果进行综合分析,联合解释地质异常体位置。

图1 施工装置示意
Fig.1 Schematic diagram of construction device
1.2 孔中数据特征
设置如图2所示模型,可研究巷道-钻孔瞬变电磁装置的数据特征,以指导资料处理方法研究。模型将一个2 m×2 m的发射线圈布置在掘进工作面孔口处,发射电流为1 A,掘进巷道规格为20 m×4 m×4 m,钻孔长度为80 m,在钻孔前方60 m处偏上5 m位置放置一个低阻异常体(积水巷道),钻孔从异常体下方经过,异常体规格为4 m×20 m×4 m,分别在钻孔孔深0,20,40,60,80 m处设置5个接收点。设置巷道电阻率为10 000 Ω·m,煤层电阻率为1 000 Ω·m,异常体电阻率为10 Ω·m。
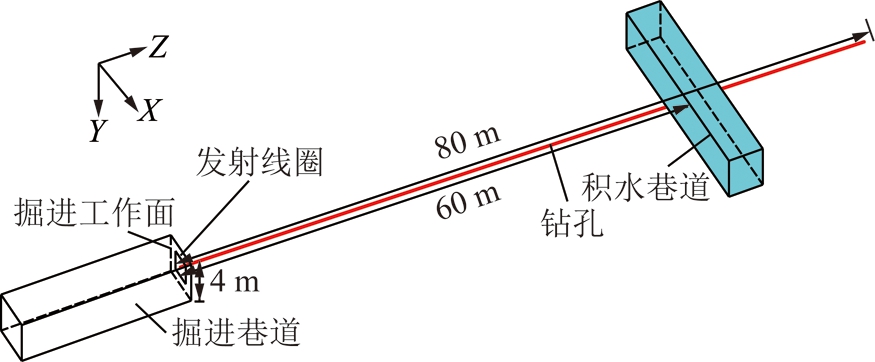
图2 模型示意
Fig.2 Schematic diagram of the model

图3 Z分量数据对比
Fig.3 Comparison of Z component data
对图2模型用时域有限差分三维正演算法模拟了含异常体和不含异常体两种情况,剖分网格边长为0.5 m。5个接收点不同情况下得到的Z分量数据对比情况如图3所示。从图3(a)可明显看出,随着入孔深度的增加,感应电动势曲线由一条单调曲线逐渐变为一条单峰曲线,孔深越深,对应测点的峰值越低,峰值对应的时间越晚。从图3(b)可看出,由于异常体体积较小,仅距离异常体最近的60 m孔深处数据曲线上对其有明显的拱起反映,其余孔深数据曲线上肉眼无法识别出异常响应特征,说明距离异常体越近,反映越强,这意味着采用孔内测量的方式确实有利于提高异常分辨能力。
但因测量曲线已不再符合单调衰减特征,所以很难对该装置的视电阻率给出类似中心回线装置晚期定义形式的简单公式,其精细的分辨能力就无法通过成像进行高精度呈现,必须考虑新的反演成像办法。
1.3 波场反变换
扩散方程到波动方程转换[27]的公式为
(1)
从式(1)可以看出,扩散场f(x,y,z,t)和波动场u(x,y,z,τ)中包含x,y,z三个空间坐标元素,说明该公式对空间任意位置的两种场量变换均适用,可将该公式用于非中心回线装置的其他瞬变电磁工作装置。
式(1)离散表达式为
(2)
式中,f(x,y,z,ti)为瞬变电磁场量;u(x,y,z,τj)为f(x,y,z,ti)所对应的虚拟波场量;τ为与瞬变电磁场的时间t相对应的虚拟波场时间;hj为积分系数;i为瞬变电磁场数据时间测道数;j为虚拟波场数据时间测道数。
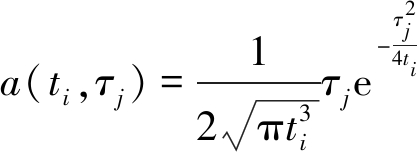
(3)
是式(2)的核函数。
式(1)的稳定性很差,数值化后的方程(2)属于极度病态的类型,其病态程度与方程组阶数是高度相关的,因此,必须大幅降低波场反变换式的线性方程组阶数,有效改善方程的不适定性。
最初提出的处理方法被称为分时段波场反变换算法,该方法认为计算过程中对方程组阶数影响较大的参数主要有两个,一是积分系数的数量,二是对数值积分离散时使用的采样点的数量,只要将这2个量降低,就能把方程组阶数降至较稳定的水平。这种办法提出根据采样时间将数据分段,对每一段数据来说,其积分系数和采样点个数均较少,可以得到较为稳定的计算结果[28]。
图4就是在均匀介质条件下采用分时段波场反变换计算的结果,介质电阻率为100 Ω·m,图中纵坐标A表示归一化的波场振幅,由图4可以看出:由于模型不存在地电界面,7个时段中的黑色直线即为理论上应得到的波场数据,点状线是按照分时段波场反变换方法计算得到的结果,显然2者存在误差,且前后时段的时间重叠部分的反变换结果也存在差异,7个时段波场数据的拼接也存在问题(图5)。

图4 均匀介质分时段反变换的波场图像
Fig.4 Results of wavefield transformation for timephased in Homogeneous medium

图5 7段波场反变换结果叠加
Fig.5 Superposition graph of 7 periods results
可以看出,分时段波场反变换算法只是权宜之计,要想更为精确得一次性完成瞬变电磁数据的波场反变换计算,必须使用一种能显著降低病态方程条件数的算法。对矩阵条件数进行预处理是一个可行的办法,使用超松弛预条件子能有效将矩阵条件数降至原来的平方,从而保证解方程(2)得到可靠且稳定的计算结果[26]。
该预条件全时段波场反变换算法效果如图6所示。图6(a)为在均匀介质条件下采用全时段波场反变换计算的结果,介质电阻率为100 Ω·m,与图4,5相比计算结果精度更高,并且可以一次将整个时段波场结果计算出来,避免了各个时段重叠部分的处理。图6(b)为一个H型地电模型采用全时段波场反变换得到的波形,模型参数见表1。由图6(b)可以看出:全时段波场反变换结果能反映模型设置的2个地电层位,但波形较宽,尤其是第2个波形,展宽现象较为严重,导致前后2个波形的分界点很难确定。

图6 全时段波场反变换的波场图像
Fig.6 Results of wavefield transformation for full time
表1 H型模型参数
Table 1 Parameter of H model

地层层序厚度/m电阻率/(Ω·m)表层80100中间层8050基底层125
综合来看,使用分时段算法和全时段算法均可以实现瞬变电磁数据的波场反变换计算,但2者均有明显的不足之处,分时段算法不够稳定,结果的精度不高,最大的问题是各个时段反变换得到的波场值在相互重叠的部分并不一致,甚至差异较大,仅通过平均算法压制的效果不佳,造成重叠段出现虚假子波;全时段算法稳定,计算精度相对较高,没有虚假子波的问题,但单个波形宽度较大,在虚拟波场时间上所包含的波数会较少,反映的地电层位界面不清晰,分辨率并不能实现显著提高解释精度的目的。
因此,笔者考虑结合以上2种算法的优势,既能通过时间分段压缩波形,提高界面分辨能力,又能保留全时段算法的稳定和精度,还能保证段与段重叠部分的真实可靠。
具体实施如图7所示,首先对分时段的波场反变换做一个改进,不再将时间分为固定段,而是设置一个固定长度的时间窗口,让它从第1个时间处按一定的时间步长向最后1个时间处滑动,每次滑动都对窗口内的瞬变电磁数据进行波场反变换,同时也要使用1.2节所述方法计算整个时段的波场反变换结果,之后将每个时间窗口计算的波场结果与全时段计算的波场结果做相关,根据相关性强弱来决定各个时间窗口波场结果是否与全时段波场结果进行叠加处理,所有与全时段结果相关性强的时窗结果与全时段结果的叠加结果即为最终的波场反变换结果。

图7 时间窗口滑动示意
Fig.7 Schematic diagram of sliding time window
相关系数可以定义为
(4)
式中,w1,w2为两个独立时窗反变换得到的虚拟波动场结果,k为它们之间的相关系数。显然,k的值越大,则w1,w2的形态也就越接近。
这种基于相关算法的滑动时窗波场反变换算法结果的好坏,主要取决于时间窗口的大小。如果时间窗口设置太大,即对整个时域分段太少,必然导致每次计算的不适定性增强,结果精度降低,同时各个时窗的反变换后波形的相关性会很大,起不到压制伪波形的目的;如果时间窗口设置太小,参与计算的采样点个数太少将导致对反变换方程的约束不足,由于方程奇异产生的数据跳变表现明显,反而掩盖了由地下电性变化引起的真实波场信息。
显然,使用滑动时窗算法时,必然有一个最优的时间窗口存在,它既能使反变换得到的波场最大限度的反映真实电性变化,又能完美压制不需要的伪波形。经过大量的正演模拟检验,得到了最优时间窗口的2个选取标准:① 一个瞬变电磁时窗转化得到的虚拟波动场时窗中至少要囊括一个整波,这使得该窗口包含的采样点个数能够对反变换方程产生足够的约束能力;② 在已经符合标准1的情况下,滑动时间窗口要尽可能缩小,这使得后期能够参与相关运算的窗口数量足够多,有效压制伪波形的出现。
确定了相关系数和最优时间窗口,很容易可以实现滑动时窗波场反变换算法,最终可得到精度很高的波场反变换结果。
图8为对应表1参数的H型地电模型采用滑动时窗波场反变换计算的结果,图8中黑色实线是理论上应得到的波场,点状线是滑动时窗波场反变换算法计算得到的波场,可以看出:波场反变换结果的幅值、位置、波形宽度均与理论波形吻合度很高,仅在波形两侧有少量震荡,相比全时段波场反变换结果受展宽效应影响较小。

图8 滑动时窗波场反变换的波场图像
Fig.8 Results of Wavefield transformation for sliding time window
显然基于相关算法的滑动时窗波场反变换算法综合了分时段和全时段波场反变换算法各自优势,是通过瞬变电磁信号求取虚拟波动场信号的最优算法。
1.4 二维“一发多收”数据的动校正
常规瞬变电磁采用中心回线装置施工,经过1.3节的工作,其数据可转化为类似于地震自激自收的一维虚拟波场数据,已有较好的反演成像方法。巷道-钻孔瞬变电磁虽然单次测量是“一发一收”,但因为发射装置位置、能量均未发生变化,故整体上类似地震勘探中 “一发多收”施工装置,本质属于二维装置,需要对其转化得到的二维虚拟波场数据进行动校正后方可反演。
二维瞬变电磁“一发多收”施工与二维地震勘探工作方式相似,只是将地震炮点的炸药激发改为用线圈或接地电极激发,将地震的检波器改为三分量瞬变电磁接收线圈或电极(图9)。

图9 二维瞬变电磁工作装置
Fig.9 2D TEM working device
为研究二维瞬变电磁“一发多收”施工装置数据的波场特征,设计一个D型模型采用1.2节中使用过的时域有限差分进行三维数值模拟,层厚与电阻率等模型参数如图10(a)所示,发射框边长定为100 m,供电电流1 A,发射框中心位于1号接收点左侧400 m,接收点距5 m。

图10 D型模型和起伏界面示意
Fig.10 Schematic diagram of the D model and undulating formation
对模拟的垂直分量感应电动势数据做波场反变换,可得如图11(a)所示的波形,对比一般地震单炮数据可以看出:瞬变电磁虚拟波场的“单炮”记录与地震反射波有明显不同,由于波形记录沿测点方向斜率很小,并未表现出明显的双曲线特征,而更符合地震直达波的直线特征,而随测点距离的增大,虚拟波场数据的能量也依次减弱,这与地震单炮记录一致。

图11 D型模型二维波场反变换结果
Fig.11 Wavefield transformation result of D model and undulating formation
为检验图11(a)中的波场时距曲线特征是否与直观感受到的一致,对反射波峰值点分别进行了直线拟合和双曲线拟合,结果如图12所示,图中红色实线为直线的结果,蓝色虚线为双曲线的结果,两条曲线几乎重合,差异很小。从拟合度上看,直线拟合度为0.976 8,双曲线拟合度为0.958 4,2者均超过0.9,都可以作为虚拟波场的时距曲线特征,但考虑到直线拟合度更高,且计算简单,后续研究将以虚拟波场的直线型时距曲线作为基准。

图12 D型模型虚拟波场时距曲线拟合结果
Fig.12 Fitting results of time curve for virtual wavefield of D model
考虑到射线理论,地震单炮记录还有一个重要特性,即反射点对应的是炮点与检波点的中点,但瞬变电磁波2次场在二维条件下是否也遵循射线理论,仍需要数值模拟结果的检验。设计一个D型起伏地层模型采用1.2节中使用过的时域有限差分进行三维数值模拟,层厚与电阻率等模型参数如图10(b)所示,在水平位置100~200 m的层面有一梯形凸起,梯形凸起下边长100 m,上边长75 m,高度30 m,发射框边长定为100 m,供电电流1 A,发射框中心位于1号接收点左侧400 m,接收点距10 m。
对模拟的垂直分量感应电动势数据做波场反变换,可得如图11(b)所示的波形,瞬变电磁虚拟波场的“单炮”记录仍然与图11(a)类似,并未表现出明显的双曲线特征,而表现为直线特征;随测点距离的增大,虚拟波场数据的能量也依次减弱。值得注意的是:在11~20号测点之间,波形记录上表现出层位的起伏特征,该位置与图10(b)所示模型设计在水平位置100~200 m的凸起位置吻合,证明波形记录点与接收点(检波点)一致,这也与常规地震的单炮记录不同。
因此,根据数值模拟结果可认为瞬变电磁二维拟地震单炮数据波形记录具有两个基本特征:① 波形记录点即接收点,即接收点处的虚拟波场记录反映的就是该接收点正下方的地电信息;② 随着收发距的增大,同一层位的反射波记录时间也逐步变大,时距曲线特征与直线特征相符。按照这两个特征,再参考地震动校正的计算方法,可以推导瞬变电磁二维拟地震单炮数据的动校正计算方法如下。
假设收发距为x的接收点波形记录时间为t(x),收发距为0的接收点波形记录时间为t(0),虚拟波场波速为v,可以得到
t(x)=t(0)+x/v
(5)
动校正量可写为
Δt=t(x)-t(0)=x/v
(6)
虚拟波场波速v可由下一节中的计算方法获得。
得到Δt后,对于收发距为x的接收点来说,从记录时间中减去该值即可完成动校正。
对于如图10(a)所示D型模型,按照上方确定的动校正算法进行校正,可以由图11(a)得到图13(a)动校正后的波场结果图,可以看到不同接收点反映层位信息的正峰波形记录时间不再倾斜,呈水平层状特征,与设计的数值模型一致,说明动校正方法有效。
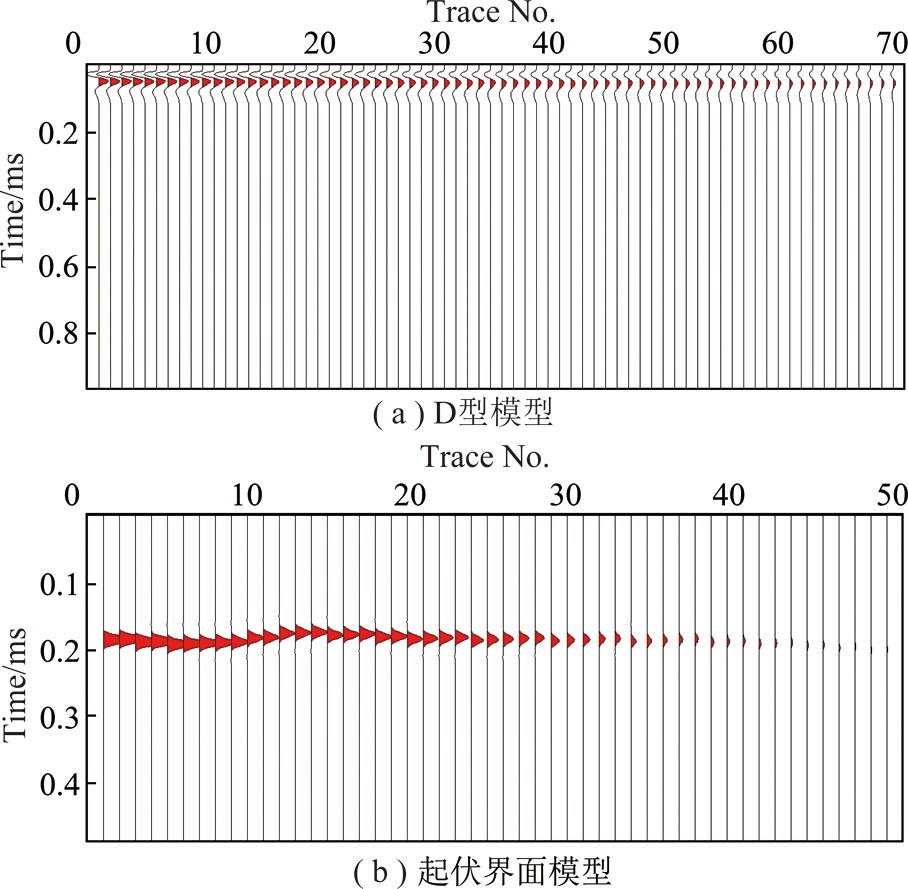
图13 D型模型和起伏地层模型动校正结果
Fig.13 Dynamic correction result of D model and undulating formation
对于如图10(b)所示D型起伏地层模型,同样按照上方确定的动校正算法进行校正,可以由图11(b)得到图13(b)的动校正后的波场结果图,可以看到不同接收点的反映层位信息的正峰波形记录时间基本不再表现出整体倾斜的特征,除11~12号测点之间的起伏特征外,其他测点大体呈水平层状特征。而11~20号测点位置与模型设计在水平位置100~200 m的凸起位置吻合,说明动校正方法有效。
1.5 初始速度模型
根据文献[31],可以从等效导电平面法出发,建立虚拟波场速度与电阻率的转换关系。
等效导电平面法是根据视纵向电导曲线的特征值直观地划分地层的一种近似方法,该方法可以形象地理解为:随着时间t的增减,等效导电平面以一定的速度上下“浮动”。可认为此速度即为虚拟波场的传播速度,可由如下公式计算
(7)
式中,σi为电导。
1.6 全波形反演
经过1.4节的动校正,二维“一发多收”瞬变电磁数据已转化为类似于地震自激自收的一维波形数据,可参考文献[32]对其进行全波形反演,实现拟地震反演成像。反演迭代公式为
 vpE(k)
vpE(k)
(8)
式中,vp为纵波速度;E为误差泛函;α为迭代步长;k为迭代次数,运算时以目标函数梯度的反向作为迭代方向,在第k次的模型上把误差函数展开就可以得到迭代步长。
2 模拟检验
2.1 数值模拟
为验证巷道-钻孔瞬变电磁二维工作方法的探测效果,设计如图14(a)所示的三维数值模型。在迎头前方有一超前钻孔,采空区异常体中心位于钻孔孔深37 m处左侧30 m,模型参数见表2。发射线圈边长为2 m,发射电流强度为1 A,测线布置如图14(b)所示,钻孔中测线上有73个测点,测点间距1 m。
对正演数据进行二维波场反变换后,可得到图15(a)所示的波形图,可以清晰看出虚拟波场对采空区异常体前后两个地电界面的响应,只是该波形沿测点方向有时间上的后移。经过动校正后可以得到图15(b)所示的波形,图中采空区左右界面的两层波形已基本校平,与模型设置基本吻合,可以进行下一步全波形反演工作。

图14 模型示意
Fig.14 Schematic diagram of the mode
表2 模型参数
Table 2 Model parameter table

地层尺寸/(m×m×m)电阻率/(Ω·m)煤层200×1 000×1 000500后方空巷道5×5×10010 000含水采空区20×40×2010
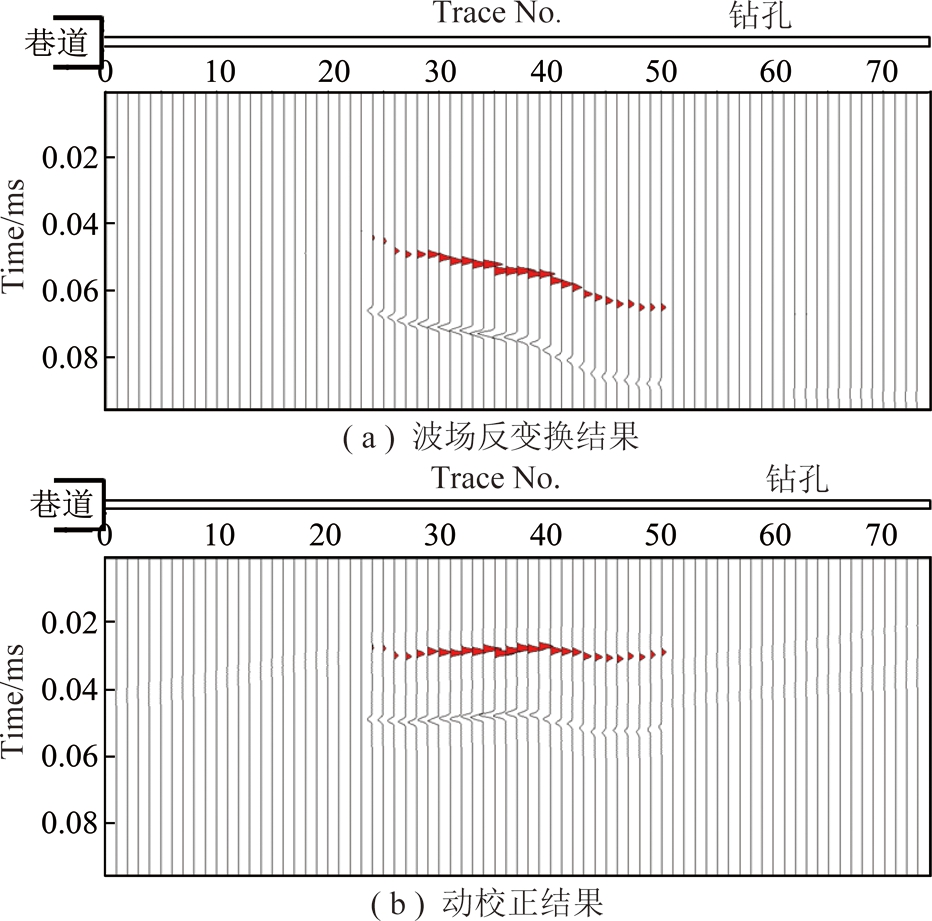
图15 三维数值模型数据虚拟波场波形
Fig.15 Waveform of virtual wavefield for 3D numerical model
对动校正后波形进行反演,可得如图16所示的结果。可以看出在孔深25~50 m内,钻孔径向15~40 m内有一明显低阻异常,异常体形状接近正方形,边长约为25 m,这一低阻异常的厚度、位置均与模型设置吻合较好,块状体的特征反映非常明显,解释精度较高。

图16 三维数值模型数据反演结果
Fig.16 Inversion results of 3D numerical model
2.2 物理模拟
为进一步验证方法对巷道-钻孔二维施工实际数据的探测效果,在长安大学地球物理专用的物理模拟实验水槽进行了模拟试验,模型设置如图17所示。采用多匝小线框激发、多匝小线框接收的施工方式取得数据,发射线圈边长为0.4 m,匝数为10匝,接收线圈面积约为0.9 m2,发射电流强度为1.5 A,施工布置如图17所示,测线上有14个测点,测点间距为0.05 m。异常体用一铜板代替,铜板规格为0.1 m×0.1 m×0.002 m,铜板布设在图17中坐标系相对发射、接收线圈中心轴线位置的第1象限内,垂直测线放置,8号测点径向约0.2 m位置。

图17 模型施工示意
Fig.17 Schematic diagram of the model
对图17中的观测数据进行二维波场反变换后,可得到图18(a)所示的波形图,可以清晰看到8号测点处有一组反映低阻体前后两个界面的强幅值波形,较其他测点波幅差距很大,显然是铜板异常的响应,只是该波形对应的时间较晚,直接反演得到的深度会比模型布置的参数偏深。经过动校正后可以得到图18(b)所示的波形,图中主要异常处的波形时间经过了校准,可以进行下一步全波形反演工作。

图18 水槽物理模型数据虚拟波场波形
Fig.18 Waveform of virtual wavefield for flume physical model
对动校正后波形进行反演,可得如图19所示的结果。可以看出在测线延伸方向长度0.35 m处得到一明显的竖条状低阻异常,沿径向长度约为0.1 m,与铜板宽度一致,距离发射、接收线圈中心轴线的距离约为0.2 m,与铜板放置位置吻合较好。
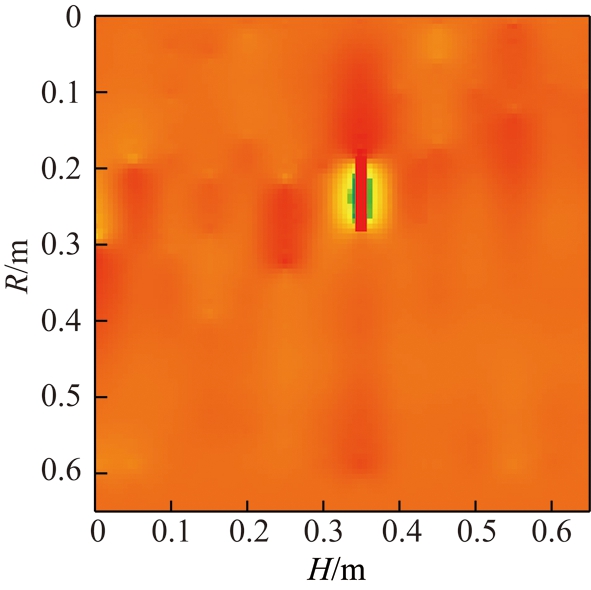
图19 水槽物理模型数据反演结果
Fig.19 Inversion results of flume physical model
水槽模型相对比较理想,为接近实际工况,选择山西大同某煤矿井下开展了1∶1物理模拟试验,施工布置如图20所示,钻孔为裸孔,无套管,使用不导电碳纤维杆人工将探头送入钻孔。采用多匝小线框激发、孔中探头接收的施工方式取得数据,发射线圈边长为2 m,匝数为40匝,接收探头等效面积约为1 000 m2,发射电流强度为10 A,施工钻孔深72 m,孔中从3 m开始有24个测点,测点间距为3 m。认为钻孔左侧掘进工作面前方放置的掘进机和胶带为异常体,掘进机在钻场前方10~15 m范围,距离钻孔径向距离约5 m。

图20 施工示意
Fig.20 Schematic diagram
对图20中的观测数据进行二维波场反变换后,可得到图21(a)所示的波形图,可以清晰看到前5个测点上有明显的异常体波形响应,与掘进机、皮带的位置对应较好,且波形记录清晰表现出“一发多收”装置的时距曲线特征。经过动校正后可以得到图21(b)所示的波形,图中对应掘进机和胶带的异常波形已基本校平,与现场实际情况基本吻合,可以进行下一步全波形反演工作。

图21 井下物理模型数据虚拟波场波形
Fig.21 Waveform of virtual wavefield for mine physical model
对动校正后波形进行反演,可得如图22所示的结果。可以看出在测线径向5 m处、延伸方向长度3~16 m范围内有明显条带状低阻异常,其中10~16 m范围内异常幅值最强,与掘进机位置基本一致,后方弱异常则与胶带位置吻合较好。

图22 井下物理模型数据反演结果
Fig.22 Inversion results of mine physical model
3 探测实例
山西阳泉某煤矿15103工作面掘进阶段,其回风巷道掘进前方为一已关闭煤矿。经调查该矿存在越界开采行为,且采空区存在大量积水。由于越界开采具体范围无法摸清,采空积水成为该回风巷道掘进过程中的重要安全隐患。15103工作面回风巷道设计长度1 020 m,已掘进750 m,根据调查推测再向前掘进60 m极有可能揭露邻矿越界开采的积水采空巷道(图23)。

图23 15103工区平面示意
Fig.23 Schematic diagram of 15103 work area
为避免揭露采空巷道,提前对工作面布局进行调整,利用掘进工作面已有钻孔设计了巷孔瞬变电磁探测工作,具体工作设计如图24所示,施工时每个钻孔发射线框中心法线方向均指向钻孔钻进方向。施工选择2号、3号和7号钻孔施工,其中2号、3号钻孔为顺煤层水平孔,7号钻孔为斜向上顶板孔,钻孔均为裸孔,无套管,使用不导电碳纤维杆人工将探头送入钻孔。孔中施工点距均为3 m,其中2号孔孔深75 m,实际测量72 m,3号孔孔深75 m,实际测量75 m,7号孔孔深65 m,实际测量63 m。

图24 施工示意
Fig.24 Schematic diagram
因篇幅关系,仅列出3号钻孔观测数据的二维波场反变换结果和动校正结果,如图25所示。由图25(a)中可以清晰看出自10号测点开始出现束状波形,符合采空巷道特征,但波形随收发距增大出现明显时间延迟现象,需要动校正处理。经过动校正后得到图25(b)所示的波形,时间延迟现象依然较为明显,结合施工巷道、钻孔以及推测采空巷道的空间位置分析,此时的时间差异应与实际采空巷道位置相关,可以进行下一步全波形反演工作。
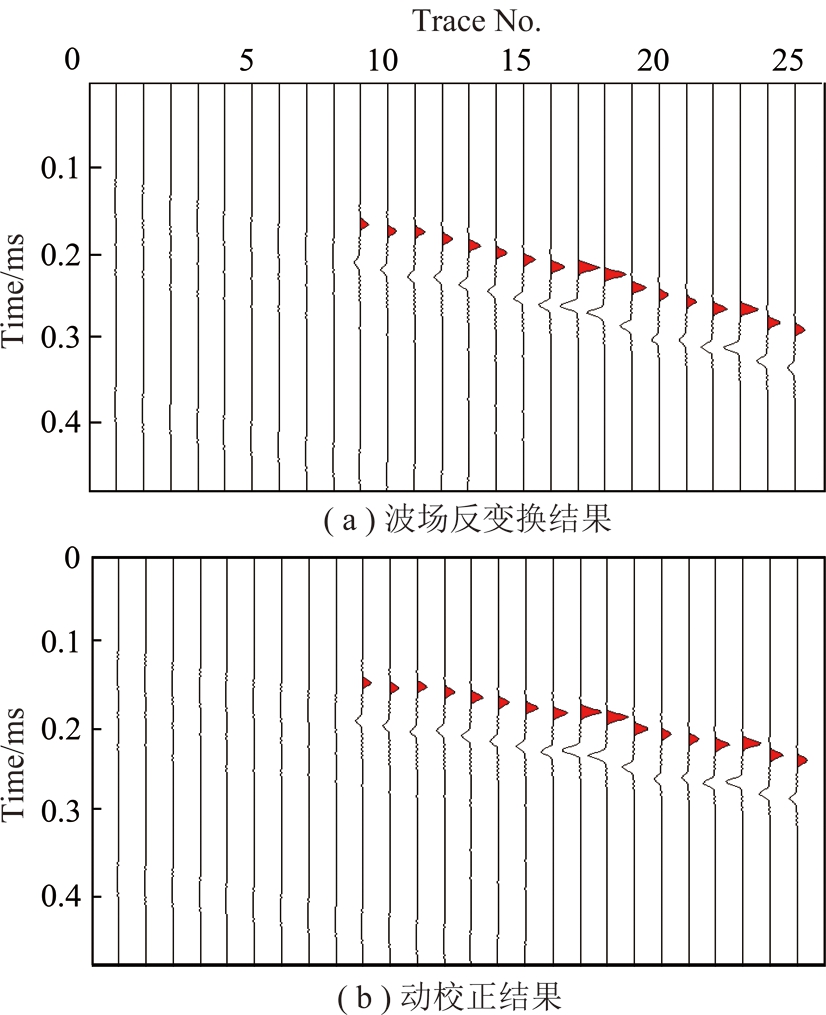
图25 3号钻孔数据虚拟波场波形
Fig.25 Waveform of virtual wavefield for No.3 borehole
对3个施工钻孔动校正后波形进行反演,可得如图26所示的结果。可以看出3个图上均有明显的条带状低阻异常,符合采空巷道特征。该异常均出现在3个钻孔孔深30 m之后,异常走向与2号孔基本平行。异常幅值与该异常和钻孔的距离存在显著相关性,图26(a)中的异常幅值最强,图26(b),(c)中的异常幅值较弱。

图26 3个钻孔实测数据反演结果
Fig.26 Inversion results of measured data from 3 boreholes
综合3个钻孔的反演结果,通过交汇定位可基本确定低阻异常体位置,得到如图27所示的积水采空巷道平面解释结果图。相比调查结果,积水采空巷道位置更偏北,角度也向北偏转更大,距离掘进工作面距离比预计的60 m小一半,仅有30 m。

图27 15103工区探测结果平面示意
Fig.27 Schematic diagram of detection results for 15103 work area
本次物探工作结果提交后,矿方邀请专家召开了会议讨论,认为物探成果可靠,立即采取措施,停止掘进,做好防治水准备工作,并重新设计了开切眼和工作面。可见,巷道-钻孔瞬变电磁二维拟地震反演方法为矿方安全掘进提供了技术支撑,为矿方下一步工作的决策提供了可靠依据。
4 结 论
(1)在距离异常体较近位置观测可获得更强的异常体响应,巷道-钻孔瞬变电磁工作装置有利于提高低阻异常体的探测精度,但测量曲线已不再符合单调衰减特征,其视电阻率定义非常困难。
(2)传统的分时段波场反变换和全时段波场反变换算法均能将瞬变电磁数据转换为虚拟波场数据,且各有长处和不足,基于相关叠加的滑动时窗波场反变换算法结合了2者的优势,又规避了各自的缺陷,波场转换效果更优。
(3)“一发多收”二维装置下瞬变电磁虚拟波场数据特征与地震单炮记录特征不同,不是双曲线形态,而是直线形态,且记录点与接收点相同,据此得出的动校正算法,可将“一发多收”二维装置虚拟波场数据转化为“自激自收”一维数据,之后可采用较为成熟的全波形反演方法对其实现高精度的拟地震反演成像。
(4)数值模拟和物理模拟对本文提出的方法做了充分的检验,反演结果与模型吻合度较高,说明巷道-钻孔瞬变电磁拟地震反演方法能够突出钻孔周围异常特征,扩大钻孔有效控制范围。
(5)井下巷道空间内的探测实例通过多个钻孔的综合探测,精细解释了一条威胁矿方安全生产的积水采空巷道,通过与前期调查结果的对比,证明巷道-钻孔瞬变电磁拟地震反演方法能提高采空巷道这类小目标体的探测准确率,对煤矿安全生产决策具有重要意义。
[1] DU Wenfeng,PENG Suping,ZHU Guowei,et al.Time-lapse geophysical technology-based study on overburden strata changes induced by modern coal mining[J].International Journal of Coal Science & Technology,2014,1(2):184-191.
[2] 刘菁华,王祝文,朱士,等.煤矿采空区及塌陷区的地球物理探查[J].煤炭学报,2005,30(6):715-719.
LIU Jinghua,WANG Zhuwen,ZHU Shi,et al.The geophysical exploration about exhausted area and sinking area in coal mine[J].Journal of China Coal Society,2005,30(6):715-719.
[3] 程建远,孙洪星,赵庆彪,等.老窑采空区的探测技术与实例研究[J].煤炭学报,2008,33(3):251-255.
CHENG Jianyuan,SUN Hongxing,ZHAO Qingbiao,et al.The detection technology of excavated region in coal mine and case study[J].Journal of China Coal Society,2008,33(3):251-255.
[4] 陈卫营,薛国强.瞬变电磁法多装置探测技术在煤矿采空区调查中的应用[J].地球物理学进展,2013,28(5):2709-2717.
CHEN Weiying,XUE Guoqiang.Application on coal-mine voids detection with multi-device TEM technology[J].Progress in Geophysics,2013,28(5):2709-2717.
[5] 苏彦丁.瞬变电磁法在山西某煤矿采空巷道探测中的应用[J].勘察科学技术,2015(5):55-57,60.
SU Yanding.Application of transient electromagnetic method in goaf roadway detection in a coal mine in Shanxi Province[J].Site Investigation Science and Technology,2015(5):55-57,60.
[6] 王季.反射槽波探测采空巷道的实验与方法[J].煤炭学报,2015,40(8):1879-1885.
WANG Ji.Experiment and method of void roadway detection using reflected in-seam wave[J].Journal of China Coal Society,2015,40(8):1879-1885.
[7] 范涛,赵兆,吴海,等.矿井瞬变电磁多匝回线电感影响消除及曲线偏移研究[J].煤炭学报,2014,39(5):932-940.
FAN Tao,ZHAO Zhao,WU Hai,et al.Research on inductance effect removing and curve offset for mine TEM with multi small loops[J].Journal of China Coal Society,2014,39(5):932-940.
[8] MACNAE J,STALTARI G.Classification of sign changes in Borehole TEM decays[J].Exploration Geophysics,1987,18:331-339.
[9] 徐正玉,杨海燕,邓居智,等.垂直接触带影响下地-井瞬变电磁响应研究[J].地球物理学进展,2015,30(3):1345-1353.
XU Zhengyu,YANG Haiyan,DENG Juzhi,et al.Research on response of down-hole TEM by vertical sheet[J].Progress in Geophysics,2015,30(3):1345-1353.
[10] 武军杰,李貅,智庆全,等.电性源地-井瞬变电磁法三分量响应特征分析[J].地球物理学进展,2017,32(3):1273-1278.
WU Junjie,LI Xiu,ZHI Qingquan,et al.Analysis of three component TEM response characteristic of electric source dill hole TEM[J].Progress in Geophysics,32(3):1273-1278.
[11] WEST R C,WARD S H.The borehole transient EM of a three-dimensional fractured zone in a conductive half space[J].Geophysics,1988,53:1469-1478.
[12] 孟庆鑫,潘和平.地-井瞬变电磁响应特征数值模拟分析[J].地球物理学报,2012,55(3):1046-1053.
MENG Qingxin,PAN Heping.Numerical simulation analysis of surface-hole TEM responses[J].Chinese Journal of Geophysics,2012,55(3):1046-1053.
[13] 杨海燕,徐正玉,岳建华,等.覆盖层下三维板状体地-井瞬变电磁响应[J].物探与化探,2016,40(1):190-196.
YANG Haiyan XU Zhengyu,YUE Jianhua,et al.3D inclined conductor behavior of down-hole transient electromagnetic method with overburden layer[J].Geophysical and Geochemical Exploration,2016,40(1):190-196.
[14] BUSELLI G,LEE S K.Modelling of drillhole TEM responses from multiple targets covered by a conductive overburden[J].Exploration Geophysics,1996,27:141-153.
[15] DYCK A V,WEST G F.The role of simple computer models in interpretation of wideband,drill-hole electromagnetic surveys in mineral exploration[J].Geophysics,1984,49:957-980.
[16] 张杰.地-井瞬变电磁异常特征分析及矢量交会解释方法研究[D].北京:中国地质大学(北京),2009.
ZHANG Jie.Analysis of anomalous character and study vector intersection for downhole transient electromagnetic method[D].Beijing:China University of Geosciences(Beijing),2009.
[17] HEE J K,KI H L,MICHAEL W A.Fast inversion method for interpreting borehole electromagnetic data[J].Earth Planets Space,2003,55:249-254.
[18] 杨毅,邓晓红,张杰,等.一种井中瞬变电磁异常反演方法[J].物探与化探,2014,38(4):855-859,864.
YANG Yi,DENG Xiaohong,ZHANG Jie,et al.A borehole TEM anomaly inversion method[J].Geophysical and Geochemical Exploration,2014,38(4):855-859,864.
[19] VELLA L.Taking downhole EM underground at hill 50 decline mount magnet Western Australia[J].Exploration Geophysics,1997,28:141-146.
[20] 王世睿.隧道掌子面-钻孔瞬变电磁超前探测方法与试验研究[D].济南:山东大学,2016.
WANG Shirui.Research on tunnel face-borehole transient electromagnetic method and experiment for advanced detection[D].Jinan:Shandong University,2016.
[21] 孙怀凤,程铭,宿传玺,等.隧(巷)道掘进工作面-钻孔瞬变电磁超前探测方法物理模拟试验研究[J].煤炭学报,2017,42(8):2110-2115.
SUN Huaifeng,CHENG Ming,SU Chuanxi,et al.Tunnel face-borehole transient electromagnetic method and its physical experimental studies[J].Journal of China Coal Society,2017,42(8):2110-2115.
[22] 范涛.孔巷瞬变电磁动源定接收方法探测采空区试验[J].煤炭学报,2017,42(12):3229-3238.
FAN Tao.Experimental study on the exploration of coal mine goaf by dynamic source and fixed reception Roadway-Borehole TEM detection method[J].Journal of China Coal Society,2017,42(12):3229-3238.
[23] 陈丁,程久龙,王阿明.矿井全空间孔中瞬变电磁响应积分方程法数值模拟研究[J].地球物理学报,2018,61(10):4182-4193.
CHEN Ding,CHENG Jiulong,WANG Aming.Numerical simulation of drillhole transient electromagnetic response in mine roadway whole space using integral equation method[J].Chinese Journal of Geophysics,2018,61(10):4182-4193.
[24] LEE K H,LIU G,MORRISON H F.A new approach to modeling the electromagnetic response of conductive media[J].Geophysics,1989,54(6):1180-1192.
[25] 戚志鹏,李貅,吴琼,等.从瞬变电磁扩散场到拟地震波场的全时域反变换算法[J].地球物理学报,2013,56(10):3581-3595.
QI Zhipeng,LI Xiu,WU Qiong,et al.A new algorithm for full-time-domain wave-field transformation based on transient electromagnetic method[J].Chinese Journal of Geophysics,2013,56(10):3581-3595.
[26] 范涛,程建远,王保利,等.应用瞬变电磁虚拟波场成像方法检测井下煤层气水力压裂效果的试验研究[J].煤炭学报,2016,41(7):1762-1768.
FAN Tao,CHENG Jianyuan WANG Baoli,et al.Experimental study on imaging method of TEM pseudo wave-field to detect the effect of underground coal-bed gas hydraulic fracturing[J].Journal of China Coal Society,2016,41(7):1762-1768.
[27] 李貅,薛国强,宋建平,等.从瞬变电磁场到波场的优化算法[J].地球物理学报,2005,48(5):1185-1190.
LI Xiu,XUE Guoqiang,SONG Jianping,et al.An optimize method for transient electromagnetic field-wave field conversion[J].Chinese Journal of Geophysics,2005,48(5):1185-1190.
[28] 范涛,鲁晶津,王冰纯,等.瞬变电磁虚拟波场反演法在井下超前探测中的应用[J].煤炭科学技术,2017,45(10):8-15,47.
FAN Tao,LU Jingjin,WANG Bingchun,et al.Inversion method of transient electromagnetic virtual wave-field applied to advance detection in underground mine[J].Coal Science and Technology,2017,45(10):8-15,47.
[29] 朱宏伟,李貅,张军,等.瞬变电磁法三维拟地震成像信息提取技术[J].地球物理学进展,2010,25(5):1648-1656.
ZHU Hongwei,LI Xiu,ZHANG Jun,et al.Information collecting technology in 3D pseudo-seismic imaging of transient electromagnetics[J].Progress in Geophysics,2010,25(5):1648-1656.
[30] 薛国强,李貅,戚志鹏,等.瞬变电磁拟地震子波宽度压缩研究[J].地球物理学报,2011,54(5):1384-1390.
XUE Guoqiang,LI Xiu,QI Zhipeng,et al.Study of sharpening the TEM pseudo-seismic wave-form[J].Chinese Journal of Geophysics,2011,54(5):1384-1390.
[31] 范涛.TEM虚拟波场三维连续速度分析及其在隧道超前预报中的应用[J].物探与化探,2011,35(2):243-247.
FAN Tao.A 3D continuous velocity analysis of tem fictitious wave-field and its application to tunnel advanced prediction[J].Geophysical and Geochemical Exploration,2011,35(2):243-247.
[32] 范涛,程建远,王保利,等.瞬变电磁虚拟波场成像方法及其对未爆弹探测的试验研究[J].地球物理学进展,2016,31(5):2326-2332.
FAN Tao,CHENG Jianyuan,WANG Baoli,et al.Imaging method of TEM pseudo wave field and application of unexploded ordnance detection[J].Progress in Geophysics,2016,31(5):2326-2332.
[33] TAE J,JUNG H S,HEE J K,et al.Electromagnetic travel time tomography using approbobility wave-field transform[J].Geophysics,2002,67(3):67-69.
[34] 李貅,戚志鹏,薛国强,等.瞬变电磁虚拟波场的三维曲面延拓成像[J].地球物理学报,2010,53(12):3005-3011.
LI Xiu,QI Zhipeng,XUE Guoqiang,et al.Three dimensional curved surface continuation image based on TEM pseudo wave-field[J].Chinese Journal of Geophysics,2010,53(12):3005-3011.
[35] 李貅,薛国强,刘银爱,等.瞬变电磁合成孔径成像方法研究[J].地球物理学报,2012,55(1):333-340.
LI Xiu,XUE Guoqiang,LIU Yinai,et al.A research on TEM imaging method based on synthetic-aperture technolog[J].Chinese Journal of Geophysics,2012,55(1):333-340.
