机械断裂事故中约80%为机械的疲劳失效问题[1],机械零部件疲劳载荷谱的编制是机械设计及疲劳寿命分析的基础[2-3],因此对机械零部件进行疲劳载荷谱编制具有重要意义。
目前关于航空、汽车、船舶、农业机械等领域的载荷谱研究取得了一定成果:文献[4]根据飞机起落架的着陆方式,提出一种飞机起落架载荷谱编制的新方法;文献[5]以某轿车摆臂载荷为对象,提出一种考虑强化载荷的载荷谱编制方案;文献[6]利用随机非线性疲劳裂纹样本,编制出船舶结构载荷加载谱;文献[7]根据采集的典型工况的传动载荷信号,利用分段处理方法,对装载机传动系的载荷谱进行编制。而针对煤矿机械,尤其是掘进机油缸的实测载荷谱研究相对匮乏。
掘进机是煤矿井下综掘工作面重要的工作设备,其摆动截割动作主要依靠液压油缸得以实现,井下恶劣的工作环境和复杂多变的外载荷往往会导致油缸发生疲劳失效。油缸载荷谱可以反映油缸工作载荷情况,是油缸疲劳强度计算和可靠性分析的前提和依据,是对油缸进行计算机辅助设计的先决条件,也是作为理论分析和疲劳试验的基础。
笔者利用前期研发的大容量数据记录仪(黑匣子),解决了煤矿井下无法长期采集掘进机工作数据这一行业难题[8],成功获取掘进机在井下长达2个月的工作载荷数据。对采集到的EBZ160型掘进机回转油缸压力数据进行提取处理和雨流计数统计,得到回转油缸载荷幅值与均值的分布规律,并绘制出回转油缸载荷谱。本文研究可为EBZ160型掘进机回转油缸载荷值的模拟提供数据基础,还可为油缸的疲劳试验提供载荷信息,这些基础信息对油缸寿命预测与设计具有重要意义。
1 载荷数据的测取
由于煤矿井下特殊的环境,并不是所有的载荷类型都能直接测取和存储。在前期研发的大容量数据记录仪(黑匣子)逐渐成熟的基础上,实时采集和储存的掘进机相关工作载荷数据成为可能。压力变送器与黑匣子通过掘进机的主控单元相连接,利用压力变送器测取油缸油压载荷数据,通过掘进机主控单元传输到黑匣子中存储[9]。由于掘进机电控箱空间有限,将黑匣子和本安电源放置在本安型控制箱中,安装在掘进机司机驾驶位置的后方,如图1所示。测试的EBZ160掘进机服役于冀中能源邢东矿1100南部采区集中配电巷,巷道为全煤巷,经过2个月井下的数据采集存储,获得了大量有效工作载荷数据。

图1 黑匣子的安装位置
Fig.1 Install location of black box
考虑到在油缸内直接加装油压传感器会引起油缸漏油,这样会给掘进机使用带来很大麻烦,所以采取在油路里加装压力变送器的方法来采集油压载荷。根据井下煤安规程,采用BYD-60型矿用隔爆型压力变送器,如图2所示,回转油缸载荷测试连接方案如图3所示。截割头水平摆动截割工作时,压力变送器能够分别检测到回转油压载荷并采集,对于左右2个回转油缸而言表现为推动回转台与拉动回转台交替运动,左右2个回转油缸工作原理相同且结构上呈对称分布[10],分析其中一个即可,本文选取左回转油缸载荷进行分析。

图2 压力变送器实物
Fig.2 Pressure transmitter picture

图3 回转油缸载荷测试方案连接
Fig.3 Load test scenario of rotary cylinder
2 载荷数据的预处理
测试系统的工作环境十分恶劣,因此测取的数据中不可避免的存在异常峰值点[11-12],这些异常峰值点会严重干扰数据的分析。为了获取反映回转油缸载荷变化规律的真实信号,根据数据的特点,采用幅值门限法去除信号中的异常峰值点,为后续载荷数据分析和载荷谱编制奠定基础。
图4为测取的回转油缸拉动载荷时间历程图(局部),数据的采样频率为1 Hz。
图4 测取的回转油缸拉动载荷时间历程图(局部)
Fig.4 Time history of rotary cylinder pull load(part)
为获得回转油缸载荷谱,必须对测取的载荷进行预处理,提取工作时回转油缸载荷的时间历程,由于压力变送器测得的工作载荷位于平衡阀之后,根据平衡阀工作原理[13],测得的大于5 MPa的载荷才为真正的工作载荷,同时掘进机停机段、截割头空载段及工作异常段等无效数据需剔除。为使获得的载荷谱具有典型性、概括性和集中性,提取的载荷时间历程必须具有足够的代表性,尽可能在统计上使可能发生的重要事件得到充分地呈现[14]。
对回转油缸拉动载荷数据进行预处理之后,取3组等时间长度的载荷数据进行时域统计,见表1。
表1 3组回转油缸拉动载荷的时域统计
Table 1 Three sets of time-domain statistics of rotary cylinder pull load
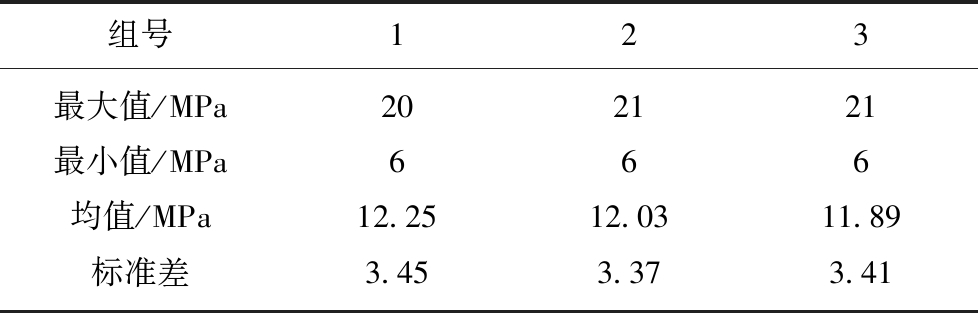
组号123最大值/MPa202121最小值/MPa666均值/MPa12.2512.0311.89标准差3.453.373.41
由表1可知,3组回转油缸拉动载荷数据的均值和标准差变化不大,基本保持在一个稳定水平,由此可以判断回转油缸载荷数据是平稳的。掘进机工作时回转油缸运动过程较简单,拉动—静止—推动交替循环进行,由此可以判断回转油缸载荷数据是各态历经的。由油缸载荷的平稳性和各态历经性检验得知,可以任取一个时间足够长或作业次数足够多的油缸载荷样本在一定统计误差下代替母体,预处理后的回转油缸拉动载荷样本数据如图5所示。
图5 预处理后的回转油缸拉动载荷样本数据
Fig.5 Pre-processed sample data of rotary cylinder pull load
3 随机载荷历程的统计处理
油缸在工作过程中,每次测得的载荷时间历程都不相同,由于这种不确定性,无法将该结果直接应用于理论分析和工程实践,所以需对预处理后的载荷样本数据进行统计处理,得到反映油缸载荷变化规律的真实历程。
3.1 基于雨流计数法的统计计数
计数法分为单参数计数法和双参数计数法,单参数计数法操作简单,但在计数中会丢失载荷的先后次序、载荷中值等一些有价值的参数,在疲劳寿命预测时精度会受到较大影响,因此选用双参数计数法。雨流计数法作为一种应用广泛的双参数计数法[15],在计数原理上与工作载荷对金属零部件的循环应力应变较相似,因此采用雨流计数法对回转油缸载荷样本数据进行统计计数。
雨流计数法的主要步骤为数据压缩和循环数提取[16],其中数据压缩把原始载荷数据处理成便于统计循环数的数组,在进行数据压缩时样本数据中最重要的信息是转折点处载荷的峰谷值大小和顺序,通常连续的随机载荷过程与载荷历程的时间是没有关系的[17],转折点数据可描述真实载荷序列,提取转折点压缩载荷数据是进行载荷统计计数的前提,提取转折点的原理如图6所示。

图6 转折点提取原理
Fig.6 Schematic of turning point extraction
对压缩处理后的回转油缸拉动载荷进行循环数提取,得到雨流计数矩阵,即幅值、均值与频次联合分布的三维柱状图,如图7所示。

图7 回转油缸拉动载荷雨流矩阵
Fig.7 Rainflow matrix of rotary cylinder pull load
3.2 幅均值概率分布及检验
为进行载荷频次外推,需得到随机载荷总体的概率分布函数。根据雨流计数矩阵获得随机载荷峰值与均值的累计频次直方图,结合大量统计分析经验,对幅值和均值概率分布分别作威布尔分布和正态分布的假设。
采用威布尔概率纸图解法对幅值数据进行威布尔分布检验,如图8所示,根据检验结果幅值服从威布尔分布。
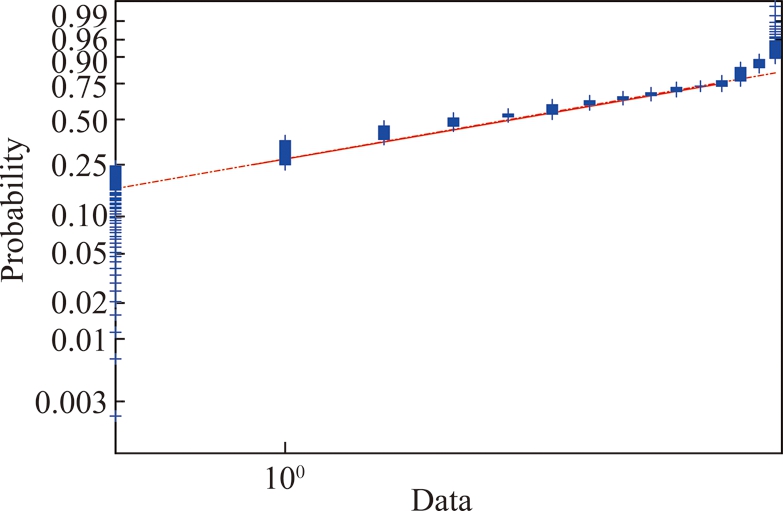
图8 载荷幅值威布尔分布检验
Fig.8 Weibull distribution test for load amplitude
载荷幅值用变量x表示,其概率分布密度函数为
(1)
式中,α为威布尔分布形状参数;β为威布尔分布尺度参数;ε为威布尔分布阈值参数。
在Matlab中对幅值进行威布尔分布拟合,如图9所示。得到幅值分布参数的估计值,在95%置信区间内,幅值服从形状参数为1.156,尺度参数为3.345的威布尔分布。
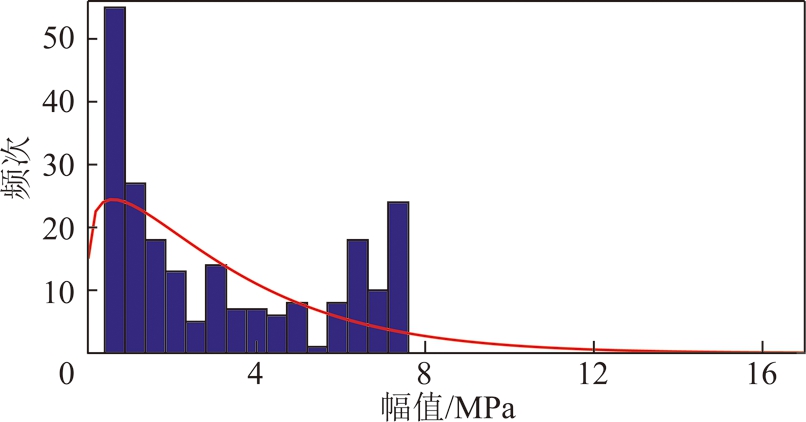
图9 载荷幅值的频次直方图与概率分布拟合
Fig.9 Frequency histogram and probability distribution fit of load amplitude
利用非参数检验[18]对均值进行检验是否服从正态分布,h=0表示接受正态分布,说明均值服从正态分布。在Matlab中对均值进行正态分布拟合,发现拟合曲线并不能很好的包括靠近极大值的数据,为使编制的载荷谱更能代表油缸真实工作情况,进一步对回转油缸载荷均值-频次直方图进行分析,发现存在多个均值出现频次集中的现象,因此提出一种三模态正态概率分布模型来描述的回转油缸载荷均值,用变量y表示载荷均值,其概率分布密度函数为
(2)
式中,wi为权重系数,具有约束关系w1+w2+w3=1;μi为第i个正态分布均值;σi为第i个正态分布的标准差。
根据频次直方图形状给出模型的初始参数,以全局最优化为目标,采用最小二乘迭代算法对回转油缸载荷均值非线性拟合,得到如图10所示的拟合曲线和表2所示的模型参数,拟合曲线可以较好的反映载荷均值统计特征,并呈现出显著的三模态正态分布。
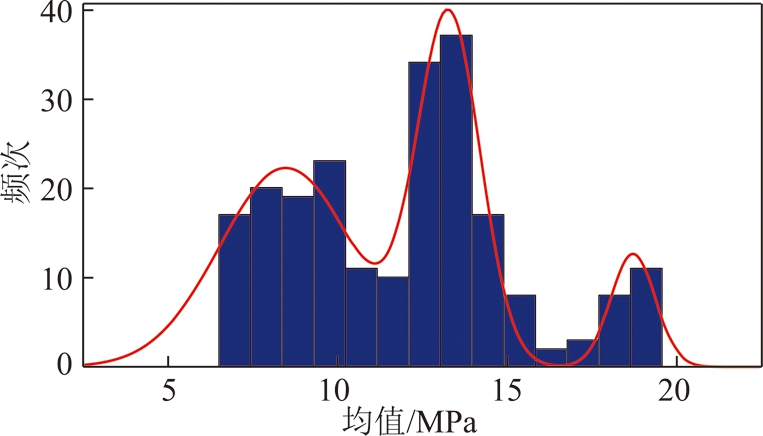
图10 载荷均值的频次直方图与三模态分布拟合
Fig.10 Frequency histogram and three modal distribution fitting of load mean
表2 载荷均值的三模态分布拟合结果
Table 2 Three modal distribution fitting result of load mean
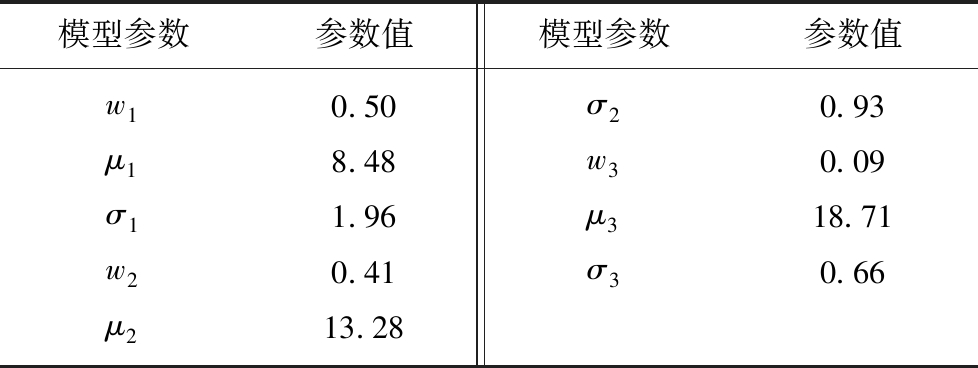
模型参数参数值模型参数参数值w10.50σ20.93μ18.48w30.09σ11.96μ318.71w20.41σ30.66μ213.28
利用卡方检验[19],对幅值和均值的独立性进行检验,原假设为H0:x与y相互独立。将幅值和均值分级,幅值分为r级,ni(i=1,2,…,r)表示幅值落在第i级的频次;均值分为s级,nj(j=1,2,…,s)表示均值落在第j级的频次;nij表示幅值落在第i级、均值落在第j级的频次;n为样本容量。若H0成立,则应该满足下式:
(3)
构造统计量:
(4)
根据Pearson定理,若H0成立,则当n→∞时,χ2的分布收敛到χ2((r-1)(s-1))。至少在样本容量n较大的时候,可近似地认为χ2~χ2((r-1)(s-1)),从而构造否定域。事实上,当H0成立时,χ2不应该太大,所以给定检验水平α,否定域为![]() 以回转油缸拉动载荷为例进行计算,r=s=15,取α=0.05,查χ2分布概率表得
以回转油缸拉动载荷为例进行计算,r=s=15,取α=0.05,查χ2分布概率表得![]() 统计量的观测值为
统计量的观测值为
(5)
因为
(6)
故在检验水平0.05条件下,原假设H0成立,得到x和y相互独立,故幅均值联合概率分布密度为
f(x,y)=f(x)·f(y)
(7)
4 载荷谱的编制
4.1 幅均值二维谱的编制
由于被测的载荷数据只能代表油缸设计寿命中很小的一部分,它不足以代表母体中少数最大载荷的发生情况,因此编制载荷谱时有必要对载荷频次进行外推。经验理论一般认为106次载荷循环对于包括很少发生的最严重情况在内的全部载荷具有足够的代表性,相当于疲劳极限寿命,因此必须对回转油缸载荷数据合成的累积频次扩展到106次循环,以便得到在总寿命中可能出现的更加真实的载荷历程[20-21]。回转油缸载荷由拉动和推动载荷共同组成,推拉工况作业时间比例约为1∶1,故拉动和推动载荷各自累积频次扩展到5×105次循环。样本拉动载荷的频次通过式(8)外推到整个生命周期。
N′=kN
(8)
式中,N′为外推后的拉动载荷累积频次数;N为测试样本的拉动载荷频次数;k为扩展倍数,其中k=5×105/N1,N1为测试拉动载荷样本雨流计数后的载荷循环。
由于载荷幅值和均值相互独立,并分别服从威布尔分布和正态分布,因此求载荷的极值就可以转化为求幅值和均值的极值,幅值与均值的极值计算公式如式(9),(10)所示。
幅值极值:
(9)
式中,P为回转油缸拉动载荷频率密度函数与极值发生概率。
均值极值:
(10)
式中,μip为第i个正态分布的标准正态偏差。
CONOVER[22]发现将载荷谱分成8级可以精确地反映其疲劳效应,采用8级载荷等级可以较好地代表连续载荷累积频数曲线,由于较大的载荷幅值对疲劳寿命影响较大,因而分级时把较大幅值分得密些。根据式(9),(10)分别得到幅、均值的极值后,对幅值采用不等间隔分级法分为8级,对均值采用等间隔分级法分为8级,根据式(11)得到对应幅均值的各级循环次数n,形成8×8级二维载荷谱,表3为回转油缸拉动载荷二维载荷谱。
(11)
式中,n为对应幅均值的各级循环次数;a1,a2分别为载荷幅值的积分上、下限;m1,m2分别为载荷均值的积分上、下限;f(x,y)为幅均值联合概率分布密度。
表3 回转油缸拉动载荷数据二维载荷谱(频次)
Table3 Two-dimensional load spectrum of the rotary cylinder pull load
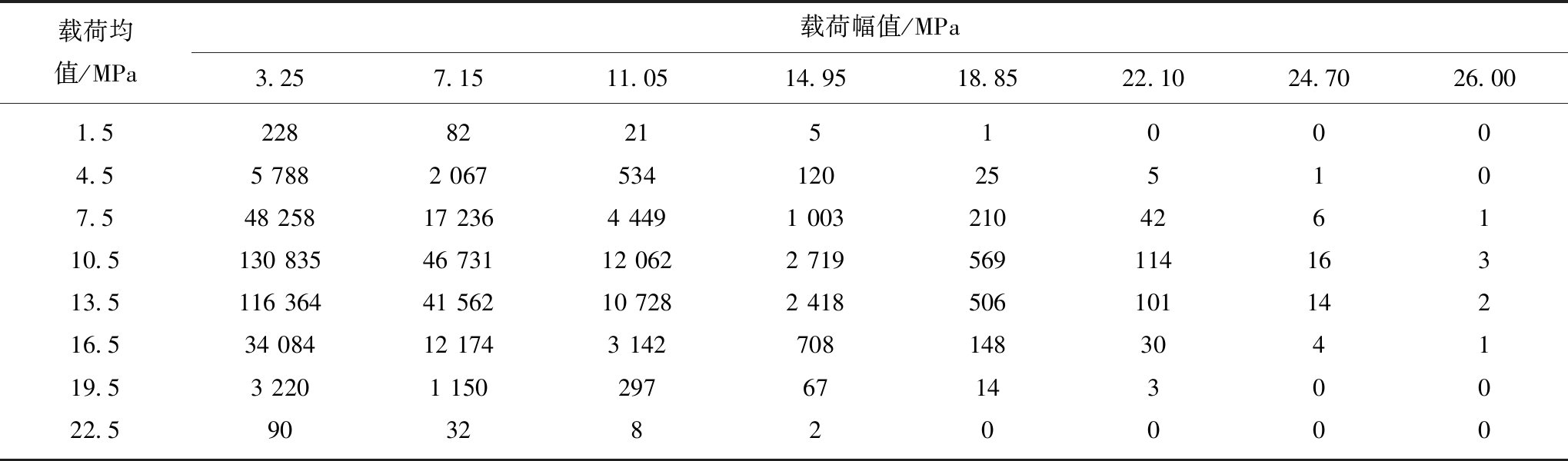
载荷均值/MPa载荷幅值/MPa3.257.1511.0514.9518.8522.1024.7026.001.52288221510004.55 7882 067534120255107.548 25817 2364 4491 003210426110.5130 83546 73112 0622 71956911416313.5116 36441 56210 7282 41850610114216.534 08412 1743 142708148304119.53 2201 150297671430022.59032820000
4.2 疲劳试验程序加载谱的编制
国内疲劳试验多采用程序疲劳试验,根据疲劳累积损伤理论,以外推后的雨流计数矩阵(幅均值二维载荷谱)为数据基础,编制程序加载谱。八级程序载荷谱是典型的程序加载谱。载荷幅值的大小是疲劳损伤的主要决定因素,在很大程度上反应了疲劳寿命估算和疲劳试验结果的可靠性与准确性,采用Goodman等寿命方法,将二维载荷谱等效为均值为0 MPa的一维程序加载谱。等效方程为
(12)
式中,Pa为载荷幅值;Peq为等效载荷幅值;Pm为载荷均值;Pb为极限压力载荷。
等效载荷幅值采用非等间隔法分为8级,8级载荷水平的大小是由等效载荷幅值最大值乘比例系数得到的
Pj=βjPeqmax (j=1,2,3,…,8)
(13)
式中,Pj为各级载荷幅值;Peqmax为等效载荷幅值最大值;βj为比例系数,通常设为1,0.95,0.85,0.725,0.575,0.425,0.275,0.125[23]。
根据式(12)将幅均值二维载荷谱中的每个载荷循环次数进行等效转换,成为对称载荷循环;然后,对转换后的循环进行累积计数,形成每个载荷幅上的累积循环数;最后,根据式(13)将连续累计曲线转换为8级程序加载谱,得到等效幅值和频次。回转油缸拉动载荷数据一维程序加载谱见表3。
5 结 论
(1)利用黑匣子采集到掘进机回转油缸载荷数据,通过对载荷时间历程进行分析和预处理,得到回转油缸载荷基于时间的一维工作载荷谱,真实地再现了煤矿井下载荷的复杂性与随机性。
表3 回转油缸拉动载荷数据一维载荷谱
Table 3 One-dimensional load spectrum of the rotary cylinder pull load
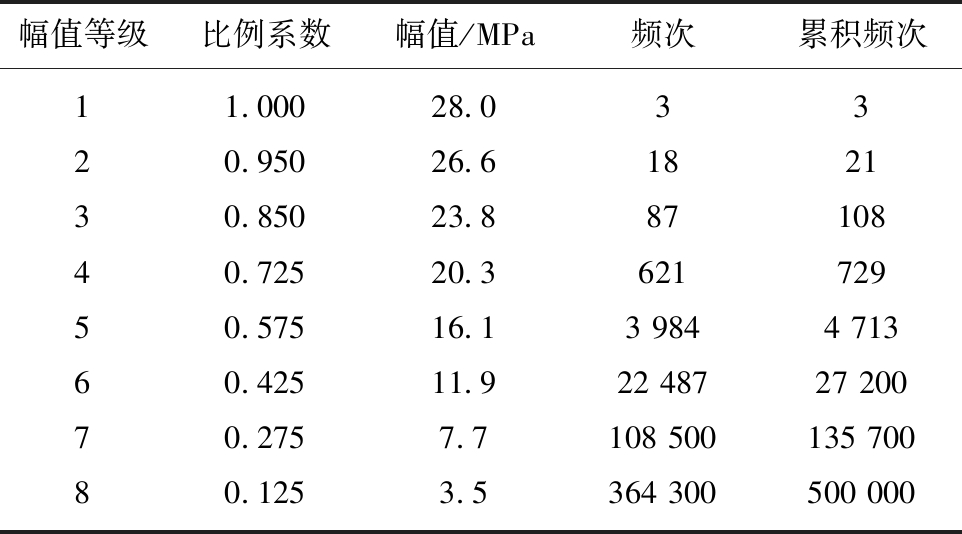
幅值等级比例系数幅值/MPa频次累积频次11.00028.03320.95026.6182130.85023.88710840.72520.362172950.57516.13 9844 71360.42511.922 48727 20070.2757.7108 500135 70080.1253.5364 300500 000
(2)基于雨流计数法,统计分析得到回转油缸拉动载荷幅值服从形状参数为1.156,尺度参数为3.345的威布尔分布,拟合出均值的三模态正态概率分布模型,实现回转油缸载荷信息的准确识别。利用卡方检验,得到在检验水平0.05的条件下,幅值和均值相互独立。
(3)根据回转油缸推拉工况作业时间比例进行频次外推,利用二维概率分布函数,编制了回转油缸拉动载荷8×8级二维载荷谱。通过工况合成与等效转换,编制了疲劳试验加载谱,为回转油缸疲劳寿命试验提供加载条件,为回转油缸疲劳设计提供依据。
[1] 叶南海.机械疲劳寿命预测与可靠性设计关键技术研究[D].长沙:湖南大学,2012.
YE Nanhai.Key technology research for mechanism fatigue life prediction and reliability design[D].Changsha:Hunan University,2012.
[2] 高云凯,徐成民,方剑光.车身台架疲劳试验程序载荷谱研究[J].机械工程学报,2014,50(4):92-98.
GAO Yunkai,XU Chengmin,FANG Jianguang.Study on the programed load spectrum of the body fatigue bench test[J].Journal of Mechanical Engineering,2014,50(4):92-98.
[3] MIKHEEVSKIY S,GLINKA G,LEE E.Fatigue crack growth analysis under spectrum loading in various environmental conditions[J].Metallurgical & Materials Transactions A,2013,44(3):1301-1310.
[4] 刘克格,闫楚良.飞机起落架载荷谱实测与编制方法[J].航空学报,2011,32(5):841-848.
LIU Kege,YAN Chuliang.Load measurement and compilation of landing gear of airplane[J].Acta Aeronauticaet Astronautica Sinica,2011,32(5):841-848.
[5] 郑松林,梁国清,王治瑞,等.考虑低幅锻炼载荷的某轿车摆臂载荷谱编制[J].机械工程学报,2014,50(16):147-154.
ZHENG Songlin,LIANG Guoqing,WANG Zhirui,et al.Compilation of automotive lower control arm spectrum based on the low-amplitude training load[J].Journal of Mechanical Engineering,2014,50(16):147-154.
[6] HODAPP D P,COLLETTE M D,TROESCH A W.Stochastic nonlinear fatigue crack growth predictions for simple specimens subject to representative ship structural loading sequences[J].International Journal of Fatigue,2015,70:38-50.
[7] 张英爽,王国强,王继新,等.工程车辆传动系载荷谱编制方法[J].农业工程学报,2011,27(4):179-183.
ZHANG Yingshuang,WANG Guoqiang,WANG Jixin,et al.Compilation method of power train load spectrum of engineering vehicle[J].Transactions of the CSAE,2011,27(4):179-183.
[8] 杨健健,王丙军,姜海,等.基于SQLite数据库的掘进机状态信息存储的研究[J].工矿自动化,2012,38(12):105-108.
YANG Jianjian,WANG Bingjun,JIANG Hai,et al.Research of operation information storage of roadheader based on sqlite database[J].Industry and Mine Automation,2012,38(12):105-108.
[9] 李旭.悬臂式掘进机关键结构的力学特性研究[D].北京:中国矿业大学(北京),2017.
LI Xu.Research on mechanical properties of key structures on boom-type roadheader[D].Beijing:China University of Mining and Technology (Beijing),2017.
[10] 李旭,顾永正,吴淼.基于微分几何的掘进机工作机构运动学分析[J].煤炭学报,2016,41(12):3158-3166.
LI Xu,GU Yongzheng,WU Miao.Kinematics analysis of roadheader’s working mechanism based on differential geometry[J].Journal of China Coal Society,2016,41(12):3158-3166.
[11] CURRAN M,ZHENG K,GUPTA H,et al.Handling rack vibrations in FSO-based data center architectures[A].In 2018 International Conference on Optical Network Design and Modeling (ONDM)[C].2018:47-52.
[12] ZHENG K,CURRAN M,GUPTA H,et al.2018.Design of data center free-space optical network:Optical and mechanical considerations[A].In ASTFE Digital Library.Begel House Inc[C].2018.
[13] 李旭,王苏彧,吉晓冬,等.EBZ160型掘进机驱动油缸实测载荷分析[J].煤炭技术,2016,35(5):250-252.
LI Xu,WANG Suyu,JI Xiaodong,et al.Load analysis of driving cylinder for EBZ160 roadheader based on measured data[J].Coal Technology,2016,35(5):250-252.
[14] 马园园,谢里阳,林文强.液压支架随机载荷历程及Monte Carlo法的应用[J].东北大学学报(自然科学版),2014,35(1):93-96.
MA Yuanyuan,XIE Liyang,LIN Wenqiang.Random load history of hydraulic support and application of monte carlo method[J].Journal of Northeastern University (Natural Science),2014,35(1):93-96.
[15] 张吉桥.雨流计数法与概率分布拟合在疲劳寿命估算中的应用[J].广东工业大学学报,2010,27(1):82-85.
ZHANG Jiqiao.Application of rain-flow counting method and probability distribution fitting technique in the estimation of fatigue life[J].Journal of Guangdong University of Technology,2010,27(1):82-85.
[16] BISPING JR,BLEICHER C,WAGENER R,et al.Fatigue life approach for large components in heavy plant engineering based on rainflow counted local strains[J].Procedia Engineering,2015,101:43-51.
[17] 邢韵.EPB6280盾构机推进油缸载荷值的提取与分析[J].材料与冶金学报,2014,13(4):298-305.
XING Yun.Extraction and analysis on load values of push cylinder for EPB6280 shield machine[J].Journal of Materials and Metallurgy,2014,13(4):298-305.
[18] BORS AG,NASIOS N.Kernel bandwidth estimation for nonparametric modeling[J].IEEE Transactions on Systems Man & Cybernetics Part B:Cybernetics,2009,39(6):1543-1555.
[19] 武爱文,冯卫国,卫淑芝.概率论与数理统计[M].上海:上海交通大学出版社,2011.
[20] 刘岩,张喜逢,王振雨,等.载荷谱外推方法的对比[J].现代制造工程,2011(11):8-11.
LIU Yan,ZHANG Xifeng,WANG Zhenyu,et al.Contrast of extrapolations in compiling load spectrum[J].Modern Manufacturing Engineering,2011(11):8-11.
[21] 宫海彬,苏建,王兴宇,等.基于极值外推的高速列车齿轮传动装置载荷谱编制[J].吉林大学学报:工学版,2014,44(5):1264-1269.
GONG Haibin,SU Jian,WANG Xingyu,et al.Compiling method of load spectrum of high-speed train gear dirve system based on extreme value extrapolation[J].Journal of Jilin University:Engineering and Technology Edition,2014,44(5):1264-1269.
[22] CONOVER J C,JAECKEL H R,KIPPOLA W J.Simulation of field loading in fatique testing[J].Journal of Terramechanics,1966,3(3):101-102.
[23] 张英爽.装载机传动系载荷谱的测取与应用研究[D].长春:吉林大学,2014.
ZHANG Yingshuang.Research on the load spectra acquisition and application of loader powertrain[D].Changchun:Jilin University,2014.
