煤矿顶底板断裂、断层滑移或煤柱破裂均会诱导应力波(动载荷)产生，应力波传播作用于采场煤岩体，导致动力灾害发生[1-4]。煤岩体冲击动力学有助于揭示矿井受扰动而产生的动力灾害，因此煤岩体冲击动力学行为特征一直是研究的热点问题。
煤岩体冲击动力学主要借助于霍普金森压杆系统[5]来测试，自从KOLSKY[6]提出该系统以来，经过不断改进，SHPB技术取得了飞速发展，尤其在煤岩动力学测试方面[7-8]。煤岩动力学测试经历了一维动载和动静组合加载等阶段。单仁亮等[9]研究了一维动载下云驾岭煤矿无烟煤的动态本构特性，发现煤体初始弹性模量、屈服强度和极限强度均随着应变率的增加而增加;刘晓辉等[10]利用SHPB系统测试了不同应变率下煤岩冲击动力学特性，煤岩在低应变率下多呈轴向劈裂破坏，高应变率下呈现压碎破坏;夏开文和姚伟[11]研究了岩石在不同预拉伸应力下的拉伸强度，动态拉伸强度随着加载率的增加而增加;王其胜和李夕兵[12]测试了动静组合条件下花岗岩的力学特性，发现花岗岩破碎分形维数随着应变率的增加而增加;宫凤强等[13]开展了动静组合加载下砂岩的动力学特性试验研究，揭示了高应力下岩石的动态强度递增、岩爆发生和诱导致裂三者之间的相互转化机制;刘少虹等[14]讨论了动静组合加载煤样破坏特性，总结得出动静载荷下煤的强度反映抵抗动载能力的强弱，碎片的分形维数衡量动载冲击破坏剧烈程度。
关于煤岩体动力学研究，不仅在煤岩动力学特征方面取得许多成就，而且在煤岩动力学本构模型方面也取得了丰厚的成果。单仁亮等[15]建立了线性黏弹性模型，以此来表达无烟煤的显著塑性流动，两个不同松弛时间的Maxwel体分别表征无烟煤的高、低应变率响应;高文蛟等[16]提出了无烟煤压缩膨胀拉伸破坏模型，建立了该模型的动态强度理论计算关系式，阐述了动力学参数之间的定量关系;付玉凯等[17]基于弹塑性理论建立了损伤体黏弹性本构模型，模型拟合曲线与实测动态本构曲线具有较好的一致性，该模型对高应变率更加敏感;为了克服元件型建模的不足，王登科等[18]提出了一种强度型动态统计损伤本构模型，该模型参数数量较少，拟合精度较高，适用于表达煤体动力学行为;朱晶晶等[19]测试了单轴循环冲击下岩石的动力学特性并建立了动态统计损伤本构模型，该模型能够充分反映岩石强度与应变和应变率的关系;李夕兵和左宇军等[20-21]分析了动静组合加载条件下岩石系统的稳定性，建立了非线性动力学本构模型，动载荷幅值和频率超过一定值会引起岩石系统振幅的突跳进而引起破坏;刘少虹[22]采用时效损伤本构模型与尖点突变理论，推导了动静加载下煤岩组合系统的破坏判据、突跳位移以及释放总能量的数学关系，建立了动静载下组合煤岩系统的非线性动力学模型，揭示了煤岩体结构和动静载相互作用是影响动载诱发冲击地压的关键。
上述一维动载和动静载组合作用下煤岩体动力学行为及本构方程对于丰富和完善煤岩体动力学具有重要的理论意义。目前，关于三轴煤体在冲击载荷作用下的动力学特性鲜见报道，而井下煤岩体真实的应力环境是三向受力，因此有必要开展冲击载荷下三轴煤体动力学研究。笔者建立了三轴分离式霍普金森压杆试验系统，开展了三轴煤体冲击动力学实验，分析了冲击载荷下三轴煤体动态应力应变曲线、应变率效应等动力学特征，提出了冲击载荷下三轴煤体动力学本构模型，该模型充分考虑了轴向静载、围压和冲击载荷3种因素，并解释了其对动态强度和破坏应变等动力学特征的影响。
1 三轴SHPB试验
1.1 试验系统
自主搭建了煤岩三轴分离式霍普金森压杆试验系统(图1)。该系统由轴向加载子系统、围压加载子系统、冲击载荷加载子系统、应变采集子系统、测速子系统及缓冲装置等构成。冲击载荷加载子系统相比以往动力学测试系统有很大改进，不同于依靠氮气钢瓶加压发射子弹，本系统通过空压机压缩空气，通过压缩空气推动子弹撞击入射杆实现冲击载荷加载，既可以减少氮气使用，节约实验成本;又可以实现较大速率加载，最高可实现40 m/s的加载速率。
图1 煤岩三轴分离式霍普金森压杆试验系统
Fig.1 Split hopkinson press bar experimental system of triaxial coal or rock
煤岩冲击动力学系统的入射杆、透射杆、子弹均采用30Crmosini2a钢材制作，弹性模量210 GPa，纵波传播速度为5 100 m/s，杆径均为100 mm，入射杆、透射杆和子弹分别长5.0，3.0，0.4 m。应变片分别贴于入射杆和透射杆中间位置以采集撞击而产生的脉冲信号，每根杆上的应变片又呈对称布置。
1.2 试验原理及方案
三轴冲击动力学试验操作过程:① 试样放入三轴腔体，通过轴向加载装置将轴向静载加到预设压力;② 通过围压加载子系统将围压加到预设压力;③ 通过空压机向钢瓶压缩空气，调整冲击气压，同时调整好测速装置及应变数据采集软件，然后按下开关，发射子弹以施加冲击载荷。一次试验完成以后，必须先卸掉围压，再卸载轴向静载。
三轴冲击动力学测试原理与一维动载试验原理相同，仍是基于一维应力波假定和应力均匀化假设。通过入射杆和透射杆上的应变片采集试验过程中的应力波信号，进一步分离提取入射波εi(t)、反射波εr(t)和透射波εt(t)，基于应力波传播理论、一维应力假设和位移连续性，可推导出试样的平均应变率
应变(ε(t))和应力(σ(t))：
式中，C为应力波在弹性杆中传播的速度;L0为试样长度;E为弹性杆的弹性模量;A为弹性杆截面积;A0为试样截面积;t为应力波脉冲持续时间。
本试验所采用煤样经加工制成φ100 mm×50 mm的煤样，符合煤岩动力学测试长径比要求。为了减少压杆与试样之间的摩擦效应，选取两端平行度在0.02 mm公差范围内的试样，试验时并在两端涂抹黄油;为了减少离散效应，尽量选取密度和波速较接近的试样进行试验，所选试样的基本物理参数见表1。
本文主要测试分析冲击载荷下三轴煤体动力学特征，为了说明动力学特征的普遍性，随机选取轴向静载、围压和动载荷冲击速度组合测试不同条件下三轴煤体动态应力应变曲线及峰值强度和破坏应变随应变率的关系，试验方案见表1。
表1 基本物理参数及试验方案
Table 1 Basic physical parameters and test scheme
试样编号密度/(kg·m-3)波速/(m·s-1)轴向静载/MPa围压/MPa冲击速度/(m·s-1)11 2301 4120.771.803.5021 2201 5062.642.133.5331 2391 3023.015.729.4141 2141 4042.604.956.7551 2251 4203.814.8310.86
2 实测煤样动力学分析
2.1 应力应变曲线
不同轴向静载、围压和冲击速度组合加载下煤样的冲击结果见表2，煤样的动态应力应变曲线结果如图2所示。从动态应力应变曲线可以看出，相比静态加载，冲击应力应变曲线几乎不存在压密阶段，在加载初期，应力应变曲线很快进入线弹性阶段，一方面，预先加载轴向静态载荷，使得原生裂隙闭合，试样更加致密，再加之围压的限制变形作用，因此试样表现出完整弹性体的特征;另一方面，试样即使仍有未闭合的原生裂隙，由于冲击破坏试验过程时间较短，动态应力应变曲线不会表现出压密阶段特征。在线弹性阶段，应变在较小范围内变化，应力极速增加，动态弹性模量较大，且不同轴向静载、围压和冲击速度组合加载下试样的线弹性阶段基本重合，说明试样在不足以导致裂纹扩展的轴向静载和围压作用下，有助于试样表现出均一性特征。当应力达到峰值强度的60%～85%阶段时，应力应变曲线呈现“跃进”现象，即应力应变曲线斜率经历先减小又增大再减小的过程，这可能与碳在晶体微破裂中的作用有关[9]。进一步，应力增加直至峰值强度，试样破坏，应力下降。
表2 试验结果
Table 2 Test results
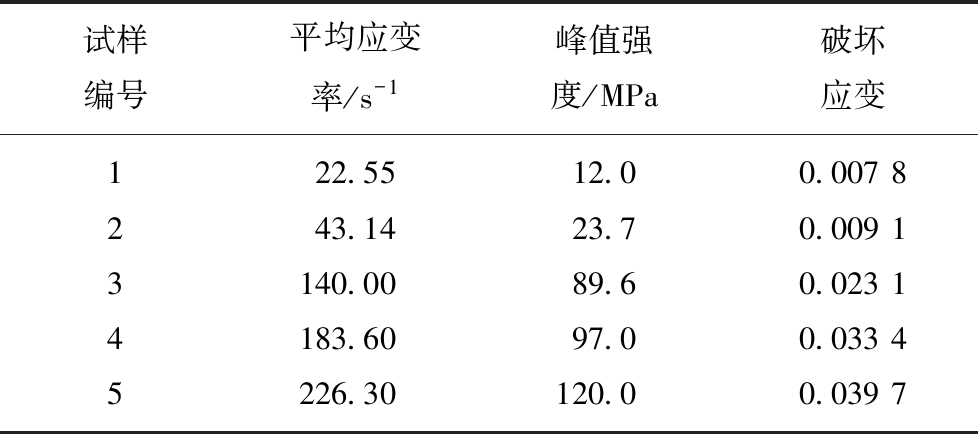
试样编号平均应变率/s-1峰值强度/MPa破坏应变122.5512.00.007 8243.1423.70.009 13140.0089.60.023 14183.6097.00.033 45226.30120.00.039 7
图2 应力应变曲线
Fig.2 Curves of stress-strain
2.2 动态峰值强度和试样平均应变率之间的关系
根据前人的研究结果，煤体材料的特征参数表现出较强的应变率相关性[9,12,17,19]。为了反映冲击载荷作用下三轴煤体材料的应变率效应，拟合了轴向静载、围压和冲击速度组合加载下各煤样峰值强度与平均应变率的关系，发现煤样峰值强度与平均应变率呈现很好的线性相关性，如图3所示。冲击载荷下三轴煤样动态峰值强度σ和平均应变率
拟合关系式为
拟合度高达97.28%，峰值强度随平均应变率呈线性增加。实验条件下的轴向静载、围压和冲击速度是任意组合的，应变率效应将这3种因素的作用归一化，它们对煤体动态强度的影响最终都反映在应变率上，只要轴向静载、围压和冲击速度组合使得煤体应变率增加，则冲击载荷作用下煤体动态强度也随之线性增加。
图3 峰值强度与平均应变率关系
Fig.3 Relationship between peak strength and average strain rate
2.3 破坏应变和试样平均应变率之间的关系
煤样动态应力应变曲线达到峰值时，试样开始破坏，因此峰值强度所对应的应变，这里称为破坏应变。同样，冲击载荷作用下三轴煤样的破坏应变与平均应变率呈现高度线性相关，拟合关系为
拟合度98.59%，随着平均应变率增加，破坏应变线性增加。而且本文通过轴向静载、围压和冲击速度的随机组合产生不同应变率，这样的试验条件更加证明了煤样特征参数应变率效应普适性。
图4 破坏应变和平均应变率的关系
Fig.4 Relationship between failure strain and average strain rate
3 三轴冲击载荷下动力学本构模型及验证
3.1 本构模型的建立
本文将岩石力学的强度理论与统计损伤理论，考虑轴向静载、围压、冲击载荷组合作用，推导三轴煤体冲击动力学本构模型。首先，作如下假定:① 煤体具有均一性，宏观表现为各向同性，即各向同性的损伤体;② 煤体破坏前服从胡克定律，即应力应变为线弹性变化，破坏后失去承载能力;③ 煤体微元体强度服从Weibull分布。
根据前述假定③，煤体各微元体强度遵循Weibull分布，其概率密度函数可以表示为
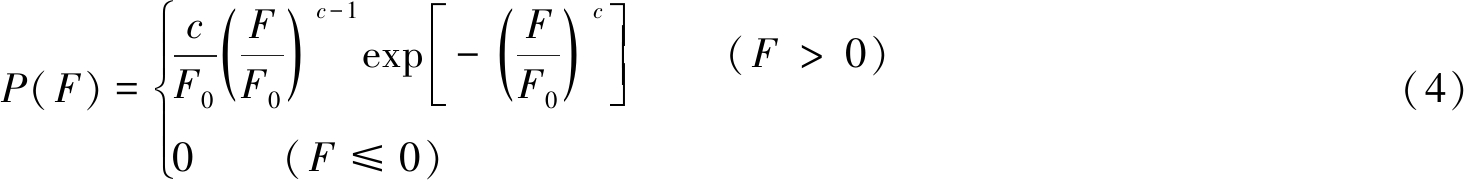
式中，F为煤体微元体强度的分布变量;c，F0为Weibull分布的表征参数，主要取决于煤体力学特性。
当煤体受载荷作用时，部分微元体将逐渐发生破坏，为了反映此渐变过程，在微元体统计分布假定的基础上，采用统计损伤变量。则在某一载荷作用下，统计损伤变量可以表示为
式中，D为统计损伤变量;Nf为某一载荷作用下已破坏微元数目;N为总的微元体数目。
在任意区间[F,F+dF]内破坏的微元数目可以表示为NP(x)dx，当外载荷从0增加到某一微元强度F时，破坏微元体数目为
将式(6)代入式(5)化简可得
由式(7)可得，损伤变量D与微元体强度F有关，而微元体强度与其所处的应力状态有关。为了体现复杂应力状态对煤体的影响，需考虑煤体的破坏准则，而Drucker-Prager(D-P)破坏准则同时考虑了中间主应力和静水压力作用，克服了M-C准则的主要弱点，而且适应于煤岩体材料，则基于该准则的煤体微元体强度为
式中，f(σ)为破坏准则;α0为煤中微元体的强度参数，与煤体材料黏聚力和内摩擦角有关;I1为应力张量的第一不变量;J2为应力偏量的第二不变量。
根据D-P准则：
I1=σ′1+σ′2+σ′3
(10)
式中，φ为内摩擦角，取煤样测试平均值35°;σ′1，σ′2，σ′3分别为损伤体有效应力，对应的名义应力分别为σ1，σ2，σ3。
三轴损伤煤体有效应力可表示为
σ′i=σi/(1-D) (i=1,2,3)
(12)
式中，下标i为应力方向，1为轴向，2和3为侧向。
本文所讨论的三轴煤体受轴向预应力加载，因此，轴向应力σ1包含两部分[11]，即
σ1=σd+σs
(13)
式中，σd为动载所施加的应力;σs为轴向静载所施加的预应力。
煤体在轴向载荷作用下，根据胡克定律，试样的轴向应变为
式中，ε1为轴向应变;ν为泊松比，取所选煤样实测平均值0.3。
由于三轴煤体冲击破坏实验系统，围压是均一的，即σ2=σ3，所以式(14)可简化为
将式(12)代入式(15)得
利用应变等效假设，可得三轴煤体冲击动力学本构关系为
σ1=Eε1(1-D)+2νσ3
(17)
进一步，结合式(7)，(13)和(17)，可得冲击载荷下三轴煤体统计损伤本构模型表达式:
该模型综合考虑了轴向静载、围压和冲击载荷等因素，从本构方程可以明显看出，围压有助于提高煤体的动态强度;轴向静载会加速煤体损伤，从而降低煤体的强度;而冲击载荷作用时间较短，煤体在瞬间表现为一个完整的弹性体，所以冲击载荷会提高煤体的弹性模量和动态强度;此本构方程所反映的三轴煤体本质特征与实验结果相吻合，且综合考虑了轴向静载、围压、和冲击载荷，有助于揭示三轴煤体动力学基本科学问题。
3.2 本构模型的验证
为了验证上述模型的正确性，以式(18)为基础，结合试验数据进行拟合，对比理论拟合曲线和试验曲线的重合性。依据上述建立的的模型关系式，确定F0和c是建立本构模型的关键。
根据D-P破坏准则，并基于式(8)，(10)～(13)和(16)可进一步推导出:
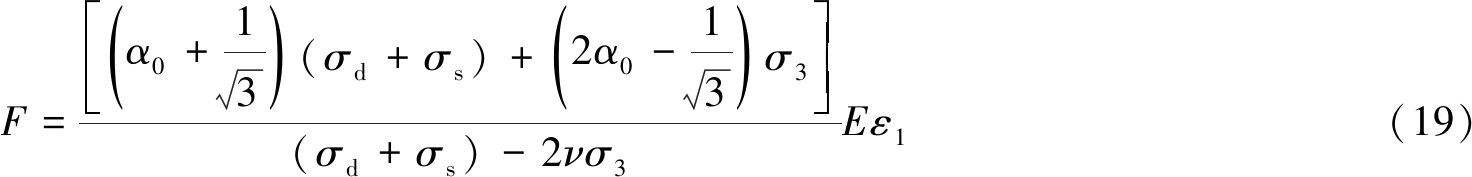
在已测试试验数据的基础上，很容易得到应力应变极值点(σd,max，εm)，而F0为式(19)对应动态应力应变曲线峰值点处所取值，因此F0:
然后采用极值法建立模型表达式和极值点的关系，最终确定模型参数c。首先，对式(18)求导，并根据极值点导数为0的性质可得
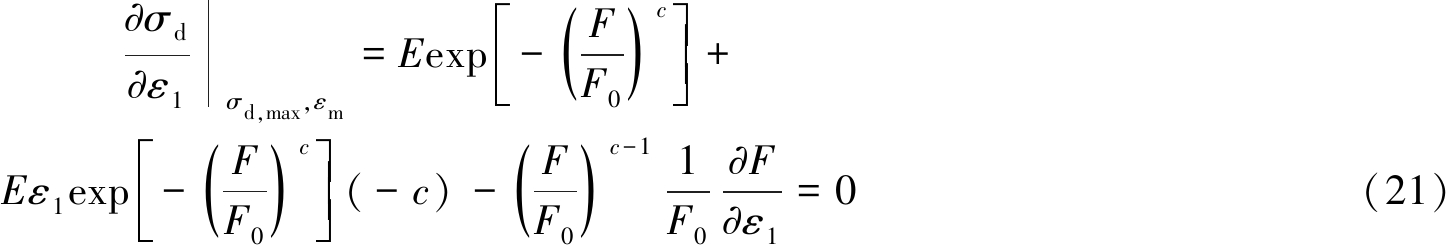
化简得
令式(19)中
则
F=Emε1
(23)
将式(23)两边同时对ε1求导，代入式(22)化简得
c=1
(24)
那么，式(18)进一步化简为
基于上述建立的模型以及三轴煤体冲击动力学实验数据，确定表1实验条件下的模型参数，计算得到了动态应力应变理论曲线，其与实验数据的对比如图5所示。由图5可得，冲击载荷下三轴煤体应力应变实验结果与理论曲线随着应变率的增加，拟合效果越来越好。主要是低应变率下应力应变实验结果波动性较强，拟合效果较差。图5(c)～(d)应力应变的实验结果和理论曲线有较好的一致性，说明已建立的冲击载荷下三轴煤体动态本构模型可以反映煤体强度、破坏应变与轴向静载、围压和冲击载荷的关系，验证了模型的合理性。当然，该模型的理论曲线和实验结果还存在差距，尤其是理论曲线不能反映应力应变的阶跃特征，与选取线弹性阶段应力应变曲线斜率有关，亦或从应变率角度出发建立动态本构模型，这也是我们未来需要对模型进一步修正的研究方向。
图 5 冲击载荷下三轴煤体应力应变曲线实验结果与理论曲线对比
Fig.5 Comparison between experimental and theory results of triaxial coal stress-strain under impact load
4 结 论
(1)冲击载荷下三轴煤体应力应变曲线不存在压密阶段，轴向静载的压密效应使得煤样原生裂隙闭合，增加其完整性，围压的限制变形同样有助于提高煤样完整性，因此试样在初始加载阶段表现出线弹性特征;当应力达到峰值强度的60%～85%阶段时，应力应变曲线呈现“跃进”现象，即应力应变曲线斜率经历先减小又增大再减小的过程，这可能与碳在晶体微破裂中的作用有关;当应力超过煤样峰值强度，试样破坏，应力下降。
(2)冲击载荷下三轴煤体的动态抗压强度和破坏应变与平均应变率高度线性相关，具有明显的应变率效应，说明应变率是影响煤体动力学特征的本质因素。应变率效应将轴向静载、围压和冲击载荷3种不同因素的影响归一化，最终都反映在应变率上，只要组合加载条件有助于提高煤体应变率，其动态强度和破坏应变就随之增加。
(3)基于岩石力学的强度理论与统计损伤理论，考虑轴向静载、围压、冲击载荷组合作用，建立了冲击载荷下三轴煤体动力学本构模型。从本构模型可以看出，轴向静载会加速煤体损伤，从而降低煤体的强度;围压有助于提高煤体的动态强度;而冲击载荷作用时间较短，煤体在瞬间表现为一个完整的弹性体，所以冲击载荷会提高煤体的弹性模量和动态强度，该本构模型反映的三轴煤体动力学本质特征与实验结果相吻合。对比分析发现理论应力应变曲线与试验应力应变曲线具有较好的一致性，且应变率越高，一致性越好。
[1] 冯俊军，王恩元，沈荣喜，等.煤体压剪破裂震源模型及远场震动特征[J].中国矿业大学学报，2016，45(3):483-489.
FENG Junjun，WANG Enyuan，SHEN Rongxi,et al.A coal shear fracture source model and its far-field seismic characteristics[J].Journal of China University of Mining & Technology，2016，45(3):483-489.
[2] 刘少虹，毛德兵，齐庆新，等.动静加载下组合煤岩的应力波传播机制与能量耗散[J].煤炭学报，2014，39(S1):15-22.
LIU Shaohong，MAO Debing，QI Qingxin，et al.Under static loading stress wave propagation mechanism and energy dissipation in compound coal-rock[J].Journal of China Coal Society，2014，39(S1):15-22.
[3] 何江，窦林名，蔡武，等.薄煤层动静组合诱发冲击地压的机制[J].煤炭学报，2014，39(11):2177-2182.
HE Jiang，DOU Linming，CAI Wu，et al.Mechanism of dynamic and static combined load inducing rock burst in thin coal sea[J].Journal of China Coal Society，2014，39(11):2177-2182.
[4] 冯俊军.应力波产生机制及对冲击地压影响研究[D].徐州:中国矿业大学，2016:72-96.
FENG Junjun.Research on stress wave formation and its influence mechanism on rockburst[D].Xuzhou:China University of Mining and Technology,2016:72-96.
[5] 夏开文，周传波.岩石动态力学参数测试综述[J].工程爆破，2014，20(2):43-53.
XIA Kaiwen,ZHOU Chuanbo.Review of testing methods for dynamic rock mechanical properties[J].Engineering Blasting，2014，20(2):43-53.
[6] KOLSKY H.An investigation of the mechanical properties of materials at very high rates of loading[J].Proceedings of the Physical Society.Section B，1949，62:676-700.
[7] 平琦，骆轩，马芹永，等.冲击载荷作用下砂岩试件破碎能耗特征[J].岩石力学与工程学报，2015,34(S2):4197-4203.
PING Qi,LUO Xuan,MA Qinyong,et al.Broken energy dissipation characteristics of sandstone specimens under impact loads[J].Chinese Journal of Rock Mechanics and Rock Engineering，2015,34(S2):4197-4203.
[8] 金解放，李夕兵，殷志强，等.轴压和围压对循环冲击下砂岩能量耗散的影响[J].岩土力学，2013,34(11):3096-3102,3109.
JIN Jiefang，LI Xibing，YIN Zhiqiang，et al.Effects of axial compression and confining pressure on energy dissipation of sandstone under cyclic impact loads[J].Rock and Soil Mechanics，2013,34(11):3096-3102,3109.
[9] 单仁亮，程瑞强，徐慧玲，等.云驾岭煤矿无烟煤的动态本构特性实验研究[J].岩石力学与工程学报，2005，24(S1):4658-4662.
SHAN Renliang，CHENG Ruiqiang，XU Huiling，et al.Experimental study on dynamic constitutive characteristics of anthracite of Yunjialing coal mine[J].Chinese Journal of Rock Mechanics and Rock Engineering，2005，24(S1):4658-4662.
[10] 刘晓辉，张茹，刘建峰.不同应变率下煤岩冲击动力试验研究[J].煤炭学报，2012，37(9):1528-1534.
LIU Xiaohui，ZHANG Ru，LIU Jianfeng.Dynamic test study of coal rock under different strain rates[J].Journal of China Coal Society，2012，37(9):1528-1534.
[11] 夏开文，姚伟.预加载下岩石的动态力学性能研究[J].工程爆破，2015，21(6):7-13.
XIA Kaiwen,YAO Wei.Dynamic mechanical properties of rock under pre-load[J].Engineering Blasting，2015，21(6):7-13.
[12] 王其胜，李夕兵.动静组合加载作用下花岗岩破碎的分形特征[J].实验力学，2009，24(6):587-591.
WANG Qisheng，LI Xibing.Fractal property of granite failure under coupled static-dynamic load[J].Journal of Experimental Mechanics，2009，24(6):587-591.
[13] 宫凤强，李夕兵，刘希灵，等.一维动静组合加载下砂岩动力学特性的试验研究[J].岩石力学与工程学报，2010，29(10):2076-2085.
GONG Fengqiang，LI Xibing，LIU Xiling，et al.Experimental study of dynamic characteristics under one-dimensional coupled static and dynamic loads[J].Chinese Journal of Rock Mechanics and Rock Engineering，2010，29(10):2076-2085.
[14] 刘少虹，李凤明，蓝航，等.动静加载下煤的破坏特性及机制的试验研究[J].岩石力学与工程学报，2013，32(S2):3749-3759.
LIU Shaohong，LI Fengming，LAN Hang，et al.Experimental study of failure characteristics and mechanism of coal undercoupled static and dynamic loads[J].Chinese Journal of Rock Mechanics and Rock Engineering，2013，32(S2):3749-3759.
[15] 单仁亮，程瑞强，高文蛟.云驾岭煤矿无烟煤的动态本构模型研究[J].岩石力学与工程学报，2006，25(11):2258-2263.
SHAN Renliang，CHENG Ruiqiang，GAO Wenjiao.Study on dynamic constitutive model of anthracite of Yunjialing coal mine[J].Chinese Journal of Rock Mechanics and Rock Engineering，2006，25(11):2258-2263.
[16] 高文蛟，单仁亮，苏永强.无烟煤单轴冲击动态强度理论[J].爆炸与冲击，2013,33(3):297-302.
GAO Wenjiao，SHAN Renliang，SU Yongqiang.Theoretical research on dynamic strength of anthracite under uniaxial impact[J].Explosion and Shock Waves，2013,33(3):297-302.
[17] 付玉凯，解北京，王启飞.煤的动态力学本构模型[J].煤炭学报，2013,38(10):1769-1774.
FU Yukai，XIE Beijing，WANG Qifei.Dynamic mechanical constitutive model of the coal[J].Journal of China Coal Society，2013,38(10):1769-1774.
[18] 王登科，刘淑敏，魏建平，等.冲击破坏条件下煤的强度型统计损伤本构模型与分析[J].煤炭学报，2016，41(12):3024-3031.
WANG Dengke，LIU Shumin，WEI Jianping，et al.Analysis and strength statistical damage constitutive model of coal under impacting failure[J].Journal of China Coal Society，2016，41(12):3024-3031.
[19] 朱晶晶，李夕兵，宫凤强，等.单轴循环冲击下岩石的动力学特性及其损伤模型研究[J].岩土工程学报，2013,35(3):531-539.
ZHU Jingjing，LI Xibing，GONG Fengqiang，et al.Dynamic characteristics and damage model for rock under uniaxial cyclic impact compressive loads[J].Chinese Journal of Geotechnical Engineering，2013,35(3):531-539.
[20] 李夕兵，左宇军，马春德.中应变率下动静组合加载岩石的本构模型[J].岩石力学与工程学报，2006,25(5):865-874.
LI Xibing，ZUO Yujun，MA Chunde.Constitutive model of rock under coupled static-dynamic loading with intermediate strain rate[J].Chinese Journal of Rock Mechanics and Rock Engineering，2006,25(5):865-874.
[21] 左宇军，李夕兵，马春德，等.动静组合载荷作用下岩石失稳破坏的突变理论模型与试验研究[J].岩石力学与工程学报，2005,24(5):741-746.
ZUO Yujun，LI Xibing，MA Chunde,et al.Catastrophic model and testing study on failure of static loading rock system under dynamic loading[J].Chinese Journal of Rock Mechanics and Rock Engineering，2005,24(5):741-746.
[22] 刘少虹.动静加载下组合煤岩破坏失稳的突变模型和混沌机制[J].煤炭学报，2014，39(2):292-300.
LIU Shaohong.Nonlinear catastrophy model and chaotic dynamic mechanism of compound coal-rock unstable failure under coupled staticdynamic loading[J].Journal of China Coal Society，2014，39(2):292-300.
