在荷载的作用下，岩石的体积逐渐减小直至最小，而当超过某一临界荷载时，岩石既有裂隙扩展与新裂隙的产生导致岩石的体积开始增加，这种现象称之为岩石扩容，早在20世纪40年代，BRIDGMAN就首次观测到岩石扩容[1]，对应的临界荷载称为扩容应力或岩石长期强度[2]。近年来，随着深部矿产资源的开发与能源储库建设、地铁及城市地下空间的开发利用、岩质隧道、边坡等的稳定性均与岩石扩容有关，且扩容也是地震与岩爆发生的先兆[3-4]。比如，油气储库的失稳将不可避免的导致储库失效、地表沉陷或油气泄露等工程事故，为了保证用于油气储存的废弃盐岩溶腔完整性，盐岩需要避免产生扩容;受应力集中和应力重分布的影响，深埋岩石工程将会发生较大范围的岩体失稳而产生较大的碎胀(扩容)变形，为了保证工程安全需要采取一定工程支护措施。因此，对岩石的扩容进行研究具有重要的科学意义。
国内外学者对岩石的扩容进行了广泛的研究，取得了较为丰富的研究成果。侯文诗等[3]通过对8种岩样的单轴、三轴压缩试验，建立了不同岩石扩容起始点的变化规律;陈宗基等[4-5]提出扩容是地下结构稳定中的基本因素，对地震预报研究具有重要的意义;尹光志等[6]研究了中间主应力对砂岩扩容的影响;MATSUSHIMA[7]提出随着围压的增加扩容应力出现了降低趋势;LAMA和VUTUKURI[8]将扩容看作是岩石微裂隙张开或延伸;许东俊等[9-10]认为扩容与岩石的物性和应力状态有关，且体积变化与应力路径有关;YUAN等[11]引入了岩石扩容指数概念;卢兴利等[12]从卸荷角度出发，研究了岩石碎裂过程中的扩容碎胀变形特性;王宇等[13]研究了岩石扩容起始应力与弹性模量、泊松比和孔隙度的关系，并建立了花岗岩和闪长岩的扩容起始应力预测方程。通过对试验数据的分析，SPIERS等[14-16]与HUNSCHE等[17-19]分别建立了线性及非线性扩容准则;LIU等[20-21]从能量角度研究了裂纹扩展规律及地下开采过程中冲击地压监测、预警及防治措施。
已有岩石扩容研究成果具有以下特点:① 侧向变形对岩石扩容具有重要影响，但较少涉及能表征侧向变形影响的泊松比;② 多采用应力偏量第二不变量
与应力张量第一不变量I1线性或非线性关系表示，但缺乏明确的物理意义;③ 陈宗基等[4-5]提出扩容对地震预报具有重要的意义，但当前扩容准则在地震预报的理论机制方面存在明显不足之处，即不能反映震源释放的应变能对岩体扩容影响或难以反映能量是材料扩容的内在机理。
基于材料破坏是能量驱动下的一种状态失稳现象[22]，从能量转化角度对岩石的扩容准则进行研究。为此，从弹性应变能角度分析了已有扩容准则的物理意义及不足之处，在此基础上建立扩容准则，并利用该准则对有能量输入情况下岩体的扩容进行理论分析。
1 弹性应变能分析
热力学第一定律[22]:
U=Ud+Ure=Ud+UreJ2+UreI2
(1)
其中,Ud为耗散能，满足熵增原理;Ure为弹性应变能，是使材料屈服(包括破坏)的根本原因;UreJ2，UreI2分别为偏量与张量弹性应变能。总能量U按式(2)计算[22]:
U=
σ1dε+
σ2dε+
σ3dε
(2)
由应力状态决定的弹性应变能
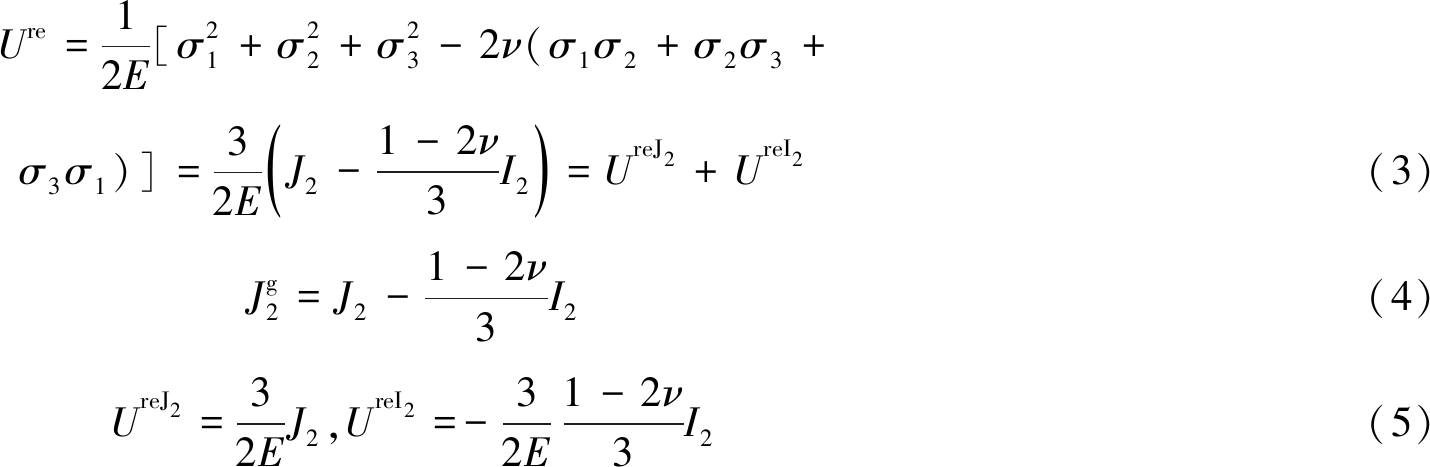
式中，σ1，σ2，σ3分别为最大主应力、中间主应力及最小主应力;E为弹性模量;ν为泊松比;I2为应力张量第二不变量;
分别为应力偏量与广义应力偏量第二不变量。
由式(1)～(5)并结合文献[22]的研究成果，可得:① 根据能量守恒定律，弹性应变能释放是材料破坏的根本原因[22]，提出弹性应变能是材料扩容的内在机理;② Ure等于UreJ2与UreI2之和，因此，仅考虑UreJ2或UreI2对材料扩容、屈服与破坏的影响，可能会导致计算结果出现较大的误差;③ UreJ2恒≥0;UreI2既可>0，又可≤0;④ 若假定材料弹性模量为定值，则
分别反映了Ure，UreJ2的大小;⑤ ν=0.5时，
即UreI2=0,Ure=UreJ2;ν≠0.5时，
即UreI2≠0,Ure≠UreJ2;⑥ 若ν<0.5且I2<0或ν>0.5且I2>0，则UreI2>0，这种情况下仅考虑UreJ2对扩容的影响，将导致计算的扩容应力偏大;反之，若ν>0.5且I2<0或ν<0.5且I2>0，则UreI2<0，这种情况下仅考虑UreJ2对扩容的影响，将导致计算的扩容应力偏小。由此可知，扩容准则若要精确的描述材料的扩容特性，显然应考虑泊松比的影响。
综上所述，一方面，从能量角度来说，
比J2更适合描述岩石的扩容特性;另一方面，忽略UreI2对扩容的影响，将会导致计算结果失真。
2 泊松比分析
2.1 试验概况
由于泊松比对弹性应变能有明显的影响，因此对岩石扩容过程中的泊松比进行了简单研究。试验所用泥质白云岩试样取自贵阳市高地-阳光建筑边坡，并将其加工成直径D=50 mm，高H=100 mm的标准圆柱体。其中，试样两端面的平行度最大误差不超过0.05 mm，在试件整个高度上，直径误差不超过0.3 mm，端面垂直于试件轴，最大误差不超过0.25°。为了研究不同应力水平下岩石变形与扩容特性，利用中科院武汉岩土所MTS815.03进行了泥质白云岩的三轴压缩试验，具体试验步骤如下:① 同步施加侧向应力与轴向应力至特定值(0,5,10,15及20 MPa)，并将其记录的变形值作为初始值;② 在整个试验过程中保持侧向应力不变，以每秒0.5～1.0 MPa的加载速率施加轴向荷载，逐级测读轴向荷载及变形值，直至试件破坏;③ 偏应力等于0时，试样变形也等于0，即图1中变形由第②步变形减去第①步中初始值所得。
图1 泥质白云岩三轴压缩试验
Fig.1 Results of triaxial compressive strength testing
2.2 试验结果分析
岩石破坏通常可划分为4个阶段:裂纹闭合阶段I、弹性阶段II(该阶段应力应变曲线呈近似直线形)、裂纹稳定扩展阶段III及裂纹非稳定扩展阶段IV[13]，εls为轴向应力应变曲线上近似直线段的起点或与弹性阶段II下限相对应应变;εld为侧向应变曲线上近似直线段的上限相对应应变;扩容应力σd对应于体应变曲线上拐点，即岩石体积被压缩至最小时应力;峰值应力σp对应于应力应变曲线的最高点;εd,εp为与扩容应力(σd)、峰值应力(σp)相对的轴向应变。
泥质白云岩的三轴压缩试验结果如表1与图1所示，其泊松比按式(6)确定。以“εls～εd”为例对泊松比计算进行简单说明:式(7)中ε3i为与扩容应力相对应的侧向主应变;ε3(i-1)为与轴向应力应变曲线上近似直线段的起点相对应侧向主应变;ε1i为与扩容应力相对应的轴向主应变;ε1(i-1)为与轴向应力应变上近似直线段的起点相对应轴向主应变。
式中，ε1i，ε1(i-1)为与轴向应力σ1i，σ1(i-1)对应的轴向主应变;ε3i，ε3(i-1)为与轴向应力σ1i，σ1(i-1)对应的侧向应变。
由图1与表1可以看出:
(1)泊松比随应力水平的改变而变化，是1个变量而非常量，这与岩石的变形参数应视为变量的结论一致[24]。
(2)单轴与三轴压缩试验数据计算的泊松比明显不同。可见，将单轴试验确定的泊松比应用于复杂应力状态，可能存在一定的问题。
(3)应力水平及应变计算范围的选取，均对计算的泊松比有影响。比如，由扩容点前、后应力应变曲线计算的泊松比分别<0.5与>0.5。需要说明:马洪岭[16]、黄润秋等[25]也曾通过试验数据计算，得出岩石泊松比会大于0.5。
(4)随围压增大扩容点呈现先接近后远离峰值应力的趋势，比如围压为0，5，10，15及20 MPa时，扩容应力约为峰值强度的0.51，0.62，0.86，0.83及0.75。造成这种结果的主要原因是弹性应变能受应力状态及泊松比影响所致，即泊松比减小可以导致弹性应变能增至岩石发生扩容(这只是一种情况，主要取决于应力状态对UreJ2与UreI2影响)，从而使扩容应力远离峰值应力。
表1 泥质白云岩的三轴压缩试验计算结果
Table 1 Calculation of triaxial compressive strength testing
参数围压/MPa05101520σd/MPa10.3442.292.9110.07128.16σp/MPa20.1868.1108.12132.51171.49σd/σp0.510.620.860.830.75εls/10-20.146 00.161 80.170 40.115 30.125 8εld/10-2-0.016 6-0.059 9-0.039 2-0.056 1-0.077 9εd/10-20.228 80.382 50.623 90.599 20.500 6εp/10-20.785 80.792 80.780 10.839 20.901 8εls～εd0.230.320.330.300.35εld～εd0.480.410.400.430.44εd～εp1.791.120.861.030.97
综上所述，由于岩石属于非理想弹塑性材料，存在各种地质缺陷，基于本文及其他研究者的试验成果，可知岩石扩容时的泊松比较为复杂，既可>0.5，又可<0.5。因此，本文中的泊松比主要通过对试验数据拟合的方法确定，且可>0.5。
3 已有扩容准则理论分析
为建立更符合岩石扩容特性的扩容准则，从弹性应变能角度对国内外学者提出的扩容准则进行了理论分析。
侯文诗等[3]用应力不变量表示硬岩扩容准则:
SPIERS[14]盐岩扩容准则:
RATIGAN等[15]盐岩扩容准则:
胡云华[24]用应力不变量表示花岗岩扩容准则:
Hunsche[17]盐岩扩容准则:
郝铁生等[19]盐岩扩容准则:
应力及应力不变量表示M-C扩容(强度)准则:
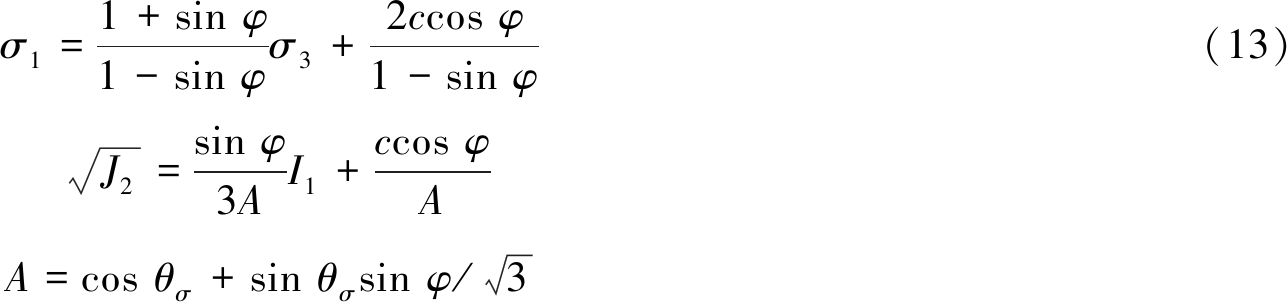
式中，c，φ分别为材料扩容时的黏聚力与内摩擦角，由M-C扩容准则确定;α为量纲常数;θσ为罗德角;N 为关系指数;D1，D2，D3，D4，D5，a及b均为由数值拟合而得材料常数。
比较式(7)～(10)与式(13)可看出，线性扩容准则与M-C强度准则均可由式(14)表达，因此，将线性扩容准则统称为M-C扩容准则。另外，无论线性或是非线性扩容准则，式(7)～(12)均可由扩容准则的一般表达式(14)表示。
式(14)左右两边同时乘以
并与式(3)及(5)比较，可得
ν=0.5时，由式(3),(5)可得
Ure=UreJ2+UreI2=UreJ2
(16)
ν=0.5时，联立式(15),(3)及(5)可得
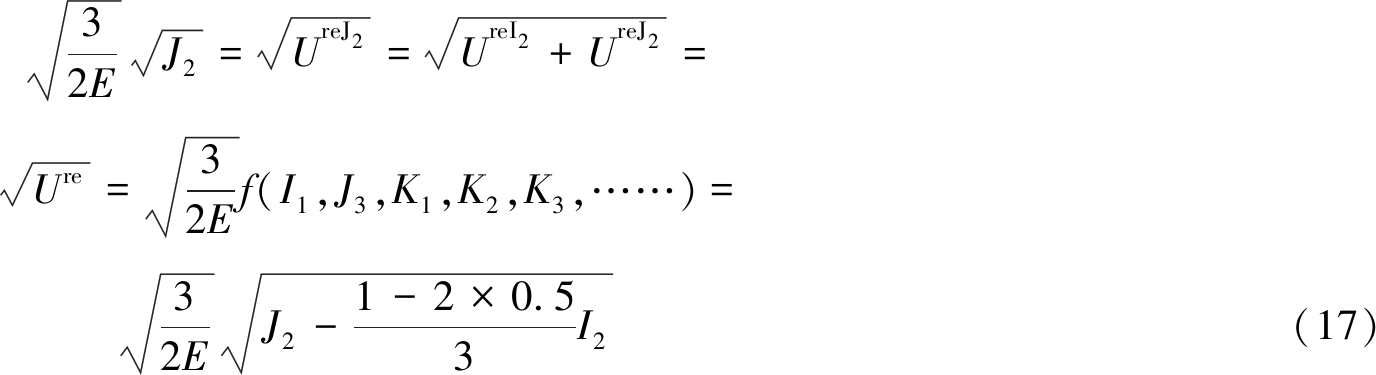
式中，J3为应力偏量第三不变量;K1，K2，Ki为材料参数或材料参数组合。
由式(1)及式(7)～(17)，可得已有扩容准则特点:① 已有扩容准则物理意义:当偏量弹性应变能UreJ2达到某一临界值时，材料开始扩容;② 从受力角度看，线性扩容准则未考虑中间主应力对材料扩容的影响，显然这将影响扩容准则在复杂应力状态下的计算精度与适用性;③ 线性扩容准则计算的扩容应力随围压线性增加，即不会降低，这显然与岩石力学中的中间主应力效应相矛盾;④ 从能量角度看，材料自加载至扩容、屈服及破坏的全过程均应满足能量守恒定律。一方面，上述扩容准则仅考虑了UreJ2，而未考虑UreI2对扩容的影响，因此，扩容时不满足能量守恒定律;另一方面，若扩容准则满足能量守恒定律，则认为材料在任意应力水平下扩容时的泊松比均为0.5，这显然与前述的岩石泊松比分析不尽一致。
综上所述，不满足能量守恒定律(仅考虑UreJ2与扩容关系)，或将材料扩容时泊松比恒看作0.5，是扩容准则只适用于特定岩土材料，或计算结果难以令人满意的根本原因。因此，提高计算精度与适用性的关键是扩容准则能满足能量守恒定律。
4 广义扩容准则
4.1 广义扩容准则的建立
在前述分析的基础上，提出Ue达到某一临界值时材料开始扩容，据此建立广义扩容准则。
式(18)左右两边同时除以可得应力不变量表示的广义扩容准则，即
显然，选择不同的f(I1,J3,K1,K2,K3,……)，即可得相应的扩容准则。
广义扩容准则特点:既满足扩容时的能量守恒定律，又能反映中间主应力对材料扩容的影响。另外，若f(I1,J3,K1,K2,K3,……)采用已有不变量与材料参数的组合函数(比如，已有扩容准则中的组合函数)，则便于广义扩容准则的推广和应用。
为便于从理论上对广义扩容准则进行分析，以式(13)右侧的函数代替式(19)中的不变量与材料参数的组合函数，可得广义M-C扩容准则。
广义M-C扩容准则:
图2为广义M-C扩容准则在π平面的扩容轨迹(I2<0):① 广义M-C扩容准则是一族随泊松比而变化的扩容准则集合，且ν=0.5时蜕化为式(13);② ν=0.5，广义M-C扩容准则的扩容轨迹与M-C强度准则屈服轨迹相似，即图2中ν=0.5时的扩容轨迹既可表示屈服与破坏轨迹，又可表示扩容轨迹;③ 泊松比越小，广义扩容准则计算的扩容应力越小;④ 当中间主应力超过某一临界值时，受泊松比变化的影响，广义扩容准则计算的扩容应力可能会降低。
图2 广义M-C扩容准则在π平面扩容轨迹
Fig.2 Trace of dilation surfaces on π plane of the generalized dilatation criterion (I2<0)
根据前述
及广义M-C扩容准则在π平面的屈服轨迹，其计算结果存在2种可能:
(1)0<ν<0.5,I2>0，或ν>0.5,I2<0时，广义扩容准则计算的扩容应力偏大;
(2)0<ν<0.5,I2<0，或ν>0.5,I2>0时，广义扩容准则计算的扩容应力偏小。
以式(8)与式(10)为基础，分别建立软岩与硬岩2种情况下岩石广义扩容准则。
(1)盐岩广义扩容准则
(2)硬岩广义扩容准则:
4.2 广义扩容准则验证
采用1stOpt软件的差分进化算法(differential evolution)，对广义M-C扩容准则的泊松比进行了识别。利用1stOpt软件对广义M-C扩容准则进行参数反演的具体步骤为:① 将式(21)与式(22)以自定义函数的形式输入软件;② 将岩石的试验数据输入软件;③ 择一种算法(本文选用差分进化法)进行计算，即可获得该准则的参数。
为保证扩容准则验证的客观性，利用式(21),(22)分别对文献[14]及[26-27]中的盐岩及文献[24]中硬岩的试验数据进行了验证，计算结果如图3～6所示。表2为广义扩容准则的拟合参数,其中，ν为由试验数据拟合而得泊松比。
图3 扩容准则对文献[14]盐岩扩容应力计算
Fig.3 Calculation results of salt rock dilation stress[14]
图4 扩容准则对文献[26-27]盐岩扩容应力计算
Fig.4 Calculation results of salt rock dilation stress[26-27]
图5 扩容准则对文献[24]硬岩扩容应力计算
Fig.5 Calculation results of hard rock dilation stress[24]
由改进的三剪能量扩容准则式(12)，对文献[14]的三轴压缩试验数据进行拟合，可得式(12)的参数如下:α=5.69,N=1.88,D1=0.02,D2=2.28,D3=39.67,D4=116.96,D5=2.56。计算结果如图3所示。
由改进的三剪能量扩容准则式(12)，对文献[14]的三轴拉伸试验数据进行拟合，可得式(12)的参数如下:α=28.58,N=1.23,D1=21.97,D2=43.23,D3=21.25,D4=45.36,D5=15.94。计算结果如图3所示。
根据表2及图3的计算结果可知:
(1)广义扩容准则可较好的模拟三轴压缩与三轴拉伸条件下的盐岩与硬岩扩容，且计算精度高于M-C扩容准则，可见基于弹性应变能建立的扩容准则是可行的。
图6 Urx,ν及E对扩容影响(I2<0)
Fig.6 Relation between the dilation and Urx,ν and E
表2 扩容准则计算成果
Table 2 Results in the dilation criteria
试验数据来源c/MPaφ/(°)广义扩容准则拟合ν数据拟合相关性系数R2广义扩容准则M-C扩容准则或扩容准则式(13)备注盐岩[14]——0.1280.997 1—θσ=30°——0.2210.997 1—θσ=-30°盐岩[26]3.5418.000.2250.998 60.975θσ=-30°盐岩[27]5.138.230.1590.999 60.990θσ=-30°硬岩[24]22.6446.330.3020.999 40.977θσ=-30°
注:黏聚力与摩擦角由式(14)对扩容时试验数据拟合而得;文献[14]中试验数据拟合相关性系数为式(13)拟合结果。
(2)其他扩容准则可较好的计算三轴压缩或三轴拉伸条件下盐岩扩容应力，但不能同时使计算的三轴压缩与三轴拉伸条件下盐岩扩容应力均精确。
(3)SPIERS等、RATIGAN等提出的经验型扩容准则认为与I1是线性关系，且认为材料扩容时的泊松比为0.5与实际情况不符，这导致了其计算精度较差;改进的三剪能量扩容准则假定材料3个复合滑动面的弹性剪切应变能之和ws为常数，而实际ws随I1变化而变化[23]。
(4)广义扩容准则计算精度较高的原因:既考虑了UreJ2对扩容的影响，又考虑UreI2的影响，即反映了能量转化是物质物理过程的本质属性。
5 广义扩容准则在地震中应用
陈宗基等[4-5]提出扩容对地震预报具有重要的意义，但包括本文提出式(18)～(22)的扩容准则，均不能计算受震源释放应变能影响的岩体是否扩容，显然若扩容准则对此能够有所反应，则这对地震预报具有重要现实意义。为此，以式(18)表示的广义扩容准则为基础，提出可释放的总能量Ur达到某一临界值时，材料开始扩容，据此建立扩容准则。考虑岩体内储存的与原岩应力相对应弹性应变能为Ure，较短时间内输入未知可释放能量为Urx，则可得
U=Ud+Ur,Ur=Urx+Ure
(23)
K2,K3,……)
(24)
其中，Ur为材料内储存的可释放总能量;Urx为未知可释放能量，除Ure之外的可释放应变能统称;R为扩容判据指数，R<1.0表示未扩容、R=1.0处于扩容极限状态及R>1.0表示已扩容。
式(24)左右两边同时除以可得新扩容准则，为表达方便称式(25)为广义扩容准则，因此，式(18)是式(25)在Urx=0情况下的特例。同理，基于可释放应变能释放是岩体扩容的内在机理，得能反映外部能量输入条件下岩石扩容的广义M-C扩容准则:
对受震源释放应变能影响的岩体，可根据岩体吸收应变能的监测数据，利用式(25)或式(26)计算岩体是否发生扩容;反之，若监测到岩体发生了扩容，则可通过式(25)或式(26)计算得出震源释放的应变能大小，显然这对地震预报具有重要现实意义。可见，式(25)或式(26)可用于地震预报。
接下来，以式(26)为例，研究θσ=-30°条件下震源释放应变能或未知可释放应变能(Urx)、ν及弹性模量(E)对岩体扩容的影响。假定最大、中间及最小原岩应力分别为15，10及10 MPa，扩容时岩体c=20 MPa、φ=30°，由式(13)可得无外部能量输入情况下岩体的扩容应力为99.28 MPa(扩容时ν=0.5)。
由式(23)～(26)及图6可以看出:① Urx,E及ν对扩容应力均有影响;② 泊松比对岩体扩容的影响近似线性，且随泊松比增加扩容判据指数R呈现为减小的趋势，即其他条件相同条件下泊松比越大岩体越不易扩容;③ 随震源释放应变能Urx增加，扩容判据指数R逐渐增加，当释放应变能足够大岩体均会发生扩容，这是广义扩容准则能够进行地震预报理论基础。比如，当Urx=0.02时，R=1.13，即岩体发生扩容;④ 岩体扩容与震源释放应变能或Urx密切相关，这是式(25)或式(26)可用于地震预报的理论基础。
综上所述，广义扩容准则式(25)满足能量守恒定律，且能反映Urx,E及ν对扩容的影响，因此，可用于有外部能量输入情况下岩体的扩容计算，这对于地震预报具有重要意义。
6 结 论
(1)从弹性应变能角度分析了已有扩容准则的特点，指出已有扩容准则认为泊松比恒为0.5是材料扩容的前提(或仅考虑了UreJ2对扩容的影响不满足能量守恒定律)，且不能反映外部输入能量(比如，震源释放应变能)、材料变形特性对扩容的影响。
(2)在对已有扩容准则总结的基础上，提出储存的可释放总能量Ur达到某一临界值时，材料就开始扩容，据此建立广义扩容准则。理论分析表明，广义扩容准则既满足能量守恒定律，又能体现Urx,E及ν对材料扩容的影响。
(3)广义扩容准则为地震预报提供了一个有效途径。由岩体吸收震源释放的应变能监测数据，广义扩容准则可计算得出岩体是否发生扩容;反之，若监测到岩体发生了扩容，可通过广义扩容准则计算得出震源释放的应变能大小，这对地震预报具有重要意义。
(4)基于试验结果，对比分析了线性、非线性及广义扩容准则的计算效果。结果表明:广义扩容准则可以较好地表述岩石的扩容特性，计算结果更为精确，并分析了产生上述结果的内在机制。
[1] BRIDGMAN P W.Volume changes in the plastic stages of simple compression[J].Journal of Applied Physics,1949,20(12):1241-1251.
[2] 柴红保,曹平,赵延林,等.花岗岩板渐进破坏过程的微观研究[J].岩土工程学报,2010,32(7):1048-1053.
CHAI Hongbao,CAO Ping,ZHAO Yanlin,et al.Implementation and application of constitutive model for damage evolution of fractured rock mass[J].Chinese Journal of Geotechnical Engineering,2010,32(7):1048-1053.
[3] 侯文诗,李守定,李晓,等.岩石扩容起始特性与峰值特性的比较[J].岩土工程学报,2013,35(8):1478-1485.
HOU Wenshi,LI Shouding,LI Xiao,et al.Comparison between dilatancy onset and peak of different rocks[J].Chinese Journal of Geotechnical Engineering,2013,35(8):1478-1485.
[4] 陈宗基,康文法.在岩石破坏和地震之前与时间有关的扩容[J].岩石力学与工程学报,1983,2(1):11-21.
CHEN Zongji,KANG Wenfa.Time dependent dilatancy prior to rock failure and eathqakes[J].Chinese Journal of Rock Mechanics and Engineering,1983,2(1):11-21.
[5] 陈宗基,石泽全,于智海,等.用8 000 kN 多功能三轴仪测量脆性岩石的扩容、蠕变及松弛[J].岩石力学与工程学报,1989,8(2):97-118.
CHEN Zongji,SHI Zequan,YU Zhihai,et al.Dilatancy creep and relaxation of brittle rocks measured with the 8 000 kN multipurpose triaxial apparatus[J].Chinese Journal of Rock Mechanics and Engineering,1989,8(2):97-118.
[6] 尹光志,鲁俊,李星,等.中间主应力对砂岩扩容及强度特性影响[J].煤炭学报,2017,42(4):879-885.
YIN Guangzhi,LU Jun,LI Xing,et al.Influence of intermediate principal stress on dilation and strength characteristics of sandstone[J].Journal of China Coal Society,2017,42(4):879-885
[7] MATSUSHIMA S.On the flow and fracture of igneous rocks and on the deformation and fracture of granite under high confining pressure[M].Japan:Bulletin of the Disaster Prevention Research Institute,Kyoto University,1960:20-26.
[8] LAMA R D,VUTUKURI V S.Handbook on mechanical properties of rocks[M].Clausthal:Trans Tech Publications,1978:203-205.
[9] 许东俊,耿乃光.岩体变形和破坏的各种应力途径[J].岩土力学,1986,7(2):17-25.
XU Dongjun,GENG Naiguang.The various stress paths causing deformation and failure in rocks[J].Rock and Soil Mechanics,1986,7(2):17-25.
[10] 许东俊,李小春,蔡忠理,等.应力状态和岩石扩容特性[J].岩土力学,1992,13(2):11-21.
XU Dongjun,LI Xiaochun,CAI Zhongli,et al.Stress path and dilatancy behavior of rocks[J].Rock and soil mechanics,1992,13(2):11-21.
[11] YUAN S C,HARRISON J P.An empirical dilatancy index for the dilatant deformation of rock[J].International Journal of Rock Mechanics and Mining Sciences,2004,41(4):679-686.
[12] 卢兴利,刘泉声,苏培芳.考虑扩容碎胀特性的岩石本构模型研究与验证[J].岩石力学与工程学报,2013,32(9):1886-1893.
LU Xingli,LIU Quansheng,SU Peifang.Constitutive model of rocks considering dilatancy-bulking behavior and its calibration[J].Chinese Journal of Rock Mechanics and Engineering,2013,32(9):1886-1893.
[13] 王宇,李晓,贲雨星,等.脆性岩石扩容起始应力预测——以花岗岩和闪长岩为例[J].岩石力学与工程学报,2014,33(4):737-746.
WANG Yu,LI Xiao,BEN Yuxing,et al.Prediction of initiation stress of dilation of brittle rocks[J].Chinese Journal of Rock Mechanics and Engineering,2014,33(4):737-746.
[14] SPIERS C J,PEACH C J,BRZESOWSKY R H,et al.Long-term rheological and transport properties of the dry and wet salt rocks[C].CEC:EUR11848,prepared for Commission of the Euorean Communities,by University of Utrecht,Utrecht,The Netherlands,1988.
[15] RATIGAN J L,VAN Sambeek L L,DEVRIES K L,et al.The influence of seal design on the Development of the disturbed rock zone in the WIPP alcove seal tests[R].American:Topical Report RSI-0400,prepared by Parsons Brinkerhoff San Francisco,CA,and RE/SPEC Inc,Rapid City,SD,for Sandia National Laboratories,Abbuquerque,NM,1991.
[16] 马洪岭.超深地层盐岩地下储气库可行性研究[D].武汉:中国科学院武汉岩土力学研究所,2010.
MA Hongling.Study on feasibility of rock salt underground gas storage in ultra-deep formation[D].Wuhan:Institute of Rock and Soil Mechanics,Chinese Academy of Sciences,2010.
[17] HUNCHE U E.Failure behavior of rock salt around underground cavities[C].7th International Symposium on Salt[A].Tokyo,1992.
[18] DEVRIES K L,MELLEGARD K D,CALLAHAN G D,et al.Cavern roof stability for natural gas storage in bedded salt[R].Pittsburgh,Pennsylvania:United States Department of Energy National Energy Technology Laboratory,2005.
[19] 郝铁生,梁卫国,张传达.基于三剪能量屈服准则的地下水平盐岩储库腔壁稳定性分析[J].岩石力学与工程学报,2014,33(10),1997-2006.
HAO Tiesheng,LIANG Weiguo,ZHANG Chuanda.Analysis of wall stability for underground horizontal gas storage in bedded salt rock based on yield criterion of triple shear energy[J].Chinese Journal of Rock Mechanics and Engineering,2014,33(10):1997-2006.
[20] LIU Peng,JU Yang,RANJITH Pathegama G,et al.Visual representation and characterization of three-dimensional hydrofracturing cracks within heterogeneous rock through 3D printing and transparent models[J].International Journal of Coal Science & Technology,2016,3(3):284-294.
[21] DOU Linming,MOU Zonglong,LI Zhenlei,et al.Research progress of monitoring,forecasting,and prevention of rockburst in underground coal mining in China[J].International Journal of Coal Science & Technology,2014,1(3):278-288.
[22] 谢和平,鞠杨,黎立云.基于能量耗散与释放原理的岩石强度与整体破坏准则[J].岩石力学与工程学报,2005,24(17):3003-3010.
XIE Heping,JU Yang,LI Liyun.Criteria for strength and structural failure of rocks baded on energy dissipation release principles[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(17):3003-3010.
[23] 周辉,李震,杨艳霜,等.岩石统一能量屈服准则[J].岩石力学与工程学报,2013,32(11):2170-2184.
ZHOU Hui,LI Zhen,YANG Yanshuang,et al.Unified energy yield criterion of rock[J].Chinese Journal of Rock Mechanics and Engineering,2013,32(11):2170-2184.
[24] 胡云华.高应力下花岗岩力学特性试验及本构模型研究[D].武汉:中国科学院武汉岩土力学研究所,2008.
HU Yunhua.Study on mechanical properties of granites under high pressure condition and its constitutive models[D].Wuhan:Institute of Rock and Soil Mechanics,Chinese Academy of Sciences,2008.
[25] 黄润秋,黄达.卸荷条件下花岗岩力学特性试验研究[J].岩石力学与工程学报,2008,27(11):2205-2213.
HUANG Runqiu,HUANG Da.Experimental research on mechanical properties of granites under unloading condition[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(11):2205-2213.
[26] 郭建强.基于弹性应变能盐岩屈服准则及其工程应用研究[D].重庆:重庆大学，2014.
GUO Jianqiang.Study on the criterion of rock salt based on energy principles and its application in engineering[D].Chongqing:Chongqing University，2014.
[27] 陈剑文.盐岩的温度效应及细观机理研究[D].武汉:中国科学院武汉岩土力学研究所，2008.
CHEN Jianwen.Study on temperature effect of mechanical properties and micro mechanism of rock salt[D].Wuhan:Institute of Rock and Soil Mechanics，Chinese Academy of Sciences，2008.
