节理的力学特性是影响岩体力学行为的主要因素,控制着岩体工程在外载荷作用下的变形与破坏特征[1]。研究岩体结构面在地震等动荷载作用下的剪切特性是进行岩体工程动力稳定性分析的重要前提。作为一种动荷载,地震加速度的大小和方向在不断变化,对于结构面而言,地震荷载既是动荷载又是循环荷载[2-3]。岩体结构面的剪切特性一方面会受动荷载幅值及加载速率的影响,另一方面也受动荷载形成的循环剪切或循环加载卸载的影响。特别地,岩体结构面的粗糙起伏会在循环剪切荷载作用下遭受周期性的磨损与钝化,造成其抗剪强度参数的劣化,进而造成岩体沿结构面发生错动和滑移,最终造成边坡岩体的破坏。因此,研究在循环荷载作用下岩体结构面累积损伤与抗剪强度的劣化机制是准确评价边坡岩体动力稳定性需要解决的关键科学问题之一。
国内外关于循环荷载作用对岩体结构面力学特性影响的研究工作较多[4-10],但大都针对强震作用来开展,此时每次循环加载均会越过节理剪切强度的峰值点,出现“左右滑移错动”现象,而在一些微小地震作用下岩体结构面遭受的循环剪切往往不会超过节理剪切强度的峰值点,岩石节理仅发生沿同一方向的“循环加卸载”,即结构面会受到峰值前的循环加卸载影响(峰前循环加载)。已有监测资料[11-12]表明,水库诱发地震的震级往往较小、发震频率较高。这种微小地震荷载对岩体结构面的影响不同于强震,因为荷载大小有限,岩体中结构面往往不会产生明显的滑移和错动现象,即结构面遭受的循环剪切荷载并没有超过其峰值抗剪强度,仅在有限的研究文献[13-15]中,才将微小地震荷载对岩体结构面的影响概括为峰前循环加载作用。可见,针对三峡水库蓄水后微小地震频发的外荷载环境,开展结构面在峰前循环剪切荷载下的累积损伤及力学特性研究,更符合库区岩质边坡中结构面的实际受力状态。
鉴于采用数值计算方法能够克服室内试验周期长、试样制作困难、均一性难以保证、成本高等难点,同时,采用数值计算方法可以针对岩石节理开展更多次数的峰前循环加载,能与室内试验结果对比验证并进一步丰富试验研究成果,其在岩土工程中的运用日益广泛。作为一种典型的细观数值模拟方法,PFC颗粒流离散元法的主要优点在于不需要通过经验设定材料的宏观本构,只依据颗粒接触的黏结机理便可从细观尺度模拟岩石颗粒间的摩擦与黏结,进而实现宏观材料的组构,这从细观上反映了颗粒胶结型材料的结构属性[16]。文献[17-19]采用PFC分别模拟了在单轴、三轴和巴西劈裂试验中岩石的力学特性,较充分阐述与论证了PFC颗粒流模拟在研究岩石细观损伤破裂演化过程和力学性质等方面的优势。另外,在PFC模拟岩石节理剪切行为方面,相关文献[20-23]较为完善地实现了岩石节理PFC数值直剪试验,并从能量转化、裂纹演化及声发射现象等细观力学特征方面,以及节理岩石的破坏形态以及强度模型等宏观方面深入分析了节理在直剪试验过程中的力学演化特征和破坏机制。上述研究结果表明PFC能较好地模拟节理岩体的剪切力学特性,弥补了室内试验中无法进行细观特性研究的缺陷。但是,以上数值模拟研究缺乏针对岩石节理遭受峰前循环剪切作用下的研究,且现有的研究大多忽略了二阶起伏体对岩石节理的剪切特性,而文献[24-27]研究表明节理剪切面上的二阶起伏体会对其剪切特性产生重要影响,特别是在节理所受法向应力较小的情况下,忽略二阶起伏体会远远低估节理的抗剪强度。
鉴于此,笔者首先进行了考虑二阶起伏体的岩石节理室内直剪试验,在此基础上,基于颗粒流理论和 PFC 程序,建立了与室内直剪试验中的3种岩石节理试样相应的PFC数值计算模型,并较为完善地实现了含二阶起伏体贯通型锯齿状岩石节理的PFC峰前循环加载直剪试验,进而从细观角度(颗粒位移、裂纹数量)等方面深入探讨了岩石节理在循环加载阶段的损伤演化机制及对其宏观力学特性的影响,结合室内直剪试验结果,从宏观、细观2个尺度分析了峰前循环加载对岩石节理剪切特性的影响。
1 直剪试验及数值模拟实现
1.1 室内直剪试验
室内试验设计了一阶起伏体分别为15°,30°以及45°三种类型试样,考虑到二阶起伏会对岩石节理的剪切特性产生重要影响,3种类型试样均设计了二阶起伏体。试样几何尺寸如图1所示(以一阶起伏角45°为例),试样长度160 mm,高度120 mm,厚度50 mm。

图1 试样的几何尺寸示意(一阶起伏角45°)
Fig.1 Schematic diagram of geometric size for specimens (first-order asperity 45°)
采用DWJ1525型水刀切割机来切割均质砂岩岩板,并通过M250型岩石试样机打磨试样边界,获得了符合图1所示尺寸的均匀一致的原岩试样,试样加工流程如图2所示。

图2 原岩试样制作过程
Fig.2 Rock samples processing flow
室内直剪试验循环加载包括2个加载阶段:循环剪切的动力加载阶段(力控制);常规静力直剪试验阶段(位移控制)。循环剪切阶段的加载方案如图3所示。由图3可知,试验的循环加载阶段需要确定加载速率、剪切幅值、加载次数以及最小循环剪切力4个参数。试验中动力加载阶段选取加载速率1.0 kN/s,同时兼顾试验目的与试验条件限制,循环加载次数设计为20,50,100,200,500次,循环剪切幅值为50%峰值剪切强度(τp)。常规静力直剪试验阶段采用位移控制方式,加载速率为0.5 mm/min,直至试样破坏。

图3 循环剪切加载方案示意
Fig.3 Schematic diagram of cyclic shear loading scheme
在开展循环加载试验前,需要对试样进行常规直剪试验,以获取试样的峰值剪切强度。试验采用位移控制方式,加载速率为0.5 mm/min。结合现有的研究成果[28],含一阶起伏体岩体结构面剪切变形模式可分为爬坡,爬坡啃断,啃断3种基本类型,不同起伏角与法向力的组合决定了岩石节理在剪切过程中的变形模式。经过多次预试验,在室内常规直剪试验中发现:试样在15°+1 MPa(起伏角+法向压力)的组合下会发生爬坡变形模式,在30°+2 MPa的组合下会发生爬坡、啃断变形模式,在45°+4 MPa的组合下会发生啃断变形模式。常规直剪试验下,不同破坏模式下典型的剪应力-剪位移曲线如图4所示。

图4 3种典型破坏模式的剪切应力-剪切位移曲线
Fig.4 Curves of shear stress versus shear displacement under three typical failure modes
其中,爬坡破坏模式剪应力-剪位移曲线上表现为出现多个峰值点。啃断破坏模式剪应力-剪位移曲线形状逐渐趋向完整岩石的剪切曲线,仅出现一个峰值剪应力,且峰值出现后曲线会出现明显的脆性跌落。爬坡啃断破坏模式兼有爬坡与啃断破坏模式的特征,剪切曲线的上升段出现多个峰值(爬坡效应),而在达到峰值抗剪强度后出现明显的脆性跌落(啃断效应)。
室内试验针对每种变形模式分别进行了5个试样的常规直剪试验,爬坡,爬坡啃断,啃断破坏模式下对应的平均峰值抗剪强度分别为1.09,3.97以及5.16 MPa,通过平均峰值抗剪强度即可确定剪切幅值。而对于最小循环剪切力,为充分体现循环剪切的影响,应尽量取较小值,基于试样在3种变形破坏模式下的平均峰值剪切力,在爬坡模式中该值取为2 kN,在爬坡啃断、啃断破坏模式中该值取为4 kN。这样,循环剪切加载方案所需的参数已全部确定。室内试验在WDAJ-600型岩石剪切流变试验机上进行,部分试验过程如图5所示。

图5 部分峰前循环剪切直剪试验过程
Fig.5 Part of pre-peak cyclic shear test process
1.2 PFC数值模拟
1.2.1 PFC直剪试样的建立
共建立6道墙体来模拟剪切盒,剪切盒的大小为高×宽=120 mm×160 mm。其中1,3,4号墙体形成上部剪切盒,共同作为加载墙体,2,5,6号墙体形成下部剪切盒,固定不动;同时为了防止在加载过程中颗粒的逃逸,建立了7,8号墙体作为翼墙,以保证整个直剪试验的正常进行。
在建立的剪切盒范围内随机生成20 316个颗粒,颗粒密度为2 700 kg/m3,颗粒半径为0.35~0.51 mm服从均匀分布,孔隙率0.14。采用平行黏结模型作为颗粒之间的细观本构模型,采用光滑节理接触模型模拟含二阶起伏的锯齿形节理,采用离散裂隙网络(DFN)创建贯通型结构面,建立了如图6(以一阶起伏角30°试样为例)所示的岩石节理直剪试样,并在裂隙0.5 mm范围内赋予颗粒光滑节理接触模型。

图6 PFC岩石节理试样(一阶起伏角30°)
Fig.6 PFC rock joint specimen(First-order asperity 30°)
以一阶起伏角45°,法向压力4 MPa下节理岩石的常规直剪试验剪应力-剪位移曲线作为标定基准,对比分析模拟与室内试验结果,采用“试错法”来反复改变细观参数,不断动态调整直至试验曲线与模拟曲线基本吻合,最终得到颗粒体为最小颗粒半径Rmin为0.35 mm;最大与最小颗粒半径比Rmax/Rmin为1.86;颗粒体密度ρ为2 700 kg/m3;粒间摩擦因数μ为0.5;颗粒弹性模量E*为10 GPa;颗粒法向、切向刚度比k*为2.6;平行黏结半径系数λ为1.1;平行黏结弹性模量E*为10 GPa;平行黏结法向、切向刚度比k*为2;平行黏结法向强度平均值为4.8 MPa;平行黏结法向强度标准差为5 MPa;平行黏结切向强度平均值为4.8 MPa;平行黏结切向强度标准差为5 MPa。光滑节理分别为法向刚度Sn为100 GPa;切向刚度Ss为100 GPa;摩擦因数μ为0.3;剪胀角ψ为0°;黏结模式为0;黏结法向强度σc为0 MPa;黏结系统黏聚力c为0 MPa;黏结系统摩擦角φ为0°。
在该组参数下数值模拟的剪应力-剪位移曲线与室内直剪试验对比如图7所示。
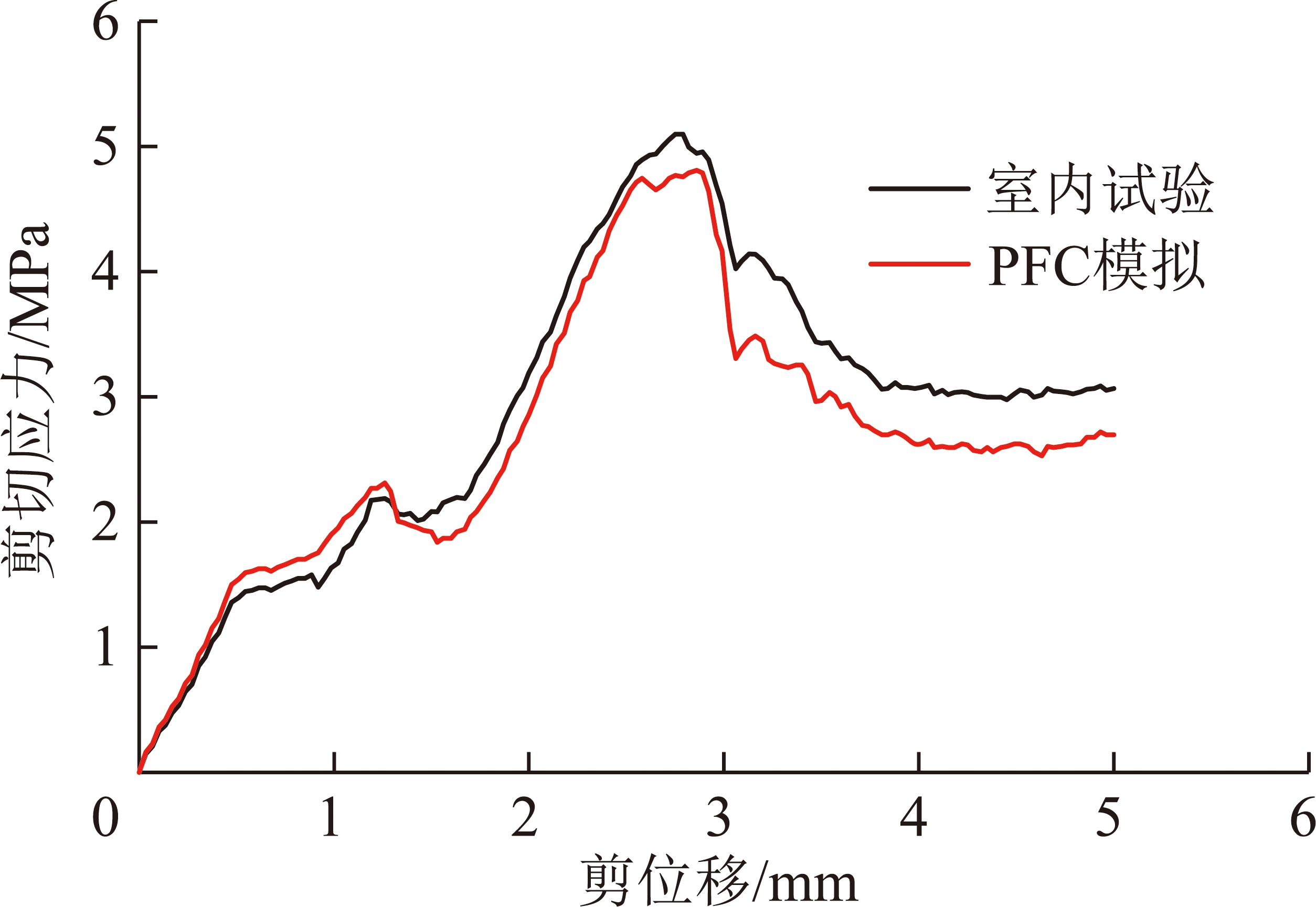
图7 室内直剪试验与PFC模拟曲线
Fig.7 Curves of direct shear test in laboratory and using PFC simulation
由图7可见,模拟曲线与试验曲线能够较好吻合,选取该组细观力学参数作为最终的细观力学参数。
1.2.2 剪切循环试验数值加载过程的实现
(1)恒定法向加载。
基于伺服机制原理,通过不断调整PFC中墙体速率以控制墙体受力,并通过FISH语言编制了伺服程序,不断指定更新顶部1号墙体的边界约束速度进行伺服加载,以作用在边界约束上的平均应力来计算试样应力,并用公式(1)计算Y方向上的应变ε,即

式中,L为Y方向上的试样当前长度;L0为Y方向上试样原始长度。
加载过程中,为保持法向应力恒定,通过数值伺服机制调整法向约束顶板的速度减小测量应力与需求应力之间的差异,伺服控制执行下列算法。
边界约束的速度等式为
式中,角标(ω)表示对应的参数为平均值;G为通过FISH函数用下列推理估测的“增量”参数;σm为在边界上监测到的应力;σr为在边界上需要施加的应力;Δσ为边界上监测应力与需要施加应力的差值。
在一个时步内由约束运动引起的约束力的最大增量为
式中,Nc为边界约束上接触面的数量;![]() 为接触面的平均刚度。因此,平均约束应力的改变量为
为接触面的平均刚度。因此,平均约束应力的改变量为
其中,A为约束区域。为保持稳定,约束应力变量的绝对值不得大于需求值与测量值的差值。在实际应用中,采用放大系数α使稳定需求变为
|Δσ(ω)|<α|Δσ|
(5)
将式(4)代入式(5),得
其中,![]() 因此有
因此有
取G>0,Δσ>0 即
因此可以通过式(9)来确定增量:
实际模拟中一般取α=0.5。
在墙体中生成均匀密实的静定试样后,对试样进行法向伺服加载。调用伺服加载程序,程序自动计算顶板1号墙体应力与应变,获取顶板1号墙体与颗粒接触数量,计算获得“增量”参数G,利用式(2)实时动态更新顶部1号墙体速度,并对整个试样内部法向应力进行实时动态监测。当法向应力和目标应力之间的差值与目标应力的比值小于0.3%后,认为对顶部墙体的应力伺服已经完成,继续计算消除试样内部不平衡力,得到密实均匀承受恒定法向伺服力的静定试样,法向伺服加载完成。
(2)切向循环加载。
切向循环加载的实现是本次模拟的关键,在室内直剪试验中的循环加载主要通过试验力的大小来控制,而在PFC中,主要通过定义墙体速度来实现剪切加载,其本质上是一种位移控制加载方式。考虑到数值模拟与试验在加载方式上的一致性,在PFC模拟中通过监测加载墙体与颗粒之间的应力值,从而获取加载过程中的剪应力大小,基于试验中循环加载的上、下限(τmax,τmin),实时调整墙体的运动方向,从而实现峰前循环加载,循环剪切加载方案如图8所示。

图8 循环剪切加载方案示意
Fig.8 Schematic diagram of cyclic shear loading scheme
峰前循环加载过程主要程序包括试件剪应力的测量以及循环过程墙体速度施加。剪切盒的受力如图9所示,其中,Fn1和Ft1分别为剪切面上部左侧面轴力和剪力;Fn2和Ft2分别为剪切面上部上表面轴力和剪力;Fn3和Ft3分别为剪切面上部右侧面轴力和剪力;σ和τ分别为剪切面上的正应力和剪应力。

图9 剪切盒受力示意
Fig.9 Force diagram of shear box
根据受力分析,作用于剪切面上的剪力假定为T。由水平方向上受力平衡得
T+Fn3=Fn1+Ft2
(10)
由于一般设定墙体摩擦因数为0,因此Ft2一般为0,则
T=Fn1-Fn3
(11)
求得剪切力后,可通过下式求剪应力:
τ=T/A
(12)
在PFC中通过FISH语言编制程序,实时监测3,4号墙体接触力,及3,4号墙体之间距离,通过式(11),(12)计算出试件中剪应力大小,根据不同起伏角节理试样的峰值剪切强度,设置峰前循环加载的上下限见表1。
表1 峰前循环加载的上下限
Table 1 Upper and lower limit of pre-peak cyclic loading
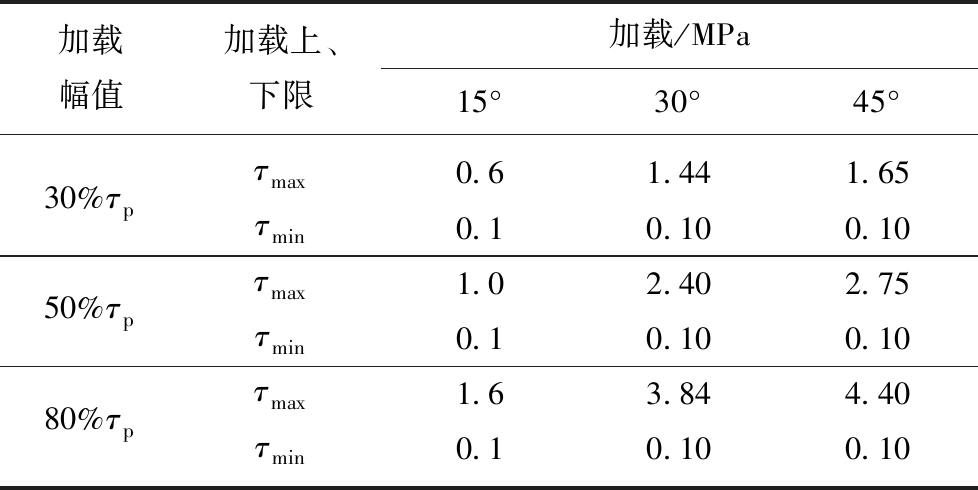
加载幅值加载上、下限加载/MPa15°30°45°30%τpτmax0.61.441.65τmin0.10.100.1050%τpτmax1.02.402.75τmin0.10.100.1080%τpτmax1.63.844.40τmin0.10.100.10
指定1,3,4号墙体以准静态速度0.3 m/s进行加载,实时监测3,4号墙体接触力,求得试件内剪应力,进行记录。当试件内剪应力达到循环峰值剪切强度上限τmax,给定1,3,4号加载墙体以反向动态加载速度-0.3 m/s,继续监测试件所受剪应力,当试件所受剪应力达到循环峰值剪切强度下限τmin,给定1,3,4号加载墙体正向动态加载速度0.3 m/s,如此往复循环,直至完成目标循环剪切次数。
(3)数值加载过程。
本文岩石节理数值直剪试验过程包括2个部分:峰前循环加载部分以及常规直剪试验部分。试验中,为了使系统对试件内部产生的不平衡力及时进行调整,保证结果的可靠性,常规直剪试验加载过程保持为拟静力加载状态。鉴于PFC采用的是显式时步算法,每一时步约为4.15×10-8 s,因此,可以采用0.3 m/s的水平速率,这相当于1.245×10-8 m/步,剪切速率非常小,已经可以视为静态加载。理论上,循环加载过程是动态加载过程,1,3,4号墙体以反复正反向速度进行循环加载,通过墙体速度方向的改变实现峰前循环加载的目的。
2 数值模拟结果与分析
2.1 起伏角的影响
分别建立了一阶起伏角为5°,15°,30°,45°,60°的岩石节理,数值模拟施加法向压力2 MPa,循环幅值50%τp,循环次数500次,用以分析起伏角对岩石节理抗剪强度的影响。峰前循环加载500次后,进行常规直剪试验直至试件破坏,试件破坏后细观裂纹对比如图10所示。图10中红色裂纹为剪切裂纹,绿色裂纹为张拉裂纹(下文同)。

图10 细观裂纹分布
Fig.10 Distribution of mesoscopic cracks
如图10所示节理破坏后的裂纹分布情况,在起伏角较小时,试件裂纹主要沿二阶起伏体分布,沿二阶起伏角形成贯通裂纹,试件沿受力侧贯通裂纹滑动,非受力侧脱空,一阶起伏尖端锯齿受到少量磨损,试件表现出典型爬坡变形模式;随着起伏角度的增大,在30°起伏角时,已经可以观察到,非受力侧脱空现象显著减小,虽有脱空但张开度不大,除了沿二阶起伏分布的裂纹外,部分锯齿在根部或锯齿中部亦开始产生贯通裂纹,表明在试件沿一阶起伏方向爬坡的过程中,部分锯齿被同时啃断;继续增大起伏角,当起伏角达到45°时,裂纹主要沿锯齿根部分布,形成贯通裂缝,二阶起伏处亦有剪切裂缝的存在,整个节理闭合性较好,此时观察到的裂纹分布情况,表现为典型的啃断变形模式;继续增加起伏角角度,起伏角角度达到60°,此时锯齿高度较高,单个锯齿类似于楔形体存在,整个试件类似于卯榫结构。因为起伏角度的增加,试件内节理占比显著增多,相对前几组试件,该组岩体更加离散。观察发现,裂纹主要分布在锯齿根部,同时,发现边界处锯齿因孤立存在,边界处没有支撑体,发生了类似于楔形体劈裂的破坏。
通过对不同起伏角裂纹分布情况的分析发现,随着起伏角的增大,试件整体上按爬坡—爬坡啃断—啃断的变形模式在发展。提取模拟中获得的各级起伏角下循环直剪试验的峰值抗剪强度,如图11所示。
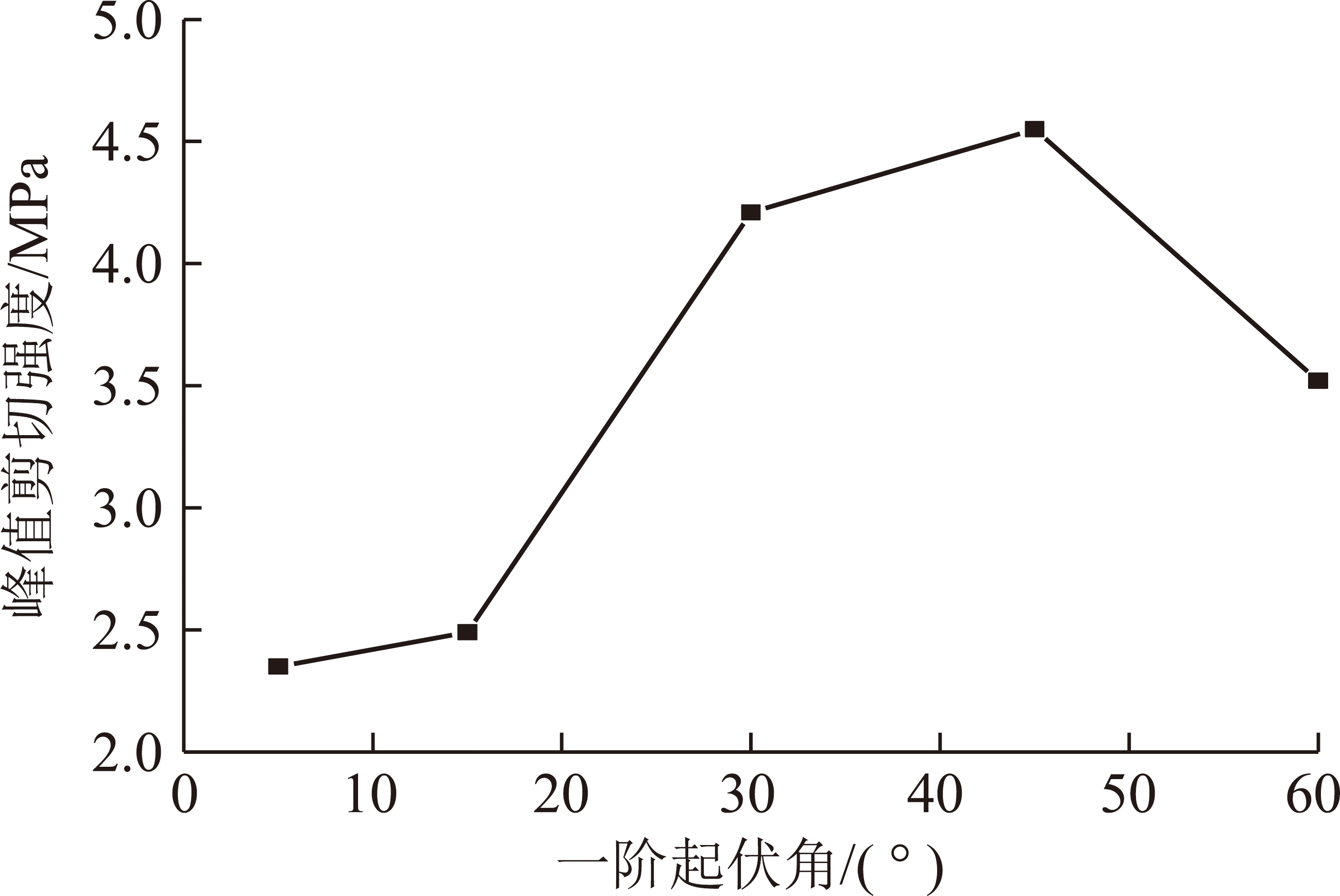
图11 峰值强度曲线
Fig.11 Shear displacement shear stress curve
由图11可见,随着起伏角的增加,节理岩体抗剪强度不断提升,这是因为锯齿高度升高,剪切过程中节理间摩阻力增大,但当起伏角度达到60°时,因为节理占比过高,试件内节理面较多,反而降低了试件强度。
2.2 法向压力对岩石节理抗剪强度的影响
以一阶起伏角30°,循环幅值50%τp,循环次数500次模型为研究对象,讨论法向压力对岩石抗剪强度的影响,对试件分别施加1,2,3,4 MPa法向压力,各级法向压力加载后,对各试件进行峰前循环剪切,循环500次后,各级法向压力下试件裂纹发展如图12所示。可见,低法向应力条件下裂纹发展较为迅速,500次循环过后,1 MPa法向压力下试件内已经出现向锯齿内发展的贯通裂纹,且二阶起伏处有密集裂纹出现,发生较严重的剪切磨损,非受压侧出现显著脱空,证明试件剪胀较为明显;随着法向压力不断增大,节理面闭合度逐渐提高,剪胀效应已不再显著。试件内贯通裂纹显著减少,裂纹主要出现在受压侧二阶起伏处,表明高法向应力条件下,法向压力对试件压密作用愈加显著,高法向应力使节理处颗粒接触面增加,颗粒更加密实,整个试件趋近于一个整体岩块。

图12 裂纹扩展
Fig.12 Crack propagation pattern
不同法向压力条件下节理抗剪强度变化如图13所示。由图13可知,随着法向压力的增加,试件峰值剪切强度、峰后残余强度随之增大。这是由于试件破坏模式按爬坡—爬坡啃断—啃断趋势发展的过程中,啃断一阶起伏体需要克服更多的阻力。
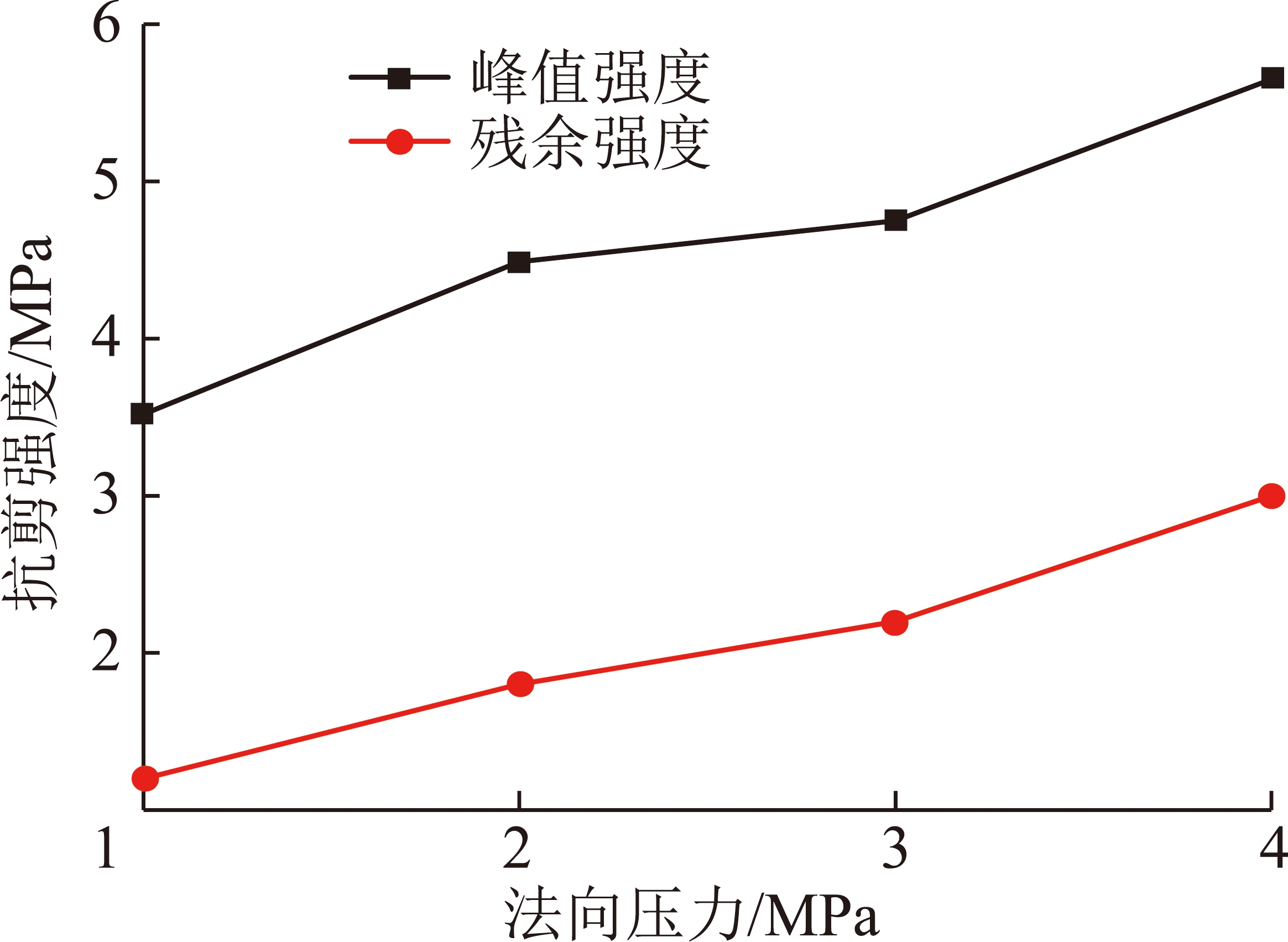
图13 法向压力与节理抗剪强度关系
Fig.13 Relationship between normal pressure and shear strength of joints
2.3 循环加载幅值的影响
选取起伏角30°,法向压力2 MPa模型试样,分别施加30%τp,50%τp,80%τp循环幅值,不同加载幅值下节理在500次循环荷载后裂隙发展如图14所示。由图14可知,加载幅值越大,对受压侧颗粒间黏结磨损越严重,裂隙产生数量越多。在30%τp加载幅值下,张拉裂纹扩展深度有限,而随着加载幅值增大,张拉裂纹进一步扩展并加深,对试样的损伤程度加剧。可见,循环加载幅值越高对节理的损伤程度越大。
进一步提取裂隙追踪数据,对比分析500次循环下各循环加载幅值的裂隙总数目,如图15所示。由图15可知,在循环加载初期,加载幅值对裂隙产生数量影响不大;随着循环次数的增多,循环加载幅值对应裂隙产生数量发生较大变化,80%τp循环加载幅值对应裂隙数量曲线剧烈上升,且随着循环次数的增加,裂隙数量增长速率逐渐增大,曲线有继续发散的趋势;50%τp循环加载幅值裂隙数量曲线在多次循环加载后,数量增加较为明显,但增加幅度与速度要明显低于80%τp;30%τp裂隙数量曲线一直较为平缓,曲线没有陡增,即裂隙数量随着循环加载次数的增加基本维持在稳定而不增长的状态。

图14 不同加载幅值下典型裂隙发展
Fig.14 Typical crack development under different loading amplitude

图15 不同加载幅值裂隙发展趋势
Fig.15 Development trend of crack with different loading amplitude
由此可以看出,循环加载幅值对节理的累积损伤程度产生重要影响,当循环荷载幅值较低时,如30%τp,节理在循环加载阶段产生的损伤裂纹数量较少,且随循环加载次数的增加不再增长,可以判断,低幅值的循环荷载对节理剪切强度的影响极为有限,甚至可以忽略;当荷载幅值进一步增加,如50%τp,节理损伤裂纹的增长速度在循环加载初期较快,而在循环加载后期的增长速度显著放缓,中等幅值的循环荷载会造成节理的累积损伤,在经历足够次数的循环加载后,节理剪切强度会出现一定程度的劣化现象;当循环荷载幅值越靠近峰值强度时,如80%τp,节理损伤裂纹的数量随循环加载次数的增加呈现阶梯型快速增长趋势,较少次数的循环加载就可能造成节理剪切强度的显著下降。
2.4 循环加载次数的影响
以起伏角30°,法向压力2 MPa,循环加载幅值50%τp试样为例,经历不同循环加载次数20,50,100,200,500,1 000以及2 000次后节理的损伤特征如图16所示。
从图16可以明显看出,低次数循环下(20,50,100次)节理裂隙发展缓慢,主要表现为受压侧颗粒压密以及受压侧张拉裂缝的产生,非受压侧有少量裂隙的产生,主要为张拉裂隙,也伴有极少数剪切裂缝。中低循环次数下(200,500次),受压侧颗粒进一步被压紧压密,二阶起伏处黏结颗粒受到压剪作用,黏结破坏,张拉裂隙沿二阶起伏进一步增多,第1级,第2级锯齿中部,出现向锯齿内发展的压致拉裂缝,裂缝处于发展初期,长度较小。随着循环次数的增加,循环次数达到1 000次,可以观察到,受压侧沿二阶起伏处已经生成较多裂隙,说明二阶起伏处可以在被压紧压密的过程中,颗粒间黏结已经在不断循环过程中被破坏,形成裂隙。第1级,第3级压致拉裂缝已经进一步发展,向锯齿中部延伸,有啃断锯齿的趋势。非受压侧有部分裂隙产生,并可以观察到节理处沿二阶起伏较小张开度的脱离。当进行到较高次数的循环(1 500,2 000次),受压侧沿二阶起伏裂隙剧烈发展,沿一阶起伏方向有形成贯通裂缝的趋势,第1级锯齿内压致拉裂缝沿平行受压侧一阶起伏方向已经贯通整个锯齿,第3级锯齿内压致拉裂缝发展到锯齿中部;非受压侧因为循环加载磨损的影响,形成了较多离散裂隙,同时可以观察到沿二阶起伏的颗粒间脱离。

图16 不同循环加载次数下节理的裂纹扩展特征
Fig.16 Crack propagation characteristics of joints under different cyclic loading times
对整个循环加载过程中的裂纹实时进行追踪,动态更新裂纹类型、产生数量,如图17所示。可见,在循环加载初期曲线较为平缓,裂隙增加不多,在循环加载中期,裂纹成线性增长,在循环加载后期,曲线陡升,裂纹数量剧烈增加,继续发散趋势明显。同时,整个剪切过程中,以张拉裂缝的产生为主,伴随少量剪切裂缝的生成。
3 数值模拟与室内直剪试验对比分析
3.1 破坏模式分析
试样的数值模拟与室内试验破坏模式对比如图18所示。

图17 裂纹数量随循环时步发展曲线
Fig.17 Growth curves of crack number with cyclic time step

图18 模拟破坏模式与试验破坏模式对比
Fig.18 Comparison between simulated failure mode and failure mode in parameter calibration
从图18可以看出,数值直剪试验与室内直剪试验中表现出的破坏模式基本吻合,进一步证明了数值模拟计算结果的有效性。其中,15°一阶起伏角试件在较小的起伏角与法向压力组合下(15°+1 MPa),剪切过程中结构面会沿着一阶起伏体受力侧坡面滑移,二阶起伏体被磨损剪断,非受力侧坡面脱空,并伴有较为明显的剪胀性质,即爬坡破坏模式。在爬坡破坏模式下,节理的剪切强度主要受剪切面上的一阶起伏体角度以及二阶起伏体(表面粗糙度)控制。
随着节理一阶起伏体的起伏角以及施加的法向压力增大(30°+2 MPa),节理在剪切过程中的爬坡效应会受到一定的抑制,在出现一定程度的爬坡效应后,节理一阶起伏体的上部尖端会因压致拉裂而发生啃断破坏,即爬坡啃断破坏模式。在爬坡啃断破坏模式下,节理的剪切强度受节理的一阶起伏体角度、二阶起伏体以及岩石的黏聚力等因素控制。
随着一阶起伏体的起伏角及试验法向压力进一步增大(45°+4 MPa),节理在剪切过程中的爬坡效应几乎被完全抑制,试验中观察到节理发生破坏时主要表现为一阶起伏体被啃断,即啃断破坏模式。在啃断破坏模式下,节理的抗剪强度主要受岩石黏聚力控制。
3.2 节理强度劣化规律
不同破坏模式下峰值抗剪强度与循环剪切次数关系如图19所示。其中,数值模拟计算了在50%τp以及80%τp循环剪切幅值下分别进行20,50,100,200,500,1 000以及2 000次峰前循环剪切后节理的峰值抗剪强度。同时,通过室内直剪试验结果进行对比验证,但限于试验条件与时间成本,室内直剪试验只获得了50%τp循环剪切幅值下进行20,50,100,200以及500次峰前循环剪切后节理的峰值抗剪强度以及残余抗剪强度。
如图19所示,3种破坏模式下不同循环剪切次数对应的峰值抗剪强度的数值模拟与室内直剪试验结果较为接近,进一步证明了数值模拟计算的准确性。可以看出,峰值抗剪强度随着循环加载次数的增加呈现出先增后减的变化趋势。同时,不同的破坏模式下,节理峰值抗剪强度变化曲线出现下降的拐点位置不同,在爬坡、爬坡啃断、啃断模式下曲线拐点位置对应的循环加载次数分别约为50,100,200次。这一规律表明,节理剪切面上发生爬坡变形模式的二阶起伏体在50次循环加载后即出现磨损劣化;随着循环加载的持续,啃断变形模式下的一阶起伏体在循环加载200次后损伤开始出现,这表明在峰前循环加载过程中,节理的累积损伤经历了从二阶起伏体向一阶起伏体的演变过程。
另外,不同循环加载幅值对应的节理直剪峰值强度也有不同,相同循环次数条件下,循环加载幅值越大,节理劣化越严重,峰值剪切强度越小,且循环加载幅值越大,峰值剪切强度随着循环次数的增加降低幅度越大。

图19 不同破坏模式下峰值强度与循环剪切次数关系
Fig.19 Relationship between peak strength and cyclic shear times under different failure modes
4 峰前循环加载对节理剪切特性的影响机理探讨
数值模拟和室内试验结果显示,节理的峰值抗剪强度随循环加载次数的增加出现先增后减的变化特征,有限次数的峰前循环加载反而能增加节理的抗剪强度。为解释这一现象,本文将峰前循环加载对节理的影响归结为2种效应:接触效应和损伤效应。其中,接触效应指的是随着峰前循环加载次数的增加,节理不断地被压紧、压密,节理剪切面的接触面积不断增加的现象,如图20(a)所示。损伤效应指的是随着循环次数的增加节理剪切面上的二阶起伏逐渐磨损劣化,一阶起伏体上部尖端出现损伤裂纹并持续扩张贯通直至被啃断的现象,如图20(b)所示。

图20 节理接触效应与损伤效应示意
Fig.20 Schematic diagram of joint contact effect and damage effect
以一阶起伏角30°,循环幅值50%τp,循环次数500次数值模拟试验为例,模型在不同法向压力条件下剪向位移与法向位移关系如图21所示。
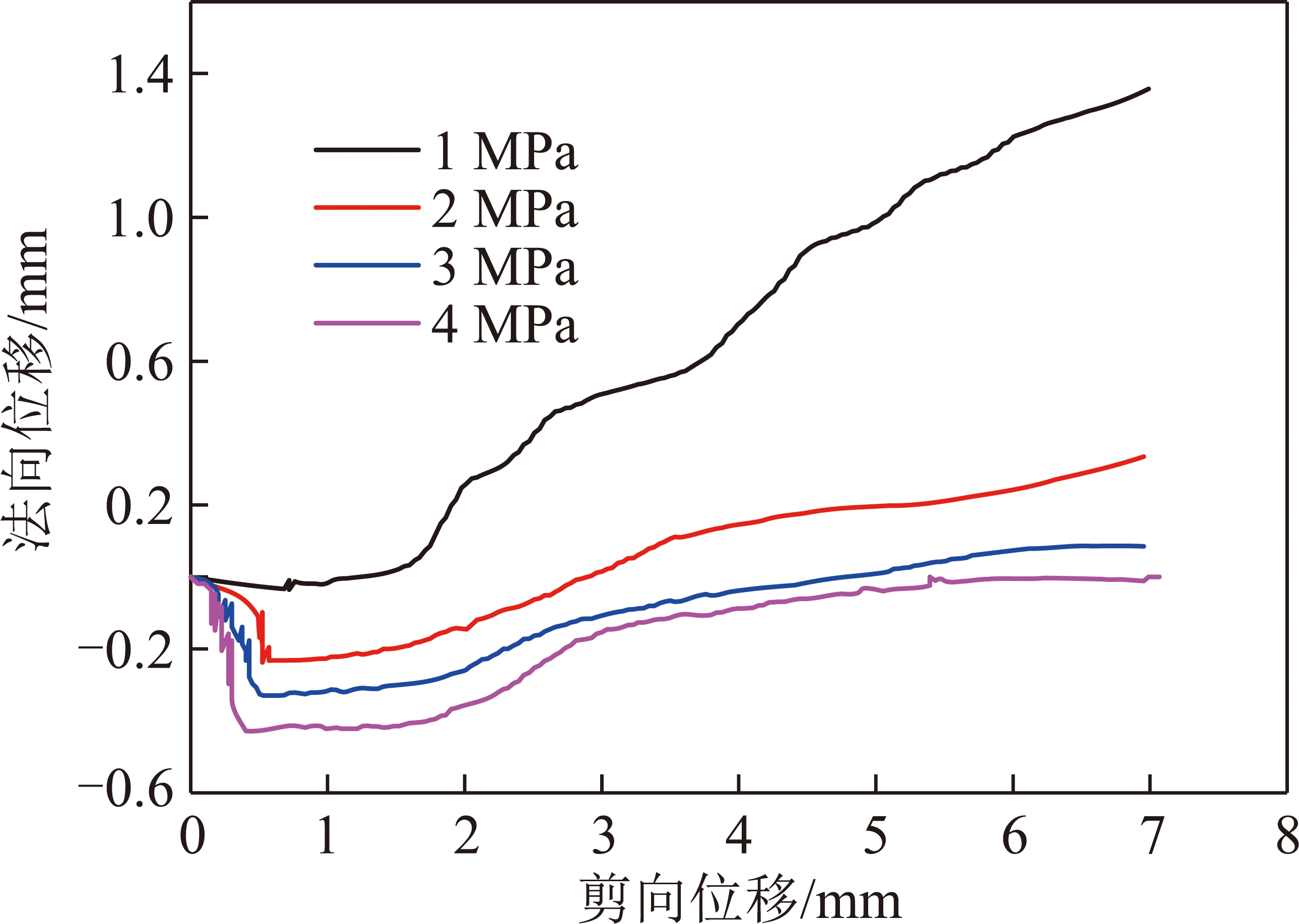
图21 剪向位移-法向位移曲线
Fig.21 Shear displacement-normal displacement curves
由图21可知,在循环加载前期,试件在各级法向应力条件下均先剪缩;在循环加载后期,低法向应力下试件表现出较大的正向剪胀,随着法向应力的增加,试件逐渐被压密,剪胀量逐渐减小,当法向压力加载到4 MPa时,试件在整个剪切过程,都是在压缩状态下进行。总体而言,在峰前循环加载初期,节理经历较少次数的循环剪切后,节理剪切面的接触效应即得到充分体现,在此阶段损伤效应还未得到充分体现,接触效应增加了节理在剪切过程中的接触面积,从而对抵抗剪切荷载产生有利的作用,使得节理的峰值抗剪强度在循环加载初期有所增长。然而,随着循环剪切次数逐步增大,节理剪切面的接触效应在经历了初始的增加后会维持在一个相对稳定的水平,而损伤效应开始体现,且随着循环剪切次数增加而增大,当损伤效应造成的抗剪强度劣化值超过接触效应产生的增加值时,节理最终的峰值抗剪强度将降低,呈现下降的趋势。
5 结 论
(1)随着岩石节理一阶起伏角、法向压力的增大,岩石节理的破坏模式按爬坡、爬坡啃断以及啃断趋势发展,且节理的抗剪强度随着一阶起伏角、法向压力的增大总体上呈增大趋势,但当一阶起伏角过大导致试件内节理面占比过大时,反而降低了试件强度。
(2)爬坡模式下,损伤裂纹主要出现二阶起伏体附近,张拉裂纹及剪切裂纹均有出现,体现出循环加载对二阶起伏的磨损效应;在啃断模式下,除了在二阶起伏体上有少许张拉及剪切裂纹外,损伤裂纹主要出现在一阶起伏体上,且以张拉裂纹为主,体现出循环加载对一阶起伏体的啃断效应;而爬坡啃断模式下,综合了上述2种模式的裂纹发展特征。
(3)低幅值的循环荷载对节理剪切强度的影响极为有限,甚至可以忽略,但随着循环加载幅值的增加,节理起伏体上裂纹的扩展贯通程度、裂纹的数量均显著增多,表明循环加载幅值的大小是决定节理起伏体累积损伤速度的关键因素。
(4)节理裂纹数量随循环加载次数的增大不断增加,且增加的速度有加快的趋势,而在循环加载次数增加到某个量级时,裂纹出现激增的现象,这一现象体现了节理疲劳裂纹的扩展贯通有累积后突变的演变特征;有限次数的循环加载将增大节理的峰值抗剪强度,而当循环加载次数进一步增大,循环加载对节理的累积损伤效应开始体现,节理的损伤将造成其抗剪强度的劣化,从而使得峰值抗剪强度出现下降的变化趋势,且循环加载幅值越大峰值强度峰值下降幅度越大。
(5)峰前循环加载对节理的影响可以归结为接触效应和损伤效应,这2种效应的演变是造成节理在峰前循环剪切过程中抗剪强度先增后减的根本原因。
[1] 李海波,刘博,冯海鹏,等.模拟岩石节理试样剪切变形特征和破坏机制研究[J].岩土力学,2008,29(7):1741-1746,1752.
LI Haibo,LIU Bo,FENG Haipeng,et al.Study of deformability behaviour and failure mechanism by simulating rock joints sample under different loading conditions[J].Rock and Soil Mechanics,2008,29(7):1741-1746,1752.
[2] 周友华,胡奉湘,饶云阶,等.地震应力产生传递与集中机制的研究[J].国际地震动态,2004(11):8-14.
ZHOU Youhua,HU Fengxiang,RAO Yunjie,et al.Researches on the mechanisms for the transform and concentration of seismic stresses[J].Recent Developments in World Seismology,2004(11):8-14.
[3] 胡志奇,郑文衡,陆明勇.岩体动态应力在地震机理中的作用研究[J].大地测量与地球动力学,2005,25(1):108-112.
HU Zhiqi,ZHENG Wenheng,LU Mingyong.Preliminary study on crustal stress and its effecton earthquake triggering[J].Journal of Geodesy and Geodynamics,2005,25(1):108-112.
[4] HOMAND F,BELEM T,SOULEY M.Friction and degradation of rock joint surfaces under shear loads[J].International Journal for Numerical & Analytical Methods in Geomechanics,2001,25(10):973-999.
[5] LEE H S,PARK Y J,CHO T F,et al.Influence of asperity degradation on the mechanical behavior of rough rock joints under cyclic shear loading[J].International Journal of Rock Mechanics & Mining Sciences,2001,38(7):967-980.
[6] JAFARI M K,HOSSEINI K A,PELLET F,et al.Evaluation of shear strength of rock joints subjected to cyclic loading[J].Soil Dynamics & Earthquake Engineering,2003,23(7):619-630.
[7] 刘博,李海波,刘亚群,等.循环荷载作用下节理凸起体概化破坏模型及剪切强度计算分析[J].岩石力学与工程学报,2013,32(S2):3000-3008.
LIU Bo,LI Haibo,LIU Yaqun,et al.Generalized damage model for asperity and shear strength calculation of joints under cyclic shear loading[J].Chinese Journal of Rock Mechanics and Engineering,2013,32(S2):3000-3008.
[8] 刘博,李海波,刘亚群.循环剪切荷载作用下岩石节理变形特性试验研究[J].岩土力学,2013,34(9):2475-2481.
LIU Bo,LI Haibo,LIU Yaqun.Experimental study of deformation behavior of rock joints under cyclic shear loading[J].Rock and Soil Mechanics,2013,34(9):2475-2481.
[9] 张雨霆,丁秀丽,邬爱清,等.有厚度天然结构面法向循环加载变形特性研究[J].岩土力学,2017,38(10):2865-2872.
ZHANG Yuting,DING Xiuli,WU Aiqing,et al.Deformation characteristics of natural structural planes with certain thickness under normal cyclic loading condition[J].Rock and Soil Mechanics,2017,38(10):2865-2872.
[10] 邓建,肖明,谢冰冰,等.循环荷载下岩体结构面本构关系与积分算法研究[J].岩土工程学报,2017,39(6):1048-1057.
DENG Jian,XIAO Ming,XIE Bingbing,et al.Constitutive relation and integration algorithm for rock discontinuities under cyclic loading[J].Chinese Journal of Geotechnical Engineering,2017,39(6):1048-1057.
[11] 陈德基,汪雍熙,曾新平.三峡工程水库诱发地震问题研究[J].岩石力学与工程学报,2008,27(8):1513-1524.
CHEN Deji,WANG Yongxi,ZENG Xinping.A study of reservoir-induced earthquake of three gorges project[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(8):1513-1524.
[12] WANG R S.Three gorges reservoir induced earthquake monitoring and prediction[J].Journal of China Three Gorges University (Natural Science),2017,39(1):30-37.
[13] 李海波,蒋会军,赵坚,等.动荷载作用下岩体工程安全的几个问题[J].岩石力学与工程学报,2003,22(11):1887-1891.
LI Haibo,JIANG Huijun,ZHAO Jian,et al.Some problems about safty analysis of rock engineering under dynamic load[J].Chinese Journal of Rock Mechanics and Engineering,2003,22(11):1887-1891.
[14] FERRERO A M,MIGLIAZZA M,TEBALDI G.Development of a new experimental apparatus for the study of the mechanical behaviour of a rock discontinuity under monotonic and cyclic loads[J].Rock Mechanics and Rock Engineering,2010,43(6):685-695.
[15] TSUBOTA Y,KUNISHI T,IWAKOKE Y,et al.Fundamental studies on dynamic properties of rock joint under cyclic loading using mortar and Ryoke gneiss[M].London:Rock Dynamics and Applications-State of the Art,2013.
[16] Itasca Consulting Group Inc.PFC2D (particle flow code in 2D) theory and background[R].Minnesota:Itasca Consulting Group Inc.,2008.
[17] POTYONDY D O,CUNDALL P A.A bonded-particle model for rock[J].International Journal of Rock Mechanics and Mining Sciences,2004,41(8):1329-1364.
[18] CHO N,MARTIN C D,SEGO D C.A clumped particle model for rock[J].International Journal of Rock Mechanics and Mining Sciences,2007,44(7):997-1010.
[19] YOON J.Application of experimental design and optimization to PFC model calibration in uniaxial compression simulation[J].International Journal of Rock Mechanics and Mining Sciences,2007,44(6):871-889.
[20] 周喻,MISRA A,吴顺川,等.岩石节理直剪试验颗粒流宏细观分析[J].岩石力学与工程学报,2012,31(6):1245-1256.
ZHOU Yu,MISRA A,WU Shunchuan,et al.Macro-and meso-analyses of rock joint direct shear test using particle flow theory[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(6):1245-1256.
[21] 夏才初,宋英龙,唐志成,等.粗糙节理剪切性质的颗粒流数值模拟[J].岩石力学与工程学报,2012,31(8):1545-1552.
XIA Caichu,SONG Yinglong,TANG Zhicheng,et al.Particle flow numerical simulation for shear behavior of rough joints[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(8):1545-1552.
[22] 王刚,张学朋,蒋宇静,等.基于颗粒离散元法的岩石节理面剪切破坏细观机理[J].中南大学学报(自然科学版),2015,46(4):1442-1453.
WANG Gang,ZHANG Xuepeng,JIANG Yujing,et al.Meso-mechanism research on shear failure of rock joint based on particle discrete element method[J].Journal of Central South University (Science and Technology),2015,46(4):1442-1453.
[23] 李晓锋,李海波,夏祥,等.类节理岩石直剪试验力学特性的数值模拟研究[J].岩土力学,2016,37(2):583-591.
LI Xiaofeng,LI Haibo,XIA Xiang,et al.Numerical simulation of mechanical characteristics of jointed rock in direct shear test[J].Rock and Soil Mechanics,2016,37(2):583-591.
[24] 朱小明,李海波,刘博.循环剪切荷载作用下含二阶起伏体模拟岩石节理力学特性研究[J].岩土力学,2014,35(2):371-379.
ZHU Xiaoming,LI Haibo,LIU Bo.Study of mechanical characteristics of simulated rock joints with second-order asperity under cyclic shear loading[J].Rock and Soil Mechanics,2014,35(2):371-379.
[25] 夏才初.工程岩体节理力学[M].上海:同济大学出版社,2002.
[26] 朱小明,李海波,刘博,等.含一阶和二阶起伏体节理剪切强度的试验研究[J].岩石力学与工程学报,2011,30(9):1810-1818.
ZHU Xiaoming,LI Haibo,LIU Bo,et al.Experimental study of shear strength of joints with first-order and second-order asperities[J].Chinese Journal of Rock Mechanics and Engineering,2011,30(9):1810-1818.
[27] 朱小明,李海波,刘博,等.含二阶起伏体的模拟岩体节理试样剪切特性试验研究[J].岩土力学,2012,33(2):354-360.
ZHU Xiaoming,LI Haibo,LIU Bo,et al.Experimental study of shear characteristics by simulating rock mass joints sample with second-order asperities[J].Rock and Soil Mechanics,2012,33(2):354-360.
[28] 黄达,黄润秋,雷鹏.贯通型锯齿状岩体结构面剪切变形及强度特征[J].煤炭学报,2014,39(7):1229-1237.
HUANG Da,HUANG Runqiu,LEI Peng.Shear deformation and strength of through-going saw-tooth rock discontinuity[J].Journal of China Coal Society,2014,39(7):1229-1237.
