随着能源需求量逐年增加,地下开采深度和强度越来越大。深部条件下地质环境愈趋复杂,在高地应力和开采强扰动条件下(动、静态应力叠加致灾原理[1]),极易发生超低摩擦效应,进而诱发超低摩擦型冲击地压等突发性工程动力灾害。如:辽宁红阳三矿冲击地压现场观察到巨量煤岩整体向巷道滑移达1~3 m,这种现象极可能是由高地应力状态下煤岩超低摩擦效应诱发的。
所谓超低摩擦效应,即在动载作用下,当冲击作用力的能量达到一定水平时,会在互相作用的块体间产生摩擦“消失”效应[2]。岩体超低摩擦理论最早由国外学者KURLENYA和OPARIN[3-5]提出并通过试验验证了其存在。ALEKSANDROVA和SHER[6-8]建立了一维块系介质模型并对应变波传播进行了实验及理论研究,发现波的传播速度和衰减程度在很大程度上取决于中间材料的黏性。RUTTER等[9]通过实验研究软弱夹层对断层泥摩擦效应的影响,发现软弱夹层对断层超低摩擦滑动起重要作用。MARK[10]认为,采矿活动及矿震等动力作用下,煤体可能会因“失去约束”而导致冲击地压等灾害发生。
国内,钱七虎院士[11]指出超低摩擦效应是深部开采中的关键科学问题以来,我国学者对超低摩擦效应发生机理和规律进行了大量研究。理论方面:王明洋等[12-13]对具有构造等级的岩体介质在变形过程中的储能性状进行了理论研究,分析其特点对块系介质动力变形与稳定性影响规律。王洪亮[14]、吴昊[15-17]等建立了深部块系岩体一维动力模型,给出了工作块体加速度及水平位移解析式。潘一山等[18-20]从摆型波传播动力模型角度,通过相邻块体间相对位移在拉伸方向的最大值给出了相邻块体间超低摩擦倾向判据,同时指出块系岩体中的动力传播还存在岩块间的“超强挤压”现象。蓝一凡[21]引入转角自由度,建立深部岩体的二维非连续块模型,发现在二维矩形隧洞围岩中存在超低摩擦现象。实验方面:崔永权等[22]研究侧向应力扰动对断层摩擦影响,发现应力降大幅度增加意味着侧向应力的小幅度扰动可能会引起“低摩擦”现象出现。王洪亮[14]、王德荣[23]、许琼萍[24]、吴昊[15-17]等基于Kurlenya的超低摩擦实验,研制出了一套深部岩体动态特性多功能实验装置,从工作块体水平位移角度,验证了超低摩擦效应。李杰等[25-27]利用自行研制的块系岩体动态力学性能测试试验系统,进行了一维块系岩体模型波动特性和不同初应力条件下冲击扰动诱发岩块滑移的物理模拟研究,获得冲击扰动诱发岩块不可逆位移、动力滑移失稳的关键力学机制、规律及充要条件。李利萍等[28-29]从塑性动力学角度解释了岩体超低摩擦效应,提出超低摩擦型冲击地压这一新概念。贾宝新等[30]等研究冲击载荷下块系岩体摆型波传播特性。任晓龙[31]以具有孔状结构的层理状花岗岩块体为研究对象,研究了不同静荷载和不同扰动荷载幅值作用下超低摩擦现象。岑夺丰[32]以汶川地震为背景,对强震触发顺层滑坡的滑动面动态摩擦特性及滑动摩擦准则、滑坡震裂-启动动力学模型等从理论到实例应用的系统研究。数值模拟方面:吕家庆[33]、李利萍[34]等以花岗岩块系模型为研究对象,用FLAC3D模拟了垂直冲击和水平静力共同作用、垂直冲击和水平冲击共同作用下的动力响应。王来贵等[35]将超低摩擦效应引入地震载荷下边坡结构面的研究,得到地震载荷下结构面法向应力状态调整规律及滑体启滑机制。
国内外学者对超低摩擦效应特别是一维动力模型进行了深入分析,但所关注指标多为块体水平位移、块体竖向加速度等参数,对表征块体间相对位置情况的竖向位移差研究较少。研究中多考虑深部条件下强冲击扰动对岩体模型的影响,上覆岩层压力对岩体影响的研究极少且所得竖向位移差表达式较为复杂。为此,在查阅了大量资料,以上述专家学者对超低摩擦效应的理论和实验研究为基础,推导出含上覆岩层压力的新块体间竖向位移差解析表达式,通过块系岩体模型的垂直冲击试验验证了理论模型的正确性。理论研究了花岗岩块系模型在垂直冲击作用下,块体质量、结构面阻尼、垂直冲击幅值及频率对模型块体间竖向位移差影响规律;最后以竖向位移差最小值(块体间最大拉伸量)作为评定超低摩擦效应易发与否的指标。研究结果以期对超低摩擦型冲击地压预测和防治提供参考。
1 超低摩擦效应理论模型
超低摩擦效应理论模型的建立,多采用弹簧或者弹簧阻尼模拟软弱夹层的力学特性,并通过连接质点来建立整体模型。
1.1 模型建立及位移差公式
深部岩体由裂隙和节理等地质构造所分割,超低摩擦效应机理与块体界面动力变形特性和块系稳定性密切相关。研究深部块体介质的变形特性必须首先确定块体界面法向和切向的动力特性。因此,块体间设置弹簧和阻尼器描述块状岩体界面间软弱连接介质对能量的传递和阻滞,刚度系数为k,阻尼系数为c。此外,在前人所做工作的基础上[17-18],将块体近似为等质量刚体,建立了如图1所示的动力计算模型。图1中,块体为尺寸相同的等质量块体,垂直冲击扰动力Pv(t),作用于块体1上表面形心,方向竖直向下。其函数形式为
式中,Pv为动力载荷幅值,N;ω=2πf,其中f为动载频率,Hz;t为动力计算时间,s。
块体的运动包含2个阶段:第1阶段为在垂直冲击作用下发生的受迫振动;第2阶段为t0时刻起块体以该时刻状态为初始条件的自由振动。

图1 受垂直冲击作用块体动力模型
Fig.1 Dynamic model of block subjected to vertical impact
块体系统由n个块体垂直叠放构成,设竖直向下为正方向,则竖直方向有运动方程:
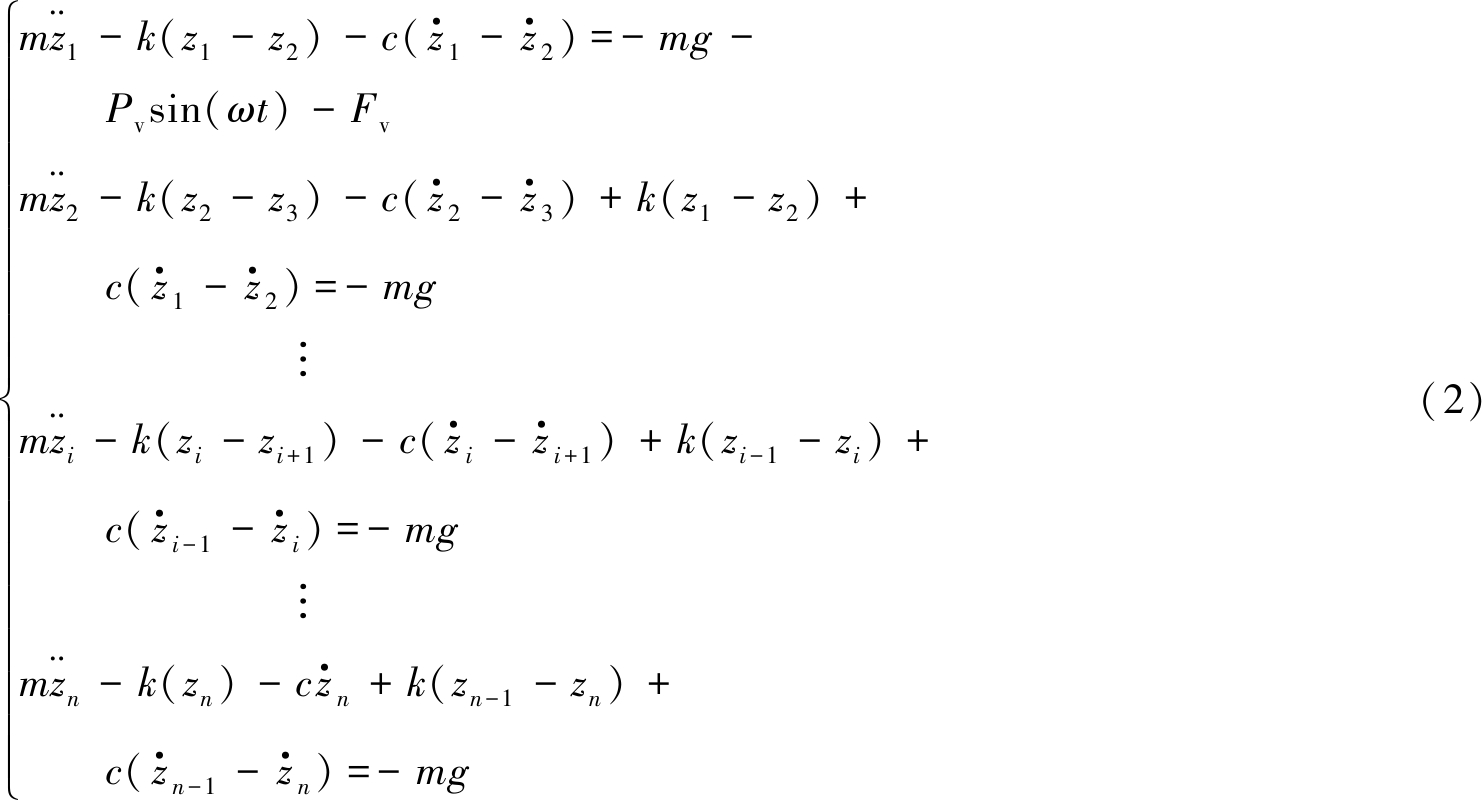
式中,m为块体质量,kg;zi为块体i的位移,m;g为重力加速度;Fv为模型垂直方向地应力合力,N。
将式(2)简化成矩阵形式,得

设z=z0+y,竖向平衡位置有
Kz0=b
(4)
解得各块体初始位移为
将z=z0+y,代入矩阵方程式(3),得
参考文献[8,16-17]的分析结果,得到模型中块体加速度及速度近似解为
z3/3)e-μz2zdz
(7)
式中,![]() 为弹簧刚度系数,N/m;c为阻尼系数,(N·s)/m;l为弹簧自由长度,m。
为弹簧刚度系数,N/m;c为阻尼系数,(N·s)/m;l为弹簧自由长度,m。
由式(7),(8)可求得各块体竖向加速度及速度,回代原方程(2)可得:
(1)2块体间竖向位移差为
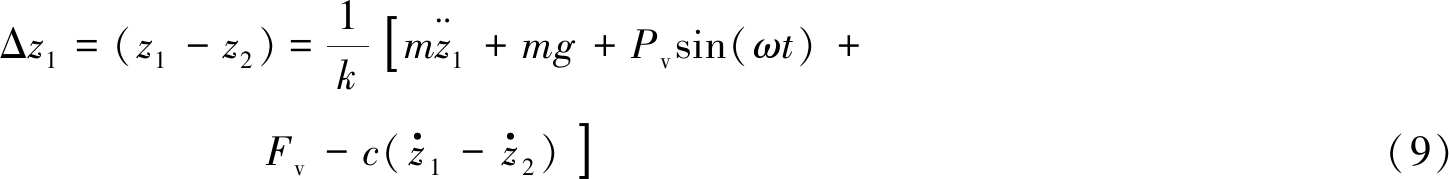
(2)3块体间竖向位移差为

(3)4块体间竖向位移差为

1.2 试验验证
为便于对比分析,验证理论模型的正确性,参考文献[2,17],进行垂直冲击试验。试验冲击装置由自由落体运动的钢球以及可调节高度的支架组成,钢球质量为116 g,冲击高度分别为5,10,15,20,25 cm,块体尺寸为100 mm×100 mm×50 mm,块体质量为1.4 kg,试验模型由5块岩块沿高度方向叠放,块间无软弱夹层,在块体1上施加垂直冲击载荷。测量装置为TST-5915数据采集仪,最高采样频率为100 kHz,加速度传感器采用江苏泰斯特CA-YD-193A型三向加速度计,量程为500g,Z向灵敏系数为0.989 mV/(m·s2)。加速度传感器分别粘贴在相邻岩块接触界面两侧,如图2所示。

图2 垂直冲击试验模型
Fig.2 Experimental model of vertical impact loading
理论公式中的计算参数,冲击频率及幅值由Hertz 撞击理论转化结果所得,见表1,其余参数参考文献[2]取值,l=0.005 m,k=107 N/m,c=260 N·s/m,Fv=0 N。以第3和第4块体加速度与冲击高度关系为例,将试验结果与理论模型计算结果进行了对比,如图3,4所示。
表1 Hertz 理论冲击能力学转化结果
Table 1 Mechanical transform results of impact pulse based on Hertz theory
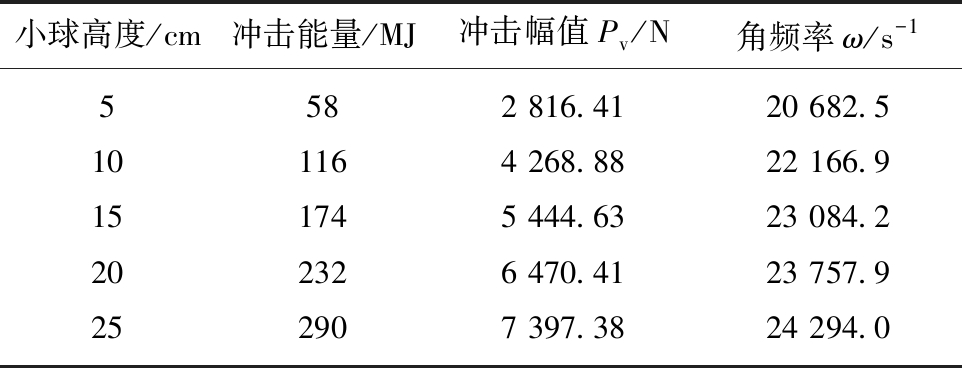
小球高度/cm冲击能量/MJ冲击幅值Pv/N角频率ω/s-15582 816.4120 682.5101164 268.8822 166.9151745 444.6323 084.2202326 470.4123 757.9252907 397.3824 294.0

图3 第3,4块体加速度试验值与理论值对比曲线
Fig.3 Comparison of experimental values and theoretical values of the acceleration of block 3 and 4 under impact loading

图4 不同冲击高度下第3,4块体加速度试验与理论最大 最小值对比曲线
Fig.4 Comparison curves for the experimental and theoretical acceleration of maximum and minimum on block 3 and 4 under different impact heights
由图3可知,本文所得加速度理论值与试验值都会随垂直扰动而产生上下波动并最终趋于稳定状态,其变化趋势一致。由图4可以看出,不同冲击高度下,第3和第4块体加速度最大值和最小值与冲击高度间关系试验结果与理论计算结果变化特征相同,第3块体加速度试验最大值和理论最大值均与冲击高度呈线性递增关系,第3块体加速度试验最小值和理论最小值均与冲击高度呈线性递减关系,两者变化趋势一致,而第4块体加速度与冲击高度间关系同样具有相同规律,试验和理论结果更为接近。以上对比分析从试验角度验证了理论模型正确性,同时也说明单向冲击试验结果是合理和可靠的。
2 竖向位移差影响因素分析
深部块系岩体超低摩擦效应机理及相关规律还不甚明晰,实际深部采矿工程实践发现,动载作用下超低摩擦型冲击地压极易发生。以n=5时3-4块体间竖向位移差变化曲线为例,进行理论分析。参数取值同上,以小球高度10 cm组的冲击载荷幅值和频率为基础组。
2.1 块体质量影响分析
块体质量大小反映了深部岩体破碎程度,质量越大,岩体越完整,为研究块体质量大小对岩体超低摩擦效应影响,取不同质量块体(0.9,1.4,2.4,3.4,4.4,5.4,6.4 kg),研究过程中其它量保持不变。在块系岩体模型各块体质量同步变化时3-4块体竖向位移差变化曲线如图5所示(图5中,竖向位移差为正,表示块体间处于压缩状态,为负,表示块体间处于拉伸状态)。

图 5 模型块体质量同步变化时3-4块体间竖向位移差曲线
Fig.5 Vertical displacement difference curves between 3-4 blocks when the block mass changes synchronously
(1)块体振动在时间尺度上分为强迫振动阶段和自由振动阶段,振动周期随着块体质量增加而逐渐增加。按竖向位移差变化情况可分为相互脱离、弱挤压、强挤压和超强挤压4个阶段(图6),超低摩擦现象发生在相互脱离阶段和弱挤压阶段。

图6 不同冲击载荷幅值时3-4块体间竖向位移差曲线
Fig.6 Vertical displacement difference curves between 3-4 blocks under different impact loading amplitudes
由图5可知,在块系模型受到垂直冲击载荷作用后,3-4块体间竖向位移差在冲击载荷作用下发生振荡,变化形式类似于准周期正弦曲线,但幅值逐渐减小,最终达到平衡。块体运动分为两个过程,在t0=0.142 ms之前,块体做强迫振动,在t0时刻之后,块体为有阻尼自由振动,最后逐渐稳定。块体间竖向位移差最大值出现在系统强迫振动阶段。此外,块体位移差达到最值的时间亦随块体质量变化而改变,表明块体质量对纵向波的传播影响明显,其振动周期随着块体质量增加而逐渐增加。
当块体开始叠放时(块体间无压缩),其竖向位移差为0;由块体间竖向位移差公式可知,块体叠放完成时(初始状态),块体在重力作用下相互挤压,出现初始竖向位移差(img+Fv)/k;如果不考虑块体间阻尼因素,当模型受冲击作用时,其最大竖向位移差(压缩量)为(img+Fv+Pv)/k;综上所述,块体的竖向运动过程按其竖向位移差变化情况可分为4个阶段:① 当Δzi<0时,为相互脱离阶段;② 当0<Δzi<(img+Fv)/k时,弱挤压阶段;③ 当(img+Fv)/k<Δzi<(img+Fv+Pv)/k时,强挤压阶段;④ 当(img+Fv+Pv)/k<Δzi时,为超强挤压阶段。
超低摩擦现象发生在相互脱离阶段和弱挤压阶段,在相互脱离阶段,块体间不再受压,其水平方向摩擦力为0,只要存在任意形式侧向力,都会发生超低摩擦效应,甚至可能导致超低摩擦型冲击地压等动力灾害发生。在弱挤压阶段,当水平扰动大于块体间最小静摩擦力时,块体会发生超低摩擦效应。(设块体在超强挤压及强挤压状态和静平衡状态时不发生侧向移动)。
(2)3-4块体间竖向位移差最小值随块体质量增加程对数规律递增,块体间的相对脱离程度越来越小,即块体越破碎,质量越小,超低摩擦效应愈趋显著。
图7为3-4块体间竖向位移差最小值随块体质量变化曲线,由图7可知,随着块体质量增加,位移差最小值以对数函数规律递增,块体质量越大,其位移差最小值越大,即块体质量越大,块体间的相对拉伸量逐渐减小(脱离程度减小),此过程中超低摩擦效应越来越不易发生,这与深部条件下岩体更趋破碎、超低摩擦效应更易发生的实际情况相一致[2]。

图7 3-4块体间竖向位移差最小值随块体质量变化曲线
Fig.7 Varies curve of minimum vertical displacement difference between 3-4 blocks with the mass of the block
2.2 块体间阻尼影响分析
块体间阻尼大小同样反应了块体间软弱介质性质,即块体间接触情况。为分析其对超低摩擦效应影响,阻尼系数c分别取:80,120,160,200,240,260,300,340,380 N·s/m,共9组,分析过程中其他变量保持不变。不同阻尼作用下块体间竖向位移差变化情况如图8所示。

图8 模型结构面阻尼不同时3-4块体间竖向位移差曲线
Fig.8 Vertical displacement difference curves between 3-4 blocks in different damping of structural surface
3-4块体竖向位移差随阻尼增加以线性规律递增,阻尼系数越大,超低摩擦效应越不易发生。
由图8可知,块体间结构面阻尼对模型强迫振动和自由振动阶段均有影响,但对模型自由振动阶段影响更为显著,随着阻尼系数增加,块体振动稳定所需时间显著减小,一方面表现为此阶段竖向位移差最小值随阻尼增加而增大(以线性规律递增),另一方面为竖向位移差趋于稳定时间逐渐减小。图9为3-4块体间竖向位移差最小值随块体间阻尼变化具体情况。模型在静力平衡状态时块体间竖向位移差保持为定值,在只改变块体间阻尼大小的过程中,3-4块体间竖向位移差的最小值逐渐增加,即块体间最大拉伸量随阻尼增加而逐渐递减,使超低摩擦效应发生的可能性逐渐减小。

图9 3-4块体间竖向位移差最小值随结构面阻尼变化曲线
Fig.9 Curve of minimum vertical displacement difference between 3-4 blocks with the damping of structural surface
2.3 冲击载荷幅值影响分析
冲击能量强度跟冲击载荷幅值大小密切相关。综放开采过程中区段煤柱在承受上覆岩层重力载荷的同时,也会受到回采作业的各种扰动(爆破震动、矿震、周期来压等)。在理论分析过程中改变冲击载荷幅值和频率大小以实现对冲击力大小和扰动周期的改变,研究其对超低摩擦效应影响规律。参考文献[2],冲击载荷幅值分别取:2 000,2 500,3 000,3 500,4000,4 500,5 000 N,共7组。此时,冲击频率及其他各变量为定值。模型在不同垂直冲击载荷幅值下工作块体竖向位移差变化曲线如图6所示。
3-4块体间竖向位移差最小值随冲击载荷幅值以线性规律递减,冲击载荷幅值越大,超低摩擦效应更容易发生。
由图6可知,冲击载荷幅值变化,使3-4块体间竖向位移差在强迫振动阶段和自由振动阶段的幅值均出现较大变化,但其周期保持不变。竖向位移差最小值随冲击载荷幅值增加呈线性规律变化,如图10所示。由于模型在静力平衡状态时块体间竖向位移差为定值,所以,在竖向位移差最小值随冲击载荷幅值以线性规律递减时,3-4块体间拉伸量(脱离程度)随冲击载荷幅值以线性规律递增,即拉伸量越来越大,更易造成超低摩擦效应的发生,这与实际情况下强扰动更易造成超低摩擦效应的实际情况相符。

图10 3-4块体间竖向位移差最小值随冲击载荷 幅值变化曲线
Fig.10 Curve of minimum vertical displacement difference between 3-4 blocks with impact loading amplitude
2.4 冲击载荷频率影响分析
冲击载荷频率反映了模型所受冲击能量集中程度,频率越大,冲击能量越集中。因此考察冲击载荷频率对块体间竖向位移差(以3-4块体间竖向位移差为例)影响,以期获得相关规律。分析过程中,垂直冲击载荷频率f取值为:500,1 000,1 500,2 000,2 500,3 000,3 500,4 000 Hz,其他变量均为定值(与基础参数相同)。不同冲击载荷频率作用下3-4块体间位移差变化曲线如图11所示。

图11 模型不同冲击载荷频率时3-4块体间竖向位移差曲线
Fig.11 Vertical displacement difference curves of 3-4 blocks under different impact loading frequencies
低频扰动对块体间竖向位移差影响最为显著,亦更易诱发超低摩擦效应。
由图11可知,模型所受垂直冲击载荷频率变化使3-4块体间竖向位移差变化显著。在冲击载荷幅值确定时,其频率增加,使冲击载荷周期减小,其作用于模型的时间减少,冲击能量减小,使块体运动趋于缓和,表现为竖向位移差最大值随冲击频率增加而逐渐减小,竖向位移差最小值随冲击频率增加而逐渐增加。而低频扰动使块体间超强挤压阶段和相对脱离变得更加突出,超强挤压压力增加会破坏块体,使之破碎化(即块体质量减小),亦造成块体间压力减小。两者相互作用,使超低摩擦型冲击地压等更容易发生,这与冲击地压的震前频率信号以低频为主相符[36]。当冲击载荷频率持续增加时,竖向位移差最小值随冲击频率的增加以对数函数关系递增,如图12所示。
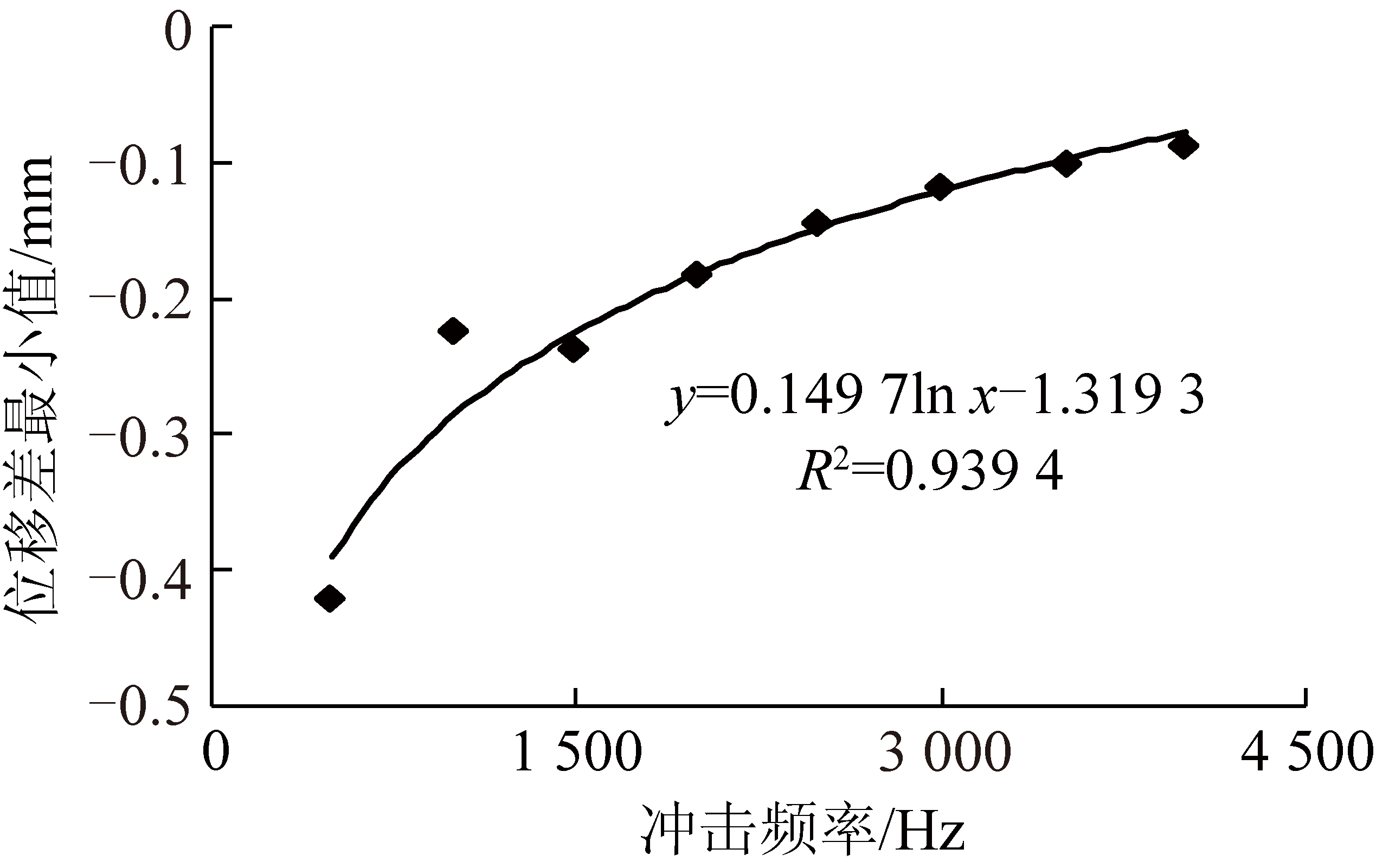
图12 3-4块体间竖向位移差最小值随冲击载荷频 率变化曲线
Fig.12 Minimum value of vertical displacement difference between 3-4 blocks with impact loading frequency
3 结 论
(1)垂直冲击作用是超低摩擦效应发生的前提条件;块系岩体模型受垂直冲击作用,块体在时间尺度上先后发生强迫振动和有阻尼自由振动,而按竖向位移差变化情况,块体所处状态分处4个阶段,即超强挤压阶段、强挤压阶段、弱挤压阶段和相互脱离阶段。
(2)模型内部因素结构面阻尼、块体质量主要影响块体自由振动阶段的运动状态,3-4块体间竖向位移差最小值随块体质量以对数规律递增、随块体间阻尼系数增加以线性规律递增;外界因素如垂直冲击载荷幅值与频率对模型中块体的整个运动过程都有较大影响,竖向位移差最小值随垂直冲击载荷幅值增加而线性递减,随冲击频率增加以对数规律递增。
(3)提出以竖向位移差最小值(对应实际情况下最大拉伸)来判断超低摩擦效应发生难易程度,得到块体间结构面阻尼越小、块体质量越小、垂直冲击频率越小而幅值越大、竖向位移差最小值越小,相对脱离程度越大,超低摩擦效应更易发生,这与实际深部情况下超低摩擦效应发生特征相一致。
[1] DOU Linming,MU Zonglong,LI Zhenlei,et al.Research progress of monitoring,forecasting,and prevention of rockburst in underground coal mining in China[J].International Journal of Coal Science & Technology,2014,1(3):278-288.
[2] 何满潮,钱七虎.深部岩体力学基础[M].北京:科学出版社,2010:547-570.
[3] KURLENYA M V,OPARIN V N,VOSTRIKOV V I.Pendulum-type waves:Part II.Experimental methods and main results of physical modeling[J].Journal of Mining Science,1996,32(4):245-273.
[4] KURLENYA M V,OPARIN V N,VOSTRIKOV V I.Effect of anomalously low friction in block media[J].Journal of Applied Mechanics and Technical Physics,1999,40(6):1116-1120.
[5] KURLENYA M V,OPARIN V N,BALMASHNOV A E G.On dynamic behavior of “self-stressed” block media,Part II:Comparison of theoretical and experimental data[J].Journal of Mining Science,2001,37(5):455-461.
[6] ALEKSANDROVA N I,SHER E N.Modeling of wave propagation in block media[J].Journal of Mining Science,2004,40(6):579-587.
[7] ALEKSANDROVA N I,CHEMIKOV A G,SHER E N.Experimental investigation into the one-dimensional calculated model of wave propagation in block medium[J].Journal of Mining Science,2005,41(3):232-239.
[8] ALEKSANDROVA N I,SHER E N,CHEMIKOV A G.Effect of viscosity of partings in block-hierarchical media on propagation of low-frequency pendulum waves[J].Journal of Mining Science,2008,44(3):225-234.
[9] RUTTER E H,HACKSTON A J,YEATMAN E.Reduction of friction on geological faults by weak-phase smearing[J].Journal of Structural Geology,2013,51:52-60.
[10] MARK Christopher.Coal bursts in the deep longwall mines of the United States[J].International Journal of Coal Science & Technology,2016,3(1):1-9.
[11] 钱七虎.深部地下工空间开发中的关键科学问题[A].第230次香山科学会议-深部地下空间开发中的基础研究关键技术问题[C].北京:2004.
QIAN Qihu.The key problems of deep underground space development[A].The key technical problems of base research in deep underground space development-the 230th Xiangshan science conference[C].Beijing:2004.
[12] 王明洋,戚承志,钱七虎.深部岩体块系介质变形与运动特性研究[J].岩石力学与工程学报,2005,24(16):2825-2830.
WANG Mingyang,QI Chenzhi,QIAN Qihu.Study on deformation and motion characteristics of blocks in deep rock mass[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(16):2825-2830.
[13] WANG M Y,LI J,MA L J,et al.Study on the characteristic energy factor of the deep rock mass under weak disturbance[J].Rock Mechanics and Rock Engineering,2016,49(8):3165-3173.
[14] 王洪亮,葛涛,王德荣,等.块系岩体动力特性理论与实验对比分析[J].岩石力学与工程学报,2007,26(5):951-958.
WANG Hongliang,GE Tao,WANG Derong,et al.Comparison of theoretical and experimental analyses of dynamic characteristics of block rock mass[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(5):951-958.
[15] 吴昊,方秦,王洪亮.深部块系岩体超低摩擦现象的机理分析[J].岩土工程学报,2008,30(5):769-775.
WU Hao,FANG Qin,WANG Hongliang.Mechanism of anomalously low friction phenomenon in deep block rock mass[J].Chinese Journal of Geotechnical Engineering,2008,30(5):769-775.
[16] WU Hao,FANG Qin,ZHANG Yadong,et al.Mechanism of anomalous low friction phenomenon in deep block rock mass[J].Mining Science and Technology,2009,19(4):409-419.
[17] 吴昊,方秦,张亚栋,等.一维块系地质块体波动特性的试验和理论研究[J].岩土工程学报,2010,32(4):600-611.
WU Hao,FANG Qin,ZHANG Yadong,et al.Propagation properties of stress waves in one-dimensional geo-block medium[J].Chinese Journal of Geotechnical Engineering,2010,32(4):600-611.
[18] 潘一山,王凯兴.岩体间超低摩擦发生机理的摆型波理论[J].地震地质,2014,36(3):833-844.
PAN Yishan,WANG Kaixing.Pendulum-type waves theory on the mechanism of anomalously low friction between rock masses[J].Seismology and Geology,2014,36(3):833-844.
[19] 王凯兴,潘一山.摆型波传播过程块系岩体频域响应反演岩块间黏弹性性质[J].煤炭学报,2013,38(S1):19-24.
WANG Kaixing,PAN Yishan.Frequency domain response of block-rock mass inversion partings viscoelastic property on pendulum-type wave propagation[J].Journal of China Coal Society,2013,38(S1):19-24.
[20] 王凯兴.基于摆型波理论的非连续岩体动力响应与防冲控制研究[D].阜新:辽宁工程技术大学,2013.
WANG Kaixing.Dynamic response of discontinuous rock mass base on the theory of pendulum-type waves and anti-impact control[D].Fuxin:Liaoning Technical University,2013.
[21] 蓝一凡.深埋洞室超低摩擦型岩爆发生机制与定量预测[D].重庆:重庆大学,2015.
LAN Yifan.The occurrence mechanism of anomalously low friction-type rockburst and its quantitative prediction in deep caverns[D].Chongqing:Chongqing University,2015.
[22] 崔永权,马胜利,刘力强.侧应力扰动对断层摩擦影响的实验研究[J].地震地质,2005,27(4):645-652.
CUI Yongquan,MA Shengli,LIU Liqiang.Effect of lateral stress perturbation on frictional behavior:An experimental study[J].Seismology and Geology,2005,27(4):645-652.
[23] 王德荣,陆渝生,冯淑芳,等.深部岩体动态特性多功能试验系统的研制[J].岩石力学与工程学报,2008,27(3):601-606.
WANG Derong,LU Yushen,FENG Shufang,et al.Development of multipurpose test system for dynamic behaviors of deep rock masses[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(3):601-606.
[24] 许琼萍,陆渝生,王德荣.深部岩体块系摩擦减弱效应试验[J].解放军理工大学学报(自然科学版),2009,10(3):285-28.
XU Qiongping,LU Yusheng,WANG Derong.Experimental study on friction weakened effect of deep block rock mass[J].Journal of PLA University of Science and Technology(Natural Science Edition),2009,10(3):285-28.
[25] 李杰,周益春,蒋海明,等.非线性摆型波问题的提出及科研仪器研制[J].湘潭大学自然科学学报,2017,39(4):22-28.
LI Jie,ZHOU Yichun,JIANG Haiming,et al.State of the nonlinear pendulum-type waves problems and development of the test equipment[J].Natural Science Journal of Xiangtan University,2017,39(4):22-28.
[26] 李杰,王明洋,蒋海明,等.爆炸与冲击中的非线性岩石力学问题(I):一维块系岩体波动特性的试验研究[J].岩石力学与工程学报,2018,37(1):38-50.
LI Jie,WANG Mingyang,JIANG Haiming,et al.Nonlinear mechanical problems in rock explosion and shock.Part I:Experimental research on properties of one-dimensional wave propagation in block rock masses[J].Chinese Journal of Rock Mechanics and Engineering,2018,37(1):38-50.
[27] 李杰,蒋海明,王明洋,等.爆炸与冲击中的非线性岩石力学问题(II):冲击扰动诱发岩块滑移的物理模拟试验[J].岩石力学与工程学报,2018,37(2):291-301.
LI Jie,JIANG Haiming,WANG Mingyang,et al.Nonlinear mechanical problems in rock explosion and shock.Part II:Physical model test on sliding of rock blocks triggered by external disturbance[J].Chinese Journal of Rock Mechanics and Engineering,2018,37(2):291-301.
[28] 李利萍,潘一山,王晓纯,等.开采深度和垂直冲击荷载对超低摩擦型冲击地压的影响分析[J].岩石力学与工程学报,2014,33(S1):3225-3230.
LI Liping,PAN Yishan,WANG Xiaochun,et al.Influence analysis of exploit depth and Vertical impact load on anomalously low Friction Rockburst[J].Chinese Journal of Rock Mechanics and Engineering,2014,33(S1):3225-3230.
[29] 李利萍,潘一山,王晓纯,等.考虑上覆岩层压力的深部岩体块系介质超低摩擦效应理论分析[J].自然灾害学报,2014,23(1):149-154.
LI Liping,PAN Yishan,WANG Xiaochun,et al.Theoretical analysis of ultra-low friction effect in deep blockrock mass considering overlying rock pressure[J].Journal of Natural Disasters,2014,23(1):149-154.
[30] 贾宝新,陈扬,潘一山,等.冲击载荷下块系岩体摆型波传播特性的试验研究[J].岩土力学,2015,36(11):3071-3076.
JIA Baoxin,CHEN Yang,PAN Yishan,et al.Experimental research on propagation characteristics of block-rock mass pendulum-type wave under shock load[J].Rock and Soil Mechanics,2015,36(11):3071-3076.
[31] 任晓龙.节理化岩体超低摩擦现象实验研究[D].北京:中国矿业大学,2017.
REN Xiaolong.Experiment study of ultra-low friction phenomenon on jointed rock mass[D].Beijing:China University of Mining & Technology,2017.
[32] 岑夺丰.强震触发顺层滑坡张性破裂及低摩擦启动机理[D].重庆:重庆大学,2017.
CEN Duofeng.Tensional rupture and low-friction initiation mechanism of bedding landslides triggered by mega-earthquakes[D].Chongqing:Chongqing University,2017.
[33] 吕家庆.深部岩体超低摩擦效应的FLAC-3D数值模拟研究[D].阜新:辽宁工程技术大学,2015.
LÜ Jiaqing.Numerical simulation of the effect of anomalously low friction of deep rock masses based on FLAC-3D[D].Fuxin:Liaoning Technical University,2015.
[34] 李利萍,王淋,邰英楼.动静组合加载作用下块系岩体动力响应分析[J].中国安全生产科学技术,2016,12(11):5-10.
LI Liping,WANG Lin,TAI Yinglou.Dynamic response analysis on block rock mass under combined static-dynamic load[J].Journal of Safety Science and Technology,2016,12(11):5-10.
[35] 王来贵,习彦会,周向.地震边坡超低摩擦效应启滑机理分析[J].防灾减灾工程学报,2016,36(4):595-600.
WANG Laigui,XI Yanhui,ZHOU Xiang,et al.Analysis of open-slip with anomalously low friction effect of slope under earthquake[J].Journal of Disaster Prevention and Mitigation Engineering,2016,36(4):595-600.
[36] 袁瑞甫,李化敏,李怀珍.煤柱型冲击地压微震信号分布特征及前兆信息判别[J].岩石力学与工程学报,2012,31(1):80-85.
YUAN Ruifu,LI Huamin,LI Huaizhen.Distribution of microseismic signal and discrimination of portentous information of pillar type rockburst[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(1):80-85.
