瞬变电磁法是以电磁感应定律为基础理论，在地面以不接地回线源或接地电性源作为发射源，在供电电流间歇期间进行观测二次场，通过研究二次场的空间和时间分布规律达到探测地下目标体的一种电法勘探方法。该方法由于对低阻体特别敏感，近年来得到了广泛的应用[1]，特别是在煤田采空区、陷落柱等构造探测及其富水性评价方面发挥了重要的作用[2-5]。

瞬变电磁对低阻体的反映比较灵敏，易于确定低阻目标的平面位置，但对于目标体埋深的确定，一直没有有效的方法，这是制约该方法进行精细探测的关键问题所在。由于影响探测深度的因素很多，实际应用中会受到许多干扰因素的影响，所以该问题一直没有得到很好的解决。探测深度对于施工设计和资料解释都是非常重要的，直流电法中不同极距、电磁法中不同频率不同时间对应目的层深度范围是地球物理工作者最关心的。自20世纪70年代以来，有许多学者对直流电法中探测深度做了详尽的研究[6-8]，ROY A对于不同装置形式探测深度进行了比较[9]，OLDENBURG D W针对激发极化法和直流电法的探测深度进行了深入研究[10]。SIMON D就电阻率成像深度和视电阻率对数计算深度等做了比较[11]。在电磁法勘探中，SPIES 在20世纪80年代就给出了频率域趋肤深度公式和时间域瞬变电磁场的扩散深度公式[12];XUE提出了一种改进的定源中心回线深部探测方式[13];接着有不同学者都对电磁法的探测深度进行了研究[14-16]。国内早在20世纪90年代，方文藻等[17]就对瞬变电磁的探测深度及分辨率做过理论研究，采用正演程序计算了二层及三层地电断面测深曲线，以归一化时间为横坐标，归一化感应电压为纵坐标，根据均匀大地情况下烟圈效应感应电流的传播速度，得到感应电压曲线偏离时间，代入计算电压的响应的公式中，把电压衰减到噪声电平的覆盖层厚度定义为最大探测深度，用噪声电平代替响应的磁场响应，获得最大探测深度。陈明生等[18]基于烟圈效应等效电流环扩散理论，推导了平面波场极大值的传播深度，并通过时频分析法阐明了时间域和频率域探测深度之间的关系，从理论上论述了瞬变电磁的探测深度;认为TEM场一般已忽略位移电流，对于第一道观测时间来说已经属似稳状态，其扩散深度即为阶跃脉冲到达的深度，主要取决于延迟时间和大地电导率，TEM场到达异常体后被异常体反射回来的阶跃脉冲被接收到，地面观测数据时间大约是瞬变电磁场扩散深度时间的2倍。闫述等[19]讨论了TEM的探测深度与大地电阻率以及上覆地层的关系，大地电阻率增加，场所到达的深度增加，反之亦然;即在低阻介质中，场的传播要比高阻介质慢，如果上覆地层是低阻，要达到相同的探测深度，则需要更大的延迟时间。上覆地层若为低阻时，常常可以观测到比较强的信号，但并不代表探测深度会增大，其主要是上覆低阻地层使电磁场衰减非常慢，掩盖了下部异常体的微弱信息，这其实是不利于探测深部地质体的。薛国强[20]通过时间域和频率域之间的等价性，研究了时间和频率之间关系，把时间换算为频率，通过频率域的平面波场的探测深度公式估算瞬变电磁的探测深度。一般认为瞬变电磁的探测深度受地下电阻率、电流、线框面积、延迟时间以及仪器最小可分辨电压等因素的影响，许多学者都对此作了研究[21-25]。王庆乙[26]对线框大小影响瞬变电磁的探测深度提出了质疑，他认为大回线探测深，小回线探测浅的认识是对实际应用的误导，小回线也可以探测深部的异常，瞬变电磁的探测深度取决于场源脉宽所含的频率，磁矩或回线边长不具备深度效应，周期脉冲函数的基频是决定探测最大深度的决定因素。

如何把延迟时间转换为实际探测深度是瞬变电磁方法中的一个关键问题，影响着该方法解释的准确性和应用效果,特别是电性分界面的确定[27-30]。李貅[31]等提出基于浮动薄板理论，计算出地下电磁响应的视纵向电导，再通过视纵向电导得到视探测深度，该方法对原始数据质量要求很高，如果计算的纵向电导有问题，会导致计算的深度变化很大，甚至下一时间道计算深度小于上一时间道计算深度。另一种方法就是依据烟圈效应原理，采用趋肤深度的公式进行计算，该方法对于理论数据应用较好，简单方便;但是对于实际数据，存在着各种干扰，计算出的视电阻率再根据该公式计算深度也会出现晚期的探测深度较早期浅的问题。基于烟圈效应理论的时深转换更加实用一些，它是首先计算出全期视电阻率，再根据全期视电阻率得到电磁场的传播速度，最后根据扩散深度公式换算出瞬变电磁探测深度，实际应用过程中根据地电断面不同，乘以经验系数。

综上所述，对于不同地电断面或实际资料的瞬变电磁精确探测深度，至今还没有一个比较通用的算法或公式能够完全解决它。目前该方法的处理解释主要以视电阻率的断面图进行定性解释为主，结合已知钻孔和地质资料进行深度校正，然后应用到整个测区，难以达到精准处理解释要求。针对此问题，我们提出以电性标志层识别技术为关键，借助于钻孔和三维地震成果资料，对测区任意点数据进行深度校正，然后结合视电阻率断面图异常特征，对整个测区的瞬变电磁资料进行精准处理解释。

1方法原理

1.1瞬变电磁时深转换方法

根据烟圈效应原理，随着时间的推移，等效感应涡流环从地面向下逐渐扩展，其传播速度与地下电导率密切相关，可导出地下涡流场传播的瞬时速度v，通过瞬时速度和涡流场传播时间可求出涡流场在地下传播的平均速度进而求出地层总厚度H(i)。

基于层状地电模型如图1所示，该算法的关键在于求层速度。首先根据测量数据dB/dt求取全域视电阻率，如果所用线框比较大，探测的目标层埋深相对偏深，为了简便起见，也可以用晚期视电阻率，即

(1)

式中，ρτ为视电阻率;M为发射磁矩;q为接收偶极矩;ε(i) 为感应电压;t(i)为采样延迟时间;B为磁感应强度。

图1 地电模型示意
Fig.1 Geo-electric model

依据电磁感应定律，计算地下每一层涡流场的扩散速度为

(2)

式中，μ0为真空中的磁导率;σ为电导率。

然后根据每一层的传播速度，对某一深度以上到地表之间这段地层，求出电磁波所用总路程和总时间，求出该段的平均速度，如式(3)所示，再依据双倍旅程的概念，即地表接收到的信号是波传播深度的2倍，求出探测深度公式。

(3)

(4)

1.2视电阻率微分极值

瞬变电磁常采用视电阻率深度等值线图进行地下电性结构的定性解释，由于视电阻率是地下介质以及地形等因素的综合影响，其只能大致反映地层的电性变化，对于电性标志层的划分以及局部异常体的边界范围的确定等都很模糊，难以适应煤矿地面瞬变电磁的精细处理要求;因此，我们采用视电阻率纵向微分极值识别电性标志层。视电阻率纵向微分其实是描述视电阻率随深度的变化率，即视电阻率的梯度，其值越大，表明视电阻率的变化越大，在电性层分界面处，视电阻率变化一般比较大，其在微分曲线上会出现极值，它比视电阻率参数对地层的分辨更敏感，我们采用视电阻率微分极值结合视电阻率参数，综合识别电性标志层。

(5)

其中，φ(z)为视电阻率纵向微分，也即视电阻率纵向一次导数，该微分极大值可识别地下电性层标志，通过已知电性层扩展到整个研究区域内每条测线求取K值，可得到整个工区内测点的K值。

1.3基于三维地震资料的任意测点深度系数校正

由于瞬变电磁探测深度确定误差非常大，常常给资料解释带来很大困难，导致解释结果和实际地层不符。三维地震数据可以较准确的确定9号煤层深度，误差不超过5%，这可以作为瞬变电磁视电阻率微分极值识别电性标志层一个标准。煤层是中高阻，瞬变电磁方法对其不灵敏，但是煤层和上覆地层电性差别比较大，是由低阻向高阻过渡的电性界面，主要通过视电阻率微分极值确定目标层的上界面位置，然后根据地震数据确定的9号煤层深度进行对比，得到各测点的深度校正系数。三维地震测线和瞬变电磁测线不是一一对应的，有些测线数据是吻合的，也有一部分瞬变电磁测线数据没有三维地震数据资料。因此，如果要对全区瞬变电磁测点进行精准的深度校正，笔者提出利用已知的地震测线成果，对未知测点进行内插，内插方法选择的是克里金插值法，该方法能够对研究对象提供一种最佳线性无偏估计，按照空间属性在空间位置上的变异分布，确定对一个待插点值有影响的距离范围，然后用此范围的采样点估计待插点的属性值，从而提取任意测线任意测点的校正系数K。图2即为任意测点K值内插图，黑色为三维地震测线确定K值对应的测点，红色为经过内插后K值对应的测点，可以看出，经过内插后所有测点都有对应的校正系数。

图2K值内插点
Fig.2 ValueKinterpolation points

图3为全区任意点K值等值线图，从图3可以清楚的看到测区不同区域，校正系数不同，整体取值为0.65～1.43，同一测线大号点的K值较小号点的K值大，中间上部K值比较大，可见，在整个测区需要根据地震成果资料对不同位置的测点采用不同的K值校正才比较合理。这主要是由于引用水平导电薄层理论，将层状大地各地层的影响等效为导电薄层的影响进行计算。实际地形和下部地层起伏不平也会造成视电阻率计算误差，从而导致全区有不同的校正系数，北部校正系数比较大与其奥灰层等高线降低以及地表地形起伏有关。因此，我们通过内插方法实现全区任意测点的K值校正。

图3 全区任意点K值等值线
Fig.3 ValueKcontour map of the any point in the whole area

2电性标志层的识别

2.1研究区概况

堡子井田位于山西省沁水煤田晋城矿区西南部。其井田含煤地层包括石炭系上统太原组及二叠系下统山西组、下石盒子组。其中太原组、山西组为主要含煤地层，前者含主要可采9号煤层，后者含主要可采2，3号煤层，下石盒子组含1～2层薄煤层。含煤地层属于中高阻，9号煤层起伏比较大，在工区范围内落差可达300 m。根据地表出露、钻孔勘探及井下揭露，井田地层由老到新发育有奥陶系中统峰峰组，石炭系中统本溪组、上统太原组，二叠系下统山西组、下石盒子组、上统上石盒子组，第四系中、上更新统及全新统。其中奥陶系中统峰峰组为含煤地层基底，厚度大于100 m，以深灰色厚层状石灰岩夹灰黄色泥灰岩和钙质泥岩薄层。灰岩中节理、裂隙和岩溶均很发育。该井田位于沁水煤田南缘，由于受区域构造带的影响总体为一走向北西，倾向北东的单斜构造，次一级构造为向南仰起的向斜构造，地层倾角一般8°～13°，局部达25°～35°。井田发现褶曲1个，断层57条，其中以往地质勘探推断16条、井下揭露41条，未发现陷落柱。

井田内主要含水层为第四系中上更新统松散岩类孔隙含水层，二叠系下统山西组、下石盒子组及上统上石盒子组碎屑岩类裂隙含水层，石炭系上统太原组碎屑岩类夹碳酸岩类岩溶裂隙含水层，奥陶系中统碳酸盐岩岩溶裂隙含水层。其中，中奥陶统峰峰组石灰岩含水层为井田内煤系地层下伏的主要充水含水层，钻探结果表明最大厚度为103 m，岩性为石灰岩、泥质灰岩、白云质灰岩、灰质白云岩和花斑状灰岩，裂隙溶洞极发育，具明显的水蚀作用，裂隙多充填有方解石结晶体。根据水文孔抽(放)水试验资料，奥灰水位标高在+950 m左右，渗透系数0.009～10.74 m/d，单位涌水量0.003 23～0.6 L/(s·m)，为弱-中等富水性含水层，水质属于HCO3·SO4-Ca·Mg型水。

以钻孔ZKB1-1为例，首先用钻孔的测井资料统计深度及电阻率数据并绘制出数据的阶梯图(图4(a))，通过阶梯图，根据等效电阻率法划分理论模型的深度及电阻率并绘制成阶梯图(图5(a)左图)，进行正演，并进行时深转换，将所得的数据绘制出正演理论曲线。

图4 测井数据统计
Fig.4 Statistical diagram of logging data

图5 典型界面确定
Fig.5 Typical interface determination

由图5(b)可知，视电阻率曲线随着深度的增加逐渐上升，说明地下电性构造的电阻率逐渐升高，与实际建立的地电模型一致。但是从视电阻率测深曲线上不易看到电性标志层的大致深度，因为视电阻率曲线是地下介质电性的综合反映，只能进行整体的定性解释，很难进行精确的电性层划分。视电阻率微分极值能够很好的反映视电阻率的变化大小，在电性层分界处，电阻率发生突变，视电阻率的梯度最大，据此，我们求出视电阻率微分曲线，即纵向一阶导数，由图5可知，视电阻率一阶导数随深度的增加逐渐增加到达最大值后开始减小，该最大值深度和电性标志层分界面的位置吻合。笔者提取该钻孔旁的实测曲线，绘制其视电阻率曲线和视电阻率微分曲线，在ZKB1-1深度为260 m处对应太原组中段，主要是石灰岩、砂岩、泥岩和煤层组成的海陆交互相地层，ZK201在深度为420 m处对应太原组下段含煤地层与建立的理论模型的计算结果进行比较，结果发现，视电阻率测深曲线和理论曲线非常接近，都呈逐渐上升态势，适合于定性解释;而视电阻率微分曲线出现了极大值，这个极大值恰好在建立的理论模型电性分界面附近。由此可见，通过视电阻率微分极值确定电性标志层是可行的，比视电阻率测深曲线更能够精细刻画地下电性分层。对于由ZK201建立的理论模型和井旁实测视电阻率曲线以及微分极值曲线，具有类似的特征。

2.2电性层的识别及校正

如图6所示，256线是经过任意点K值校正后的视电阻率断面图对比。由于煤层为中高阻，但煤层与上覆地层电阻率差异较大，可以此进行电性层识别。视电阻率曲线是地下介质综合电性的反映，难以对分界面反映清楚，通过视电阻率微分可放大这种微小的变化，更容易识别出电性层，然后再进行深度校正。在校正前，视电阻率等值线图在大号点处视电阻率基本沿水平方向变化，甚至在尾部有点上翘，而且探测深度明显偏浅，造成这种现象的原因有两点，一是该区域地层发生了变化，不是均匀层状地层，用视深度计算公式计算的结果就会和实际有偏差;另一个因素是由于实测数据受到干扰，发生畸变，浅部视电阻率计算结果偏小，导致相应的深度整体也偏小。根据地震成果资料，实际煤层等高线从小号点到大号点是由浅变深，逐渐倾斜的，解释结果与实际不太符合。

图6 256线视电阻率校正断面对比
Fig.6 256 apparent resistivity correction section comparison

依据视电阻率微分极值等值线图(图6)，可以看到视电阻率微分能够精细的刻画电阻率参数的变化，非常有利于电性标志层的识别。可以清楚的看到，在视电阻率微分等值线图近似中间层位，等值线出现极大值，呈封闭或半封闭形态，从纵向上看，是视电阻率微分局部极值的位置，横向上变化平缓，在大号点处向上移动，在点号270～290下方附近存在隐伏状体，很可能在9号煤层下方存在另一隐伏电性构造。校正后的视电阻率断面图，出现了局部多层状极值，主要是由于采用多个K值校正后，原来的深度数据会发生变化，导致本是光滑的曲线在网格化时发生了细微变化，但整体电性变化和原始视电阻率一致。在实际使用时，需结合目标煤层等高线的位置，对原始视电阻率进行深度校正，得到新的校正后视电阻率等值线图(图6(c))。可以看到，视电阻率等值线基本沿煤层等高线分布，在点号240～250处，273～293处出现了2个明显的凹陷，且在2个断层之间，说明这两处是明显的低阻异常，有较强富水性，校正后的视电阻率等值线图解释更加合理了。

图7 344线视电阻率校正断面对比
Fig.7 344 apparent resistivity correction section comparison

同样，由图7可知，没有经过校正的视电阻率断面图结果存在深度不够的现象，特别是在大号点区域，深度明显偏浅，等值线由小号点到大号点逐渐上升，而9号煤层等高线是逐渐向深部倾斜，显然与实际不符。我们依据地震数据成果，在该条测线上对K系数进行平面上内插，得到该条测线的任意测点的K系数，然后结合视电阻率微分极值图，对整条测线计算深度进行校正。从图7(b)可以看出，视电阻率微分等值线图在纵向中间接近煤层附近出现封闭的高值形态，在两边出现3字形态，我们依据极值原理，把极值连线作为电性层标志，然后根据地震成果资料确定的9号煤层等值线，计算校正系数K值，得到校正后的视电阻率断面图，如图7(b)所示。经过校正后的视电阻率等值线基本沿煤层等高线方向，在断层附近等值线沿纵向变化比较大，呈S或封闭的低阻形态，与实际地层吻合的比较好。

所以，经过视电阻率微分极值来确定电性标志层实际深度与时深转换深度的系数K值，K值深度校正后的视电阻率在实际地层对应、异常区域及深度的确定方面都有所改进，经过此方法校正后具有很明显的优势，处理后与实际地层资料符合。

3测区资料精准处理成果

3.1测区富水区分布成果

依据视电阻率的特征对全区的TEM断面进行了解译,然后把断面异常放在平面图上，异常相关性较好的平面上至少相邻两条线上有异常，把其平面位置圈起来，形成平面异常分布。对奥灰顶异常区进行了圈定(图8)，可见异常区基本分布全区，具有沿北西向分带的特点。异常区均为低阻，依据奥灰岩电阻率与含水性的关系，推断上述异常区为奥灰顶富水区。

图8 奥灰顶界面富水区分布
Fig.8 Distribution map of water-rich zone at Ordovician Ash top interface

3.2异常验证试验

2018年4月以来堡子矿施工了8个钻孔，钻孔出水量情况如下:① 奥灰出水情况:钻孔B1-1奥灰抽水涌水量为0.36 m3/h;钻孔B1-2奥灰抽水涌水量为10.37 m3/h;钻孔B1-4奥灰抽水涌水量为1.52 m3/h;钻孔Of4奥灰抽水涌水量为23.6 m3/h;钻孔Of5奥灰抽水涌水量为6 m3/h。② K2出水情况:钻孔Of6,K2灰岩抽水涌水量1.0 m3/h;钻孔B1-1,K2灰岩抽水涌水量0.36 m3/h;钻孔B1-2,K2灰岩抽水涌水量0.75 m3/h;钻孔B1-4,K2灰岩抽水涌水量0.95 m3/h;钻孔B1-5,K2灰岩抽水涌水量1 m3/h;钻孔Kf3，K2灰岩抽水涌水量24 m3/h。根据各钻孔出水情况，与精准处理成果进行对比分析。

图9为奥灰层视电阻率平面图，红色代表高阻，蓝色代表低阻。即在线号136～240，点号251～351区间，视电阻率表现为高阻，阻值范围在380～580 Ω·m，且对应钻孔B1-1,B1-4，其奥灰抽水涌水量分别为0.36，1.52 m3/h;线号272～356内，视电阻率表现为中低阻，阻值范围在260～360 Ω·m，对应钻孔B1-2,Of4,Of5，分别为10.37，23.6，6 m3/h，奥灰抽水涌水量较钻孔B1-4多，中高阻区域对应钻孔涌水量较小，低阻区域对应涌水量相对较大，精准处理成果与钻探成果基本吻合。

图9 奥灰层视电阻率平面
Fig.9 Apparent resistivity plane map of Ordovician Grey Layer

3.3导水通道的确立

如图10所示，钻孔Kf3出水点位于308测线221测点附近，其左右两边均出现断层F35，F36，且随着测点号的减小低阻异常随之向测区南部移动;校正后的视电阻率图的等值线在该出水点附近呈现近S非层状，纵向梯度大，综合其他几条断面分析有可能在钻孔Kf3西南方向，K2层位存在导水通道。再从测区西南边得知有一条前沟河流，且该河流位置地处于背斜构造，使得地表水沿着断层F35，F36之间侧向补给进去。据此，可以判断虽然此处电阻率并非低阻，但存在导水通道，从而导致Kf3水量较大。

图10 308线视电阻率断面
Fig.10 308 apparent resistivity section map

3.4任意测点深度计算误差

将时深转化后的数据求取纵向一阶导，绘制出纵向一阶导数断面图，进而寻找圈闭极大值区域(电性标志层)数据，然后再与三维地震推断的9号煤层数据，做一深度比值得出K值，再经过K值深度矫正来绘制最终的视电阻率断面图。该方法依赖于三维地震数据的准确性，三维地震数据确定9号煤层的深度误差不超过5%，因此，计算该误差也是依赖于此的，与先验资料的精准性有莫大关系。把经过视电阻率微分极值方法校正后的深度，与验证钻孔实际深度进行误差计算。经过K值深度校正后的标志层高程与后期施工钻孔资料中的9号煤层高程计算相对误差应小于5%。当然，这与三维地震数据可教准确探测到9号煤层深度为前提。具体计算以钻孔B1-4为例，地表标高为1 106.304 m，9号煤层深度为227.77 m，即9号煤层标高为地表标高与9号煤层深度之差。相对误差为

d=(|x-μ|)/μ×100%=(|840-

878.534|)/878.534×100%=4.386%<5%

其中，x为电性标志层经过K值校正后的高程;μ为9号煤层标高。后期施工的钻孔资料的地层层位与孔旁瞬变电磁测点计算的相应层位深度计算误差小于5%。

4结 论

(1)根据钻孔电阻率测井曲线，建立研究区相应的地球物理模型，通过正演计算和时深转换，获得电性标志层的微分极值响应特征，通过理论与孔旁实测视电阻率曲线及微分极值曲线的对比，确定微分极值点与电性标志层的对应关系，由此实现基于视电阻率曲线微分极值点的电性标志层识别。

(2)基于三维地震成果数据，提取研究区内任意测点处标志层的准确深度，通过对同一测点处该标志层准确深度与基于视电阻率曲线微分极值点电性标志层深度对比，得到瞬变电磁测点深度校正系数K值，进而通过内插实现测区内瞬变电磁任意测点深度的校正。

(3)建立了一套煤矿地面瞬变电磁资料精准处理方法系统，以视电阻率微分极值识别电性标志层为基础，通过三维地震成果对任意TEM测点进行深度校正，可达到对目标层异常的精准解释。

(4)依据视电阻率微分极值校正后视电阻率断面图不连续非层状等特征，结合多条断面图相关关系以及地表水的补给关系，确立了测区导水通道的存在。

(5)采用该方法对堡子矿测区瞬变电磁资料进行了精细处理，由点及线，再由线及面逐一解释了该区的奥灰顶富水性异常特征，根据相关性原理，划分了该区富水性异常范围，与实际基本吻合，通过钻孔验证，深度误差小于5%。

视电阻率微分极值识别电性层虽然有一定的效果，但该方法也有一定的适用性，其电性层主要是指低阻高阻层的分界面，如果是很薄的煤层，效果不明显;另外，实际数据中夹杂着各种噪音，视电阻率微分后放大了噪音，实际应用中需结合地质钻孔等已知资料仔细区分。

参考文献 :

[1] 薛国强,于景邨.瞬变电磁法在煤炭领域的研究与应用新进展[J].地球物理学进展,2017,32(1):325-332.

XUE Guoqiang,YU Jingcun.New development of TEM research and application in coal mine exploration[J].Progress in Geophysics,2017,32(1):325-332.

[2] 陈康,薛国强,陈卫营,等.一种煤层顶板富水性快速评价方法[J].地球物理学进展,2017,32(4):336-341.

CHEN Kang,XUE Guoqiang,CHEN Weiying,et al.Rapid evalution method for the water abundance of coal seam roof[J].Progress in Geophysics,2017,32(4):336-341.

[3] 代凤强.瞬变电磁法探测煤层顶板岩层赋水性的应用[J].工程地球物理学报,2017,14(2):225-230.

DAI Fengqiang.The application of transient electromagnetic method in detection of water bearing property of Coal Seam Roof Strata[J].Chinese Journal of Engineering Geophysics,2017,14(2):225-230.

[4] 梁庆华.矿井瞬变电磁法在煤矿中的探测方法及异常特征分析[J].矿业安全与环保,2015,42(2):72-75.

LIANG Qinghua.Detection method and abnormal characteristics analysis ofmine transient electromagnetic technique in coal mine[J].Mining Safety & Environmental Protection,2015,42(2):72-75.

[5] 杨建军,吴汉宁,冯兵,等.煤矿采空区探测效果研究[J].煤田地质与勘探,2006,34(1):67-70.

YANG Jianjun,WU Hanning,FENG Bing,et al.Research on prospecting effect for gob area of coal mines[J].Coal Geology & Exploration,2006,34(1):67-70.

[6] BHATTACHARYA B B,SEN M K.Depth of investigation of collinear electrode arrays over homogeneous anisotropic half-space in direct current methods[J].Geophysics,1981,46(5):768-780.

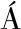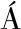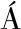[7] SNDOR Szalai,ATTILA Novk,LSZL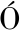Szarka.Depth of investigation and vertical resolution of surface geoelectric arrays[J].Journal of environment and Engineering Geophysics,2009,14(1):15-23.

[8] ROY A,APPARAO A.Depth of investigation in direct current methods[J].Geophysics,1971,36(5):943-959.

[9] ROY A.Depth of investigation in Wenner,Three-electrode and dipole-dipole DC resistivity methods[J].Geophysical Prospecting,2010,20(2):329-340.

[10] OLDENBURG D W,LI Y.Estimating depth of investigation in DC resistivity and IP surveys[J].Geophysics,1999,64(2):403-416.

[11] SIMON D Carrière,KONSTANTINOS Chalikakis,CHARLES Danquigny,et al.Using resistivity or logarithm of resistivity to calculate depth of investigation index to assess reliability of electrical resistivity tomography[J].Geophysics,2017,82(5):EN93-EN98.

[12] SPIES B R.Depth of investigation in electromagnetic sounding methods[J].Geophysics,1989,54(7):872-888.

[13] XUE G,BAI C,YAN S,et al.Deep sounding TEM investigation method based on a modified fixed central-loop system[J].Journal of Applied Geophysics,2012,76,23-32.

[14] JAMES E R,JAMES C M.Doubling the effective skin depth with a local source[J].Geophysics,1999,64(3):732-738.

[15] HUANG H P.Depth of investigation for small broadband electromagnetic sensors[J].Geophysics,2005,70(6):G135-G142.

[16] ZHOU Chao,ZHAO Siwei.The application of OCTEM in exploration of coal mine gob[A].International Geophysical Conference[C].2018:1631-1634.

[17] 方文藻,李予国,李貅,等.瞬变电磁测深法的探测深度及分辨率[A].中国地球物理学会学术年会[C].北京:1991.

FANG Wenzao,LI Yuguo,LI Xiu，et al.The detection depth and resolution of transient electromagnetic method[A].Annual Meeting of Chinese geophysics Society[C].Beijing:1991.

[18] 陈明生,石显新.对瞬变电磁测深几个问题的思考(四)——从不同角度看瞬变电磁场法的探测深度[J].煤田地质与勘探,2017,45(5):144-150.

CHEN Mingsheng,SHI Xianxin.Detecting depth of transient electromagnetic method from different points of view[J].Coal Geology & Exploration,2017,45(5):144-150.

[19] 闫述,石显新,陈明生.瞬变电磁法的探测深度问题[J].地球物理学报,2009,52(6):1583-1591.

YAN Shu,SHI Xianxin,CHEN Mingsheng.The probing depth of transient electromagnetic field method[J].Chinese Journal Geophysics,2009,52(6):1583-1591.

[20] 薛国强.论瞬变电磁测深法的探测深度[J].石油地球物理勘探,2004,39(5):575-578.

XUE Guoqiang.On surveying depth by transient electromagnetic sounding method[J].Oil Geophysical Prospecting,2004,39(5):575-578.

[21] 王善勋,刘军,雷振.瞬变电磁(TEM)中心回线装置发射框边长与最佳探测深度关系的探讨[J].物探化探计算技术,2012,34(5):548-551.

WANG Shanxun,LIU Jun,LEI Zhen.The relationship between the loop size and the optimal detecting depth in in-loop TEM[J].Computing Techniques for Geophysical and Geochemical Exploration,2012,34(5):548-551.

[22] 吴信民,杨海燕,杨亚新,等.论电法勘探的理论探测深度[J].东华理工大学学报(自然科学版),2013,36(1):60-64.

WU Xinmin，YANG Haiyan，YANG Yaxin，et al.Theoretical depth of investigation of electric method prospecting[J].Journal of East China Institute of Technology,2013,36(1):60-64.

[23] 吴信民,张振坤,徐剑波.瞬变电磁法理论的探测深度问题[J].地球物理学进展,2015,30(3):1333-1336.

WU Xinmin,ZHANG Zhenkun,XU Jianbo.Theoretical depth of investigation of transient electromagnetic method[J].Progress in Geophysics,2015,30(3):1333-1336.

[24] 陈魁奎，王心义.瞬变电磁法探测盲区深度减少和探测深度增加技术[J].河南理工大学学报(自然科学版)，2016，35(6):796-801.

CHEN Kuikui，WANG Xinyi.The technology of reduce the detection blind area depth and increase the detection depth of transient electromagnetic method[J].Journal of Henan Polytechnic University(Natural Science)，2016，35(6):796-801.

[25] 徐剑波.瞬变电磁法理论探测深度的研究及应用[D].南昌:东华理工大学，2014.

XU Jianbo.The study and application of transient electromagnetic sounding on the theoretical depth of investigation[D].Nanchang:East China Institute of Technology,2014.

[26] 王庆乙.对瞬变电磁法回线边长决定探测深度的质疑[J].物探与化探,2007,31(4):327-332.

WANF Qingyi.Querying the depth formula of TEM’S[J].Geophysical & Geochemical Exploration,2007,31(4):327-332.

[27] 敬荣中,林剑,肖志强.K剖面法在岩溶勘查中的应用[J].地质与勘探,2002,38(2):78-81.

JING Rongzhong,LIN Jian,XIAO Zhiqiang.Application of K section method to KARST exploration[J].Geology and Exploration,2002,38(2):78-81.

[28] 薛国强,宋建平,李貅.用瞬变电磁法识别地下电性分界面[J].煤田地质与勘探,2003,31(5):49-51.

XUE Guoqiang,SONG Jianping,LI Xiu.Recognizing electrical interface with the transient electromagnetic method[J].Coal Geology & Exploration,2003,31(5):49-51.

[29] 冉云.瞬变电磁测深数据的小波分析处理与电性层划分[D].太原:太原理工大学，2010.

RAN Yun.Wavelet analysis processing and electrical layer division for transient electromagnetic data[D].Taiyuan:Taiyuan University of Technology,2010.

[30] 李超.瞬变电磁视纵向电导微分成像应用研究[D].西安:长安大学2010.

LI Chao.The study of differential coefficient imaging of apparent vertical conductance in transient electromagnetic method[D].Xi’an:Chang’an University，2010.

[31] 李貅.瞬变电磁测深的理论与应用[M].西安:陕西科学技术出版社，2002.