随着矿井开采水平不断延伸，煤炭资源开采的水害问题日益严重。含/导水异常体的探测是水害防治的基础，在众多的探测手段中，矿井瞬变电磁法具有对低阻体敏感、距离目标体近异常强度大、施工方便等优点，在巷道掘进超前探测、工作面富水区域探测等领域得到了广泛的应用。开展矿井瞬变电磁法的三维正演研究，不仅能指导实际工作中的资料解释、提高解译精度，还能为尚处于研究阶段的三维反演奠定基础，对该方法的发展具有重要的促进作用。

针对矿井瞬变电磁法正演问题，姜志海采用2.5维有限差分法正演了全空间条件的涡流扩散，指出与半空间的“烟圈”扩散方式不同，全空间条件下涡流的中心始终位于发射线圈平面[1]。谭代明、占文峰、陈健强采用三维节点有限元法也得到了相同的结论[2-4]。刘志新将发射源简化为磁偶源并采用三维节点有限元法正演了巷道的影响，指出巷道的存在使瞬变电场响应值减小，巷道规模越大，对探测结果影响越大[5]。杨海燕和岳建华采用三维有限差分法正演了巷道、关断电流等对矿井瞬变电磁响应的影响，结果表明巷道的影响主要集中在早期，线性和半正弦关断电流的影响主要表现在“早期”，关断时间越长，关断效应对瞬变场的影响越向瞬变“晚期”延伸[6-9]。于景邨和常江浩采用三维有限差分法对老空水的矿井瞬变电磁响应进行了研究，老空水正对发射回线法线时响应最强，当老空水位于巷道一侧时，会在巷道另一侧产生范围和幅值都相对较小的假异常[10-11]。胡博和岳建华采用边界元法对巷道的影响进行了正演，指出围岩电阻率越低，巷道的影响越大[12]。刘晓和谭捍东初步验证了伪谱法对矿井瞬变电磁法正演的适用性[13]。陈丁和程久龙则采用积分方程法对全空间条件下孔中瞬变电磁响应进行了研究，指出孔中瞬变电磁应同时观测瞬变电磁的竖直和水平分量[14]。程久龙和黄少华采用有限差分法正演了各向异性介质的瞬变电磁场响应，指出各向异性介质的对称主轴与探测方向之间夹角对瞬变电磁响应具有较大影响[15]。

综上所述，前人通过对矿井瞬变电磁法的2.5维或三维正演得到了很多有益的成果，采用的方法主要为有限差分法、积分方程法和节点有限元法，这些方法应用于复杂地质模型时均受到一定的限制[16]。而矢量有限元法(由于基函数位于棱边，又称棱边有限元法)的出现很好地解决了节点有限元法的“伪解”以及与结构相关的奇异性问题[17]，具有对模型适用性强、精度高等优点。鉴于此，笔者开展基于时域矢量有限元法的矿井瞬变电磁法三维正演研究，提高复杂地质模型正演的精度。

1时域矢量有限元正演算法

1.1控制方程推导

针对地学问题，准静态条件(忽略位移电流)下，时间域中的麦克斯韦方程组为

×H=J+Js

(1)

(2)

·D=0

(3)

·B=0

(4)

式中，为哈密顿算子;H为磁场强度;E为电场强度;D为电位移矢量;B为磁感应强度;t为时间;Js为场源电流密度;J为场源激发的传导电流密度。

此外，还有3个辅助的介质特性方程如下

B=μH，D=εE，J=σE

(5)

其中，μ，ε，σ分别为磁导率、介电常数和电导率。针对地学问题，常见矿物的磁导率与真空磁导率μ0十分接近，故设μ=μ0。

由式(2)，(4)可假设

B=×A

(6)

φ

(7)

式中，A为磁矢量势;φ为标量势。

在引入库仑规范·A=0(矢量有限元中该条件自动满足)的条件下，φ=0，证明如下:

根据式(3)，(5)和(7)可得

在每个单元体内，假设ε是均匀的，由上式得·(φ)=0，且×(φ)≡0，故φ=0。因此

(8)

将式(6)，(8)和介质特性方程代入式(1)，可得磁矢量势的赫姆霍兹(Helmholtz)方程为

×(

(9)

1.2弱形式方程

假设场源距离模型边界足够远，则在模型外边界上可采用理想导体边界条件，即电场、磁场在外边界上的切向分量为0，即

式中，n为模型外表面的单位法向量。

根据Galerkin加权余量法，基于上述边界条件和控制方程(9)的电磁场问题的弱形式经变换、简化后为

∭Ω[(×A)·(

∭Ωμ0(Js·N)dV

(10)

式中，N为矢量基函数;Ω为模型区域。

1.3单元分析

为更好地模拟复杂地电模型，采用一阶四面体矢量单元进行单元分析。单元的节点(阿拉伯数字)与棱边(罗马数字)间的编码规则如图1所示。

图1 四面体矢量单元的节点和棱边
Fig.1 Nodes and edges in a tetrahedral vector element

单元e中，点(x,y,z)处的矢量势A在某一时刻t的值可由六条棱边的矢量基函数表示为

(11)

式中，上标e为棱边i、矢量A等均为基于单元的局部编码或变量。其中矢量基函数

(12)

式中，下标i1和i2为棱边i对应的节点编号;为棱边长度;和为2个节点对应的标量基函数。可以证明，矢量基函数的散度为0，即

(13)

结合式(11)，(13)，即可证明·A=0。

基函数还具有如下性质:在其对应的棱边i上的切向分量为1，在其他5条棱边上的切向分量为0，在不包含棱边i的面上的切向分量也为0。

将式(11)代入式(10)，式(10)左端的第1部分可写为

∭Ωe(×Ae)·(×

式中，为某一条边的基函数;{Ae}为6×1的列向量，其元素为为6×6的对称矩阵。

同理，式(10)左端体积分中第2部分离散后可表示为同样为6×6的对称矩阵。矩阵元素的表达式详见参考文献[17]。

对于式(10)的右端的计算，为减小线电流引起的奇异性，可将回线源看做多个较短导线元的组合，并在源附近采用较密的网格剖分。ANSARI、李建慧等以该方法处理导线源，取得了好的效果[18-19]。设发射源位于z=0的平面上，其中通过的电流如图2所示。

图2 发射回线示意
Fig.2 Sketch map of transmitter loop

以图2中的Ⅰ边为列，详述计算过程，网格剖分后，设Ⅰ边分布于若干个单元中，且总是与这些单元的某一个棱边重合，其中的源电流密度为

式中，I(t)为随时间变化的电流强度;δ为冲激函数;dl为导线元的长度;(x0,y0)为其中心坐标;ex为x方向的单位矢量。设置不同的I(t)即可加载不同波形的发射电流。

令{Fe}为6×1的列向量，其元素为

根据基函数的性质，只有导线元所在棱边的其余棱边均为0。

将上述单元矩阵组按照局部-全局编码规则装起来后，最终得到形如下式的总体矩阵方程

(14)

1.4时间离散

由于式(14)中包含对时间的微分，因此求解未知数A(t)需对时间进行离散，本文采用无条件稳定的向后差分法进行。为提高精度，采用如下具有二阶精度的差分格式[20]，假设t时刻之前的A均为已知，则

(15)

其中，Δt为时间步长。将式(15)代入式(14)，可得

上式即为A(t)的递推公式，可见求解时需对这一与步长Δt相关的矩阵求逆。根据瞬变电磁场前期变化剧烈、后期变化平缓的特点，先使用一个固定的时间步长(比如Δt0)计算至某一时刻，然后增大时间步长(如增大为2Δt0)，再计算到某一时刻，而后再次增大时间步长，以此类推，直至计算结束。

2算法验证

通过均匀全空间模型的解析解和有限元解的对比，验证上述算法的正确性。模型大小为8 km×8 km×8 km，电导率0.01 S/m(电阻率100 Ω·m)，发射源为边长2 m的正方形回线，水平置于模型的中心，关断时间为0，采用中心回线接收，接收线圈等效面积100 m2，在10-6～10-2s的时间内对数等间距分布41个时间门(电流开始关断的时刻为0时间)。

模型的网格剖分采用Delaunay法剖分非结构化四面体网格，单元尺寸随着与发射源距离的增加而逐渐增大，剖分后共有30 021个单元，在CPU为E3-1230 V2、内存32 GB的台式机上的计算时间为166 s。均匀全空间模型的有限元解和解析解的对比如图3所示，41个时间门的相对误差的绝对值均小于1.5%，均方相对误差为0.84%，有限元解和解析解吻合良好。

图3 均匀全空间有限元解及其相对误差
Fig.3 FEM solution of homogeneous whole-space and its relative errors

3算例分析

3.1关断效应

实际施工时，发射电流不可能瞬变为0，总是需要经过一段时间后才能衰减为0。实际与理想电流关断波形的偏差，也会使实际的瞬变电磁响应偏离理论值，称之为“关断效应”。在均匀全空间模型的基础上，分别设置关断时间为10 μs的线性和指数关断电流以及关断时间为100 μs的线性关断电流(图4)，研究电流关断波形和关断时间引起的矿井瞬变电磁响应畸变。

图4 关断电流示意
Fig.4 Sketch map of ramp current

由图5可知，关断时间均为10 μs时，指数关断相比线性关断，引起的畸变更小，激发的响应也能更快地接近解析解，这是因为与线性关断相比，指数关断电流的波形更接近理想的阶跃电流。线性关断时，电流完全关断之前的感应电压基本不衰减，推断是因为电流关断过程中，接收线圈中的感应电压U可以分为由发射回线中电流变化引起的部分(称之为U1)和由大地中感应涡流衰减引起的部分(称之为U2)，U1∝ dI/dt，而电流线性关断时，dI/dt为常数，且U1的强度要远大于U2，因此U基本不变，图5中两种线性关断电流在10 μs之前的U基本相差10倍也验证了上述推论;在电流完全关断的瞬间，U1消失，因此感应电压出现了明显的突降;此外，与关断时间10 μs相比，关断时间100 μs引起的畸变更加向晚期延伸。

图5 不同关断电流的U-t曲线
Fig.5U-tcurves under different ramp current

3.2巷道影响

矿井瞬变电磁法的施工总是在巷道中进行的，不考虑巷道中的支护和机械设备，巷道空间可视为电导率为0的高阻异常体，破坏了理想的全空间条件，引起瞬变电磁响应的畸变。

围岩的电阻率和发射回线边长保持不变，在均匀全空间模型中设置横截面10 m×10 m、长1 000 m的巷道，分别在巷道的掘进工作面和中心设置如图6所示的2组相互垂直的发射回线(Tx1～Tx4)，由模型的对称性和发射电流的矢量分解可知，巷道引起的最大畸变必然在这4个线圈之中。

图6 巷道和发射回线布置示意
Fig.6 Sketch map of tunnel and transmitting loop layout

关断时间为0时，由巷道引起的瞬变电磁响应畸变如图7所示。巷道的影响主要表现为使早期的感应电压降低，随着电磁波的扩散，巷道影响迅速降低，20 μs后含巷道影响的数据与理想全空间的相对误差小于10%。巷道引起的畸变随发射回线位置的变化规律如下:发射回线位于巷道中心时的畸变程度大于回线位于掘进工作面时，回线朝向顶底板或侧帮时的畸变程度要大于朝向掘进工作面时，具体为Tx4>Tx3>Tx2>Tx1。

图7 有无巷道的U-t曲线(关断时间为0)
Fig.7U-tcurves of models with and without tunnel (turn off time 0)

巷道的影响主要集中在早期，而在实际施工中，仪器一般为线性关断且有着数百微秒的关断时间，因此无需考虑由巷道引起的数据畸变。为验证上述推论，在Tx4发射回线中加载线性关断时间为100 μs的发射电流，正演结果如图8所示。含巷道影响的数据与理想全空间的最大相对误差小于6%，实际施工中可以忽略不计。本文之所以设置规模超过实际的巷道，就是为了能更好地说明上述结论。

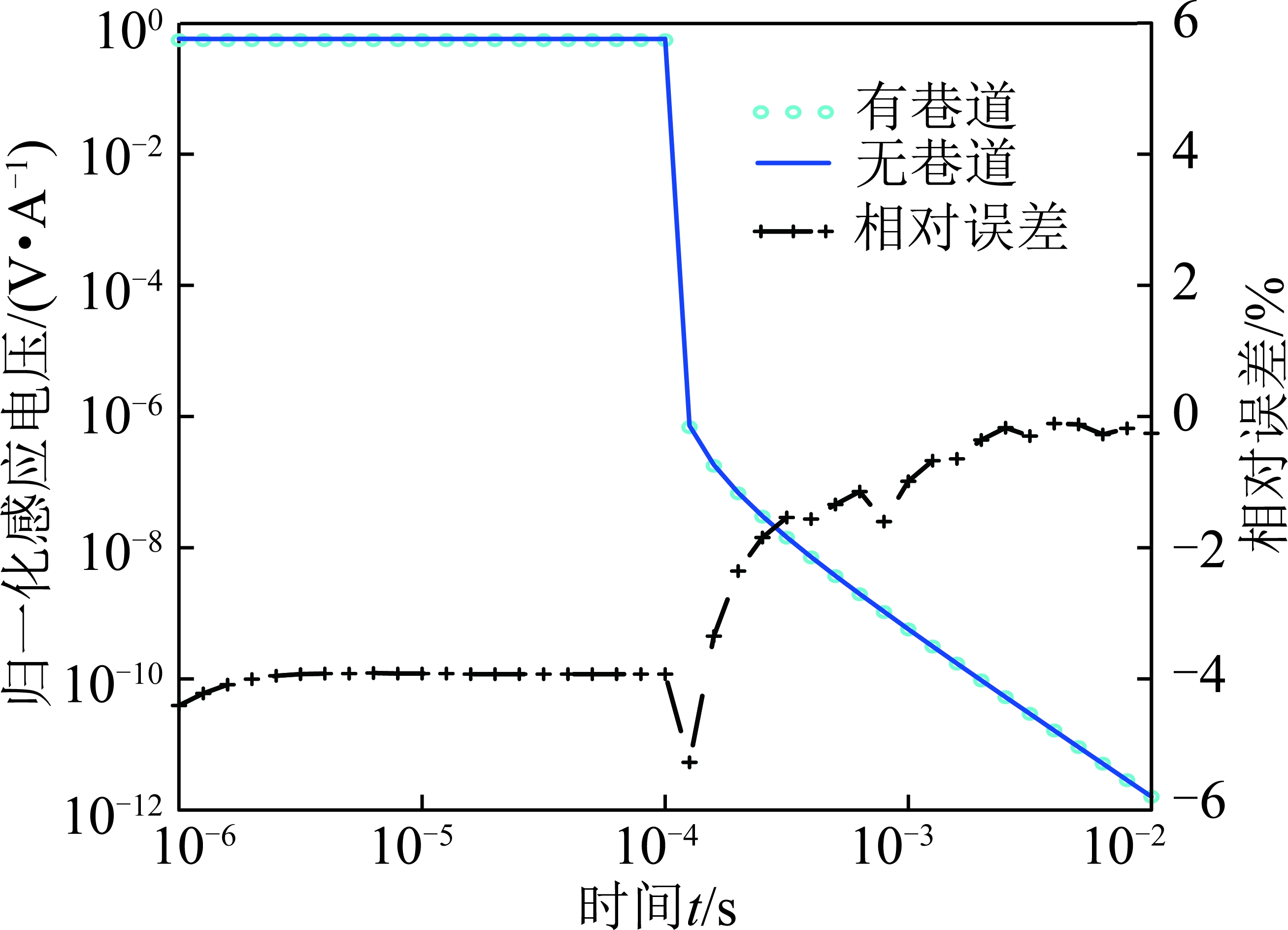
图8 有无巷道的U-t曲线(关断时间100 μs，Tx4回线)
Fig.8U-tcurves of models with and without tunnel (turn off time 100 μs,Tx4 loop)

3.3积水采空区

积水采空区是矿井瞬变电磁法的重要探测对象之一，研究其响应特征对于指导实际工作中的资料解释具有重要意义。模型设置如图9所示，在电导率为0.01 S/m(电阻率100 Ω·m)的围岩中，有一电导率为0.002 5 S/m(电阻率400 Ω·m)、厚10 m的高阻煤层，在煤层中有一规模为50 m×50 m×10 m大小的积水采空区，其电导率为4 S/m(电阻率0.25 Ω·m)。模型整体大小、发射回线边长与3.2节中的一致，发射电流线性关断，关断时间100 μs。发射回线Tx的中心点为原点O，它与积水采空区左侧面中心O′的连线定义为z方向，OO′的长度为r，本文取r=25 m。为更好地显示积水采空区，图中隐去了围岩和大部分煤层。正演时采用转动发射线圈的方式模拟实际施工中的扇形探测，引入类球坐标的角度参数(θ,φ)以更好地描述发射回线法向量nT的朝向。图9中，σ1，σ2，σ3分别为围岩、煤层和积水采空区的电导率;(θ,φ)为回线指向引入的类球坐标的角度参数。

图9 积水采空区模型示意
Fig.9 Sketch map of watery goaf

图10为φ=90°时不同角度θ(nT指向在水平面上变化，故称之为“水平剖面”，如图11所示)的U-t曲线对比，为突出异常只显示了电流完全关断之后的20个时间门，简洁起见只显示了θ=0°～90°的曲线，θ=-90°～0°的响应可由模型的对称性得到。不论线圈角度如何，相比无采空区时，感应电压在500 μs之前都有一定的增长，500 μs之后随着电磁波扩散出低阻异常体，接收到的感应电压趋于无采空区时。随着θ趋近于0，即nT逐渐指向异常体的中心，500 μs之前的感应电压逐渐升高。

图10 不同θ角度的U-t曲线(φ=90°)
Fig.10U-tcurves of variousθ(φ=90°)

图11 水平剖面示意(φ=90°)
Fig.11 Sketch map of horizontal section(φ=90°)

图12为φ=0°时不同角度θ(称之为“垂直剖面”，即nT的指向在竖直面上变化，图13)的U-t曲线对比，同样基于模型的对称性图中只显示了θ=0°～90°的曲线。与φ=90°相同，感应电压相比正常煤层有明显的升高，但φ=0°时，最强的低阻异常响应并不是nT指向积水采空区中心(θ=0°)时，而是在nT指向顶底板(θ=90°)时。

图12 不同θ角度的U-t曲线(φ=0°)
Fig.12U-tcurves of variousθ(φ=0°)

图13 垂直剖面示意(φ=0°)
Fig.13 Sketch map of vertical section(φ=0°)

图14 500 μs时感应涡流密度分布
Fig.14 Distribution of induced eddy current density at 500 μs

对于这种看似反常的现象，本文以500 μs时nT指向积水采空区中心(φ=0°,θ=0°)和顶底板(φ=0°,θ=90°)时感应涡流分布为例进行解释。nT指向采空区中心和顶底板时x=0平面的涡流密度分布如图14所示。可见感应涡流主要集中在异常体内(图中红色线框所示)，此时瞬变电磁响应主要取决于异常体内的涡流，而nT指向顶底板时异常体内的涡流密度远大于指向采空区中心时，因此nT指向顶底板时的低阻异常响应更强。该现象也可作如下定性解释:全空间条件下介质中的涡流可以看作一系列平行于发射回线、并以椭球面的方式扩散的电流环，因此，体积和形状一定的异常体，其平行于发射回线的规模对瞬变电磁响应的影响更大，而根据本文的模型设置，nT指向顶底板时，异常体平行于发射回线的规模更大，更有利于涡流的产生和发展，因此低阻异常响应更强。

4结 论

(1)基于时间域麦克斯韦方程和矢量有限元天然满足的库仑规范推导了磁矢量势的赫姆霍兹方程，结合齐次边界条件推导了相应的弱形式方程，采用对模型适用性强的一阶四面体矢量单元对弱形式方程进行了单元分析，并在单元分析时将回线源视为多个电流元克服了源的奇异性，时间离散则采用具有二阶精度、步长逐渐增大的向后差分法进行，实现了复杂地质模型的矿井瞬变电磁法全波形响应计算。均匀全空间模型的有限元数值解相对于解析解的均方相对误差为0.84%，表明本文算法是正确且具有较高精度的。

(2)关断效应会使感应电压升高，关断时间相同时，线性关断波形的影响大于指数关断，关断波形相同时，关断时间越长，关断效应的影响越向晚期延伸。

(3)巷道会使早期的感应电压减小，但对晚期的数据影响很小，因此考虑实际仪器的关断时间后，巷道的影响基本可以忽略。

(4)对前方长方体状积水采空区的正演结果表明，积水采空区会使感应电压升高，在水平剖面上最强的低阻异常响应出现在发射回线指向采空区中心时，但在垂直剖面上却出现在发射回线指向顶底板时。对这种现象，本文从涡流角度给出了一些解释，但仍需进行更深入的研究，以揭示更深层次的机理。

参考文献 :

[1] 姜志海.巷道掘进工作面瞬变电磁超前探测机理与技术研究[D].徐州:中国矿业大学,2008.

JIANG Zhihai.Study on the mechanism and technology of advanced detection with transient electromagnetic method for roadway drivage face[D].Xuzhou:China University of Mining and Technology,2008.

[2] 谭代明.隧道超前探水全空间瞬变电磁理论及其应用研究[D].成都:西南交通大学,2009.

TAN Daiming.Research on theory and application for advanced prediction of water by whole space transient electromagnetism[D].Chengdu:Southwest Jiaotong University,2009.

[3] 占文锋,武玉梁.全空间瞬变电磁法三维正演模拟与现场试验研究[J].中国煤炭，2016，42(5):42-47.

ZHAN Wenfeng,WU Yuliang.Study on 3d forward modeling and field test of full-space transient electromagnetic method[J].China Coal,2016,42(5):42-47.

[4] 陈健强.采空区全空间瞬变电磁响应特征与应用研究[D].北京:煤炭科学研究总院,2017.

CHENG Jianqiang.Study on response characteristics and applications of whole-space transient electromagnetic method in goafs[D].Beijing:China Coal Research Institute,2017.

[5] 刘志新.矿井瞬变电磁场分布规律与应用研究[D].徐州:中国矿业大学,2007.

LIU Zhixin.Study on the distribution and application of mine transient electromagnetic field[D].Xuzhou:China University of Mining and Technology,2007.

[6] 岳建华,杨海燕,胡搏.矿井瞬变电磁法三维时域有限差分数值模拟[J].地球物理学进展,2007,22(6):1904-1909.

YUE Jianhua,YANG Haiyan,HU Bo.3D finite difference time domain numerical simulation for TEM in-mine[J].Progress in Geophysics,2007,22(6):1904-1909.

[7] 岳建华,杨海燕.巷道边界条件下矿井瞬变电磁响应研究[J].中国矿业大学学报,2008,37(2):152-156.

YUE Jianhua,YANG Haiyan.Research on response of transient electromagnetic field in underground mine with boundary condition of laneway[J].Journal of China University of Mining & Technology,2008,37(2):152-156.

[8] 杨海燕,岳建华.瞬变电磁法中关断电流的响应计算与校正方法研究[J].地球物理学进展,2008,23(6):1947-1952.

YANG Haiyan,YUE Jianhua.Research on response calculation and correction technique of turn-off current in the transient electromagnetic method[J].Progress in Geophysics,2008,23(6):1947-1952.

[9] 杨海燕.矿用多匝小回线源瞬变电磁场数值模拟与分布规律研究[D].徐州:中国矿业大学,2009.

YANG Haiyan.Study on numerical simulation and distribution regularity of transient electromagnetic field with mine-used multi small loop[D].Xuzhou:China University of Mining and Technology,2009.

[10] 于景邨,常江浩,苏本玉,等.老空水全空间瞬变电磁法探测三维数值模拟研究[J].煤炭科学技术,2015,43(1):104-108,112.

YU Jincun,CHANG Jianghao,SU Benyu,et al.Study on whole space transient electromagnetic method prospect three dimensional numerical modeling of gob water[J].Coal Science and Technology,2015,43(1):104-108,112.

[11] CHANG Jianghao,YU Jincun,LIU Zhixin.Three-dimensional numerical modeling of full-space transient electromagnetic responses of water in goaf[J].Applied Geophysics,2016,13(3):119-132,161-162.

[12] 胡博,岳建华,于润桥.巷道对全空间瞬变电磁场影响的边界元数值模拟[J].中国矿业大学学报,2013,42(5):774-781.

HU Bo,YUE Jianhua,YU Runqiao.Numerical simulation of the roadway effect on whole-space transient electromagnetic fields by boundary element method[J].Journal of China University of Mining & Technology,2013,42(5):774-781.

[13] 刘晓,谭捍东.瞬变电磁法全空间三维伪谱法模拟[J].地球物理学进展,2016,31(1):268-273.

LIU Xiao,TAN Handong.3D pseudo-spectral method for TEM modeling in whole-space[J].Progress in Geophysics,2016,31(1):268-273.

[14] 陈丁,程久龙,王阿明.矿井全空间孔中瞬变电磁响应积分方程法数值模拟研究[J].地球物理学报,2018,61(10):300-311.

CHEN Ding,CHENG Jiulong,WANG Aming.Numerical simulation of drill hole transient electromagnetic response in mine roadway whole space using integral equation method[J].Chinese Journal of Geophysics,2018,61(10):300-311.

[15] 程久龙,黄少华,温来福,等.矿井全空间三维主轴各向异性介质瞬变电磁场响应特征研究[J].煤炭学报,2019,44(1):285-293.

CHENG Jiulong,HUANG Shaohua,WEN Laifu,et al.Response characteristics of three-dimensional axial anisotropic media for transient electromagnetic method in underground whole-space[J].Journal of China Coal Society,2019,44(1):285-293.

[16] 李建慧.基于矢量有限单元法的大回线源瞬变电磁法三维数值模拟[D].长沙:中南大学,2011.

LI Jianhui.3D numerical simulation for transient electromagnetic field excited by large source loop based on vector finite element method[D].Changsha:Central South University,2011.

[17] JIN Jianming.The finite element method in electromagnetics (Third edition)[M].New Jersey:Wiley,2014.

[18] ANSARI S,FARQUHARSON C G.3D finite-element forward modeling of electromagnetic data using vector and scalar potentials and unstructured grids[J].Geophysics,2014,79(4):E149-E165.

[19] 李建慧,胡祥云,陈斌,等.复杂形态回线源激发电磁场的矢量有限元解[J].石油地球物理勘探,2017,52(6):1324-1332.

LI Jianhui,HU Xiangyun,CHEN Bin,et al.3D electromagnetic modeling with vector finite element for a complex-shaped loop source[J].Oil Geophysical Prospecting,2017,52(6):1324-1332.

[20] JOHN H M,KURTIS K F.Numerical methods using MATLAB(Fourth edition)[M].New Jersey:Prentice Hall,2004.