气固流化床以其燃料来源广、适应性强，气固流动可操控等优点被广泛应用在能源，化工等工业生产过程[1]。在流化床内稠密气固两相流体系中，由于流体相与固体相相互作用直接影响到床内质量、动量与能量交换以及反应速率与效率，因此，深入探讨流化床内气固流动机理对流化床反应器设计制造与精准操控具有重要意义。

目前，用于模拟气固两相流的传统模型主要有基于欧拉-欧拉法的双流体模型[2]与基于欧拉-拉格朗日法的颗粒轨道模型[3]。其中，对流体相而言，两种模型都需要求解相对复杂的N-S方程，且边界难以处理。近些年来发展起来的格子Boltzmann方法[4]能够有效克服以上传统数值模拟方法的缺陷。格子Boltzmann方法(LBM)是介于宏观连续模拟与微观分子动力学模拟之间的介观模拟方法[5]，近年来一些学者将其与离散单元法(DEM)耦合以模拟气固两相流动特性。ZHANG等[6]在LBM-DEM耦合模型的基础上引入浸入边界法对双颗粒在黏性流体中的沉降过程进行数值模拟，成功复现了双颗粒沉降过程中的经典DKT现象。在此基础上，ZHANG等[7]进一步将双松弛时间加入到LBM-DEM耦合模型中，再次复现了二维单颗粒沉降过程中的DKT现象。HABTE等[8]将硬球模型引入到LBM-DEM耦合方法中，模拟了7 200个颗粒的沉降过程。HASHEMI等[9]将传热的影响引入LBM-DEM耦合模型，同时，考虑了流体温度、流体密度等因素对牛顿流体沉降过程的影响，成功模拟了单颗粒与多颗粒沉降过程。CUI等[10]应用LBM-DEM耦合模型对土壤在局部射流作用下二维空腔的大小变化进行了数值模拟，结果表明当射流速度增加或颗粒之间的黏聚力增强时空腔范围扩大，若射流速度过高，床体将破裂并形成“井喷”现象。GUI等[11]将LBM-DEM耦合模型应用于二维气固两相交叉射流的研究。在模拟时忽略了颗粒对流体的作用力。得到了在不同斯托克斯数下射流的涡结构、颗粒分布和回弹率的分布特征。YAN等[12]将浸入边界法引入到LBM-DEM耦合模型中，模拟得到在外加磁场的影响下个别颗粒随外加磁场变化的运动规律。HAN等[13]采用LBM-DEM耦合模型模拟了重力作用下颗粒在球面柱内的沉降过程，模拟时将流体填充的空隙空间简化为静水状态，证明了介观耦合系统中具有的浮力效应。WANG等[14]应用LBM-DEM耦合模型模拟了在一股射流作用下，一段时间内气泡在鼓泡床中的演化过程，同时将空隙率、气固相对滑移速度等物理特征添加到标准的格子Boltzmann方程中，由于采用硬球模型处理两颗粒之间的碰撞，因而对三颗粒及以上颗粒碰撞细节问题难以准确描述，存在一定的局限性。

以上应用LBM-DEM耦合模型主要集中在颗粒数目较少的稀疏两相流，而对流化床、鼓泡床等设备中稠密气固两相流动特性少有深入探讨。因此，笔者将修正后的格子Boltzmann方法与基于软球模型的离散单元法相结合，引入适用于B类颗粒的Gidaspow曳力模型[15]，从介观角度建立LBM-DEM耦合模型，采用Fortran语言编程实现以上模型算法，分析多孔射流过程典型参数变化以研究颗粒在喷动床中流动作用机理。

1数学模型

基于LBM-DEM耦合的数学模型，考虑固体运动对流场的影响，采用修正后的格子Boltzmann方法对流体相进行模拟，离散单元法软球模型求解颗粒-颗粒、颗粒与壁面间的碰撞，颗粒所受曳力由Gidaspow模型计算所得。

标准的格子Boltzmann方法用来求解单相流体的流动。其中，二维条件下采用D2Q9模型控制方程，固体颗粒在流场中的示意图如图1所示。

图1 固体颗粒在流场的位置示意
Fig.1 Schematic diagram of position of solid particles in the control body

1.1流体运动模型(LBM)

为了考虑颗粒运动对流体相的影响，将附加碰撞相加入到格子Boltzmann方程中。

(1)

式中，为附加碰撞相;fi(x,t)为t时刻格点x处i方向分布函数;为平衡态分布函数;ρ为流体密度;us为网格内所有颗粒的平均速度;-i与i表示方向相反。

修正后的格子玻尔兹曼方程演变为

(2)

权函数B(εs,τ)和结构修正因子ω(εg)表达式为

(3)

其中，εs为颗粒体积分数;τ为无量纲松弛时间。将大涡模拟(LES)应用到LBM模拟高雷诺数流动，即亚网格的小尺度的涡对流动结构的影响用湍流黏度系数υe来反映。在Smagorinsky亚网格尺度应力模型中υe由应变速率决定:

(4)

式中，Cs为Smagorinsky常数;Sij为应变速率张量。

通过τt=τ+τe代替式(2)中的τ来实现LES应用到LBM，其中τe为有效碰撞涡松弛时间，则:

(5)

式中，υe为湍流黏度系数；υ为黏度系数；υt=υ+υe;c为格子长度与时间长度的比值。

求解得到修正后的松弛时间τt为

(6)

式中，Q为动量通量。

1.2颗粒运动模型(DEM)

牛顿第二定律用来描述颗粒的运动，单颗粒i受力运动方程可以表示为

(7)

式中，m为颗粒质量;Fy,i为颗粒所受曳力;Fp为颗粒所受周围颗粒的碰撞力。

颗粒与颗粒之间受力由弹性力与阻尼力组成。法向力fn,ij分解为法向弹性力fcn,ij和法向阻尼力fdn,ij，切向力ft,ij分解为切向弹性力fct,ij和切向阻尼力fdt,ij。

根据胡克定律，颗粒之间的作用力可表示如下：颗粒所受法向力:

fcn,ij(t)=fcn,ij(t-Δt)-knΔδn

(8)

(9)

颗粒所受切向力:

fct,ij(t)=fct,ij(t-Δt)-ktΔδt

(10)

(11)

(12)

式中，Δδ为相对位移增量;μ为摩擦因数;k为弹性系数;η为黏性系数;t与n分别为法向与切向。

1.3气固耦合(LBM-DEM)

采用牛顿第三定律解决气固之间的耦合问题。在一个控制体内，采用修正后的格子Boltzmann方法求解颗粒对流体的作用力，Gidaspow模型求解流体对颗粒的作用力。

颗粒对流体的作用力可表示为

(13)

式中，h为格子长度;B为权函数;ei为离散速度。

流体对颗粒的作用力可表示为

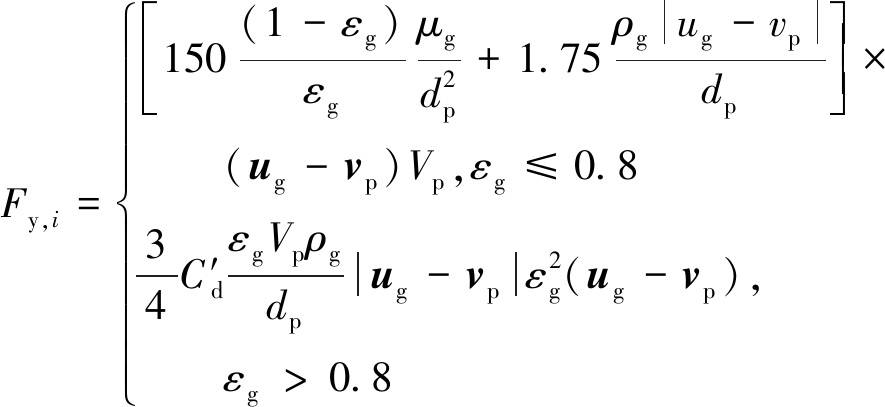
(14)

式中，dp为颗粒直径;ρg为流体密度;ug为流体速度;vp为颗粒速度;μg为流体黏度;Vp为颗粒体积;εg为空隙率;C′d为有效曳力系数，且为单颗粒曳力系数，其表达式如下:

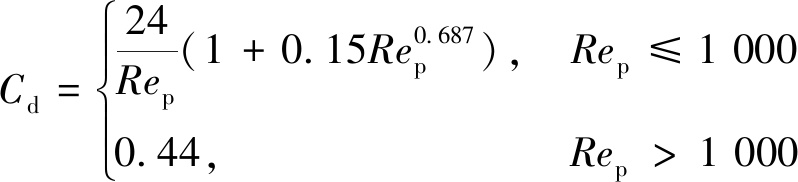
(15)

颗粒雷诺数

(16)

为了减小二维系统与三维系统的差异，本文采用文献[16-17]中提出的方法来计算空隙率:

(17)

式中，ε2d与ε3d分别为二维、三维系统空隙率。

控制体内流固之间的相互作用力以Boltzmann理论计算出的力为基准，所以要对颗粒所受曳力进行修正，来满足牛顿第三定律。

通过标度因子对控制体内每一个颗粒受到的曳力进行修正:

(18)

式中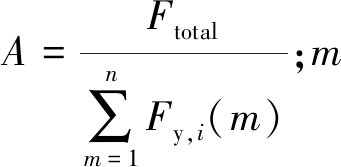，为颗粒数量;n为颗粒总数。

2模拟对象及参数

无量纲下，流化床的宽×高×厚=75×200×0.5，喷口宽度为2的结构设置，进行单喷口、双喷口与三喷口系统数值模拟。模拟对象几何尺寸以三喷口系统为例。如图2所示，采用8 910个直径为135 μm、密度为2 500 kg/m3的球型颗粒。气相密度为1.179 5 kg/m3，气体黏度为1.887 2×10-5kg/(m·s)。具体模拟参数见表1。本文模拟二维矩形流化床内颗粒在底部射流作用下的运动过程。气体在壁面处设置为无滑移边界条件，颗粒在壁面处设置为滑移边界条件。

图2 模拟对象几何尺寸(无量纲)
Fig.2 Geometry size of simulated object (dimensionless)

表1 模拟参数
Table 1 Simulation parameters

类型参数数值床宽/m0.020 25床高/m0.054射流入口宽度/m5.4×10-4气相 气体密度/(kg·m-3)1.179 5气体黏度/(kg·(m·s)-1)1.887 2×10-5气相网格长度/m2.7×10-4气相时间步长/s2.4×10-5弹性系数0.9摩擦因数0.1颗粒相颗粒密度/(kg·m-3)2 500颗粒直径/m1.35×10-4颗粒数8 910固相时间步长/s4.8×10-6

3结果与讨论

3.1模型验证

首先，对程序的正确性进行验证，对比参考WANG等[14]的研究，本文采用相同的模拟参数(表2)，模拟了一股时间为182 ms的射流在鼓泡床中所形成气泡的变化过程。模拟结果如图3所示。图3(a)～(b)气体从床的底部射入，在床底部生成锥状气泡雏形，并逐渐长大。图3(c)～(d)气泡与底面床体分离并逐渐上升。图3(e)～(f)气泡不断上升，在气泡底部出现尾迹。图3(g)～(h)气泡运动到床层表面发生破裂。采用的基于曳力模型为Gidaspow的软球模型与原文稍有差别，其它变量设置相同。考虑到上述因素，整个过程与文献[14]模拟得到的结果相一致，复现了单个气泡在鼓泡床中的演化过程。同时，将文献[18]中通过实验方法获得的瞬时气泡图4(a)与本文模拟得到的瞬时气泡空隙率云图4(b)进行对比，可知模拟与实验的颗粒运动趋势以及气泡形态具有较好的一致性，进一步验证了LBM-DEM耦合模型的准确性。

表2 模拟参数
Table 2 Simulation parameters

类型参数数值床宽/m0.006 75床高/m0.027射流入口宽度/m8.1×10-4气相 气体密度/(kg·m-3)1.179 5气体黏度/(kg·(m·s)-1)1.887 2×10-5气相网格长度/m2.7×10-4气相时间步长/s2.4×10-5弹性系数0.9摩擦因数0.1颗粒相颗粒密度/(kg·m-3)930颗粒直径/m5.4×10-5颗粒数15 000固相时间步长/s4.8×10-6

图3 气泡的演化过程
Fig.3 Process of bubble evolution

图4 实验与模拟结果气泡形态比较
Fig.4 Comparison of bubble form between experiment and simulation results

3.2单喷口系统

3.2.1空隙率分布

图5为射流速度分别为0.7，0.9 m/s时，单喷口系统的空隙率分布云图。由图10可知在2种速度下，由于颗粒到达顶部时曳力减小，颗粒受重力作用向下落回到床内。因而，射流中心区域都存在较高的空隙率，且随着高度的增加射流中心向两侧扩展。当射流速度增加时，颗粒所受曳力变大，与图5(a)中心喷口顶部存在一个小的喷泉区相比，图5(b)所示的喷泉区明显扩大，该趋势与文献[19]所得实验结果一致。

图5 时均空隙率分布
Fig.5 Distribution of time averaged porosity

3.2.2颗粒拟温度分布

颗粒拟温度是描述床层颗粒随机性的一个参数，同时也代表了颗粒拥有的平均脉动动能。图6为射流速度分别为0.7，0.9 m/s时，单喷口系统的颗粒拟温度分布云图。颗粒拟温度在接近喷口中心时达到峰值。同时随着高度的增加而减少，并向两侧延伸而降低。气流速度为0.7 m/s时，如图6(a)所示。颗粒拟温度向两侧传播较弱，脉动范围较小，表明颗粒之间横向碰撞较弱。气流速度为0.9 m/s时，如图6(b)所示。颗粒拟温度向两侧传播明显，颗粒之间横向碰撞增强，速度脉动范围扩大。以上分析表明射流速度大小是影响颗粒分布的重要参数。

图6 颗粒拟温度分布
Fig.6 Distribution of particle pseudo-temperature

3.2.3床层膨胀高度

床层膨胀高度反应射流强度的大小。规定以平均颗粒体积分数为0.1时的床高为床层膨胀高度。图7为不同射流气速下平均颗粒体积分数沿床高的分布。当射流速度在0.7 m/s与0.9 m/s时，床层膨胀高度分别为0.007 6 m与0.007 9 m。这是由于射流速度提高，使得颗粒所受气体曳力增加，颗粒之间碰撞几率变大，床层膨胀高度增加。

图7 不同射流速度下颗粒体积分数沿床高分布
Fig.7 Different jet velocity of particle volume fraction distribution along the bed height

3.3多喷口系统

3.3.1空隙率分布

图8为射流速度在0.7 m/s时，双喷口、三喷口时均空隙率分布对比图。两种情况都存在射流合并现象，这表明喷口数量增加，死区范围减小，射流之间相互影响加剧，因而三喷口在较低的高度进行射流合并。这与文献[20]中所描述的床底部开始出现合并射流且死区范围扩大结论不太一致。主要是因为在介尺度范围模拟时，颗粒直径较小，相同质量下颗粒重力较小，回落颗粒对壁面两侧颗粒影响范围有限，死区范围影响有限。

图8 时均空隙率分布
Fig.8 Distribution of time averaged porosity

3.3.2颗粒拟温度分布

图9为射流速度在0.7 m/s时，双喷口、三喷口在床内不同高度下颗粒拟温度分布图。颗粒拟温度随着高度的增加逐渐减小。在床高较低时，双喷口(图9(a))中心区颗粒拟温度较低，表明还未到达射流合并高度，射流作用不明显;三喷口时(图9(b))，由于一个中心喷口的引入使得射流中心扩大，且射流合并高度降低，中心区颗粒拟温度增加。

图9 不同高度下颗粒拟温度分布
Fig.9 Pseudo-temperature distribution of particles at different heights

3.3.3床层膨胀高度

图10为射流速度在0.7 m/s，双喷口、三喷口颗粒平均体积分数沿床高的分布。由图可知，双喷口、三喷口床层膨胀高度分别为0.009 7 m与0.012 0 m。这是由于喷口数量的增加使其射流相互影响剧烈，颗粒所受气体曳力的加强使得向上运动整体颗粒数增加，因而床层膨胀高度增大。

图10 双、三喷口颗粒体积分数沿床高分布
Fig.10 Particle volume fraction of double and triple jets along the bed height distribution

3.3.4能量分布

图11为射流速度在0.7 m/s时，0～1.2 s内双喷口、三喷口势能与动能对比图。颗粒势能大于颗粒动能，表明颗粒堆积产生的势能含有总能效应。

图11 能量分布
Fig.11 Energy of distribution

在0～0.3 s，颗粒循环处于初始阶段，动能与势能能量转化强烈，能量变化显著;而在0.3～1.2 s，颗粒循环基本建立，因此能量变化趋于稳定。由图11(a)可知，喷口数量增加使得射流混合强度变大，向上运动颗粒增多，床层底部颗粒减少，颗粒势能增加66.07%。如图11(b)所示，根据能量守恒原理，从而颗粒动能随喷口数量的增加而减少，当喷口数量由2个增加为3个时，颗粒动能减少48.48%。

4结 论

(1)通过对模拟与实验得到的颗粒瞬时流化过程图进行对比，发现数值模拟与实验所得结果具有良好的一致性，有效验证了LBM-DEM耦合模型的正确性。

(2)对于单喷口系统，射流气速由0.7 m/s增加到0.9 m/s后，气体对颗粒的携带能力增强，从而进一步扩大了颗粒层喷泉区的作用范围，同时床内空隙率分布增大，速度脉动变大，颗粒拟温度升高，床层整体膨胀高度由0.007 6 m增加到0.007 9 m。

(3)对于多喷口系统，由于相邻喷口间存在较强的横向扰动，同一射流速度下，喷泉区出现明显的射流合并现象，在喷口数量增加时，射流合并高度降低28.57%，床层内时均空隙率扩大明显，沿床高分布的时均颗粒拟温度升高;而射流数量的增加使其颗粒横向脉动范围扩大，势能提高66.07%，床层膨胀高度提高27.50%。由于横向脉动增强干扰了颗粒轴向脉动强度，因而动能降低48.48%。

(4)以上分析结论与传统的模拟结果和实验结论相一致，表明基于修正格子Boltzmann方法与离散单元法相结合的耦合模型可以作为分析稠密气固两相流内在机理的有效工具。

参考文献 :

[1] BAHNG M K,MUKARAKATE C,ROBICHAUD D J,et al.Current technologies for analysis of biomass thermochemical processing:A review[J].Analytica Chimica Acta,2009,651(2):117.

[2] 陈巨辉,殷维杰,于广滨,等.流化床气固相间脉动能量作用分析[J].中国电机工程学报,2017,37(19):5674-5681.

CHEN Juhui,YIN Weijie,YU Guangbin,et al.Analysis of the gas-solid interphase fluctuating energy interaction in fluidized bed[J].Proceedings of the CSEE,2017,37(19):5674-5681.

[3] 戴群特,时凯,祁海鹰.基于介尺度特性分析的流态化过程数值方法[J].煤炭学报,2016,41(10):2508-2513.

DAI Qunte,SHI Kai,QI Haiying.Research progress of simulation methods of fluidization process in CFB based on meso-scale characteristics analysis[J].Journal of China Coal Society,2016,41(10):2508-2513.

[4] 李龙,贾晓东,刘永文,等.两相格子Boltzmann方法模拟大密度比下双液滴冲击液膜的流动过程[J].动力工程学报,2015,35(6):457-462.

LI Long,JIA Xiaodong,LIU Yongwen,et al.Simulation of flow process of two droplets with large density ratio impacting on liquid film by two-phase lattice boltzmann method[J].Chinese Journal of Power Engineering,2015,35(6):457-462.

[5] REN S,ZHANG J Z,ZHANG Y M,et al.Phase transition in liquid due to zero-net-mass-flux jet and its numerical simulation using lattice Boltzmann method[J].Acta Physica Sinica,2014,63(2):024702.

[6] ZHANG H,TAN Y,SHU S,et al.Numerical investigation on the role of discrete element method in combined LBM-IBM-DEM modeling[J].Computers & Fluids,2014,94(2):37-48.

[7] ZHANG P,GALINDO-TORRES S A,TANG H,et al.An efficient Discrete Element Lattice Boltzmann model for simulation of particle-fluid,particle-particle interactions[J].Computers & Fluids,2017,147:63-71.

[8] HABTE M A,WU C J.Particle sedimentation using hybrid lattice boltzmann-immersed boundary method scheme[J].Powder Technology,2017,315:486-498.

[9] HASHEMI Z,AOUALI O,KAMALI R.Three dimensional thermal Lattice Boltzmann simulation of heating/cooling spheres falling in a Newtonian liquid[J].International Journal of Thermal Sciences,2014,82(1):23-33.

[10] CUI X,LI J,CHAN A,et al.A 2D DEM-LBM study on soil behaviour due to locally injected fluid[J].Particuology,2012,10(2):242-252.

[11] GUI N,XU W K,LIANG G,et al.LBE-DEM coupled simulation of gas-solid two-phase cross jets[J].Science China(Technological Sciences),2013,56(6):1377-1386.

[12] YAN L,ZHENG Z,BO S,et al.SUMO modification stabilizes enterovirus 71 polymerase 3D to facilitate viral replication[J].Journal of Virology,2016,90(23):10472.

[13] HAN Y,CUNDALL P A.LBM-DEM modeling of fluid-solid interaction in porous media[J].International Journal for Numerical & Analytical Methods in Geomechanics,2013,37(10):1391-1407.

[14] WANG L,ZHANG B,WANG X,et al.Lattice Boltzmann based discrete simulation for gas-solid fluidization[J].Chemical Engineering Science,2013,101(14):228-239.

[15] GIDASPOW D.Multiphase flow and fluidization:Continuum and kinetic theory descriptions[M].San Diego:Academic Press,1994.

[16] OUYANG J,LI J.Particle-motion-resolved discrete model for simulating gas-solid fluidization[J].Chemical Engineering Science,1999,54(13-14):2077-2083.

[17] TRAORE P,LAURENTIE J C,DASCALESCU L.An efficient 4 way coupling CFD-DEM model for dense gas-solid particulate flows simulations[J].Computers & Fluids,2015,113:65-76.

[18] TRAPRE P,LAURNTIE J C,DASCALESCU L.An efficient 4 way coupling CFD-DEM model for dense gas-solid particulate flows simulations[J].Computers & Fluids,2015,113(31):65-76.

[19] HE Y,LIM C J,GRACE J R,et al.Measurements of voidage profiles in spouted beds[J].Canadian Journal of Chemical Engineering,2010,72(2):229-234.

[20] DEB S,TAFTI D.Investigation of flat bottomed spouted bed with multiple jets using DEM-CFD framework[J].Powder Technology,2014,254(2):387-402.