综合机械化放顶煤开采的关键技术之一是放顶煤液压支架技术[1],液压支架在煤炭开采中起到了支撑顶层煤矸,防止端面冒顶、架间漏矸的作用。综采工作面上的液压支架经常遇到的现象是煤岩垮落导致的冲击载荷[2],冲击载荷发生后,支架的工作状态、运动形式会发生变化,严重时会导致销轴变形破坏、立柱爆缸、活柱弯曲、掩护梁和尾梁的冲击变形,中断综放工作面的正常工作。例如,2008年某矿曾出现过的直接顶来压较大导致两架ZZ5600/17/35型支撑掩护式液压支架“压死”的事故,造成了严重的经济损失。液压支架的适应性和可靠性决定着采煤工作能否正常进行[3],影响着放顶煤开采的支护安全,对支架的强度分析和结构优化起着指导性的作用。自20世纪60年代起,国外主要采煤国就开始了综采技术与装备的研究[4-6],但由于国情的影响,这方面的研究逐渐陷入了停滞。目前,国内学者对于液压支架的研究,主要集中于对液压支架的静力学研究及对液压支架在载荷作用下的动态响应。胡登高和范迅[7]应用有限元法对液压支架进行了强度分析,通过对液压支架整架进行划分网格等前处理,在立柱横断面上施加均匀定载荷,分析底座扭转、顶梁偏载等工况,得到了顶梁及底座的应力情况。杨胜利等[8]通过建立顶板动载冲击的力学模型,求得了不同条件下的最大冲击载荷和支架伸缩量的解析表达式,得到了判别是否压架的准则。梁利闯等[9]研究了冲击载荷作用下液压支架的力传递特性,得到冲击载荷作用位置不同,支架各铰接点力传递特性不同,各铰接点对作用位置敏感度也不同的结论。万丽荣等[10]通过研究冲击载荷作用于支架掩护梁后支架的运动及受力情况,提出冲击载荷作用位置不同,支架的动力学变化趋势不同。文献[11-17]对液压支架的承载特性、工作阻力进行了研究,深入探讨并完善了液压支架的力平衡区理论,指出了提高液压支架承载能力的方法。
然而,以上文献尚未涉及放顶煤液压支架受冲击时的动态响应研究。通过施加集中载荷进行掩护式液压支架冲击载荷研究的方式忽略了物体间的碰撞接触过程,没有考虑物体变形及能量转化,不符合实际。通过实地考察,发现放煤部的实际工况为松散煤的整体滑移及冒落冲击。为此,笔者针对煤矸垮落冲击某架型放顶煤液压支架尾梁的放煤工况,以煤岩直接作用于尾梁,重点研究尾梁承受冲击载荷后的动态响应。通过对单颗粒煤岩冲击尾梁后的动态响应分析得到尾梁的动载规律、受力状况,为冲击载荷下放顶煤液压支架顶梁、掩护梁、立柱等主要部件的动态研究提供借鉴。
1 放煤机构刚柔耦合模型
放顶煤液压支架放煤机构主要由尾梁、插板、尾梁平衡千斤顶和插板千斤顶等部件构成,其中,尾梁是实现挡矸和放煤的关键部件。尾梁上侧和掩护梁相铰接,下侧通过平衡千斤顶连接于掩护梁下侧,并通过插板千斤顶与插板相连。本文主要研究煤岩冲击尾梁后对尾梁振动特性的影响,插板和插板千斤顶虽然和尾梁相连接,但煤岩冲击尾梁后插板和插板千斤顶对尾梁的瞬态特性影响不大,完全考虑只会增大模拟时间,因此省略这些部件,简化后的放煤机构如图1所示。放顶煤液压支架放煤时,煤岩与尾梁发生碰撞,真实情况下,尾梁及煤岩均会发生变形,为更贴合实际工况,将尾梁及煤岩颗粒处理为柔性体。图2为经前处理软件Hypermesh划分网格后生成的包含材料属性的柔性体文件,用此柔性体替换掉原来模型中的刚性体。尾梁平衡千斤顶起到支撑尾梁的作用,稳定后达到平衡状态,其运动特性与Adams中弹簧阻尼系统的刚度和黏滞阻尼系数等特性相对应,因此千斤顶可由弹簧阻尼系统等效代替。其余均处理为刚性体。
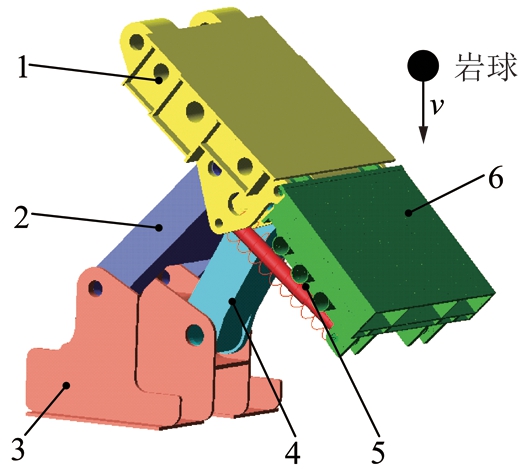
图1 放煤机构示意
Fig.1 Sketch map of coal caving machine
1—掩护梁;2—前连杆;3—底座;4—后连杆;
5—弹簧阻尼系统;6—尾梁

图2 尾梁及煤岩颗粒柔性体文件
Fig.2 Flexible body file of tail beam and coal-rock particle
1.1 基于Adams的接触碰撞模型
直接顶和顶煤的垮落,会导致煤岩对支架的冲击作用,煤矸和尾梁的碰撞接触是一种经典的力学行为。本文中,煤岩和尾梁均为质量均匀、各向同性材料,其接触表面光滑,不考虑摩擦力的影响。放顶煤液压支架上方存在着一层强度较低的顶煤,松散的顶煤下落时,形状各异,若分别建模,会给研究工作带来极大的困难,因此将下落的煤岩颗粒统一简化为球体。煤岩颗粒与尾梁发生碰撞后,接触区尺寸与接触物体尺寸相比非常小,可以忽略。满足以上条件后,可以采用基于弹性半空间假设的Hertz接触理论来解决这种碰撞问题。
Hertz接触理论[18]指出,两弹性体发生碰撞时,接触区内会产生接触变形量δ和法向接触力Fn,两者之间有如下关系:
![]()
(1)
其中,R为弹性体等效接触半径,m;E为等效弹性模量,Pa。等效接触半径和等效弹性模量分别满足:
![]()
(2)
![]()
(3)
式中,R1,R2分别为两碰撞物体的曲率半径,m;μ1,μ2分别为两接触物体的泊松比;E1,E2分别为两碰撞物体弹性模量,Pa。
由式(1)可推得碰撞过程中产生的相对变形量为
![]()
(4)
Adams采用基于非线性弹簧阻尼模型的接触函数[19]来对接触碰撞进行定义,不考虑碰撞过程中的摩擦损耗时,可以按照式(5)计算碰撞时产生的接触力。
![]()
(5)
式中,k1为接触刚度系数;e为接触力的非线性指数;a为两接触物体相对运动速度,m/s;c为接触过程中的最大阻尼系数;d为接触阻尼达到最大值时的两接触物体的最大切入深度,m。
由式(5)可以看出,接触函数计算两物体碰撞产生的接触力时分成两部分,一部分是基于Hertz接触理论的弹性力,另一部分是对碰撞系统产生约束的阻尼力,式(5)中函数step(δ,0,0,d,c)是解决阻尼力不连续的阶跃函数,其具体形式如下:
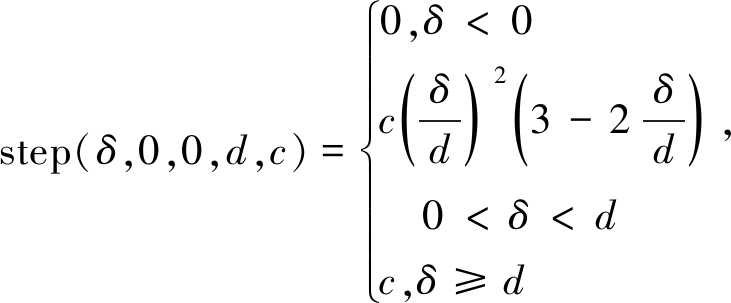
(6)
Adams接触碰撞模型的参数中,材料的接触刚度k1是影响碰撞结果的重要因素,其大小与材料属性、尺寸等因素有关。在确定此参数的具体数值时,可根据Hertz接触理论确定,如式(7)所示。
![]()
(7)
尾梁和煤岩的材料属性见表1。
表1 尾梁、煤岩材料参数
Table 1 Material parameters of tail beam and coal-rock

项目材料密度/(kg·m-3)弹性模量/GPa泊松比尾梁Q3457 8502100.30煤岩煤1 3802.260.28
煤岩颗粒粒径取R=0.025 m,质量为0.090 3 kg,和煤岩颗粒相比,尾梁的接触半径及质量均可认为为无穷大,根据式(2),(3),(7)计算出煤岩冲击尾梁的接触刚度k1=5.115 452 343×108。
1.2 等效弹簧阻尼模型
尾梁平衡千斤顶内部的高压乳化液在受载时体积会发生变化,缸体在乳化液压力作用下也会发生一定变形,缸体和乳化液可以视为两个串联的弹簧。千斤顶的等效刚度k称为固液耦合刚度[20],具体的计算公式为
![]()
(8)
式中,kq为千斤顶内部高压乳化液刚度;kg为千斤顶缸体刚度。
本文所用尾梁千斤顶的型号为单伸缩立柱型,其等效刚度可以用下式计算。
![]()
(9)
其中,S为乳化液有效承压面积;ξ,Eg分别为缸体厚度和缸体弹性模量;L,ky分别为乳化液液柱高度及乳化液体积压缩系数。液体体积弹性模量Ep为液体积压缩系数ky的倒数,故式(9)可以改写为
![]()
(10)
尾梁平衡千斤顶缸体材料为45号钢,其材料属性及乳化液的相关属性见表2。
表2 尾梁千斤顶及乳化液主要参数
Table 2 Main parameters of tail beam jack and emulsion

项目参数缸体内径/mm140缸体壁厚/mm14千斤顶弹性模量/GPa210乳化液体积弹性模量/GPa1.95
2 数值模拟及结果分析
本文以“煤岩直冲”方式对尾梁直接进行加载,等效弹簧阻尼系统在尾梁自身重力的作用下发生振动,由于阻尼的存在,弹簧在一段时间后达到稳定状态。煤岩颗粒与尾梁接触时,在很短的时间内,岩球的动能转移到尾梁上,产生巨大的碰撞接触力,对尾梁-弹簧阻尼系统产生外激励,导致尾梁的的受迫振动,从而使尾梁的速度、加速度、位移发生突变,如图3所示,以下将针对尾梁的这些响应量及瞬时接触力进行探讨。

图3 尾梁冲击响应
Fig.3 Impact responses of the tail beam
2.1 尾梁承载区冲击响应分析
为探讨煤岩冲击尾梁上顶面不同位置时,尾梁的动态响应差异,选取尾梁上顶面中心0.8 m×0.8 m的正方形区域为承载区,约定尾梁对称轴所在方向为纵向,与掩护梁相铰接的一端为承载区上侧。由于尾梁自身形状的对称性,煤岩冲击对称轴两侧相同位置时对尾梁造成的影响是相同的,因此选取对称轴左侧承载区域作为研究对象。在左侧承载区内等间距(ΔL=0.2 m)地选取15个点作为冲击点,并按顺序标定,冲击点分布情况如图4所示。
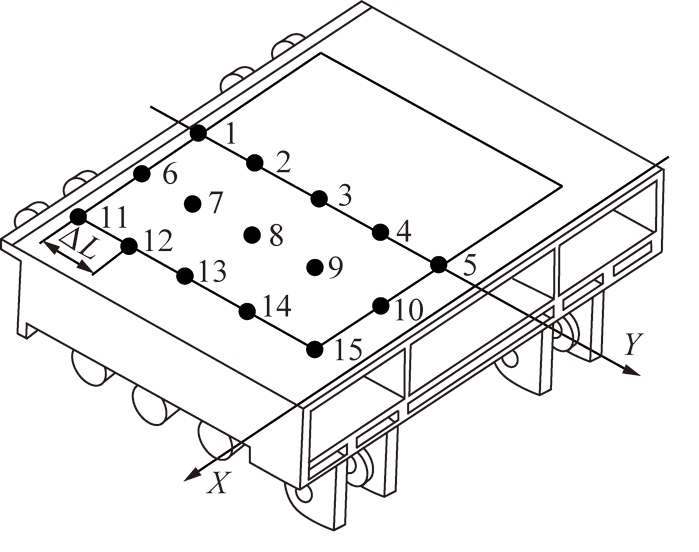
图4 上顶面冲击点分布
Fig.4 Distribution of impact points on the top surface
根据兖州矿区某矿1303工作面煤层厚度8.61~9.32 m,放煤高度5.1~5.8 m等赋存情况[21],取煤岩颗粒自由下落高度为4 m。本文所用架型放煤机构采用强扰动式尾梁插板放煤机构,放煤角可达20°~60°,控制尾梁放煤角为45°不变,此时测得尾梁平衡千斤顶内乳化液柱的高度为136.32 mm,按式(10)求得弹簧阻尼模型的等效刚度为2.122 5×108,忽略空气阻力,只考虑重力加速度(g=9.8 m/s2)的影响,进行数值模拟。
提取碰撞接触力及尾梁动态响应量的最大值并绘制曲线,其结果如下。
图5为碰撞发生的瞬间,接触区域内产生的最大接触力,纵轴表示接触力,横轴表示冲击点位置。可以看出,尾梁纵向5个点分别组成的3条曲线高度相似,变化规律相同。每一纵向从上往下的5个冲击点,产生的最大接触力先增大,然后减小,最后再次增大,承载区中心点3所在横向的3个冲击点3,8,13处的最大接触力最小,位于中心点横向以上的冲击点(1,2,6,7,11,12)的最大接触力明显大于中心点横向以下冲击点(4,5,9,10,14,15)的最大接触力。这是因为尾梁的连接方式类似于上端铰接,另一端添加弹簧约束的简支梁,位于承载区上侧铰接点附近的区域相较于下侧的区域,可在一定意义上认为是刚性区域,煤岩碰撞后变形相较于下侧很小,消耗的能量少,因此产生的碰撞力大。分析尾梁上顶面同一横向的冲击点,可以看出,煤岩颗粒碰撞尾梁时所产生的最大接触力,数值大小基本相同,在远离尾梁对称轴的方向上,最大接触力有减小的趋势。综上可以发现,煤岩冲击承载区不同位置,产生的瞬间接触力不同,冲击点与尾梁掩护梁铰接点的距离对接触力的影响很大,距铰接点距离越近,碰撞产生的接触力越大;同一横向位置的冲击点,越靠近轴心位置,冲击产生的接触力越大,但数值非常接近。
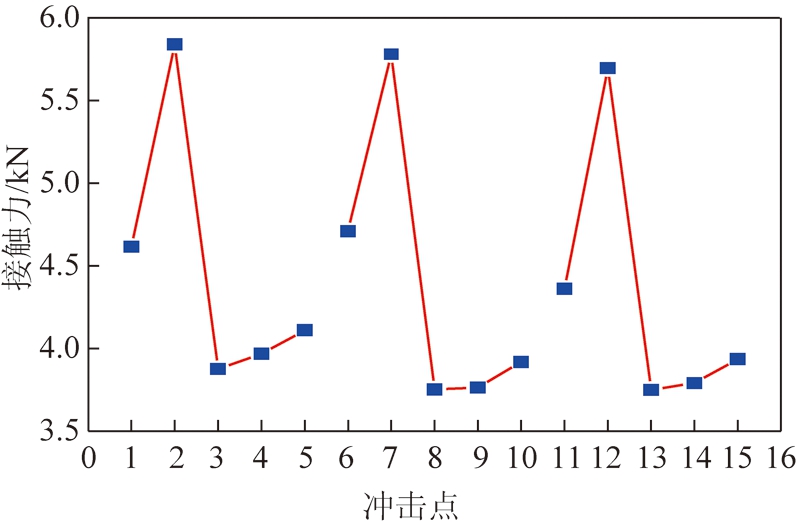
图5 最大接触力
Fig.5 Maximum contact force
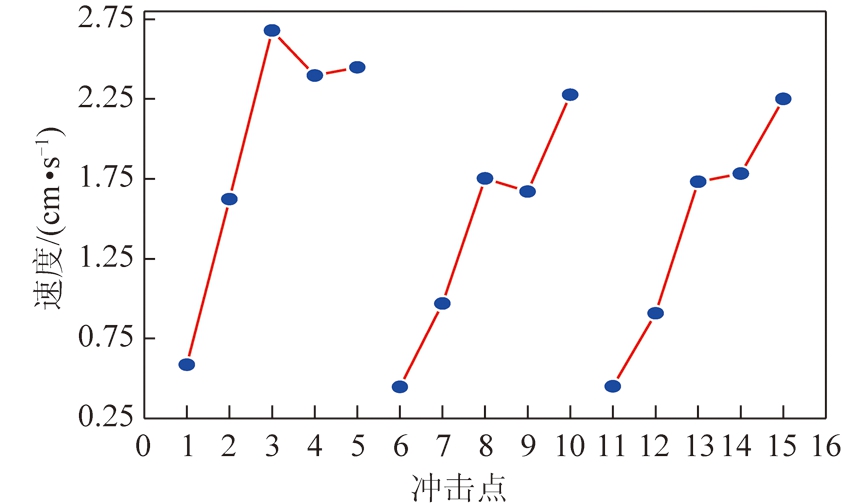
图6 最大速度响应
Fig.6 Maximum velocity response
图6为碰撞后尾梁质心的最大速度响应,3条曲线基本上呈现出相同的走势。煤岩颗粒碰撞承载区同一纵向自上而下的5个冲击点后,均使尾梁质心速度发生突变,质心的最大速度基本上可以认为呈现出先上升再下降最后继续上升的特性。结合图5,6可以看出,3条曲线均在中心点所处位置的冲击点处发生偏转。由于中间点所处位置上的冲击点均为曲线的拐点,具有“临界点”特性,因此将穿过这些冲击点的直线称之为“水平临界线”。承载区同一纵向,尾梁质心速度的总趋势是随冲击点位置的下降而上升,虽然出现了拐点,但拐点两侧的曲线趋势相同,水平临界线以上的冲击点,质心的最大速度响应明显小于水平临界线以下冲击点的,这是由两种因素导致的。一种因素是越靠近尾梁下侧,碰撞消耗的能量越多,尾梁吸收的能量也越多,导致尾梁动能增大。另一个因素是水平临界线以下的冲击点,靠近弹簧阻尼模型与尾梁的连接点,临界线以上的冲击点,更靠近尾梁-底座的铰接点。相较于铰接这种“刚性连接”方式,弹簧连接这种“柔性连接”方式更容易运动,其附近区域运动能力更强,拐点可能是由于水平临界线处于两种连接方式中间,弹簧阻尼连接与铰接同时作用于尾梁造成的。同一横向上的冲击点,位于尾梁对称轴上的冲击点,最大速度响应的值最大,远离对称轴的两个冲击点,最大速度响应的值稍小,且这两个冲击点的最大速度相差并不大。
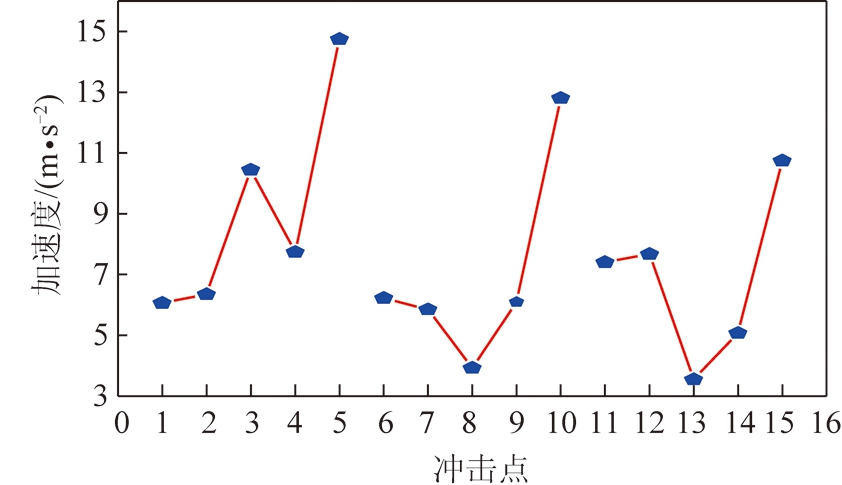
图7 最大加速度响应
Fig.7 Maximum acceleration response
图7为尾梁质心的最大加速度响应曲线,图中第1条曲线的线型与右侧两条曲线的线型稍有差异,但水平临界线经过的冲击点仍为曲线的拐点。从纵向上看,分别观察水平临界线以上和以下的冲击点,其最大加速度响应随冲击点位置的下降基本上呈上升趋势。水平临界线上方的冲击点产生的最大加速度非常接近,差值不超过1 m/s2。6,7点的加速度曲线下降的原因可能是求解器的敛散性,但两点的数值相差并不大,可以认为是正常情况。对于水平临界线上的点,除中心点3外,其余2个点是所在曲线上的最低点。与最大接触力不同,虽然最下侧产生的接触力较小,但加速度的数值却是最大的。这是因为尾梁下侧与弹簧阻尼系统相连接的区域,运动趋势最强,较小的接触力也能产生较大的瞬时加速度。从横向上看,水平临界线上包括其以下的冲击点,最大加速度有个明显的特征,同一横向上的点,越靠近轴心位置,其最大加速度越大;而水平临界线以上同一横向上的点,越远离轴线方向,最大加速度越大,由于靠近掩护梁尾梁相铰接的区域,运动趋势较弱,总的来说上方6个点的最大加速度响应相差并不大,最大值和最小值相差不超过2 m/s2。
尾梁质心受迫振动后远离平衡位置的最大距离是碰撞后尾梁质心的最大振幅。由图8 可以看出,3条曲线的线型基本一致,随着冲击点位置从上到下,尾梁质心的最大振幅越来越大,但上升趋势越来越平缓。同一横向位置上3个冲击点的最大振幅基本一致。这是由于煤岩颗粒冲击弹簧连接点附近的区域时,消耗的能量更多,尾梁吸收的能量也更多,动能增大,振动特性更强。由于振幅曲线沿承载区纵向冲击点变化平稳,没有拐点的出现,因此综合3条曲线可以推断出整个承载区的振幅响应规律,相同冲击条件下,尾梁承载区的最大振幅响应和冲击位置的关系如图9 所示。

图8 最大振幅
Fig.8 Maximum amplitude
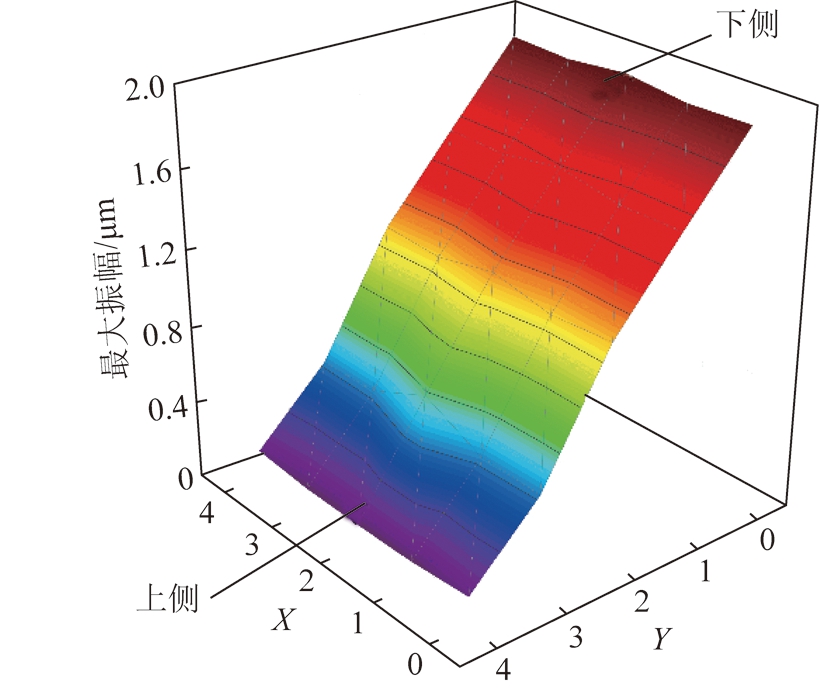
图9 承载区最大振幅
Fig.9 Maximum amplitude of the bearing area
综上可以看出,尾梁的最大振幅主要与承载区位置有关,冲击点位置越接近承载区下侧区域时,尾梁吸收能量越多,质心的最大振幅越大,尾梁振动越明显。
2.2 放煤角对冲击响应的影响
摆动式放煤机构通过尾梁上下摆动以松动顶煤并维持落煤空间,尾梁与水平线之间的夹角称之为放煤角。放煤角变化时,尾梁的承载特性及动态响应会发生变化。为研究不同放煤角下尾梁的冲击响应变化,在放煤角为20°~50°(增量为5°)时建立不同的刚柔耦合模型,分别测出每一放煤角下相应尾梁千斤顶内乳化液的液柱高度,并根据式(10)求出对应的弹簧阻尼模型的固液耦合刚度,将其记录在表3中。为最大程度降低Adams求解器的敛散性对于仿真结果的影响,选取尾梁承载区中心点及纵向上下两个点作为冲击点,自上而下将其重新标记为点1,2,3,如图10所示,进行多组仿真实验。同时,设定煤岩自由下落高度均为4 m。
表3 不同放煤角下液柱高度及等效刚度
Table 3 Liquid column height and equivalent stiffness under different coal caving angles
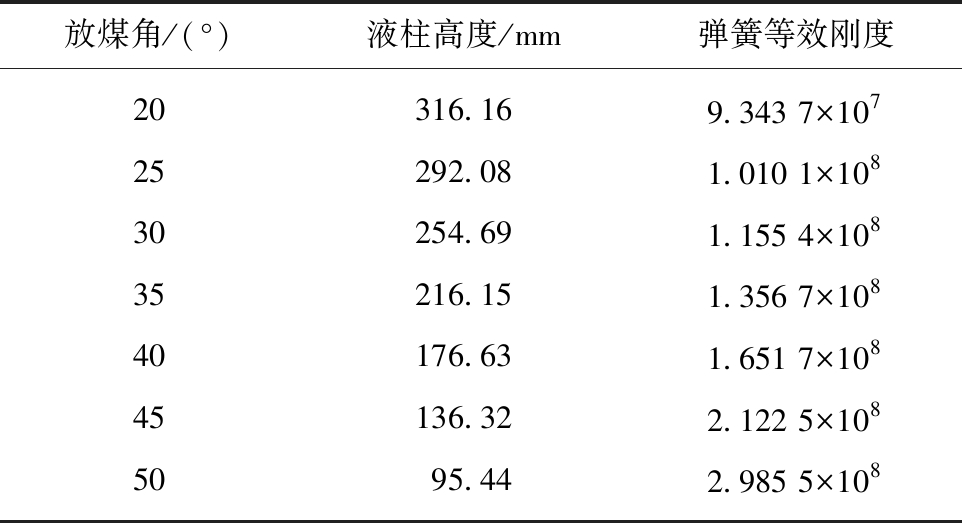
放煤角/(°)液柱高度/mm弹簧等效刚度20316.169.343 7×10725292.081.010 1×10830254.691.155 4×10835216.151.356 7×10840176.631.651 7×10845136.322.122 5×1085095.442.985 5×108

图10 冲击点位置
Fig.10 Position of impact points
图11为不同放煤角下最大接触力曲线,横轴为放煤角,纵轴为碰撞瞬间产生的最大接触力。可以看出,随着放煤角的增大,最大接触力逐步减小,3条曲线的下降趋势基本一致,下降的速度越来越慢,最终接触力将趋于稳定。放煤角35°是3条曲线的分界点,小于35°时,曲线下降速度极快,大于35°后,曲线下降速度趋于平缓。造成接触力下降的原因是,同一高度下落的煤岩冲击尾梁时,其碰撞初速度相同。煤岩和尾梁接触时,两者之间的相对速度可以分解成垂直于尾梁上顶面方向的法向速度和平行于尾梁上顶面方向的切向速度,而对接触物造成冲击影响的主要是两接触物之间的法向速度。随着尾梁放煤角的增大,煤岩的法向速度逐渐减小,导致了接触力的逐渐减小。而接触力的变化规律与煤岩的法向动能变化规律一致,接触力初期的急速下降可能是由于煤岩法向动能的快速下降造成的。通过以上分析可以看出,尾梁放煤角较小时,冲击产生的接触力极大,放煤机构易受到冲击破坏,应针对此情况对尾梁及连接处进行结构强度的优化,防止特殊集中力对尾梁造成的冲击破坏及连接处销轴的弯曲和断裂等情况的出现。
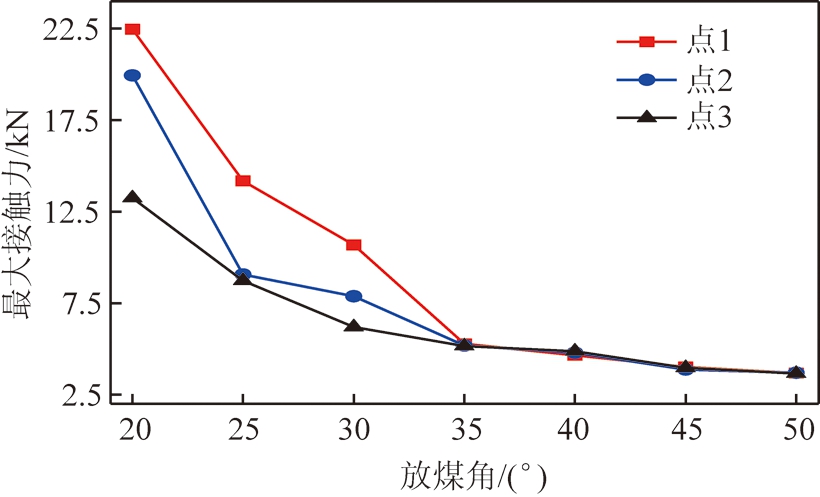
图11 最大接触力
Fig.11 Maximum contact force
图12为尾梁质心最大速度响应曲线,从图中可以发现,随着放煤角的增大,尾梁质心的最大速度减小,且减小的速度越来越快,这种现象是由于尾梁质心的最大速度响应和煤岩法向速度有关,煤岩颗粒法向速度与放煤角呈余弦函数关系,随放煤角的增大,法向速度减小得越来越快,带动尾梁质心的最大速度也随这种关系变化。煤岩和尾梁质心相似的速度变化关系可以认为是煤岩颗粒和尾梁之间的“速度传递”,煤岩碰撞尾梁后,带动尾梁运动,且尾梁质心能达到的最大速度随煤岩法向速度以相同趋势变化,当放煤角达到一定角度后,尾梁速度趋于0,将不再发生运动。
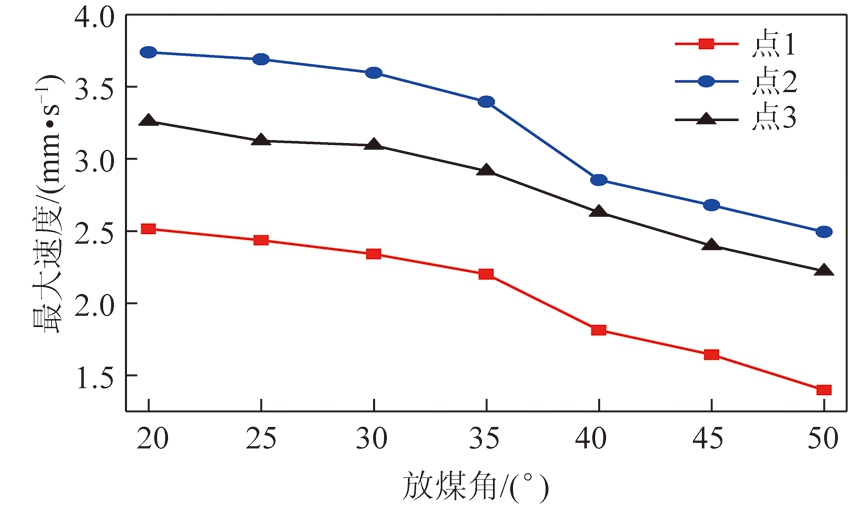
图12 最大速度响应
Fig.12 Maximum velocity response
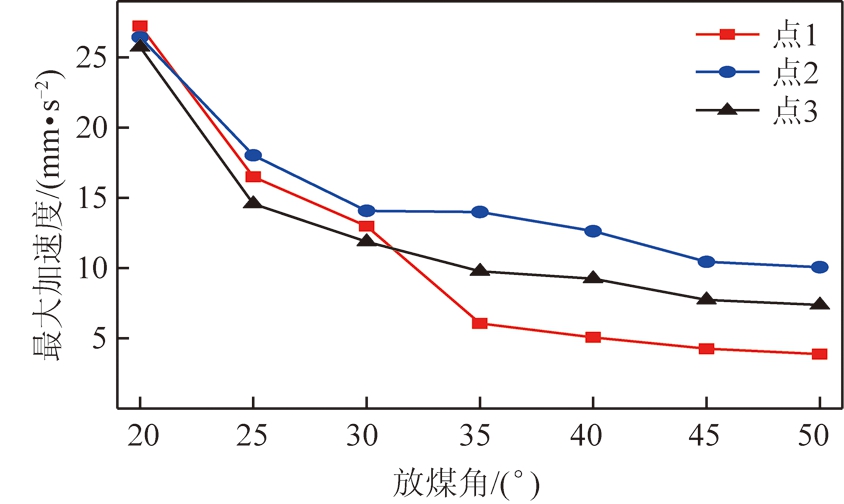
图13 最大加速度响应
Fig.13 Maximum acceleration response
图13为碰撞后尾梁质心最大加速度随放煤角的变化曲线。根据牛顿第二运动定律,加速度和接触力为正相关关系,虽然尾梁上侧和掩护梁铰接,下侧连接着弹簧,但在极短的时间内,尾梁运动仍遵循牛顿定律,其最大加速度响应和最大接触力变化相同,随放煤角的增大而减小,且减小的速度越来越慢。与图11相比,在35°之后,加速度曲线趋于稳定,3个冲击点的差值也趋于稳定,但曲线差值远大于35°之前的曲线差值。这种现象可以解释为,随放煤角的增大,尾梁的运动趋势更敏感,放煤角较小时,接触力相差较大,但最大加速度却基本相同;放煤角较大时,接触力相差不大,最大加速度的区别却很大。
图14为尾梁质心的最大振幅曲线,从图中可以看出,随着放煤角的增大,尾梁质心的最大振幅减小,且在放煤角较小时,下降速率更快,超过30°后,基本上呈线性形式减小。这是因为随着放煤角的增大,碰撞产生的接触力激励变小,尾梁在和煤岩的能量转移中吸收的能量变少,动能增量小,导致其振动能力变弱,更难以运动。最大振幅在放煤角较小时下降速度较快的原因可以归结于最大冲击力在角度较小时的高速下降。
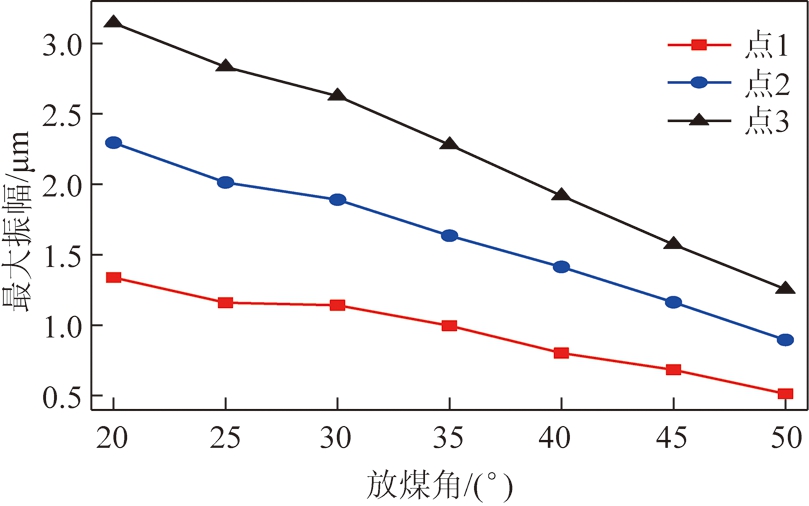
图14 最大振幅
Fig.14 Maximum amplitude
3 基于不同模拟方式的对比验证
为探讨本文采用方法的合理性,将所用模型处理为刚性体,在刚体冲击方式下进行仿真对比,验证本文研究方法的合理性。
在不同放煤角条件下建立煤岩冲击尾梁的多刚体动力学模型,如图15所示,参照表1设置模型的材料属性,岩球半径为25 mm,下落高度为4 m。煤岩和尾梁接触时的接触参数仍采用Hertz接触理论确定,取刚度系数为5.115 452 343×108,根据经验,设置阻尼系数为接触刚度的1%。
图15 多刚体模型
Fig.15 Multi-rigid body model
对20°~50°放煤角(增量为5°)条件下建立的7个刚体模型分别进行仿真计算,提取冲击力的最大值,结合刚柔耦合模型获得的数据,对两种模拟方式取得的结果进行比较,如图16所示。
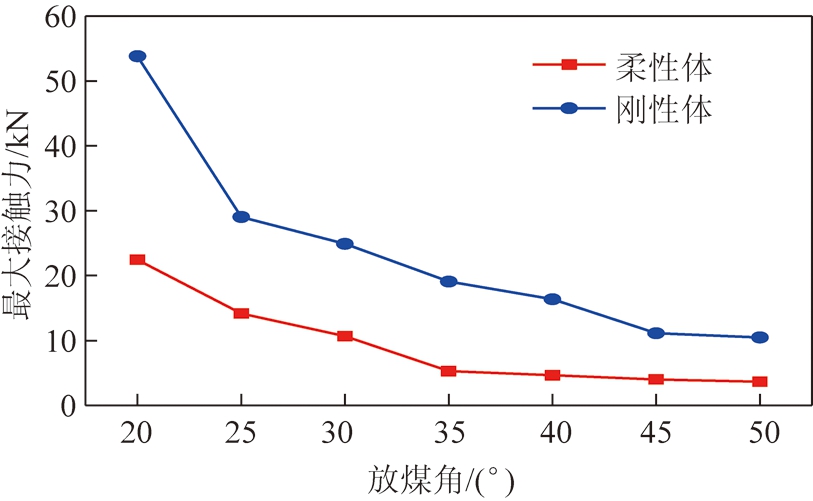
图16 两种仿真方式比较
Fig.16 Comparison of two simulation methods
由图16可以看出,刚性体冲击和柔性体冲击得到的最大接触力均随放煤角的增大而较小,且两条曲线的线型一致,在放煤角较大时,曲线趋于平稳。不同的是,刚体冲击得到的最大冲击力均大于同条件下柔性体冲击方式得到的仿真数据。这种结果是正确的,产生这种情况的原因是本文所用模型经前处理软件Hypermesh划分网格后,生成了带有材料属性的柔性体文件,在碰撞发生的瞬间,接触的网格相互挤压,节点发生偏移,两接触物之间出现相对变形,会吸收一定的能量[22],且刚柔耦合模型中尾梁和弹簧阻尼系统的运动也会吸收大量的能量。而多刚体动力学模型中,无弹簧阻尼模型,放煤机构通过固定副固连在地面上,煤岩冲击过程中只发生穿透而不发生相对变形及尾梁的运动,消耗的能量极少,这对结果产生了显著的影响。综上可知,相同冲击条件下,多刚体模型较刚柔耦合模型而言,产生的冲击力更大。
通过以上两种模拟方式的对比可以发现,采用刚体冲击方式得到的结果偏大,仅能对冲击结果的趋势起指导作用,而本文采用的研究方式更接近真实工况,具有合理性,得到的结论具有可靠性。
4 结 论
(1)与“集中载荷”加载方式相比,采用“煤岩直冲”方式对尾梁进行加载,既考虑了煤岩和尾梁的材料属性、外形、尺寸对整个碰撞过程的影响,也考虑了碰撞过程中两接触物体的相对变形及能量消耗,体现了碰撞过程的“瞬时性、复杂性”,以更接近实际的方式对煤岩冒落冲击工况进行了处理,其结果可以更准确地反映尾梁的动态特性及受力状态。
(2)煤岩冲击尾梁不同位置时,其动态特性有差异。尾梁-弹簧阻尼系统连接处附近的的区域碰撞时消耗的能量较多,冲击力较小。此时,尾梁会吸收较多的能量,导致振动特性变强,动态响应量在这些区域取得极值,应对这部分区域进行结构优化。提出了承载区 “水平临界线”的定义,位于此临界线上的冲击点是冲击响应曲线上的拐点,除振幅外的其他响应量均在此处发生突变。振幅是所有响应参量中变化最稳定的,随冲击点位置的下降平稳上升,可凭借此响应量对尾梁进行动态监测。
(3)放煤角是影响尾梁的运动趋势和受力情况的重要因素。通过模拟结果可以看出,放煤角较小时,尾梁吸收的能量多,运动能力强,放煤角较大时,振动特性差,运动能力较弱。随着尾梁放煤角的增大,碰撞接触力及尾梁的动态响应量均在减小,可以作为控制放煤角度的动态反馈量。相同冲击条件下,放煤角较小时接触力的数值巨大,易对尾梁造成冲击破坏,应针对这种情况对放煤机构进行强度校核。
(4)本文研究成果可以为放顶煤液压支架放煤机构强度校核、结构优化提供参考,为放煤机构的动态控制提供参考量。
[1] 王国法,刘俊峰,任怀伟.大采高放顶煤液压支架围岩耦合三维动态优化设计[J].煤炭学报,2011,36(1):145-151.
WANG Guofa,LIU Junfeng,REN Huaiwei.Design and optimization of high seam-caving coal hydraulic support based on model of support and wall rock coupling[J].Journal of China Coal Society,2011,36(1):145-151.
[2] 陈赫宇,孙姣,贾雷永,等.提高液压支架抗冲击能力技术研究[J].煤矿机械,2015,36(2):69-71.
CHEN Heyu,SUN Jiao,JIA Leiyong,et al.Improve impact resistance hydraulic support technology research[J].Coal Mine Machinery,2015,36(2):69-71.
[3] 王国法.液压支架技术体系研究与实践[J].煤炭学报,2010,35(11):1903-1908.
WANG Guofa.Study and practices on technical system of hydraulic powered supports[J].Journal of China Coal Society,2010,35(11):1903-1908.
[4] NEVOLIN N V,SHILKOV B P,POTEPKO V M.Sudden rock failures in mining coal seams of the Kizel Basin[J].Journal of Mining Science,2003,39(1):21-26.
[5] YASITLI N E,UNVER B.3D numberical modeling of long wall mining with top coal caving[J].International Journal of Rock Mechanics & Mining sciences,2005,42(2):219-225.
[6] LI C C.Rock support design based on the concept of pressure arch[J].International Journal of Rock Mechanics and Mining Science,2006,43(7):1083-1090.
[7] 胡登高,范迅.液压支架强度可靠性及敏感性分析[J].辽宁工程技术大学学报(自然科学版),2016,35(6):636-641.
HU Denggao,FAN Xun.Reliability and sensitivity analysis of hydraulic support[J].Journal of Liaoning Technical University (Natural Science),2016,35(6):636-641.
[8] 杨胜利,王家臣,杨敬虎.顶板动载冲击效应的相似模拟及理论解析[J].煤炭学报,2017,42(2):335-343.
YANG Shengli,WANG Jiachen,YANG Jinghu.Physical analog simulation analysis and its mechanical explanation on dynamic load impact[J].Journal of China Coal Society,2017,42(2):335-343.
[9] 梁利闯,田嘉劲,郑辉,等.冲击载荷作用下液压支架的力传递分析[J].煤炭学报,2015,40(11):2522-2527.
LIANG Lichuang,TIAN Jiajin,ZHENG Hui,et al.A study on force transmission in a hydraulic support under impact loading on its canopy beam[J].Journal of China Coal Society,2015,40(11):2522-2527.
[10] 万丽荣,刘鹏,孟昭胜,等.冲击载荷作用于掩护梁对液压支架的影响分析[J].煤炭学报,2017,42(9):2462-2467.
WAN Lirong,LIU Peng,MENG Zhaosheng,et al.Analysis of the influence of impact load on shield beam of hydraulic support[J].Journal of China Coal Society,2017,42(9):2462-2467.
[11] 周永昌.掩护式液压支架力学特性的初步分析[J].煤炭学报,1981(1):1-17.
ZHOU Yongchang.Preliminary analysis of mechanical characteristics of shield supports[J].Journal of China Coal Society,1981(1):1-17.
[12] 徐亚军,王国法,任怀伟.液压支架与围岩刚度耦合理论与应用[J].煤炭学报,2015,40(11):2528-2533.
XU Yajun,WANG Guofa,REN Huaiwei.Theory of coupling relationship between surrounding rocks and powered support[J].Journal of China Coal Society,2015,40(11):2528-2533.
[13] 徐亚军,王国法,刘业献.两柱掩护式液压支架承载特性及其适应性研究[J].煤炭学报,2016,41(8):2113-2120.
XU Yajun,WANG Guofa,LIU Yexian.Supporting property and adaptability of 2-leg powered support[J].Journal of China Coal Society,2016,41(8):2113-2120.
[14] 孟昭胜,曾庆良,万丽荣,等.掩护式液压支架顶梁承载特性及其适应性研究[J].煤炭学报,2018,43(4):1162-1170.
MENG Zhaosheng,ZENG Qingliang,WAN Lirong,et al.Supporting performance and canopy adaptability of shield support[J].Journal of China Coal Society,2018,43(4):1162-1170.
[15] 杨培举,刘长友,韩纪志,等.平衡千斤顶对放顶煤两柱掩护支架适应性的作用[J].采矿与安全工程学报,2007,24(3):278-282.
YANG Peiju,LIU Changyou,HAN Jizhi,et al.Role of equilibrium jack in a daptability of 2-leg shield support of top coal caving[J].Journal of Mining and Safety Engineering,2007,24(3):278-282.
[16] 杨培举,刘长友,金太.两柱掩护式综放支架的承载规律及工艺研究[J].采矿与安全工程学报,2010,27(4):512-516.
YANG Peiju,LIU Changyou,JIN Tai.Research on the load variation laws and technologic effect of two-leg sublevel caving shield support[J].Journal of Mining and Safety Engineering,2010,27(4):512-516.
[17] 韩光远,刘长友,杨伟,等.四柱综放支架总阻力及其作用点位置确定探讨[J].煤炭工程,2011(4):39-41.
HAN Guangyuan,LIU Changyou,YANG Wei,et al.Discussion of determining total resistance and its position acting on four pillar caving support[J].Coal Engineering,2011(4):39-41.
[18] YANG Yang,ZENG Qingliang,WAN Lirong.Dynamic response analysis of the vertical elastic impact of the spherical rock on the metal plate[J].International Journal of Solids and Structures,2019,158:287-302.
[19] IMED Khemili,LOTFI Romdhane.Dynamic analysis of a flexible slider-crank mechanism with clearance[J].European Journal of Mechanics,2008,27(5):882-898.
[20] 刘欣科,赵忠辉,赵锐.冲击载荷作用下液压支架立柱动态特性研究[J].煤炭科学技术,2012,40(12):66-70.
LIU Xinke,ZHAO Zhonghui,ZHAO Rui.Study on dynamic features of leg applied to hydraulic powered support under bumping load[J].Coal Science and Technology,2012,40(12):66-70.
[21] 王国法.放顶煤液压支架与综采放顶煤技术[M].北京:煤炭工业出版社,2010:35-36.
[22] 丁叁叁.高速列车车体设计关键技术研究[D].北京:北京交通大学,2016:85-86.
DING Sansan.Study on the key technology of the high-speed train carbody[D].Beijing:Beijing Jiaotong University,2016:85-86.
