近年来，随着社会对基础设施建设和能源资源的需求日益增大，众多大型岩体工程建设相继开展。如石油天然气的开采，油气能源的地下存储，矿产资源开采，以及高放核废料的地下处置等，无不涉及岩石在高温热开度及岩体在高温作用下渗透特性的变化。例如，在高放核废料的地下处置中，在较长时间内仍会产生大量余热，致使周围的岩石温度上升，随后逐渐冷却至之前状态[1]，因此开展高温作用后岩石裂隙渗流的研究具有重要意义。
国内外一些学者对岩石非线性渗流特性进行了研究。FORCHHEIMER等[2]认为，压力梯度与渗流流量之间的关系是由流体和渗流通道的形态共同决定的，在低渗流流量情况下，压力梯度和渗流流量为线性关系，可由Darcy定律来描述;而当渗流流量较大时，Darcy定律[3]无法描述非线性渗流特征。
SOMERTON等[4]考虑大气压力和模拟油藏压力，在400～800 ℃条件下对大量砂岩岩芯进行了加热试验，发现岩样渗透率至少增加了50%。LI等[5]研究了岩石裂隙的渗流流量与温度之间的关系，结果表明，温度越高，岩石裂隙开度和渗流流量越大。冯子军等[6]采用高温高压岩体三轴试验机对一系列花岗岩试样进行热破裂渗流率的测定，并定量地观察了岩石裂隙的发展过程。薛娈鸾等[7]考虑温度对流体运动黏度的影响，建立三维裂隙岩体渗流耦合的模型，能够真实地反映岩石裂隙中的渗流过程，且具有较高的可靠性。以上研究表明岩石在高温作用后，其渗透特性会显著增加，但对于高温裂隙渗流的规律与机制的研究仍然不够深入。
胡大伟等[8]对峰后大理岩的非线性渗流特性进行了研究，得到渗流速率随压力梯度的演化规律。尹乾等[9]基于人工裂隙网络试样，通过改变围压大小，分析不同围压条件下岩体非线性渗流特性的演化过程。刘日成等[10]通过对岩石试样裂隙网络的渗流试验，观测到裂隙内部存在非线性渗流区域，得到了流量Q与压力P的非线性关系曲线，并通过数值模拟与试验结果相对比，使结果更具有说服力。杨天鸿等[11]提出了破碎岩体非线性渗流突水的研究机理，研究了不同围压、水力梯度和流速条件下破碎岩石渗流规律。于洪丹等[12]通过改变含有裂隙网络岩石试样渗透压力及围压的大小，推导出渗透系数在不同环境下的变化规律。郭保华等[13]通过研究不同种类岩石裂隙渗流的发展规律，划分了岩石裂隙渗流的阶段以及各阶段渗流的演化特征。李顺才等[14]建立了岩石裂隙的非Darcy渗流运动方程，得到了与应力场耦合的渗流场控制方程。以上研究工作极大地推动了岩石裂隙渗流的研究，揭示了岩石裂隙渗流的基本特征，然而现有研究大部分是对常温下的岩石裂隙开展的，对裂隙岩石在高温应力作用后的裂隙非Darcy渗流以及流体动量损失等方面的研究并不多见。
针对高放核废料地质处置、深部地热开采、以及煤炭深部开采等岩体工程遇到的渗流问题，开展高温岩石裂隙的渗流研究对于评价岩体工程安全性具有重要意义。为此，笔者开展高温后不同渗透压力作用下的岩石非线性渗流试验，得到了渗流性质随水头压力的演化规律;同时，根据CT三维扫描结果，深入探讨了试验现象的物理机制。
1 试验系统和步骤
1.1 试验系统
在进行高温后岩石非线性渗流试验时，由于试验中渗透压力较大，试样腔密闭困难，并且对围压的控制精度要求较高，因此，在一般的三轴试验仪上很难实现本试验。根据此次试验的特殊性，本文采用由中国科学院武汉岩土力学研究所与南昌大学合作研制的“温度-应力-渗流耦合的岩石力学试验系统”进行试验研究。该系统由围压、轴压和渗透水压3套相互独立的加载部分组成，具有以下功能和特点:① 特殊设计的渗透压力施加系统，具有准确控制流量、压力大小的特点，高围压(可达100 MPa)和高轴压(可达 500 MPa)输出，可实现应变和应力加载控制方式，控制精度高，其误差为±0.1 MPa，满足高渗透压条件下稳态法渗流试验的要求;② 特殊设计的氟化橡胶套，能保证将渗透水压力和围压完全隔开，可实现渗透压力和围压的独立施加，同时，完全密封的油缸系统也可保证试验过程中渗透压力和围压的稳定性;③ 全自动控制和数据采集;④ 设备的实体照片，如图1所示。
图1 温度-应力-渗流多场耦合仪实体
Fig.1 Test apparatus for coupling temperature,stress and seepage
1.2 试验步骤
试验所用的岩样为玄武岩，玄武岩的成岩过程和所处的地质环境与高温作用密切相关。采用取芯抽样的方法，制成直径为50 mm、高度为100 mm的标准玄武岩试样共8个。经测量其基本的物理和力学性质如下:密度为2.95×103 kg/m3、单轴抗压强度为283.5 MPa、内摩擦角为52°、黏聚力为48.5 MPa、弹性模量为58 GPa、泊松比为0.28。本文主要研究其高温过后岩石渗透性质的演化规律，具体的操作步骤如下:
(1)将岩石试样放在800 ℃的高温炉中加热6 h;
(2)岩样冷却后，将其安装到温度-应力-渗流多场耦合仪中进行试验;
(3)使用恒定荷载控制施加围压稳定在1 MPa，模拟岩石在工作情况下的围压条件;
(4)在恒定围压条件下，在进水口分级施加渗透压力(渗透压力为0～6 MPa)，出水口无水压力，保持为大气压;
(5)每级水头压力梯度保持一段时间，待水流稳定后，测量在该级水头压力梯度条件下一段时间内渗透水的质量;试验水温为25 ℃，水的密度和动力黏度分别为ρ=0.997×103 kg/m3和μ=0.891 mPa·s;
(6)将试样放入diondo d2高分辨率全能型微焦点CT检测系统进行裂隙性状分析。
1.3 diondo d2高分辨率全能型微焦点CT检测
采用diondo d2高分辨率全能型微焦点CT检测系统(图2)对渗透试验后的岩样进行三维扫描，得到岩样的多视图裂隙扫描结果和裂隙开度的分布分别如图3，4所示。
图2 Diondo d2高分辨率全能型微焦点CT检测系统
Fig.2 Diondo d2 high resolution all-round micro-focus CT detection system
图3 CT扫描裂隙分布四视图
Fig.3 Four-view display of rock fracture distribution by CT scanning
图4 裂隙开度分布的CT扫描结果
Fig.4 Aperture distribution of rock fracture by 3D CT scanning
由图3可知，从不同观测角度均可发现宏观裂隙的存在，其中沿进水-出水方向可见贯通裂隙，为渗透水提供了渗流通道。由图4可知裂隙的开度主要在0～1.6 mm，根据图4裂隙扫描结果，提取岩样裂隙开度数值，可得如图5所示的裂隙开度分布占比图。
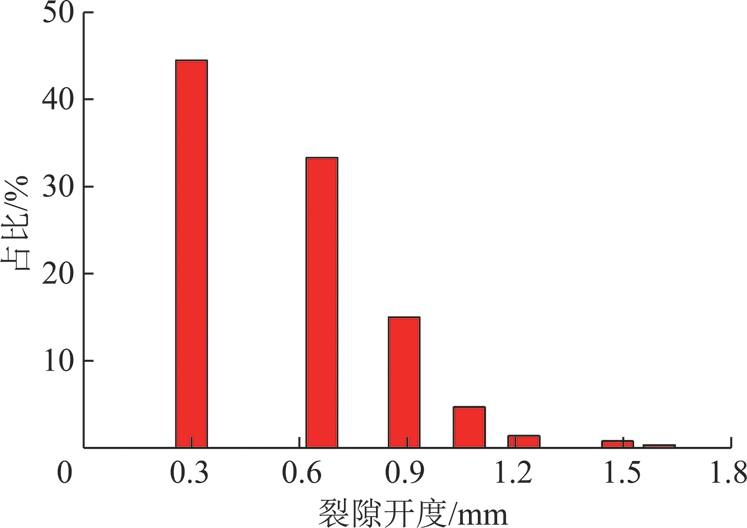
图5 CT扫描裂纹开度统计分析
Fig.5 Statistical analysis of CT scanned crack thickness
根据图5中裂隙的开度分布可知，裂隙开度主要分布在0.3～0.7 mm，裂隙平均开度h=0.572 6 mm。由于裂隙开度分布比较集中，因此，为方便计算岩石裂隙渗流的平均速度，本文采用裂隙的平均开度。由图3～5可知，通过CT扫描能清楚的看到岩石内部裂隙的网络结构，得到岩石裂隙网络分布图，从而获得裂隙开度和尺寸等一系列岩石裂隙分布特征参数，可为分析岩石裂隙非线性渗流提供依据。利用微焦点CT对岩样整体进行高分辨率三维扫描，基于分析软件对岩样进行三维逐层检测，分析其内部结构，并可进行缺陷统计和分析，得到了图6所示的逐层孔隙率统计结果。
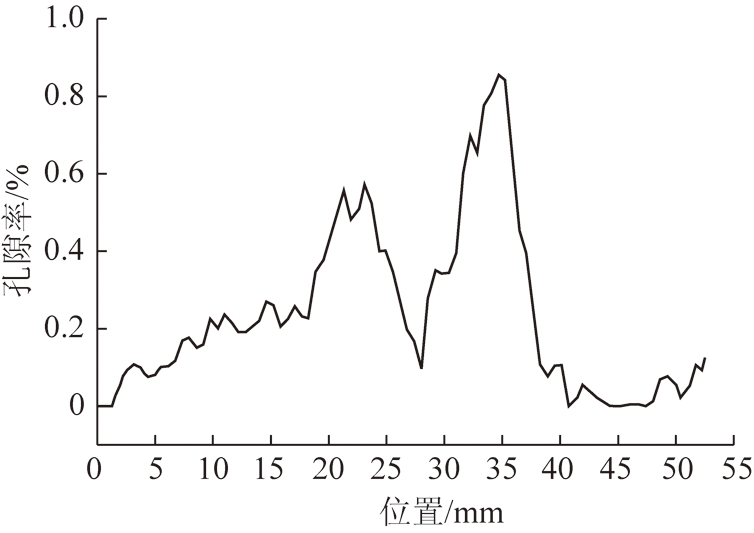
图6 CT扫描逐层孔隙率统计分布
Fig.6 Layer-by-layer porosity statistics by CT scanning
张志镇等[15]利用压汞法测试不同高温热处理后岩样的孔隙特征，得到温度对岩石孔隙率及孔隙空间分布的影响规律。其研究表明:随着温度的升高，岩石的孔隙率呈指数函数增长。根据图6的统计分析可知，本文试验所用的玄武岩即使在800 ℃高温作用后的内部孔隙率也极小(小于0.9%)，由此可知其在常温下的孔隙率更小。由LOSKUTOV和ZHAKOV等[16]对孔隙率和渗透率之间的回归关系来评价岩芯的渗流能力研究可知，当孔隙率较低时，对岩石裂隙渗流基本没有影响。因此，可以认为本文试验中的渗流基本是在岩石裂隙中进行的，而孔隙率的影响可以忽略不计。
2 试验现象和结果
2.1 高温下岩石裂隙发展
将岩样放入高温炉中，在800 ℃的恒温条件下加热6 h，等待冷却后，岩石内部会形成裂隙网络，如图7所示。
图7 岩石加温过后宏观图和透视图
Fig.7 Macro and perspective view of rock specimen after heating
2.2 渗流试验结果
根据1.2节试验步骤，得到了不同渗透压下8个岩样的非线性渗流试验结果，图8给出了围压为1 MPa时的非线性渗流曲线。
通过分析图8可以发现，对于全部岩样，其渗流流量均随着渗透压力梯度的增加而增大。同时，试验结果还表明，随着渗透压力的增加，
P和Q曲线的斜率逐渐增大，最后趋于一个大致稳定的值。可以将图8中渗流流量的演化过程分为2个阶段进行分析:① 初始阶段:当渗透压力较小时，流体在岩石裂隙中的流动相对来说比较困难，水流的流态比较稳定，为Darcy流。在这一阶段，流体的流动符合Darcy定律;② 非线性渗流阶段:当渗透压力逐渐增大时，裂隙中的流体流动速率逐渐增大，从而转变成非Darcy流。在这一阶段，Darcy定律不再适合流体的流动。
3 试验分析
3.1 非线性渗流分析
通过分析以上结果，本文采用Forchheimer方程来拟合渗流流量和渗流压力梯度的关系。
P=aQ+bQ2
(1)
其中，P为水力梯度;Q为渗流流量;a和b均为拟合系数，分别代表黏聚力损失项和惯性力损失项[3]。基于式(1)，通过origin软件得到拟合系数a和b，所得结果如图9及表1所示。
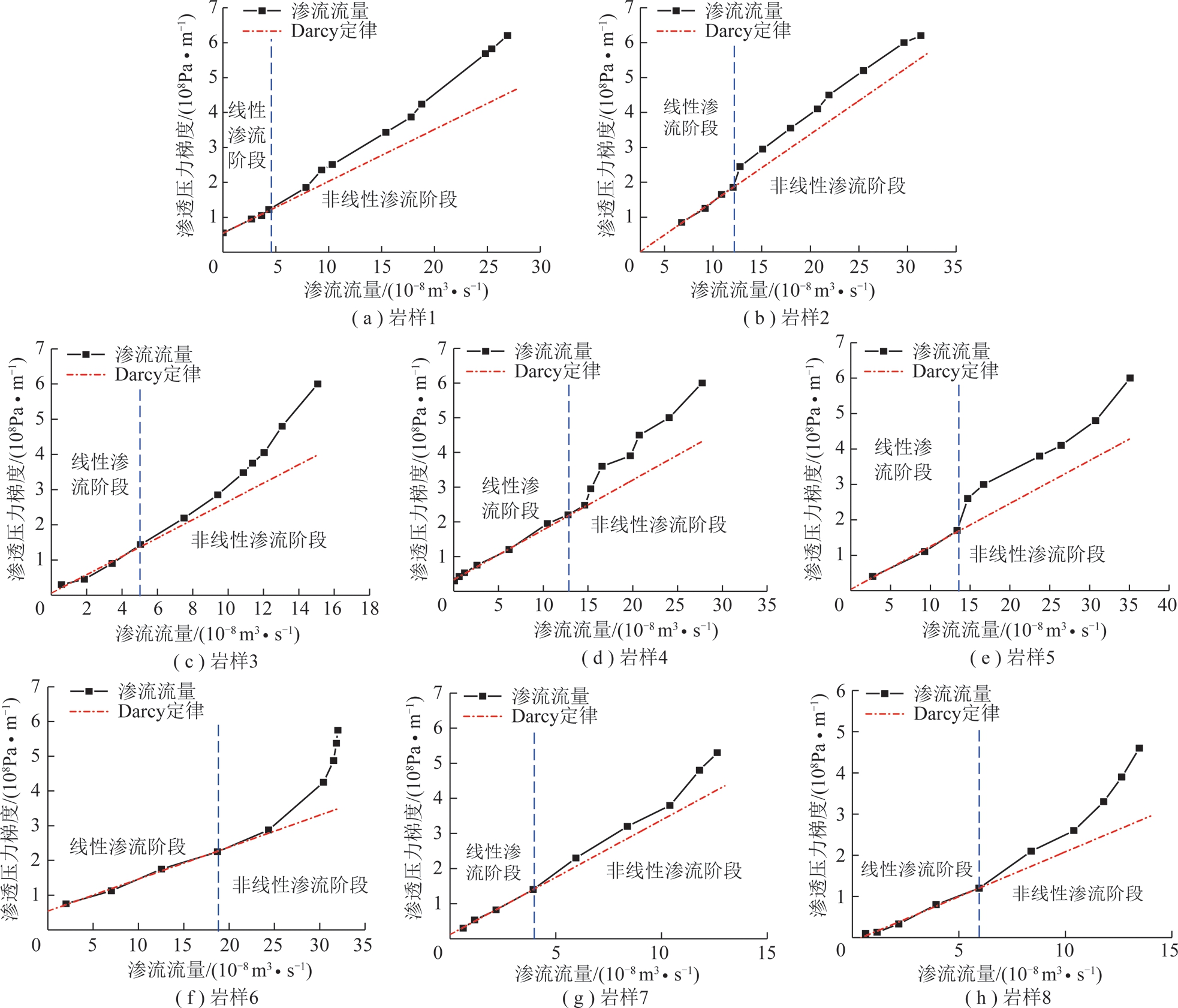
图8 渗流流量与渗透压力梯度的关系曲线
Fig.8 Relationship curves of seepage flow and seepage pressure gradient
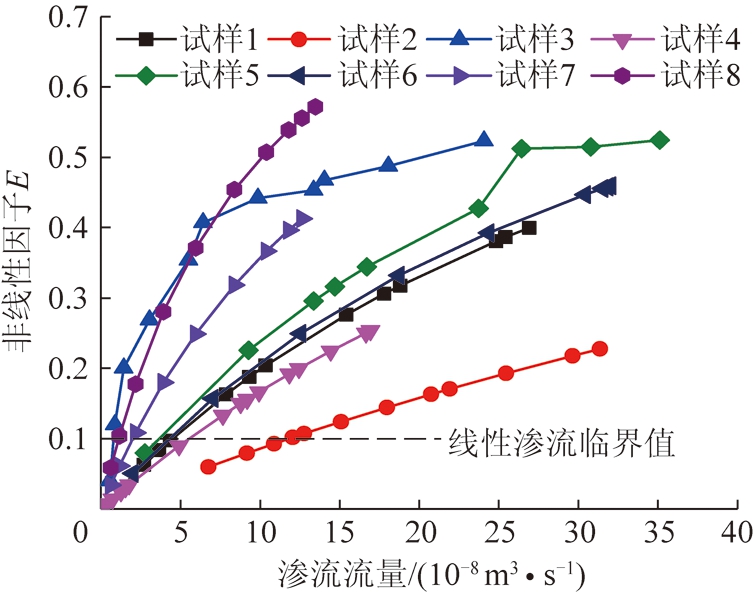
图9 非线性因子E与渗流流量的关系
Fig.9 Relationship between nonlinear factor E and seepage flow
由表1可知，Forchheimer方程能够很好的拟合本文高温作用后岩石裂隙渗流试验中水力梯度与流量之间的关系，相关系数均在0.94以上，精度很高。
3.2 临界雷诺数的判别
裂隙渗流的控制性方程为流体动力学中的Navier-Stocks方程，该方程指出，流体运动过程中的水力损失，主要来源于黏滞力损失和惯性力损失这两项。其中，惯性力损失项与流体流速的平方成正相关的关系[17-18]。式(1)中的非线性系数 b 主要表征流体流动过程中的惯性力耗散机制。
表1 拟合参数的大小及误差
Table 1 Values and errors of the fitting parameters
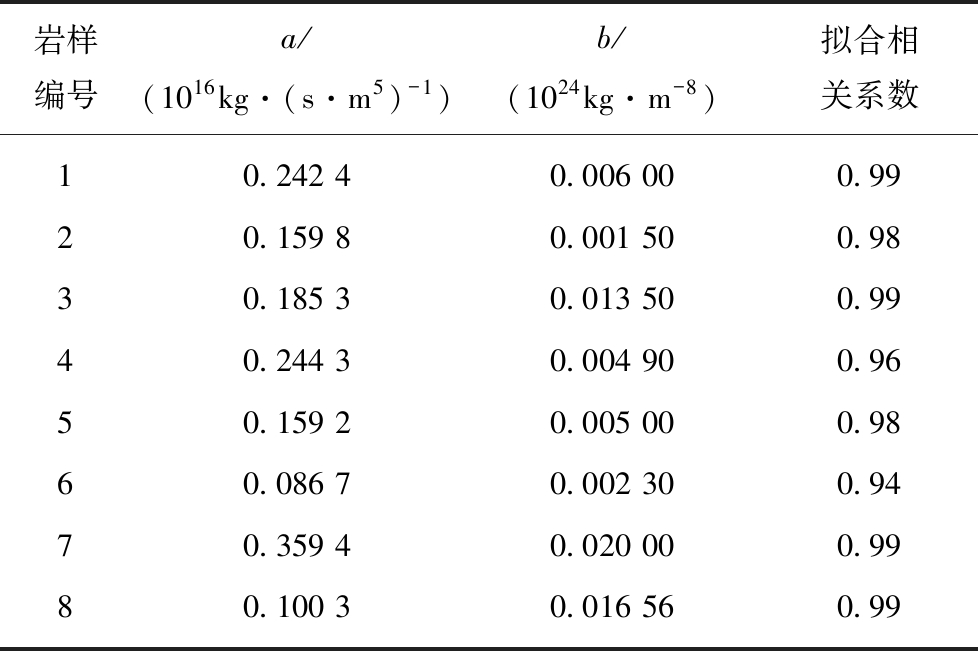
岩样编号a/(1016kg·(s·m5)-1)b/(1024kg·m-8)拟合相关系数10.242 40.006 000.9920.159 80.001 500.9830.185 30.013 500.9940.244 30.004 900.9650.159 20.005 000.9860.086 70.002 300.9470.359 40.020 000.9980.100 30.016 560.99
岩石裂隙渗流试验结果表明，随着流速的增加，达西定律已经变得不适用。为了进一步量化岩石节理渗流的非线性程度，ZENG和GRIGG(2006)[19]定义了一个非线性因子E，即
(2)
在裂隙渗流的研究中，一般认为，当E<0.1时，渗流为Darcy流，而当非线性因子E=0.1时，渗流的非线性效应就变得不可忽略[20]。因此，在实际岩体工程中大多定义E=0.1作为线性流和非线性流的分界点。
在水力学中，雷诺数表征惯性力和黏性力的比值，相应的在裂隙渗流研究中有如下定义:
(3)
其中，ρ为流体密度;v为裂隙的平均流速;h为裂隙的平均开度;μ为动力黏滞系数;w为试样宽度。根据以上描述，定义非线性因子E=0.1时的雷诺数为临界雷诺数Rec，其具体计算表达式[21]为
(4)
根据渗流流量与岩石裂隙开度可以求得流体的流动速度，其表达式为
(5)
式中，A为流体流过的横截面积。
根据式(2)可求得非线性因子E与渗流流量的关系，如图9所示。
由图9可知，随着渗流流量的增加，非线性因子E逐渐变大，到最后趋于一个定值。以岩样8为例，当E=0.1时，可知渗流流量Q=1.167 9×10-8 m3/s。
根据式(4)，(5)可以得到(临界)雷诺数与渗透压力梯度的关系曲线，如图10所示。
图10 (临界)雷诺数与渗透压力梯度的关系
Fig.10 Relationship between(critical) Reynolds number and seepage pressure gradient
图10中，符号“▲”代表临界雷诺数为0.26。随着压力梯度的增加，雷诺数也逐渐增加，当到达临界雷诺数之后，裂隙渗流就转化为非线性渗流。故临界雷诺数为裂隙渗流由Darcy流转化为非线性渗流的关键点。
3.3 动量相对损失率——欧拉数
欧拉数(Euler Number)是一个工程中常见的参数，在流体力学中欧拉数的符号为Eu，描述动量传递的特征数。其具体的表达式为
(6)
式中，ΔP为压力差。
根据式(6)可以得到欧拉数与压力梯度的关系曲线，如图11所示。
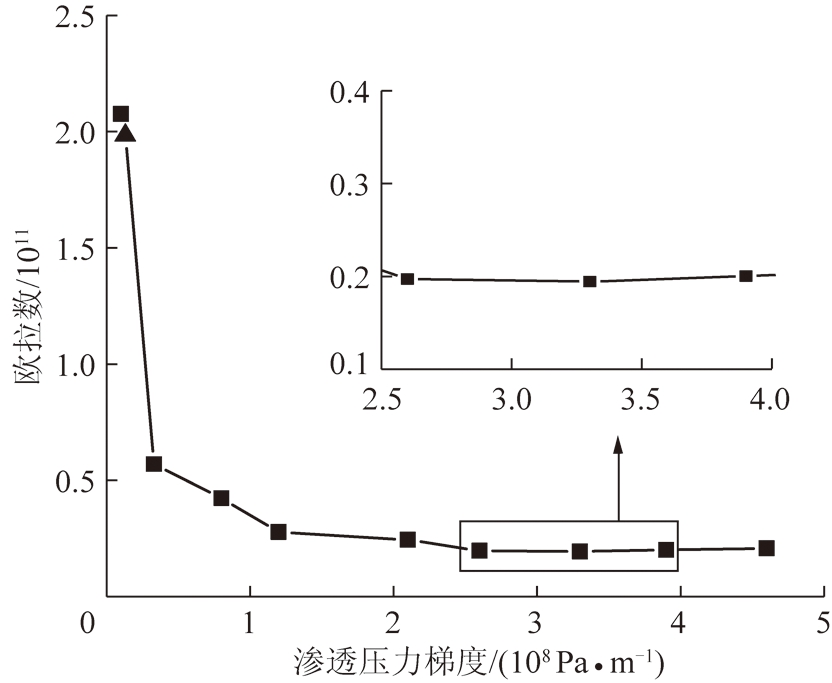
图11 欧拉数与压力梯度的关系曲线
Fig.11 Relationship between Euler number and pressure gradient
由图11可知，当渗透压力梯度逐渐增大时，欧拉数呈现出先急速减小后缓慢增加的趋势。产生该现象的原因在于，当渗透压力较小的时候，裂隙中流体的流动较困难，需要克服较多的阻力，因此动量损失较大;而当渗透压力逐渐增加时，流体在裂隙中的流动变得容易，其动量损失量减小;当渗透压力增大到一定程度时，渗透压力对降低流体动量损失的效应不明显，同时，裂隙的约束又会使其动量损失缓慢增加。
4 结 论
(1)采用三维CT扫描技术对岩样内部裂隙逐层扫描，能清楚的观测到岩石内部裂隙的网络结构，得出裂隙开度和尺寸等岩石裂隙分布特征参数，可为研究岩石多裂隙渗流提供依据。
(2)对高温作用后岩样的渗流试验数据采用Forchheimer方程进行拟合，得到Forchheimer方程中系数a，b的值，其拟合精度较高，为分析岩石裂隙渗流流量随压力梯度的变化提供理论依据。
(3)岩石裂隙渗流试验结果表明，随着流速的增加，达西定律已经变得不适用。因此定义了非线性因子E，根据E的数值大小，可判断岩石裂隙渗流的流态，当E=0.1时，可得到临界Darcy流对应的临界雷诺数，为裂隙渗流由Darcy流转化为非线性渗流的关键点。
(4)随着渗透压力梯度的增加，动量相对损失率—欧拉数呈先急速减小后缓慢增大的变化趋势，可直观的得到岩石裂隙中渗流动量的损失情况，对研究岩石中流体的运动损失提供理论支持。
[1] 高红梅.高温作用下岩石渗透规律的研究[D].阜新:辽宁工程技术大学,2005.
GAO Hongmei.Study on law of rock permeability under high-temperature[D].Fuxin:Liaoning Technical University,2005.
[2] FORCHHEIMER P.Wasserbewegung durch boden[J].Zeitz Vereines Deutsch Ingenieure,1901,45(1782):1781-1788.
[3] ERGRUN S.Fluid flow through packed column[J].Chemical Engineering Progress,1952,48:89-94.
[4] SOMERTON W H,SOYLEMEZOGLU I M,DUDLEY R C.Effect of stress on permeability of coal[J].International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts，1975,12(5-6):129-145.
[5] LI Z W,FENG X T,ZHANG Y J,et al.Experimental research on the convection heat transfer characteristics of distilled water in manmade smooth and rough rock fractures[J].Energy,2017(133):206-218.
[6] 冯子军,赵阳升,张渊,等.热破裂花岗岩渗透率变化的临界温度[J].煤炭学报,2014,39(10):1987-1992.
FENG Zijun,ZHAO Yangsheng,ZHANG Yuan,et al.Critical temperature of permeability change in thermally cracked granite[J].Journal of China Coal Society,2014,39(10):1987-1992.
[7] 薛娈鸾.裂隙岩体渗流-传热耦合的复合单元模型[J].岩土力学,2016,37(1):263-268，278.
XUE Luanluan.A composite element model for coupled seepage-heat transfer of fractured rock mass[J].Rock and Soil Mechanics,2016,37(1):263-268，278.
[8] 胡大伟,周辉,谢守益,等.峰后大理岩非线性渗流特征及机制研究[J].岩石力学与工程学报,2009,28(3):451-458.
HU Dawei,ZHOU Hui,XIE Shouyi,et al.Research on character and mechanism of nonlinear seepage in post-peak marble[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(3):451-458.
[9] 尹乾,靖洪文,刘日成,等.不同侧压力系数下裂隙网络岩体非线性渗流特性[J].岩土力学,2019,40(2):1-9.
YIN Qian,JING Hongwen,LIU Richeng,et al.Nonlinear fluid flow behaviors in fracture networks subjected to various lateral pressure ratios[J].Rock and Soil Mechanics,2019,40(2):1-9.
[10] 刘日成,蒋宇静,李博,等.岩体裂隙网络非线性渗流特性研究[J].岩土力学,2016,37(10):2817-2824.
LIU Richeng,JIANG Yujing,LI Bo,et al.Nonlinear seepage behaviors of fluid in fracture networks[J].Rock and Soil Mechanics,2016,37(10):2817-2824.
[11] 杨天鸿,师文豪,李顺才,等.破碎岩体非线性渗流突水机理研究现状及发展趋势[J].煤炭学报,2016,41(7):1598-1609.
YANG Tianhong,SHI Wenhao,LI Shuncai,et al.State of the art and trends of water-inrush mechanism of nonlinear flow in fractured rock mass[J].Journal of China Coal Society,2016,41(7):1598-1609.
[12] 郭保华,苏承东.多级加载下岩石裂隙渗流分段特性试验研究[J].岩石力学与工程学报,2012,31(S2):3787-3794.
GUO Baohua,SU Chengdong.Test research on piecewise seepage characteristics of rock fracture under multistage loadings[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(S2):3787-3794.
[13] 于洪丹,陈飞飞,陈卫忠,等.含裂隙岩石渗流力学特性研究[J].岩石力学与工程学报,2012,31(S1):2788-2795.
YU Hongdan,CHEN Feifei,CHEN Weizhong,et al.Research on permeability of fractured rock[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(S1):2788-2795.
[14] 李顺才,陈占清,缪协兴,等.破碎岩体流固耦合渗流的分岔[J].煤炭学报,2008,33(7):754-759.
LI Shuncai,CHEN Zhanqing,MIAO Xiexing,et al.Bifurcation of fluid-solid coupling flow in broken rock[J].Journal of China Coal Society,2008,33(7):754-759.
[15] 张志镇,高峰,高亚楠,等.高温影响下花岗岩孔径分布的分形结构及模型[J].岩石力学与工程学报,2016,35(12):2426-2438.
ZHANG Zhizhen,GAO Feng,GAO Yanan,et al.Fractal structure and model of pore size distribution of granite under high temperatures[J].Chinese Journal of Rock Mechanics and Engineering,2016,35(12):2426-2438.
[16] LOSKUTOV V,ZHAKOV S.Dependence of the liquid transverse relaxation time T2 in porous media on fluid flow velocity[J].International Journal of Heat and Mass Transfer,2016,101:692-698.
[17] SCHRAUF T W,EVANS D D.Laboratory studies of gas flow through a single natural fracture[J].Water Resources Research,1986,22(7):1038-1050.
[18] HASSANIZADEH S M,GRAY W G.High velocity flow in porous media[J].Transport in Porous Media,1987,2(6):521-531.
[19] ZENG Z,GRIGG R A.Criterion for non-darcy flow in porous media[J].Transport in Porous Media,2006,63(1):57-69.
[20] ZIMMERMAN R W,Al-YAARUBI A,PAIN C C,et al.Non-linear regimes of fluid flow n rock fractures[J].International Journal of Rock Mechanics and Mining Sciences,2004,41(3):163-169.
[21] JAVADI M,SHARIFZADEH M,SHAHRIAR K,et al.Critical Reynolds number for nonlinear flow through rough-walled fractures:The role of shear processes[J].Water Resources,2014,50(2):1789-1804.
