露天矿山路径优化问题是满足特定物理和经济约束之下搜索最佳运输线路的组合优化问题,长期以来一直都是卡车调度、物料流规划等相关领域的重点研究课题之一,对于降低矿山运营成本具有重要意义[1-2]。
目前,针对于露天矿山路径优化算法大致可分为两类,第一种方法是使用等效运距作为权重或优化指标,采用静态网络分析方法来搜索最佳路线。如,WHITE和OLSON[3]以全局等效运距的总和最小化为优化目标,建立露天矿山运输路径优化模型;CHANG等[4]在综合考虑等效距离和运输系统收益的情况下,针对卡车调度需求,提出一种寻径算法;ADENSO-DIAZ[5]指出煤矿的运输路线存在波动变化,并结合这种动态特点,提出了一种用于自动更新静态网络的新方法;LI J Q等[6]提出了一种同时考虑设备作业和时效性成本最小化的露天矿山洒水车线路优化策略;HU[7]采用和声搜索算法设计了露天矿山路径优化算法;陈应显[8]、孙臣良[9]、李勇[10]等分别将群智能算法引入静态运输网络图中,提出适用于露天矿路径优化问题的解决方案;另一类方法则是在多种约束条件下,结合图论中网络分析方法,通过求解数学规划模型来实现矿山运输路径优化,颇有代表性的研究如CHOI,PARK和 SUNWOO[11]指出“目前很少有关于卡车最佳运输路线的研究,这主要是因为在以前的研究中,人们总是假设路面状况在其生命周期内总是相同的,这种假设对露天矿山进行优化分析往往是不现实的”,基于此种考虑将多指标评价方法与最小成本路径分析方法相结合,提出适用于大型露天矿山线路优化的新方法;CHOI和NLETO[12]通过对最小成本路径分析算法的改进,提出一种适用于不同路面类型的优化方法,并对地形和曲线设计变化对交通效率的影响进行了分析。
事实上,路径优化算法在物流、交通运输和路由器寻址[13-14]等相关领域有着极为广泛的应用,近年来也形成了一系列极为成熟的动态网络寻径算法,但这些算法很难被直接应用于露天矿山路线优化问题中,其主要原因在于:在露天矿山实际作业场景中,运输系统常受到多种综合因素限制,运输成本常表现出周期性的随机波动效应,如直接采用传统的物理距离或单一静态常量来表征,则存在明显的局限性。特别是当路面受到频繁碾压破坏和周期性维护后,这种成本波动效应的周期性特征则更为明显。笔者在充分考虑上述问题的基础上,将Clifford代数引入到露天矿山路径优化问题中,利用其拓扑连通性计算与标量表达的无关性,构建了线路拓扑逻辑计算方法,并建立了标量场动态表达模型;考虑道路运输网络具有动态随机特性,提出基于时变运输功最小化的优化目标,并定义了时变运输功公式,提出了一种有效估计时变滚动阻力系数的新方法,给出了计算此类时变指标的优化计算策略;最终结合遗传算法构建了路径优化算法。经多组仿真对比实验验证,文中算法对于求解矿山路径优化问题可行且有效。
1 基于Clifford代数的运输网络建模
1.1 有向图的几何代数编码
在Clifford代数空间内进行基于有向图的路径分析,实质上是对欧式空间内的网络分析法的一种多维推广,是有效降低网络分析复杂度的重要手段之一。在Clifford代数空间内,任意欧式空间中的一条带有n个节点的路径方案,均可以被抽象表达为一个n阶片积对象(n-blade),并总是可以通过blade对象的几何代数运算来实现路径拓扑关系的生成、遍历和筛选[15]。因此,对于一个包含n个路径节点的运输系统有向图G=(V,E),则可进行如下的几何代数描述:对于有向图G,存在一簇向量{e1,e2,…,en}为几何代数空间Cln,0的向量集合,其中每一个元素ei均对应有向图网络中的惟一节点;同理,空间中的另一簇向量{e13,e24,…,eij};for 1<i<n,1<j<n,其可表示有向图中的有向边集合。根据几何代数空间内蕴的反对称特性,其有向边的方向性,即可表示为eij=-eji,并且这些有向边的关联函数可由标量uij来进行表示,uijeij。
1.2 Cln,0空间内拓扑关系计算
Cln,0空间中对象的维度扩张和形体的构建与表达均是通过外积运算来实现,这种内蕴的外积拓扑延拓特性能建立网络图中节点、有向边以及路径间的统一表达。因此,对于网络图中节点与有向边间的二目几何运算关系则可形式化表达为
![]()
(1)
式(1)描述了有向图节点到有向边的拓扑延拓方法,对于路径中有向边之间的进一步延拓也可以采用类似的外积运算来实现。故对于图中具备连通性的n个节点v1,v2,…,vn,其有序排列所组成的有效路径则可描述为具有n个基向量ei的连续外积形式,即L=e1∧e2…∧en=e1,2,…,n,e1,2,…,n为空间中的n阶片积对象,它所对应的路径即为可行解。
上述运算介绍了路径拓扑延拓的具体方法,但并不能判断出路径间的拓扑连通性。为此,文中引入片积维度的概念,并通过片积的维度运算实现延拓路径的连通性判断。由路径Cln,0可以看出,对具备连通性的路径进行连续的外积运算,其本质上是将一维向量ei扩展拉伸为n维片积对象e1,2,…,n的过程。因此,可以广义的认为基的每一次外积运算,其维度均向上延拓一阶,也就是说片积的重复外积运算将满足维度的可加性条件。根据这种可加性,就可以通过外积的维度变化来判别路径的连通性。因此,文中采用判据:grade(ei∧ej)=grade(ei)+grade(ej)来判断拓扑延拓的连通性。相反,当路径间不具备连通性时,由于有向边运算结果为变量0,可加性判别则将不再成立,即grade(0)≠grade(ei)+grade(ej)。综合上述两组判据,即可实现路径延拓与连通性拓扑的快速识别。
按照上述的几何拓扑关系,将有向图中的有向边的几何拓扑关系抽象为几何邻接矩阵描述为A,矩阵A中的任意一个元素皆描述了图中任意两点之间的几何拓扑关系和连通性。

(2)
观察式(2)不难发现,其本质上就是2-blade有向边的矩阵表达,因此外积运算仍适用于其所对应的矩阵表达。基于此种考虑,根据邻接矩阵的运算特性,将外积运算进一步推广,按照矩阵“叉乘”运算定义邻接矩阵的外积运算规则:A2 =A∧A,按照此种运算规则,几何邻接矩阵A每参与外积运算(A∧A)就等同于片积维度延拓一次,也就是向外扩展一层节点的路径,其路径延拓原理如图1所示,对于图1中包含有9个节点的有向图,带有2-blade有向边的几何邻接矩阵A,经过一次外积运算即可计算出所有3-blade的路径,即包含3个任意节点的有效路径(其中A2矩阵中“+”并不指代数学运算,仅表示可能路径的组合)。故通过多次迭代上述外积运算即可得到任意节点间的拓扑连通性关系。
1.3 Cln,0空间内标量计算
权重信息是寻径问题的求解基础,在露天矿山的路径优化问题中,这种权重信息多表现为数值型变量,且变量常以节点或有向边的关联函数形式存在。但在之前定义的几何代数空间中,空间对象间所有二目运算均基于外积的形式参与代数运算,这使得标量场数据均以积的形式表达,导致部分标量场数据丧失了可加性关系。为保证计算模型的合理性,需要对标量场内的关联函数进行如下可加性变换:考虑网络自身与权重间的无关性,将如式(3)所示的带有标量权重的外积拓扑运算的标量部分嵌入可加性映射Φ。
aei∧bej=(a*b)ei∧ej
(3)
文中可加性映射Φ采用:![]() 故其数乘运算关系即可表达为式(4)形式,从而实现标量数据的可加性。
故其数乘运算关系即可表达为式(4)形式,从而实现标量数据的可加性。
eaei∧ebej=(ea*eb)ei∧ej=ea+beij
(4)

图1 几何邻接矩阵外积运算原理
Fig.1 Operation principle of geometric adjacency matrix exterior product
2 数值约束标量场建模
2.1 定义模型变量
为定义模型方便,文中首先对约束模型中的参数变量做以下说明,其中:
(1)已知参数:V={1,2,3,…,n}为路径的非空节点集合;E为相邻节点间的有向边集合;ei,j=(i,j)∈E,节点i和j间的有向边,i,j∈V;Δheij为相邻节点间的高程差,m;Nk为实动卡车数量,k∈K;K为卡车所属类型;![]() 为路径相邻节点间的实动卡车数,
为路径相邻节点间的实动卡车数,![]() 为计划路径的待排物料总量,Mm3;PS为装载点;PE为卸载点;
为计划路径的待排物料总量,Mm3;PS为装载点;PE为卸载点;![]() 为第i辆k类型卡车的载重量,
为第i辆k类型卡车的载重量,![]() 为第i辆k类型卡车的自重,
为第i辆k类型卡车的自重,![]() 为待排量的计划排弃周期,
为待排量的计划排弃周期,![]() 为两相邻节点间的平均行车速度,km/h;ΔLei,j为两相邻节点间的物理距离,
为两相邻节点间的平均行车速度,km/h;ΔLei,j为两相邻节点间的物理距离,![]() 为两相邻节点间的行车安全距离上限,km;Kei,j为两相邻节点间的车流密度,辆/km;lk为 k类型卡车车身长度,
为两相邻节点间的行车安全距离上限,km;Kei,j为两相邻节点间的车流密度,辆/km;lk为 k类型卡车车身长度,![]() 为两相邻节点间的车流密度上限,辆/km;KE为所选路径的车流密度,辆/km;p为车道数量,双车道取2,单车道取1;kb为车辆行驶的不平衡系数;kr为车辆作业的时间利用系数;
为两相邻节点间的车流密度上限,辆/km;KE为所选路径的车流密度,辆/km;p为车道数量,双车道取2,单车道取1;kb为车辆行驶的不平衡系数;kr为车辆作业的时间利用系数;![]() 为卡车的风挡面积,m2;r为坡度阻力系数;C为空气阻力系数;ρ为大气密度,kg/m2;α为路面坡度,(°);f(t)为阻力系数的时变函数。
为卡车的风挡面积,m2;r为坡度阻力系数;C为空气阻力系数;ρ为大气密度,kg/m2;α为路面坡度,(°);f(t)为阻力系数的时变函数。
(2)待估计参数:Fei,j为相邻有向边之间的阻力集合,kN。
(3)规划模型的决策变量:xi为各弧段上决策变量。
2.2 数值型约束模型
数值型约束是描述路径属性特征的依据,也是建立路径优化问题的数值计算基础。对于文中所述的优化问题与传统的混合整数规划模型建模过程相同,只是无需在考虑模型中的决策变量和相关约束。因此,对于有向边约束的标量场建模,仍可采用规划建模的思路,按照全局时变运输功最小化进行建模,其优化问题的目标函数如式(5)所示。
![]()
(5)
式中,Fei,j阻力为时变函数,其主要由3部分组成:滚动阻力Ffeij、坡度阻力Freij以及空气阻力Fweij,其关联函数的形式化表达如式(6)所示。
考虑所选路径差异以及因路面频繁碾压而造成的路面阻力系数变化,定义相邻节点路径间的阻力公式:
![]()
(6)
不等约束以及等式约束条件如下:
(1)对于各个路径弧段的车流密度约束:
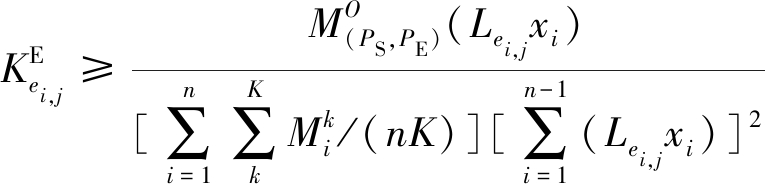
(7)
式中,![]() 满足计算条件
满足计算条件
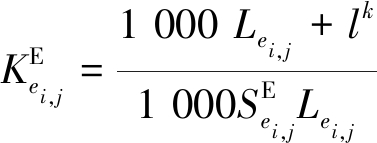
(8)
(2)所选路径的总体车流密度约束:

(9)
式中,KE应满足计算条件如下式:
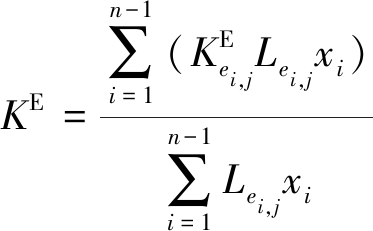
(10)
(3)道路通过能力约束:
![]()
(11)
式中,N应满足计算条件如下:
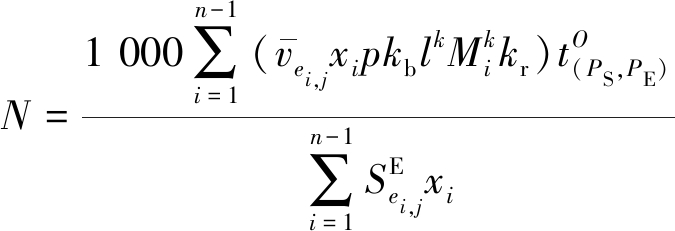
(12)
2.3 时变阻力系数估计
由权重指标的关联函数式(5),(6)不难看出,模型中最难计算的参数即为对模型中时变阻力系数的估计,这主要是因为该参数在不同路段以及相同路段的不同养护周期内均存在波动变化,进而导致阻力系数存在时变效应。因此,为了更好地模拟卡车在运输道路上因滚动阻力系数变化而造成的这种阻力时变效应,笔者采用多标签模式识别(分类)和趋势面技术来构建阻力系数的时变参数估计。其估计算法的基本思路是:首先利用统计所得路面属性指标和特定的人为路面分级,建立多标记的模式分类模型;利用模式分组后所得的指标参数进一步构建其阻力系数趋势面模型;最终按照给定路径的指标参数,实现阻力系数的时变估计,其算法实现过程如下:
第1步,道路表面类型的分类。根据露天矿山的运输道路状况及文献[16]中汇总的各类路面特征和阻力系数分布范围,对扎哈淖尔露天煤矿不同养护周期内的路面特征进行分类,并将各类路面特征及阻力系数分布范围进行统计,其分类统计结果见表1。
表1 不同路面条件下的滚动阻力系数分类
Table 1 Classification of rolling resistance coefficient under different road conditions

路面类型分类阻力系数范围1.非常坚硬,光滑的路面或污垢表面,没有渗透或弯曲0.010~0.0182.坚硬、光滑、稳定的路面,不渗透、浇灌、定期养护0.018~0.0203.坚固、光滑、滚动的道路,有泥土或弯曲的表面,微微弯曲,保持轻微,保持相当的规律性浇水0.020~0.0304.泥路,在负荷作用下弯曲,很少维护,没有水,25 mm的轮胎渗透或弯曲0.030~0.0455.泥路,在负荷作用下弯曲,很少维护,没有水,50 mm的轮胎渗透或弯曲0.045~0.0606.坑坑洼洼的土路,在负荷作用下变柔软,没有维护,不稳定,100 mm的轮胎渗透或弯曲0.060~0.0757.坑坑洼洼的土路,在负荷作用下变柔软,没有维护,不稳定,200 mm的轮胎渗透和弯曲0.075~0.1008.非常柔软,泥泞,坑坑洼洼的道路,300 mm的轮胎渗透,没有弯曲0.100~0.140
第2步,多标签模式分类训练数据处理。根据滚动阻力系数的测试表明[16-17],车辆的滚动阻力系数易受多种因素综合影响,如路面条件、行驶速度、轮胎结构、轮胎材料和轮胎压力等,但考虑问题自身、数学模型抽象及问题求解的复杂性,本文仅讨论因路面频繁碾压和因周期性路面养护,而引起的滚动阻力系数波动变化。为此,笔者将对路面碾压破坏的三大主要因素作为多标签分类模型的属性指标,即路段上平均行驶速度、养护周期内的累积运输物料量以及距上一个路面养护周期的时间间隔。按照上述属性和对应路面类型,统计扎矿2017年指标数据作为模式分组的训练数据,数据统计结果如图2所示。

图2 训练数据样本
Fig.2 Training data sample
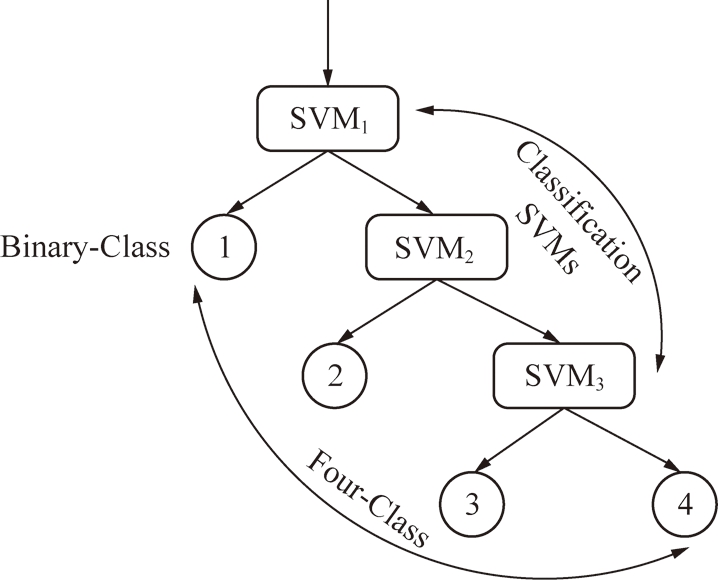
图3 四分类逻辑流程
Fig.3 Four-classification logic flow
第3步,多标记模式分类建模。将人为划定的8种路面类型作为分类标签,并按照二分类模式进行建模,具体的处理逻辑如图3所示(图中仅以四分类分组建模过程为例),对于训练样本(Xi,yi),i=1,2,…,l,其训练样本属性集为![]() 可以按照式(13)形式构建二分类支持向量机模型,其中分类指标yi∈{+1,-1}分别表示:+1表示被分类模型选出的一种特定路面类型,而-1则表示混杂有其他未被选出的路面类型集合。对于多标签分类,则如图3所示,进一步在-1所表示的路面集合中迭代构建二分类支持向量机,即可最终实现8种路面类型的多标签分类识别。
可以按照式(13)形式构建二分类支持向量机模型,其中分类指标yi∈{+1,-1}分别表示:+1表示被分类模型选出的一种特定路面类型,而-1则表示混杂有其他未被选出的路面类型集合。对于多标签分类,则如图3所示,进一步在-1所表示的路面集合中迭代构建二分类支持向量机,即可最终实现8种路面类型的多标签分类识别。
![]()
(13)
式中,K(x·xi)为核函数,笔者选用高斯径向基核函数。
第4步,趋势面模型和滚动阻力系数估计。经步骤3处理后,算法可通过属性指标识别出指标所属路面,但无法根据属性指标直接明确给出具体的系数估计。考虑阻力系数在对应的路面区间内周期性变化与其路面破损存在特定的内蕴关联(为降维考虑去掉指标![]() 文中采用二次多项式来描述其中的内蕴关联,其二次多项式趋势面模型如式(14)所示:
文中采用二次多项式来描述其中的内蕴关联,其二次多项式趋势面模型如式(14)所示:
![]()
(14)
并进一步采用最小二乘估计,建立规划模型如式(15)所示,8组路面的二次多项式趋势面拟合结果如图4所示。

图4 不同路面类型的趋势面估计
Fig.4 Trend surface estimates for different road types
![]()
(15)
3 基于Clifford代数的路径优化算法
传统的路径优化算法都是建立在求解整数规划模型的基础上,并结合群智能算法提高求解效率。这类规划模型计算常采用决策变量控制路径的拓扑连通性,求解过程需要同时考虑拓扑连通性计算和数值约束指标的目标寻优。当大型网络中数值约束存在动态特性时,求解这类问题的复杂度就会明显增加,易导致优化算法陷入局部最优,而无法获得全局最优解。在充分考虑这些因素的基础上,笔者将几何代数引入动态运输网络中,将传统欧式空间的有向图推广到Clifford代数空间,实现网络中的节点、有向边和路径的统一表达,利用迭代外积运算来表达出路径的拓扑连通性,从而实现拓扑计算和数值约束优化计算的分离,并且拓扑连通性计算结果可直接为群智能优化算法提供启发式拓扑关系。因此,文中路径优化算法设计的重点即为考虑如何将数值型约束嵌入有向图中,实现在几何代数空间内处理拓扑解析计算和动态有向边权重的标量计算,并利用外积的几何邻接矩阵计算结果为群智能算法提供启发式编码方案,最终实现复杂大型动态网络的快速寻径。
3.1 权重关联函数优化策略
第2节定义了关于路面养护时间间隔(t)的卡车时变行驶阻力的表达方式和计算方法,它标定了网络中各有向边之间的数值约束关系,但对于这样一个动态网络,特别是当网络节点规模较大时,这类数值计算仍极为复杂。出于简化计算提高算法收敛性考虑,文中基于随机理论和数理统计知识,引入两组推论和一组数值计算优化策略。
推论1:对于任意两个随机变量X,Y,如果其期望E(·)满足E(X)≤E(Y),则事件所对应的概率P(X≤Y)>0.5也成立。
为进一步说明该推论的正确性,笔者结合数理统计知识推导出此推论的证明过程如下:
假设:
E(X)≤E(Y)
(16)
可推知:
E(X)-E(Y)≤0⟺E(X-Y)≤0
(17)
引入相关变量Z:
Z=X-Y
(18)
可推得:
E(Z)≤0
(19)
根据期望定义可推知:
![]() ZP(Z)dZ
ZP(Z)dZ
(20)
将公式分为A,B两部分讨论:
![]() ZP(Z)dZ=
ZP(Z)dZ=
考虑公式A,B所在区间,可推知:
因为
![]()
(22)
又
E[Z]≤0
(23)
所以,式A绝对值一定大于式B绝对值:
![]()
(24)
故可推得如下P之间的关系:
P(Z≤0)≥P(Z≥0)
(25)
又因为整个概率空间和恒等于1:
P(Z≤0)+P(Z≥0)=1
(26)
进而推得:
P(Z≤0)≥1-P(Z≤0)⟺2P(Z≤0)≥1
(27)
整理即可证明出推论结果正确,即
P(Z≤0)≥0.5⟺P(X≤Y)≥0.5
(28)
推论2:对于路径优化问题中具备联通性且参与对比的两条路径L和K,可采用P(L≤K)和P(L>K)分别描述L和K成为最优路径的概率。因此,根据推论1结论,文中广义的认为min{E(L),E(K)}为最优路径的判据,判据所对应的路径即为最优路径。
结合上述2组推论,采用随机理论进行优化建模,其数值计算优化策略可表述为:假设道路运输网络中存在有效的可行路径r边的全路径运输功能耗可以表示为一个l维的随机变量Ω={W1(t),W2(t),…,Wl(t)},其联合概率密度分布函数可以表示为
fr=f[w1(t),…,wl(t)]=
![]()
(29)
因此,对于表征全路径中最优路径为r的事件γ,且该事件满足如下路径间的能耗条件:
wγ(t)≤w1(t),…,wγ(t)≤wl(t),该路径成为全局最优路径的概率即可表示为:
Pγ[wγ(t)≤w1(t),…,wγ(t)≤wl(t)]=
![]()
(30)
再进一步结合推论1,将路径事件的概率估计转化为求全局能耗期望值问题,即可实现数值约束的优化计算。
3.2 路径优化算法流程
为进一步提高算法的收敛特性,笔者将几何代数空间外积计算所得的几何邻接矩阵结果嵌入遗传算法,利用拓扑计算结果启发式的枚举路径基因编码,并将3.1节所介绍的优化策略嵌入到遗传算法的适应度函数(M/U(t),其中M为一个较大的常数,防止适应度值过小)中,用于简化时变动态网络中的标量场计算,算法具体处理流程将如图5所示。

图5 算法逻辑流程
Fig 5 Algorithm logic flow
4 仿真实验对比分析
为了直观地表达算法的优化效果,文中以扎哈淖尔露天矿为研究对象,选择了5组测试路径,对文中算法各代最优解的运输功能耗进行统计,如图6所示。
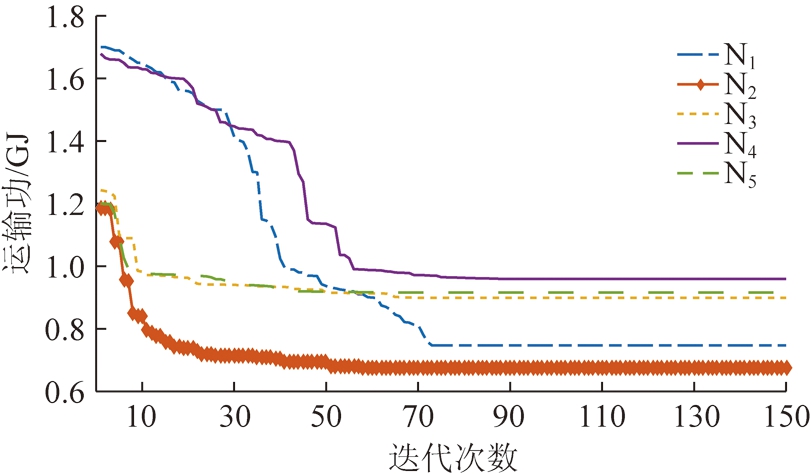
图6 路径优化结果
Fig.6 Route optimization results
对比分析图6可知,N1和N4两组路径节点数分别为74和77,在早期路径优化过程中运输功值较大,并在第30~40代左右算法开始快速收敛,最终收敛于全局最优解。
考虑现阶段对于遗传算法的精度、可信度和计算复杂程度尚没有有效的定量分析方法,为进一步论证文中算法的鲁棒特性,笔者采用上述5组测试路径进行20次重复测试,其20次重复实验的统计数据见表2。对比表2数据可知,20组重复实验除N1存在错误估计外,均收敛于最优解。通过平均相对误差水平和计算用时对比,说明算法具有较强的稳定性和较高执行效率。
表2 重复实验对比数据(20组)
Table 2 Repeated test comparison data(20 groups)
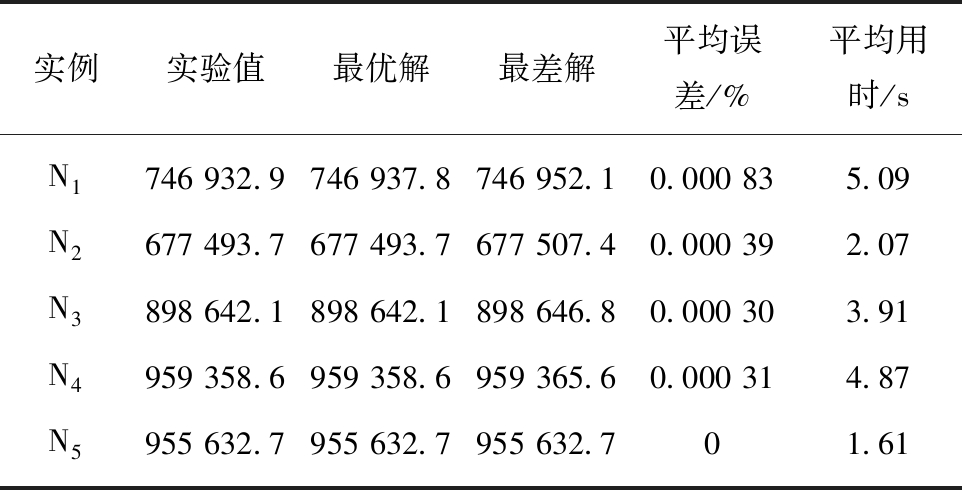
实例实验值最优解最差解平均误差/%平均用时/sN1746 932.9746 937.8746 952.10.000 835.09N2677 493.7677 493.7677 507.40.000 392.07N3898 642.1898 642.1898 646.80.000 303.91N4959 358.6959 358.6959 365.60.000 314.87N5955 632.7955 632.7955 632.701.61
笔者曾在文献[18]中论证过基于时变运输功最小化的路径优化方法,并采用改进的遗传算法对路径优化模型进行求解。为进一步说明引入Clifford代数计算后对于提高寻径算法效率的改善作用,笔者将此5组测试路径代入文献[18]算法模型进行仿真,其各代最优解的运输功能耗统计如图7所示。

图7 基于改进遗传算法的路径优化结果
Fig.7 Route optimization results based on IGA
对比图6和7可发现,图7中N1和N4两组模型迭代前期收敛速度缓慢,并且伴有过早熟现象。而图6中引入几何代数方法后算法的收敛速度更快,而且能消除图7中的过早熟现象,能够快速的优化出全局最优解。对比N2,N3和N5节点相对较少的路径,图6中3组曲线收敛方向上的梯度明显大于图7中曲线。因此,可以说明文中算法具有更快的收敛速度和过早熟控制能力。
最后为论证采用时变运输功作为寻径问题目标函数的优势,笔者进一步利用经典静态网络路径优化算法对5组测试路径进行仿真实验,其仿真计算结果见表3。通过对比表格中数据可看出,较之经典算法,文中算法能快速的找出路径中的能耗最优解,对于求解路径优化问题具有更强的现实意义。
表3 对比算法的优化效果
Table 3 Comparison of the effect of algorithmic optimization

CaseLoad StatusAlgorithmsNodeAverage speed/(km·h-1)Haul dist-ance/kmTransport energy/kJExecution time/sN11Clifford-GA74341.39746 932.95.16Dijkstra/PSO321.27776 826.421.17/7.79N21Clifford-GA31311.17677 493.72.02Dijkstra /PSO291.08704 826.58.77/3.04N31Clifford-GA39341.68898 642.13.97Dijkstra /PSO331.59914 732.311.87/3.73N41Clifford-GA77351.93959 358.65.07Dijkstra /PSO321.87967 439.525.02/9.35N51Clifford-GA36271.94955 632.71.59Dijkstra /PSO221.67979 261.87.07/4.72
5 结 论
(1)从有向图网络分析法出发,将经典欧式空间内网络分析方法推广至几何代数空间,建立了一套路径的几何拓扑连通性和约束指标计算的方法,实现了几何拓扑和数值最优化问题的分离,降低了传统露天矿多约束条件路径优化问题的复杂度。
(2)将路径分析中的数值型约束嵌入到几何代数空间,并根据露天矿山工程实际,建立了基于时变运输功的路径优化模型,并结合数理统计和随机理论,提出两组推论和一组优化策略,显著提高了算法的收敛效率。
(3)针对传统遗传算法的随机路径编码易存在冗余编码问题,通过引入外积拓扑运算结果进行启发式遗传编码,能有效提高遗传算法的收敛速度。
(4)通过对比多组寻径算法,证明采用Clifford代数与遗传算法进行组合来构建路径优化算法是现实可行的,对于降低矿山能耗、指导矿山生产具有极为重要的现实意义。
[1] 白润才,马云东,李建刚.露天矿卡车实时调度及安全保证预警理论与应用研究[M].沈阳:沈阳大学出版社,2005.
[2] 孙效玉,赵松松,刘恒,等.露天矿车流路网均衡分配模型[J].煤炭学报,2017,42(6):1607-1613.
SUN Xiaoyu,ZHAO Songsong,LIU Heng,et al.Equilibrium distribution model of traffic flow on road network for traffic flow of open pit[J].Journal of China Coal Society,2017,42(6):1607-1613.
[3] WHITE J,OLSON J.On improving truck/shovel productivity in open-pit mines[A].In Proceedings of the 23rd International Symposium on Application of Computers and Operations Research in the Minerals Industries(APCOM’92)[C].1992:739-746.
[4] CHANG Yonggang,REN Huizhi,WANG Shijie.Modelling and optimizing an open-pit truck scheduling problem[J].Discrete Dynamics in Nature and Society,2015(2015):8.
[5] DIAZ B A,LEV B,ARTIME R.Simulation in dynamic environments:Optimization of transportation inside a coal mine[J].IIE Transactions,2010,36(6):547-555.
[6] LI J Q,MIRCHANDANI P B,KNIGHTS P F.Water truck routing and location of refilling stations in open pit mines[A].Proceedings of 2008 Australian Mining Technology Conference The Australian Institute of Mining and Metallurgy[C].2008:141-156.
[7] HU T.Improved harmony search algorithm in strip mine vehicle route research[J].Advances in EECM,2012,1:559-564.
[8] 陈应显,韩明锋.改进粒子群算法的露天矿路径优化研究[J].微电子学与计算机,2011,28(11):61-68.
CHEN Yingxian,HAN Mingfeng.Improved particle swarm optimization on open-pit vehicle routing problem[J].Microelectronics & Computer,2011,28(11):61-68.
[9] 孙臣良,刘静.露天矿运输道路网络的建立及其路径优化[J].科技导报,2011,29(30):47-51.
SUN Chenliang,LIU Jing.Establishing of surface mine road networks and optimization of their transportation route[J].Science and Technology Review,2011,29(30):47-51.
[10] 李勇,胡乃联,李国清.基于改进粒子群算法的露天矿运输调度优化[J].中国矿业,2013,22(4):98-105.
LI Yong,HU Nailian,LI Guoqing.Open-pit hauling dispatching optimization based on improved PSO algorithm[J].China’s Mining Industry,2013,22(4):98-105.
[11] CHOI Y,PARK H D,SUNWOO C.Multi-criteria evaluation and least-cost path analysis for optimal haulage routing of dump trucks in large scale open-pit mines[J].International Journal of Geographical Information Science,2009,23(12):1541-1567.
[12] CHOI Y,NIETO ANTONIO.Optimal haulage routing of off-road dump trucks in construction and mining sites using google earth and a modified least-cost path algorithm[J].Automation in Construction,2011,20:982-997.
[13] SCHIFFER M,WALTHER G.Strategic planning of electric logistics fleet networks:A robust location-routing approach[J].Omega,2018,80:31-42.
[14] GAI Wenmei,JIANG Zhongan,et al.Multi-objective route planning model and algorithm for emergency management[J].Mathematical Problems in Engineering,2018:113-150.
[15] VINCE J.Geometric Algebra:An Algebraic System for Computer Games and Animation[M].New York:Springer Verlag,2009.
[16] TANNANT D,REGENSBURG B.Guidelines for mine haul road design[J].Canada Vancourer:UBC Faculty Research and Publications,2001.
[17] 余志生.汽车理论[M].北京:机械工业出版社,2000.
[18] 柴森霖,白润才,刘光伟,等.基于改进遗传算法的露天矿运输路径优化[J].重庆大学学报,2018,41(2):87-95.
CHAI Senlin,BAI Runcai,LIU Guangwei,et al.Open-pit path optimization based on improved genetic algorithm[J].Journal of Chongqing University,2018,41(2):87-95.
