现代浮选技术(泡沫浮选法)出现于20世纪初[1],早期研究方向主要集中在浮选药剂在矿物表面的作用规律以及矿物表面的润湿现象[2]。20世纪40年代,人们逐渐认识到矿物颗粒与气泡间的相对运动会对浮选结果产生重要影响,并展开了系列研究。然而因浮选槽中充斥着大量颗粒与气泡,流场环境十分复杂,因此有关浮选过程中颗粒-气泡间相对运动的研究一直是重点及难点[3]。
早期研究中,由于对实际浮选过程认识的不足,研究者主要通过不同流态下的流线方程对颗粒-气泡间的相对运动进行理论推导。随着研究的深入,人们逐步考虑到颗粒性质、气泡性质等因素对颗粒-气泡间相对运动的影响并对该过程进行了探索[2]。
对于颗粒-气泡间相对运动的研究不仅促使人们对浮选机理有进一步的了解,而且对开发新型浮选机和提高浮选效率均具有指导意义。JAMESON[4]通过研究颗粒-气泡间的相对运动,提出剧烈碰撞有助于提高浮选回收率,进而开发了Jameson浮选柱。曾克文和余永富[5]发现,浮选槽中矿浆紊流强度过大会降低萤石的最大浮选粒度,从而提出降低紊流强度反浮选脱除萤石。微细颗粒-气泡间相对运动研究表明,强紊流会促使微细颗粒挣脱流线的束缚进而与气泡发生碰撞,为此WANG等[6]通过在旋流静态微泡浮选柱上增设涡流发生器增大矿浆的紊流度,提高了浮选回收率和可燃体回收率。基于此,笔者对颗粒-气泡间相对运动的研究进展进行了综述。
1 基于流线方程的颗粒-气泡相对运动
早期研究认为,当颗粒粒度远小于气泡直径时,可认为颗粒随流线运动。为此提出了2个重要假设:① 颗粒惯性力可以忽略,即认为颗粒沿流线运动;② 气泡为刚性球体,不会发生形变。为此,早期对颗粒-气泡间相对运动的研究主要通过求解不同流态下的流线方程进行[7-8]。
SUTHERLAND[7]首次对浮选速率与流体之间的关系进行了定量描述,并根据势流下的绕流方程(式(1))建立了首个颗粒-气泡碰撞概率表达式(式(2))。
![]()
(1)
![]()
(2)
其中,ψ为流函数;Pc为碰撞概率;vb为气泡上升速度;Rb为气泡半径;r和θ分别为极坐标下的半径坐标和角坐标;Rc为临界碰撞半径;dp为颗粒直径;db为气泡直径。SUTHERLAND等的研究具有里程碑式的意义,提供了一种关于颗粒-气泡间相对运动的研究方法,为后续研究奠定了基础。
GAUDIN[9]在SUTHERLAND的基础上,根据Stokes流下的绕流方程(式(3))建立了类似的碰撞概率表达式(式(4))。
![]()
(3)
![]()
(4)
由于早期对中等雷诺数下流线方程认识的不足,随后的研究也都集中在Stokes流和势流。如REAY[10]和ANFRUNS[11]等都利用了Stokes流线方程对碰撞概率公式进行了推导。FLINT和HOWARTH[12]发现当Stokes数接近0时,无论气泡周围的流动是Stokes流还是势流,二者碰撞概率的极限值相同,具体表达式为
![]()
(5)
![]()
(6)
式中,ρp为颗粒密度;ρf为液体密度;Rp为颗粒半径;μ为流体动力黏度;U为气泡上升速度。
上述研究的基础为势流和Stokes流,势流是一种最简单的模型,计算过程中不考虑流体本身的黏性,并认为流体是无旋的,Stokes流是速度极为缓慢的流动。上述两种情况与实际浮选流态相差较大,因此适用性较差。随着对浮选过程认知的深入,中等雷诺数下的颗粒-气泡间的相对运动逐渐得到了关注。
WEBER和PADDOCK[13]通过求解Navier-Stokes方程,推导了中等雷诺数下的碰撞概率公式:
(200<Re<300)
(7)
YOON和LUTTERLL[14]认为浮选槽中的流态介于Stokes流与势流之间,通过结合Stokes流线方程与势流流线方程,提出了适用于雷诺数在0~100的流线方程(式(8))。式中x=r/Rb,根据该方程推导的碰撞概率如式(9)所示。
![]()
(8)
![]()
(9)
自此,基于流线方程的颗粒-气泡间相对运动的研究便形成了一个较为完整的体系,然而因上述研究过程中假设颗粒运动轨迹与液体流线一致,这一假设在随后的研究中被认为存在较大局限性。VERRELLI等[15]指出,利用流线方程推导颗粒轨迹的基本假设中存在一定矛盾,在推导过程中,颗粒既被看作大小有限的物体又被认定是不会对流动产生干扰的点。当颗粒粒度较小时,颗粒实际运动轨迹与理论计算结果吻合度较高,随着颗粒粒度和密度增大,由于惯性力和重力等因素的影响,颗粒轨迹会偏离流线。此外,后续研究者发现[16],颗粒-气泡间的疏水作用力是导致颗粒黏附在气泡表面的主要原因。在疏水力的作用下,颗粒会刺破颗粒-气泡间的水化膜进而形成三相润湿周边,三相润湿周边的不断扩展使得黏附更加牢固。采用流线方程研究颗粒-气泡相对运动时,液体显然无法模拟颗粒与气泡黏附的具体过程,因此基于流线方程的颗粒-气泡相对运动研究具有局限性。
2 各因素作用下颗粒-气泡间相对运动
随着对浮选过程中颗粒-气泡间相对运动了解的深入,研究发现颗粒-气泡间的相对运动除受颗粒周围流场的影响之外,还受到颗粒性质及气泡性质等因素的影响。
2.1 颗粒性质对颗粒-气泡间相对运动的研究
2.1.1 颗粒惯性的影响
早期研究过程中通常忽略颗粒惯性力的影响,然而,随着颗粒粒度及密度的增大,颗粒轨迹会在惯性力的影响下偏离流线。MICHAEL和NOREY[17]研究认为,一旦颗粒Stokes数大于1/12,惯性力对颗粒运动的影响便无法忽略。
LANGMUIR和BLODGETT[18]首次考虑了颗粒惯性力对颗粒运动的影响,并利用Stokes数量化了颗粒惯性力的影响。Stokes数是一个无量纲数,用于描述颗粒在流体中的行为,反映了颗粒惯性力和黏性力的比,当颗粒Stokes数较小时,颗粒容易跟随流体运动,反之颗粒运动的跟随性减弱,颗粒Stokes数St的计算公式为
![]()
(10)
LANGMUIR等假设颗粒为质点,通过数值计算近似推导了颗粒-气泡的碰撞概率(式(11)),该公式只适用于颗粒Stokes数较大的情况。
![]()
(11)
DOBBY和FINCH[19]同样引入了Stokes数表示颗粒惯性力的影响,通过多元回归计算了颗粒-气泡的碰撞概率(式(12))。
![]()
(12)
其中,Pc0为Stokes数为0时的碰撞概率;u*为颗粒速度与气泡速度的比值;Reb为气泡雷诺数。相较于LANGMUIR等的研究,该碰撞概率对于中等雷诺数下的流场具有较好的适用性,其适用条件为200<Reb<300,St<0.8,u*<0.25。
SCHULZE[20]提出颗粒-气泡间相对运动受截流效应、重力和惯性力3者共同影响,并分别推导了各因素作用下颗粒-气泡的碰撞概率公式。其中由惯性力引起的碰撞概率计算公式为

(13)
其中,a,b为与雷诺数相关的系数;vp为颗粒速度。SCHULZE的研究综合了颗粒流线、颗粒惯性力及重力的影响,然而由于缺乏对颗粒负惯性作用的认识,因此碰撞概率的计算结果较高。此外,SCHULZE认为,颗粒-气泡的碰撞概率是上述3种因素对应碰撞概率的简单累加,这一观点并未得到严格的证明,因此其准确性值得商榷。
DAI等[21-22]在SUTHERLAND等基础上考虑了颗粒惯性力及气泡表面流动性的影响,利用颗粒运动方程(式(14))对碰撞概率进行了推导,该方程被称为GSE(Generalized Sutherland Equation)方程(式(15))。

(14)

(15)
其中,Pc-SU为SUTHERLAND等推导的碰撞概率;v为颗粒速度;w为水流速度,推导过程中将颗粒作用在气泡表面的力分解为指向气泡中心的压力和远离气泡中心的离心力,随着θ增大,压力逐渐减小,离心力逐渐增大;θt为压力与离心力平衡点对应的角度,如图1所示。

图1 气泡表面受力示意
Fig.1 Schematic of forces acting on the surface of bubble
DAI等将理论计算结果与Hallimond管测得的碰撞概率相比较,发现当颗粒直径在7~60 μm,Stokes数小于0.27时,GSE方程的计算结果与试验结果吻合度较高。
GSE方程推导时将颗粒惯性作用分为正惯性作用和负惯性作用,当颗粒与气泡趋于在气泡前部(θ<45°)碰撞时,正惯性作用占主导地位,颗粒在惯性作用下脱离流线,趋于沿垂直方向与气泡碰撞,正惯性作用增大了颗粒与气泡的碰撞概率。当颗粒与气泡趋于在气泡后部(45°<θ<90°)碰撞时,负惯性作用占主导地位,流体切向速度的增大使得惯性力呈现出离心力的形式,颗粒趋于远离气泡,碰撞概率减小[23]。
NGUYEN等[24]通过求解颗粒运动方程计算了大小不同的球形颗粒(半径0~50 μm,密度2.5 g/cm3)与气泡(半径0.385 mm)的碰撞概率。将计算结果与GSE方程对比发现,当颗粒半径小于10 μm时,二者之间吻合度较好,随着颗粒半径逐渐增大,由颗粒运动方程得到的碰撞概率逐渐大于GSE方程的计算结果。
综上所述,为量化颗粒惯性力对颗粒运动轨迹的影响,学者们引入了Stokes数,然而由于缺乏对颗粒负惯性作用的认识,因此碰撞概率的计算结果偏大。GSE方程考虑了颗粒负惯性作用的影响,认为颗粒负惯性作用会降低碰撞概率,然而仅考虑颗粒惯性力显然无法准确表述颗粒-气泡间相对运动,需进一步考虑其他动力学因素的影响。
2.1.2 颗粒重力的影响
重力作为颗粒沉降的驱动力,会对颗粒-气泡间的相对运动产生较大影响,当颗粒体积相同时,颗粒所受重力由颗粒密度决定,为此在研究过程中通常会把密度的影响作为研究重点。
NGUYEN等[25-27]利用Galileo数量化了颗粒重力的影响,Galileo数反映了重力与黏性力的比,计算公式为
![]()
(16)
NGUYEN等随后推导了颗粒与气泡碰撞概率的计算公式,如式(17)所示,式中φ为固体体积分数,n取值与颗粒雷诺数和阿基米德数有关。

(17)
由式(17)可以看出,同一雷诺数下,碰撞概率随颗粒密度的增大而增大。NGUYEN等随后在GSE方程的基础上,考虑到重力的影响,建立了颗粒的运动方程,如式(18)所示,式中vg反映了重力对颗粒运动轨迹的影响。
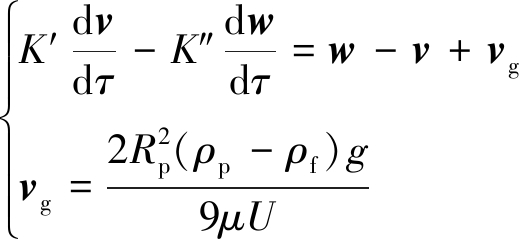
(18)
NGUYEN等计算时假设颗粒密度为1.3,2.0,3.0,4.0,5.0,6.0和7.0 g/cm3,气泡直径为0.77 mm。计算结果显示,对于细颗粒而言(粒度<20 μm),碰撞概率随颗粒密度的增大而减小,分析认为这是由于流经气泡的液体对颗粒产生负惯性作用导致的,对于粗颗粒而言,碰撞概率随颗粒密度的增大而增大。
KOUACHI等[28]利用石英(ρ=2.65 g/cm3)和黄铜矿(ρ=4.10 g/cm3)2种矿物比较了GSE方程和Schulze方程碰撞概率的计算结果,计算过程中气泡直径设为1.2 mm,计算结果如图2所示。

图2 GSE和Schulze模型中,石英和黄铜矿的碰撞效率
随颗粒大小的变化规律
Fig.2 Collision efficiency of quartz and chalcopyrite as a function of particle size calculated for both GSE and Schulze models
由图2可知,颗粒粒度较小时,GSE方程和Schulze方程的计算结果相差不大,随着颗粒体积增大,Schulze方程的计算结果逐渐大于GSE方程的结果。分析认为这是由于Schulze方程在计算过程中忽略了负惯性力的影响,从而导致上述结果。对于GSE模型,当颗粒粒度小于57 μm时,石英与气泡的碰撞概率大于黄铜矿与气泡的碰撞概率,当颗粒粒度大于57 μm时,石英与气泡的碰撞概率小于黄铜矿与气泡的碰撞概率。
上述研究表明,对于细颗粒而言,颗粒-气泡间的相对运动会受颗粒周围水流产生的负惯性作用影响,导致颗粒与气泡的碰撞概率随着颗粒密度的增大而减小;对于粗颗粒而言,颗粒与气泡的碰撞概率随着颗粒密度的增大而增大。
2.1.3 颗粒形状和粗糙度的影响
随着研究的深入,人们发现除惯性力和重力之外,颗粒的形状和粗糙度同样会影响颗粒-气泡间的相对运动进而造成浮选结果的差异。
矿物颗粒形状差异较大,可细分为类球形、多角形、整粒状、片状和纤维状等多种形状[26]。长久以来,人们一直推测某些形状的颗粒具有更高的可浮性并展开了大量研究。
KOH等[29]比较了相同条件下球形玻璃微珠和玻璃颗粒(球形系数0.41)的浮选结果,发现同粒度下球形玻璃微珠的浮选速率常数要低于玻璃颗粒的浮选速率常数。WEN和XIA[30]利用煤颗粒进行实验,结果与KOH等的结果一致。XIA等[31]研究发现,长时间磨矿会磨平煤颗粒表面的棱角,降低了煤的可浮性,上述实验均表明颗粒形状会对浮选结果产生较大影响,而造成上述现象的原因一直是研究的重点。
DIPPENAAR[32]利用高速摄影技术研究了颗粒形状对颗粒-气泡间液膜薄化、破裂的影响,发现疏水性较强球形颗粒的诱导时间反而大于疏水性较弱的棱角形颗粒。VERRELLI等[33-34]直接观测了玻璃微珠和玻璃颗粒在气泡表面的滑落、黏附过程,发现不规则玻璃颗粒的诱导时间要低于玻璃微珠的诱导时间。KRASOWSKA和MALYSA[35]发现上升气泡在空腔尺寸较小(约小于1 μm)的Teflon板表面需回弹4~5次才会黏附在Teflon板上,而在空腔尺寸较大(约大于50 μm)的Teflon板上,气泡不发生回弹直接黏附在Teflon板上,并认为这是由于粗糙颗粒的表面凸起会加速颗粒-气泡间液膜的排液,降低诱导时间。上述研究证明,形状不规则颗粒的诱导时间要低于球形颗粒,这意味着不规则颗粒具有更高的可浮性。
LECRIVAIN等[36]研究了疏水玻璃纤维在气泡表面的滑行及黏附过程,发现玻璃纤维与气泡的碰撞位置影响二者的黏附状态。如图3所示,当玻璃纤维与气泡在气泡上游区域发生碰撞时,玻璃纤维沿长轴方向与气泡相切,二者之间为强黏附,反之玻璃纤维沿短轴方向与气泡相切,二者之间的黏附十分不牢固,玻璃纤维极易从气泡表面脱附。

图3 玻璃微珠及玻璃纤维在气泡表面滑行
Fig.3 Glass beads and glass fibers slide on the surface of the bubble
HANSS等[37]研究了颗粒形状和表面粗糙度对颗粒-气泡间相对运动的影响,通过研磨改变玻璃微珠的形状,利用氢氟酸(HF)溶液腐蚀玻璃微珠得到表面粗糙度不同的玻璃微珠。实验发现,不规则颗粒的临界碰撞半径小于玻璃微珠的临界碰撞半径,如图4所示,且不规则颗粒的浮选回收率要高于玻璃微珠。经腐蚀后表面粗糙度较高颗粒与气泡之间的黏附强度要大于玻璃微珠与气泡之间的黏附强度,这一结果与KARKAS和HASSAS[38]的研究结果一致。分析认为颗粒形状会影响液体对颗粒的作用力,导致颗粒运动轨迹发生改变,颗粒表面粗糙度主要影响颗粒与周围介质之间的相互作用。

图4 不规则颗粒和球形颗粒碰撞示意
Fig.4 Schematic representation of bubble particle collision for ground and spherical particles
由上述研究可知,不规则颗粒与气泡间的诱导时间小于球形颗粒,这是因为不规则颗粒的表面凸起会促进颗粒-气泡间液膜的薄化及破裂,颗粒的形状会影响颗粒周围的流体对颗粒的作用力,改变其运动轨迹,且不规则颗粒与气泡之间的黏附强度受颗粒与气泡碰撞位置及颗粒表面粗糙度的影响。然而,上述研究多以玻璃微珠作为比较对象,缺乏不同形状矿物颗粒之间的相互比较,需在该方面进一步研究。
2.2 气泡性质对颗粒-气泡间相对运动的研究
除颗粒性质外,气泡表面性质也会影响颗粒-气泡间的相对运动。早期研究认为,因实际浮选时加入了表面活性剂,表面活性剂吸附在气泡表面导致气泡表面呈现非流动性。关于气泡表面的流动性,为便于理解,可假设气泡外包裹着一层环形液体层,当气泡表面呈现非流动性时,液体层固定在气泡表面,速度与气泡速度相同,当气泡表面呈现流动性时,该液体层可以自由移动。
SAM等[39]测量了自来水和表面活性剂溶液中气泡(直径0.9~2.7 mm)的上升速度。结果显示,气泡在两种液体中的初始上升速度相同,然而气泡在表面活性剂溶液中的上升末速要小于在自来水中的上升末速。这一结果与LOGLIO等[40]的实验结果类似,LOGLIO认为气泡在初始上升区域(约1 m)内其表面仍可视为流动性表面,随着气泡不断上升,杂质吸附在气泡表面会降低气泡表面的流动性从而导致气泡速度减小。上述研究均表明气泡表面的流动性会影响气泡的运动,然而气泡表面流动性对颗粒-气泡间相对运动的作用机理尚不明确。
DUCKHIN等[41]进一步研究指出,若溶液中污染物物质的量浓度低于10-2 mol/L,气泡上半球仍为流动性表面,这与目前普遍观点类似,即气泡表面流动性可用“滞留帽”(Stagnant cap)模型表示。具体来说,表面活性剂会吸附在气泡表面,由于气泡在上升过程中受到周围流体的作用,上半球吸附的表面活性剂、污染物等会被扫到下半球,故气泡上半球仍可视为流动性表面。因气泡表面流动性会对颗粒-气泡间的相对运动产生较大影响,故考虑了气泡表面性质的研究将会更接近实际浮选过程。
NGUYEN等[42-45]认为,当颗粒-气泡间距离减小到与颗粒直径相当时,二者之间的水化阻力层会影响颗粒的运动,颗粒所受阻力可分解为径向阻力Fr和切向阻力Fφ,如式(19)所示。
![]()
(19)
其中,f1~f4为阻力系数,该阻力系数受气泡表面的流动性的影响,计算方法见表1,表中h为颗粒与气泡间的距离;Vr为颗粒径向速度;Vφ为颗粒切向速度;Wr为水流径向速度;Wφ为水流切向速度。NGUYEN等量化了气泡表面流动性对颗粒所受水化阻力的影响,然而其研究仅考虑了流动性表面和非流动性表面两种情况,并未对表面部分污染气泡进行研究。
表1 流体阻力系数近似方程
Table 1 Approximate equation of fluid drag coefficient

非流动性表面流动性表面f1=[1+(Rp/h)0.89]1.124f1={1+[Rp/(4h)]0.719}1.394f2=2.022+(h/Rp)0.626+(h/Rp)f2=1.707+(h/Rp)0.836+(h/Rp)f3=1+0.498ln1.207Rph()0.986+1[]{}1.027{}0.979f3=1.106+(h/Rp)1.501+(h/Rp)f4=1.288+(h/Rp)0.724+(h/Rp)f4=1.107+(h/Rp)1.502+(h/Rp)
气泡表面流动性受气泡表面污染程度的影响,通常采用清洁角θclean量化气泡表面的污染程度。具体来说,当气泡表面无污染物吸附时,θclean=180°,此时气泡为流动性表面;当气泡表面被污染物包覆时,θclean=0°,此时气泡为非流动性表面;当0°<θclean<180°,气泡表面部分污染,可用“滞留帽”模型描述气泡表面的流动性。
CUENOT[46]分析了受污染气泡周围的流体运动,图5为雷诺数Re=100,θclean=45°时气泡周围的流线分布。由图5可知,在θclean附近,流线会突然远离气泡,分析认为这是由于涡量局部增强导致的。

图5 Re=100,θclean=45°的气泡周围的流线分布
Fig.5 Streamline distribution around the bubble
(Re=100,θclean=45°)
SARROT等[47]分别推导了颗粒与流动性气泡、非流动性气泡以及部分污染气泡之间的碰撞概率,发现颗粒与气泡的碰撞概率随气泡表面污染程度的增大而减小。LEGENDRE等[48]进一步研究表明,对于部分污染气泡,碰撞概率计算时存在一个临界值,如式(20)所示,式中n取值与雷诺数有关。
![]()
(20)
当颗粒与气泡的半径比小于该临界值时,碰撞概率与颗粒-气泡的半径比线性相关,反之则与该值的二次方相关。HUANG等[49]在LEGENDRE的研究基础上提出,存在一个临界角θcrit(式(21)),若θclean>θcrit,掠过轨迹只能与气泡在流动性部分碰撞,若θclean<θcrit,则掠过轨迹的碰撞点没有这一限制。
![]()
(21)
综上所述,气泡表面的流动性可用“滞留帽”模型描述,气泡表面流动性会影响颗粒与气泡接近过程中水化阻力的大小。颗粒与气泡的碰撞概率随气泡表面污染程度的增大而减小,且存在一个临界角θcrit会影响颗粒-气泡的相对运动。
3 颗粒-气泡相对运动的试验
上述研究多为理论推导,因实际浮选过程中颗粒-气泡间的相对运动受众多因素的影响,十分复杂,故通常采用简化试验装置研究颗粒-气泡间的相对运动。
颗粒沉降装置作为一种直接观测颗粒-气泡间相对运动的装置被广泛应用于实际研究,这一装置可追溯至1956年WHELAN和BROWN[50]的研究,其示意如图6所示。

图6 WHELAN和BROWN的试验装置
Fig.6 Experimental device of WHELAN and BROWN
试验过程中气泡通过毛细管C产生,颗粒储存在注射器F中并通过水流被带入水槽中,L为高速摄像机,用于记录颗粒的运动轨迹,R为阀门,M为反射镜装置。WHELAN首次观测并记录了颗粒-气泡间的相对运动,发现当颗粒-气泡间距离减小到一定程度后,颗粒会偏离垂直方向并向远离气泡的方向运动,并认为该过程与颗粒的Stokes数相关。WHELAN提供了一种直接观测颗粒-气泡相对运动的方法,为后续研究指出了方向,然而受当时条件的限制,该设备调节及观测精度较差。
WANG等[51-52]在WHELAN等基础上搭建了一套颗粒沉降装置用于观测颗粒-气泡间的相对运动,如图7所示,并以疏水性不同的玻璃微珠(dp=131 μm)为研究对象,利用相机记录了玻璃微珠在气泡(流动性表面)和球形玻璃(非流动性表面)上的运动过程。

图7 WANG等的试验装置
Fig.7 Experimental device of WANG
试验显示,亲水玻璃微珠只能在气泡上半球滑行,到达气泡赤道位置附近后便离开气泡,而疏水玻璃微珠越过气泡赤道后会继续沿气泡表面滑行并最终黏附在气泡底部,WANG分析了玻璃微珠的受力并推导了颗粒的滑落速度:
![]()
(22)
其中,ks为玻璃微珠在气泡表面滑行时的阻力系数,与试验比较发现,ks随气泡表面流动性增大而减小,玻璃微珠的滑落速度随气泡表面流动性增大而增大。
此外,试验发现颗粒与气泡之间的黏附效率除与颗粒疏水性相关之外,还受颗粒-气泡碰撞位置的影响,颗粒与气泡的碰撞位置越接近气泡中轴,黏附效率越大。上述研究观测了颗粒与表面流动性不同气泡之间的相对运动,并通过阻力系数ks量化了颗粒在气泡表面滑行时所受的阻力。
澳大利亚联邦科学与工业研究组织(CSIRO)同样开发了一套颗粒沉降装置并命名为“Milli-Timer”,装置示意图如图8所示。

图8 Milli-Timer试验装置
Fig.8 Milli-Timer experimental device
NGUYEN和EVANS[53]利用该装置记录了疏水玻璃微珠在气泡表面的运动过程,并观测到疏水玻璃微珠刺破水化膜的过程,该过程中颗粒与气泡间径向距离的变化如图9所示。

图9 颗粒径向位置相对气泡随时间的变化
Fig.9 Particle radial position relative to the bubble surface as a function of time
当玻璃微珠与气泡碰撞并在气泡表面滑行一段距离后,玻璃微珠与气泡之间的径向距离突然减小,这一现象是水化膜薄化至临界液膜厚度后刺破水化膜的瞬间,随后形成了三相润湿周边。VERRELLI等[54]同样观测到这一现象,并发现颗粒滑行速度在气泡赤道两侧并非完全对称,这一现象与假设气泡表面为流动性表面时的颗粒速度更为接近。
上述研究均是颗粒在自由沉降状态下与气泡间的相对运动,且研究对象均为表面性质均匀的玻璃微珠等材料。
HUBICKA等[55]研究了上升气泡(直径0.5~0.8 mm)与下降玻璃球(直径14.11 mm)之间的相对运动,试验装置如图10所示。
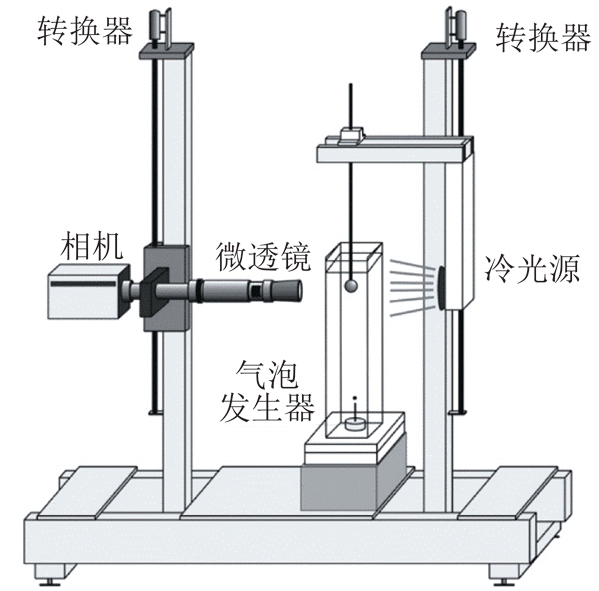
图10 HUBICKA等的试验装置
Fig.10 Experimental device of HUBICKA
试验时气泡由底部产生,玻璃球和光源一起固定在移动装置上并能以50 mm/s或100 mm/s的速度下降,高速相机固定在另一侧的移动装置上。气泡所处的溶液环境包括去离子水和表面活性剂溶液(187 mg/L)。试验结果显示,气泡的运动轨迹受气泡上升速度以及玻璃球下降速度的影响,推导了气泡运动轨迹的表达式,如式(23)所示,并验证了其准确性。

(23)
式中,x为气泡水平位置。
HUBICKA等的试验装置中气泡自由上升,颗粒下降速度在一定范围内可调,实现了运动颗粒与运动气泡间相对运动的研究。然而该装置使用的玻璃球的尺寸远大于实际浮选颗粒尺寸,且玻璃球并非实际矿物,缺乏代表性。
卓启明等[56-57]同样搭建了一套颗粒沉降试验装置(图11),该装置可精确调节气泡位置及颗粒初始沉降位置,并开发了一套多目标追踪软件,实现了对大量颗粒与气泡相对运动的自动处理。在该装置的基础上,卓启明等以实际煤样为研究对象,统计了大量煤颗粒与气泡的相对运动行为,试验结果表明,煤颗粒在与气泡碰撞前其运动轨迹会偏离垂直方向,且煤颗粒与气泡的黏附效率随碰撞角和密度的增大而减小。

图11 卓启明等试验装置
Fig.11 Experimental device of ZHUO Qiming
1—漏斗微移模块;2—LED阵列光源;3—入料定位漏斗;
4—观察室;5—气泡微移模块;6—摄像机;7—气泡产生调节模块
上述研究对于颗粒-气泡间相对运动的试验研究主要采用颗粒沉降法,其研究对象由追踪单个玻璃微珠与气泡之间的相对运动发展为对大量实际矿物颗粒与气泡间相对运动的研究,且出现了关于运动玻璃球与上升气泡之间相对运动的研究。然而,上述研究均在静水中进行,与实际浮选环境相差较大,而关于如何在实际浮选环境下追踪颗粒与气泡的相对运动尚未得到有效的解决,值得进一步加强研究。
4 结 论
(1)对颗粒-气泡间相对运动的研究进展进行了系统综述,当颗粒粒度较小时,利用流线方程推导颗粒-气泡间相对运动具有较好的适用性,随着颗粒粒度增大,受惯性力的影响,颗粒挣脱流线的束缚,颗粒惯性力的影响可细分为正惯性作用和负惯性作用,正惯性作用会促使颗粒沿垂直方向与气泡碰撞,增大碰撞概率,负惯性作用表现为离心力,减小碰撞概率。
(2)颗粒粒度较小时,碰撞概率随颗粒密度的增大而减小,颗粒粒度较大时,碰撞概率随颗粒密度的增大而增大。此外,颗粒形状的不规则性首先会改变流体对气泡的作用力,其次会促进颗粒-气泡间液膜的薄化及破裂,减少诱导时间,增大颗粒表面粗糙度会加大黏附强度。
(3)气泡表面的流动性可用“滞留帽”模型描述,气泡表面的流动性会影响颗粒所受水化阻力大小,且碰撞概率随气泡表面污染程度的增大而减小。
(4)目前关于颗粒-气泡间相对运动的试验研究多采用颗粒沉降法,然而研究多在静水中进行,缺乏实际浮选环境下真实矿物颗粒与气泡间相对运动的试验研究。
[1] 谢广元.选矿学[M].徐州:中国矿业大学出版社,2016.
[2] FUERSTENAU M C,JAMESON G,YOON R H.Froth flotation:A century of innovation[M].American:Society for Mining Metallurgy & Exploration,2007.
[3] NGUYEN A V,SCHULZE H J.Colloidal science of flotation[M].London:CRC Press,2004.
[4] JAMESON G J.A new concept in flotation column design[M].Arizona:SME,Phoenix,AZ,1988.
[5] 曾克文,余永富.浮选矿浆紊流强度对矿物浮选的影响[J].金属矿山,2000(9):17-20.
ZENG Kewen,YU Yongfu.Effect of the turbulent strength of the flotation pulp on mineral flotation[J].Metal Mine,2000(9):17-20.
[6] WANG L,Wang Y,Yan X,et al.A numerical study on efficient recovery of fine-grained minerals with vortex generators in pipe flow unit of a cyclonic-static micro bubble flotation column[J].Chemical Engineering Science,2017,158:304-313.
[7] SUTHERLAND K L.Physical chemistry of flotation.XI.kinetics of the flotation process[J].Journal of Physical & Colloid Chemistry,1948,52(2):394.
[8] DAI Z,FORNASIERO D,RALSTON J.Particle-bubble collision models-a review[J].Advances in Colloid and Interface Science,2000,80:231-256.
[9] GAUDIN A M.Flotation[M].New York:MCGRAW-HILL,1957.
[10] REAY D,RATCLIFF G A.Removal of fine particles from water by dispersed air flotation:Effects of bubble size and particle size on collection efficiency[J].Canadian Journal of Chemical Engineering,1973,51(2):178-185.
[11] ANFRUNS J F,KITCHENER J A.Rate of capture of small particles in solution[J].Transactions of the Institution of Mining and Metallurgy,Section C:Mineral Processing and Extractive Metallurgy,1977,86:9-15.
[12] FLINT L R,HOWARTH W J.The collision efficiency of small particles with spherical air bubbles[J].Chemical Engineering Science,1971,26(8):1155-1168.
[13] WEBER M E,PADDOCK D.Interceptional and gravitational collision efficiencies for single collectors at intermediate Reynolds numbers[J].Journal of Colloid & Interface Science,1983,94(2):328-335.
[14] YOON R H,LUTTRELL G H.The effect of bubble size on fine particle flotation[J].Mineral Processing & Extractive Metallurgy Review,1989,5(1-4):101-122.
[15] VERRELLI D I,KOH P T L,NGUYEN A V.Particle-bubble interaction and attachment in flotation[J].Chemical Engineering Science,2011,66(23):5910-5921.
[16] XING Y,GUI X,CAO Y.The hydrophobic force for bubble-particle attachment in flotation-a brief review[J].Physical Chemistry Chemical Physics,2017,19(36):24421-24435.
[17] MICHAEL D H,NOREY P W.Particle collision efficiencies for a sphere[J].Journal of Fluid Mechanics,1969,37(3):565-575.
[18] LANGMUIR I,BLODGETT K.Mathematical investigation of water droplet trajectories[J].Atmospheric Phenomena,1961:335-347.
[19] DOBBY G S,FINCH J A.Particle size dependence in flotation derived from a fundamental model of the capture process[J].International Journal of Mineral Processing,1987,21(3):241-260.
[20] SCHULZE H J.Probability of particle attachment on gas bubbles by sliding[J].Advances in Colloid & Interface Science,1992,40:283-305.
[21] DAI Z,DUKHIN S,FORNASIERO D,et al.The inertial hydrodynamic interaction of particles and rising bubbles with mobile surfaces[J].Journal of Colloid & Interface Science,1998,197(2):275.
[22] DAI Z,FORNASIERO D,RALSTON J.Particle-bubble collision models-a review[J].Advances in Colloid & Interface Science,2000,85(2):231-256.
[23] KOUACHI S,HASSAS B V,HASSANZADEH A,et al.Effect of negative inertial forces on bubble-particle collision via implementation of schulze collision efficiency in general flotation rate constant equation[J].Colloids & Surfaces A Physicochemical & Engineering Aspects,2017,517.
[24] NGUYEN C M,NGUYEN A V,MILLER J D.Computational validation of the generalized sutherland equation for bubble-particle encounter efficiency in flotation[J].International Journal of Mineral Processing,2006,81(3):141-148.
[25] NGUYEN P T,NGUYEN A V.Validation of the generalized sutherland equation for bubble-particle encounter efficiency in flotation:Effect of particle density[J].Minerals Engineering,2009,22(2):176-181.
[26] NGUYEN A V,KMET’ S.Collision efficiency for fine mineral particles with single bubble in a countercurrent flow regime[J].International Journal of Mineral Processing,1992,35(3-4):205-223.
[27] NGUYEN A V.The Collision between fine particles and single air bubbles in flotation[J].Journal of Colloid & Interface Science,1994,162(1):123-128.
[28] KOUACHI S,HASSAS B V,HASSANZADEH AHMAD,et al.Effect of negative inertial forces on bubble-particle collision via implementation of Schulze collision efficiency in general flotation rate constant equation[J].Colloids and Surfaces A:Physicochemical and Engineering Aspects,2017,517:72-83.
[29] KOH P T L,HAO F P,SMITH L K,et al.The effect of particle shape and hydrophobicity in flotation[J].International Journal of Mineral Processing,2009,93(2):128-134.
[30] WEN B,XIA W.Effect of particle shape on coal flotation[J].Energy Sources Part A Recovery Utilization & Environmental Effects,2017,39(13):1390-1394.
[31] XIA W,NIU C,ZHANG Z.Effects of attrition on coarse coal flotation in the absence of collectors[J].Powder Technology,2017,310:295-299.
[32] DIPPENAAR A.The destabilization of froth by solids.I.the mechanism of film rupture[J].International Journal of Mineral Processing,1982,9(1):1-14.
[33] VERRELLI D I,BRUCKARD W J,KOH P T L,et al.Particle shape effects in flotation.Part 1:Microscale experimental observations[J].Minerals Engineering,2014,58(4):80-89.
[34] VERRELLI D I,KOH P T L,BRUCKARD W J,et al.Variations in the induction period for particle-bubble attachment[J].Minerals Engineering,2012,36-38(10):219-230.
[35] KRASOWSKA M,MALYSA K.Wetting films in attachment of the colliding bubble[J].Advances in Colloid & Interface Science,2007,134(21):138-150.
[36] LECRIVAIN G,PETRUCCOI G,RUDOLPH M,et al.Attachment of solid elongated particles on the surface of a stationary gas bubble[J].International Journal of Multiphase Flow,2015,71:83-93.
[37] HASSAS B V,CALISKAN H,GUVEN O,et al.Effect of roughness and shape factor on flotation characteristics of glass beads[J].Colloids & Surfaces A Physicochemical & Engineering Aspects,2016,492:88-99.
[38] KARAKAS F,HASSAS B V.Effect of surface roughness on interaction of particles in flotation[J].Physicochemical Problems of Mineral Processing,2016,52(1):19-35.
[39] SAM A,GOMEZ C O,FINCH J A.Axial velocity profiles of single bubbles in water/frother solutions[J].International Journal of Mineral Processing,1996,47(3-4):177-196.
[40] LOGLIO G,PANDOLFINI P,MILLER R,et al.Novel methods to study interfacial layers[M].Amsterdam:Elsevier,2001.
[41] DUKHIN S S,KRETZSCHMAR G,MILLER R.Dynamic of adsorption at liquid interfaces-theory,experiment,application[M].Amsterdam Elsevier,1995.
[42] NGUYEN A V.One-step analysis of bubble-particle capture interaction in dissolved-air flotation[J].International Journal of Environment & Pollution,2007,30(2):227-249.
[43] NGUYEN A V.Particle-bubble encounter probability with mobile bubble surfaces[J].International Journal of Mineral Processing,1998,55(2):73-86.
[44] NGUYEN A V,EVANS G M.Exact and global rational approximate expressions for resistance coefficients for a colloidal solid sphere moving in a quiescent liquid parallel to a slip gas-liquid interface[J].Journal of Colloid & Interface Science,2004,273(1):262-270.
[45] NGUYEN A V.Hydrodynamics of liquid flows around air bubbles in flotation:A review[J].International Journal of Mineral Processing,1999,56(1-4):165-205.
[46] CUENOT B B.The effects of slightly soluble surfactants on the flow around a spherical bubble[J].Journal of Fluid Mechanics,1997,339:25-53.
[47] SARROT V,GUIRAUD P,LEGENDRE D.Determination of the col-lision frequency between bubbles and particles in flotation[J].Chemical Engineering Science,2005,60(22):6107-6117.
[48] LEGENDRE D,SARROT V,GUIRAUD P.On the particle inertia-free collision with a partially contaminated spherical bubble[J].International Journal of Multiphase Flow,2009,35(2):163-170.
[49] HUANG Z,LEGENDRE D,GUIRAUD P.Effect of interface contamination on particle-bubble collision[J].Chemical Engineering Science,2012,68(1):1-18.
[50] WHELAN P F,BROWN D J.Particle-bubble attachment in froth flotation[J].Transactions of the Institution of Mining and Metallurgy,1956,65:181-192
[51] WANG W,ZHOU Z,NANDAKUMAR K,et al.Effect of surface mobility on the particle sliding along a bubble or a solid sphere[J].Journal of Colloid & Interface Science,2003,259(1):81-88.
[52] WANG W,ZHOU Z,NANDAKUMAR K,et al.Attachment of individual particles to a stationary air bubble in model systems[J].International Journal of Mineral Processing,2003,68(1):47-69.
[53] NGUYEN A V,EVANS G M.Movement of fine particles on an air bubble surface studied using high-speed video microscopy[J].Journal of Colloid & Interface Science,2004,273(1):271-277.
[54] VERRELLI D I,KOH P T L,NGUYEN A V.Particle-bubble interaction and attachment in flotation[J].Chemical Engineering Science,2011,66(23):5910-5921.
[55] HUBICKA M,BASAROVA P,VEJRAZKA J.Collision of a small rising bubble with a large falling particle[J].International Journal of Mineral Processing,2013,121:21-30.
[56] 卓启明,刘文礼,刘伟.煤颗粒与气泡黏附行为的试验研究[J].煤炭学报,2018,43(7):2029-2035.
ZHUO Qiming,LIU Wenli,LIU Wei.Experimental study on the attachment behavior of coal particles and bubbles[J].Journal of China Coal Society,2018,43(7):2029-2035.
[57] ZHUO Q,LIU W,XU H.The effect of collision angle on the collision and adhesion behavior of coal particles and bubbles[J].Processess,2018,6(11):1-15.
