随着地下工程向深部发展,地下围岩在复杂地应力的作用下表现出的随时间发展的大变形、难支护以及失稳破坏等工程问题日益增多。因此在岩基、边坡、水利工程以及隧道等地下工程领域进行岩石工程流变学的研究具有重要的价值[1-3]。岩体流变理论就是研究岩石或岩体在外力、水力、温度、地质特征及施工扰动等各种环境、地质与工程因素作用下,岩体材料及岩体结构与时间相关的力学特性[4-6]。
于立业等[7]对高煤级原生结构煤进行了不同温度及不同应变速率流变试验,并进行红外光谱检测,探讨了其流变特征与流变形态转换条件。结果表明温度对其脆韧性流变有影响,内部结构发生重大变化。沈才华等[8]基于应变能理论,从内能角度出发,将Perzyna黏塑性理论与西原模型相结合,采用Drucker-Prager屈服准则考虑应力状态对加速蠕变阶段的影响,建立了能预测加速蠕变并能反映蠕变三阶段的简化蠕变本构模型。张泷等[9]基于Rice不可逆内变量热力学理论对岩石蠕变与松弛的一致性问题进行讨论,通过不同约束条件建立了黏弹—黏塑性蠕变与应力松弛本构方程,并通过模型相似性材料蠕变试验得以验证。高文华等[10]基于粉砂岩蠕变实验,建立了MCVISC模型,并利用FLAC3D进行了自定义模型的开发,并对该程序进行了验证,数值模拟结果与试验曲线吻合较好。
对于岩土类材料的加速蠕变阶段特性,如何进行判断和描述破坏机理还具有较大的争议,往往对于加速蠕变的研究都是基于试验结果的拟合,或者将传统的本构模型添加新建立的元件,来判别和模拟材料的加速蠕变过程。目前国内外学者认为,蠕变的产生主要由于微裂缝的产生和演变[11-12],尤其岩石蠕变过程与裂纹的扩展密不可分。因此,笔者基于最小能耗原理研究岩石蠕变断裂破坏的机理,建立一种基于能量耗散理论的非线性加速蠕变模型,最终结合岩石三轴蠕变试验数据,对模型的正确性与合理性进行验证。
1 基于能量耗散理论的加速蠕变模型建立
基于对岩石蠕变试验曲线特征的分析,可知岩石的蠕变变形都具有明显的黏弹塑性行为。当应力小于屈服强度值时,岩石蠕变变形会随着时间的发展而呈现出衰减态势,并且变形最终趋于稳定;当应力高于屈服强度值时,蠕变变形由减速蠕变过渡到等速蠕变,应变速率近似为一定值,应变随时间线性增长。当蠕变应变达到某一值时,岩石变形便会进入加速蠕变阶段,产生不可逆的变形,并最终变形导致断裂破坏。
一般常用西原体模型(图1)对岩石蠕变变形进行描述,其一维流变模型的蠕变方程为

(1)
式中,E0为弹性模量;E1为黏弹性模量;η1和η2为黏滞系数;σ为总应力;ε为总应变;σs为长期强度;t为蠕变时间。

图1 西原模型
Fig.1 Nishihara model
西原模型不能较好地描述黏塑性阶段的加速蠕变特性,故需要建立一种新型的模型来弥补西原体的缺点。由于Perzyna黏塑性理论对于岩石的黏塑性特性具有较好地呈现,也较好地描述加速蠕变阶段的力学特性,故选Perzyna黏塑性模型[13-14]来代替西原体原有黏塑性模型,其黏塑性应变率![]() 为
为
![]()
(2)
式中,η为黏塑性黏滞系数;F为岩石屈服函数;{m}黏塑性流动方向;“〈〉”是麦考利括号,括号内的函数为分段函数;{·}为向量表述形式。
其中φ(F)为F的任意函数,一般可以表示为
![]()
(3)
式中,n为参数;σs1为初始屈服强度。
对于岩土类这种耗散型材料来说,它们应力来自于应变或者温度变化历史,由于不同“历史”的应变与温度可以对应不同的应力,故只是简单地测量观察其外部变量是不能确定本构关系,必须加以可以反映材料内部变化的内部变量,才可以真正建立耗散型材料的本构关系[15]。一般认为产生蠕变加载过程中的能耗主要来源于材料内部的内能变化,它会进一步导致材料蠕变损伤,故可以运用能耗理论结合蠕变过程中蠕变速率来反映黏塑性蠕变变化特性。为了更好地分析岩石蠕变在黏塑性阶段蠕变特性,现采用耗散率值来定义不同蠕变阶段的控制阈值,将稳定蠕变与衰减蠕变的临界点采用临界耗散率值γ1来表示,其临界值下限值为![]() 当耗散率超过此临界值,岩石进入稳定蠕变阶段;稳定蠕变与加速蠕变的临界点采用临界耗散率值γ2来表示,其临界值下限值为
当耗散率超过此临界值,岩石进入稳定蠕变阶段;稳定蠕变与加速蠕变的临界点采用临界耗散率值γ2来表示,其临界值下限值为![]() 当耗散率超过此值岩石变进入加速蠕变阶段,其具体示意如图2所示。
当耗散率超过此值岩石变进入加速蠕变阶段,其具体示意如图2所示。

图2 蠕变分段临界示意
Fig.2 Creeping piecewise critical sketch map
根据能耗理论[16-17]可知,耗散率是关于应力与不可逆应变率函数,在黏塑性变形阶段耗能率γ为
![]()
(4)
式中,![]() 为耗散引起不可逆非线性应变率;σi为不同方向的应力。
为耗散引起不可逆非线性应变率;σi为不同方向的应力。
假设岩石在屈服函数约束下:
![]()
(5)
式中,λ为比例常数。
结合式(3)和(5)将F的任意函数φ(F)重新定义为
![]()
(6)
在岩石加载蠕变过程中,当耗散率值大于临界值γ1时,蠕变就会进入稳定蠕变阶段,假设此时产生的蠕变变形都是不可逆变形,故对于应变取值为临界点处的蠕变变形值εγ1,故根据式(4)中将蠕变变形值求导得出临界耗散率为
![]()
(7)
根据式(7)得出临界耗散率下限值为
![]()
(8)
式中,σs为长期强度;![]() 为长期强度对应的蠕变应变率。
为长期强度对应的蠕变应变率。
由于{m}在一维状态下采用相关联流动法则时,流动方向与塑性流动方向一致,故取值为{m}=1,同时结合式(4)得出蠕变耗散率可表示为
![]()
(9)
式中,σ为蠕变应力;![]() 为蠕变应变率。
为蠕变应变率。
联立式(6)~(9)代入到式(2)中得到改进后黏塑性应变率模型为
![]()
(10)
其中,作为稳定蠕变阶段耗散率中的蠕变变形率,实质是蠕变试验曲线在各数据点的斜率,同时由文献[18]可知采用对数以及多项式结合的经验公式可以很好地岩石的蠕变变形特性,即
εt=a+bln t+ct+dtk
(11)
式中,a,b,c,d,k均为材料参数,当处于非破坏应力水平时k=0,此时a+d为瞬时应变;t为蠕变时间。
将式(11)进行求导运算得到蠕变变形速率为
![]()
(12)
同时假设岩石的长期强度与初期屈服强度呈线性关系[19],将式(12)代入到式(10)中得到
![]()
(13)
式中,σ0为初始屈服强度。
同时根据岩石耗散能定义可知,耗散率与临界耗散率具有以下关系
![]()
(14)
式中,εs为长期强度σs所对应的蠕变变形值。
从而应力σ与长期强度σs的关系可以表示为临界耗散率的关系,将式(13)和式(14)结合西原体,得到改进后的黏塑性蠕变本构模型为

(15)
而对于加速蠕变阶段而言,耗散率的求解方法与稳定蠕变阶段一致,不存在由于加速蠕变各稳定蠕变两个蠕变阶段特性的不一致,导致岩石黏塑性蠕变速率出现较大差异,其中对于岩石耗散率的求解也只需要考虑该阶段的蠕变变形率。因此,通过耗散率和文中假设得出加速蠕变和稳定蠕变临界下限耗散率为
![]()
(16)
式中,![]() 为长期强度对应的蠕变应变率。
为长期强度对应的蠕变应变率。
岩石处于加速蠕变阶段时,即岩石应力已经处于破坏应力水平,此时岩石的应变速率为
![]()
(17)
将式(17)代入到式(2)中得到改进后加速蠕变阶段的黏塑性应变率模型为

(18)
综上所述,可以得到基于能耗理论一维状态下,岩石的黏弹塑性本构模型为
![]()
(19)
![]()
(20)

(21)
式中,λ1为衰减蠕变和稳定蠕变临界点处的比例常数;λ2为稳定蠕变和加速蠕变临界点处的比例常数;σ0为屈服应力。
通常情况下,在实际的地下结构中工程岩体都处在复杂的二向、三向受力状态,为更好地模拟工程岩石所处的这种受力状态,常在岩石室内流变试验时进行三轴压缩流变试验,旨在揭示其流变力学特性,为建立适合的流变本构模型、并为进行工程岩体流变数值分析提供有关流变参数[20-22]。因此,建立岩石在三维应力状态下的蠕变本构方程具有重要意义。
然后将一维西原体转化为三维西原体,本文将上述基于能耗理论一维状态下黏弹塑性本构模型推广到三维状态如下,即
![]()
(22)
![]()
(23)

![]()
(24)
式中,G0为弹性体的剪切模量;K为体积模量;G1为黏弹性体的剪切模量;n为试验常数,通常取n=1[23]。
一般认为在蠕变过程中,屈服函数选取连续可微的广义Mises中的Druck-Prager屈服函数为[24]:
![]()
(25)
式中,J2为应力偏量第二不变量。
将式(25)代入到式(22)~(24)中得到三维状态下基于能耗理论岩石的非线性黏弹塑性本构模型。
2 砂岩室内试验
2.1 试验仪器
本次试验是在矿业学院采矿重点实验室 MTS815.02 型三轴试验机上进行的(图3(a))。该试验机是美国 MTS 公司生产的专门用于岩石及混凝土实验的多功能电液伺服控制的刚性试验机,配有伺服控制的全自动三轴加压和测量系统,试验系统由加载部分、测试部分和控制部分3部分组成,具备轴压、围压和孔隙水压3套独立的闭环伺服控制功能。该设备性能好,测试数据客观可靠,双均值轴向引伸计以及周向引伸计测试精度高,伺服控制方式多样化,是目前世界上最先进的岩石与混凝土测试系统。试验机的主要技术参数:试验框架整体刚度为7.0 GN/m,最大轴向压力1 600 kN,最大围压70 MPa,最大孔隙水压70 MPa,满足试验要求。试验所采用的砂岩试样如图3(b)所示。

图3 试验仪器与试样
Fig.3 Rock mechanics test system and sandstone rock sample
2.2 常规三轴压缩试验
首先进行围压分别为0,10与15 MPa条件下的砂岩三轴常规压缩试验。以500 N/s的加载速率同步施加侧向压力及轴向压力至预定的围压值,使试件处于静水压力状态并保持侧向压力在实验过程中不变,注意围压活塞的进程,避免实验过程中围压的减少。设计相应加载程序,设定位移上限值,采用位移控制方式以0.002 mm/s的加载速率施加轴向荷载,试验数据由试验机自动采集并换算成对应的应变与应力输出到数据采集系统,采样间隔为2 s,并绘制出砂岩应力-应变曲线如图4所示。三轴压缩试验结果见表1。
表1 常规三轴压缩试验结果
Table 1 Test results of conventional triaxial compression

围压/MPa01015峰值强度/MPa42.7682.05104.16轴向峰值应变/%0.573 380.302 440.359 53径向峰值应变/%-0.411 03-0.232 18-0.336 07体积峰值应变/%-0.248 68-0.161 92-0.312 62E50/GPa29.5433.5934.64
注:E50为轴向应变等于峰值应变50%时对应的弹性模量。

图4 常规三轴压缩偏应力-应变关系
Fig.4 Deviatoric stress-strain relationship of conventional triaxial compression
由图4可知,随着围压的增大,砂岩峰值强度增大,弹性模量增大,抵抗变形以及承受荷载的能力增大,围压的增大将会使得砂岩各向峰值应变增大,增大了砂岩的扩容量,使得砂岩更不容易破坏。
2.3 蠕变试验方案
本文决定采用单体逐级增量加载进行室内蠕变试验,由室内三轴压缩试验所测各围压条件下的最大偏应力,来确定蠕变试验各级应力水平大小,为了更好地验证建立加速蠕变模型的合理性与适用性,本文进行的蠕变试验分为加载蠕变试验(定围压分级增轴压三轴蠕变试验)和卸载蠕变试验(定轴压分级卸围压三轴蠕变试验)两种。
在设计加载蠕变试验时,为了保证试验的可行性,采用分级加载的方式,对于围压10 MPa的试样,起始荷载选取三轴压缩最大偏应力的50%,为了计算方便将起始荷载取整为40 MPa,对于围压15 MPa的试样,起始荷载也选取三轴压缩最大偏应力的50%,为了计算方便将起始荷载取整为50 MPa,分级荷载依次均增加10 MPa,加载速率设定为500 N/s,各级荷载在变形稳定之后,将测试进入下一应力水平直至破坏。卸载蠕变试验采用分级卸载的方式,初始围压设定为15 MPa,围压卸载速率为500 N/s,每次围压减少5 MPa,两组蠕变试验轴压分别设定为80 MPa与60 MPa,卸载蠕变试验按照图5中加载速率先施加轴向荷载,在施加第1级应力水平的稳定之后,再施加围压荷载到预定值并保持恒定,测量和记录岩石试样的轴向应变和时间关系,然后按照试验方案逐步进行围压卸载。同时为保证实现如图5所示的卸载路径,必须保证在卸荷过程中轴向应力σ1恒定,各级荷载持续时间在变形稳定之后,试验进入下一应力水平直至破坏。

图5 试验应力路径卸载示意
Fig.5 Schematic diagram of test stress path
三轴蠕变试验步骤与三轴常规试验大致相当,仅加载方式稍有不同:设计相应加载程序,设定位移上限值,分级增轴压蠕变试验时采用荷载控制方式以500 N/s的加载速率施加轴向荷载直至预定荷载,并设定荷载持续时间为25 h,同理设定后1级荷载以及持续时间,而分级卸围压蠕变试验时亦按照同样的荷载速率卸围压至预定值,试验数据由试验机自动采集并换算成对应的应变与应力输出到数据采集系统,采样间隔为5 s,并绘制出轴向应变-时间历时曲线。
2.4 蠕变试验结果分析
由图6可知,在轴向应力水平下,试件轴向均有瞬时应变产生,而后进入衰减蠕变与稳定蠕变阶段,当应力水平较高时,就会出现加速蠕变阶段。对各级应力状况下的轴向瞬时应变进行分析,就会发现瞬时应变的大小与应力水平有关,应力水平越高,瞬时应变值也就越大,但瞬时应变占总应变的比例先增大后减小,这是由于加载初期岩石内部空隙的挤压闭合以及后期荷载作用下裂纹扩张贯通所引起的。例如围压10 MPa情况下,40 MPa轴向应力作用下的瞬时应变为0.076 8%,占总应变的94.2%,50 MPa轴向应力作用下的瞬时应变占总应变的95.4%,70 MPa轴向应力作用下的瞬时应变值为0.223 2%,占总应变的80.4%。瞬时应变的增大不仅与荷载应力水平有关,而且受到前期加载历史的影响。对各级应力状态下的轴向蠕变变形进行分析可以发现轴向蠕变变形总体上随应力水平的增加而增加,但蠕变变形占总变形的的比例先减小再增大,反映了试样内部结构的不断损伤与劣化过程。例如围压15 MPa情况下,50 MPa轴向应力作用下的蠕变变形为0.004%,占总应变的4.4%,70 MPa轴向应力作用下的蠕变变形占总应变的2.5%,90 MPa轴向应力作用下的蠕变变形为0.044%,占总应变的14.65%,60 MPa比50 MPa轴向应力作用下的蠕变变形量稍小,可能原因是50 MPa荷载作用下试件的变形还包含空隙的压密带来的轴向变形。各级应力状态下蠕变变形量的增大的影响因素与瞬时应变增大的因素一致。

图6 不同轴向应力下轴向蠕变(加载)
Fig.6 Creep of axial under different axial stress state(loading)
综合分析瞬时应变与蠕变变形占总变形的比例值,可以发现瞬时变形在总变形中占有绝对的比重,试件破坏的主要因素还是外部荷载引起的瞬时变形。

图7 分级卸围压
Fig 7 Unloading confining pressure
由图7可知,以轴向60 MPa作用下砂岩卸围压蠕变试验为例,在轴压60 MPa条件下试样共经历了3级围压,分别为15,10,5 MPa,砂岩试样蠕变历时为62.28 h,轴向最终破坏极限应变为0.311 5%,大于分级增轴压定围压三轴蠕变试验轴向最终变形值,反映了卸围压对砂岩试样极限变形的影响较增轴压更大,围压越低,破坏时的变形量越大。通过对比分级增轴压三轴蠕变试验,可以发现分级卸围压引起的偏应力增大更容易使试样由衰减蠕变过渡到稳定以及加速蠕变阶段,卸围压蠕变变形更为显著,比如围压10 MPa条件下的分级增轴压试验破坏偏应力为60 MPa,而轴压60 MPa条件下的分级卸围压试验破坏偏应力为55 MPa,且破坏时间更短。主要原因是岩样内部积累的能量向卸荷方向释放,因而造成裂隙尖端拉应力超过该点抗拉强度,从而裂纹逐渐扩张,横向变形逐渐增大,岩样内部结构损伤加剧,最终局部丧失承载能力而失稳破坏。在较高的围压(σ3= 15 MPa)作用下,各向变形呈现衰减蠕变形态,在中等围压(σ3= 10 MPa)作用下,各向变形最终呈现稳定蠕变形态,在较低围压(σ3=5 MPa)作用下,各向变形最终呈现加速蠕变破坏形态。对各级围压作用下的各向蠕变变形进行分析可以发现各向蠕变变形总体上随围压的降低而增加,蠕变变形占总变形的比例随围压的降低而增大,瞬时变形随围压的降低而增加,但占总变形的比例随围压的降低而降低。例如围压15 MPa情况下径向瞬时应变量为-0.058 63%,占总应变的92.6%,10 MPa围压作用下的径向瞬时应变为-0.112 74%,占总应变的76.5%,5 MPa围压作用下的瞬时径向应变值为-0.232 93%,占总应变的64.4%。
3 模型参数识别
3.1 模型临界参数确定
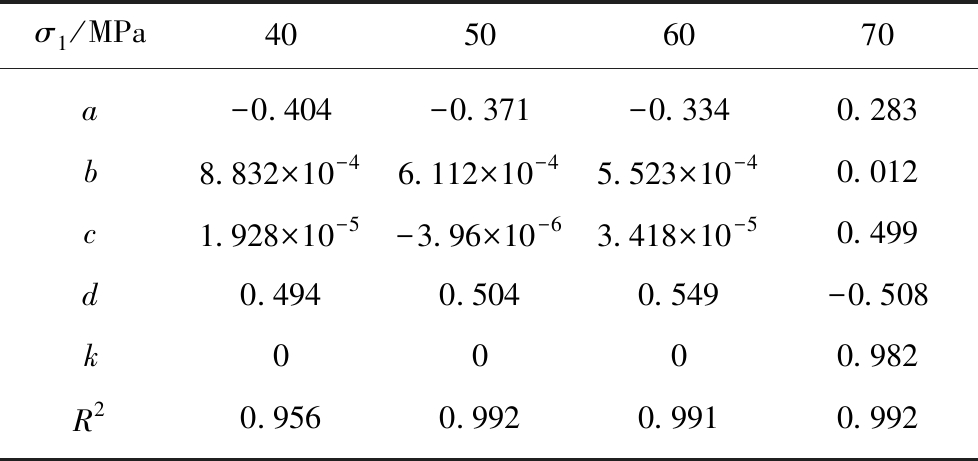
由于实验过程中试样的非均匀性,各向异性以及微缺陷的存在,造成试验数据的震荡,由原始试验数据进行蠕变速率的确定势必造成蠕变速率发展趋势上下波动较大,不利于对蠕变速率进行分析,难以反映蠕变变形规律,故采用经验公式(11)对时间t求导后进行拟合,以定围压分级加载轴压试验方案中的围压10 MPa为例,拟合参数见表2。
表2 定围压分级加载轴压的轴向蠕变拟合参数
(σ3= 10 MPa)
Table 2 Fitting parameters of axial creep under staged loading with constant confining pressure(σ3= 10 MPa)
σ1/MPa40506070a-0.404-0.371-0.3340.283b8.832×10-46.112×10-45.523×10-40.012c1.928×10-5-3.96×10-63.418×10-50.499d0.4940.5040.549-0.508k0000.982R20.9560.9920.9910.992
绘制出在不同围压条件下的蠕变速率与时间的规律曲线,如图8所示,然后根据图8得出模型曲线有关蠕变变形速率的参数。

图8 蠕变速率(σ3= 10 MPa)
Fig.8 Creep strain rate when σ3= 10 MPa
由图8可知,当应力水平较低时(σ1= 40 MPa),轴向与蠕变蠕变速率最终趋于0,说明了试样仅经历衰减蠕变阶段;当位于中等应力水平时(σ1= 50,60 MPa),轴向蠕变速率逐渐减小最终趋于一个稳定值,说明试样经历了衰减蠕变与稳定蠕变两个阶段;当应力水平较高时(σ1= 70 MPa),蠕变速率先减小趋于稳定,而后迅速增大直至岩样破坏,说明了试样经历了蠕变3阶段。
根据图2中经典蠕变曲线关系可知,时间t=0~t1段内包括了岩土体的瞬间蠕变和衰减蠕变两部分,其中衰减蠕变的特征为蠕变变形速度随时间而减小;到t=t1~t2段内岩土体进入了稳定蠕变阶段,此阶段内蠕变速度近于常数,几乎呈现一条水平直线;而到t>t2段内岩土体进入加速蠕变阶段,此阶段内蠕变速度随时间而增加直至岩土体失稳破坏,故可以根据上述对于蠕变速率的变化特征来区分临界点。因此,结合图7砂岩的蠕变速率得出在不同临界点处蠕变阶段转化对应的时间分别为t1,t2;临界耗散率所对应的蠕变应变速率为![]() 具体数值见表3,其中“-”表示没有这项数值,由于在轴压为50 MPa和60 MPa时岩石并未发生加速蠕变,只存在衰减和稳定蠕变2个阶段。
具体数值见表3,其中“-”表示没有这项数值,由于在轴压为50 MPa和60 MPa时岩石并未发生加速蠕变,只存在衰减和稳定蠕变2个阶段。
表3 临界点对应参数值
Table 3 Corresponding parameters of critical point

σ1/MPa506070t1/h4.7355.0320.847t2/h——5.245ε·sγ11.192×10-41.689×10-41.273×10-4ε·sγ2——2.763×10-4
3.2 模型计算值与试验值对比
现将上述对于临界参数的数值代入到改进后蠕变公式(22)~(24)中,然后通过Origin基于最小二乘法(Levenberg-Marquard优化算法)对定围压分级加载轴压试验中的围压10 MPa和定轴压分级卸围压试验中的轴压60 MPa下的三轴蠕变试验曲线进行参数辨识[25],得到其模型参数见表4,5,其中相关系数均在0.95以上。同理,可以得到其他定轴压分级卸围压和定围压分级加载轴压条件下三轴模型计算值与试验值对比。
表4 定围压分级加载轴压三轴蠕变模型参数(σ3= 10 MPa)
Table 4 Three-axis creep model parameters of axial compression loading(σ3=10 MPa)

σ1/MPaG0/GPaK/GPaG1/GPaη1/(GPa·h-1)η2/(GPa·h-1)η3/(GPa·h-1)λλ1λ′λ240138.752210.314 296.244 175.188 ——————50146.966 251.561 604.906 363.527 1 012.224 —8.5222.641 ——60153.461 293.365 1 805.797 256.090 1 545.442 —7.8915.723 ——7059.680 250.373 122.514 123.307 1 301.0183 190.5217.06710.553 4.909 1.197
表5 定轴压分级卸围压三轴蠕变模型参数(σ1= 60 MPa)
Table 5 Three-axis creep model parameters of fixed axial compression and unloading confining pressure(σ1= 60 MPa)

σ3/MPaG0/GPaK/GPaG1/GPaη1/(GPa·h-1)η2/(GPa·h-1)η3/(GPa·h-1)λλ1λ′λ215279.362 423.444 596.152 648.119 ——————10295.899 506.488 1 217.707 686.485 4 317.153 —7.033 10.661 ——5120.158504.096 246.679 278.768 2 247.710 5 502.7637.450 12.751 6.008 4.186

图9 试验结果与计算值对比
Fig.9 Experimental results contrast calculated values
根据前文所建立的基于能耗理论岩石的黏弹塑性非线性蠕变方程,对围压10 MPa四级蠕变试验曲线反演所获得的参数和轴压60 MPa三级蠕变试验曲线反演所获得的参数,代入改进后蠕变损伤方程(22)~(24)中,绘制出蠕变变形与时间关系的曲线,如图9所示。
如图9所示,推导出的非线性蠕变损伤模型在围压为10 MPa和15 MPa(加载蠕变试验)、以及轴压60 MPa和80 MPa(卸载蠕变试验)下都符合蠕变曲线变化规律,从以上不同围压、不同应力下砂岩蠕变试验曲线与模型曲线的对比图中可以充分地说明,对基于能耗理论改进传统的黏塑性应变率本构模型的方式来反映岩石蠕变全过程变形规律是合适可行的。该模型不仅准确地反映衰减和稳定蠕变阶段的蠕变特性,也克服了传统西原体难以描述加速蠕变的缺点,总体上该模型具有更高的拟合度,对三轴蠕变试验数据具有一个良好的预测分析。
4 结 论
(1)基于弹塑性理论对传统西原模型进行改进,可以较好地描述岩土类材料的黏弹性蠕变和黏塑性蠕变特性,也为研究蠕变模型和蠕变力学特性提供一个思路。
(2)蠕变加载过程中的能耗和蠕变损伤主要来源于岩土类材料内部的内能变化,基于能量耗散理论和考虑蠕变速率变化构建的岩石加速蠕变模型能更好地描述岩石黏弹塑性蠕变特性,更好地反映了岩石能量耗散与蠕变变化之间的关系,也突出了蠕变速率和蠕变应力状态对于加速蠕变的影响。
(3)基于能耗理论改进传统的黏塑性应变率本构模型,不仅准确地反映衰减和稳定蠕变阶段的蠕变特性,也克服了传统西原体难以描述加速蠕变的缺点,总体上该模型具有更高的拟合度,对三轴蠕变试验数据具有一个良好的预测分析。
(4)试验数据与模型曲线结果良好的一致性,也说明本文通过运用耗散率值来定义不同蠕变阶段的控制阈值方法是可行的,为预测蠕变变形全过程和划分蠕变变形各阶段提供一个新的方法。
[1] 陈沅江.岩石流变的本构模型及其智能辨识研究[D].长沙:中南大学,2003.
CHEN Yuanjiang.Study on the reological constitutive model of rock and its intelligent identification[D].Changsha:Central South University,2003.
[2] CHEN L,WANG C P,LIU J F,et al.A damage-mechanism-based creep model considering temperature effect in granite[J].Mechanics Research Communications,2014,54(11):76-82.
[3] 孙钧.岩石流变力学及其工程应用研究的若干进展[J].岩石力学与工程学报,2007,26(6):1081-1115.
SUN Jun.Rock rheological mechanics and its advance in engineering applications[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(6):1081-1115.
[4] 黄海峰,巨能攀,黄敏,等.朱俊霖软岩非线性蠕变损伤模型及其试验研究[J].水文地质工程地质,2017,44(3):49-60.
HUANG Haifeng,JU Nengpan,HUANG Min,et al.Nonlinear creep damage model of soft rock and its experimental study[J].Hrdrogeology and Engineering Geology,2017,44(3):49-60.
[5] 梁冰,张涛,王俊光,等.片麻岩蠕变特性试验研究[J].实验力学,2018,33(3):451-460.
LIANG Bin,ZHANG Tao,WANG Junguang,et al.Experimental study of geneiss creep properties[J].Journal of Experimental Mechanics,2018,33(3):451-460.
[6] 肖世武,周雄,胡小玲,等.分数阶导数线性流变固体模型及其应用[J].工程力学,2012,29(10):354-358.
XIAO Shiwu,ZHOU Xiong,HU Xiaoling,et al.Linear rheological solid model with fractional derivative and itsapplication[J].Engineering Mechanic,2012,29(10):354-358.
[7] 于立业,琚宜文,李小诗.基于流变实验和红外光谱检测的高煤级煤流变特征[J].煤炭学报,2015,40(2):431-438.
YU Liye,JU Yiwen,LI Xiaoshi.Rheological charateristic study of high rank coal based on rheological experiments and FTIR[J].Journal of China Coal Society,2015,40(2):431-438.
[8] 沈才华,张兵,王文武.一种基于应变能理论的加速蠕变本构模型[J].煤炭学报,2014,39(11):2195-2200.
SHEN Caihua,ZHANG Bin,WANG Wenwu.A new accelerated creep constitutive model based on the strain energy theory[J].Journal of China Coal Society,2014,39(11):2195-2200.
[9] 张泷,刘耀儒,杨强,等.基于不可逆内变量热力学的岩石材料粘弹-粘塑性本构方程[J].工程力学,2015,32(9):34-41.
ZHANG Long,LIU Yaoru,YANG Qiang,et al.A Viscoelastic-viscoplastic constitutive equation of rock materials based on irreversible internal variable thermodynamics[J].Engineering Mechanics,2015,32(9):34-41.
[10] 高文华,刘正,朱建群.岩石MCVISC流变模型及其在FLAC3D程序中的实现[J].防灾减灾工程学报,2015,35(2):219-225.
GAO Wenhua,LIU Zheng,ZHU Jianqun.MCVISC rheological model and its implementation in FLAC3D program[J].Journal of Disaster Prevention and Mitigation Engineering,2015,35(2):219-225.
[11] SIH G C.Strain-energy-density factor applied to mixed mode crack problems[J].International Journal of Fracture,1974,10(3):305-321.
[12] SIH G C.From monoscale to multiscale modeling of fatigue crack growth:Stress and energy density factor[J].Science China Physics,Mechanics and Astronomy,2014,57(1):39-50.
[13] ZHOU H W,WANG C P,HAN B B,et al.A creep constitutive model for salt rock based on fractional derivatives[J].International Journal of Rock Mechanics and Mining Sciences,2011,48(1):116-121.
[14] ZHOU H W,WANG C P,MISHNAEVSKY Jr L,et al.A fractional derivative approach to full creep regions in salt rock[J].Mechanics of Time-Dependent Materials,2013,17(3):413-425.
[15] 高玮,汪磊,杨大勇.岩石损伤演化的能量方法研究[J].岩石力学与工程学报,2011,30(S2):4087-4092.
GAO Wei,WANG Lei,YANG Dayong.Rock damage evolution based on energy principle[J].Chinese Journal of Rock Mechanics and Engineering,2011,30(S2):4087-4092.
[16] 唐松花,罗迎社,周筑宝.基于最小耗能原理的混凝土损伤演变方程[J].暨南大学学报(自然科学与医学版),2005,26(1):69-71.
TANG Songhua,LUO Yingshe,ZHOU Zhubao,et al.Establishing the damage developing equation of con-crete through the principle of minimum dissipation of energy[J].Journal of Jinan University:Natural Science & Medicine Edition,2005,26(1):69-71.
[17] 邱战洪,张我华,陈云敏.基于最小耗能原理的黏弹塑性损伤模型[J].岩土力学,2007,28(S1):160-164.
QIU Zhanhong,ZHANG Wohua,CHEN Yunmin.The visco elastic-plastic damage model based on the principle of minimum energy consumption[J].Rock and Soil Mechanics,2007,28(S1):160-164.
[18] 王有涛.海棠山隧道砂岩蠕变特性试验研究[D].阜新:辽宁工程技术大学,2016.
WANG Youtao.Experimental study on creep characteristics of sandstone in Haitangshan tunnel[D].Fuxin:Liaoning Technical University,2016.
[19] RUTTER E H.On the creep testing of rocks at constant stress and constant force[J].International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts,1972,9(2):191-195.
[20] 张树光,孙成鑫,王有涛,等.海棠山隧道砂岩变参数蠕变特性研究[J].公路交通科技,2016,33(10):105-110.
ZHANG Shuguang,SUN Chengxin,WANG Youtao,et al.Study on variable parameter creep characteristics of sandstone in haitangshan tunnel[J].Journal of Highway and Transportation Research and Development,2016,33(10):105-110.
[21] 何志磊,朱珍德,朱明礼,等.基于分数阶导数的非定常蠕变本构模型研究[J].岩土力学,2016,37(3):737-744.
HE Zhilei,ZHU Zhende,ZHU Mingli,et al.An unsteady creep constitutive model based on fractional order derivatives[J].Rock and Soil Mechanics,2016,37(3):737-744.
[22] 韩阳,谭跃虎,李二兵,等.岩石非定常 Burgers 蠕变模型及其参数识别[J].工程力学,2018,35(3):201-217.
HAN Yang,TAN Yuehu,LI Erbin,et al.Non-stationary Burgers creep model of rock and its parameter identification[J].Engineering Mechanics,2018,35(3):201-217.
[23] 齐亚静,姜清辉,王志俭,等.改进西原模型的三维蠕变本构方程及其参数辨识[J].岩石力学与工程学报,2012,31(2):347-355.
QI Yajing,JIANG Qinghui,WANG Zhijian,et al.3D creep constitutive equation of modified Nishihara model and its parameters identification[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(2):347-355.
[24] 宇晓龙.花岗岩三轴蠕变过程特征分析及本构模型研究[D].阜新:辽宁工程技术大学,2014.
YU Xiaolong.Research on triaxial creep characteristics of granites and its constitutive models[D].Fuxin:Liaoning Technical University,2014.
[25] 刘开云,薛永涛,周辉.参数非定常的软岩非线性黏弹塑性蠕变模型[J].中国矿业大学学报,2018,47(4):921-928.
LIU Kaiyun,XUE Yongtao,ZHOU Hui.A nonlinear viscoelastic-plastic creep model of soft rock with unsteady parameters[J].Journal of China University of Mining & Technology,2018,47(4):921-928.
