随着工业化进程的不断加速以及国家重大战略的需求，地下工程项目不断增多，土压平衡盾构机被越来越广泛的应用到各种软土地下施工中。土压平衡盾构机在掘进过程中必须维持开挖面稳定，否则会引起地表变形甚至是灾难性事故[1]。因此，建立密封舱土压预测模型对土压力进行实时精确预报，以提供决策依据是非常必要的。由于密封舱土压受多子系统、多场耦合等诸多因素影响，构建密封舱土压机理模型极其困难。因此，一些学者开始研究基于现场施工数据的建模方法。YEH[2]提出基于数据采用BP神经网络建立密封舱土压控制模型,这也是首次提出基于数据建立密封舱土压模型。文献[3]基于模糊神经系统建立了盾构机的控制模型。MANUEL[4]采用DEM方法构建了密封舱压力的数值模型。文献[5]首先建立了系统间简单的机理关系，在此基础上利用LS-SVM进行参数优化以构建土压控制模型。文献[6]利用LS-SVM建立了土压预测模型并采用智能方法进行控制参数优化。李守巨[7]采用自回归滑动平均模型方法建立了密封舱土压模型。上述研究没有考虑初始训练样本的分布差异会对分类器性能产生影响，以及在进行大规模计算时的效率、实时性等问题，因此模型在线预测、辨识等的效果会受到很大影响。
为此，笔者提出了一种基于多粒子群协同优化的并行支持向量机密封舱土压建模方法。支持向量机作为一种先进的机器学习方法以结构风险最小化为原则，泛化能力强、不易陷入局部极值等优点，广泛应用于模式识别、非线性系统建模[8-9]。其中，惩罚因子C和核参数σ是支持向量机中最重要的两个参数，直接影响建模的精度和效率。因此，本文将支持向量进行分层并行学习，并利用粒子群之间的相互协同来优化SVM的参数C和σ,完成基于大规模数据的土压快速预测。最后，通过仿真实验证明了方法的有效性。
1 支持向量机回归算法
支持向量机回归是利用非线性映射函数φ(·)将样本数据x映射到高维特征空间F，然后在此空间进行线性回归，即
(1)
式中，ω为权矢量;b为阈值;Rn为n维实数空间。
在特征空间最优化逼近f(x)使其结构风险最小，其目标函数记为
(2)
其中，C为惩罚因子;ε为不敏感损失函数。最后转化为二次规划问题进行求解，得到线性回归函数:
(3)
式中，K(xi,x)为核函数;αi为拉格朗日乘子;
为其最优解;b为偏置项;l为样本数量。
由于RBF核函数是一种前馈学习网络，具有学习速度快、全局收敛等特性，为此，本文选用RBF核函数，即
(4)
其中，σ为核参数决定数据在新特征空间的分布状态，影响模型的分类精度。惩罚因子C用于平衡模型的逼近误差和复杂度。二者是影响支持向量机回归模型性能的2个重要参数。
2 SVM回归模型的参数优化
2.1 协同粒子群算法
粒子群算法是一种智能仿生优化技术，通过群体中个体之间的信息传递及共享来搜索最优解,算法参数少、收敛速度快[10]。粒子每次迭代依据两个“极值”来修正其位置和速度，但往往容易出现在最优解附近“震荡”的现象，进而得到局部最优解。为此，本文采用了如下粒子群速度[11]计算公式:
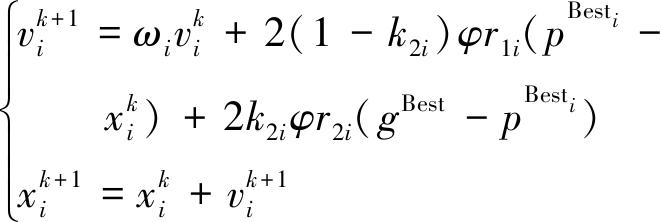
(5)
其中，
为衡量接近局部最优解的程度;k2i为衡量接近全局最优解的程度;k1i为收敛程度;
为粒子在k+1时刻的位置;r1i和r2i是学习因子，通常在0～2之间取值;pBesti表示第i个粒子的最优解;gBest为所有粒子当前的最优解;
为第i个粒子在k时刻的位置。各参数对算法收敛性的影响是:0≤ωi<1收敛性随着ωi变小而加强;0<k1i<1,收敛性随着k1i变大而发散;如果0<k2i<1，当k2i→1时将收敛于全局最优，而当k2i→0时将收敛于局部最优。
算法全局极值设为gBest，局部极值为pBesti。在算法开始阶段，个体xi和局部极值pBesti一般差距较大，因此，惯性因子ωi趋近于l;而此时gBest和pBesti差距也较大，因此取k2i趋近于0。k1i随着迭代次数的增加，下降趋势显著，呈指数下降。当算法接近收敛时,gBest和pBesti的差距逐渐趋近于0,此时参数自动调整，惯性因子ωi趋于0,k2i趋于1。根据以上分析,设计如下参数:
ωi=ωmax-(ωmax-ωmin)Tmax/Ti
(6)
k1i=k0exp(-αi)
(7)
(8)
式中，ωmax，ωmin为惯性因子的最大和最小值;Ti为当前迭代次数;Tmax为最大迭代次数;k0为影响因子;α为收敛调整参数。
2.2 SVM模型的参数优化
本文利用协同粒子群优化算法具有全局快速寻优的特点，来优化SVM的模型参数C和σ。由于群体每次寻优都要经历二次优化计算，耗时、效率低，因此，本文将协同粒子群并行化寻优，即在各独立的进程内进行独立搜索，不但保证了种群的多样性又提高了加速比，易于找到最优值[12-13]。粒子群不同的运动方式会得到不同的参数ωi,k1i,k2i,最后各群体汇集到主进程，计算得到模型的全局最优参数C和σ。算法如下:
(1)初始化种群。给各并行进程分配粒子群,在每次优化后粒子群的结构向量为:Xj=(x1j,…,xpj)T,p是进程数,j是优化次数;第i个粒子第j次优化后的结构向量为Xij=(xij1,…,xijk)T，xijk为二维变量，代表参数C和σ，表示在第i个进程进行第j次优化的第k个粒子。
(2)读取训练集T={(x1,y1),…,(xk,yk)}∈(X,Y)k，其中xi∈X=Rn，yi∈Y=Rn，i=1,…,k。给定模型初始参数，建立SVM土压预测模型，得到土压预测值y′。
(3)定义粒子群的适应度函数，取能反映SVM预测模型性能的均方误差为适应度函数f，即
(9)
式中，y′i为第i次土压预测值;yi为第i次土压实测值。基于适应度函数的最小值来判断算法是否收敛，如果适应值大于设定值，则继续寻优计算，否则结束。
(4)各个进程的局部粒子群优选如下:
pBesti,j=
(10)
最后汇聚到主进程，得到全局优选粒子群如下:
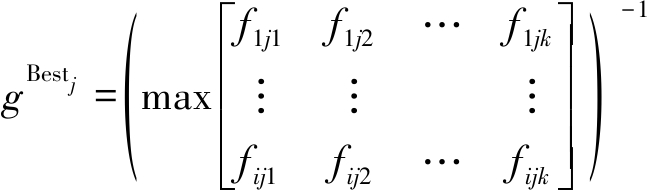
(11)
式中，fijk为第i个进程第j次优化的第k个粒子的适应值;(·)-1为由适应值反向求得的中心数。
(5)得到本次搜索的全局最优解gBestj，同时根据式(5)更新粒子速度和位置，式(6)～(8)修正参数。
(6)主进程判断是否满足结束条件，即达到最大训练次数或适应值满足要求，若满足结束条件，即可得到优化的参数组合C和σ;否则返回步骤(2)。
3 基于并行SVM的土压预测模型的建立
本文采用了支持向量机的并行学习算法进行建模，算法具有良好的可扩充性，计算效率高[14-15]。利用三层结构对分类器进行更新，避免了初始样本的分布差异对模型性能产生影响，使模型具有更强的泛化能力和更高的预测精度。三层并行 SVM 算法的结构示意图如图1所示。
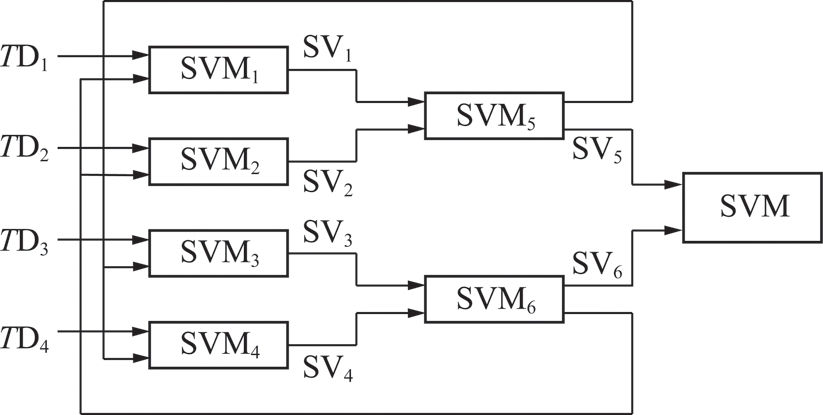
图1 三层并行SVM的结构
Fig.1 Structure of three layers parallel SVM
算法的具体步骤:
(1)将原训练样本集T分解为 4 个训练子集TD1,TD2,TD3,TD4,基于2.2节优化后的模型参数分别对4个子集按照通常训练SVM 的方法并行地处理而得到 4 个支持向量机SVM1,SVM2,SVM3,SVM4，得到的4个支持向量集合分别为:SV1,SV2,SV3和SV4。
(2)将SV1和SV2,SV3和SV4分别合并得到两个新的训练集，再并行训练支持向量机SVM5和SVM6，最后得到两个支持向量集SV5和SV6。
(3)交叉反馈SV5和SV6，即将SV5合并到TD3和TD4中,将SV6合并到TD1和TD2中，然后重新训练，转步骤(1)重新执行，得到集合SV′5和SV′6。
(4)如果SV′5-SV5=φ且SV′6-SV6=φ;或者SV5和SV′5，SV6和SV′6的差集是一些固定的样本，则合并SV′5和SV′6。加入SV5和SV′5，SV6和SV′6的差集。
4 仿真实验与分析
4.1 工程概况
实验数据来至于北京地铁10号线某标段。该段地质主要为粉质黏土、细沙等，隧道埋深12.6 m，水位埋深7.1 m。盾构机采用土压平衡盾构机，直径为6.25 m，4个压力传感器位于密封舱承压隔板上过圆心的水平和竖直的两条垂线上，分别距圆周0.9 m，其分布如图2所示，规格参数见表1。
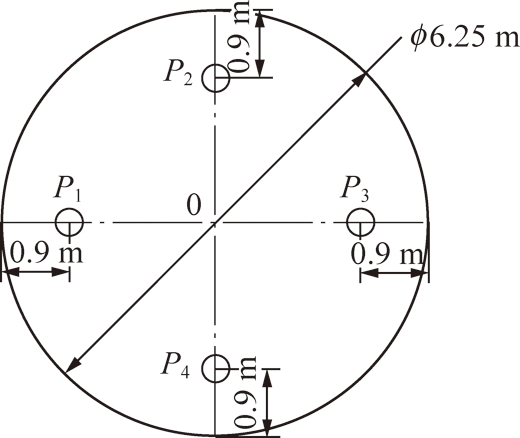
图2 密封舱压力传感器分布
Fig.2 Pressure sensors distribution in soil chamber
4.2 数据采集与参数设置
根据盾构机的施工控制经验可知，密封舱土压p(k)主要受螺旋输送机转速vs(k)、推进速度va(k)、总推力F(k)、刀盘转速vc(k)等参数影响。因此，将x(k)=(vs(k),va(k),F(k),vc(k))′作为预测模型的输入，将密封舱土压力p(k)作为模型的输出。采集现场第320～350环施工数据，剔除异常数据后得到数据样本集T={x(k),p(k)}，k=1,…,1 500，其中1 300组为训练样本，200组为测试样本。
表1 盾构机参数
Table 1 Dimensions of the shield machine
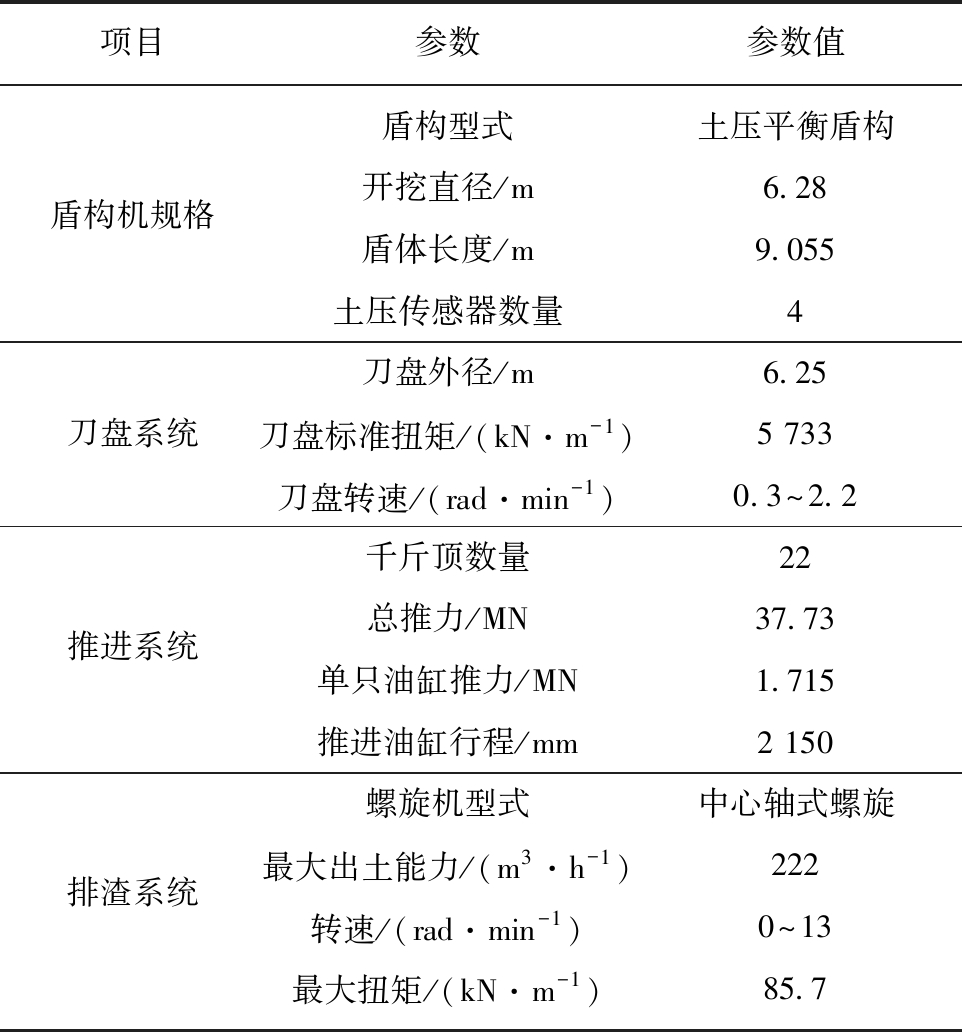
项目参数参数值盾构型式土压平衡盾构盾构机规格开挖直径/m6.28盾体长度/m9.055 土压传感器数量4刀盘外径/m6.25刀盘系统刀盘标准扭矩/(kN·m-1)5 733 刀盘转速/(rad·min-1)0.3～2.2 千斤顶数量22推进系统总推力/MN37.73 单只油缸推力/MN1.715 推进油缸行程/mm2 150 螺旋机型式中心轴式螺旋排渣系统最大出土能力/(m3·h-1)222转速/(rad·min-1)0～13 最大扭矩/(kN·m-1)85.7
协同粒子群算法对支持向量机的参数(C,σ)进行优化，初始参数设定如下:粒子种群规模为200，每个粒子的维度是2，种群随机平均分给4个进程进行计算，惯性因子ωmax=1.2，ωmin=0.1，系数α=0.8，k0=1.2，最大迭代次数Tmax=200。据此，优化支持向量机参数并建立土压预测模型。
实验用计算机型号为ThinkPadXlCarbon,Intel(R)Co re(TM)i5-4210U CPU@1.7 GHz。
4.3 实验结果与分析
4.3.1 预测模型的有效性验证
为了准确反映整个密封舱内土压变化情况，对舱内4个压力监测点P1，P2，P3，P4(分别位于承压隔板的左、上、右、下4个位置)进行土压预测，各监测点取200个样本进行预测，预测结果如图3所示，误差图如图4所示，相应的定量统计分析结果见表2。
图3中，星实线为土压实测值，圈实线为土压预测值，可以看出P1，P2，P3，P4 4个监测点的预测值与实测值都很接近，预测效果较好;从表2中的平均绝对误差及百分误差也可以看出，样本整体预测的误差都较小，平均绝对百分误差在1.75%～2.96%，说明模型具有较高的预测精度。由于P4点靠近螺旋输送机口，实时排渣对该点土压力会有不确定性影响，因此该点土压力波动较大，与实际工况相符;但其平均绝对百分误差仅为2.08%，说明预测精度较高。从表2的最大误差可以看出，4个监测点的个别时刻预测误差较大，P2点达到了9%，这可能是控制参数或工况突变导致的，但其仍在密封舱土压平衡控制的稳定域范围内，属正常工况。所以，综合以上分析可知，完全可以基于这4个压力监测点做出整个开挖面的土压力预测，以对密封舱土压失衡做出提前预警。
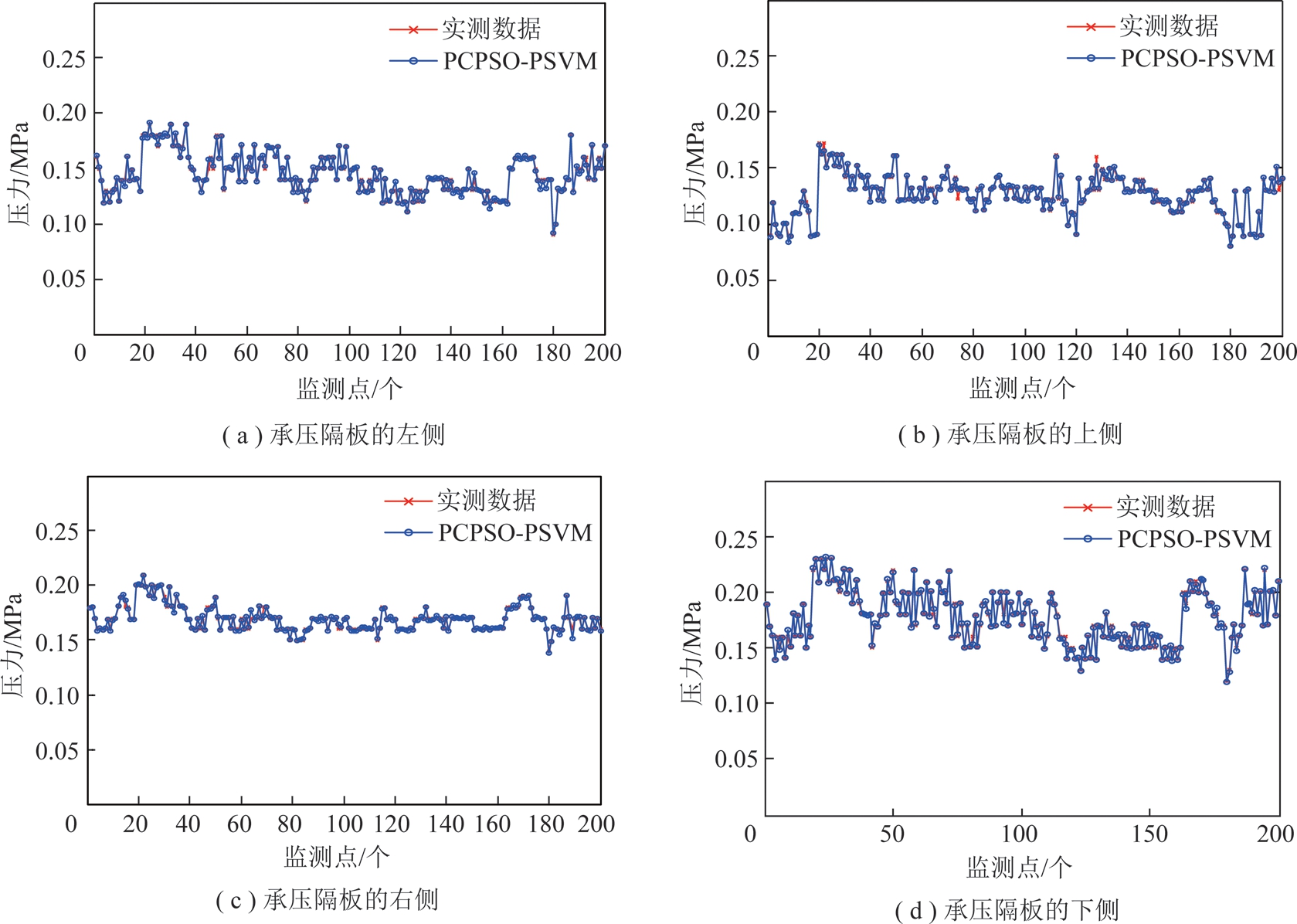
图3 4个监测点的土压预测结果
Fig.3 Prediction results of the four monitoring points earth pressure
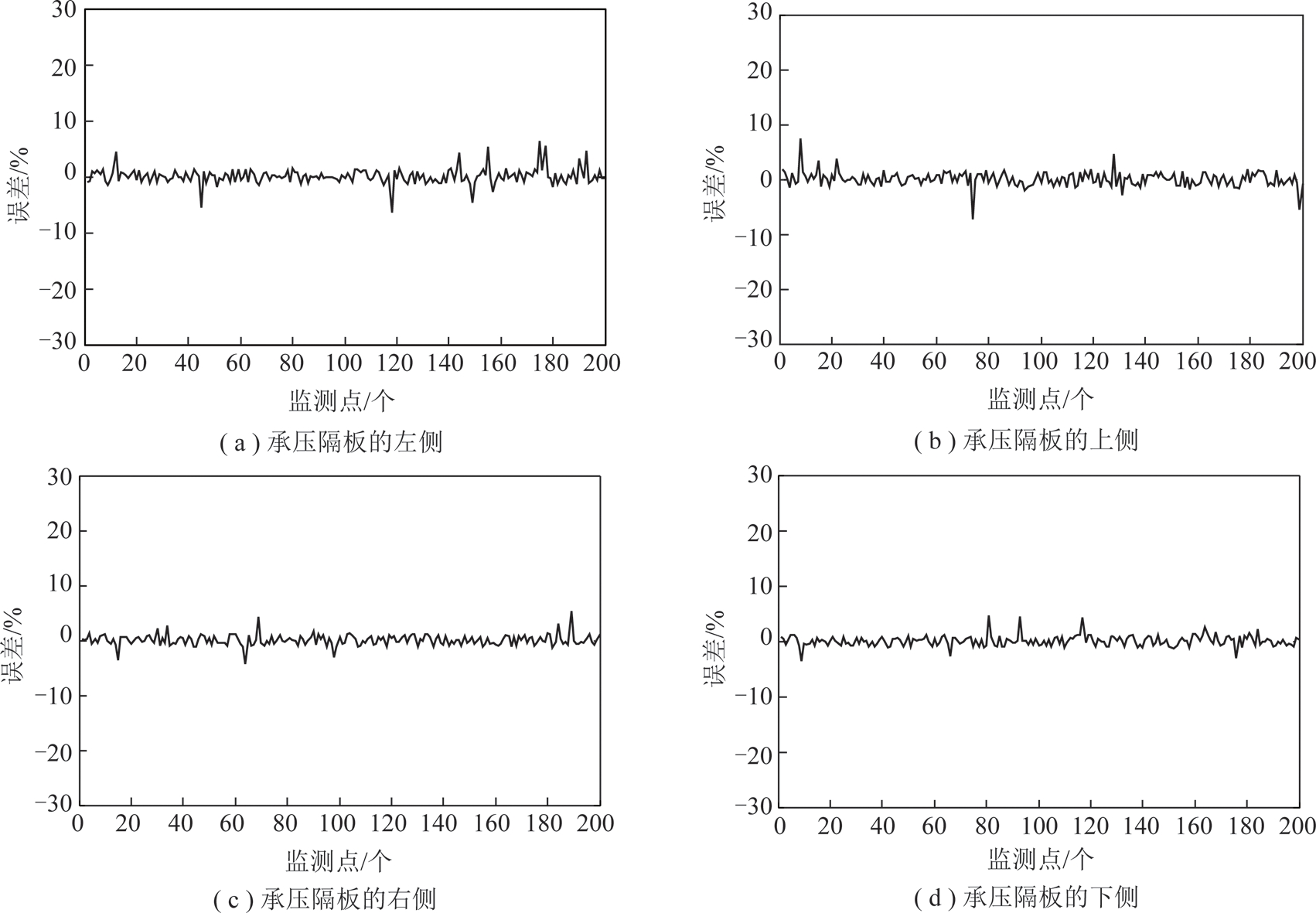
图4 4个监测点的土压预测误差
Fig.4 Prediction errors of the four monitoring points earth pressure
表2 4个监测点的预测结果统计
Table 2 Prediction results statistics of four sensors
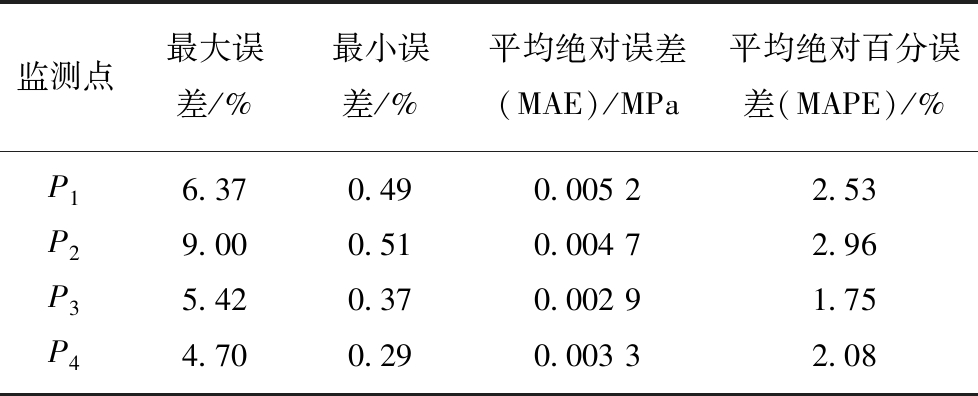
监测点最大误差/%最小误差/%平均绝对误差(MAE)/MPa平均绝对百分误差(MAPE)/%P16.370.490.005 22.53P29.000.510.004 72.96P35.420.370.002 91.75P44.700.290.003 32.08
4.3.2 预测结果对比分析
为了检验预测效果，与标准的SVM进行了对比。为了效果更明显、直观，仅利用100个数据样本进行预测，图5为预测结果对比图，图6为对应的预测误差图。
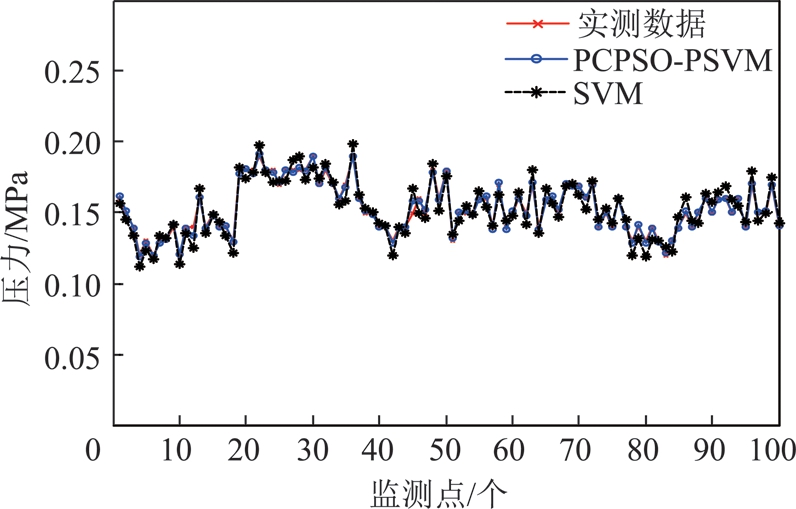
图5 2种方法预测结果对比
Fig.5 Contrast of the prediction results of the two methods
图6 2种方法预测误差对比
Fig.6 Contrast of the prediction error of the two methods
图5中星实线是土压实测值，圈实线为本文的预测值，虚线为标准SVM的预测结果，从图中可以看出，与SVM方法相比本文预测效果更好，与实测值吻合程度更高。误差对比如图6所示，实线为本文预测误差，虚线为SVM预测误差，可以看出本文预测误差明显小于SVM预测误差，预测精度较高。另外，为了更全面的展现方法的特性，也从计算时间和预测的均方根误差(RMSE)两个方面进行了比较，结果见表3。
表3 PCPSO-PSVM与SVM计算结果对比
Table 3 Contrast of the results of PCPSO-PSVM and SVM
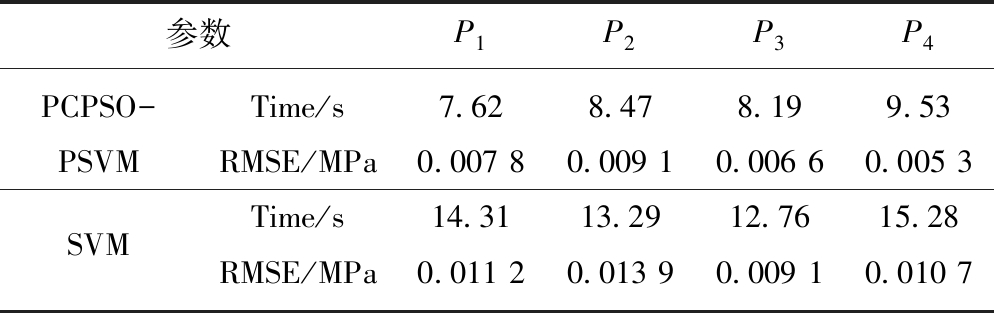
参数P1P2P3P4PCPSO-Time/s7.628.478.199.53PSVMRMSE/MPa0.007 80.009 10.006 60.005 3SVMTime/s14.3113.2912.7615.28RMSE/MPa0.011 20.013 90.009 10.010 7
由表3中可以看出，本文方法的均方根误差明显小于SVM方法;计算时间也明显缩短，最大缩短至原来的53.92%。因此，本文方法的计算精度和效率均有所提高。
5 结 论
(1)提出采用并行支持向量机方法进行密封舱土压建模，利用交叉反馈的方式更新初始样本，避免了初始样本的分布差异对模型性能产生影响，显著提高了密封舱土压预测精度。
(2)利用协同粒子群并行优化SVM的模型参数C和σ，实验表明有效提高了模型的预测精度和效率。根据实际工况，可以满足在线计算的实时性要求。
(3)基于现场数据验证了方法的有效性，方法可以应用于盾构实际施工中基于大规模数据的土压预测，为实施密封舱土压平衡控制提供决策依据，具有实际的工程指导意义。
[1] 刘宣宇，邵诚.盾构机自动控制技术现状与展望[J].机械工程学报，2010,46(20):152-160.
LIU Xuanyu,SHAO Cheng.Present status and prospect of shield machine automatic control technology[J].Journal of Mechanical Engineering,2010,46(20):152-160.
[2] CHENG I-Yeh.Application of neural networks to automatic soil pressure balance control for shield tunneling[J].Automation in Construction,1997,5(5):421-426.
[3] ALVAREZ G M,BRUINES P A,VERHOEF P N W.Modeling tunnel boring machine performance by Neuro-Fuzzy methods[J].Tunneling and Underground Space Technology,2000,15(3):259-269.
[4] MANUEL J M,LUIS E R.Discrete numerical model for analysis of earth pressure balance tunnel excavation[J].Journal of Geotechnical and Geoenvironmental Engineering,2005(10):1234-1242.
[5] 刘宣宇,邵诚,刘任喜.盾构掘进土压控制模型的建立及仿真[J].煤炭学报,2010,35(4):575-579.
LIU Xuanyu,SHAO Cheng,LIU Renxi.Modeling and simulation on earth pressure control for shield tunneling[J].Journal of China Coal Society,2010,35(4):575-579.
[6] LIU Xuanyu,SHAO Cheng,MA Haifeng,et al.Optimal earth pressure balance control for shield tunneling based on LS-SVM and PSO[J].Automation in Construction,2011,20:321-327.
[7] 李守巨，霍军周，曹丽娟.盾构机土压平衡系统的ARMA模型及其参数估计[J].煤炭学报,2014,39(11):2201-2205.
LI Shouju,HUO Junzhou,CAO Lijuan.Autoregressive moving average model and its parameter estimation for earth pressure balance system of shield[J].Journal of China Coal Society,2014,39(11):2201-2205.
[8] VAPNIK V N.The nature of statistical learning theory[J].Neural Networks IEEE Transactions,1995,10(5):988-999.
[9] HUANG G B,MAO K Z,SIEW C K,et al.Fast modular network implement action for support vector machines[J].IEEE Trans Neural Networks,2005,16(6):1651-1663.
[10] DORIGO M,BLUM C.Ant colony optimization theory:A survey[J].Theoretical Computer Science,2005,344(2-3):243-278.
[11] 王华秋，廖晓峰.一种并行协同粒子群优化的支持向量机预测模型[J].控制理论与应用，2006,23(6):934-940.
WANG Huaqiu,LIAO Xiaofeng.Prediction model of support vector machine based on parallel cooperative particle swarm optimization[J].Control Theory & Applications,2006,23(6):934-940.
[12] COLLOBERT R,BENGIO Y,BENGIO S.A parallel mixture of SVMs for very large scale problems[J].Neural Computation,2002,14(7):1105-1114.
[13] DO T N,NGUYEN V H,POULET F.GPU-based Parallel SVM Algorithm[J].Journal of Frontiers of Computer Science and Technology,2009,3(4):368-377.
[14] COELLO C A C,PULIDO G T,LECHUGA M S.Handling multiple objectives with particle swarm optimization[J].IEEE Trans on Evolutionary Computation,2004,8(3):256-279.
[15] COOREN Y,CLERC M,SIARRY P,et al.An adaptive multiobjective particle swarm optimization algorithm[J].Computational Optimization and Applications,2011,49(2):379-400.
