煤炭是我国的主要能源,也是山西经济发展的支柱产业之一,然而,采煤造成的水土资源损毁以及衍生的资源环境问题尤为突出,它的影响涉及到了社会、经济、生态等方方面面[1]。煤炭开采破坏了原有的地形、地貌以及水文条件,引发了生态环境与社会条件的失衡[2]。煤炭开采不仅使得矿区水土资源的时空匹配遭受影响,水土资源的持续利用能力受到约束,同时制约着煤炭资源的开发与区域经济的发展。因此迫切要求在煤矿区协调煤炭、水、土地资源,建立煤矿区水土资源优化配置模式与方法,以充分保护和挖掘煤矿区煤炭、水、土地资源的开发和产出潜力。在矿产资源和水土资源并存区,如何做到在进行煤炭资源开采时,保护水土资源在国内外都已有研究[3-4]。
通过分析开采煤炭引发的问题,找出最优开采规模一直是国内外都在关注的热点。ANNE和 AUDE[5]分析了技术不确定性对最优开采速度的影响,得出如果消费者的瞬时替代弹性小于1,则技术不确定性延缓了煤炭资源的开采速度;当替代弹性大于1时,情况则正好相反。WAQAR和DIMITRAKOPOULOS[6]通过对煤矿开采作业的分析,探讨了矿产资源在不确定性供应和长期储存条件下的最优生产规模,指出生产能力优化模型应注重资源边界品位理论与生产能力之间的联系,在多个级别品位资源曲线的认识基础上构建了矿山的最优生产能力模型。李静[7]运用经济学采矿学动态最优化等理论,对储量价格技术环境约束及政策等不确定条件下我国煤炭资源的最优开采规模进行了研究,针对我国煤炭资源开采的实际情况,提出了煤炭资源实现最优开采的政策及建议;姜杰[8]打破了以往研究忽略煤矿生产主要影响因素的动态不确定性及煤矿开采所造成的外部性等缺陷的研究局限,利用动态最优化理论和方法对我国煤矿跨期最优生产规模进行了研究;翟燕妮[9] 为了使煤炭资源能够得到更好的保护利用,通过分析煤炭工业进出壁垒状况、煤炭资源开采利用的正负效应、以及煤炭资源流通过程中存在的问题,对煤炭资源开采规模影响因素如价格、开采率、成本、技术等及相互关系进行系统分析,引入煤炭资源开采引起的生态环境约束条件,建立煤炭资源开采规模的线性规划模型。
总之,关于煤矿的研究多侧重于研究煤矿的最大经济效益,忽略了资源等同于经济发展的重要地位。笔者以长河流域为研究区,介绍研究区概况与数据来源,分析煤炭开采规模-水土资源经济系统的运行过程并构建因果关系图,然后建立煤炭开采规模-水土资源经济系统的流图与变量方程,并进行模型验证,最后定义长河流域未来发展可能的几种主要情景,用SD模型模拟不同煤炭开采规模情景下的水土资源利用结构,并根据模拟过程阐述实现这些水土利用结构的路径,找出煤炭-资源经济效益双效最优的煤炭开采模式,为长河流域煤炭开采规模的调控提供借鉴。
1 长河流域现状分析
长河流域的面积是113.16 km2,在丰富的矿产资源中,煤炭资源探明储量占到泽州县的3/4。因此,长河流域存在着很大的经济发展潜力。自20世纪80年代以来,长河流域内的采矿等能源重化工企业大量兴起,从2009年开始,山西省扎实推进煤炭资源整合和煤矿企业兼并重组,该地区统计整合煤矿企业达到了11个,采矿业大约占到第2产业的30%(数据来源于泽州统计年鉴),矿业的快速发展带动了该区的经济发展。目前,该地区正处于快速进入工业化和城市化的阶段,资本的形成和积累对经济的增长具有非常重要的影响。然而,长河流域受煤炭开采的影响较大,煤矿开采给该区的生态环境带来了很大的损害。土地塌陷、地下水位下降、粮食减产、房屋裂缝等问题已经严重影响到了当地人民的经济发展与生活。长河流域的土地资源问题突出,农田人均占有量少,根据泽州统计年鉴显示,长河流域在2014年的人均耕地大约只有120 m2。而煤炭的开采对土地造成了破坏,加剧了该地区土地资源的紧张局面。并且,保证粮食产量,就离不开水的灌溉,长河流域水资源不仅总量较少,且时空分布不均。人均水资源拥有量仅为世界人均拥有量的3.6%,全国人均量的14.4%,山西人均量的81.3%,该区属于严重缺水地区,而且在开采资源的过程中,那些矿石、废渣等有毒成分污染水资源,如今地表水利用率低,浅、中层地下水资源已遭破坏、用水浪费现象严重、水资源破坏严重等问题始终存在,而农业用水占比较大,大约占到全部用水量的50%,生活用水占约23%,工业用水占约20%(数据来源于泽州统计年鉴),水资源的破坏,对农业、生活、工业发展都造成了一定程度的影响。
从2007年山西省人民政府印发的《山西省煤炭工业可持续发展政策措施试点工作总体实施方案》的说明强调充分发挥山西省的煤炭资源优势,发展煤炭生产必须坚持开发与保护并重,实行合理开发,综合利用,在提高社会经济效益的同时必须防治环境污染,保护自然资源,维持生态平衡,可以看出国家对于“山西煤炭工业可持续发展政策措施试点”的大力支持。因此,最优开采模式的研究对促进该地区的煤炭和水土资源的协同利用就尤为重要。
2 长河流域“煤炭开采规模-水土资源经济”仿真系统构建
2.1 煤炭开采规模-水土资源经济系统因果关系图
煤炭开采规模、水资源、土地资源、系统经济4个子系统基本涵盖了矿区发展工作涉及的主要方面,在相互耦合作用力下,共同构成矿区煤炭开采规模与水土资源协调发展的仿真系统(图1)。在煤炭开采规模-水土资源经济系统因果关系图中,煤炭开采量的增加,会带来水资源损毁量的增加,继而造成水资源不足和产生较多的废水污染土地,因此,一方面通过提高生态环境治理投资,治理废水改善水资源环境,构成一个正因果回路;另一方面,减小煤炭开采量,减少水资源消耗,保证水资源环境的健康发展,构成一个负因果回路。又因为该地区煤炭资源丰富,是目前该地区的主要发展产业,因此,煤炭开采量加大,可以很大程度上提高该地区的国民产值的增长速度,经济的进步使得采煤技术提高,更好的服务于煤炭产业,构成一个正因果回路[10]。

图1 煤炭开采规模-水土资源经济系统的因果关系
Fig.1 Causal relationship diagram of coal mining scale-water and soil resources economic system
2.2 模型建立数据来源
研究中数据的主要来源有历年山西省晋城市泽州县统计年鉴、水资源规划、国民经济和社会发展统计公报、水资源公报、耕地资源公报、环境状况公报、水土保持概况以及泽州县相关的规划资料等。系统分析的时间为2011—2030年,以2011年为基期年,系统仿真模拟了2011—2016年数据,仿真步长为1 a,模型最终预测时间为2030年。其他参数及变量逻辑关系的确定,有3种情况:① 借鉴其他学者前期的测定和研究;② 根据指标的定义进行计算;③ 建立相应计量经济学模型[11-13]。
2.3 系统关系流图
模型要研究的煤炭最优开采模式是一个多层次的复杂问题,煤炭的开采规模受到耕地面积、社会经济、水资源量、政策制度等多方面因素的约束,当我们有了这些资源约束系数,就可以建立起相应的动态模型。
根据煤炭开采规模-水土资源经济系统因果关系图用vensim 软件得到系统各变量之间的流图,如图2所示:模型选择了69个参数变量,其中有耕地面积、耕地损毁面积、总人口、煤炭总量、农业生产投资、固定资产投资、生态环境投资、总需水量以及总供水量9个变量设为状态变量。10个速率变量,26个常数量,25个辅助变量。在模型中耕地面积与农业生产投资、煤炭开采量有关,农业生产投资与国民产值有关,国民产值与煤炭开采量有关;水资源量与生态环境投资、煤炭开采量有关,生态环境投资量与国民产值有关,国民产值与煤炭开采量有关;煤炭开采量直接影响着国民生产总值;煤炭开采量与固定资产投资、水资源供需差、耕地面积供需差有关。如前所述,通过模型找出最优开采规模,关系到该地区煤炭资源、水资源和土地资源能否得到高效利用。

图2 基于“煤炭开采规模-水土资源经济系统”的系统流
Fig.2 System flow diagram based on “coal mining scale-water and soil resources economic system”
2.4 系统动力学方程
为了验证构建模型的有效性并进行仿真,需要对模型中的状态变量方程、参数、表函数等进行初始值赋值。根据因果关系图、系统关系流图,通过趋势外推法、回归分析法等确定模型的方程和参数如下:
耕地面积 = INTEG(土地复垦量-矿区土地面积损毁量,耕地面积初始量),km2;
耕地损毁面积=INTEG(矿区土地损毁量-土地复垦量,耕地损毁面积初始量),km2;
总人口 = INTEG(总人口×人口增长率,总人口初始量),万人;
矿区土地损毁量=塌陷面积+压占面积+水污染耕地面积,km2;
耕地供需差=耕地面积-耕地需求量,km2;
人口增长速率用表函数表示:
([(2011,-0.06)-(2030,0.1)],(2011,0.001 9),(2012,0.004 7),(2013,0.003 5),(2014,-0.000 61),(2015,0.000 2),(2016,0.000 2));
耕地供需差= IF THEN ELSE(耕地面积-耕地需求量>0,耕地面积-耕地需求量,0),km2;
总供水量= INTEG(水资源增加量-水资源减少量,总供水量初始量),万t;
总需水量= INTEG(工业新鲜用水量+农业用水量+活用水量+生态用水量,总需水量初始量),万t;
水资源供需差=IF THEN ELSE(总供水量-总需水量>0,总供水量-总需水量,0),万t;
万吨煤开采废水排水量=万t煤开采废水排放量系数×固定资产投资;
煤炭总量= INTEG(煤炭开采量-煤炭利用量-煤炭销售量,煤炭总量初始量),万t;
采出率=(耕地供需差影响因子0.3+水资源供需差影响因子0.2+固定资产投资影响因子0.5)×采出率表格;
开采储量= STEP(39 000,1),万t;
农业生产投资= INTEG(农业生产投资率,农业生产投资率初始量),万元;
固定资产投资= INTEG(固定资产投资率,固定资产投资初始量),万元;
生态环境投资= INTEG(生态环境投资率,生态环境投资初始量),万元;
煤矿业产值=单位煤炭产值×煤炭销售量。
2.5 模型检验
本研究构建了流图,并设置了其中的变量方程与相关参数,下面用该模型以2011年为基期模拟2012—2016年长河流域煤炭开采与水土资源利用的关系,并与真实的2012—2016年数据对比验证模型的模拟效果,结果详见表1。可见相对误差在5%内,传统认为模拟精度在5%以内即可,于是可认为构建的SD模型具有较高的模拟精度,其结构合理、逻辑可行,是用于目标年不同情景下水土资源利用状况模拟预测的有效工具,下文用该模型模拟长河流域2030年不同情景下水土资源利用状况[14-17]。
表1 长河流域土地资源-水资源-煤炭开采规模-经济系统主要变量仿真数据与历史数据对比
Table 1 In the long river the basin land resources-water resources-coal mining scale-economic system comparison of the main variable simulation data with historical data

主要变量比较2012年2013年2014年2015年2016年仿真值98.1998.1998.6298.6198.61耕地面积/km2历史值98.1898.1798.6098.6098.60 偏差/%0.010.020.020.010.01仿真值433 931434 792436 905438 314440 740国民生产总值/万元历史值435 468435 433437 753438 819440 873偏差/%-0.350.210.050.29-0.03仿真值2 5192 5062 5762 6432 651总供水量/103t历史值2 5202 5052 5652 6332 650偏差/%-0.040.040.430.380.04仿真值148.5137.7129.4131.7124.8煤炭开采量/103t历史值148.0137.0128.7131.2124.3偏差/%0.340.510.540.380.40
3 煤炭开采方式仿真模拟方案的设定
3.1 煤炭开采方式仿真模拟方案的设定
矿区煤炭资源的发展存在很多的不确定性,提前判定不同煤炭资源开采模式下矿区水土资源经济系统的发展结构并分析实现该方式的路径对矿区的发展管理具有重要意义。该地区的基本矛盾是煤炭开采损毁水土资源与水土资源需求间的矛盾,即有限水土资源既要满足民生需求和维持生态空间,又要支持矿业的发展,长河流域是典型煤炭主产区,担负着该煤炭资源的供给任务,同时长河流域地区部分耕地沙化严重,又是水资源比较紧张的生态环境敏感区,而作为欠发达地区,又需要维持经济的稳步发展,因此合理控制煤炭资源的开采规模,促进煤炭、水土资源的同步高效利用是该地区发展的关键。从关键矛盾出发把长河流域的未来发展情景划分为经济优化型、资源优化型、SD-MOP优化型3类。
情景模拟最关键的是识别不同情景的主要指标,由各指标值来定义每一情景的内容,笔者认为经济优化型的情景的标示指标是煤炭开采规模,即煤炭采出率,资源优化型情景主要是土地复垦率与废水治理率,而SD-MOP优化型情景主要是煤炭开采规模与水土资源的双效控制。 具体指标的大小设置详见表2。
表2 不同发展情景下关键指标数值确定
Table 2 Determination of key indicators in different development scenarios %
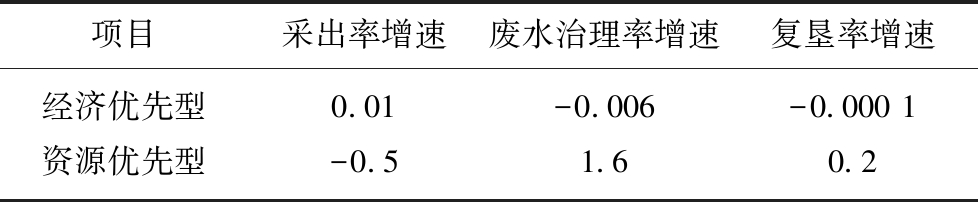
项目采出率增速 废水治理率增速复垦率增速经济优先型0.01-0.006-0.000 1资源优先型-0.51.60.2
本文指标设置参考了3种数据:长河流域发展的历史数据、山西省经济发展资源量最低保留量数据以及与地区延轨迹发展的预测数据。对采出率指标设置,根据历史数据预测长河流域未来煤炭开采量的增速的上限为1.96%,通过模拟运行找出采出率的增速上限为0.01%,若考虑到长河流域未来经济转型及资源束缚压力,本文选择-7.43%作为长河流域煤炭开采量增速的下限,即采出率下限为-0.02%,因为经过对历史数据、资源最低保留数据分析在经济转型压力下煤矿开采增长率将长期维持在-7.43%以上。同理,对废水治理率指标设置,总供水量的增速上限是3%,即废水治理率的增速上限为1.6%,总供水量的增速下限是-0.59%,即废水治理率的增速下限为-0.006%;对复垦率指标设置,根据历史数据预测长河流域耕地面积的增速上限是0.4%,下限为-0.01%,即复垦率的增速上限为0.02%,下限为-0.000 1%[18]。
3.2 长河流域经济优化型、资源优化型煤炭开采方式的情景模拟
分别把表中这2种不同情景的关键指标值代入所构建的SD模型中,模拟不同情景下2030年长河流域煤炭开采模式,模拟结果如图3所示。

图3 经济优化型、资源优化型模拟仿真方案
Fig.3 Economic optimization,resource optimization simulation program
通过对模型及数据的分析可以得,在经济优化型发展模式中,随着煤炭开采量不断增加,年国民生产总值由2016年的440 389万元增加到2030年的506 770万元,较2016年增加了15.07%,但是总供水量由2016年的2 650万t减少到2030年的2 435万t,较2016年减少了8.11%,耕地也出现了小幅度减少,由2016年的98.60 km2减少到2030年的98.46 km2,较2016年减少了0.14%;在资源优化型发展模式图形中,国民生产总值增长幅度明显减少,由2016年的440 389增加到2030年的453 378万元,仅增长了2.95%,耕地面积由2016年的98.60 km2增加到2030年的104.27 km2,增长了5.75%,总供水量由2016年的2 650万t增加到2030年的4 008万t,增长了51.24%。
通过分析可以得出,长河流域的煤炭产业对当地的经济发展和水土资源都有很大的影响,实施经济优化型发展方案,即加大煤炭开采规模,使得国民生产总值的增长率大幅度提高,但是煤炭资源的开采给水资源带来了很大影响,在本就水资源不充足的地区这种发展模式是行不通的;而实施资源优化型发展方案,在以煤炭资源发展为主的地区,大幅度减少其煤炭开采规模,虽然提高了耕地面积和水资源供应量,但是很大程度上减小了当地国民产值的增长速度,煤炭经济发展的控制很大程度上限制了该区的经济发展。
总结可得,经济优化型发展模式不符合社会经济发展的长远利益,会导致当地水资源不足,难以实现可持续发展的战略目标;资源优化型发展模式虽然保证了当地资源环境,但是不利于经济的发展,因此,为更好的实现经济-生态双重效益的同步发展,我们利用多目标规划模型和系统动力学模型相结合的方式找出煤炭最优开采模式。
3.3 SD-MOP优化型仿真方案的模拟
通过建立SD模型,仿真模拟了经济优化型、资源优化型煤炭开采规模方式。为保持水资源和土地资源利用的良性循环,提高土地和水资源的最大效率和效益,使土地和水资源可持续利用,最大限度促进区域经济发展。因此,利用SD与多目标规划整合模型,对2030年长河流域煤炭开采规模-水土资源状况进行仿真与优化,旨在提高煤炭、水和土地的效率和效益,维持煤炭资源-水土资源经济系统的相对平衡,实现该地区煤炭、土地、水资源的可持续利用。
3.3.1 敏感性因素识别
在构建SD模型时,利用线性回归等方法建立各因素之间的关系式时,通过对模型不断的运行调整,可以看出敏感性较强的因素,因此,经过大概筛选,对应耕地面积选取了粮食自给率、塌陷因子、压占因子、复垦率;对应煤炭开采量选取了采出率和固定资产投资系数;对应水资源供应量选取了万吨煤开采废水排放量、废水治理率,生态环境投资系数;对应国民生产总值选取了煤炭销售系数,总共有10个参数。然后,分别以耕地面积、煤炭开采量、总供水量和国民生产总值为输出变量,将以上10个参数分别代入公式中,并结合回归分析模型得出各参数之间的关系式,进行系统的原始模拟运行。最后根据灵敏度公式计算得出影响煤炭开采规模-水土地资源损毁系统最大的敏感性因素为采出率、废水治理率和复垦率[19]。
灵敏度计算公式为
![]()
(1)
式中,S为灵敏度;X为变化参数;Y为输出变量;t为模拟时间。
当S(t)<1时,表明该参数为非敏感性因子;当S(t)>1时,表明该参数为敏感性因子。
3.3.2 多目标规划模型构建
根据煤炭开采规模-水土资源经济系统结构优化的敏感性因素,将采出率、废水治理率和复垦率分别定义为x1,x2与x3,将煤炭开采量、耕地面积、总供水量、废水排放量、耕地损毁面积分别定义为y1,y2,y3,y4,y5。
(1)经济效益目标函数为
![]()
(2)
式中,k1为单位煤炭的价格,元/t;k2,k3为耕地和总供水量单位面积的产值,万元/km2,现设定为多年平均值,经测算k1=450,k2=0.68,k3=0.23。
(2)生态效益目标函数为
![]()
(3)
式中,z2为耕地绿当量系数;z3为最低供水量系数,结合该地区的实际状况,设定耕地绿当量z2=0.2,z3=0.9。
(3)各元素与敏感性因素的回归关系为
y1=39 431x1+330x2-2 476x3+1 994
y2=-229 692x1+x2+2 380x3+5 275
y3=22 230x1-x2+180x3+2 411
y4=34 710x1-125x2-1 500x3+240
y5=9 104x1-x2-531x3+733
(4)
(4)煤炭开采量、耕地面积、总供水量、废水排放量、耕地损毁量的约束
煤炭开采量约束。根据该地区的煤炭存储量、煤炭探明量以及各煤炭企业批准最高煤炭开采量等因素的测算,到2030年该地区的煤炭开采量不得超过600万t。因此,煤炭开采量的约束条件是y1≤600万t。
耕地面积约束。采用插值法测算,到2030年长河流域耕地保有量只有为31.25 km2才可保证区域人口粮食安全。因此,耕地保有量约束条件为y2≥3 125。
总供水量约束。根据该地区人口等因素分析得出,总供水量约束条件是y3≥1 872。
废水排放量约束。根据对历史数据的趋势预测以及水资源储量的分析得出,废水排放量的约束条件是y4≤70。
耕地损毁面积约束。根据耕地面积即投资开垦费用等因素的分析得出,耕地损毁面积约束条件是y5≤678。
变量约束x1>0;x2>0;x3>0。利用lingo11.0软件求解,得出优化值x1=0.001 5,x2=0.57,x3=0.07。根据结果可以推出:采出率是以-0.3%的增速运行;污水处理率是0.8%的增速运行;复垦率是以0.1%的增速运行。再将其代入系统流图,模拟各类元素变化情况,对系统进行优化。方案模拟结果如图4所示。
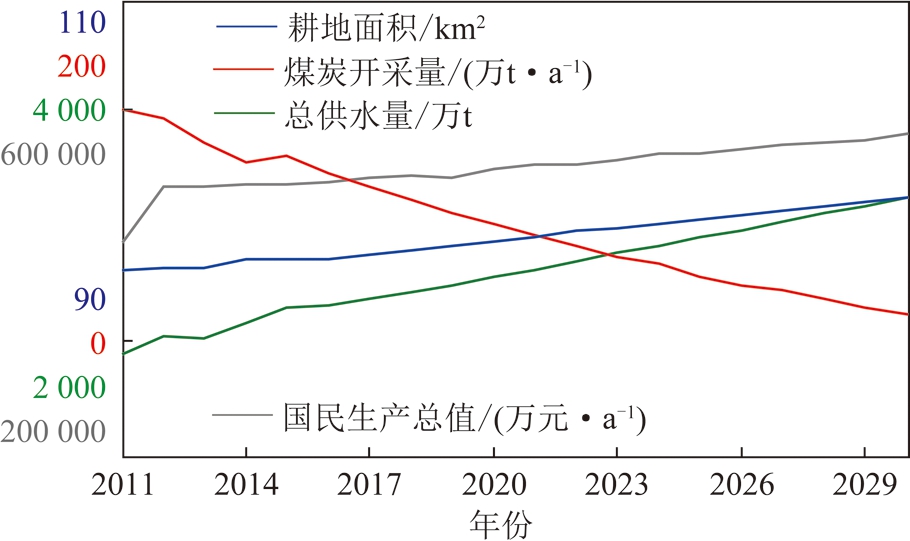
图4 SD-MOP优化型模拟仿真方案
Fig.4 SD-MOP optimized simulation solution
通过数据分析,到2030年,长河流域年国民生产总值从2016年的440 872.7万元增加到2030年的479 385.5万元,较2016年增加了8.74%,经济效益得到很大提高;耕地面积从2016年的98.60 km2增加到2030年的101.40 km2,增加了2.84%;总供水量从2016年的2 650万t增加到了3 131.65万t/a,增加了18.17%。该方案既保证了水土资源的健康持续发展,也确保了该地区的经济能够稳步持续增长。因此,经济-生态双重效益同步发展的优化型方案是矿区煤炭开采形式的最理想方案。
4 结 论
(1)经济优化型。经济优化型方案以高资源消耗率以及低效能的资源保护投入为主要特征,实现社会经济快速发展的目的。分析得出:随着煤炭开采量不断增加,年国民生产总值也在快速增长,但是供水量也在快速减少,耕地面积也出现了小幅度减小。可见,经济型发展模式不符合社会经济发展的长远利益,会导致矿区陷入“水资源不足”的威胁中,难以实现可持续发展的战略目标。
(2)资源优化型发展方式。资源型发展模式以保护土地和水资源为主,减少煤炭的开采规模,同时增加生态环境和农业生产投资。结果显示:年国民生产总值增速较大幅度减小,耕地面积在加大农业投资和减少开采规模的作用下快速增长,总供水量也快速增加。可见,资源型发展模式维护资源的健康稳步发展,但是不利于经济的发展。
(3)SD-MOP整合优化模型,对长河流域煤炭开采规模的设定进行了综合考虑,既考虑了经济效益又重视了生态环境,其优化方案是朝着煤炭资源、土地资源和水资源的合理利用,经济-生态双优化的改造过程,是在提高研究区煤炭资源、水和土地资源的利用效率的过程,有助于优化长河流域煤炭、水和土地资源的数量结构、层次结构与效益结构。因此,此方案是科学可行的。
未来,长河流域若想要健康发展,就要对煤炭开采规模进行严格控制,必须改变现状,向土地保护、水资源保护等方面综合调整,并辅之以科学的管理,来提高煤炭、土地和水资源的利用效率,减少土地和水资源损毁,保护土地和水资源的质量安全,实现该区域煤炭资源、水资源和土地资源的高效利用。
[1] 匡伟,时代,刘立忠,等.采煤沉陷土地损毁程度评价软件系统研究[J].金属矿山,2015,44(4):15-17.
KUANG Wei,SHI Dai,LIU Lizhong,et al.Study on the software system for evaluating the damage degree of coal mining subsidence land[J].Metal Mine,2015,44(4):15-17.
[2] 董丽丽.区域生态环境背景下煤矿区水土资源协调利用研究[D].徐州:中国矿业大学,2015.
DONG Lili.Study on the coordinated utilization of water and soil resources in coal mines under the background of regional ecological environment[D].Xuzhou:China University of Mining and Technology,2015.
[3] 黄程希,王瑾,毕如田,等.压煤区开采规模与水土资源承载力协调性分析[J].灌溉排水学报,2018,37(1):91-97.
HUANG Chengxi,WANG Jin,BI Rutian,et al.Analysis of the coordination between mining scale and water and soil resources carrying capacity in coal-pressed areas[J].Journal of Irrigation and Drainage,2018,37(1):91-97.
[4] 李强,李永春,陈大勇,等.神东矿区水资源可持续利用问题研究[J].干旱区资源与环境,2013,27(9):141-147.
LI Qiang,LI Yongchun,CHEN Dayong,et al.Study on the sustainable utilization of water resources in shendong mining area[J].Resources and Environment in Arid Areas,2013,27(9):141-147.
[5] ANNE E,AUDE P.Optimally eating a stochastic cake:A Recursive utility approach[J].Resource and Energy Economics,2003,25:129-139.
[6] WAQAR Ali Asad M,DIMITRAKOPOULOS R.Optimal production scale of open pit mining operations with uncertain metal supply and long-term stockpiles[J].Resources Policy,2012,37(1):81-89.
[7] 李静.不确定条件下我国煤炭资源最优开采规模研究[D].西安:西安科技大学,2012.
LI Jing.Research on the optimal mining scale of coal resources in China under uncertain conditions[D].Xi’an:Xi’an University of Science and Technology,2012.
[8] 姜杰.煤矿跨期生产规模的优化研究[D].西安:西安科技大学,2014.
JIANG Jie.Optimization of intertemporal production scale in coal mines[D].Xi’an:Xi’an University of Science and Technology,2014.
[9] 翟燕妮.煤炭资源开采规模研究[D].太原:山西财经大学,2009.
ZHAI Yanni.Research on the scale of coal resource exploitation[D].Taiyuan:Shanxi University of Finance and Economics,2009.
[10] BI Yinli,ZOU Hui,ZHU Chenwei.Dynamic monitoring of soil bulk density and infiltration rate during coal mining in sandy land with different vegetation[J].International Journal of Coal Science & Technology,2014,1(2):198-206.
[11] 胡宗楠,李鑫,楼淑瑜,等.基于系统动力学模型的扬州市土地利用结构多情景模拟与实现[J].水土保持通报,2017,37(4):211-218.
HU Zongnan,LI Xin,LOU Shuyu,et al.Multi-scenario simulation and implementation of land use structure in Yangzhou City based on system dynamics model[J].Bulletin of Soil and Water Conservation,2017,37(4):211-218.
[12] HE Chunyang,SHI Peijun,CHEN Jin.Developing land use scenario dynamics model by the integration of system dynamics model and cellular automata model[J].Science in China(Series D:Earth Sciences),2005(11):1979-1989.
[13] WANG Hao,ZHANG Kai,CHEN Junhua,et al.System dynamics model of taxi management in metropolises:Economic and environmental implications for Beijing[J].Journal of Environmental Management,2018,213:555-565.
[14] 高亚,章恒全.基于系统动力学的江苏省水资源承载力的仿真与控制[J].水资源与水工程学报,2016,27(4):103-109.
GAO Ya,ZHANG Hengquan.Simulation and control of water resources carrying capacity in Jiangsu Province based on system dynamics[J].Journal of Water Resources and Water Engineering,2016,27(4):103-109.
[15] 秦欢欢,张保祥,孟凡海.基于系统动力学的龙口市水资源供需问题研究[J].水资源与水工程学报,2017,28(4):45-49,57.
QIN Huanhuan,ZHANG Baoxiang,MENG Fanhai.Study on supply and demand of water resources in Longkou City based on system dynamics[J].Journal of Water Resources and Water Engineering,2017,28(4):45-49,57.
[16] 李保杰,顾和和,纪亚洲.基于CLUE_S模型的矿区土地利用变化情景模拟——以徐州市贾汪矿区为例[J].热带地理,2018,38(2):274-281.
LI Baojie,GU Hehe,JI Yazhou.Scenario simulation of land use change in mining area based on CLUE_S Model——Taking Jiawang mining area in Xuzhou city as an example[J].Tropical Geography,2018,38(2):274-281.
[17] TONG Lei,DOU Yuanyuan.Simulation study of coal mine safety investment based on system dynamics[J].International Journal of Mining Science and Technology,2014,24(2):201-205.
[18] 胡宗楠,李鑫,楼淑瑜,等.基于系统动力学模型的扬州市土地利用结构多情景模拟与实现[J].水土保持通报,2017,37(4):211-218.
HU Zongnan,LI Xin,LOU Shuyu,et al.Multi-scenario simulation and implementation of land use structure in Yangzhou based on system dynamics model[J].Bulletin of Soil and Water Conservation,2017,37(4):211-218.
[19] 李秀霞,徐龙,江恩赐.基于系统动力学的土地利用结构多目标优化[J].农业工程学报,2013,29(16):247-254,294.
LI Xiuxia,XU Long,JIANG Enci.Multi-objective optimization of land use structure based on system dynamics[J].Transactions of the Chinese Society of Agricultural Engineering,2013,29(16):247-254,294.
