随着采煤装备的不断发展,开采的地层越来越复杂,开采速度越来越快,对镐型截齿的质量提出了更高的要求。硬质合金头脱落作为镐型截齿一种常见的失效形式[1],会大大降低镐型截齿的寿命,增加煤矿开挖成本,降低施工效率。在截齿工作过程中,钎焊接头处的工作温度、破岩载荷以及钎焊残余应力等因素均会导致硬质合金头的松动,直至脱落。截齿合金头脱落的主要原因是焊缝质量差、强度低,钎料层厚度的合理选择能有效增强截齿的钎焊强度[2]。根据不同的施工地层,镐型截齿可分为两种,不加耐磨层的普通截齿与加耐磨层的耐磨截齿。耐磨层在增强截齿耐磨性的同时,对其钎焊接头处的连接性能也有一定的影响,有必要对两种截齿的钎焊接头分别进行钎焊性能分析与最优钎料层厚度的选择。
近年来,国内外大量学者对截齿展开了研究。王立平等[3-4]基于Evans截割模型,通过理论推导的方式,提出了镐齿截割力的修正模型。BAKAR M Z A[5],JEONG H Y等[6]通过实验的方式,研究了如截线间距、截割深度、岩石饱和度等参数对截齿截割力及比能耗的影响。张倩倩等[7]通过实验和数值模拟方法,研究了镐型截齿的耐磨性能及其磨损特征对截割力的影响。现有的对于截齿的研究主要集中在其截割力与磨损方面[8-12],解决的是关于截齿截割性能与截齿磨损方面的问题,缺乏有关镐型截齿合金头脱落失效的研究。探究镐型截齿的合金头脱落现象,需要研究截齿工作过程中钎焊接头处的应力分布情况。目前国内外对于焊缝应力方面的研究,主要体现在简单模型的焊接残余应力分布规律上[13-15]。但是,镐型截齿硬质合金头脱落现象均出现在其工作过程中,仅研究残余应力,无法体现破岩载荷与工作温度对硬质合金头脱落的影响。而且考虑到镐型截齿刀体结构、钎料成分及焊接工艺的特殊性,已有研究并不能很好地解释镐型截齿硬质合金头脱落的现象。
本文基于ANSYS软件,以u85截齿为例,分别针对普通截齿与耐磨截齿,建立有限元模型,设置其材料热物性参数随温度而变化,仿真得到两种镐型截齿钎焊接头的残余应力场。将镐型截齿的工作温度与破岩载荷加载到钎焊接头残余应力场上,求解得到镐型截齿钎焊接头的工作应力分布规律。分析研究堆焊耐磨层对镐型截齿工作过程接头应力的影响,并提出两种镐型截齿钎料层厚度的优化决策方法。
1 数值模型的建立
1.1 截齿钎焊的热传导模型
截齿钎焊冷却过程中,产生的应变包含了弹性应变、塑性应变以及热应变[16]。其中,热应变是截齿高温冷却时产生的收缩以及弹性模量和线膨胀系数随温度变化而引起的。其表达式可以写成:
![]()
(1)
式中,εT为截齿热应变;α为截齿的热膨胀系数;T0为截齿的钎焊温度;De为弹性模量矩阵;σ为截齿弹性应力;T为瞬时温度。
截齿钎焊过程主要通过热对流、热传导和热辐射等方式进行热能传递,热对流主要发生在截齿外表面与空气之间。截齿的焊后冷却过程是一个非稳态导热过程,导热方程可表示为
![]()
(2)
式中,λ为截齿的导热系数;Cp为定压比热容;ρ为密度;x,y,z为系统内每个位置的坐标;Q为热量。
截齿钎焊之后的冷却过程中存在潜热的释放问题,采用热焓法处理,热焓H的表达式可以写成
H=H0+![]() CdT+(1-fs)Lf
CdT+(1-fs)Lf
(3)
式中,H0为钎焊温度T0时钎料的比焓;C为等压热容;fs为钎料熔化状态下固体的含量;Lf为熔融钎料的比热系数。
1.2 仿真模型的建立
镐型截齿是由42CrMo刀体、HSCuZnNi铜基钎料及YG15硬质合金头组成,为了增强截齿的耐磨性,部分镐型截齿在刀体前端堆焊了Fe-Cr-Nb-C系耐磨层,如图1所示。硬质合金头直径为11.85 mm,底部定心锥面的锥角为55°,合金头侧面上下两处圆角分别为1 mm与2 mm。截齿前端的耐磨堆焊层厚度最大,达到1.75 mm,最薄位置厚度为0.5 mm。在钎焊过程中,由于铜钎料的溢出,会在硬质合金头与刀体表面覆盖一层很薄的铜钎料。考虑到表面钎料对工作应力的影响,建立镐型截齿仿真模型时采用自由边界钎料形状。
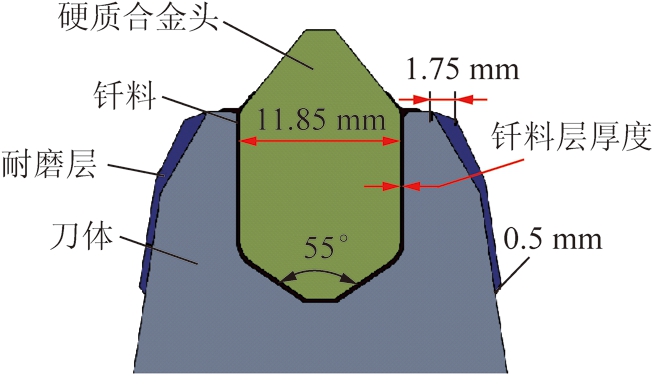
图1 截齿钎焊连接示意
Fig.1 Schematic diagram of brazing connection of pick
镐型截齿齿柄部分结构对焊缝应力的影响不大,只取镐型截齿齿尖部分进行仿真模型建立,如图2所示。为了研究镐型截齿钎料层厚度对工作应力的影响规律,考虑实际焊接工艺的影响,硬质合金头与耐磨层结构保持不变,改变刀体孔的内径,取0.050~0.225 mm的钎料层厚度,分别对普通截齿与耐磨截齿进行模型建立。采用Solid279单元,对模型进行网格划分,钎焊接头区域选用更细密网格。
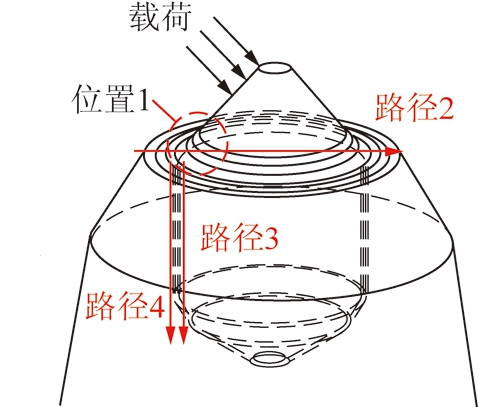
图2 截齿模型
Fig.2 Pick model
1.3 材料参数
引入以下假设:
(1)考虑钎料层弹塑性变形对接头应力的影响,忽略熔池内部化学反应;
(2)与温度有关的物理和力学性能、应力应变在微小的时间增量内线性变化;
(3)材料的物理、力学性能各向同性。
HSCuZnNi作为钎焊硬质合金最常用的钎料之一,在室温下,其硬质合金钎焊接头的抗剪强度达到320 MPa,抗拉强度达到450 MPa;当温度达到300 ℃时,钎焊接头的抗剪强度为250 MPa,抗拉强度为380 MPa。
截齿采用理想弹塑性线性强化模型,在镐型截齿高温钎焊后的冷却过程中,材料的物理和力学性能参数随温度变化而改变,考虑各材料的屈服强度对热应力的影响,具体材料参数见表1。
表1 截齿材料的性能参数
Table 1 Performance parameters of pick material
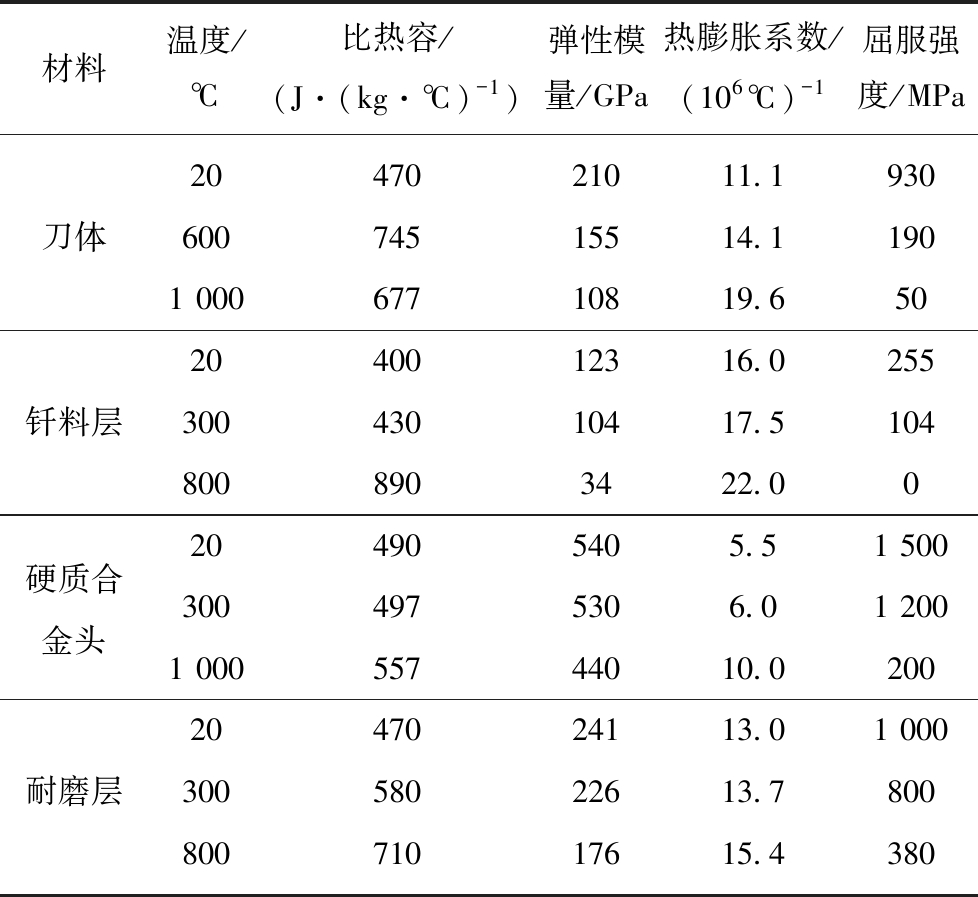
材料温度/℃比热容/(J·(kg·℃)-1)弹性模量/GPa热膨胀系数/(106 ℃)-1屈服强度/MPa2047021011.1930刀体60074515514.11901 00067710819.6502040012316.0255钎料层30043010417.51048008903422.00204905405.51 500硬质合3004975306.01 200金头1 00055744010.02002047024113.01 000耐磨层30058022613.780080071017615.4380
1.4 边界条件
温度达到800 ℃以上时,截齿上钎料层与耐磨层均呈软化状态,所承受应力很小,对截齿残余应力影响较小,不做考虑。本文研究截齿从800 ℃冷却到20 ℃室温过程的钎焊残余应力。
利用生死单元法,模拟耐磨截齿先堆焊耐磨层后钎焊硬质合金头的工艺。设置镐型截齿的初始温度为钎焊温度1 000 ℃,通过与空气对流换热的方式,将截齿冷却到800 ℃后,激活钎料层的单元,模拟钎料层的凝固成形,再空冷至室温,钎焊完成。通过改变对流换热系数的方式进行截齿的焊后热处理,模拟截齿860 ℃加热保温、淬火以及360 ℃回火,最后空冷至室温的工艺过程,得到镐型截齿的温度场。采用间接法顺序耦合分析,将温度场作为体载荷施加到镐型截齿上,得到截齿的钎焊残余应力。在截齿残余应力场的基础上,施加外部载荷与工作温度,得到镐型截齿工作过程中钎焊接头的应力分布情况。
2 钎焊残余应力仿真与实验验证
2.1 钎焊残余应力模拟结果
根据工程上的截齿实际结构参数,选择钎料层厚度为0.075 mm的镐型截齿模型,进行钎焊残余应力仿真。将笛卡尔坐标系转化成圆柱坐标系,查看仿真结果中的径向残余应力σX、周向残余应力σY与轴向残余应力σZ。
路径1位于截齿钎焊接头外表面,自刀体沿径向过渡到硬质合金头,如图3所示。
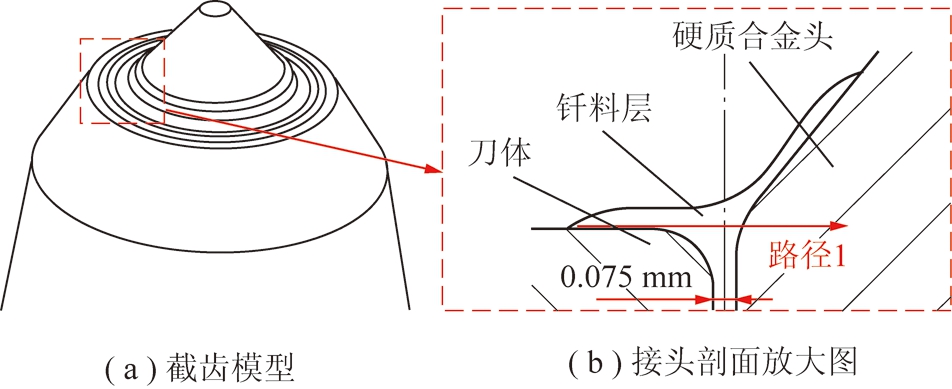
图3 路径1示意
Fig.3 Schematic diagram of path 1
提取普通截齿与耐磨截齿路径1上的钎焊残余应力数据进行分析,得到其残余应力分布曲线,如图4所示。

图4 钎焊接头残余应力分布
Fig.4 Distribution of residual stresses in brazing joints
可以看出普通截齿与耐磨截齿沿路径1的钎焊残余应力变化趋势大致相同,两者的等效残余应力σEQ最大值均出现在钎料层与硬质合金头交界面附近,说明该处为截齿钎焊接头的危险位置,容易发生因热应力过大导致的钎缝开裂。这是因为钎料与硬质合金的热膨胀系数差异较大,在冷却过程中产生较大应力集中[17]。在该位置,普通截齿的径向残余应力σX达到214 MPa,周向残余应力σY达到230 MPa;耐磨截齿的径向残余应力σX达到253 MPa,周向残余应力σY达到238 MPa。堆焊耐磨层使得截齿钎焊接头的径向残余应力σX增大了39 MPa,对周向残余应力σY影响不大。轴向残余应力σZ对钎焊接头的连接强度影响较小。
2.2 实验验证
利用Proto iXRD残余应力仪对截齿进行残余应力测试,如图5所示。该仪器采用X射线衍射方法进行非破坏性残余应力测试,可得到试件表面的沿其工作臂轴线方向的正应力,测试精度为±10 MPa。分别对钎料层厚度为0.075 mm的未钎焊截齿、普通截齿、耐磨截齿进行残余应力测试。测试未钎焊截齿得到加工初始残余应力,测试两个钎焊后截齿,得到总残余应力。

图5 残余应力测试实验
Fig.5 Residual stress test
根据应力叠加原理,总残余应力为加工初始残余应力与钎焊残余应力的矢量叠加[18],根据测试结果获得截齿上各点的钎焊残余应力。对两种镐型截齿残余应力影响区域的外表面进行取点,如图6所示。在刀体顶部边缘位置分别取2个对称点;普通截齿刀体处沿母线方向取3个间距为7 mm的点,耐磨截齿在耐磨层下方的刀体处沿母线方向取两个间距为2.5 mm的点。

图6 残余应力测量位置示意
Fig.6 Location of residual stress test point
将镐型截齿竖直放置,对顶上所取点分别进行周向残余应力σY与径向残余应力σX测试;将镐型截齿水平放置,对母线上所取点分别进行周向残余应力σY与轴向残余应力σZ的测试。分析计算得到其钎焊残余应力,将实验与仿真得到的截齿残余应力做比较,得到结果见表2。
由表2可以看出,镐型截齿的钎焊残余应力仿真值与实测值较为吻合,沿截齿刀体母线方向,截齿残余应力的变化趋势一致,证明了仿真模型的正确性。但仿真结果与实测结果仍存在一定偏差,所测点的周向残余拉应力仿真值略大于实测值,径向残余压应力略小于实测值。其中,靠近刀体顶部点的周向残余应力平均误差达到5%,截齿母线上点的平均误差达到6%。原因可能是钎焊仿真过程未考虑熔池内部的化学反应,影响了仿真结果。
表2 钎焊残余应力测量值与仿真值对比
Table 2 Comparisons of brazing residual stress between computational and experimental resultsMPa
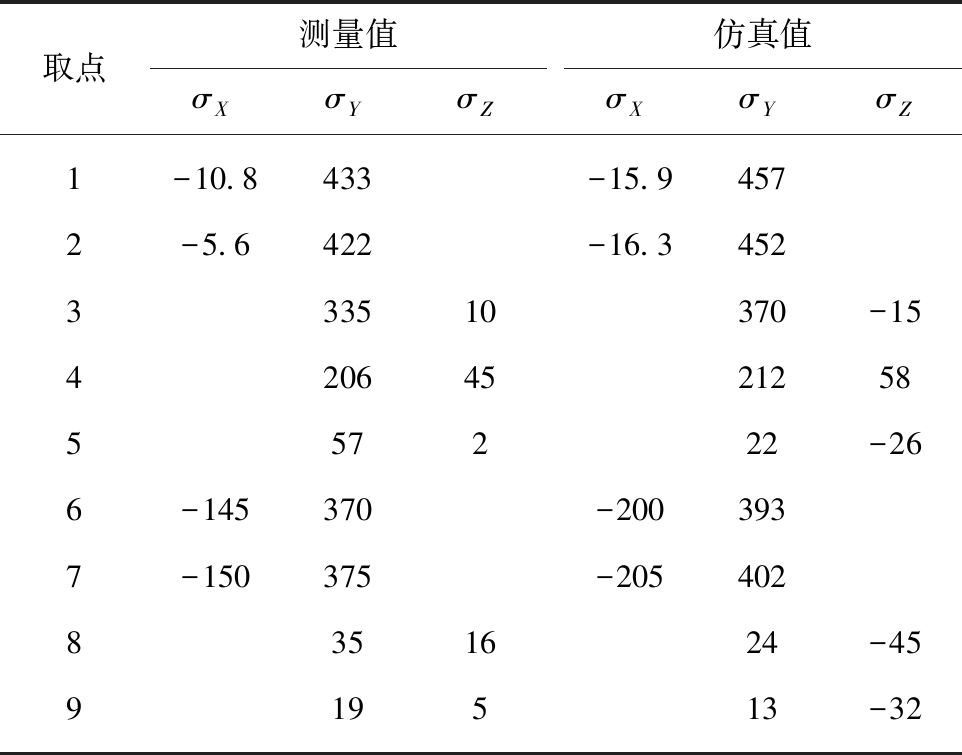
取点测量值σXσYσZ仿真值σXσYσZ1-10.8433-15.94572-5.6422-16.3452333510370-1542064521258557222-266-145370-2003937-150375-2054028351624-45919513-32
3 工作过程的钎焊接头应力模拟
3.1 镐型截齿外部载荷的获取
对截齿工作过程中接头应力仿真所需的载荷输入进行了实验研究[19]。镐型截齿破岩实验在回转切削实验台上进行,齿座上方安装有三向力传感器,设置截割速度为40 mm/s,截割深度为12 mm,进行截割角度为45°的镐型截齿三向力测试实验,如图7所示。

图7 镐型截齿三向力
Fig.7 Three-axis cutting force diagram of pick
实验取样时间为200 s,由三向力传感器可得到镐型截齿的截割阻力、牵引阻力以及侧向阻力。将实验得到的截割阻力F1与牵引阻力F2数据通过计算转化成轴向阻力FZ与径向阻力FX,侧向阻力FY保持不变,得到的载荷曲线如图8所示。
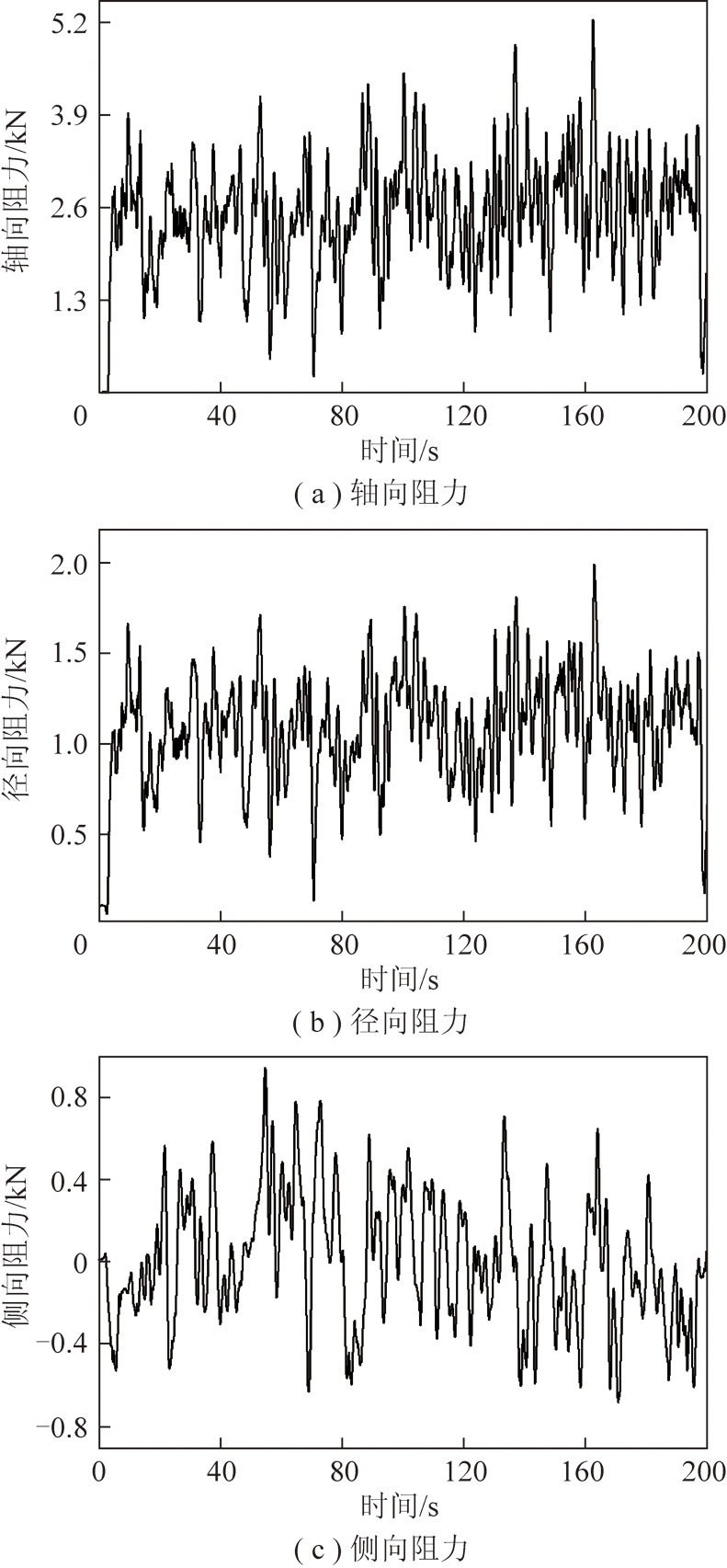
图8 镐型截齿三向载荷曲线
Fig.8 Three-axis cutting force curves of pick
通过对实验数据的分析处理,可以得到镐型截齿所受到的最大载荷与平均载荷,见表3。将三向载荷的最大值作为镐型截齿仿真的外部载荷输入。
表3 镐型截齿所受外部载荷
Table 3 Cutting force of pick N

载荷轴向阻力FZ径向阻力FX侧向阻力FY最大值5 2572 080952平均值2 5011 1230
3.2 工作温度对钎焊接头应力的影响
在镐型截齿截割煤岩时,煤岩硬度、工作时长以及喷嘴对截齿的降温效果等都会影响到截齿齿尖的工作温度。根据工程实际,截齿的工作温度在100~700 ℃。在截齿残余应力模型的基础上,分别施加工作温度100~700 ℃,进行热结构耦合分析,得到其应力分布情况。研究工作温度对截齿受载侧钎焊接头最大应力的影响,如图9所示。
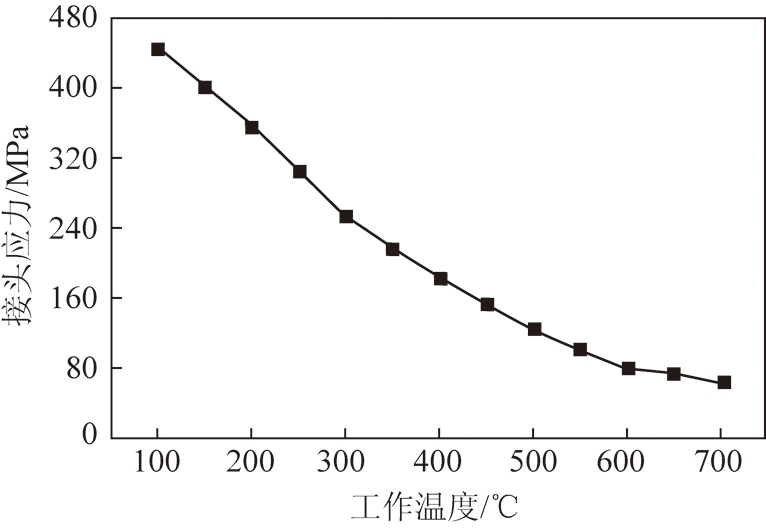
图9 工作温度对接头最大应力的影响
Fig.9 Effect of working temperature on maximum stress of joint
可以看出,截齿工作过程中的钎焊接头应力随着工作温度的增大而减小,且下降趋势逐渐变缓。当工作温度达到700 ℃时,接头应力仅为63 MPa。主要原因在于温度的升高导致了钎焊残余应力下降,且较高的工作温度使得钎料层出现了轻微软化,导致其与两侧材料之间的拉力变小了,连接强度大大降低。
3.3 不同截齿工作过程的钎焊接头应力分布规律
取截齿工作温度300 ℃,研究其工作过程中的接头应力分布规律,提取仿真结果中的等效应力σeq、径向应力σx与周向应力σy展开分析。
3.3.1 截齿径向路径的应力分析
路径2是截齿齿尖沿径向穿越刀体、钎料层与硬质合金头的直线路径。分别对普通截齿与耐磨截齿工作时沿路径2的接头应力分布规律进行分析,如图10,11所示。

图10 普通截齿路径2应力分布
Fig.10 Stress distribution of common pick in path 2

图11 耐磨截齿路径2应力分布
Fig.11 Stress distribution of wear-resistant pick in path 2
可以看出,两种截齿工作时,钎焊接头处均存在明显的拉应力,且在钎料层附近出现应力集中现象。两者的等效应力σeq最大值都出现在截齿受载侧的钎料层处,即图2中的位置1,分别达到212 MPa与210 MPa。其中,普通截齿的最大等效应力位于钎料层与刀体的交界面处,耐磨截齿的最大等效应力出现在钎料层与硬质合金头的交界面处,说明这两个位置分别是两种截齿钎焊接头最易发生破坏的危险部位。原因在于,钎焊残余应力最大的位置在钎料层与硬质合金头的交界面处,但高温的工作环境下,钎焊残余应力大幅降低,使得其对工作过程中接头应力的影响有所降低;在外部载荷的作用下,普通截齿钎焊接头的危险位置转移至钎料层与刀体的交界面处。耐磨截齿由于耐磨层结构的存在,增大了钎焊接头处的残余应力,减小了外部载荷对接头应力的影响,使得其危险位置仍出现在钎料层与硬质合金头的交界面处。
普通截齿钎焊接头在危险位置上的周向应力σy达到219 MPa,远大于径向应力σx,说明周向应力σy是导致普通截齿工作过程中钎焊接头结构破坏,引起硬质合金头脱落的主要原因。耐磨截齿在其危险位置,径向应力σx与周向应力σy分别为102 MPa与96 MPa,二者相差无几,说明耐磨截齿是在径向应力σx与周向应力σy的共同作用下,导致钎缝开裂从而使合金头脱落的。
3.3.2 截齿轴向路径的应力分析
为了进一步研究钎焊接头处的应力分布规律,提取其轴向直线路径上的应力数据。路径3位于钎料层与硬质合金头的交界面处,路径4位于钎料层与刀体的交界面处。对两种截齿工作过程中钎焊接头在路径3上的应力进行分析,得到其应力分布曲线如图12所示。
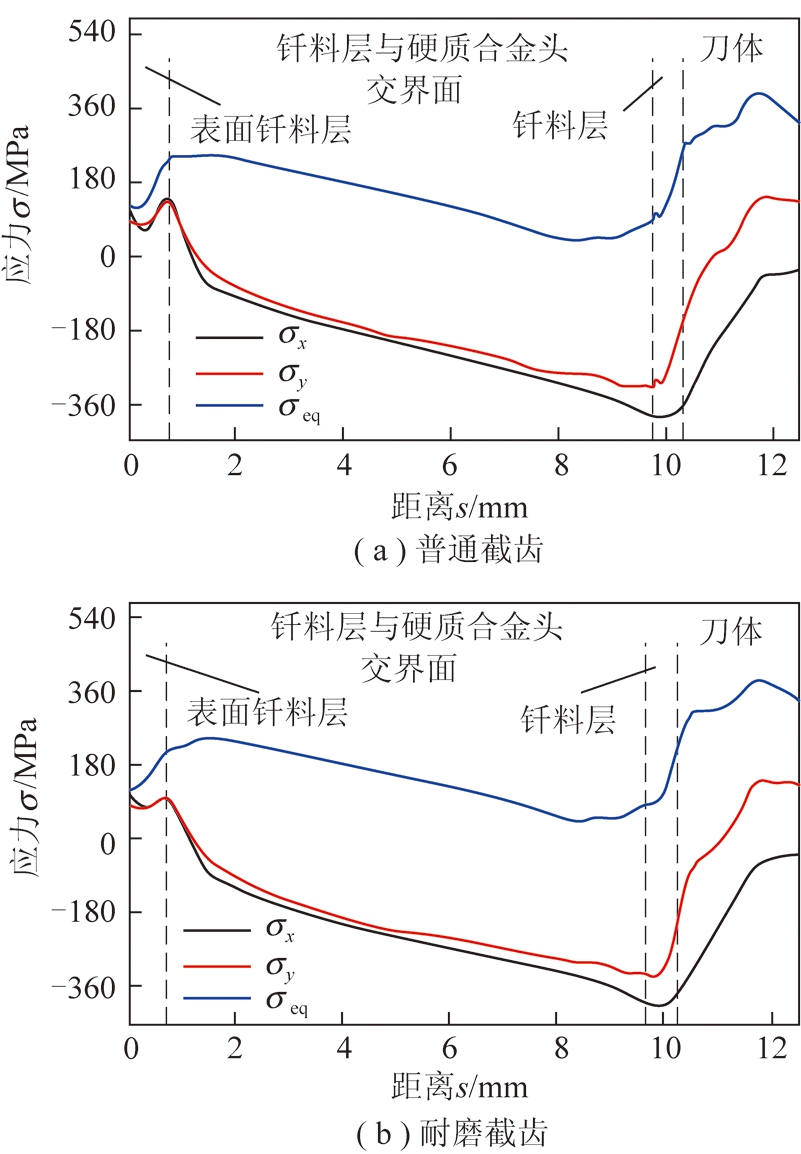
图12 钎焊接头路径3应力分布
Fig.12 Stress distribution of brazed joint in path 3
可以看出,普通截齿与耐磨截齿在路径3上的接头应力分布趋势大致是相同的,从外至内都是先增大后减小,在靠近刀体的部位再增大。等效应力σeq在表面钎料层与硬质合金头连接处以及钎料层与刀体连接处取到极值。在表面钎料层附近,径向应力σx与周向应力σy均为拉应力且数值相近,普通截齿的σx与σy达到130 MPa左右,耐磨截齿的该数值下降至大约90 MPa。在靠近刀体位置,截齿的σx与σy变为压应力,且径向应力σx要大于周向应力σy。
对两种截齿工作过程中钎焊接头在路径4上的应力进行分析,得到其应力分布曲线如图13所示。
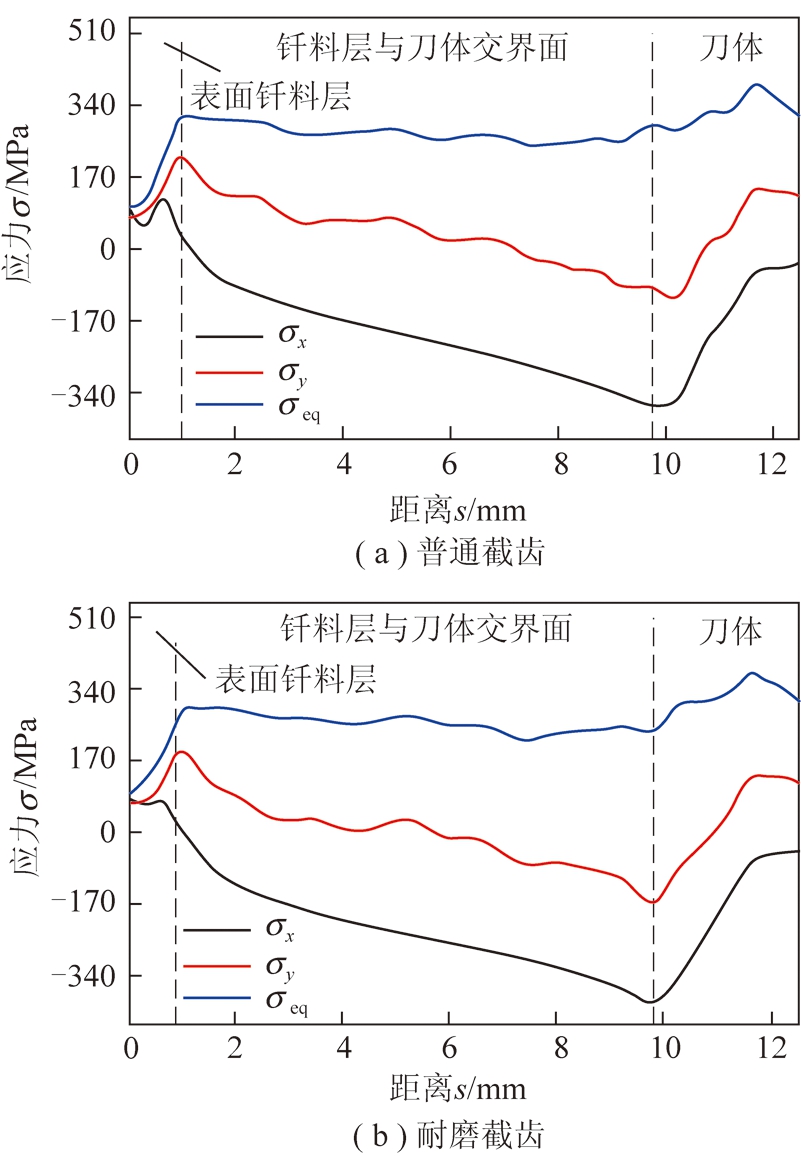
图13 钎焊接头路径4应力分布
Fig.13 Stress distribution of brazed joint in path 4
可以看出,等效应力σeq从外到内呈现先增大然后逐渐趋于平缓的趋势,在表面钎料层与刀体连接处达到峰值。在表面钎料层附近,径向应力σx与周向应力σy均为拉应力,普通截齿的σx与σy分别达到24 MPa和220 MPa,耐磨截齿的σx与σy分别为3 MPa和198 MPa。可见耐磨层使得工作过程中的截齿钎焊接头应力有所降低。
3.4 钎料层厚度对钎焊接头工作应力的影响
镐型截齿在冷却降温过程中,通过钎料层的塑形变形来协调钎焊接头的收缩差异,缓解接头部位的残余应力[20]。在工作过程中,不同钎料层厚度也对镐型截齿的载荷传递及应力分布产生影响。为了研究了不同厚度的钎料层(0.050~0.225 mm)对工作过程中接头应力的影响,在接头表面选择最大应力的节点,提取该节点的径向应力σx与周向应力σy,如图14所示。

图14 钎料层厚度对接头最大应力的影响
Fig.14 Effect of brazing filler thickness on maximum joint stress
可以看出,钎料层厚度从0.05 mm增大到0.225 mm过程中,普通截齿与耐磨截齿的最大应力均呈现先下降后上升的趋势,在0.1 mm处得到最小值。钎料层厚度为0.1 mm时,普通截齿的径向应力σx与周向应力σy分别为11 MPa和215 MPa,耐磨截齿的径向应力σx与周向应力σy分别达到18 MPa和213 MPa,钎焊接头内部应力最小,镐型截齿接头的连接强度最好。说明两种镐型截齿最优钎料层厚度的选择是一致的。从图14也可以看出,堆焊耐磨层使得镐型截齿钎焊接头的周向应力σy减小,一定程度上增强了接头的连接性能。
4 结 论
(1)普通截齿与耐磨截齿的等效残余应力σEQ最大值均出现在钎料层与硬质合金头交界面附近,这说明该处容易发生因热应力过大导致的镐型截齿钎缝开裂。堆焊耐磨层使得截齿钎焊接头该处的径向残余应力σX增大了39 MPa,对周向残余应力σY影响不大。
(2)两种镐型截齿钎焊残余应力的测量结果与数值分析结果基本吻合,说明了模型的正确性。
(3)分析镐型截齿工作过程中接头应力沿径向路径的分布情况,得到:普通截齿的最大等效应力位于钎料层与刀体的交界面处,达到212 MPa,周向拉伸应力σy是其结构破坏的主要原因;耐磨截齿的最大等效应力出现在钎料层与硬质合金头的交界面处,达到210 MPa。耐磨层对截齿整体应力的分布影响不大,但却使得截齿最大应力出现的位置发生了偏移,这使得截齿硬质合金头脱落的危险位置发生变化。
(4)分析镐型截齿工作过程中接头应力沿轴向路径的分布情况,得到:在钎料层与硬质合金头的交界面处,等效应力σeq在表面钎料层与硬质合金头连接处以及钎料层与刀体连接处达到极值;钎料层与刀体的交界面处,等效应力σeq在表面钎料层与刀体连接处达到峰值。
(5)普通截齿与耐磨截齿的最优钎料层厚度选择是一致的,均在钎料层厚度为0.1 mm时得到接头应力最小值。堆焊耐磨层使得镐型截齿的周向应力σy减小,一定程度上增强了接头的连接性能。
[1] 张强,刘志恒,王海舰,等.BP神经网络在截齿合金头失效识别中的应用[J].振动,测试与诊断,2018,38(3):508-516.
ZHANG Qiang,LIU Zhiheng,WANG Haijian,et al.Application of BP neural network in failure identification of pick alloy head[J].Journal of Vibration,Measurement & Diagnosis,2018,38(3):508-516.
[2] 高瑞婷,李晓延,朱永鑫,等.加载速率和钎料厚度对SnAgCu/Cu焊点剪切行为影响[J].焊接学报,2016,37(2):94-98,133.
GAO Ruiting,LI Xiaoyan,ZHU Yongxin,et al.Effect of loading rates and solder thickness on shear behavior of SnAgCu/Cu lead-free solder joint[J].Transactions of the China Welding Institution,2016,37(2):94-98,133.
[3] 王立平,蒋斌松,张翼,等.基于Evans截割模型的镐型截齿峰值截割力的计算[J].煤炭学报,2016,41(9):2367-2372.
WANG Liping,JIANG Binsong,ZHANG Yi,et al.Calculation of peak cutting force of conical picks based on Evans’ cutting model[J].Journal of China Coal Society,2016,41(9):2367-2372.
[4] 王立平,蒋斌松,张强.镐型截齿截槽非对称的峰值截割力计算[J].煤炭学报,2016,41(11):2876-2882.
WANG Liping,JIANG Binsong,ZHANG Qiang.Calculation of peak cutting force of conical picks under conditions of dissymmetrical slotting[J].Journal of China Coal Society,2016,41(11):2876-2882.
[5] BAKAR M Z A.Evaluation of saturation effects on drag pick cutting of a brittle sandstone from full scale linear cutting tests[J].Tunnelling and Underground Space Technology,2013,34(1):124-134.
[6] JEONG H Y,JEON S.Characteristic of size distribution rock chip produced by rock cutting with a pick cutter[J].Geomechanics & Engineering,2018,15(3):811-822.
[7] 张倩倩,韩振南,张梦奇,等.冲击载荷作用下锥形截齿磨损的实验和数值模拟研究[J].振动与冲击,2016,35(13):58-65.
ZHANG Qianqian,HAN Zhennan,ZHANG Mengqi,et al.Tests and simulation for wear of conical pick under impact load[J].Journal of Vibration and Shock,2016,35(13):58-65.
[8] WANG S,LI X,DU K,et al.Experimental investigation of hard rock fragmentation using a conical pick on true triaxial test apparatus[J].Tunnelling & Underground Space Technology,2018,79:210-223.
[9] LIU S,LIU Z,CUI X,et al.Rock breaking of conical cutter with assistance of front and rear water jet[J].Tunnelling & Underground Space Technology,2014,42:78-86.
[10] LIU X,LIU S,JI H.Mechanism of rock breaking by pick assisted with water jet of different modes[J].Journal of Mechanical Science & Technology,2015,29(12):5359-5368.
[11] 刘春生,王庆华,李德根.镐型截齿截割阻力谱的分形特征与比能耗模型[J].煤炭学报,2015,40(11):2623-2628.
LIU Chunsheng,WANG Qinghua,LI Degen.Fractal characteristic and specific energy model of conical picks cutting resistance spectrum[J].Journal of China Coal Society,2015,40(11):2623-2628.
[12] 王想,王清峰,梁运培.截割参数对镐型截齿截割比能耗的影响[J].煤炭学报,2018,43(2):563-570.
WANG Xiang,WANG Qingfeng,LIANG Yunpei.Effects of cutting parameters affecting on specific cutting energy of conical picks[J].Journal of China Coal Society,2018,43(2):563-570.
[13] DERAKHSHAN E D,YAZDIAN N,CRAFT B,et al.Numerical simulation and experimental validation of residual stress and welding distortion induced by laser-based welding processes of thin structural steel plates in butt joint configuration[J].Optics & Laser Technology,2018,104:170-182.
[14] MIRZAEE-SISAN A.Welding residual stresses in a strip of a pipe[J].International Journal of Pressure Vessels & Piping,2018,159:28-34.
[15] RIKKEN M,PIJPERS R,SLOT H,et al.A combined experimental and numerical examination of welding residual stresses[J].Journal of Materials Processing Technology,2018,261:98-106.
[16] 种晓宇,汪广驰,杜军,等.ZTAp/HCCI复合材料凝固过程中的温度场和热应力的数值模拟[J].金属学报,2018,54(2):314-324.
CHONG Xiaoyu,WANG Guangchi,DU Jun,et al.Numerical simulation of temperature field and thermal stress in ZTAp/HCCI composites during solidification process[J].Acta Metallurgica Sinica,2018,54(2):314-324.
[17] SALERNO G,BENNETT C,SUN W,et al.On the interaction between welding residual stresses:A numerical and experimental investigation[J].International Journal of Mechanical Sciences,2018,144:654-667.
[18] PARK J U,AN G,WOO W.The effect of initial stress induced during the steel manufacturing process on the welding residual stress in multi-pass butt welding[J].International Journal of Naval Architecture & Ocean Engineering,2017,10(2):129-140.
[19] 梁运培,王想,王清峰.截割厚度与截线距对镐型截齿破岩力学参数的影响[J].振动与冲击,2018,37(3):27-33.
LIANG Yunpei,WANG Xiang,WANG Qingfeng.Effects of cut depth and cut spacing on tool forces acting on a conical pick in rock cutting[J].Journal of Vibration and Shock,2018,37(3):27-33.
[20] 杜金松,颜家振,曹建国,等.蓝宝石/4J33合金钎焊接头残余应力的数值模拟分析[J].焊接学报,2017,38(8):87-90,132-133.
DU Jinsong,YAN Jiazhen,CAO Jianguo,et al.FEM analysis of distribution of thermal stresses at sapphire/kovar alloy brazed joint[J].Transactions of the China Welding Institution,2017,38(8):87-90,132-133.
