煤炭开采逐渐进入千米深井时代,深部效应易使深部矿井巷道围岩呈现出“大变形、难维护、渐进破坏”的宏观失稳特征,进而易降低深部矿井巷道围岩的稳定性[1-3]。同时,深部巷道围岩一般处于三向不等的高地应力环境中,而砂岩又是深地工程中最为常见的地质岩体之一[4]。因此,深入研究真三轴条件下砂岩渐进破坏特征及其力学行为演化规律可为深部矿井巷道围岩稳定性控制提供一定的指导与借鉴。
国内外学者对真三轴条件下煤岩体的力学行为演化规律及其破坏特征进行了深入研究,均获得了较为丰富的研究成果。陈景涛、冯夏庭[5]为了探究深部岩体在高地应力条件下的复杂应力路径演化特征,对拉西瓦花岗岩进行了真三轴试验,得出了花岗岩在真三轴条件下的破坏模式主要取决于其破坏截面上的剪应力与拉伸应变之间的竞争演化机制;VACHAPARAMPIL A等[6]深入研究了3种页岩在真三轴条件下的强度及其变形特征,较好地揭示了3种页岩的破坏机制;ZHAO[7]对锦屏大理岩进行了真三轴蠕变试验,深入研究了时间效应、蠕变速率以及长期强度三者与时效力学行为之间的关联,得出了应力水平是影响大理岩时效力学行为的主要因素;STRAHLER A等[8]深入研究了真三轴条件下的Kanaskat砂砾岩的应力-应变响应特征,较好地揭示了Kanaskat砂砾岩在真三轴条件下的力学响应机制;LU[9]对赤峰市玄武岩进行了微波-应力耦合下的真三轴试验,获得了真三轴条件下玄武岩的微波冲击力学行为响应规律;尹光志等[10-12]对不同工况下的煤岩体进行了大量的真三轴试验,分别从能量、渗透率、强度、变形、破坏模式等角度较好地表征了真三轴条件下的煤岩体破裂力学行为特征;LI[13],ZUO[14],ZHANG[15],ZHENG[16],HOEK E[17]等采用理论推导、试验研究、数值模拟等手段,深入研究了不同工况下的真三轴岩石强度准则,均较好地揭示了各类岩石在真三轴条件下的非线性破坏机制。
然而,国内外学者多数集中研究中主应力对煤岩体强度准则的影响及其准则的修正,而忽略了对真三轴条件下煤岩体渐进破坏机制方面的研究。基于此,笔者对砂岩进行了不同应力路径、不同模拟深度下的真三轴力学试验,进一步获得了真三轴条件下砂岩的渐进破坏力学行为演化规律,从而为深部巷道开挖、支护及稳定性控制提供一定的基础理论依据。
1 试验准备与试验方法
1.1 试样制备
根据《水利水电工程岩石试验规程》、《工程岩体试验方法标准》及国际岩石力学学会推荐标准[18],对所取的粗糙砂岩岩芯进行切割,打磨,精细加工,制成100 mm×100 mm×100 mm的正方体试件。另外,为了避免摩擦效应[19]对真三轴条件下的砂岩渐进破坏力学行为演化规律产生影响,特将砂岩试件端面平整度控制在0.02 mm以内。同时,通过单轴压缩和巴西劈裂力学试验测得试验所用砂岩的单轴抗压强度为62.5 MPa,单轴抗拉强度为4.6 MPa,泊松比为0.201,弹性模量为14.99 GPa。从宏观看,砂岩色相为灰黑色,且其外表面光滑,无明显孔洞、节理及宏观裂隙。另外,砂岩在真三轴压缩腔室中所受各向作用力示意如图1所示。
1.2 试验设备
本试验采用试验仪器装置为重庆大学多功能真三轴流固耦合试验系统,又名真三轴固气耦合试验系统,相应的试验装置如图2所示,试验装置功能见表1。

图1 砂岩所受各向作用力示意
Fig.1 Diagram of the forces in all directions of sandstone
2 试验方案
本次试验设计的正交试验条件为:模拟深度梯度分别为1 000,1 500,2 000 m,应力路径分别为:① 路径1:σx单面卸载;② 路径2:σx双面卸载;③ 路径3:σx,σy同时单面卸载。

图2 多功能真三轴流固耦合系统
Fig.2 Multi-function true triaxial fluid-solid coupling system
表1 多功能真三轴流固耦合系统功能详情
Table 1 Function detail table of multifunctional true triaxial fluid-solid coupling system

性能参数功能1.试验试件适用尺寸:长宽高均为100 mm或长宽高均为200 mm方形试件2.压力阈值:2个方向的载荷阈值可达6 000 kN,另一方向载荷阈值可达4 000 kN;渗透压力阈值可达40 MPa3.具备3种新的加卸载控制方式可保证试件中心点不变4.系统采取两向刚性+一向柔性或刚性加载,尽量减小端部摩擦效应的影响1.不同应力路径下单轴、双轴、真三轴煤岩力学试验2.真三轴条件下的煤岩体水力压裂试验3.煤岩体渗透率测试
其中,依据公式[20-21]以及图3中世界各国地应力测量典型结果[22]:
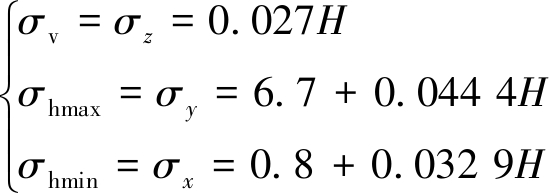
(1)
其中,σv为垂直应力;σhmax, σhmin,σh,av分别为最大水平主应力,最小水平主应力和平均水平主应力;H为埋深,σz,σy,σx分别为Z方向、Y方向以及X方向主应力。
可求得模拟深度1 000,1 500,2 000 m对应地层所存在的初始高地应力状态点三向应力值分别为σz=27 MPa,σy=51 MPa,σx=33 MPa;σz=40 MPa,σy=73 MPa,σx=50 MPa;σz=54 MPa,σy=95 MPa,σx=66 MPa。
整个试验对应的空间应力路径示意图如图4所示。整个试验的应力加卸载过程分为2个阶段,分别为O→A阶段:初始高地应力状态还原阶段,A→B阶段:真三轴各向应力加卸载阶段。3种应力路径下的O→A阶段应力加载程序是一致的。
具体的O→A阶段应力加载程序详细步骤如下:
(1)试验加载系统以2 kN/s的加载速率将三向应力以静水加压方式加载至各初始高地应力σz值。
(2)在步骤(1)基础上,保持各初始高地应力σz值不变,继续以2 kN/s的加载速率将σx,σy同步加载至各初始高地应力σx值。
(3)在步骤(2)基础上,保持各初始高地应力σz,σx值不变,继续以2 kN/s的加载速率将σy加载至各初始高地应力σy值。
(4)完成以上3步表明O→A阶段应力加载程序完成。
3种应力路径下的A→B阶段应力加载程序则是存在一定差异的,产生的差异便形成了不同的应力路径。具体的A→B阶段应力加卸载程序详细步骤:
(1)σx单面卸载路径:在O→A阶段完成的基础上,σz,σy,σx由试验加载系统同步控制,保持σy值不变,σx以卸载速率2 kN/s的应力控制方式进行单面卸载至0,σz则以加载速率0.003 mm/s的位移控制方式持续加载至砂岩失稳破坏。
(2)σx双面卸载路径:在O→A阶段完成的基础上,σz,σy,σx由试验加载系统同步控制,保持σy值不变,σx以卸载速率2 kN/s的应力控制方式进行双面卸载至0,σz则以加载速率0.003 mm/s的位移控制方式持续加载至砂岩失稳破坏。
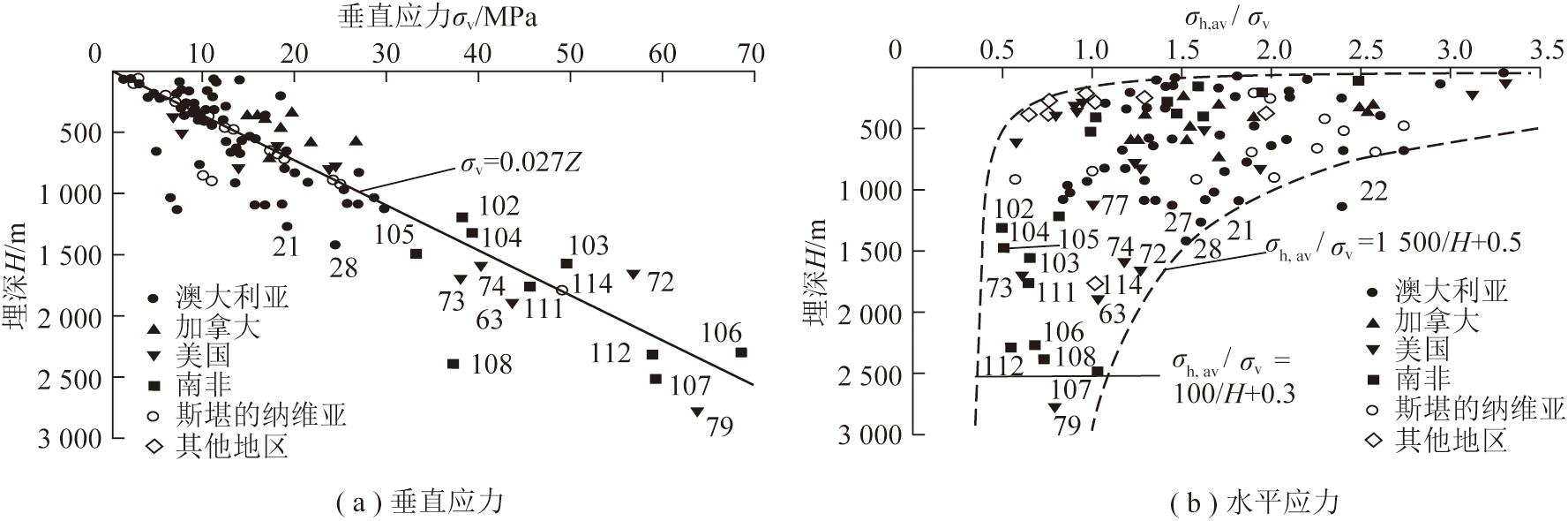
图3 世界各国地应力测量典型结果[22]
Fig.3 Typical in-situ stress measurement results in various countries around the world[22]
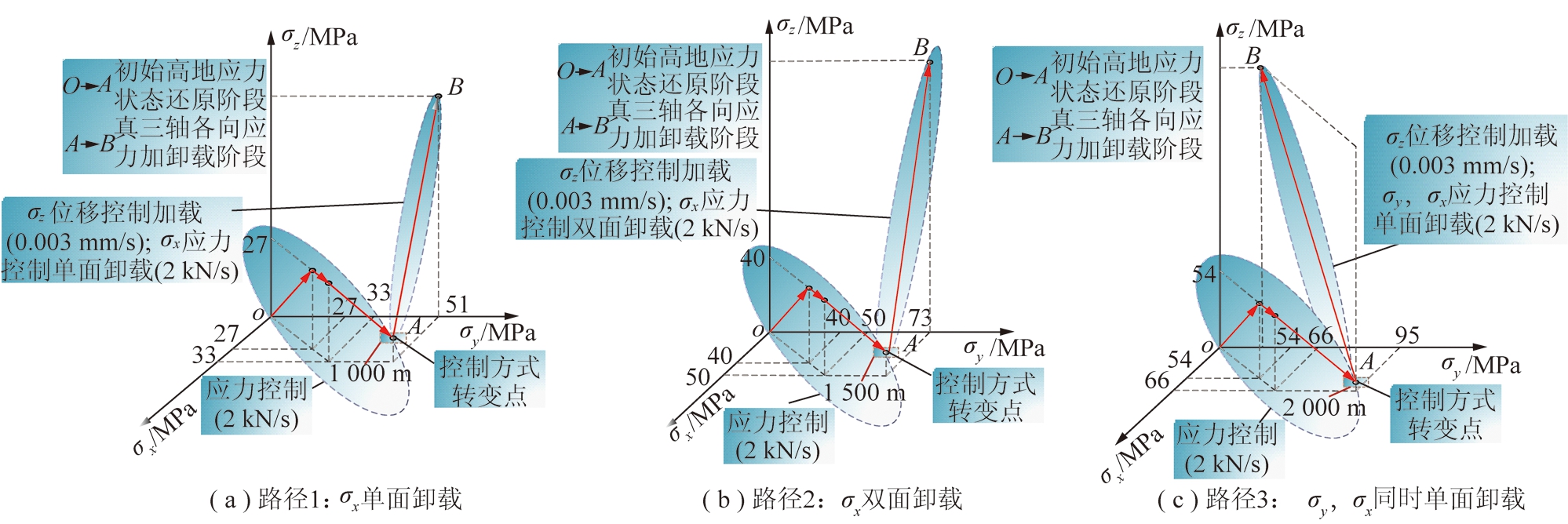
图4 真三轴条件下砂岩空间应力路径示意
Fig.4 Spacial stress paths of sandstone under true triaxial condition
(3)σx,σy同时单面卸载路径:在O→A阶段完成的基础上,σz,σy,σx由试验加载系统同步控制,σx,σy以卸载速率2 kN/s的应力控制方式进行相邻面单面卸载,σz则以加载速率0.003 mm/s的位移控制方式持续加载至砂岩失稳破坏。其中,由于σx明显低于σy,故σx卸载至0时,σy卸载至一定值。
3 试验结果分析
3.1 真三轴条件下砂岩变形全过程应力-应变曲线
如图5,6所示,不难发现,同一模拟深度、不同应力路径下的砂岩强度演化规律存在一定差异。在同一模拟深度、不同应力路径下,砂岩峰值强度演化特征为:σcf1>σcf2>σcf3,如模拟深度为1 500 m下的砂岩强度呈现出σcf1=161.11 MPa>σcf2=131.16 MPa>σcf3=127.28 MPa的演化特征,产生此特征的原因可能是砂岩在不同应力路径下的卸载程度不一造成的。卸载程度越大,砂岩表现出的峰值强度越小,这表明卸载程度会明显降低砂岩抵抗变形的能力。同时,这也与在地下工程巷道开挖时,一般选用单向独头掘进而不选取双向或相邻方向掘进巷道的事实相符。另外,从图5,6中不难发现,在同一应力路径、不同模拟深度下,真三轴条件下的砂岩强度存在明显的演化规律,具体表现在:砂岩峰值强度随模拟深度的增加而不断增大,深部效应显著。如路径1,模拟深度分别为2 000,1 500,1 000 m下的砂岩峰值强度分别为178.41,161.11,121.76 MPa。模拟深度对应的是深部地层存在的高地应力作用于煤岩体所表现出来的深部效应。深部地层埋深越大,存在此地层中的中硬及其以上的岩石在初始高地应力状态下越易表现出类硬岩性质,抵抗变形的能力便越强。同时,岩石内部也极易存储大量的弹性能,当深部巷道开挖卸压时,易导致岩爆,矿震等矿井灾害现象频发。这表明,深部效应可能是引发地下工程中事故频发的主要影响因素之一。为此,进行还原初始高地应力状态下的煤岩体力学试验,可为深部效应对煤岩体破坏机制影响规律的探索与获取提供一定的指导与参考。
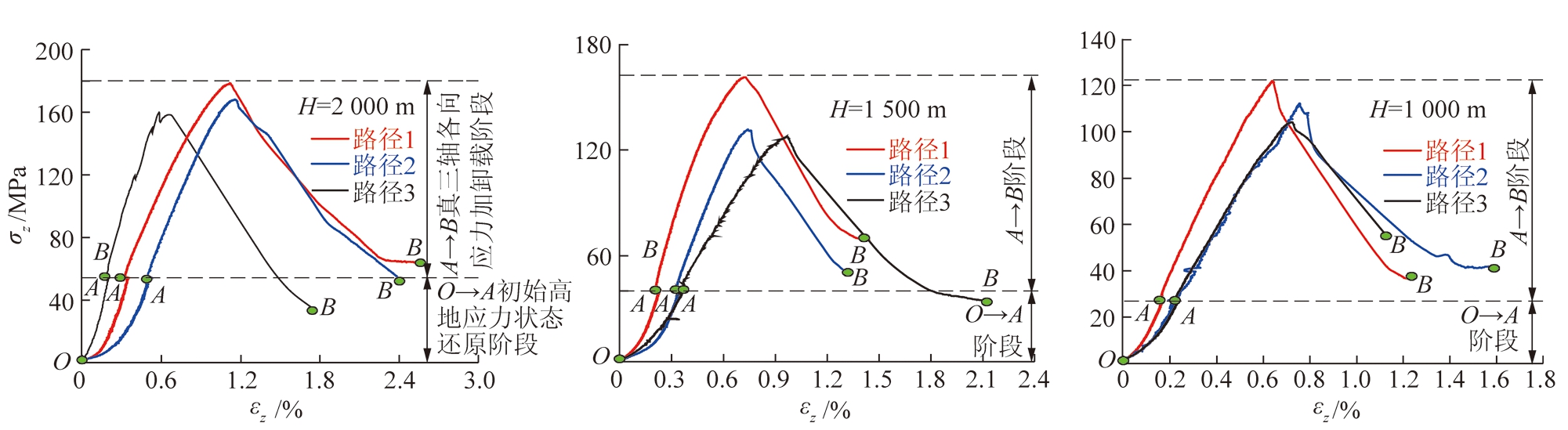
图5 不同模拟深度、不同应力路径下砂岩应力-应变曲线
Fig.5 Stress-strain curves of sandstone under different simulation depths and stress paths
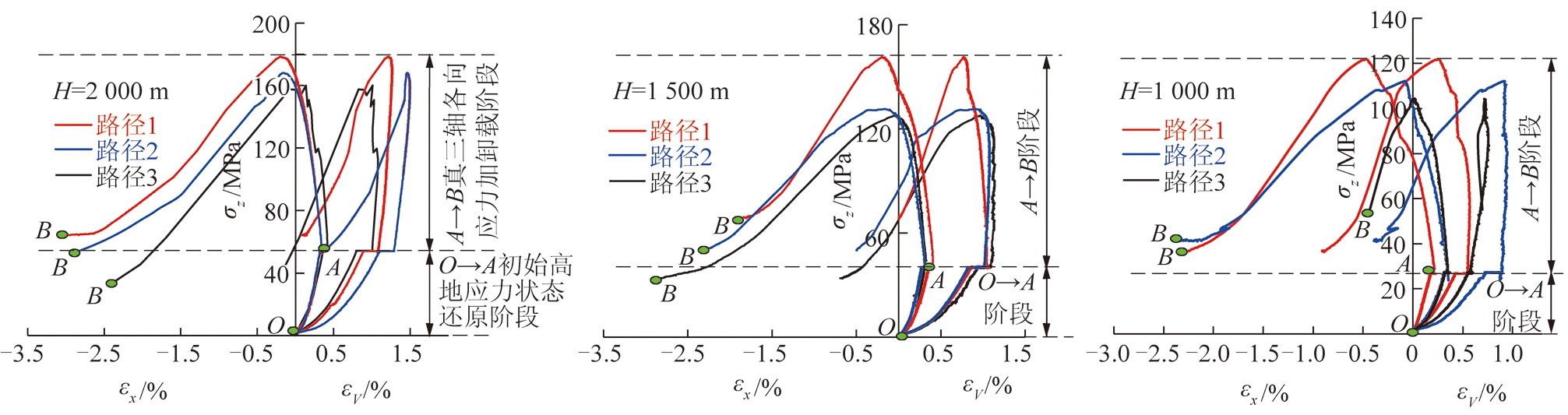
图6 不同模拟深度、不同应力路径下砂岩Z向主应变与体应变曲线
Fig.6 Z direction principal and volume strain curves of sandstone under different simulation depths and stress paths
另外,可以发现,各工况下的砂岩真三轴变形全过程应力-应变曲线外观存在一定的相似性,这主要是由于砂岩在受到外界场作用时产生的变形具有一定的记忆效应[23],但各工况下的砂岩应力-应变曲线与传统常规三轴力学试验所获得的应力-应变曲线有所不同,图5,6中的各砂岩变形全过程应力-应变曲线中均出现了长短不一的“平台”特征。产生此现象的原因是:在O→A初始高地应力状态还原阶段时,砂岩对应的模拟地层初始高地应力各向值不同,进而在还原初始高地应力时,系统需控制Z向主应力保持恒定,直至Y向主应力及X向主应力达到预设值才进行下一阶段加载,从而使砂岩变形全过程应力-应变曲线呈现出了一定长度的“平台”特征。
3.2 强度分界点的确定与阶段划分
砂岩在真三轴条件下的变形存在一定的自相似性[24],因此选取模拟深度为1 500 m,应力路径3下的砂岩变形全过程应力-应变曲线上的强度分界点进行确定及阶段划分。文献[25-29]提出了确定煤岩体全应力-应变曲线上闭合应力σcc与起裂应力σci的多种方法,如轴向最大应变差法确定闭合应力σcc,裂纹体积应变法确定损伤应力σcd及起裂应力σci,声发射法确定闭合应力σcc,起裂应力σci及损伤应力σcd等。本文则采用了轴向最大应变差法确定了闭合应力σcc,裂纹体积应变法确定了损伤应力σcd及起裂应力σci,并由此将砂岩A→B阶段的峰前应力-应变曲线划分为4个阶段:初始裂纹闭合阶段、线弹性变形阶段、稳定裂纹扩展及非稳定裂纹扩展阶段。另外,砂岩三轴加卸载过程产生的体积应变表达式为
εV=εz+εy+εx
(2)
砂岩三轴加卸载过程产生的体积应变可表示[30]为
![]()
(3)
Z,Y,X三向主应变表达式分别为
![]()
(4)
由广义胡克定律可得,Z,Y,X三向弹性主应变的表达式分别为
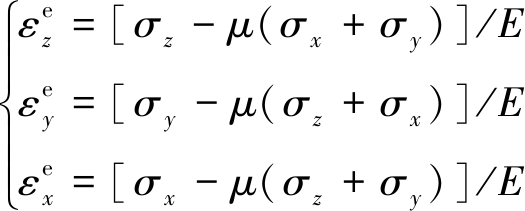
(5)
则砂岩三轴加卸载过程产生的体积弹性应变可表示为
![]()
(6)
联立式(4)~(6)可得,Z,Y,X三向塑性主应变的表达式分别为
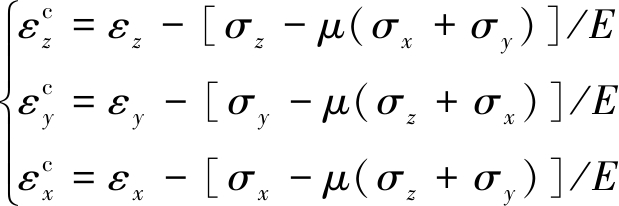
(7)
联立式(2)~(3),(6)~(7)可得,砂岩三轴加卸载过程产生的裂纹体积应变可表示为
![]() (8)
(8)
式中,εz,εy,εx,εV分别为砂岩在真三轴条件下产生的Z,Y,X三向主应变及体积应变;![]() 分别为砂岩在真三轴条件下产生的Z,Y,X三向弹性主应变及体积弹性应变;
分别为砂岩在真三轴条件下产生的Z,Y,X三向弹性主应变及体积弹性应变;![]() 分别为砂岩在真三轴条件下产生的Z,Y,X三向塑性主应变及裂纹体积应变;σz,σy,σx分别为砂岩在Z,Y,X三个方向上所受的主应力;E为砂岩弹性模量;μ为泊松比。
分别为砂岩在真三轴条件下产生的Z,Y,X三向塑性主应变及裂纹体积应变;σz,σy,σx分别为砂岩在Z,Y,X三个方向上所受的主应力;E为砂岩弹性模量;μ为泊松比。
根据上述计算以及图7给出的各强度分界点的确定及其阶段划分依据,可得到各工况下砂岩各分界点及其对应的各向应变值,各工况下砂岩强度特征点详情表见表2,变形特征点详情表见表3。

图7 真三轴条件下砂岩强度分界点确定与阶段划分依据示意
Fig.7 Basis for strength boundary point and stage division of sandstone under true triaxial condition
表2 各工况下砂岩强度特征点详情
Table 2 Detailed table of sandstone strength characteristic points under different working conditions
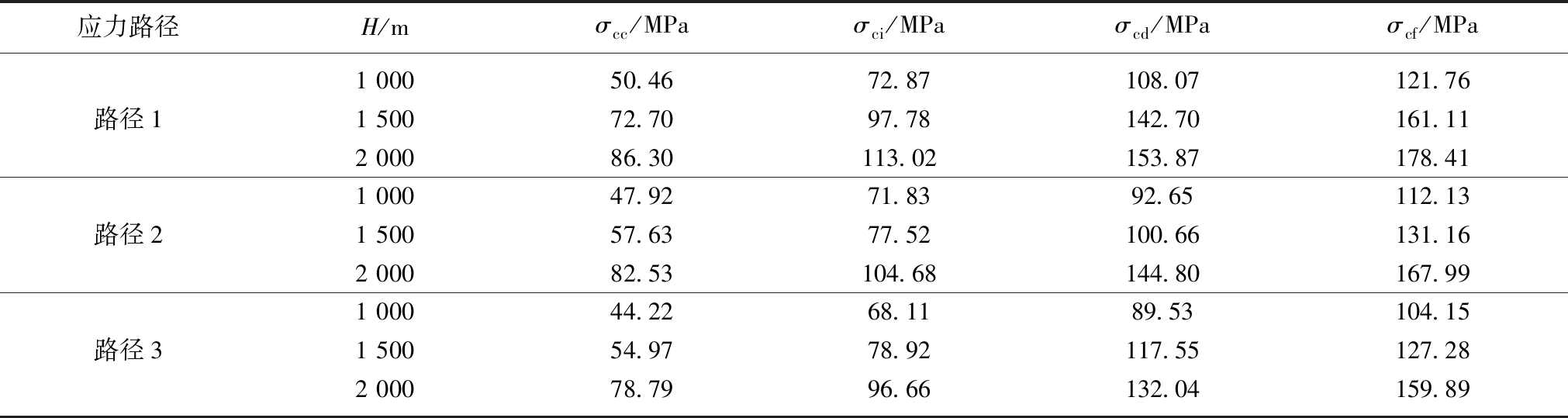
应力路径H/mσcc/MPaσci/MPaσcd/MPaσcf/MPa1 00050.4672.87108.07121.76路径11 50072.7097.78142.70161.112 00086.30113.02153.87178.411 00047.9271.8392.65112.13路径21 50057.6377.52100.66131.162 00082.53104.68144.80167.991 00044.2268.1189.53104.15路径31 50054.9778.92117.55127.282 00078.7996.66132.04159.89
3.3 砂岩Z向主应变渐进演变特征分析
如图8所示,同一模拟深度、不同应力路径下的砂岩Z向主应变渐进演变规律较好地响应了对应工况下的砂岩各强度分界点的演变特征,砂岩各强度分界点对应的Z向主应变均是随着Z向主应力的增大而不断增加。如模拟深度为1 000 m,路径1、路径2及路径3下的砂岩各强度分界点对应的Z向主应变渐进演变特征分别为2.53×10-3→3.57×10-3→5.45×10-3→6.39×10-3; 2.89×10-3→4.78×10-3→7.40×10-3→7.56×10-3;3.15×10-3→4.55×10-3→5.90×10-3→7.21×10-3,其他工况下的砂岩各强度分界点对应的Z向主应变均呈现出类似演变特征。然而,同一模拟深度、不同应力路径下的砂岩Z向主应变渐进演变程度还是存在一定差异的。产生此种差异的主要原因为:路径1和路径2下的砂岩主要是X向主应力卸载以及Z向主应力加载耦合作用导致砂岩发生变形破坏。根据格里菲斯强度理论[31],X向主应力的卸载意味着控制砂岩X方向变形的抑制作用会被减弱。同时,砂岩内部X方向因X向主应力卸载会产生的大量微裂隙,其微裂隙端部衍生出的集中拉应力会间接加快砂岩Z方向产生压缩变形。另外,Z向主应力的持续加载会直接加快砂岩Z方向产生压缩变形,Y,X方向产生膨胀变形;而路径3下的砂岩主要是Y向、X向主应力卸载及Z向主应力加载三向应力的耦合作用导致砂岩发生变形破坏。根据正交八面体强度理论[32],砂岩中的双剪应力蕴含有中主应力和静水应力效应,随之产生的Z向主应变的渐进演变程度自然而然地便与路径1和路径2的Z向主应变的渐进演变程度有所不同。
表3 各工况下砂岩变形特征点详情
Table 3 Detailed table of sandstone deformation characteristic points under different working conditions

路径H/mεzcc/10-3εycc/10-3εxcc/10-3εzci/10-3εyci/10-3εxci/10-3εzcd/10-3εycd/10-3εxcd/10-3εzcf/10-3εycf/10-3εxcf/10-31 0002.531.0902.0483.570.8601.055.450.76-2.376.390.87-4.64路径11 5002.896.0502.8393.71-2.9401.515.672.520.117.222.58-2.022 0004.68-2.2103.2606.094.6602.068.65-0.130.5811.202.82-1.951 0003.363.6702.1314.783.4930.167.402.870.547.562.43-0.78路径21 5003.823.8002.8504.613.8492.255.563.671.537.443.40-1.162 0006.154.1103.2207.244.5602.329.404.641.8611.604.65-1.591 0003.151.8433.2204.55-0.0032.665.90-0.121.777.21-0.070.10路径31 5005.043.2032.8305.862.6222.837.972.440.789.690.06-0.202 0002.864.3503.0103.104.3603.224.624.021.465.812.062.22
注:H为模拟深度,εjcc,εjci,εjcd,εjcf(j=z,y,x)分别表示强度分界点σcc,σci,σcd,σcf对应的Z,Y,X三向主应变。
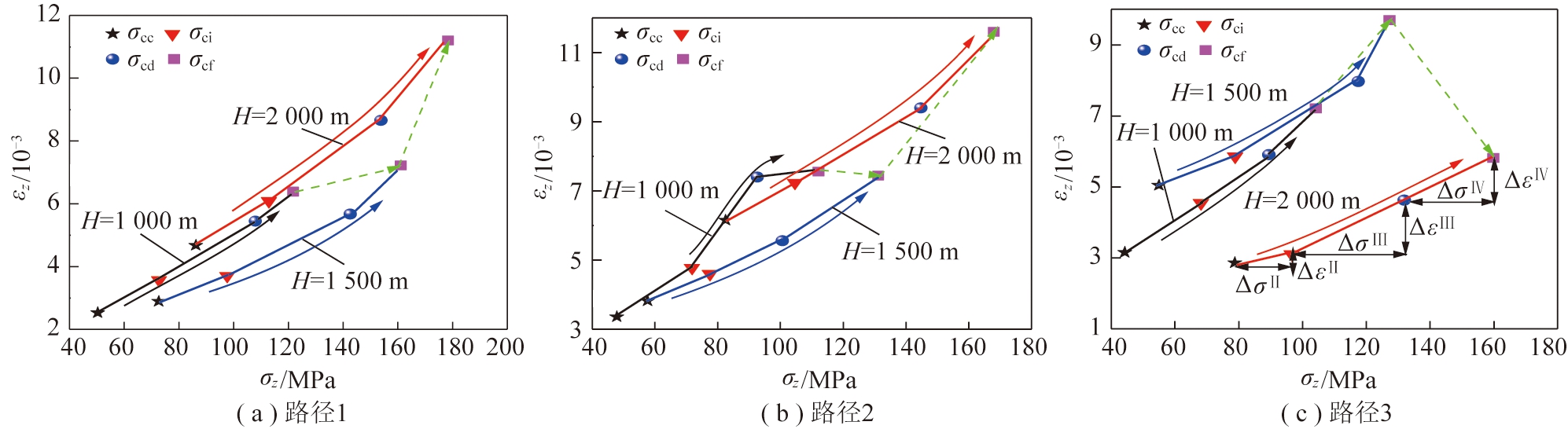
图8 不同应力路径下砂岩Z方向渐进变形特征
Fig.8 Z direction progressive deformation characteristics of sandstone under different stress paths
另外,路径1与路径2下的砂岩各强度分界点对应的Z向主应变均是随着模拟深度的增加而不断增大,深部效应显著;但路径3下的砂岩各强度分界点对应的Z向主应变渐进演变规律与路径1、路径2的渐进演变规律有所不同。随着模拟深度的增加,路径3下的砂岩各强度分界点对应的Z向主应变呈现出先增大后减小的渐变规律。如路径1,模拟深度为1 000,1 500,2 000 m下的砂岩各强度分界点对应的Z向主应变渐进演变特征分别为:εzcc:2.53×10-3→2.89×10-3→4.68×10-3,εzci:3.57×10-3→3.71×10-3→6.09×10-3,εzcd:5.45×10-3→5.67×10-3→8.65×10-3,εzcf:6.39×10-3→7.22×10-3→11.2×10-3;路径2,模拟深度为1 000,1 500,2 000 m下的砂岩各强度分界点对应的Z向主应变亦存在类似渐进演变特征。而路径3、模拟深度为1 000,1 500,2 000 m下的砂岩各强度分界点对应的Z向主应变渐进演变特征分别为:εzcc:3.15×10-3→5.04×10-3→2.86×10-3,εzci:4.55×10-3→5.86×10-3→3.10×10-3,εzcd:5.90×10-3→7.97×10-3→4.62×10-3,εzcf:7.21×10-3→9.69×10-3→5.81×10-3,渐进演变特征与路径1,2,模拟深度为1 000,1 500,2 000 m下的砂岩各强度分界点对应的Z向主应变渐进演变特征存在明显差异。
3.4 砂岩Y向主应变渐进演变特征分析
如图9所示,同一模拟深度、不同应力路径下的砂岩各强度分界点对应的Y向主应变渐进演变规律存在显著差异。随着Z向主应力的持续加载,Y向、X向主应力的不断卸载,同一模拟深度、路径3下的砂岩各强度分界点对应的Y向主应变也随之减小。如模拟深度为1 500 m、路径3下的砂岩各强度分界点对应的Y向主应变渐进演变特征为3.203×10-3→2.622×10-3→2.44×10-3→0.06×10-3,路径3、其他模拟深度下的砂岩各强度分界点对应的Y向主应变均呈现出类似演变特征。然而,路径1与路径2下的砂岩各强度分界点对应的Y向主应变渐进演变特征明显受深部效应的影响。模拟深度为1 000,1 500 m,路径1与路径2下的砂岩各强度分界点对应的Y向主应变随着Z向主应力的增大而减小,而模拟深度为2 000 m、路径1与路径2下的砂岩各强度分界点对应的Y向主应变却随着Z向主应力的增大而增大。如模拟深度为1 000 m、路径2下的砂岩各强度分界点对应的Y向主应变渐进演变特征3.67×10-3→3.493×10-3→2.87×10-3→2.43×10-3,而模拟深度为2 000 m、路径2下的砂岩各强度分界点对应的Y向主应变渐进演变特征为4.11×10-3→4.56×10-3→4.64×10-3→4.65×10-3。这表明,应力路径与深部效应均会显著影响砂岩Y向主应变的渐进演变规律。

图9 不同路径下砂岩Y方向渐进变形特征
Fig.9 Y direction progressive deformation characteristics of sandstone under different stress paths
另外,路径2与路径3下的砂岩各强度分界点对应的Y向主应变均是随着模拟深度的增加而不断增大,深部效应显著;但路径1下的砂岩各强度分界点对应的Y向主应变渐进演变规律与路径2、路径3的渐进演变规律有所不同。随着模拟深度的增加,路径1下的砂岩各强度分界点对应的Y向主应变呈现出先增大后减小的渐变规律。如路径3、模拟深度为1 000,1 500,2 000 m下的砂岩各强度分界点对应的Y向主应变渐进演变特征分别为εycc:1.843×10-3→3.203×10-3→4.35×10-3,εyci:-0.003×10-3→2.622×10-3→4.36×10-3,εycd:-0.12×10-3→2.44×10-3→4.02×10-3,εycf:-0.07×10-3→0.06×10-3→2.06×10-3;路径2、模拟深度为1 000,1 500,2 000 m下的砂岩各强度分界点对应的Y向主应变亦存在类似渐进演变特征。而路径1、模拟深度为1 000,1 500,2 000 m下的砂岩各强度分界点对应的Y向主应变渐进演变特征分别为εycc:1.09×10-3→6.05×10-3→-2.21×10-3,εyci:0.86×10-3→-2.94×10-3→4.66×10-3,εycd:0.76×10-3→2.52×10-3→-0.13×10-3,渐进演变特征与路径2,3,模拟深度为1 000,1 500,2 000 m下的砂岩各强度分界点对应的Y向主应变渐进演变特征存在明显差异。
3.5 砂岩X向主应变渐进演变特征分析
如图10所示,同一模拟深度、不同应力路径下的砂岩各强度分界点对应的X向主应变渐进演变规律大体一致,均是随着Z向主应力的增大,砂岩各强度分界点对应的X向主应变随之减小。产生此种规律的原因为:在O→A阶段,各路径下的砂岩Z,Y及X方向上均被压密。之后,各路径下的砂岩在A→B阶段均包含了X向主应力的卸载,从而使得各路径下的砂岩在此方向上的抑制作用被大大减弱,使砂岩在此方向上发生膨胀变形,进而导致各路径下的砂岩强度分界点对应的X向主应变呈现出随着Z向主应力的增大而减小的特征。如模拟深度为1 500 m、路径1,路径2及路径3下的砂岩各强度分界点对应的X向主应变渐进演变特征分别为2.839×10-3→1.51×10-3→0.11×10-3→-2.02×10-3;2.85×10-3→2.32×10-3→1.53×10-3→-1.16×10-3;2.83×10-3→2.83×10-3→0.78×10-3→-0.20×10-3;其他模拟深度下的砂岩各强度分界点对应的X向主应变均呈现出类似演变特征。
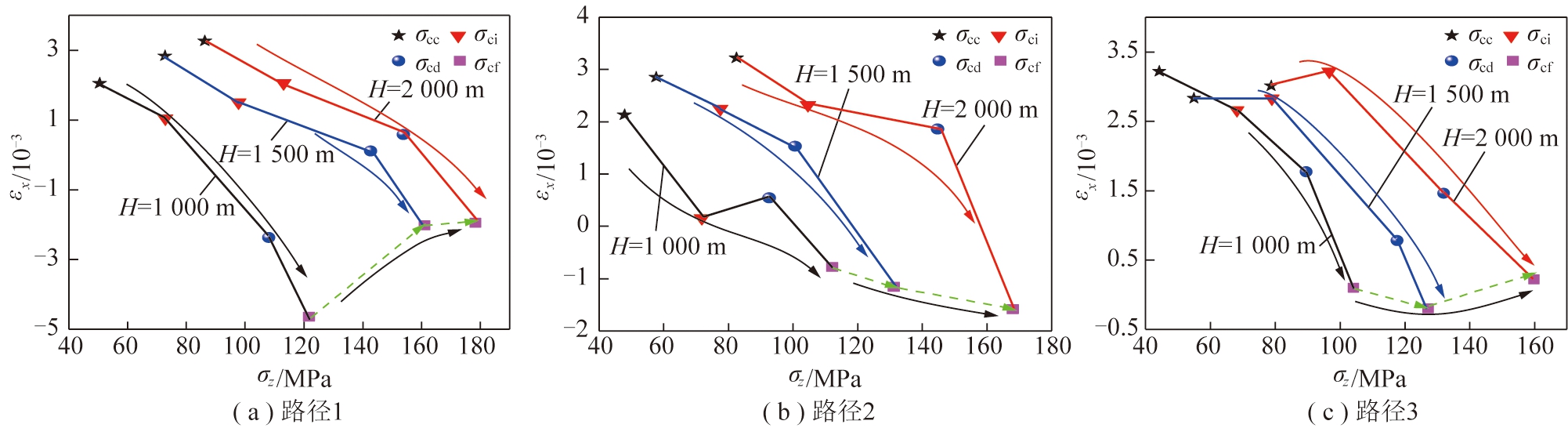
图10 不同路径下砂岩X方向渐进变形特征
Fig.10 X direction progressive deformation characteristics of sandstone under different stress paths
另外,各应力路径下的砂岩强度分界点对应的X向主应变均是随着模拟深度的增加而增大,深部效应显著。如路径1、模拟深度为1 000,1 500,2 000 m下的砂岩各强度分界点对应的X向主应变渐进演变特征分别为εxcc:2.048×10-3→2.839×10-3→3.26×10-3,εxci:1.05×10-3→1.51×10-3→2.06×10-3,εxcd:-2.37×10-3→0.11×10-3→0.58×10-3,εxcf:-4.64×10-3→-2.02×10-3→-1.95×10-3;路径1与路径2、模拟深度为1 000,1 500,2 000 m下的砂岩各强度分界点对应的X向主应变亦存在类似渐进演变特征。
4 结 论
(1)在同一模拟深度、不同应力路径下,砂岩峰值强度演化特征为:σcf1>σcf2>σcf3;同一应力路径、不同模拟深度下的砂岩峰值强度随模拟深度的增加而不断增大。
(2)同一模拟深度、不同应力路径下的砂岩Z向主应变随着Z向主应力的增大而不断增加;但同一模拟深度、不同应力路径下的砂岩Z向主应变渐进演变程度却存在一定的差异。
(3)路径2,3下的砂岩Y向主应变均是随着模拟深度的增加而不断增大,深部效应显著;随着模拟深度的增加,路径1下的砂岩Y向主应变呈现出先增大后减小的渐变规律。这表明,应力路径与深部效应均会显著影响砂岩Y向主应变的渐进演变规律。
(4)同一模拟深度、不同应力路径下的砂岩X向主应变均是随着Z向主应力的增大而不断减小;不同应力路径下的砂岩X向主应变均是随着模拟深度的增加而不断增大,深部效应显著。
[1] 袁亮.破解深部煤炭开采重大科技难题的思考与建议[J].科技导报,2016,34(2):1.
YUAN Liang.Thoughts and suggestions on solving the major scientific and technological problems of deep coal mining[J].Science and Technology Review,2016,34(2):1.
[2] LI Z L,WANG L G,LU Y L,et al.Experimental investigation on true triaxial deformation and progressive damage behaviour of sandstone[J].Scientific Reports,2019,3386(9):1-19.
[3] 袁越,王卫军,袁超,等.深部矿井动压回采巷道围岩大变形破坏机理[J].煤炭学报,2016,41(12):2940-2950.
YUAN Yue,WANG Weijun YUAN Chao,et al.Large deformation failure mechanism of surrounding rock for gateroad under dynamic pressure in deep coal mine[J].Journal of China Coal Society,2016,41(12):2940-2950.
[4] 周宏伟,谢和平,左建平.深部高地应力下岩石力学行为研究进展[J].力学进展,2005(1):91-99.
ZHOU Hongwei,XIE Heping,ZUO Jianping.Developments in researchs on mechanical behaviors of rocks under the condition of high ground pressure in the depths[J].Advances in Mechanics,2005(1):91-99.
[5] 陈景涛,冯夏庭.高地应力下岩石的真三轴试验研究[J].岩石力学与工程学报,2006,25(8):1537-1543.
CHEN Jingtao,FENG Xiating.True triaxial experimental study on rock with high geostress[J].Chinese Journal of Rock Mechanics and Engneering,2006,25(8):1537-1543.
[6] VACHAPARAMPIL A,GHASSEMI A.Failure characteristics of three shales under true-triaxial compression[J].International Journal of Rock Mechanics and Mining Sciences,2017,100(12):151-159.
[7] ZHAO J,FENG X T,ZHANG X W,et al.Time-dependent behaviour and modeling of Jinping marble under true triaxial compression[J].International Journal of Rock Mechanics and Mining Sciences,2018,110(8):218-230.
[8] STRAHLER A,W.STUEDLEIN A,W.ARDUINO P.Stress-strain response and dilatancy of sandy gravel in triaxial compression and plane strain[J].Journal Geotechnical and Geoenvironmental Engineering,2016,142(4):1-11.
[9] LU G M,FENG X T,LI Y H,et al.The microwave-induced fracturing of hard rock[J].Rock Mechanics and Rock Engineering,2019,8:1-16.
[10] 尹光志,刘玉冰,李铭辉,等.真三轴加卸载应力路径对原煤力学特性及渗透率影响[J].煤炭学报,2018,43(1):131-136.
YIN Guangzhi,LIU Yubing,LI Minghui,et al.Influence of true triaxial loading-unloading stress paths on mechanical property and permeability of coal[J].Journal of China Coal Society,2018,43(1):131-136.
[11] 尹光志,马波,刘超,等.真三轴应力条件下加卸荷速率对砂岩力学特性与能量特征的影响[J].煤炭学报,2019,44(2):454-462.
YIN Guangzhi,MA Bo,LIU Chao,et al.Effect of loading and unloading rates on mechanical properties and energy characteristics of sandstone under true triaxial stress[J].Journal of China Coal Society,2019,44(2):454-462.
[12] 尹光志,李星,鲁俊,等.真三轴应力条件下层状复合岩石破坏准则[J].岩石力学与工程学报,2017,36(2):261-269.
YIN Guangzhi,LI Xing,LU Jun,et al.A failure criterion for layered composite rock under true triaxial stress conditions[J].Chinese Journal of Rock Mechanics and Engineering,2017,36(2):261-269.
[13] LI X B,DU K,LI D Y.True triaxial strength and failure modes of cubic rock specimens with unloading the minor principal stress[J].Rock Mechanics and Rock Engineering,2015,48(6):2185-2196.
[14] ZUO J P,LI H T,XIE H P,et al.A nonlinear strength criterion for rock-like materials based on fracture mechanics[J].International Journal of Rock Mechanics and Mining Sciences,2008,45(4):594-599.
[15] ZHANG Q,LI C,QUAN X W,et al.New true-triaxial rock stre-ngth criteria considering intrinsic material characteristics[J].Acta Mechanica Sinica,2018,34(1):130-142.
[16] ZHENG Z,FENG X T,ZHANG X W,et al.Residual strength characteristics of CJPL marble under true triaxial compression[J].Rock Mechanics and Rock Engineering,2019,52(4):1247-1256.
[17] HOEK E,MARTIN C.D.Fracture initiation and propagation in intact rock-A review[J].Journal of Rock Mechanics and Geotechnical Engineering,2014,6(4):287-300.
[18] 郑虹,冯夏庭,陈祖煜.岩石力学室内试验ISRM建议方法的标准化和数字化[J].岩石力学与工程学报,2010,29(12):2456-2468.
ZHENG Hong,FENG Xiating,CHEN Zuyu.Standardization and digitization of recommended methods for indoor test ISRM rock mechanics[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(12):2456-2468.
[19] 范鹏贤,李颖,赵跃堂,等.茂木式真三轴试验机的端部摩擦效应[J].岩石力学与工程学报,2017,36(11):2720-2730.
FAN Pengxian,LI Ying,ZHAO Yuetang,et al.End friction effect of Mogi type of true-triaxial test apparatus[J].Chinese Journal of Rock Mechanics and Engineering,2017,36(11):2720-2730.
[20] 沈明荣,陈建峰.岩体力学[M].上海:同济大学出版社,2006:1-250.
[21] 司雪峰,宫凤强,罗勇,等.深部三维圆形洞室岩爆过程的模拟试验[J].岩土力学,2018,39(2):621-634.
SI Xuefeng,GONG Fengqiang,LUO Yong,et al.Experimental simultion on rockburst process of deep three-dimensional circular cavern[J].Rock and Soil Mechanics,2018,39(2):621-634.
[22] BROWN E T,HOEK E.Trends in relationships between measured in-situ stresses and depth[J].International Journal of Rock Mechanics and Mining Sciences,1978,15(4):211-215.
[23] 王海军,汤雷,任旭华,等.低应力区岩石变形记忆效应形成机制及失忆性[J].岩土力学,2014,35(4):1007-1014.
WANG Haijun,TANG Lei,REN Xuhua,et al.Mechanism of rock deformation memory effect in low stress region and its memory fading[J].Rock and Soil Mechanics,2014,35(4):1007-1014.
[24] 曹平,罗磊,刘涛影,等.岩石节理面粗糙度的分形效应与试件尺寸影响分析[J].科技导报,2011,29(24):57-61.
CAO Ping,LUO Lei,LIU Taoying,et al.Analysis of the fractal and sample size effects of the rock joint surface roughness[J].Science and Technology Review,2011,29(24):57-61.
[25] 汪斌,朱杰兵,严鹏,等.大理岩损伤强度的识别及基于损伤控制的参数演化规律[J].岩石力学与工程学报,2012,31(S2):3967-3973.
WANG Bin,ZHU Jiebing,YAN Peng,et al.Identification of damage strength of marble and parameter evolution law based on damage control[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(S2):3967-3973.
[26] RANJITH P,JASINGE D,CHOI S K,et al.The effect of CO2 saturation on mechanical properties of Australian black coal using acoustic emision[J].Fuel,2010,89(8):2110-2117.
[27] NICKSIAR M,MARTIN C D.Evaluation of methods for determining crack Initiation in compression tests on low-porosity rocks[J].Rock Mechanics and Rock Engineering,2012,45(4):607-617.
[28] MARTIN C D,CHRISTIANSSON R.Estimating the potential for spalling around a deep nuclear waste repository in crystalline rock[J].International Journal of Rock Mechanics and Mining Sciences,2009,46(2):219-228.
[29] 陈世万,杨春和,王贵宾,等.不同围压下花岗岩σcc,σci和σcd的确定[J].东北大学学报(自然科学版),2016,37(12):1789-1793.
CHEN Shiwan,YANG Chunhe,WANG Guibing,et al.Experimental study on the determination method of σcc,σci and σcd for granite under different confining pressures[J].Journal of Northeastern University (Natural Science),2016,37(12):1789-1793.
[30] 刘先珊,王科,许明.低渗储层砂岩渗流-应力-损伤渐裂过程的渗透特性演化研究[J].岩土工程学报,2018,40(9):1584-1592.
LIU Xianshan,WANG Ke,XU Ming.Study on permeability characteristics of sandstone seepage-stress-damage gradient process in low permeability reservoirs[J].Journal of Geotechnical Engineering,2018,40(9):1584-1592.
[31] 郑安兴,罗先启.压剪应力状态下岩石复合型断裂判据的研究[J].岩土力学,2015,36(7):1892-1898.
ZHENG An’xing,LUO Xianqi.Research on combined fracture criterion of rock under compression-shear stress[J].Rock and Soil Mechanics,2015,36(7):1892-1898.
[32] 黄辉,杨正浩,段文付,等.正交八面体应力空间的强度理论综述[J].武汉轻工大学学报,2007,26(4):97-101.
HUANG Hui,YANG Zhenghao,DUAN Wenfu,et al.Overview on strength theory of orthogonal octahedron stress space[J].Journal of Wuhan Polytechnic University,2007,26(4):97-101.
