采场覆岩变形规律一直是采矿工程研究的核心内容[1-2]。巨厚复合关键层作为一种特殊的含煤地层结构,采后易形成大面积悬空,长步距破断,导致工作面矿压显现异常剧烈,甚至会引发不同程度的矿震和动力灾害事故[3-6]。因而掌握具体采动条件下巨厚复合关键层的运动形式与破断规律,是煤矿安全生产的重要保障。
国内外学者在研究采场巨厚复合关键层变形规律方面取得了一定的成果。在理论研究方面,茅献彪等[7]分析了多层坚硬岩层的复合效应,利用有限单元方法计算了复合关键层的破断跨距;侯忠杰[8]推导出组合关键层承受载荷、弹性模量和破断跨距的计算公式;史红等[9]建立了两端嵌固梁力学模型,提出了大厚度坚硬岩层的3种破坏方式的力学判据;姜福兴等[10]以水平应力作用下弹性矩形薄板为力学模型,研究了高位厚硬顶板极限垮落步距;蒋金泉等[11]建立了高位硬厚岩层的Winkler基础正交梁力学模型,推导出特征弯矩及其位置的计算公式。在试验研究方面,许家林等[12]利用物理模型试验研究了松散承压含水层对复合关键层的载荷传递规律及破断影响机制;杨培举等[13]运用理论分析与相似材料试验研究了巨厚关键层的变形规律和支承压力分布特征;魏振全[14]采用数值模拟方法研究了厚硬关键层不同赋存条件下采动应力变异特征;张培鹏等[15]研究了上覆单层和双层高位硬厚岩浆岩结构及其演化特征,分析了典型采动覆岩结构致灾机理;笔者[16-17]将分布式光纤传感技术应用于模型试验,提出用光纤频移平均变化度表征巨厚岩层下开采覆岩岩层变形、来压及其变化情况。但是,采场巨厚复合关键层厚度大、与煤层间距大,垮落步距大,传统弹性薄板理论研究其破断规律与工程实际存在较大误差;另外,在立体物理模拟实验中也未能建立有效的实时监测系统对巨厚复合关键层移动变形动态演化规律进行研究。
笔者基于符拉索夫(Власов)厚板模型,结合巨厚复合关键层与煤层空间位置关系,得到了巨厚复合关键层极限垮落步距计算方法。实验室中构建大型三维立体模型,利用分布式光纤传感技术开展巨厚复合关键层运移演化规律研究,并将工作面1,2覆岩移动变形数据对比分析,揭示巨厚复合关键层运动与动压显现的关系,为采场巨厚复合关键层破断距预测以及矿山动力灾害预测提供理论依据。
1 巨厚复合岩层破断距的理论计算
1.1 力学模型的建立
在经典力学理论中,通常将板的厚度与板中面最小尺寸之比为1/7~1/5的板视为薄板,将比值大于1/4的板视为厚板[18]。因此根据采场上覆岩层厚度与跨度之比可将其简化为薄板和厚板两种模型。厚岩层破断规律的研究,由于自身重力影响和板端剪切变形已不能忽略,因而采用厚板理论分析其破断规律更加合理。建立如图1(a)所示坐标系,将厚岩层简化为四边固支的矩形厚板,定义厚板长边为a,短边为b。随着工作面的推进,厚岩层的长、短边中点先后形成张拉裂隙而进入塑性变形状态,而后分别扩展形成塑性铰,最终4个边界全部成为可以自动转动的铰支边界,边界条件由固支变成了简支,四边固支厚板演化为四边简支厚板,如图1(b)所示。此时,厚岩层只是边界约束减弱了,整体性并没有破坏。
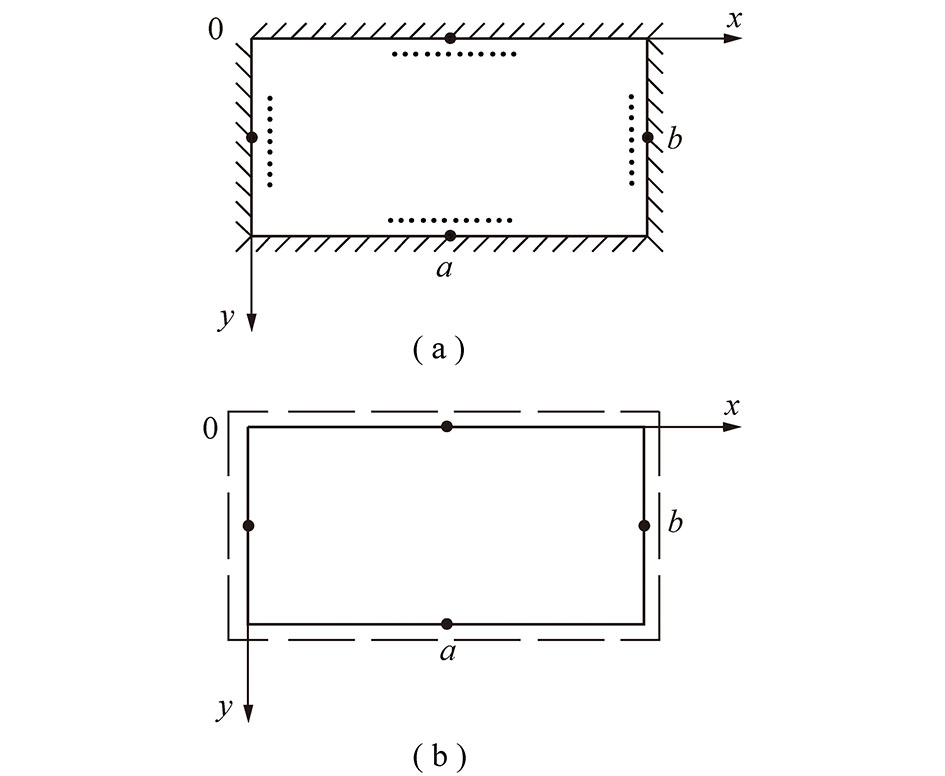
图1 四边固支及简支板模型
Fig.1 Model of four-side fixed and simply supported plates
根据厚板理论[19],得到弯曲微分方程组为
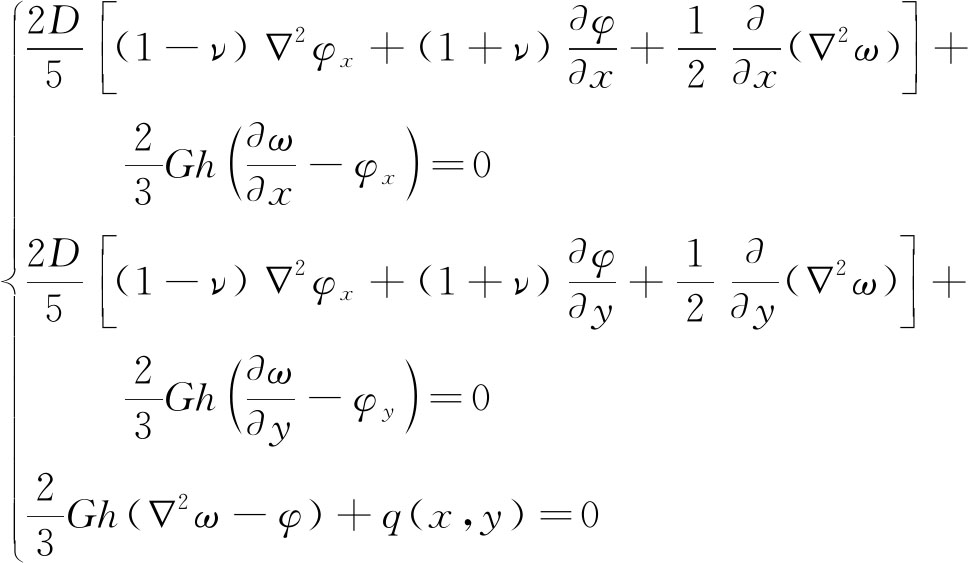
(1)
用挠度和转角表示内力和力矩的表达式为
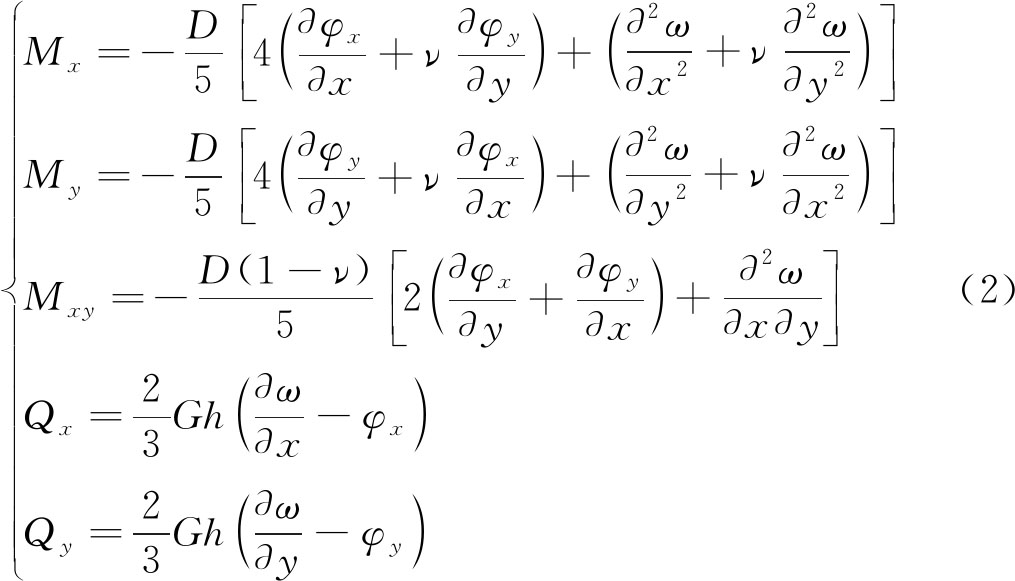
其中, 2为拉普拉斯算子;ν为泊松比;h为板厚度;ω为挠度;φ为横向剪应变;φx,φy分别为x=const和y=const两截面的转角;D为抗弯曲刚度,D=Eh3/[12(1-ν2)];G为剪切模量,G=E/[2(1+ν)];q(x,y)为横向载荷;Mx为x方向的弯矩;My为y方向的弯矩;Mxy为扭矩;Qx为x方向的横向剪力;Qy为y方向的横向剪力。图1(b)为四边简支矩形厚板,其边界条件为当x=0,和x=a处,ω=0,φy=0,Mx=0;当y=0,和y=a处,ω=0,φx=0,My=0。
2为拉普拉斯算子;ν为泊松比;h为板厚度;ω为挠度;φ为横向剪应变;φx,φy分别为x=const和y=const两截面的转角;D为抗弯曲刚度,D=Eh3/[12(1-ν2)];G为剪切模量,G=E/[2(1+ν)];q(x,y)为横向载荷;Mx为x方向的弯矩;My为y方向的弯矩;Mxy为扭矩;Qx为x方向的横向剪力;Qy为y方向的横向剪力。图1(b)为四边简支矩形厚板,其边界条件为当x=0,和x=a处,ω=0,φy=0,Mx=0;当y=0,和y=a处,ω=0,φx=0,My=0。
设挠度和转角等位移函数分别为
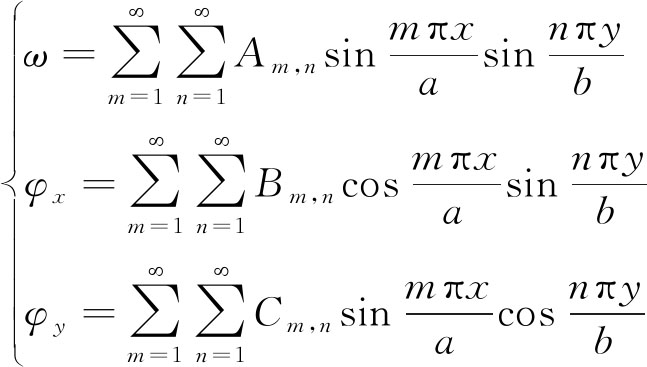
(3)
式中,Am,n,Bm,n,Cm,n为挠度和转角等位移函数的系数,由微分方程确定;m,n为1,2,3,……。
同样将横向荷载也展开成双三角级数得
![]()
(4)
式中,qm,n为双三角级数的系数。
将式(3),(4)代入式(1),联立方程转化得到Am,n,Bm,n,Cm,n分别为
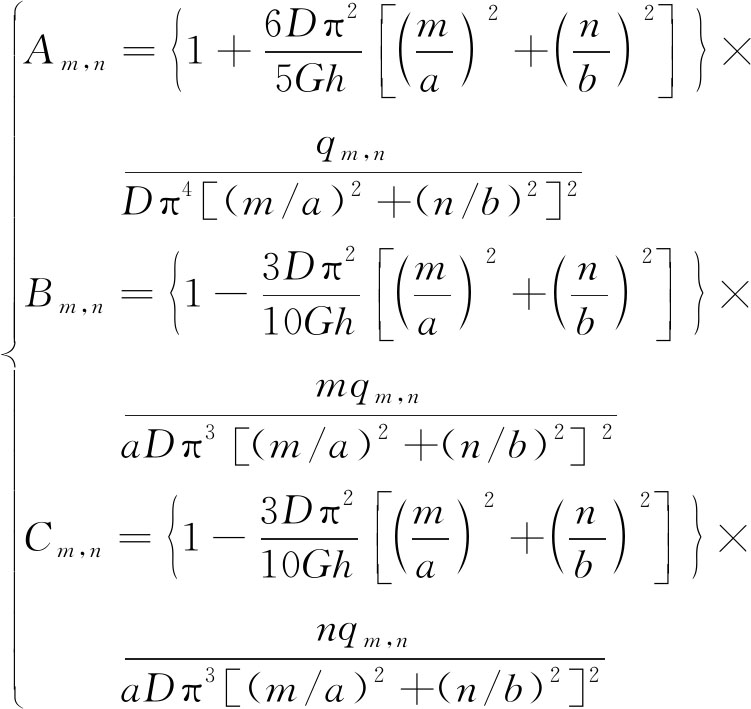
(5)
因式(3),(4)中的双三角级数收敛很快,在确保一定精度下,为简化计算可取m=n=1,联立式(2)~(5)求解板的最大力矩为
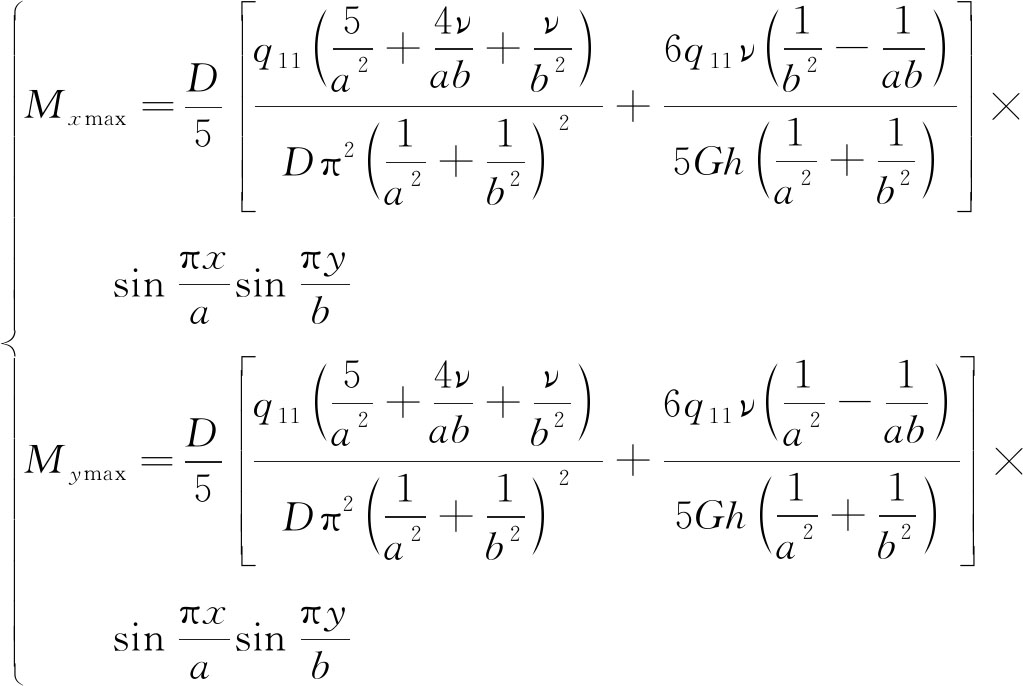
(6)
因Mx和My在结构上良好的轮换性,故只需对其中一个方向进行分析即可。显然,Mx,My都在x=a/2和y=b/2处有最大值,则
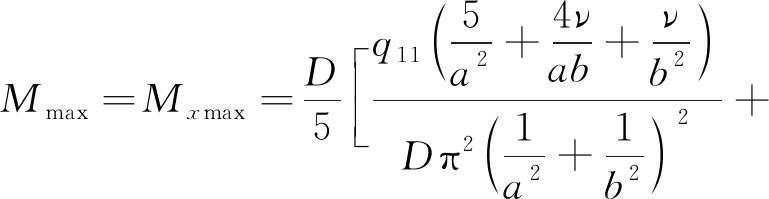
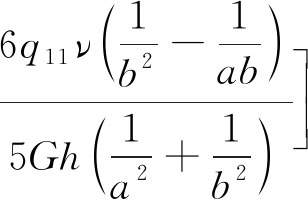
(7)
式中,q11为施加于厚岩层的单位面积载荷。
由弯矩与应力关系得
![]()
(8)
式中,σt为抗拉强度。
将式(8)代入式(7),可求得厚岩层初次破裂步距a的一元四次方程为
c1a4+c2a3+c3a2+c4a+c5=0
(9)
式中,c1,c2,c3,c4,c5均为常数项。
采空区覆岩变形是按照一定角度由下向上发展,由于高位岩层与煤层间距较大,因此高位岩层跨度与工作面推进长度相差较大,为准确得到高位岩层的破断步距,必须考虑高位岩层跨度与工作面推进长度2者之间的关系,如图2所示。
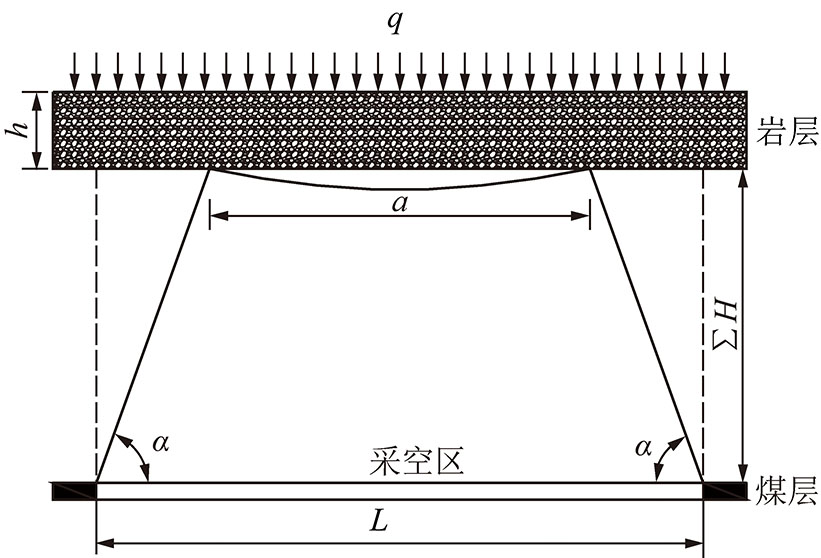
图2 岩层悬空跨度与工作面长度关系
Fig.2 Relation between thick hard strata suspension span and working face length
则高位岩层破断时岩层跨度a与工作面推进长度L的关系为
L=a+2∑Hcot α
(10)
式中,L为推进长度,m;∑H为岩层与煤层间距,m;α为垮落角,本条件取值为65°~80°。
1.2 计算条件及结果
根据岩层控制的关键层理论,利用关键层判别软件(KSPB)对千秋煤矿的关键层及位置进行判别,得出覆岩中3个厚硬岩层构成复合关键层。
(1)亚关键层1。细砂岩,位于上覆岩层112 m位置处,厚度h=40 m,ν=0.32,σt=6.5 MPa。取上覆载荷q11=2.59 MPa,工作面长度b=320 m,由式(9),(10)可得初次破断距L1≈415 m。
(2)亚关键层2。下组巨厚砾岩,位于覆岩225 m位置处,h=160 m,ν=0.28,σt=5.0 MPa。取q11=4.21 MPa,b=320 m,得出L2≈772 m。
(3)主关键层。上组巨厚砾岩,位于覆岩386 m位置处,h=250 m,ν=0.28,σt=5.0 MPa。取q11=10.25 MPa,b=320 m,得出L3≈1 253 m。
2 物理相似模拟试验
2.1 工程地质概况
千秋煤矿生产能力为210 万t/a,地处河南省义马市南部。矿井主要可采煤层为2号煤,平均厚度约24.0 m,倾角为3°~11°,平均埋深约800 m,开采方式为走向长壁综放开采,采用全部垮落法管理顶板。上覆岩层总厚度约806 m,存在3层厚硬岩层共同构成该矿井复合关键层。细砂岩(亚关键层1)厚度约为40 m,距煤层上方约112 m;在煤层上方225~636 m处发育有段高约410 m的巨厚砾岩,砾岩中部存在约1 m的软弱夹层将其分为上下两组,其中下组砾岩(亚关键层2)厚度约160 m,上组砾岩(主关键层)厚度约250 m。砾岩成份以石英砂岩和灰岩为主,其次为火成岩,砾石大小不一,磨圆较好,球度一般,泥和钙质胶结,以泥质为主。
2.2 相似常数
根据研究区域地质条件及试验目的,结合相似模拟试验条件,确定选用长×宽×高为3 600 mm×2 000 mm×2 000 mm的三维立体模型架。模拟试验相似参数见表1。
表1 主要相似参数
Table 1 Main similar parameters

名称参数几何相似比1∶400容重相似比1∶1.6应力相似比1∶640位移相似比1∶400时间相似比1∶20
2.3 模型铺装
三维立体模型铺设时,为了便于煤层开采,设计选用60 mm×40 mm的矩形镀锌方管替代煤层,每次抽出1根方管,即代表模拟煤层开挖1次。考虑到模型高度受限,将新生界岩层置换成模型顶部荷载,经换算约为2.5 t,加载方式为沙袋有序堆积在模型顶部。模型分为2个工作面开采,倾向长度800 mm,走向长度2 400 mm,在走向、倾向方向上各留设600,200 mm的煤柱,作为边界条件。铺装完成的模型如图3所示。
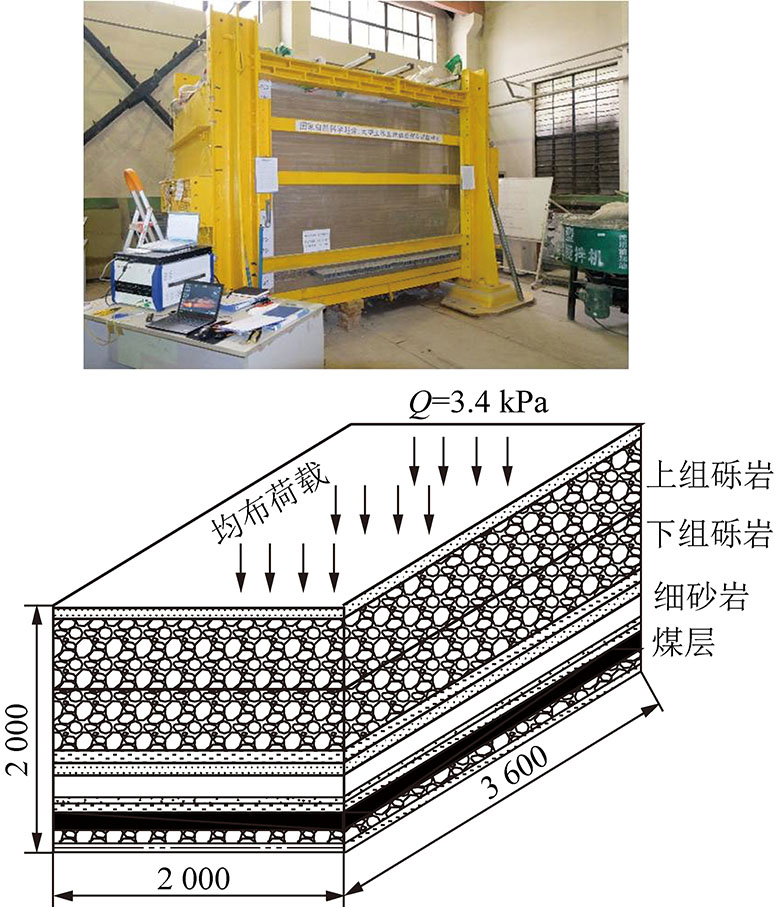
图3 三维模型开采设计
Fig.3 Mining design of three-dimensional model
2.4 试验测试系统
2.4.1 压力传感器
将已标定的CL-YB-114型压力传感器预埋在煤层底板中,利用32路数据采集仪实时监测开采过程中工作面前后支承压力变化规律。压力传感器分为2组,分别沿工作面1,2煤层走向进行布设,从开切眼开始至终采线终止,每组布设48个传感器,编号分别为1~48号和49~96号。在压力传感器上方铺设了约20 mm厚的相似材料,以避免煤层开挖过程中对压力传感器产生干扰,影响采集数据的准确性。
2.4.2 内部位移测量装置
内部位移测量装置原理为预埋在岩层中的位移测点与岩层同步变形,当测点位移发生变化,拉动渔线带动读数刻度盘旋转,刻度盘转角产生变化。立体模型中,分别在工作面1,2覆岩中沿走向布置3套测量装置(分别距离开切眼600,1 200,1 800 mm),每套测量装置上的3个测点分别位于3个关键层的中部。
2.4.3 分布式传感光纤
为了全面监测复合关键层移动变形规律,在试验模型中布设了网式传感光纤监测系统。光纤铺设方式采用预埋式,通过固定卡尺每隔一定距离固定光纤,保证光纤平直埋设在岩层中部,并施加一定的预紧力,然后装入相似材料,用工具捣压夯实。光纤分为两组,分别沿工作面1,2走向方向进行水平布设,每组3条光纤分别位于工作面上方亚关键层一、亚关键层二和主关键层的中部,共6条,分别命名为V11,V12,V13和V21,V22,V23,具体参数见表2。
表2 水平光纤布置参数
Table 2 Horizontal optical fiber layout Parameters mm

布置参数V11V12V13V21V22V23走向长度3 6003 6003 6003 6003 6003 600边界位置600600600600600600布设高度4608601 3804608601 380
整套监测系统由NBX-6055光纳仪、CL-YB-114型压力传感器、32路数据采集仪、内部位移测量装置、计算机、φ900 μm普通单模紧套光纤组成,如图4所示。
3 岩层变形的光纤响应特性
为了便于监测岩层变形,将传感光纤埋设于岩层中,光纤与岩层间为直接全面接触,两者间无黏结材料,无空隙。同时对岩层-光纤的力学结构进行如下简化:① 岩层-光纤的变形各向同性;② 纤芯与包层的力学特性相同;③ 不考虑岩层对光纤径向的挤压影响;④ 光纤在模型两端固定约束,并施加一定的预应力。
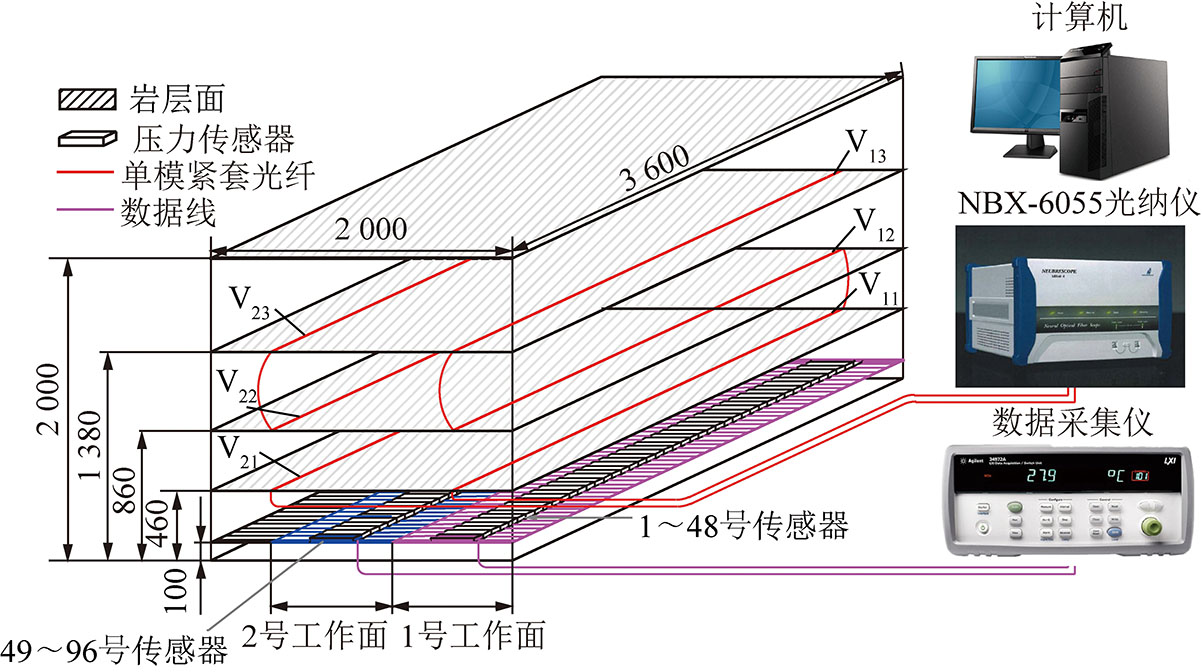
图4 试验监测系统
Fig.4 Test monitoring system
建立岩层-光纤变形示意,如图5所示,对岩层产生变形时光纤的受力状态进行分析[20]。根据假设可知,传感光纤主要受沿光纤轴向方向的拉压两种受力。图6(a)为岩层水平弯曲引起的2号,3号光纤受力状态示意,岩层中未出现水平张拉裂隙,岩层-光纤力学结构视为简支梁结构,光纤受力视作岩层变形施加在光纤上的连续荷载。根据材料力学可得其弯矩分布图,最大弯矩发生在光纤中部位置。图6(b)为岩层破断引起的1号光纤受力状态示意,随着开采岩层达到极限跨距发生破断,将岩层破断产生的张拉裂隙对光纤产生的作用力简化为岩层施加于光纤的点载荷,光纤受力视作岩层变形施加在光纤上的连续载荷和点载荷共同作用。根据叠加法可得光纤的弯矩分布图,最大弯矩发生在岩层破断位置。

图5 岩层-光纤变形示意
Fig.5 Mechanical structure of rock layer-optical fiber
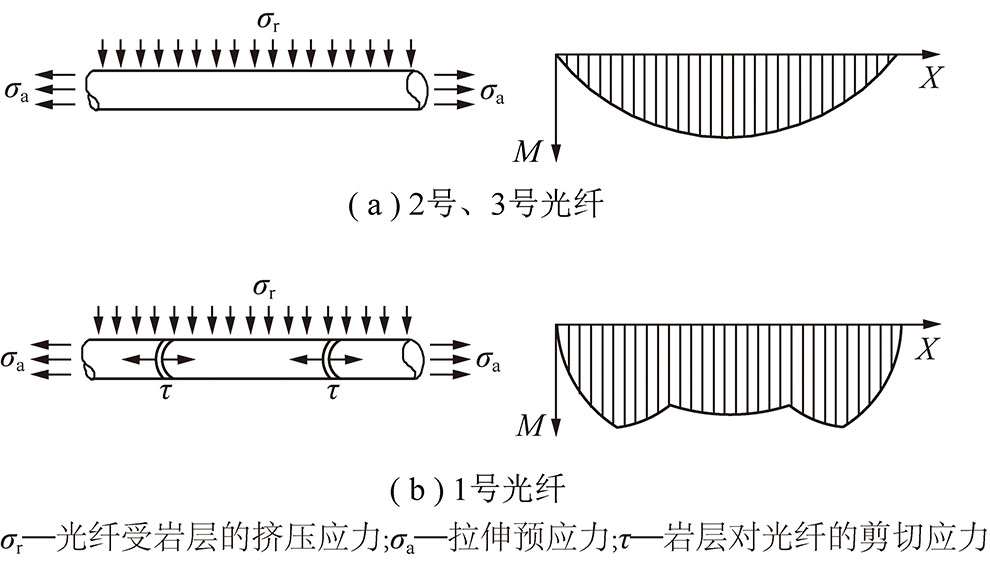
图6 光纤受力状态示意
Fig.6 Stress state of optical fibers
4 实验结果及分析
4.1 光纤监测复合关键层变形
4.1.1 工作面1
(1)亚关键层1细砂岩
传感光纤V11位于工作面1煤层上方亚关键层1细砂岩中,测试结果如图7(a)所示。工作面沿走向推进一段距离后,由于光纤所在层位细砂岩距离煤层较远,未受到采动影响,故开采前期光纤频移曲线未产生明显变化。当工作面推进至600 mm时,频移明显变化,此时频移曲线呈单峰状,峰值为136.89 MHz。随着工作面继续推进频移峰值不断增大,当推进至920 mm时,频移达到最大值,左侧峰值为438.98 MHz,右侧峰值为424.86 MHz,此时频移曲线由单峰状转变为双峰状,说明此时细砂岩发生初次破断,破断距离为920 mm。在工作面推进920~2 400 mm,频移峰值整体上变小,左侧峰值约为342.84 MHz,且位置和大小基本不变;右侧峰值随开采前移,大小呈周期性变化,分别在1 360,1 840,2 320 mm出现了3次最大峰值,分别为313.85,304.27和288.97 MHz,说明细砂岩出现了3次周期性破断,破断距约为467 mm。
(2)亚关键层2下组巨厚砾岩
传感光纤V12位于工作面1煤层上方亚关键层2下组巨厚砾岩中,测试结果如图7(b)所示。工作面从开切眼处推进,光纤频移峰值不断增大,频移曲线整体上呈单峰状。当工作面推进至1 840 mm时,频移峰值达到最大值165.94 MHz,随后继续推进频移峰值整体变小,约为140.39 MHz,较最大峰值减小了约25.55 MHz,频移曲线仍呈单峰状,说明砾岩层在开采过程中仅在1 840 mm位置时发生初次破断;光纤V12峰值相比V11峰值降低了约273 MHz,说明下组巨厚砾岩并未像细砂岩一样完全破断失稳,仅发生较大弯曲变形在中部岩层产生裂缝。
(3)主关键层上组巨厚砾岩
传感光纤V13位于工作面1煤层上方主关键层上组巨厚砾岩中,测试结果如图7(c)所示。工作面推进距离在0~800 mm,光纤频移值约为0,开采未影响到上组砾岩。推进距离在800~2 400 mm,频移曲线呈单峰状,频移峰值不断增大,最大峰值约为38.61 MHz,但远远小于光纤V11和V12的频移峰值,比下组巨厚砾岩的频移峰值减小了约127.33 MHz,比细砂岩的频移峰值减小了约400.37 MHz,说明上组巨厚砾岩受开采扰动而产生的弯曲变形量非常微小。
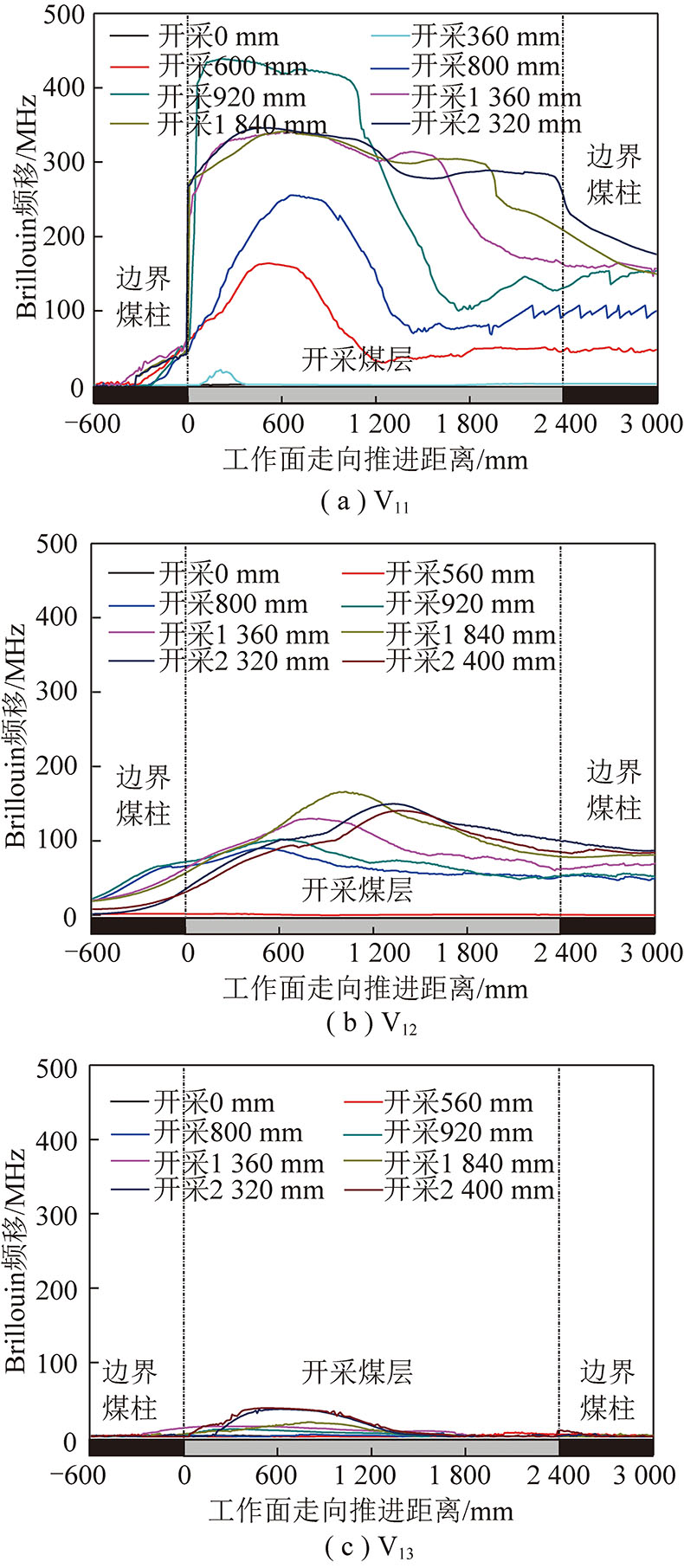
图7 工作面1复合关键层光纤频移测试曲线
Fig.7 Optical fiber frequency shift test curves of compound key layer in working face 1
4.1.2 工作面2
(1)亚关键层1细砂岩
传感光纤V21位于工作面2煤层上方亚关键层1细砂岩中,测试结果如图8(a)所示。工作面从开切眼开始推进,前期频移曲线呈单峰状,频移峰值不断增大。当推进至840 mm时,频移曲线由单峰状转变为双峰状,频移峰值达到最大,左侧峰值为319.83 MHz,右侧为311.65 MHz,说明细砂岩在岩层两端部发生破断,光纤受拉应力影响出现峰值。在工作面推进840~2 400 mm,峰值整体变小,左侧峰值位置保持不变,大小基本在261.8~264.9 MHz内;右侧峰值位置会不断前移,峰值影响范围不断增大,峰值大小呈周期性变化,共出现了3次最大峰值,位置分别为1 320,1 760,2 200 mm,大小分别为247.31,235.74,254.49 MHz,说明亚关键层1初次破断后,又出现了3次周期性破断,破断距平均约为453 mm。

图8 工作面2复合关键层光纤频移测试曲线
Fig.8 Optical fiber frequency shift test curves of compound key layer in working face 2
(2)亚关键层2下组巨厚砾岩
传感光纤V22位于工作面2煤层上方亚关键层2下组巨厚砾岩中,测试结果如图8(b)所示。随着工作面向前推进,光纤频移峰值不断增大,频移曲线整体上呈单峰状。当推进至1 760 mm时,光纤频移峰值达到最大值201.78 MHz,随后继续开采直至结束,频移峰值整体上变小,约为165.68 MHz,较最大峰值减小了约36.0 MHz,频移曲线仍呈单峰状,说明下组巨厚砾岩在整个开采过程中,仅发生初次破断,破断距离为1 760 mm;光纤V22相较V21频移峰值减小约118 MHz,说明下组巨厚砾岩相比细砂岩未整体性断裂,仅发生大弯曲变形局部产生裂缝。
(3)主关键层上组巨厚砾岩
传感光纤V23位于工作面2煤层上方主关键层上组巨厚砾岩中,测试结果如图8(c)所示。推进距离在0~720 mm内,光纤频移值基本为0,说明此时开采扰动未影响到上组砾岩;推进距离在720~2 400 mm内,频移曲线呈单峰状,频移峰值不断增大,最大峰值为40.98 MHz,但远远小于光纤V21和V22的频移峰值,比下组砾岩的频移峰值减小了约160.80 MHz,比细砂岩的频移峰值减小了约278.85 MHz,说明上组巨厚砾岩受开采扰动的变形量非常微小。
模型试验中,关键层发生大变形时,光纤与岩层体会发生相对滑移,故测试结果存在一定误差,但在一定程度上仍可反映岩体的变形。
4.2 工作面支承压力分布
立体模型两个工作面推进过程中,压力传感器监测的支承压力峰值变化曲线如图9所示。工作面1的支承压力峰值为29.5~95.8 MPa,集中系数为1.1~3.5;当推进至92 0 mm时,第1次出现峰值,约为77.5 MPa;当推进至1 360 mm时,第2次出现峰值,约为68.4 MPa;当推进至1 920 mm,第3次出现峰值,约为95.8 MPa;当推进至2 320 mm,第4次出现峰值,约为65.6 MPa;支承压力峰值明显呈现一大三小周期性变化规律。工作面2的支承压力峰值为31.5~102.4 MPa,集中系数为1.2~3.7,在推进距离840,1 320,1 760,2 240 mm位置上也出现了4次峰值,分别为73.5,70.5,102.4,73.3 MPa,也明显呈现“一大三小”周期性变化规律。

图9 支承压力峰值分布
Fig.9 Peak distribution of abutment pressure
综合分析得:① 对比工作面1,2,发现工作面2来压步距小于工作面1,说明工作面2开采受工作面1影响;但支承压力峰值大于工作面1,这是由于上覆巨厚砾岩关键层悬而不垮产生的;② 工作面呈现大小周期来压的现象,主要是由于复合关键层非同步破断产生的,低位亚关键层破断时形成小周期来压,当高位关键层达到极限承载跨度破断时,形成采场大周期来压。
4.3 工作面1,2关键层移动变形对比
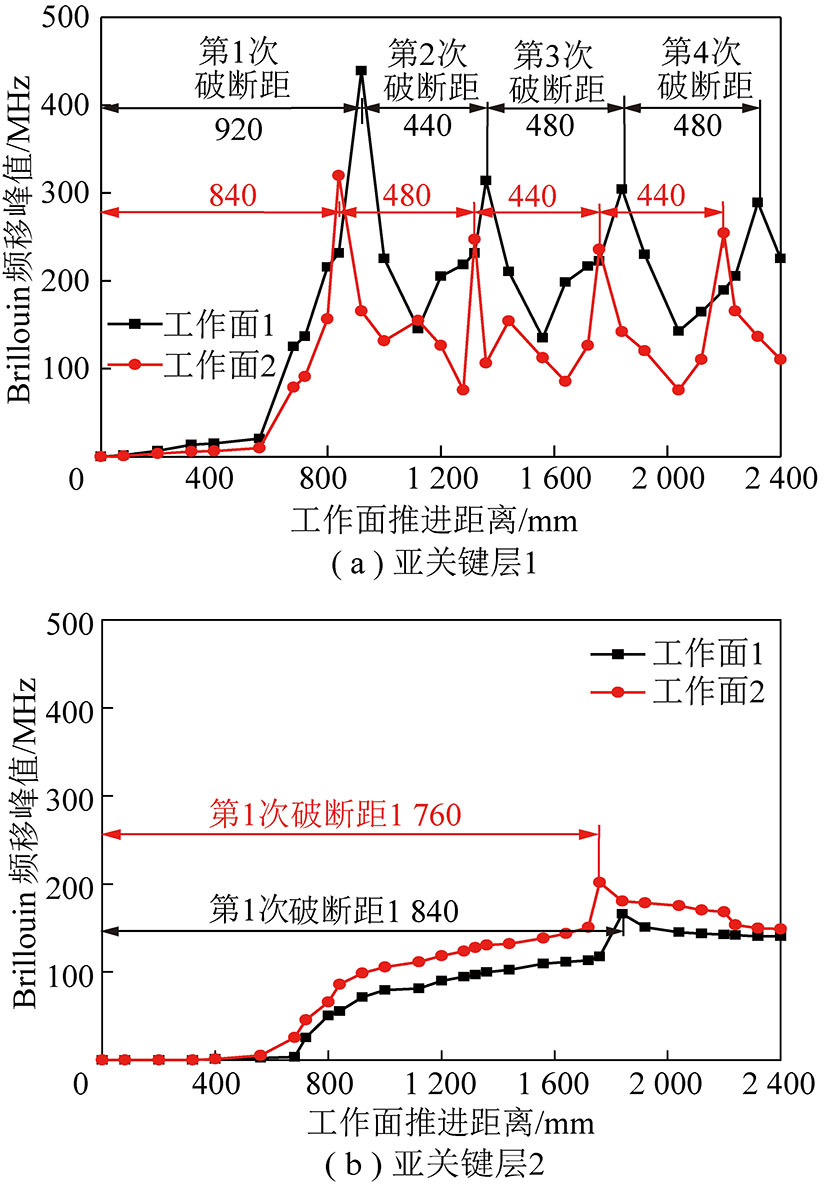
图10 光纤频移峰值分布
Fig.10 Peak distribution of frequency shift in optical fiber
工作面1,2传感光纤频移分布与覆岩移动变形如图10所示,工作面2的光纤频峰值规律与工作面1的变化趋势一致。亚关键层一频移峰值变化如图10(a)所示,工作面1中,光纤V11最大频移峰值分别为438.98,313.85,304.27和288.97 MHz,破断距离分别为920,440,480,480 mm;工作面2,光纤V12最大频移峰值分别为319.83,247.31,235.74和254.49 MHz,破断距离分别为840,480,440,440 mm;工作面1中的最大频移峰值明显大于工作面2,约为工作面2的1.1~1.4倍;工作面1的破断距离也大于工作面2,平均比工作面2破断距大约50 mm;说明工作面1的开采对工作面2产生了影响。
亚关键层2频移峰值变化如图10(b)所示,工作面1中,当推进至1 840 mm时,达到最大频移峰值为165.94 MHz;随着工作面继续推进,频移峰值位置前移,频移峰值变小,为140.39~149.53 MHz;由于模型试验推进距离的限制,未能观测到第2次最大频移峰值,预测继续推进至约3 000 mm时会再次出现最大频移峰值。工作面2的频移峰值变化趋势与工作面1相同,出现频移峰值时的推进距离小于工作面1,减小约120 mm;但工作面2的最大峰值高于工作面1,增大约35.8 MHz,说明工作面1开采时下组巨厚砾岩受采动影响破断但结构并未失稳,随着工作面2继续开采,开采范围增大,下组巨厚砾岩回转变形加剧,表现为频移值不断增大。
内部位移测试结果显示,工作面1亚关键层1的下沉量为13.7~8.9 mm,亚关键层2的下沉量为4.5~4.2 mm,主关键层的下沉量为0.95 mm;工作面2的岩层下沉量同工作面1[21]。复合关键层内部位移峰值和光纤频移峰值对比见表3。内部位移峰值与光纤频移峰值变化趋势基本一致,位移与频移的对应在27~40 MHz/mm。
表3 复合关键层内部位移峰值和频移峰值
Table 3 Peak displacement and frequency shift in compound key layer

物理变量工作面1复合关键层细砂岩下组砾岩上组砾岩工作面2复合关键层细砂岩下组砾岩上组砾岩位移峰值/mm13.705.400.9513.806.101.10频移峰值/MHz438.9165.938.6339.9201.730.70对应关系/(MHz·mm-1)32.0430.7240.6324.6233.0727.91
复合关键层破断距理论计算值和模型试验值见表4。理论计算值比模型试验值大,但整体上数值偏差不大,说明符拉索夫厚板理论计算方法适用于厚岩层破断距的计算,与物理相似模拟试验结果较为一致。
表4 复合关键层破断距理论值和试验值
Table 4 Theoretical and experimental values of breaking distance of compound key stratam

计算方法工作面1复合关键层细砂岩下组砾岩工作面2复合关键层细砂岩下组砾岩理论计算415772模型试验368736352720
5 结 论
(1)复合关键层破断距理论值与物理模型试验数值较为一致,说明符拉索夫厚板理论适用于采场厚岩层初次破断距的计算。
(2)采场巨厚复合关键层移动变形规律,亚关键层1(细砂岩)发生初次破断和3次周期性破断;亚关键层2(下组巨厚砾岩)仅发生初次破断,但结构并未失稳;主关键层(上组巨厚砾岩)仅发生弯曲变形。
(3)工作面1,2对比分析,亚关键层1在工作面1的破断距离比工作面2大,初次破断距大32 m,周期破断距大16 m;亚关键层2在工作面1的破断距离比工作面2大,初次破断距大48 m;主关键层在工作面1中的频移峰值比工作面2小,均未破断。预测随着后续接替工作面的开采,开采的范围不断增大,会出现复合关键层同步和非同步的破断现象,工作面呈现大、小周期来压现象,尤其当工作面出现大来压时,采场易发生强矿压动力灾害事故。
(4)建立了关键层结构演化的分布式光纤动态响应关系,得出了关键层位移峰值与光纤频移峰值变化趋势基本一致,位移与频移在数量上的对应关系为27~40 MHz/mm,揭示了岩层变形破坏及其结构演化的光纤频移关系。
[1] 钱鸣高,缪协兴,许家林,等.岩层控制的关键层理论[M].徐州:中国矿业大学出版社,2003:17-27.
[2] XU Jialin,XUAN Dayang,HE Changchun.Innovative backfilling lon-gwall panel layout for better subsidence control effect—separating adjacent subcritical panels with pillars[J].International Journal of Coal Science & Technology,2014,1(3):297-305.
[3] 钱鸣高,缪协兴,许家林.岩层控制中的关键层理论研究[J].煤炭学报,1996,21(3):2-7.
QIAN Minggao,MIAO Xiexing,XU Jialin.Theoretical study of key stratum in ground control[J].Journal of China Coal Society,1996,21(3):2-7.
[4] DU Wenfeng,PENG Suping,ZHU Guowei,et al.Time-lapse geophysical technology-based study on overburden strata changes induced by modern coal mining[J].International Journal of Coal Science & Technology,2014,1(2):184-191.
[5] DOU Linming,MU Zonglong,LI Zhenlei,et al.Research progress of monitoring,forecasting,and prevention of rockburst in underground coal mining in China[J].International Journal of Coal Science & Technology,2014,1(3):278-288.
[6] 王树立,张开智,蒋金泉,等.超厚高位红层砂岩破断运动与矿震活动规律[J].采矿与安全工程学报,2016,33(6):1116-1122.
WANG Shuli,ZHANG Kaizhi,JIANG Jinquan,et al.The fracture and rockburst laws of high-position hard and extremely thick red beds[J].Journal of Mining & Safety Engineering,2016,33(6):1116-1122.
[7] 茅献彪,缪协兴,钱鸣高.采动覆岩中复合关键层的断裂跨距计算[J].岩土力学,1999,20(2):1-4.
MAO Xianbiao,MIAO Xiexing,QIAN Minggao.Calculation for fracture span of conpound key strata in mining rocks[J].Rock & Soil Mechanics,1999,20(2):1-4.
[8] 侯忠杰.组合关键层理论的应用研究及其参数确定[J].煤炭学报,2001,26(6):611-615.
HOU Zhongjie.Study on application of combinatorial key stratum theory and parameters determining[J].Journal of China Coal Society,2001,26(6):611-615.
[9] 史红,姜福兴.采场上覆大厚度坚硬岩层破断规律的力学分析[J].岩石力学与工程学报,2004,23(18):3066-3069.
SHI Hong,JIANG Fuxing.Mechanical analysis of rupture regularity of hard and massive overlying strata of long wall face[J].Chinese Journal of Rock Mechanics & Engineering,2004,23(18):3066-3069.
[10] 王平,姜福兴,冯增强,等.高位厚硬顶板断裂与矿震预测的关系探讨[J].岩土工程学报,2011,33(4):618-623.
WANG Ping,JIANG Fuxing,FENG Zengqiang,et al.Relationship between fracture of high-position thick and hard roof and mine quake forecast[J].Chinese Journal of Geotechnical Engineering,2011,33(4):618-623.
[11] 蒋金泉,王普,武泉林,等.高位硬厚岩层弹性基础边界下破断规律的演化特征[J].中国矿业大学学报,2016,45(3):490-499.
JIANG Jinquan,WANG Pu,WU Quanlin,et al.Evolutionary characteristics of fracture laws of high-position hard thick strata with elastic foundation boundary[J].Journal of China University of Mining & Technology,2016,45(3):490-499.
[12] 许家林,陈稼轩,蒋坤.松散承压含水层的载荷传递作用对关键层复合破断的影响[J].岩石力学与工程学报,2007,26(4):699-704.
XU Jialin,CHEN Jiaxuan,JIANG Kun.Effect of load transfer of unconsolidated confined aquifer on compound breakage of key strata[J].Chinese Journal of Rock Mechanics & Engineering,2007,26(4):699-704.
[13] 杨培举,何烨,郭卫彬.采场上覆巨厚坚硬岩浆岩致灾机理与防控措施[J].煤炭学报,2013,38(12):2106-2112.
YANG Peiju,HE Ye,GUO Weibin.Disaster-causing mechanism and control measures of extremely thick and hard magmatic rock above working face[J].Journal of China Coal Society,2013,38(12):2106-2112.
[14] 魏振全.厚硬岩层下采动应力突变及冲击地压防治研究[J].煤炭科学技术,2017,45(8):103-108.
WEI Zhenquan.Study on mining stress variance and pressure bump prevention and control under thick and hard rock strata[J].Coal Science and Technology,2017,45(8):103-108.
[15] 张培鹏,蒋力帅,刘绪峰,等.高位硬厚岩层采动覆岩结构演化特征及致灾规律[J].采矿与安全工程学报,2017,34(5):852-860.
ZHANG Peipeng,JIANG Lishuai,LIU Xufeng,et al.Mining-induced overlying strata structure evolution characteristics and disaster-triggering under high level hard thick strata[J].Journal of Mining & Safety Engineering,2017,34(5):852-860.
[16] 柴敬,薛子武,郭瑞,等.采场覆岩垮落形态与演化的分布式光纤检测试验研究[J].中国矿业大学学报,2018,47(6):1185-1192.
CHAI Jing,XUE Ziwu,GUO Rui,et al.Experimental study of overlying mine strata collapse and its evolution by a distributed optical fiber system[J].Journal of China University of Mining & Technology,2018,47(6):1185-1192.
[17] CHAI Jing,DU Wengang,YUAN Qiang,et al.Analysis of test method for physical model test of mining based on optical fiber sensing technology detection[J].Optical Fiber Technology,2018,48:84-94.
[18] 成祥生.应用板壳理论[M].济南:山东科学技术出版社,1989:1-22.
[19] 何福保,沈亚鹏.板壳理论[M].西安:西安交大出版社,1993:160-189.
[20] 袁强.采动覆岩变形的分布式光纤检测与表征模拟试验研究[D].西安:西安科技大学,2017:24-35.
YUAN Qiang.Experimental study on detection and repersentation of mining-induced overburden deformation with distributed optical fiber sensing[D].Xi’an:Xi’an University of Science and Technology,2017:24-35.
[21] 钱云云.三维模型采场覆岩变形分布式监测及其数据处理软件开发[D].西安:西安科技大学,2017:35-55.
QIAN Yunyun.Distributed monitoring of deformation of overlying strata in the three-dimensional model and software development for processing the data it monitors[D].Xi’an:Xi’an University of Science and Technology,2017:35-55.
