采掘机械的研发由传统的静态设计发展到目前的动态虚拟设计，截齿载荷谱的历程和幅值大小是动态虚拟设计关键，研制高性能采掘机械和智能化开采的重要基础，通过揭示截齿截割煤岩载荷谱的变化规律和特征，能够为研究高效、高可靠破岩方法提供理论支撑。由于煤岩破碎的不确定性，致使载荷谱具有复杂性和随机性，传统截齿尖截割煤岩载荷的理论模型，通常根据事先假设的受拉和受剪切破坏准则理论推演各结构参数、运行参数和煤岩特性等参数表征的截齿载荷模型，由于理论推演的载荷模型常常是在某种假设条件下，如煤岩大块崩落状态时截齿所受的载荷，其能够准确计算对载荷线性影响因素条件下煤岩破碎载荷，但对截齿截割煤岩破碎的历程及非线性影响因素未能很好地进行表征。如EVANS[1]提出的最大拉应力理论，认为煤岩破碎是由于刀具切入煤岩时的拉应力造成的，引起材料脆性断裂破坏的因素是最大拉应力。NISHIMATSU[2]指出煤岩体破碎面遵守库仑-莫尔准则。ROXBOROUGH等[3]基于截割孔大小相对截深及齿岩之间摩擦力均不可忽略的前提条件下提出了峰值截割力的理论计算公式。文献[4-5]建立了直线截割试验装置，研究了镐型截齿截割岩石物理力学特性。BAO R H等[6]从断裂力学的角度给出了镐型截齿截割力的力学模型，指出最大截割力与截割厚度呈幂律关系。刘晋霞等[7]以EVANS 镐型截齿直线截割力模型为基础，提出了镐型截齿旋转截割力模型。刘春生等[8-9]给出了不同截割状态下镐型截齿侧向力的实验与理论模型。王力平等[10]基于EVANS的截割模型,认为截割时齿头的锥形表面因与岩石的夹制效应而接触应力分布有所不同,理论推导建立了峰值截割力计算公式。也有众多学者通过实验研究截齿截割煤岩的载荷历程[11-17]，上述研究均是在一定的实验条件下进行的，通常对该参数下的载荷特性有很好的研究，但对于其他参数下的规律特性较难推演。通过借鉴上述学者对煤岩破碎载荷的理论模型和实验研究成果，笔者建立截齿截割煤岩载荷理论推演模型，基于有限实验载荷谱通过熵权进行综合，将载荷理论推演模型与实验载荷谱结合起来，构建能够表征截割历程的载荷谱，应用正则化神经网络对构建的截割载荷谱进行模型化综合，根据最小二乘法原理，提出根据有限楔入角的载荷谱族的载荷预测方法，以实现对不同楔入角的截割载荷谱进行预测。
1 截齿载荷理论推演模型
1.1 不同切削位置的切削厚度
当截齿截割煤岩时，截齿旋转截割一周切削厚度由小到最大再到最小，呈月牙状，截割阻力随着切削厚度也发生相应的变化。传统切削厚度的计算以一种近似的方法，即截齿在不同位置的切削厚度hi=hmaxsin φ计算[18]，文中综合考虑截齿截割煤岩形成的月牙特征，给出一种准确计算切削厚度的方法，截齿不同位置切削厚度如图1所示，其中，R为滚筒半径，m;vq为采煤机牵引速度，m/s;hmax为最大切削厚度，mm;b，R，hmax为ΔOO′B的3条边。
图1 截齿不同切削位置切削厚度
Fig.1 Cutting thickness of pick at different position
由图1可知，截齿不同位置切削厚度准确值为hj，hj≠hi。在ΔOO′B中由余弦定理得
(1)
式中，φ为截齿截割位置角，(°)。
取b为正值，计算求得截齿不同位置切削厚度
(2)
式(2)给出了切削厚度随截齿位置角变化的数学模型，其可以描述切削厚度与采煤机滚筒半径、最大切削厚度和位置角的关系，当φ=π/2时hj=hmax，当φ=0时，
符合截齿切削月牙形成规律，分析表明，R和hj越小，近似计算的误差就越大。
1.2 煤岩崩落角
根据文献[18]韧性煤和脆性煤随不同切削厚度与崩落角的实验数据，采用指数函数关系，给出了脆性煤和韧性煤的崩落角与切屑厚度关系曲线，如图2所示。通过图2的脆性煤和韧性煤的崩落角与切削厚度的拟合曲线可知，建立了脆性煤和韧性煤切削厚度与崩落角度的数学关系。
脆性煤崩落角φ0c与切削厚度h的关系为
φ0c=45+40e-0.024h
(3)
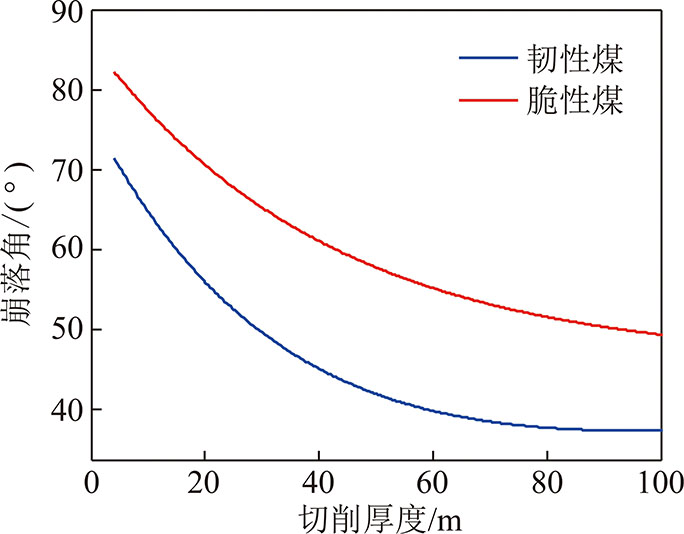
图2 崩落角与切削厚度的关系
Fig.2 Relationship between caving angle and chip thickness
韧性煤崩落角φ0r与切削厚度的关系为
φ0r=28+50e-0.029h
(4)
1.3 截割阻力的理论推演模型
螺旋滚筒式采煤机截齿在截割煤岩时，切削厚度为月牙状，截齿的不同位置切削厚度和崩落角是变化的。为获得截齿在截割煤岩过程中截割阻力的规律和幅值大小，基于不同切削位置的切削厚度和煤岩崩落角，构建截齿截割过程响应的理论推演模型。截齿截割煤岩时所受截割阻力示意如图3所示[19]。图3(a)为截齿以一定角度楔入煤岩，距离齿尖l处截齿微元所受截割阻力分析。图3(b)给出了截齿在截割过程中圆锥左右两侧的压应力产生的合力F1和F2，二者的合力F大于煤岩所产生拉应力的合力时，煤岩发生崩裂破碎，其中φ0=φ1+φ2,φ0为煤岩崩落角，(°);φ1，φ2分别为截齿单侧压应力产生的合力与崩裂线之间的夹角，(°)。一般φ2=(0.55～0.60)φ0。
图3 截齿截割阻力与煤岩崩落角
Fig.3 Cutting force and coal rock caving angle
由图3可知，
根据图3的截割阻力分析和煤岩崩落角的关系有
(5)
式中，l为截齿齿尖与煤岩的接触长度;FZ为截割阻力;dFZ为DE截面等效成圆其力的微元表达式,
为截齿表面微元面积，dA=rdφdl，mm2;ri为截圆半径，dri=sin(α+β″)dl，dl=sin(α+γ)dri，dφ为微元弧所对应的夹角;dl为接触微元长度;γ为截齿齿尖圆周0～π/2内等效倾斜角度，γ=φ2βi/φ0，(°);σt为煤岩抗拉强度，MPa;σy为煤岩抗压强度，MPa;α为截齿半锥角，(°);βi为截齿楔入角，(°);K为系数，即
(6)
由式(6)可知，该模型反映了截齿结构参数、煤岩性质参数等对截割阻力的影响关系，揭示了截割阻力随截齿位置角的变化规律特性。
2 载荷谱的预测模型
截齿截割煤岩系统的载荷谱具有一定随机性，通过熵可以度量截割系统无序的程度[19]。由于截割载荷谱随着截齿的结构参数和运行参数变化而变化，以及煤岩的各向异性，致使载荷谱具有一定的随机性，即使同一楔入角和相同截割条件下，重复实验的载荷谱也存在显著的差异，但其载荷谱幅值及变化趋势具有一定的内在关联性，为此，利用信息熵计算由截割阻力过程响应的理论推演模型和实验载荷谱的熵权[20-21]，构建相同实验条件下实验载荷谱与理论推演载荷的熵权综合模型。
2.1 载荷谱的熵权综合
令有N个载荷谱，其中N为同一楔入角等条件下实验载荷谱和理论推演载荷谱曲线总和，令当i′=1时为理论推演载荷谱。
(1)载荷归一化处理。第i′个载荷谱上第j′离散点载荷幅值占载荷幅值总和的占比[9]ki′j′为
(7)
式中，Fi′j′为第i′个载荷谱的第j′离散点载荷幅值。
(2)第i′个载荷谱熵值Si′为
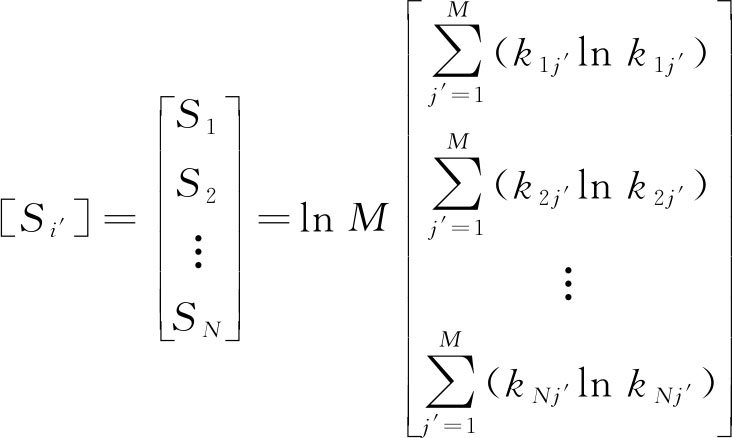
(8)
(3)第i′个载荷谱的熵权ωi′为
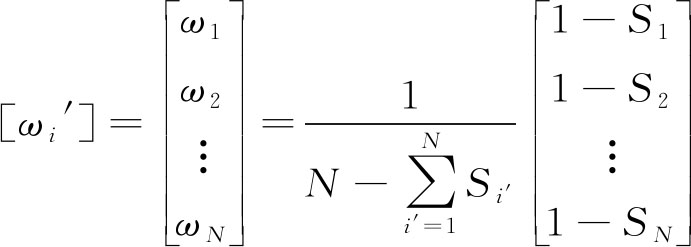
(9)
由式(6)，(9)可推导出第j′点熵权的理论与实验载荷谱综合Fj′为
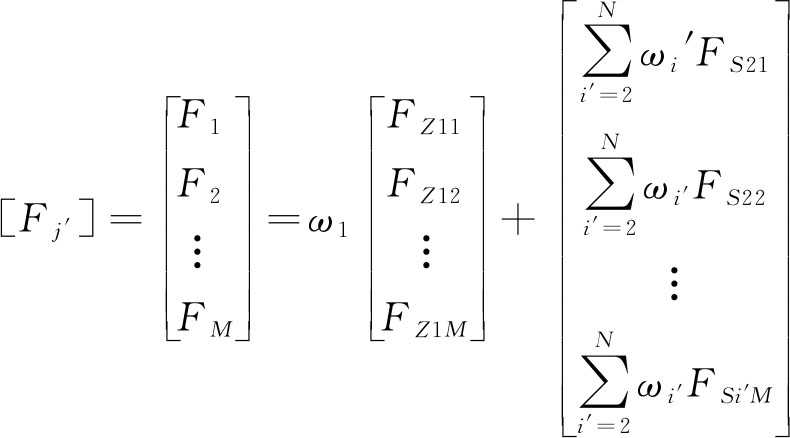
(10)
式中，ωi′为载荷的熵权，当i′=1时,ω1为理论推演载荷谱的熵权，当i′=2,3,…,N时，即ω2，ω3，…，ωN为相同实验条件下实验载荷谱的熵权重;FZ1j′为理论推演载荷谱上第j′点载荷幅值;FSi′j′为第i′个实验载荷谱上第j′点载荷幅值。
由式(10)可知，基于熵权的理论与实验载荷谱的综合载荷谱，是由M个幅值离散点构成。
2.2 载荷谱的神经网络模型化重构
截割载荷谱体现的是截齿截割煤岩复杂的非线性系统，其受截齿的运行参数和结构参数影响。神经网络具有良好的函数逼近能力[22-24]，文中选取正则化神经网络对综合的载荷谱进行逼近，实现载荷谱模型化重构。
神经网络第l层第j″个神经元的输出为
(11)
式中，f为神经元激活函数;
为第l-1层的第i″个神经元到l层第j″个神经元的权值;
为第l层第j″个神经元的偏置。
神经网络的误差函数fe(ω,b)为
(12)
式中，w为权重；b为偏置;Nn为样本总数;x为原始输入数据;f(x)为输入x对应的目标输出;fo(x)为神经网络模型的最终输出。
由梯度下降方法可知，神经网络模型的权值和偏置值不断沿梯度下降方向进行调整，使误差函数最小化，即式(12)最小化。
权值ωi″的调整为
(13)
式中，fe为误差函数;η为学习因子。
由式(13)可知，神经网络是一种全局逼近的网络，采用的梯度下降法，容易陷入局部极小点，影响神经网络的泛化能力。正则化方法可以提高神经网络的泛化能力，通过在误差函数中增加一个正则项可以改善神经网络的过拟合进而提高网络的泛化能力。文中采用L2正则化方法，式(12)可表示为
(14)
其中，λ为正则系数。由式(12)～(14)整理得L2正则化下权值调整公式为
(15)
由式(15)可知，通过引入L2正则化，神经网络在调整权值时，同时正则系数λ参与调整。式(15)的关键是如何确定正则系数λ，传统L2正则系数λ是基于固定的先验假设，根据文献[25-29]及互相关系数法，随机初始化λ和权值，利用高斯-牛顿法逼近Hessian矩阵，对正则参数进行确定。
2.3 载荷预测模型
通过实验获得一组由不同楔入角βi(β1,β2,…,βn)的载荷谱曲线族，根据理论推演模型和有限几组楔入角的实验载荷谱曲线族，利用熵权和正则化神经网络，构建不同楔入角重构载荷谱曲线族的模型，根据文献[9]与载荷谱的统计分析可知，截齿截割载荷谱的平均值、峰值最大值呈月牙形，均随楔入角βi(安装角为π/2-βi)呈现二次函数多项式关系，故有月牙形载荷谱上任意一载荷的统计值也随楔入角 βi呈现二次函数关系，即
(16)
针对式(16)需要确定拟合参量a0，a1，a2，采用最小二乘法确定载荷预测模型的系数，对载荷谱以楔入角单影响变量对系列载荷谱进行拟合，求解拟合参量的方程，即
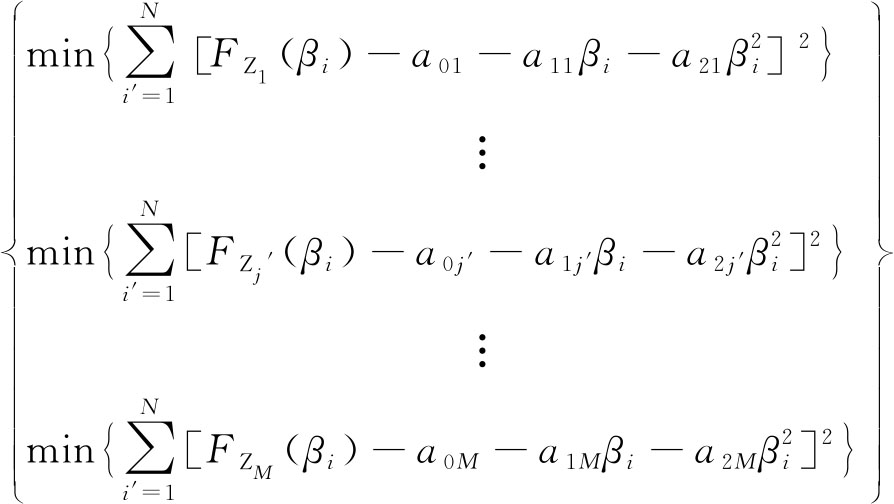
(17)
式(17)可简写为
式中，FZj′为第j′个载荷谱的离散载荷;a0j′为对应的第j′个载荷谱最小二乘的系数。
对式(17)求其偏导数有
求得
进而得到任意βi的载荷谱曲线方程系数的矩阵:
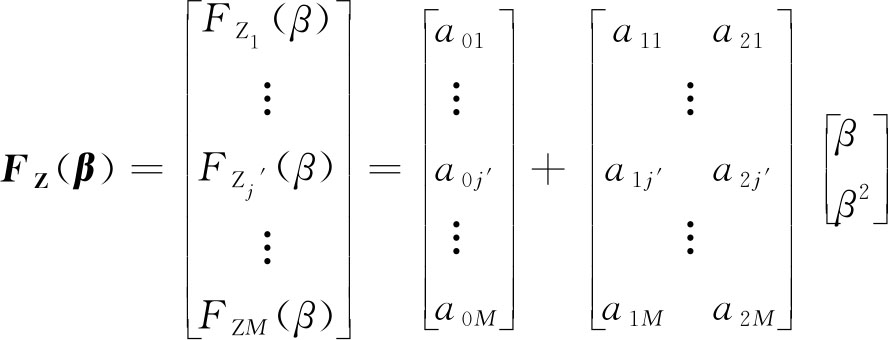
(18)
计算求得式(18)的系数，进而建立不同楔入角重构载荷谱曲线的载荷离散幅值预测模型，对于截齿截割煤岩其他的运行参数和结构参数，同理，采用上述方法与正交试验方法相结合，可对楔入角、切削厚度和轴向倾角等多变量的截割阻力进行预测。不同截齿切削厚度FΖ(hmax)、截齿轴向倾角FΖ(θ)等载谱曲线离散预测数值，在正交试验获取一系列不同的参数下载荷谱曲线基础上，利用上述方法建立多变量的载荷预测模型，进而获得FZj′(β,hmax,θ,……)。
3 应用实例
3.1 实验载荷谱
多截齿旋转截割实验系统主要由截割机构、截割煤壁、控制系统、信号采集系统和液压系统等构成，如图4所示。截割电动机经减速器和转速转矩仪驱动截割臂旋转，采用变频调速方法调节截割臂转速，截割试验台的进给运动通过液压缸实现，经速度传感器反馈，可自动和手动调速。截齿的载荷测试系统由测力装置、压力传感器、信号放大器和Dasp v10智能数据采集和信号处理系统等组成。实验条件:截齿楔入角为30°～50°，模拟滚筒半径R为730 mm，煤岩抗压强度σy为18～23 MPa，hmax为15 mm。抗拉强度一般为抗压强度的0.07～0.23，平均值为0.15。测试得到的不同楔入角的截齿轴向载荷与径向载荷，限于篇幅，文中仅给出βi=30°楔入角的轴向与径向载荷谱，如图5所示。
图4 截齿截割煤岩实验系统
Fig.4 Picking cutting coal rock experimental system
图5 βi=30°楔入角的轴向与径向载荷谱
Fig.5 Axial and radial load spectra for βi=30°
由截齿载荷的测量原理可知，实验截割阻力FS与轴向载荷F3和径向载荷F4的关系[12],即
FS=F3sin βi+F4[fnsin βi(1+k1)+k1cos βi]
(19)
式中，fn为齿套与支撑结构的摩擦因数，fn=0.1;k1为截齿测力传感器的结构尺寸系数，k1=0.739。
根据式(19)，可将不同楔入角的轴向载荷与径向载荷转化为截齿的截割载荷，图6为βi=30°楔入角的截割阻力谱。
3.2 载荷谱综合结果
由式(6)结合煤岩与截齿的结构参数，计算可得楔入角30°～50°的理论截割阻力谱，由式(7)～(10)以及不同楔入角的实验载荷，获得理论与实验载荷熵权综合的载荷谱，如图7所示。图7(a)中F301～F303代表楔入角为30°时，相同截割实验条件1～3次的截齿截割阻力谱，其他楔入角度的标注含义同理。
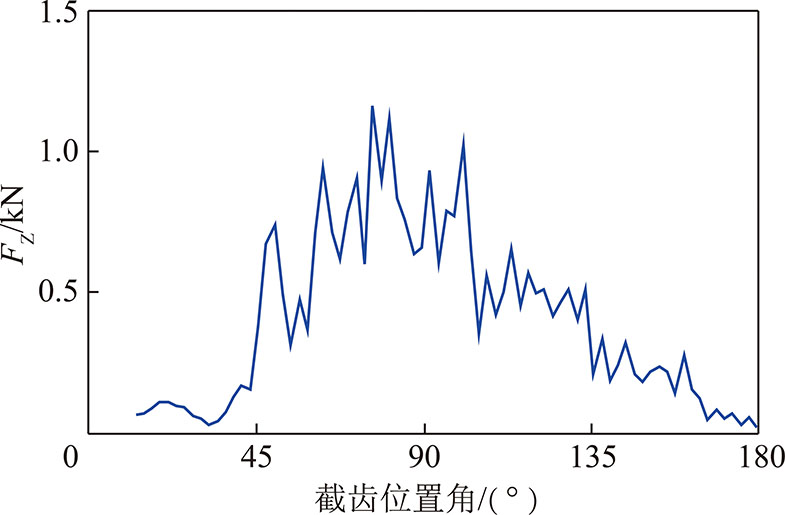
图6 βi=30°的截割阻力谱
Fig.6 Cut resistance spectrum of βi=30°
由图7可知，不同楔入角截割阻力谱综合蕴含了理论与实验截割阻力谱的特征，截割阻力谱幅值的随机特征表征了煤岩崩落的随机性。30°～50°楔入角的截割阻力谱综合不仅能够表征截齿截割煤岩的历程特征，还可以表征截齿截割煤岩的载荷幅值特征。
图7 30°～50°楔入角截割阻力谱综合
Fig.7 Comprehensive cutting resistance spectrum of 30°-50° wedge angle
3.3 截割阻力谱模型化重构结果
以不同楔入角的熵权截割阻力谱综合为基础，利用正则化神经网络对其学习模型化重构。根据式(14)，随机初始化λ和权值，使用高斯-牛顿法逼近Hessian矩阵，计算更新正则参数λ，通过正则化神经网络对图7的截割阻力谱综合进行神经网络模型化重构的截割阻力谱，如图8所示。
由图8可知，正则化神经网络可以对基于理论与实验的截割阻力谱综合进行模型化重构，其表征截割阻力谱细观信息的同时，还能表征截割阻力谱的规律，避免了传统神经网络的过度泛化，使模型适用性更好。
图8 正则化神经网络模型化重构的截割阻力谱
Fig.8 Reconstructed cutting resistance load spectrum of regularized neural network modeled
图9 不同楔入角的预测截割阻力谱
Fig.9 Load spectrum prediction for different installation angles
3.4 不同楔入角截割阻力谱的预测
根据所建立的预测模型，给出了30°，33°，50°和55°楔入角度下的预测截割阻力谱，如图9所示。
由图9可知，通过不同楔入角重构截割阻力谱曲线族的载荷预测模型，结合熵权和正则化神经网络重构的截割阻力谱可以实现不同楔入角的截割阻力谱预测。30°和50°楔入角的预测与重构截割阻力谱的互相关系数分别为0.971 7和0.983 9，根据互相关性分析相关系数在0.7～1.0是高度相关可知，30°和50°楔入角的预测截割阻力谱与正则化神经网络模型化重构的截割阻力谱呈高度相关性，30°和50°楔入角的预测截割阻力谱与正则化神经网络模型化重构截割阻力谱的幅值相对误差分别为4.04%和5.21%，从相关系数和幅值相对误差可知，预测的载荷谱具有很好符合度和准确性。在此基础上，对33°和55°楔入角的截割阻力谱进行了预测，实现了不同楔入角载荷的预测。
4 结 论
(1)通过分析截齿的截割状态，基于不同切削位置的切削厚度与煤岩崩落角的变化规律，构建了截割阻力过程响应的理论推演模型，其可以表征截齿截割煤岩历程的幅值。
(2)采用熵权方法构建了可以反映截割煤岩历程与幅值的载荷谱，以30°～50°截齿楔入角为例，计算求得理论推演模型的载荷，结合实验截割阻力谱，基于其熵权的理论与实验截割阻力谱综合，表征理论模型与实验截割阻力谱的幅值变化规律，为研究截齿不同条件下的载荷谱表征截割煤岩历程提供了方法。
(3)基于熵权截割阻力谱综合离散序列的非数学模型描述，采用正则化神经网络对不同楔入角的截割阻力谱综合进行模型化重构，以30°～50°截齿楔入角的截割阻力谱综合为例进行正则化神经网络模型化重构，很好地对截割阻力谱综合进行模型化重构。
(4)提出基于有限实验和理论综合与重构的不同楔入角的截割阻力谱曲线族，基于最小二乘法原理，构建其楔入角的预测模型，以30°～50°截齿楔入角的正则化神经网络模型化重构的截割阻力谱为基础，对30°，33°，50°和55°楔入角的截割阻力谱实现了预测。其中楔入角为30°和50°的预测截割阻力谱与正则化神经网络模型化重构截割阻力谱的互相关系数分别为0.971 7和0.983 9，呈高度相关，而幅值相对误差分别为4.04%和5.21%，表明预测模型的准确性。
[1] EVANS I.A theory of the cutting force for point-attack picks[J].International Journal of Rock Mechanics and Mining Science,1984,2(1):67-71.
[2] NISHIMATSU Y.The mechanics of rock cutting[J].International Journal of Rock Mechanics and Mining Science,1972,9(3):261-270.
[3] ROXBOROUGH F F，LIU Z C.Theoretical considerations on pick shape in rock and coal cutting[A].Proceedings of the 6th Underground Operator’s Conference[C].Kalgoorlie,1995:189-193.
[4] BALCI C,DEMIRCIN M A,COPUR H,et al.Estimation of optimum specific energy based on rock properties for assessment of road header performance[J].The Journal of South African Institute of Mining and Metallurgy，2004,104(11):633-641.
[5] BILGIN N,DEMIRCIN M A,COUPUR H,et al.Dominant rock properties affecting the performance of conical picks and the comparison of some experimental and theoretical results[J].International Journal of Rock Mechanics and Mining Sciences，2006,43:139-156.
[6] BAO R H，ZHANG L C，YAO Q Y，et al.Estimating the peak indentation force of the edge chipping of rocks using single point-attack pick[J].Rock Mechanics and Rock Engineering，2011,44(3):339-347.
[7] 刘晋霞，马超，曾庆良，等.镐型截齿截割煤岩过程的截割力研究[J].煤炭学报，2017，42(5):1325-1330.
LIU Jinxia，MA Chao，ZENG Qingliang，et al.Research on cutting force of conical pick in cutting coal process[J].Journal of China Coal Society，2017，42(5):1325-1330.
[8] 刘春生，李德根.不同截割状态下镐型截齿侧向力的实验与理论模型[J].煤炭学报，2016，41(9):2359-2366.
LIU Chunsheng，LI Degen.Experimental research and theoretical model on lateral force of conical pick under different cutting conditions[J].Journal of China Coal Society，2016，41(9):2359-2366.
[9] 刘春生，王庆华，李德根.镐型截齿截割阻力谱的分形特征与比能耗模型[J].煤炭学报，2015，40(11):2623-2628.
LIU Chunsheng，WANG Qinghua，LI Degen.Fractal characteristic and specific energy model of conical picks cutting resistance spectrum[J].Journal of China Coal Society，2015，40(11):2623-2628.
[10] 王立平，蒋斌松，张翼，等.基于 Evans 截割模型的镐型截齿峰值截割力的计算[J].煤炭学报，2016，41(9):2367-2372.
WANG Liping，JIANG Binsong，ZHANG Yi，et al.Calculation of peak cutting force of conical picks based on Evans’cutting model[J].Journal of China Coal Society，2016，41(9):2367-2372.
[11] 刘春生,任春平,李德根.修正离散正则化算法的截割煤岩载荷谱的重构与推演[J].煤炭学报,2014,39(5):981-986.
LIU Chunsheng,REN Chunping,LI Degen.Reconstruction and deduction of cutting coal and rock load spectrum on modified discrete regularization algorithm[J].Journal of China Coal Society,2014,39(5):981-986.
[12] 刘春生，任春平.改进分数阶Tikhonov 正则化的截割煤岩载荷识别方法[J].煤炭学报，2019，44(1):332-339.
LIU Chunsheng，REN Chunping.Identification method of cutting coal and rock load based on improved fractional Tikhonov regularization[J].Journal of China Coal Society，2019,44(1):332-339.
[13] 刘春生，袁昊，李德根，等.载荷谱细观特征量与截割性能评价的熵模型[J].煤炭学报，2017，42(9):2468-2474.
LIU Chunsheng，YUAN Hao，LI Degen，et al.Meso-feature of load spectrum and entropy model for cutting performance evaluation[J].Journal of China Coal Society，2017，42(9):2468-2474.
[14] 张强，顾颉颖，刘峻铭，等.基于小波包与 SOM 神经网络的截齿磨损状态识别[J].煤炭学报，2018，3(7):2077-2083.
ZHANG Qiang，GU Jieying，LIU Junming，et al.Pick wear condition identification based on wavelet packet and SOM neural network[J].Journal of China Coal Society，2018，43(7):2077-2083.
[15] 王春华,丁仁政,李贵轩,等.截齿截割煤体变形破坏过程模拟试验[J].煤炭学报,2006,31(1):121-124.
WANG Chunhua,DING Renzheng,LI Guixuan,et al.Simulation experimental on the deformation and destruction course of coal body under the function of pick cutting[J].Journal of China Coal Society,2006,31(1):121-124.
[16] DEWANGAN S,CHATTOPADHYAY S.Performance analysis of two different conical Picks used in linear cutting operation of coal[J].Arabian Journal for Science & Engineering,2016,41(1):1-17.
[17] CHOI S O,LEE S J.Three-dimensional numerical analysis of the rock-cutting behavior of a disc cutter using particle flow code[J].Ksce Journal of Civil Engineering,2015,19(4):1129-1138.
[18] 刘春生.滚筒式采煤机理论设计基础[M].徐州:中国矿业大学出版社，2003.
[19] 刘春生，李德根.截齿截割煤岩的力学模型与性能评价[M].哈尔滨:哈尔滨工业大学，2017.
[20] WANG Z,WEI Z.Dynamic engineering multi-criteria decision making model optimized by entropy weight for evaluating bid[J].Systems Engineering Procedia,2012,5:49-54.
[21] MA H Q,WANG S F,LI C.Water security dynamic assessment based on entropy-markov chain model[J].Advanced Materials Research,2013(610/613):845-848.
[22] HU H,MA B,SHEN J,et al.Robust object tracking using manifold regularized convolutional neural networks[J].IEEE Transactions on Multimedia,2019,21(2):510-521.
[23] YIN P,XIN J,QI Y.Linear feature transform and enhancement of classification on deep neural network[J].Journal of Scientific Computing,2018,76(10):1-11.
[24] SHAN D,ZHENG X.Multi-label learning model based on multi-label radial basis function neural network and regularized extreme learning machine[J].Pattern Recognition & Artificial Intelligence,2017,30(9):833-840.
[25] GOUTTE C，LARSEN J.Adaptive regularization of neural networks using conjugate gradient[A].Processing Proceedings of the 1998 IEEE International Conference on Acoustics[C].Speech and Signal,1998,2:1201-1204.
[26] FORESEE F D,HAGAN M T.Gauss-Newton approximation to Bayesian learning[A].International Conference on Neural Networks[C].1997,3:1930-1935.
[27] WANG Jinhua.Development and prospect on fully mechanized mining in Chinese coal mines[J].International Journal of Coal Science & Technology,2014,1(3):253-260.
[28] LI Yaqing,GALECKI G,AKAR G,et al.Application of the fractal theory for evaluating effects of coal comminution by waterjet[J].International Journal of Coal Science & Technology,2014,1(4):450-455.
[29] MAHAPATRA S S,SOOD A K.Bayesian regularization-based Levenberg-Marquardt neural model combined with BFOA for improving surface finish of FDM processed part[J].International Journal of Advanced Manufacturing Technology,2012,9:1223-1235.
