煤层瓦斯含量是确定井下瓦斯涌出量、矿井瓦斯储量的重要参数,直接法测瓦斯含量操作简便,是当前井下普遍采用的瓦斯含量测定方法。直接法得到的煤层瓦斯含量由损失量、可测解吸量和残余量3部分组成[1]。在3者中,损失量为拟合值,其余2者皆为真实读数。因此,损失量拟合结果的准确度决定了直接法测煤层瓦斯含量的准确性。在实际操作中,煤样的暴露时间是可以准确测定的,因此在不考虑操作误差的基础上[2],该暴露时间段中的解吸规律,即解吸模型的准确性是决定损失量测定误差大小的关键。
近年来,国内外学者根据现场测试数据和前人研究的结果,总结出各自的煤样瓦斯解吸模型。在此基础上,我国确定了直接法测定瓦斯含量的国家标准——《煤层瓦斯含量井下直接测定方法》(GB/T 23250—2009),指出了![]() 法和幂函数法2种常用的损失瓦斯量计算方法[3]。由于上述模型均属于经验式,对不同条件下的瓦斯解吸的拟合相关系数不等,业界学者对损失量计算模型进行了进一步的研究与探讨。秦跃平等[4-6]提出累计解吸量倒数与时间开方倒数呈现较好的线性关系,并通过现场数据和实验结果进行了论证。LI等[7]假设拟合损失量与实际损失量的差值服从正态分布,提出基于幂函数特性的贝叶斯概率法进行损失量推算。孙健等采用实验手段精确测定了损失量、解吸量和残余量,认为损失时间对损失量估算有关键影响[1]。李成武等[8-9]、WANG等[10]分别通过实验研究不同因素对煤的瓦斯吸附解吸能力的影响,前者着眼于煤的粒度、温度等特征的影响,后者着重研究外加静电场、应力场等外部条件的作用。SAGHAFI A[11]分析了澳大利亚运用直接法测损失量过程中的误差与不确定性,提出了估算测定误差的方法。刘彦伟等[12]、CHENG等[13]、LIN等[14]、李祥春等[15]、康志勤等[16]分别通过煤瓦斯解吸实验,从孔型、孔径等微观角度阐释了孔隙结构对气体解吸速度、解吸量的影响机理。YANG等[17]通过实验研究不同钻孔液介质对煤层气解吸扩散的影响,发现当暴露时间较长时,建模求出的解吸量更接近真实损失量。张慧杰等[18]、李云波等[19]分别通过实验探究影响构造煤瓦斯解吸初期解吸量与解吸速度的因素,认为在解吸不同时间段内,解吸规律具有分段性。
法和幂函数法2种常用的损失瓦斯量计算方法[3]。由于上述模型均属于经验式,对不同条件下的瓦斯解吸的拟合相关系数不等,业界学者对损失量计算模型进行了进一步的研究与探讨。秦跃平等[4-6]提出累计解吸量倒数与时间开方倒数呈现较好的线性关系,并通过现场数据和实验结果进行了论证。LI等[7]假设拟合损失量与实际损失量的差值服从正态分布,提出基于幂函数特性的贝叶斯概率法进行损失量推算。孙健等采用实验手段精确测定了损失量、解吸量和残余量,认为损失时间对损失量估算有关键影响[1]。李成武等[8-9]、WANG等[10]分别通过实验研究不同因素对煤的瓦斯吸附解吸能力的影响,前者着眼于煤的粒度、温度等特征的影响,后者着重研究外加静电场、应力场等外部条件的作用。SAGHAFI A[11]分析了澳大利亚运用直接法测损失量过程中的误差与不确定性,提出了估算测定误差的方法。刘彦伟等[12]、CHENG等[13]、LIN等[14]、李祥春等[15]、康志勤等[16]分别通过煤瓦斯解吸实验,从孔型、孔径等微观角度阐释了孔隙结构对气体解吸速度、解吸量的影响机理。YANG等[17]通过实验研究不同钻孔液介质对煤层气解吸扩散的影响,发现当暴露时间较长时,建模求出的解吸量更接近真实损失量。张慧杰等[18]、李云波等[19]分别通过实验探究影响构造煤瓦斯解吸初期解吸量与解吸速度的因素,认为在解吸不同时间段内,解吸规律具有分段性。
从当前研究结果来看,学界对于采用何种解吸规律进行损失量计算仍未达成共识。笔者进行了不同压力、不同暴露时间的瓦斯解吸实验,采用了现行国标规定的![]() 法和幂函数法2种损失量计算模型计算损失量,对比了2种测试方法的误差,分析了误差产生的原因,提出了直接法测含量的各阶段瓦斯解吸过程的数学模型。
法和幂函数法2种损失量计算模型计算损失量,对比了2种测试方法的误差,分析了误差产生的原因,提出了直接法测含量的各阶段瓦斯解吸过程的数学模型。
根据国标GB/T 23250—2009规定的直接法测含量中井下瓦斯解吸量的测定步骤,实验室采用排水集气法,首先让煤吸附一定瓦斯,测试煤自然解吸瓦斯的全过程数据;然后让吸附平衡的煤暴露一段时间后,再测试煤解吸瓦斯数据,并且依据测试的数据和国标规定的![]() 法和幂函数法分别计算煤暴露这段时间的损失量,再与刚开始测试的全过程瓦斯曲线相应时间段的瓦斯解吸量进行对比,确定损失量的误差;改变瓦斯的吸附量和暴露时间,反复对比计算损失量误差,则可对国标GB/T 23250—2009的2种损失量计算方法的准确性进行判断。
法和幂函数法分别计算煤暴露这段时间的损失量,再与刚开始测试的全过程瓦斯曲线相应时间段的瓦斯解吸量进行对比,确定损失量的误差;改变瓦斯的吸附量和暴露时间,反复对比计算损失量误差,则可对国标GB/T 23250—2009的2种损失量计算方法的准确性进行判断。
实验根据国标GB/T 23250—2009的规定进行设计,模拟井下直接法测含量的过程,对损失量测定环节进行研究。实验方案设计如下:
(1)实验煤样被真空脱气后充入不同压力的甲烷,使其吸附饱和,以模拟井下煤样未暴露时的瓦斯吸附状态。
(2)为模拟井下煤样脱离煤体到装入煤样罐密封解吸的过程,实验室中吸附饱和的煤样会在空气中暴露一定时间,然后再连接瓦斯解吸测定仪进行解吸测定。
(3)根据国标对读数及测定时间的规定,对解吸过程观测120 min,前30 min每隔1 min读1次数,之后每隔5 min读1次数,读数保留2位小数[3]。
(4)考虑到井下煤层瓦斯压力的不同,参考突出危险性指标中煤层瓦斯压力指标的临界值为0.74 MPa,设置了0.4,0.7,1.0 MPa三组瓦斯压力。
(5)在井下测定煤层瓦斯含量的采样过程中,暴露时间并不相同,根据国标规定暴露时间不应超过5 min,考虑到井下实测钻屑瓦斯解吸指标测定的是3~5 min的瓦斯解吸量,本实验在每组压力下设计0,1,2,3 min四组暴露时间。
(6)为还原井下真实测试过程,实验室不测定暴露时间内瓦斯解吸量,而是将暴露时间为0 min的瓦斯解吸量测试数据作为标准值,将其与暴露1,2,3 min的瓦斯解吸量进行对比,判断国标规定的损失量计算方法的误差。
实验采用通用的煤瓦斯吸附解吸实验系统进行研究,该系统由真空脱气系统、吸附解吸系统、解吸集气系统、数据采集系统及温控辅助系统等部分组成,示意图如图1所示。吸附过程由压力表进行观测,压力稳定视为吸附平衡,解吸过程采用传感器进行读数,采样频率为20 Hz。
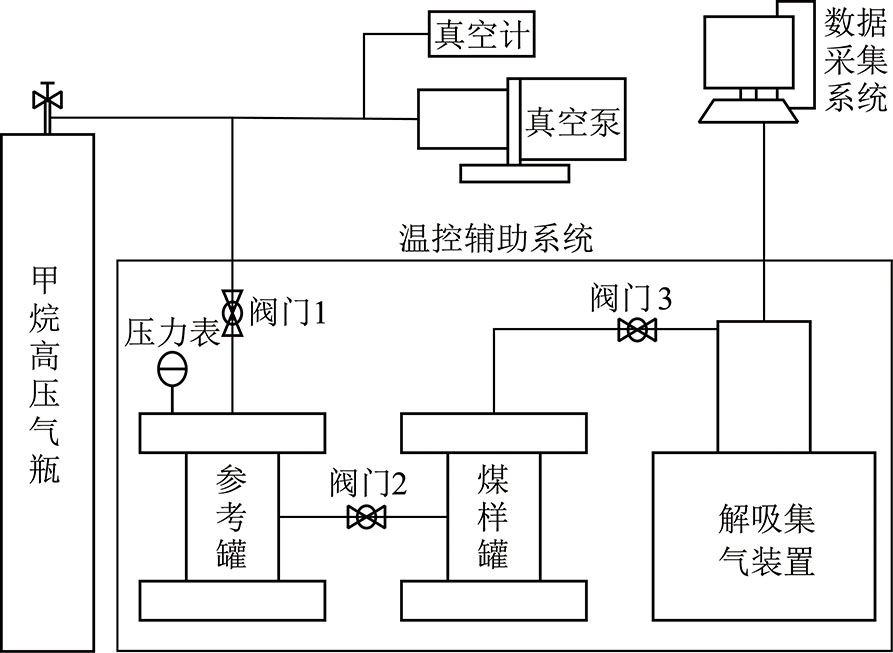
图1 瓦斯吸附解吸实验系统示意
Fig.1 Experimental system for gas adsorption and desorption
实验取用山西晋城凤凰山矿9号煤,全程密封至实验室内进行研磨筛分,得到5种粒径煤样,分别为0.25 mm以下、0.25~0.5,0.5~1,1~2和2~3 mm。实验中每组煤样均选用等量5种粒度煤样进行均匀混合,排除粒度干扰,每组煤样质量为200 g。
实验选取0.4,0.7,1.0 MPa三个瓦斯压力值进行瓦斯解吸实验,每个压力值下设煤样暴露时间分别为0,1,2,3 min的4组,共计12组实验,以模拟井下不同煤层压力下取出的煤样在不同暴露时间下的瓦斯解吸规律。实验过程包括以下步骤:① 利用温控装置将实验装置温度控制为22 ℃;② 将煤样装入煤样罐中,连接实验管路,检测气密性;③ 对实验系统进行真空脱气至10 Pa;④ 向参考罐内注入甲烷至计算压力值后打开阀门2,两罐压力达到预定压力值并开始吸附;⑤ 吸附平衡后打开阀门1,将煤样暴露在空气中,到达设定的暴露时间后关闭阀门1;⑥ 调节数据采集系统,打开阀门3进行解吸集气,根据实验设计,采集120 min解吸数据;⑦ 重复步骤①~⑥,按组改变步骤④中计算压力值和步骤⑤中暴露时间,完成不同压力、不同暴露时间下的解吸实验。
根据实验设计,读取解吸时间和累计解吸量,确定原始数据,见表1。
图2为瓦斯压力为0.4,0.7,1.0 MPa下分别暴露0,1,2,3 min后的累计瓦斯解吸量数据曲线。
目前国标中采用![]() 法和幂函数法对累计瓦斯解吸量数据进行损失量计算。
法和幂函数法对累计瓦斯解吸量数据进行损失量计算。![]() 法依据累计解吸量V与总解吸时间的平方根
法依据累计解吸量V与总解吸时间的平方根![]() 在煤样暴露后一定时间内的线性关系来计算[3],表达式为
在煤样暴露后一定时间内的线性关系来计算[3],表达式为
![]()
(1)
式中,t为瓦斯解吸时间,min;t0为煤样暴露时间,min;V为t时间段的累计解吸量,cm3;V′s为t0时间段的瓦斯解吸量,cm3;K为待定常数。
幂函数法先将解吸量与时间数据转化为解吸速度与时间数据,对解吸速度按照式(2)进行拟合求出q0和n[3]:
表1 不同压力、不同暴露时间的瓦斯累计解吸量
Table 1 Cumulative desorption of gas at different pressures and exposure times
mL/g

解吸时间/min0.4 MPa累计解吸量暴露时间/min01230.7 MPa累计解吸量暴露时间/min01231.0 MPa累计解吸量暴露时间/min0123000000000000010.300.060.050.070.310.110.100.130.350.190.160.1020.320.110.090.110.400.170.150.190.490.320.230.1730.380.150.120.140.500.260.220.270.590.410.310.2440.410.160.170.190.550.310.280.320.680.490.360.2950.450.210.190.220.600.360.340.330.760.570.420.3460.490.230.220.240.650.410.370.380.840.630.480.3970.510.260.260.280.700.460.400.420.890.680.540.4580.550.300.270.290.740.500.440.470.950.730.590.4990.560.300.310.310.790.530.470.501.000.780.610.54100.590.340.320.330.840.560.500.521.040.830.650.58110.610.350.320.340.850.620.530.561.080.880.700.62120.650.360.370.380.900.650.570.581.130.900.700.64130.650.400.390.380.940.680.590.611.170.940.750.68140.680.400.420.390.990.700.620.621.220.970.790.72150.700.450.420.421.000.750.640.661.231.020.800.73160.700.450.460.431.040.750.680.661.271.020.840.78170.720.450.460.441.070.790.700.711.271.070.890.78180.750.490.470.471.090.800.730.711.321.080.890.83190.750.500.490.481.130.850.740.751.361.120.940.83200.780.500.510.481.130.850.780.761.371.140.940.88210.790.530.510.511.180.880.780.801.401.170.990.89220.800.550.520.531.180.900.820.811.421.190.990.92230.810.550.550.531.200.910.830.811.431.221.020.93240.840.580.560.531.230.950.840.861.471.221.040.97250.840.590.560.541.240.950.870.861.471.261.060.97260.850.600.570.571.280.970.880.861.521.271.091.02270.860.600.610.581.280.990.900.901.521.311.091.02280.890.620.610.581.311.010.920.901.541.311.141.03290.890.640.610.581.331.020.930.931.571.351.141.07300.890.640.620.581.331.040.940.931.571.361.171.07350.940.690.660.631.411.141.021.001.671.461.241.17400.990.740.730.681.471.191.081.051.761.551.331.27451.040.790.760.721.531.271.141.111.831.611.381.32501.080.840.800.751.611.331.181.171.911.661.461.40551.090.840.850.771.661.381.221.201.961.751.581.46601.140.890.850.821.721.431.271.242.021.801.631.51651.170.910.900.831.741.471.311.292.101.851.681.56701.200.940.900.871.771.521.351.342.151.901.731.61751.230.990.930.871.821.541.401.382.201.951.771.66801.240.990.950.911.861.581.421.392.262.001.851.70851.281.030.950.921.911.631.461.442.302.041.891.75901.291.031.000.931.941.671.471.482.342.091.921.80951.331.081.000.961.961.681.511.492.392.111.961.851001.331.081.030.971.981.721.551.522.442.172.011.901051.351.101.050.972.011.761.561.542.492.192.041.911101.381.131.051.002.051.771.571.582.502.242.071.971151.391.131.061.022.061.801.601.592.542.292.112.001201.411.151.101.042.101.821.611.632.592.292.162.04
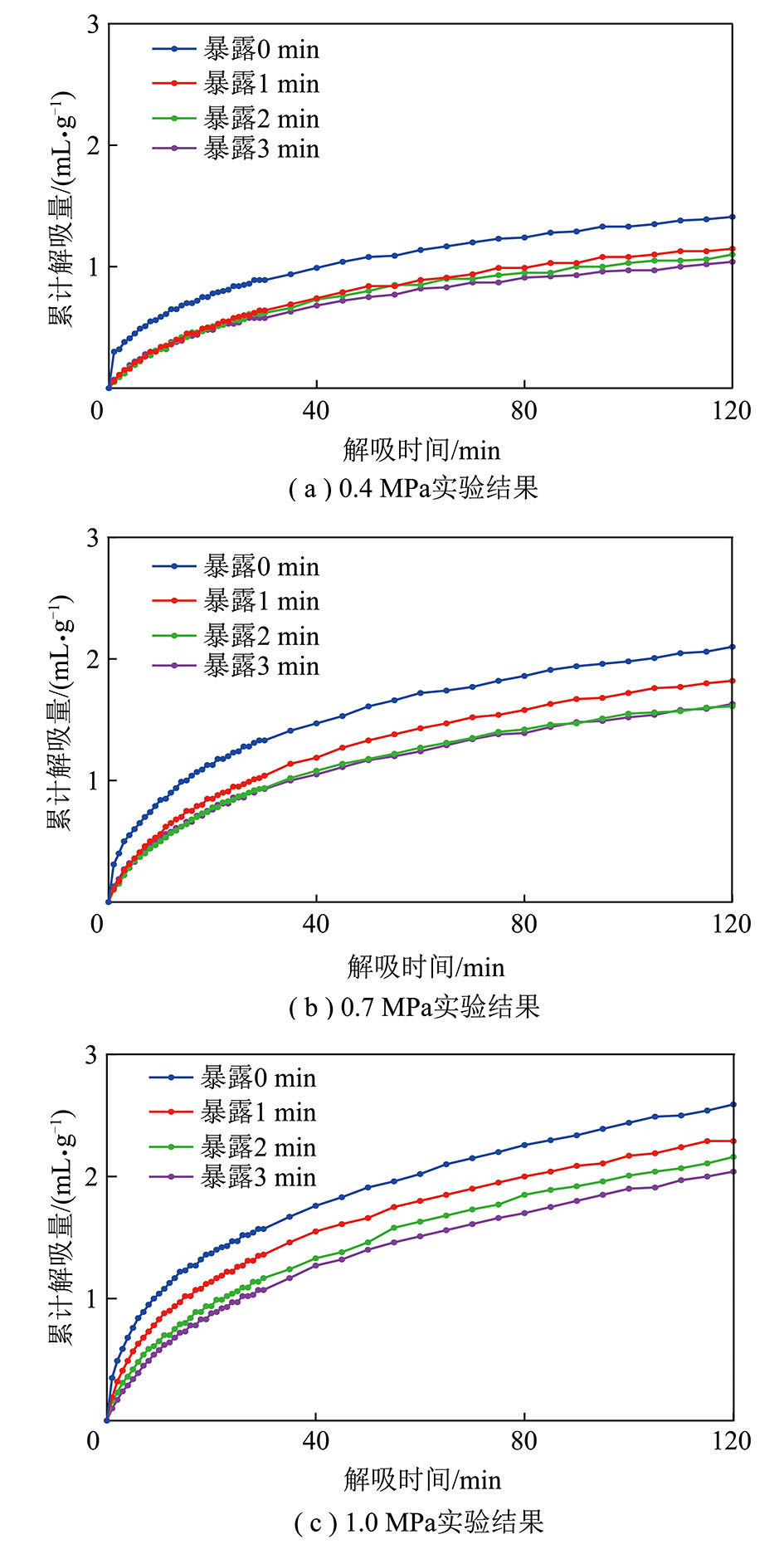
图2 不同压力和暴露时间下瓦斯解吸曲线
Fig.2 Coal gas desorption curves at different pressure and sampling time
qt=q0(1+t)-n
(2)
式中,qt为t时间的解吸速度,mL/min;q0为t=0时的瓦斯解吸速度,mL/min;n为瓦斯解吸速度衰减系数,0<n<1。
幂函数法的煤样损失瓦斯量依据式(3)计算:
![]()
(3)
表2~4反映了不同压力下![]() 法与幂函数法损失量的计算结果。其中标准值是煤样在没有暴露条件下即暴露时间为0时瓦斯解吸量的实际测定值;表2~4中暴露时间为1,2,3 min的标准值分别对应为在暴露时间为0时的1,2,3 min实测的瓦斯解吸量。根据国标对这2种方法应用的规定,对暴露1,2,3 min实验组的数据通过
法与幂函数法损失量的计算结果。其中标准值是煤样在没有暴露条件下即暴露时间为0时瓦斯解吸量的实际测定值;表2~4中暴露时间为1,2,3 min的标准值分别对应为在暴露时间为0时的1,2,3 min实测的瓦斯解吸量。根据国标对这2种方法应用的规定,对暴露1,2,3 min实验组的数据通过![]() 法和幂函数法计算损失量,将计算结果与暴露0 min的标准值进行比对,计算两者之间的偏差值和偏差比例。0.4,0.7,1.0 MPa下计算结果分别见表2~4,暴露时间的单位为min,损失量的单位为mL/g。
法和幂函数法计算损失量,将计算结果与暴露0 min的标准值进行比对,计算两者之间的偏差值和偏差比例。0.4,0.7,1.0 MPa下计算结果分别见表2~4,暴露时间的单位为min,损失量的单位为mL/g。
观察发现,2种方法在不同压力和暴露时间下的拟合损失量与损失量标准值均存在较大偏差,![]() 法计算的损失量与标准值的偏差范围为0.11~0.22 mL/g,偏差幅度为31.22%~57.49%,幂函数法计算的损失量与标准值的偏差范围为0.15~0.34 mL/g,偏差幅度为42.86%~80.00%。2种方法拟合损失量的偏差程度在各实验条件下均超出
法计算的损失量与标准值的偏差范围为0.11~0.22 mL/g,偏差幅度为31.22%~57.49%,幂函数法计算的损失量与标准值的偏差范围为0.15~0.34 mL/g,偏差幅度为42.86%~80.00%。2种方法拟合损失量的偏差程度在各实验条件下均超出![]() 方法偏差程度比幂函数法低。
方法偏差程度比幂函数法低。
![]() 法计算损失量的原理是认为累计解吸量V与解吸时间的平方根
法计算损失量的原理是认为累计解吸量V与解吸时间的平方根![]() 符合线性规律,其损失量计算结果的物理意义是按照
符合线性规律,其损失量计算结果的物理意义是按照![]() 函数,暴露t0时间下的瓦斯累计解吸量。
函数,暴露t0时间下的瓦斯累计解吸量。
幂函数法计算损失量的原理是认为解吸速度q与解吸时间t符合幂函数的关系,幂指数为绝对值小于1的负数,其损失量计算结果的物理意义是按照幂函数,暴露t0时间下的瓦斯累计解吸量。
上述试验结果表明,损失量的计算只与暴露时间和暴露时间内的瓦斯解吸规律有关,既然暴露时间是相同的,采用的测试数据是同一组数据,其偏差产生的原因只能是暴露时间内的瓦斯解吸规律不够准确,
表2 0.4 MPa瓦斯压力![]() 与幂函数法损失量计算结果
与幂函数法损失量计算结果
Table 2 Loss calculation results of ![]() method and power function method at 0.4 MPa gas pressure
method and power function method at 0.4 MPa gas pressure

暴露时间/min标准值/(mL·g-1)损失量/(mL·g-1)t法幂函数法偏差值/(mL·g-1)t法幂函数法偏差百分比/%t法幂函数法10.300.140.060.160.2451.9380.0020.320.200.100.120.2236.9768.7530.380.200.150.180.2348.2660.53
表3 0.7 MPa瓦斯压力![]() 与幂函数法损失量计算结果
与幂函数法损失量计算结果
Table 3 Loss calculation results of ![]() method and power function method at 0.7 MPa gas pressure
method and power function method at 0.7 MPa gas pressure

暴露时间/min标准值/(mL·g-1)损失量/(mL·g-1)t法幂函数法偏差值/(mL·g-1)t法幂函数法偏差百分比/%t法幂函数法10.310.200.110.110.2036.1664.5220.400.270.170.130.2333.2857.5030.500.290.260.210.2442.4848.00
表4 1.0 MPa瓦斯压力![]() 与幂函数法损失量计算结果
与幂函数法损失量计算结果
Table 4 Loss calculation results of ![]() method and power function method at 1.0 MPa gas pressure
method and power function method at 1.0 MPa gas pressure

暴露时间/min标准值/(mL·g-1)损失量/(mL·g-1)t法幂函数法偏差值/(mL·g-1)t法幂函数法偏差百分比/%t法幂函数法10.350.150.200.200.1557.4942.8620.490.270.240.220.2544.1451.0230.590.410.250.180.3431.2257.63
即采用![]() 法和幂函数法进行损失量计算,其方法是不够准确的。也就是说,暴露时间内的累计瓦斯解吸量不完全符合
法和幂函数法进行损失量计算,其方法是不够准确的。也就是说,暴露时间内的累计瓦斯解吸量不完全符合![]() 和幂函数规律。
和幂函数规律。
从煤样的解吸过程进行分析,由于待解吸瓦斯所处结构的差异,解吸速度在不同的时间段应该有一定的差别,不应该符合同一物理规律[20]。瓦斯的最初解吸状态主要是煤中的裂隙和大的孔隙中的游离瓦斯的释放,其释放速度是很快的;然后是煤样表面小孔和微孔中的吸附瓦斯开始解吸,由于其瓦斯的释放要克服吸附力,因此与游离瓦斯的快速释放相比,其释放瓦斯的速度开始变慢;最后是煤样颗粒内部更小的孔隙中吸附的瓦斯开始释放出来,其不仅要克服吸附力,还要克服瓦斯扩散到煤样表面的流动阻力,其释放瓦斯的速度就更慢了,当瓦斯解吸量非常少时,不能克服流动阻力,则瓦斯的累计解吸量趋于平衡。
采用单一的![]() 法和幂函数法进行损失量计算,忽视了瓦斯解吸过程中解吸速度的变化,因此造成了较大的误差。
法和幂函数法进行损失量计算,忽视了瓦斯解吸过程中解吸速度的变化,因此造成了较大的误差。
为更准确地计算损失量,需要对直接法测含量过程中的累计瓦斯解吸曲线的特征进行深入研究,确定各时段瓦斯解吸规律,建立相应的数学模型,才能得到更准确的损失量计算方法。需要以不同压力下暴露0 min的累计瓦斯解吸曲线作为研究对象,研究其曲线的特征规律。
本组实验中,暴露1,2,3 min的瓦斯损失量计算均存在较大的误差,说明其误差产生在3个暴露时间的重合段,即0~1 min时间段内瓦斯解吸规律不符合![]() 与幂函数规律。于是把0~1 min的瓦斯解吸曲线进行局部放大,对比分析不同压力下暴露0 min的累计解吸量与解吸时间t的关系,如图3所示。
与幂函数规律。于是把0~1 min的瓦斯解吸曲线进行局部放大,对比分析不同压力下暴露0 min的累计解吸量与解吸时间t的关系,如图3所示。
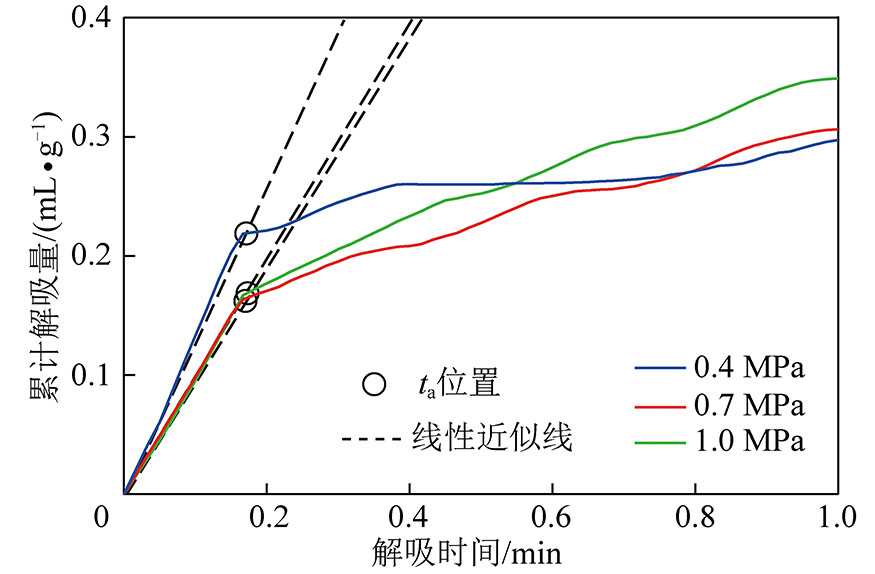
图3 不同压力下暴露0 min累计解吸量与时间的关系
Fig.3 Desorption amount and time with 0 min exposure at different pressures
观察图3发现,3次实验的瓦斯曲线规律均在10 s附近发生明显变化,10 s前累计解吸量与解吸时间基本符合线性规律,10 s后累计解吸量增速变缓。据此分析认为,在瓦斯解吸过程中存在时刻ta,在0~ta内,瓦斯解吸近似符合线性规律,在ta时间后,解吸速度开始持续降低。在0~ta时间内,累计解吸量与解吸时间的关系式应为
V=at
(4)
其中,a为解吸速度。0~ta时间段认为是初期高速释放阶段。
参考![]() 法对解吸规律的描述,以解吸时间平方根
法对解吸规律的描述,以解吸时间平方根![]() 为横坐标、以累计解吸量为纵坐标,绘制了10 s后的解吸曲线,如图4所示。观察图4发现,不同压力下累计解吸量与解吸时间的平方根
为横坐标、以累计解吸量为纵坐标,绘制了10 s后的解吸曲线,如图4所示。观察图4发现,不同压力下累计解吸量与解吸时间的平方根![]() 在一定时间内呈线性关系,然后在tb时刻解吸量发生偏离。不同压力下偏离起始点不同,0.4 MPa时位于25~30 min,0.7 MPa时位于14~25 min,1.0 MPa时位于9~14 min。依据分析认为,初期高速释放阶段以后,仍然存在偏离时间点tb,累计解吸量与解吸时间的平方根
在一定时间内呈线性关系,然后在tb时刻解吸量发生偏离。不同压力下偏离起始点不同,0.4 MPa时位于25~30 min,0.7 MPa时位于14~25 min,1.0 MPa时位于9~14 min。依据分析认为,初期高速释放阶段以后,仍然存在偏离时间点tb,累计解吸量与解吸时间的平方根![]() 在tb时间点前基本符合线性关系,在tb时间点后开始偏离线性关系,tb的位置随压力升高而前移。在ta~tb时间段内,累计解吸量与解吸时间的关系式应为
在tb时间点前基本符合线性关系,在tb时间点后开始偏离线性关系,tb的位置随压力升高而前移。在ta~tb时间段内,累计解吸量与解吸时间的关系式应为
![]()
(5)
式中,m为待定常数;n为ta阶段的瓦斯累计解吸量;ta~tb时间段认为是中期快速解吸阶段。
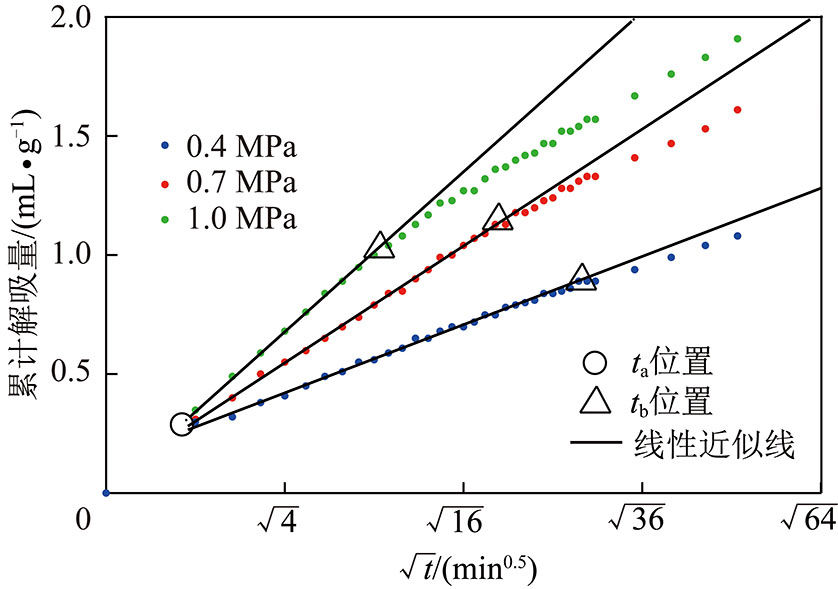
图4 不同压力下暴露0 min累计解吸量与![]() 的关系
的关系
Fig.4 Desorption amount and ![]() with 0 min exposure at different pressures
with 0 min exposure at different pressures
根据幂函数法中解吸量与解吸时间的幂函数关系,对tb后的累计解吸量与解吸时间做幂函数拟合,如图5所示。可以发现,幂函数对该时间段拟合效果良好,在tb前解吸量与幂函数拟合曲线存在一定偏差,偏差点随压力升高向后移动,即压力越高,拟合结果与原数据吻合范围越小。在tb~120 min时间内,累计解吸量与解吸时间的关系式为
![]()
(6)
其中,q0,n为待定常数;tb~120 min时间段认为是后期缓速放散阶段。
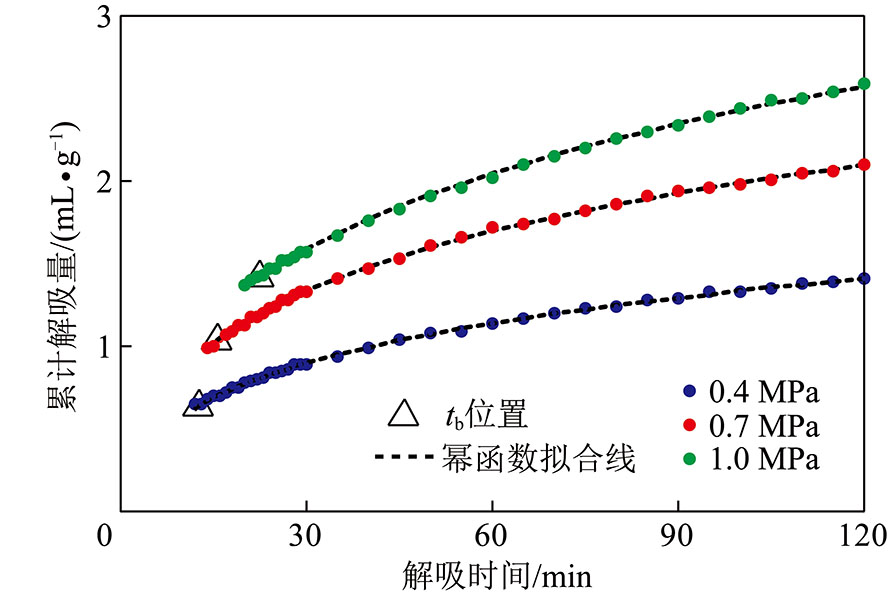
图5 tb后的累计解吸量与解吸时间的幂函数拟合结果
Fig.5 Power function fitting result of cumulative desorption and time after tb
依据上面的分析,直接法测瓦斯含量的累计解吸曲线应分为3个阶段,即符合线性规律的初期高速释放阶段、符合![]() 规律的中期快速解吸阶段、符合幂函数规律的后期缓速放散阶段。该3个阶段的数学模型分别为
规律的中期快速解吸阶段、符合幂函数规律的后期缓速放散阶段。该3个阶段的数学模型分别为

(7)
(1)模拟煤矿井下测试条件,建立了瓦斯解吸实验系统,同时设置了0.4,0.7,1.0 MPa三种的瓦斯吸附压力来改变瓦斯含量条件,设置了0,1,2,3 min煤样暴露4个时间段来改变瓦斯解吸的损失量条件,得到了12组测试数据,并依据现行的直接法测含量的国家标准(GB/T 23250—2009)规定的![]() 法和幂函数法分别确定了瓦斯损失量,对比0 min暴露时间的标准值进行分析。分析结果表明,
法和幂函数法分别确定了瓦斯损失量,对比0 min暴露时间的标准值进行分析。分析结果表明,![]() 法和幂函数法的损失量计算误差较大,
法和幂函数法的损失量计算误差较大,![]() 法计算的损失量与标准值偏差幅度为31.22%~57.49%,幂函数法计算的损失量与标准值偏差幅度42.86%~80%,并从微观角度分析了误差产生的原因。
法计算的损失量与标准值偏差幅度为31.22%~57.49%,幂函数法计算的损失量与标准值偏差幅度42.86%~80%,并从微观角度分析了误差产生的原因。
(2)研究了直接法测含量累计瓦斯解吸量与解吸时间的关系,认为存在ta和tb两个时间分界点,将解吸过程分为了3段,0~ta时间段为符合线性规律的初期高速释放阶段,ta~tb时间段为符合![]() 规律的中期快速解吸阶段,tb~120 min时间段为符合幂函数规律的后期缓速放散阶段,给出了不同阶段对应的解吸量与解吸时间的数学表达式。
规律的中期快速解吸阶段,tb~120 min时间段为符合幂函数规律的后期缓速放散阶段,给出了不同阶段对应的解吸量与解吸时间的数学表达式。
[1] 孙健,魏强,晏波,等.煤层吸附气的全解吸过程及组分与碳同位素变化:基于热模拟实验结果[J].煤炭学报,2018,43(10):2848-2856.
SUN Jian,WEI Qiang,YAN Bo,et al.Full desorption process of coalbed adsorbed gas and changes of components and carbon isotopes:Results based on thermal simulation experiments[J].Journal of China Coal Society,2018,43(10):2848-2856.
[2] 张淑同.井下瓦斯含量直接法测定关键技术研究[J].采矿与安全工程学报,2014,31(2):328-332.
ZHANG Shutong.Research on the key technologies of direct determination of underground gas content[J].Journal of Mining & Safety Engineering,2014,31(2):328-332.
[3] GB/T 23250—2009,煤层瓦斯含量井下直接测定方法[S].
[4] 秦跃平,王健,罗维,等.定压动态瓦斯解吸规律实验[J].辽宁工程技术大学学报(自然科学版),2012,31(5):581-585.
QIN Yueping,WANG Jian,LUO Wei,et al.Experimental study on dynamic gas desorption in constant pressure[J].Journal of Liaoning Technical University(Natural Science),2012,31(5):581-585.
[5] 秦跃平,郝永江,刘鹏,等.煤粒瓦斯放散模型对比分析[J].煤矿安全,2015,46(4):144-147.
QIN Yueping,HAO Yongjiang,LIU Peng,et al.Comparative analysis of coal particle gas dispersion model[J].Safety in Coal Mines,2015,46(4):144-147.
[6] LIU Peng,QIN Yueping,LIU Shimin,et al.Non-linear gas desorption and transport behavior in coal matrix:Experiments and numerical modeling[J].Fuel,2018,214:1-13.
[7] LI Xiaobin,LI Yunbo,TANG Junting.Determining the initial stage loss content of tectonic coal gas desorption via the Bayesian probability method[J].Natural Hazards,2019,97(1):83-97.
[8] 李成武,薛洪来,刘文彪.承压煤体瓦斯解吸-扩散特性实验研究[J].煤炭学报,2018,43(3):717-723.
LI Chengwu,XUE Honglai,LIU Wenbiao.Experimental study on gas diffusion in coal under stress[J].Journal of China Coal Society,2018,43(3):717-723.
[9] 李成武,雷东记.静电场对煤放散瓦斯特性影响的实验研究[J].煤炭学报,2012,37(6):962-966.
LI Chengwu,LEI Dongji.Experimental study on the influence of electrostatic field on the gas release characteristics of coal release[J].Journal of China Coal Society,2012,37(6):962-966.
[10] WANG Fakai,LIANG Yunpei,LI Xuelong,et al.Orthogonal experimental study on multifactor conditions for gas desorption in coal[J].Advances in Civil Engineering,2019,2019:1-12.
[11] SAGHAFI A.Discussion on determination of gas content of coal and uncertainties of measurement[J].International Journal of Mining Science and Technology,2017,27(5):741-748.
[12] 刘彦伟,刘明举.粒度对软硬煤粒瓦斯解吸扩散差异性的影响[J].煤炭学报,2015,40(3):579-587.
LIU Yanwei,LIU Mingju.Effect of particle size on the difference of gas desorption and diffusion of soft and hard coal particles[J].Journal of China Coal Society,2015,40(3):579-587.
[13] CHENG Yuanping,JIANG Haina,ZHANG Xiaolei,et al.Effects of coal rank on physicochemical properties of coal and on methane adsorption[J].International Journal of Coal Science & Technology,2017,4(2):129-146.
[14] LIN Baiquan,LI He,YUAN Desheng,et al.Development and application of an efficient gas extraction model for low-rank high-gas coal beds[J].International Journal of Coal Science & Technology,2015,2(1):76-83.
[15] 李祥春,李忠备,张良,等.不同煤阶煤样孔隙结构表征及其对瓦斯解吸扩散的影响[J].煤炭学报,2019,44(S1):142-156.
LI Xiangchun,LI Zhongbei,ZHANG Liang,et al.Pore structure characterization of different coal rank coal samples and its effect on gas desorption and diffusion[J].Chinese Journal of Coal Society,2019,44(S1):142-156.
[16] 康志勤,李翔,李伟,等.煤体结构与甲烷吸附/解吸规律相关性实验研究及启示[J].煤炭学报,2018,43(5):1400-1407.
KANG Zhiqin,LI Xiang,LI Wei,et al.Experimental research on the correlation between coal structure and methane adsorption/desorption law and its enlightenment[J].Journal of China Coal Society,2018,43(5):1400-1407.
[17] YANG Zhaobiao,QIN Yong,WANG Zhaofeng,et al.Desorption diffusion model and lost gas quantity estimation of coalbed methane from coal core under drilling fluid medium[J].Science China Earth Sciences,2010,53(4):626-632.
[18] 张慧杰,张浪,汪东,等.构造煤的瓦斯放散特征及孔隙结构微观解释[J].煤炭学报,2018,43(12):3404-3410.
ZHANG Huijie,ZHANG Lang,WANG Dong,et al.Gas emission characteristics and microscopic interpretation of pore structure of tectonic coal[J].Journal of China Coal Society,2018,43(12):3404-3410.
[19] 李云波,张玉贵,张子敏,等.构造煤瓦斯解吸初期特征实验研究[J].煤炭学报,2013,38(1):15-20.
LI Yunbo,ZHANG Yugui,ZHANG Zimin,et al.Experimental study on initial characteristics of gas desorption in structural coal[J].Journal of China Coal Society,2013,38(1):15-20.
[20] ROMANOV V N,GRAESER L C,JIKICH S A,et al.Coal-gas interaction:Implications of changes in texture and porosity[J].International Journal of Coal Science & Technology,2016,3(1):10-19.