巷道前方岩层中含水体的存在会严重威胁矿井巷道的安全掘进。目前可用于巷道前方水害超前探测的方法中,地质钻探法可实现岩层富水性的准确判断,但其仅为一孔之见;地球物理超前探测方法仅能定性评价巷道前方岩层富水性相对强弱。因此,开展巷道前方岩层富水性的近定量或定量预测研究,对巷道安全掘进具有较重要指导意义和应用价值[1]。
富水性或水量预测常规方法有数学模型法和统计分析,但实际预测误差较大。为提高预测准确度,基于地球物理方法的探测结果被作为己知信息引入到富水性预测中[2]。田伟[3]利用AVO技术和伪泊松比属性预测了灰岩层的富水性。此外,神经网络等非线性预测方法同样被用来预测水量。刘国辉等[4]提出与含水量相关的多个地球物理参数,并利用支持向量机对含水层水量进行预测。在矿井瞬变电磁法探测中,吴红霞[5]采用人工神经网络实现对砂岩层的富水性进行预测。在隧道超前探测中,聂利超[6]、TONG M[7]等利用激发极化衰减信息与水量的定量相关关系,初步实现了隧道掘进工作面前方岩层水量预测。
作为常用于巷道超前探测的矿井瞬变电磁法目前仅能定性评价巷道前方低阻异常体的富水性相对强弱,且判断结果依赖解释人员的经验,还无法做到含水量或者富水性的近定量或定量判断。此外,在其探测时仅能获得随采样时间变化的感应电动势值,参数信息过于单一,目前也仅通过物理模拟等手段验证瞬变电磁响应特征与巷道前方岩层中含水体水量多少有关[8]。至于二次场衰减信息与岩层含水量或富水性的定量关系还鲜有报道。因此,笔者在矿井瞬变电磁法观测数据的基础上挖掘可用于定量预测岩层富水性的特征参数,将改进的蝙蝠算法和BP神经网络结合,建立含水体富水性预测模型,并通过仿真测试和现场试验,检验该方法的可行性和有效性。
1 含水体电性参数与特征提取
1.1 含水体水量与电性参数关系
电阻率通常被用来描述岩石的导电性,矿物成分、孔隙度、温度及含水量等都是影响岩石电阻率的主要因素。岩层的含水量主要取决于岩层本身的孔隙度及所处地域的水文地质条件。通过试验统计得出岩石电阻率与孔隙度、含水饱和度等关系的经验公式——阿尔奇式(Archie,1962),其表达式为
ρ=αΦ-mS-nρw
(1)
式中,α为岩性附加导电系数;Φ为岩石孔隙度;S为含水饱和度;m为胶结系数;n为饱和度指数;ρw为孔隙水体的电阻率。
由式(1)可知,在进行巷道超前探测时,矿井瞬变电磁法有限的探测范围内,除了孔隙度和含水饱和度以外的地质参数一定,巷道前方含水体水量或富水性预测就可以简化为两个主控因素的预测:孔隙度和含水饱和度。
1.2 特征提取
影响含水体富水性的特征对预测起到了至关重要的作用。矿井瞬变电磁法巷道超前探测时采集的数据仅为随采样时间变化的感应电动势值,可用的特征过于单一,不利于实现含水体富水性预测。因此需要在采样时间和感应电动势值的基础上尽可能挖掘由感应电动势和采样时间衍生出的特征。
基于阿尔奇公式中地质参数与电阻率的关系,建立超前探测模型,发射线圈(Tx)和接收线圈(Rx)位于掘进工作面(图1)。模型中含水体的电阻率取值见表1,部分地质参数采用常见取值:α=1,m=2,n=1.7,ρw=1.1 Ω·m。在验证程序正确性后、采用全空间三维时域有限差分法(FDTD)进行模型正演[9],根据正演结果从感应电动势和采样时间两方面分析并提取与含水体富水性相关的特征。
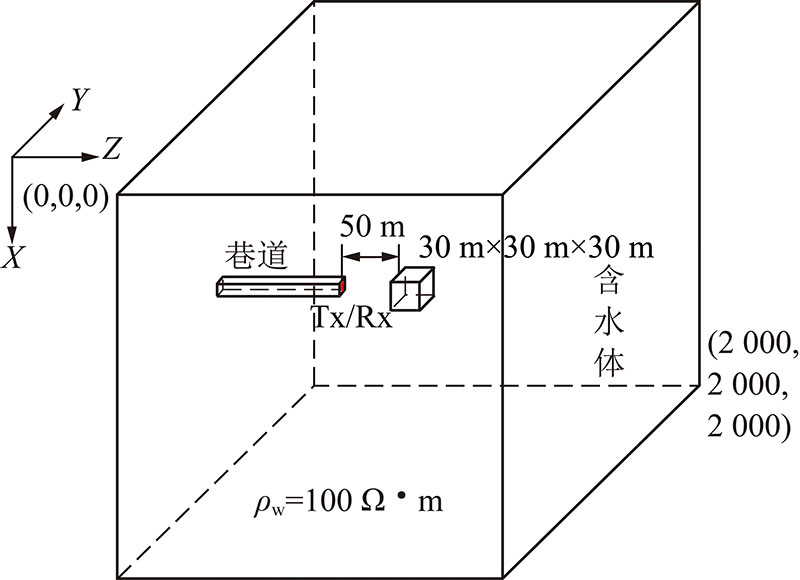
图1 巷道前方存在含水体的超前探测模型示意
Fig.1 Advanced detection model of a single water-bearing body in front of the roadway
表1 含水地质体电阻率值
Table 1 Resistivity of water-bearing geological bodies

Φ/%51015202530S/%100100100100100100ρw/(Ω·m)48.619.711.68.06.04.7
(1)感应电动势及其衍生特征
感应电动势大小与含水体富水性或水量多少的关系已得到验证[8]。矿井瞬变电磁法通常采用视电阻率描述富水性,并且感应电动势的衰减速率也能一定程度反映介质的导电性,所以采用视电阻率和感应电动势衰减速率作为感应电动势的衍生特征。
在含水饱和度为100%,含水体取不同孔隙度值时,计算所得的感应电动势衰减速率如图2(a)所示;采用优化二分搜索法[10]计算视电阻率结果如图2(b)所示。由图2(a)可以看出,在受含水体影响的时间范围内电动势衰减速率总是先变慢再变快,最后趋于一致,且随着孔隙度增大(含水量增加,富水性增强),变化趋势越明显。由图2(b)可以看出,随着孔隙度增大(含水量增加),含水体视电阻率与围岩的差别越大,当孔隙度为5%时,视电阻率与围岩电阻率最接近。

图2 不同孔隙度下电动势衰减速率和视电阻率对比
(对数坐标)
Fig.2 Comparison of attenuation rate of electromotive force and apparent resistivity under different porosity (logarithmic coordinates)
(2)采样时间及其衍生特征
除感应电动势外,另一个可直接获得的信息就是采样时间,根据采样时间通过时深转换可获得深度信息。基于烟圈理论推导获得的巷道超前探测时深转换公式[8]为
![]()
(2)
式中,ti-1和D(ti-1)分别为前一个测道的时间和深度;G(d)为全空间深度系数;ρs(ti)为视电阻率。
考虑到实际地质情况中控制含水体富水性的因素是随空间变化的,为了避免数据在空间上不匹配,采用式(2)将上述3个特征统一到深度域来,这样基于瞬变电磁法的特征参数可以和地质参数在空间域进行配准。因此,将采样时间和时深转换后的探测距离同时作为特征。
在孔隙度不变,含水饱和度变化时可获得同样的规律。因此,针对矿井瞬变电磁法超前预测含水体富水性问题,最终提取了5个特征:感应电动势(V)、采样时间序列(t)、视电阻率(ρs)、探测距离(L)和对数坐标下的感应电动势衰减速率(k)。
2 LBA-BP神经网络预测方法
2.1 LBA-BP神经网络
BP神经网络是一种多层网络的“逆推”学习前馈型网络,其3层网络理论上可任意逼近非线性映射关系。标准BP算法的初始权值、阈值是随机给定的,选取不当则会造成收敛速度变慢和陷入局部极值。针对这种情况,采用具有Lévy飞行特征的蝙蝠算法(LBA)对BP神经网络进行优化[11-13]。
蝙蝠算法利用蝙蝠的回声定位行为。其将可行域内分布的各个可行解视为蝙蝠个体,第i个蝙蝠在空间位置Xi上随机飞行(位置表征问题的解),同时具有独立的速度vi、频率fi、波长λi、响度Ai和脉冲频度ri。在模拟蝙蝠搜索过程中,速度和新解的更新公式[12]为
![]()
(3)
![]()
(4)
式中,![]() 为当前寻找得到的最优解。
为当前寻找得到的最优解。
蝙蝠算法的模型、参数简单且通用性强,但其标准算法缺乏有效的变异机制,导致蝙蝠个体易陷入局部极值、收敛精度低。对此,刘长平等提出采用Lévy飞行策略改进蝙蝠算法的全局搜索性能[14]。利用Lévy飞行的不均匀随机游走特性对蝙蝠算法进行优化,避免了蝙蝠个体被局部极值吸引,同时还拓展了搜索空间,提高蝙蝠算法的优化效果[15-16]。改进的方式是将Lévy飞行引入原有算法的位置更新公式[15],具体如下:
![]()
(5)
式中,Lévy(λ)为步长服从Lévy分布的随机搜索向量;λ∈[1,3]为尺度函数;x*为当前最佳蝙蝠所处位置。
2.2 可行性分析
矿井瞬变电磁法超前探测结果主要为巷道前方岩层的富水性相对强弱的定性评价,无法做到富水性或含水量的近定量或定量判断。采用LBA-BP神经网络解决此类复杂预测问题是非常有效的方法,这得益于BP神经网络具有以下特点:
(1)具有较强的非线性映射能力。把含水体富水性或水量与地球物理特征参数、地质特征参数之间的关系看成某种映射关系时,就可用BP网络模型来模拟这种关系。
(2)良好的容错性。当部分矿井瞬变电磁法观测数据因干扰无效或因观测失误导致信息错误时,预网络模型仍然可以给出较为正确的预测结果。其在不完全信息时的预测能力是其他定量预测数学模型不具备的。
(3)自组织、自适应、自学习的能力。BP网络模型通过自组织和自适应的机制,找出含水体富水性与特征参数之间的非线性映射关系,此外,还能通过新的实例进行自学习和再励学习,一旦遇到相似特征参数组合,网络就能正确的给出含水体富水性的定量结果。
(4)数据融合能力。BP神经网络能够同时处理定量信息(地球物理观测数据等)和定性信息(水文地质和钻孔信息等),提高预测准确度。
3 预测模型建立及仿真测试
3.1 参数选择
预测模型的建立依赖于要解决的实际问题。基于矿井瞬变电磁法的特征和预测目标确定了LBA-BP神经网络结构,如图3所示。

图3 LBA-BP神经网络结构示意
Fig.3 Topological structure of BP neural network
预测效果最优特征组合为5个特征全部采用。网络隐含层为1,隐层节点数为10;隐层传递函数选用S型函数,输出层选用双曲正切S型函数;学习率η=0.01;最大迭代次数为2 000次;目标精度0.001;蝙蝠初始种群数n=20,最大迭代次数为40,Amin=0,α=γ=0.98,f∈[0,2],v∈[-10,10]。
3.2 仿真测试
考虑到巷道掘进工作面前方岩层富水性不均匀,同时参考煤系地层中主要含水层岩性的孔隙度和含水饱和度取值范围[3-4],建立超前探测正演模型,并通过FDTD数值模拟结果提取相应特征与模型实际Φ和S构成预测网络模型所需的样本数据。正演模型尺寸与图4相同;异常单元电阻率分布如图5所示,单元的参数设置见表2。按照巷道超前探测工作角度(左偏60°~右偏60°,间隔15°,共9个角度)进行数值模拟,整理后共获得405组样本数据。训练、测试结果见表3。
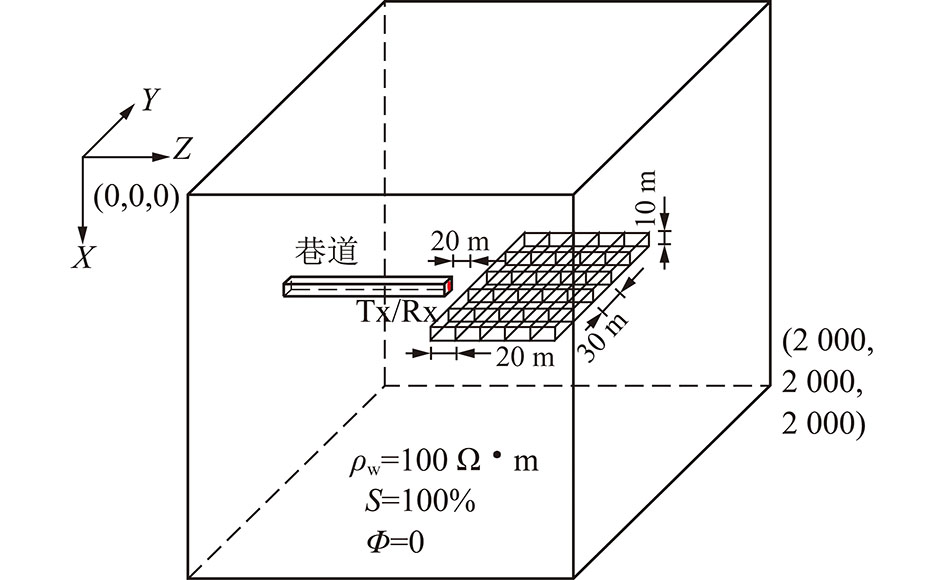
图4 巷道前方岩层富水性不均匀模型示意
Fig.4 Water-inhomogeneous model of rock formation in front of roadway

图5 异常单元电阻率分布
Fig.5 Resistivity distribution of abnormal unit
表2 异常单元地质参数
Table 2 Abnormal unit geological parameter
%
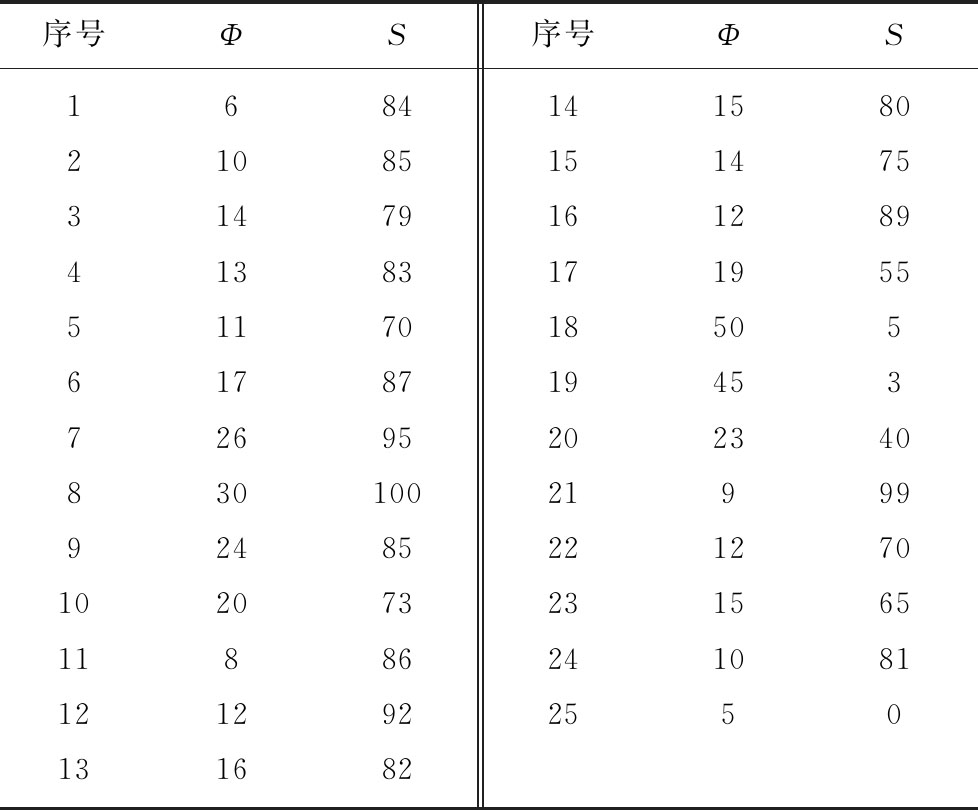
序号ΦS序号ΦS168414158021085151475314791612894138317195551170185056178719453726952023408301002199992485221270102073231565118862410811212922550131682
表3 均方误差对照
Table 3 Comparison of mean square error

种类训练集测试集孔隙度(Φ)3.5×10-32.6×10-3含水饱和度(S)2.3×10-21.1×10-2
由表3可知,测试样本误差接近且略小于训练样本误差,说明建立的预测模型具有良好的性能和泛化能力。为了验证预测模型的可靠性,建立一个类似的模型对训练好的预测网络进行验证。
为了与实际情况更为接近,以探测方向0°(正前方)为例,对模拟数据不加噪声、加噪声的预测结果进行对比,如图6所示。

图6 验证集预测结果
Fig.6 Output of verification set network
由图6可以看出,孔隙度和含水饱和度定量预测的均方误差随着噪声的增大而增大。当模拟数据不含噪声时,预测精度最高,预测值与真实值基本对应;当存在噪声时,预测值出现明显的波动,且当噪声程度增大时,预测结果波动愈加明显。然而,预测的均方误差均不超过1%,表明预测准确度仍处在一个较高的水平。
仿真测试结果表明采用LBA-BP神经网络进行基于矿井瞬变电磁法超前探测数据的巷道前方含水体的孔隙度、含水饱和度定量预测是可行的,具有较高的预测精度。
4 现场试验
4.1 地质概况
本次现场试验是结合某矿-980边界进风下山巷的矿井瞬变电磁法超前探测工程进行。巷道在3煤层顶板砂岩中掘进。巷道掘进的直接充水含水层是3煤层的顶板砂岩含水层和太原组三灰含水层。其中顶板砂岩含水层富水性不均,径流不畅、补给条件差,基本以静储存水量为主。巷道掘进过程中主要受3煤顶底板砂岩含水层影响。因此,顶板砂岩含水层成为巷道充水的最直接充水水源,而在巷道掘进过程中,基本不扰动三灰含水层,正常情况下三灰层不会出水。
4.2 矿井瞬变电磁法数据采集与处理
本次巷道超前探测仪器采用Terra-TEM瞬变电磁仪,采集时间序列选用标准时间序列,发射、接收线圈采用边长2 m×2 m的方形回线,发射、接收回线匝数分别为40匝和60匝,装置形式采用重叠回线,发射电流为1.75 A。此次超前探测的角度布置如图7所示。矿井瞬变电磁法数据处理中视电阻率计算同样采用优化二分搜索法,时深转换采用的是基于烟圈理论推导的时深转换超前探测(式(2))。
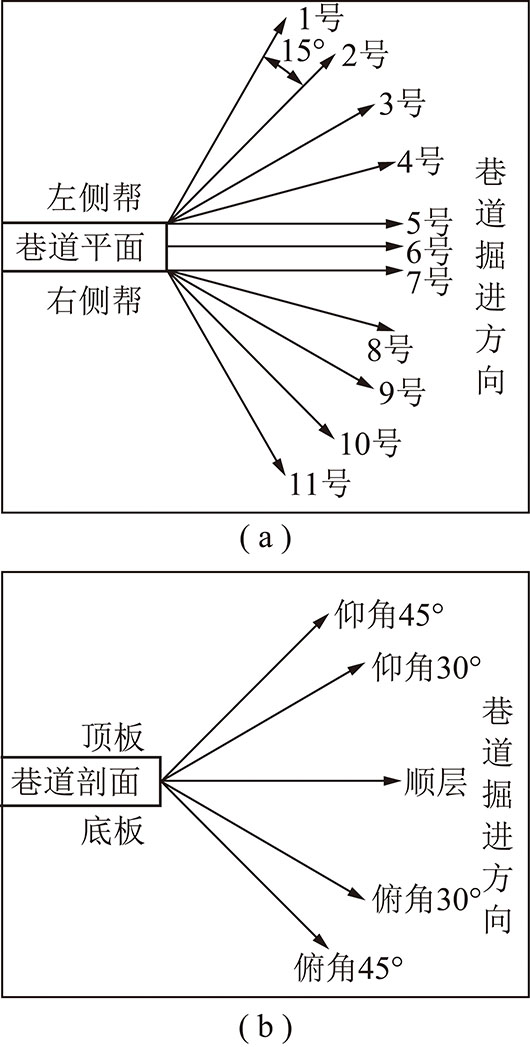
图7 探测角度示意
Fig.7 Detection angle diagram
4.3 岩层富水性定量预测试验
实际地层结构中,巷道前方含水体的富水性受多因素影响,无法对其进行定量或近定量预测,因此将富水性划分等级并与孔隙度和含水饱和度建立对应关系。根据富水性分级标准,以近定量预测的结果(孔隙度、含水饱和度)来判别巷道前方岩层的富水性情况。通过以上方法获得的含水体富水性客观且精度较高,避免了判断结果依赖人为经验。
(1)富水性预测分级标准
由巷道掘进地质资料可知,巷道在3煤层顶板砂岩中掘进可能受3煤层顶板砂岩水威胁,该砂岩含水层位于3煤顶板,以细砂岩为主,次为中砂岩和粉砂岩,局部发育裂隙,岩石孔隙度参数见表4。
表4 煤层顶、底板岩石孔隙度统计
Table 4 Coal seam top and bottom rock porosity statistics table

指标泥岩粉砂岩细砂岩中砂岩孔隙度/%3.04~4.463.943.57~8.695.101.73~9.825.693.30~3.723.51
注:![]()
根据巷道掘进过程中大部分砂岩未出水,且巷道附近区域的砂岩孔隙度平均值不超过6%,参考富水性划分标准[6],将探测范围内砂岩层的富水性按孔隙度大小划分为不含水(或极弱含水)、弱含水、中等含水和强含水4个等级。此外,潜水面之下的岩石孔隙通常几乎充满水,所以在此次钻孔未提供含水饱和度具体信息的情况下,认为探测范围内所有的岩石含水饱和度都在92%~100%。综上可以得出砂岩富水性的划分标准,见表5。
表5 富水性评价分级标准
Table 5 Classification standard for water abundance assessment

富水性分级不含水弱富水中等富水强富水孔隙度/%0~66~1212~20>20含水饱和度/%92~10092~10092~10092~100
(2)预测模型构建及训练
此次巷道掘进工作面共布设3个超前探查孔,如图8所示。将其中2个钻孔(1-2号,1-3号)的信息与矿井瞬变电磁法实测数据对应方向采集数据按照距离进行空间配准,提取5个特征与钻孔信息中的孔隙度和含水饱和度信息相结合构成样本数据。其中含水饱和度在92%~100%随机赋值。
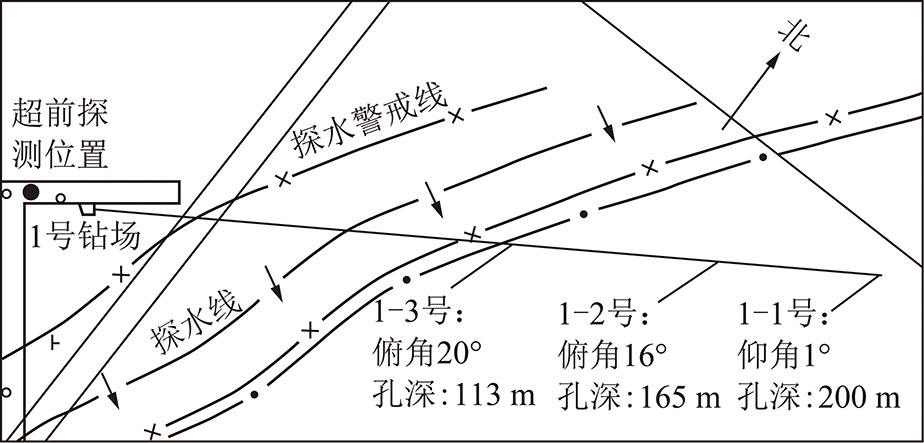
图8 钻孔位置平面示意
Fig.8 Plane sketch of drilling position
预测模型及参数设置与仿真测试相同,将上述样本数据按3∶1∶1的比例分为训练样本、测试样本和验证样本进行训练,直至预测模型可以保证富水性预测在无验证信息下的准确性为止。
(3)预测效果评价
在确保训练后的预测模型具有良好的性能和泛化能力后,对探查孔1-1号进行预测,预测结果如图9所示。由图9可以看出,1-1号钻孔经过的岩层含水饱和度预测值在95.5%~98.0%;孔隙度在前50 m处于5%左右,到58 m时达到6%,到66 m时孔隙度最大为8.5%,到77 m时减小到6%以下,之后随着距离的增大,孔隙度略微有所增大,但都维持在6%以下。对照富水性划分标准可知58~76 m段岩层为弱富水反映,其余段砂岩均不含水或极弱含水。

图9 预测输出结果
Fig.9 Output of prediction
图10为1-1号钻孔所在水平探测扇面的视电阻率断面成果图(红色虚线表示1-1号钻孔位置)。按照常规电阻率解释方法,图中在钻孔位置20~40 m范围内岩层为不含水-极弱含水反映,55~70 m为不含水反映,在70 m之后岩层的富水性逐渐增强,到90 m时岩层表现为相对弱含水,但由于晚期数据受干扰影响较为严重,因此大于100 m范围视电阻率结果参考意义较小。

图10 超前探测视电阻率断面
Fig.10 Advanced detection apparent resistivity profile
对比预测结果和视电阻率解释结果可知,两者主要在58~75 m段存在差别,预测结果显示此段的岩层为弱含水,而视电阻率解释结果显示此段岩层的富水性比周围岩层的富水性差,为不含水反映。实际钻孔1-1号在63 m处见水,水量0.5 m3/h,说明巷道前方63 m附近确实存在弱富水区,这与预测结果峰值对应的66 m吻合较好。
由此可以看出,采用基于LBA-BP的富水性预测方法实现了岩层富水性的定量解释,对巷道前方岩层富水性的预测准确度要明显优于常规视电阻率解释方法。
5 结 论
(1)在岩性及地层电阻率等参数稳定时,含水体的电阻率主要与孔隙度和含水饱和度有关,含水体富水性的预测可以简化为预测含水体的孔隙度和含水饱和度。
(2)感应电动势、采样时间序列、视电阻率、探测距离和感应电动势衰减速率等5个参数可作为进行富水性或水量预测的特征,且最优的特征组合为5个特征同时采用。
(3)采用LBA-BP神经网络进行基于矿井瞬变电磁法超前探测数据的含水体富水性预测是可行的,可以实现孔隙度和含水饱和度的定量预测以及岩层富水性的定量或近定量预测。
(4)基于LBA-BP神经网络的预测方法对巷道前方岩层富水性的解释准确度要优于常规视电阻率解释方法,能够提高矿井瞬变电磁法的解释精度。
[1] 程久龙,李飞,彭苏萍,等.矿井巷道地球物理方法超前探测研究进展与展望[J].煤炭学报,2014,39(8):1742-1750.
CHENG Jiulong,LI Fei,PENG Suping,et al.Research progress and development direction on advanced detection in mine roadway working face using geophysical methods[J].Journal of China Coal Society,2014,39(8):1742-1750.
[2] 林传年,李利平,韩行瑞.复杂岩溶地区隧道涌水预测方法研究[J].岩石力学与工程学报,2008,27(7):1469-1476.
LIN Chuannian,LI Liping,HAN Xingrui.Research on forecast method of tunnel water inrush in complex karst areas[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(7):1469-1476.
[3] 田伟,邹冠贵,汤小明,等.基于AVO技术与伪泊松比属性预测灰岩富水性的方法[J].煤炭学报,2017,42(10):2706-2717.
TIAN Wei,ZOU Guangui,TANG Xiaoming,et al.Method of predicting the water abundance of limestone based on AVO technique and pseudo Poisson’s ratio attribute[J].Journal of China Coal Society,2017,42(10):2706-2717.
[4] 刘国辉,侯征,王天意,等.一种新型的地下含水层涌水量预测模型[J].地球物理学进展,2012,27(3):1268-1273.
LIU Guohui,HOU Zheng,WANG Tianyi,et al.A new model to predict the water in flow of aquifer[J].Progress in Geophysics,2012,27(3):1268-1273.
[5] 吴红霞.基于神经网络的矿井瞬变电磁法预测岩层富水性研究[D].北京:中国矿业大学(北京),2013.
WU Hongxia.Research on transient electromagnetic method to locate water-rich area based on artificial neural networks[D].Beijing:China University of Mining and Technology(Beijing),2013
[6] 聂利超.隧道施工含水构造激发极化定量超前地质预报理论及其应用[D].济南:山东大学,2014.
NIE Lichao.Quantitative identification theory and its application of advanced geological prediction for water-earing structure using induced polarization in tunnel construction period[D].Jinan:Shandong University,2014.
[7] TONG M,LI L,WANG W,et al.Determining capillary-pressure curve,pore-size distribution,and permeability from induced polarization of shaley sand[J].Geophysics,2006,71(3):33-40.
[8] 胡雄武.巷道前方含水体的瞬变电磁响应及探测技术研究[D].淮南:安徽理工大学,2014.
HU Xiongwu.Research on transient electromagnetic response of water ahead of tunnel and its detection technology[D].Huainan:Anhui University of Science and Technology,2014.
[9] 程久龙,黄少华,温来福,等.矿井全空间三维主轴各向异性介质瞬变电磁场响应特征研究[J].煤炭学报,2019,44(1):278-286.
CHENG Jiulong,HUANG Shaohua,WEN Laifu,et al.Response characteristics of three-dimensional axial anisotropic media for transient electromagnetic method in underground whole-space[J].Journal of China Coal Society,2019,44(1):278-286.
[10] 姜国庆,程久龙,孙晓云,等.全空间瞬变电磁全区视电阻率优化二分搜索算法[J].煤炭学报,2014,39(12):2482-2488.
JIANG Guoqing,CHENG Jiulong,SUN Xiaoyun,et al.Optimized binary search algorithm of full space transient electromagnetic method all-time apparent resistivity[J].Journal of China Coal Society,2014,39(12):2482-2488.
[11] KHAN Koffka.A Comparison of BA,GA,PSO,BP and LM for training feed forward neural networks in e-learning context[J].International Journal of Intelligent Systems and Applications,2012,4(7):23-29.
[12] YANG X,GANDOMI AH.Bat algorithm:A novel approach for global engineering optimization[J].Engineering Computations,2012,29(5):464-483.
[13] BANGVAL WH,AHMAD J,RAUF HT.Optimization of neural network using improved bat algorithm for data classification[J].Journal of Medical Imaging and Health Informatics,2019,9(4):670-681,12.
[14] 刘长平,叶春明.具有Lévy飞行特征的蝙蝠算法[J].智能系统学报,2013,8(3):240-246.
LIU Changping,YE Chunming.Bat algorithm with the characteristics of Lévy flights[J].Journal of Intelligent Systems,2013,8(3):240-246.
[15] REYNOLDS A M.Cooperative random Lévy flight searches and the flight patterns of honeybees[J].Physics Letters A,2006,354(5-6):384-388.
[16] MRIDUL C,MANOJ D.Lévy Flights in metaheuristics optimization algorithms-a review[J].Applied Artificial Intelligence,2018:1-20.
