岩体初始应力场是岩石工程数值模拟计算与工程稳定性分析的必要条件,也是岩石工程设计与施工的重要依据。地应力是煤矿开采等地下工程围岩变形与破坏的根本驱动力,因此应力场研究是岩石力学与采矿工程中最基本、最重要的工作之一[1]。在地应力研究初期,基本上将地应力简单地处理为求解侧压力系数,复杂地质条件下误差较大,根本不适合实际使用。1983年,郭怀志等[2]提出了采用实际工程地应力实测资料,运用有限元数学模型回归分析方法求解出岩体初始应力场。具体作法是依据弹性力学应力叠加原理,将复杂的边界应力条件分解为几个简单的边界条件的线性组合,通过回归方法求解组合系数来实现,奠定了多元回归方法拟合初始地应力方法的基础。此后,诸多学者开始研究地应力场的反分析方法,朱伯方[3]提出通过利用地下工程掘进过程中实测位移进行小范围的地应力反演;2000年以后,大量文献引入遗传算法与神经网络等优化算法寻求地应力反演最优解[4-10],在诸多岩土工程的地应力场反演中广泛使用这些反演方法,岩体被简化为理想的各向同性材料,采用弹性模型分析,基本都能得出比较理想的结果[11-12]。为了进一步提高反演精度,郭运华等[13]提出了一种基于FLAC3D改进的初始地应力场回归方法,该方法对各应力分量分别进行回归,以提高局部异常应力区域的拟合精度。
近年来,地应力反演方法也应用于煤矿领域,取得了一定的成效[14-17]。对于煤层岩体,有其特殊的层状结构,特别是多层构造的煤系地层其力学性质在垂直和平行于岩层走向的两个方向上,差异很大,具有横观各向同性弹性体典型的特征。因此对于初始地应力场的反演,可以将这种深部层状构造煤岩体假设为横观各向同性弹性体进行研究。笔者近几年在淮南矿区,接触到了诸多典型的层状结构煤层,含煤地层一般是沉积岩,除煤层外,地层中含有多层岩石夹层,其最常见的岩性有泥岩和砂岩,其厚度从几厘米至几米,几十米不等,复杂结构含煤地层中夹层数一般多达几十层,而且岩层一般具有一定倾角,倾角随着岩层变化,岩层的力学性质在方向上也不相同,有的甚至显著不同,这样的层状结构增加了求取力学参数和进行数值模拟的难度[18]。因此,对具有典型横观各向同性岩体的应力场研究很有现实意义。陈宇龙和张宇宁[19]研究了横观各向同性岩石在不同层面倾角条件下的单轴压缩破坏过程及声发射特性,结果显示互层岩体有特殊的破坏形式。张志增[20]对横观各向同性岩体做了系统的研究,提出了一种用于反演横观各向同性岩体地应力的方法,该方法通过巷道内岩体位移来反演横观各向同性岩体地应力,通过测量岩体位移,根据巷道位移解析公式得到地应力表达式。
煤系地层由于厚度及倾角变化等,通过实测得到各层岩体的力学参数具有一定的难度。笔者介绍了一种基于FLAC3D横观各向同性模型,通过实测地应力参数,对具有板状岩层构造的矿区进行地应力场反演的方法。
1 基本原理
1.1 多元回归原理
多元回归方法是建立在弹性力学应力叠加原理基础上,在岩土天然应力状态下,可以认为岩土体处于平衡状态且无持续的塑性变形的变化,将地质体所受的复杂地应力分解为图1中6种简单的边界应力形式,通过在边界施加单位荷载获得内部单元的基本初始应力,然后将基本初始应力当做自变量,实测地应力当做因变量进行偏最小二乘回归分析,最终求解回归系数。
假设经过复杂地质运动后的地应力由图1中6种简单地质运动叠加影响形成,则地应力可由式(1)得到。将实测结果与图1中6种简单加载方式求得的相同位置的地应力结果进行回归分析,可以求得式(1)中的系数,将实测值表示为几种简单加载方式计算值的组合,回归方程为

图1 边界应力分解组合示意
Fig.1 Decomposition of boundary stress
σd=l1σx+l2σy+l3σm+l4τxy+l5τxz+l6τyz+e
(1)
式中,σd为初始地应力;σm为自重应力引起的应力;σx,σy,τxy,τxz,τyz分别为水平x向挤压、水平y向挤压、xy平面内剪切、xz平面内剪切、yz平面内剪切运动引起的应力;e为常数;l1~l6为回归系数。
1.2 FLAC3D横观各向同性模型
大型三维软件FLAC3D已经广泛地应用于岩土力学工程分析中,FLAC3D程序自带有横观各向同性弹性材料、莫尔-库仑弹塑材料和应变软化和硬化塑性材料等多种本构模型。横观各向同性弹性材料本构模型主要模拟层状结构的弹性介质,模型中垂直于层状介质的弹性模量和平行于介质的弹性模量明显不同。含煤地层的沉积岩正符合了横观各向同性弹性材料模型的特点。FLAC3D横观各向同性弹性材料模型包含了5个独立的弹性常量和2个岩层物理量,其中5个独立弹性常量为各向同性平面内的弹性模量、垂直于各向同性平面内弹性模量、垂直于各向同性平面内的剪切模量以及2个不同平面内的泊松比,2个岩层物理量为各向同性平面的倾向、各向同性平面的倾角。本文通过数值试验得到2个方向的弹性模量、剪切模量以及泊松比;通过截面岩层的数学关系计算得到各向同性平面平均的倾向和倾角与所建坐标系的关系式。
2 应力场加载至模型
通过多元回归拟合,得到地应力回归方程。地应力加载即将满足回归方程的应力分量载入模型单元及求解边界节点力实现模型力平衡,用于下一步分析设计、数值计算的过程。在已有的地应力场回归反演文献中,基本上都只介绍了求解回归方程的过程,而对地应力场如何加载至模型很少提及。郭运华等[13]提出如下一套加载方案:通过上述提到的6种简单的加载方式,得到每种加载方式下模型单元的应力分量,并将其作为回归方程的一个自变量,实测值作为因变量进行偏最小二乘回归,求解得到回归方程系数。按回归方程计算各单元地应力分量,并赋值给模型单元应力分量。此时模型单元只有内力,节点力均为0,并不能达到平衡。此时需要计算模型节点不平衡力,将求得的节点荷载(与不平衡力大小相等,方向相反)加载至模型中,这样便满足了模型的边界应力条件,同时应力场也满足实测地应力回归估计值。
3 潘一矿东区地应力反演分析
3.1 工程概况
潘一矿东区位于安徽省淮南市北部潘集区。南以淮河与淮南老矿区相隔,西与张谢矿区相邻。潘一矿井东起第0勘探线与潘二矿毗邻,西至第Ⅸ勘探线及技术边界线与潘三矿相接,北以F2、潘集背斜轴、F4、F5、F5-1断层与潘二、潘北矿为界,南至13-1煤层-800 m底板等高线地面投影线。矿井东西走向长14.6 km,倾斜宽约4 km,面积约58.4 km2,如图2所示。

图2 潘一东矿区范围示意
Fig.2 Map of Panyi east mining area
潘一矿东区位于潘集背斜及东部倾伏转折端东南翼。总体形态为褶曲构造,发育纵贯全区的轴向东西转南东向的潘集背斜,其间次级褶曲较为发育;区内共发育断层142条,其中正断层113条,逆断层29条,构造复杂程度中等,断层的走向以北西西向为主,其次为北东向等;断层倾向以南南西向为主,其次为北西向等,笔者主要考虑了规模较大的F32,FS2,FS8,FS9四条断层,其走向基本为EW向,倾向为S或N向,倾角40°~70°,如图2所示。已有研究成果[4]显示淮南矿区应力场以水平应力为主,构造应力占绝对优势。最大主应力为NEE—EW向,部分区为NW—SE向。
根据潘一矿东区煤层及巷道的布置以及初始地应力测点的位置,本次模拟选取包含了大部分采区区域,矿区宽度3 500 m,长度5 000 m,深度1 300 m,坐标原点取在整个矿区右下角,y轴沿正北方向,x轴沿正东向,z轴沿深度方向,向上为正。
3.2 地质模型概化
勘查报告显示潘一东区地层自老至新有石炭系、二叠系、第四系,主要是由30多层层厚从1 m至100多米的砂质泥岩、粉砂岩、中砂岩、泥岩、细砂岩、煤层组成,地层综合岩性见表1。数值模型中很难详尽地反映地层情况,有些岩层厚度0.5~2.0 m,而且岩性交互变化,因此必须找到一种有效可行的简化建模方法。笔者将力学性质相近的地层合并,对于层厚较小、层数较多且层面平行的多种岩性交互的地层,则采用等效模型、等效参数代替。具体做法是:首先将力学性质相近、层厚较小的岩层合并;从地面至深部,可按照上覆层(包括强风化岩层)、岩性及交互规律一致的岩层、新岩体等概化地层;同时模型也主要考虑了规模较大的F32,FS2,FS8,FS9四条断层。通过数值模拟计算得到上述交互岩层等效的各向同性和横观各向同性材料参数。根据通过上述方法,可得潘一矿东区地层概化模型如图3所示。

图3 潘一东矿区地质概化分区
Fig.3 Geological overview division of Panyi east mining area
淮南矿业集团及有关单位对潘一矿东区地应力场分析做了大量实测工作,其地应力特征实测数据转换为模型坐标系统见表2。
表2 地应力实测值转换计算结果
Table 2 Results of the conversion of measured stress values

测点埋深/m坐标/mxyz应力分量/MPaσxσyσzτxyτyzτxz1252(1)开切眼底板巷道(C1)800-33551893420-34.51-19.01-19.793.92-0.853.191231(1)运输巷底板巷道(C2)850-14361988370-31.20-21.14-22.255.87-1.834.77外水仓(C3)840-11061032380-12.79-30.44-18.75-1.06-7.15-0.47-848西翼主带式输送机大巷(C4)850-20001221370-20.08-27.62-20.158.00-1.677.28
3.3 材料等效参数计算
自然界中大部分岩石都是各向异性的,特别是沉积岩具有显著的层状构造特征。目前在理论上可将层状岩体处理成横观各向同性介质,其力学关系包含5个弹性常数[20]。
潘一东矿区地层主要是由30多层层厚从1 m至100多米的砂质泥岩、粉砂岩、中砂岩、泥岩、细砂岩、煤层组成。地层综合岩性见表1。为了探索解决这种多层岩体参数的问题,本文采用数值模拟的方法,计算得到岩层的等效参数[21]。
表1 地层综合岩性
Table 1 Comprehensive lithology

概化分层深度/m厚度/m岩性描述225.80表层黏土与强风化层第1层226171.55砂质泥岩与粉砂岩互层,层厚5~6m9.30砂质泥岩7.80泥岩与粉砂岩互层,层厚1m62.15砂质泥岩与中砂岩互层,层厚3~4m21.80砂质泥岩与细砂岩互层,层厚3~4m第2层626102.90砂质泥岩与粉砂岩互层20.40中砂岩与砂质泥岩互层,层厚2~5m5.0018煤5.50粉砂岩82.05砂质泥岩与泥质砂岩互层6.55粉细砂岩第3层76443.40砂质泥岩5.25中砂岩50.50砂质泥岩为主,砂岩为辅8.25中砂岩18.30砂质泥岩与细砂岩互层,层厚2m8.55中砂岩第4层90819.25砂质泥岩与细粒砂岩互层,层厚2m34.15砂质泥岩7.00中粒砂岩13.65泥岩6.30细粒砂岩26.90泥岩16.55中粒砂岩+细砂岩第5层104323.00砂质泥岩23.55细砂岩18.00砂质泥岩第6层1196153.00粉砂岩与泥岩互层
首先根据各岩层的力学性质、岩性互层规律等进行概化分区,将矿区的岩层自上而下简化分为6层,见表3。根据本文等效假设,再对每一层进行数值加载试验,得出各岩层的等效参数。
表3 岩层分区简化
Table 3 Simplified rock partition

岩层编号层厚/m深度/m岩性描述第1层220220第四系松散层和强风化岩层第2层400620砂质泥岩与砂岩互层第3层150770粉砂岩与泥质砂岩互层第4层150920中砂岩、细砂岩和泥质砂岩互层第5层1301050中砂岩、泥岩和泥质砂岩互层第6层2001250粉砂岩、泥岩互层
以第3层为例,该层层厚约150 m,由粉砂岩与砂质泥岩互层组成,倾角随着位置而变化。岩层累计10层,其每层的厚度4~10 m,建立数值计算模型,如图4所示。

图4 层状岩体等效模型
Fig.4 Equivalent model of layered rock mass
模型中各岩层参数分别由实验获得,分别通过对模型轴向加载试验、横向加载试验等数值试验(图5),得出模型的等效参数,见表4,5。

图5 加载试验应力应变曲线
Fig.5 Stress and strain curves of loading test
表4 各向同性材料力学参数
Table 4 Mechanical parameters of isotropic materials

岩层弹性模量/GPa泊松比密度/(kg·m-3)第1层2.00.362200第2层17.00.242650第3层14.00.242650第4层15.00.252650第5层16.80.232600第6层12.30.232600
表5 横观各向同性材料力学参数
Table 5 Mechanical parameters of transverse isotropic materials

岩层弹性模量/GPaExEz泊松比NxyNxz剪切模量Gxz/GPa密度/(kg·m-3)第3层14.514.00.260.245.72650第4层16.515.00.260.256.22650第5层18.416.80.240.237.12600第6层16.812.30.220.235.62600
注:① xy平面为各向同性平面。Ex和Nxy分别为各向同性平面内的弹性模量和泊松比;Ez,Nxz和Gxz分别为垂直于各向同性平面内的弹性模量、泊松比和剪切模量。② 未给出参数的岩层按各向同性弹性模型计算。
另外通过截面岩层的数学关系计算得到各向同性平面平均的倾向和倾角与所建坐标系的关系式。
FLAC3D横观各向同性材料模型中包括2个物理常数,分别为各向同性岩层面的倾向和倾角。研究范围内,岩层的倾向SE—SW,倾角为5°~23°。为了简化计算,岩层的倾向取优势方向0°,倾角根据yz平面内岩层线的几何关系求得,如图6所示。

图6 岩层yz平面剖面
Fig.6 Section of the rock formation in the yz plane
第3层岩层线在yz平面内拟合的方程式为:z=-8×105y2+0.297y+65.53,则岩层的倾角为:θ=-16×10-5y+0.297,rad,其中y为模型中单元的y轴坐标值。通过倾角的关系式即可编写接口文件进行计算。
断层的宽度根据经验及断层附近巷道掘进过程中揭露的断层影响范围,取为40 m,其力学参数为:弹性模量为5 GPa,泊松比为0.35,密度为2 000 kg/m3。至此,全部参数都已求得,可进行地应力反演计算。
3.4 地应力反演
通过以上得到的横观各向同性模型中7个参数,编制FLAC3D计算文件,进行地应力反演计算。整个反演过程通过编写的接口文件读写操作完成。得到横观各向同性条件下对应的地应力回归方程为
σd=2.334σx+2.5σy+1.357σm+1.703τxy+
6.576τxz-8.318τyz+7 611 039.518
反演结果表明初始地应力90%以上的变动都可以被该模型所解释,拟和度较高。由此表明显著性检验是合理的。经应力场平衡计算,得到计算坐标系下测点的地应力实测值与回归值对比见表6,7。
表6 测点实测值与回归值对比
Table 6 Comparison of measured and regression values of points MPa

测点σx实测值回归值横观同性各向同性σy实测值回归值横观同性各向同性σz实测值回归值横观同性各向同性C1-34.5-33.6-28.0-19.0-22.2-24.0-18.8-19.0-20.0C2-31.2-26.7-25.0-21.1-14.6-15.0-22.2-20.1-15.0C3-12.8-14.9-17.0-30.4-28.6-30.0-18.8-19.0-20.0C4-20.1-26.5-27.0-27.6-26.7-24.0-20.1-22.5-23.0测点τxy实测值回归值横观同性各向同性τyz实测值回归值横观同性各向同性τxz实测值回归值横观同性各向同性C13.9224.0614.51-0.847-0.7021.8703.1904.131.210C25.8706.0650.93-1.830-2.230-0.3994.7702.533.820C3-1.060-1.3108.27-7.150-5.5101.110-0.473-0.613-0.823C48.0005.5807.82-1.670-2.1500.1877.2805.232.690
表7 测点实测值与回归值对比
Table 7 Comparison of measured and regression values of points

测点σ1/MPa实测值回归值横观同性各向同性σ1方向/(°)实测值回归值横观同性各向同性σ2/MPa实测值回归值横观同性各向同性σ3/MPa实测值回归值横观同性各向同性C136.136.4-53.1103.511012119.1-23.0-15.918.119.31.54C235.835.0-59.6114.311812620.424.6-19.818.417.0-0.655C333.928.8-36.2183.516815615.417.9-13.812.712.01.01C434.729.2-59.9145.214716118.623.4-16.014.616.4-0.133
由表6,7可知,采用横观各向同性材料进行反演计算的拟合结果误差较小,大部分回归值与实测值之间的绝对误差在30%以内,这些误差产生的原因主要是简化计算模型与实际地质原型之间的差异,需要通过细化计算模型、详尽地质勘察来减少误差。结果还表明采用横观各向同性模型进行计算更能体现具有层状构造的煤系地层力学性质的方向差异性,能提高局部区域的反演精度。
按回归方程计算得到各单元应力值并加载至模型,得到精确满足实测地应力分布的地应力场。通过编写接口文件,计算得到-850 m水平标高平面主应力等值线图(图7)、-850 m水平标高平面最大主应力倾角云图(图8)和-850 m水平标高平面最大主应力方位角云图(图9)。

图7 -850 m水平标高平面最大主应力等值线
Fig.7 -850 m contour map of maximum principal stress in depth
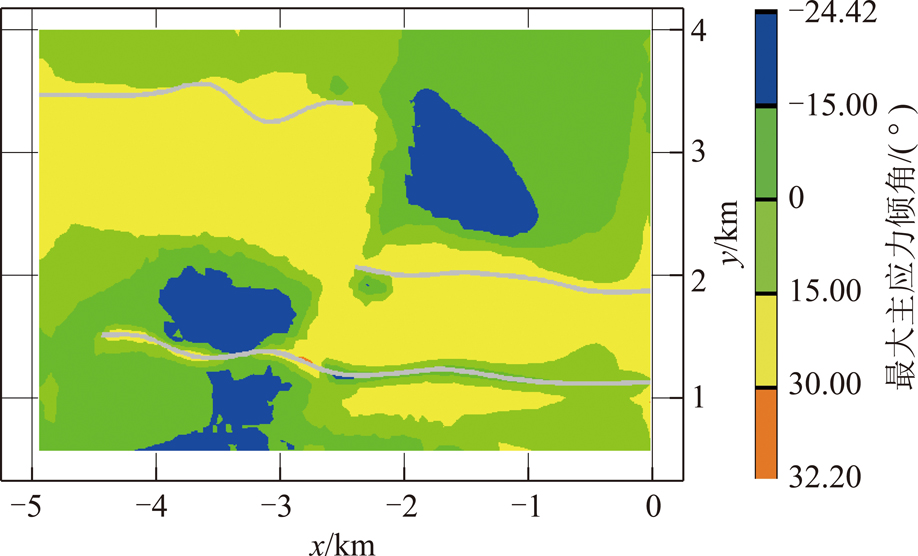
图8 -850 m水平标高平面最大主应力倾角云图
Fig.8 -850 m maximum principal stress inclination cloud indepth

图9 -850 m水平标高平面最大主应力方位角云图
Fig.9 -850 m maximum principal stress azimuth in depth
由图7可知,-850 m水平标高平面岩层的最大主应力值为20~45 MPa,大部分区域最大主应力在35~40 MPa,属高应力水平;总体来看东北区域和西南区域较西北、东南区域最大主应力要稍大。分析原因,所研究的4条断层所在区域与应力降低的区域基本一致,进一步说明断层对地应力的影响。
将最大主应力倾角定义为最大主应力矢量与xy平面的夹角(向上为正),方位角定义为沿正北向(y轴正向)顺时针旋转至最大主应力矢量在xy平面上的投影的角度(0°~360°)。由图9可知,最大主应力方位角优势方向为100°~150°和300°~350°,即主应力的优势方向为NW-SE向。图8表明最大主应力倾角为-24°~32°,大部分倾角为15°~30°,向下倾,近似水平。因此可知最大水平主应力即最大主应力,在布置巷道及煤层开采走向设计时应予以考虑。
4 结 论
(1)选择了分区域横观各向同性模型与各向同性模型相结合的计算方法,反演精度进一步得到提升。
(2)通过煤层分布的几何关系,对煤层倾角作了动态计算,有利于提高数值计算精度。
(3)通过对复杂的地层进行地质概化,建立与实际岩层一致的计算模型,进行数值试验,得到了多层岩体等效力学参数,该方法优化了建模过程,提高了数值计算效率。
[1] 康红普.煤矿井下应力场类型及相互作用分析[J].煤炭学报,2008,33(12):1329-1335.
KANG Hongpu.Analysis on types and interaction of stress fields in underground coal mines[J].Journal of China Coal Society,2008,33(12):1329-1335.
[2] 郭怀志,马启超,薛玺成,等.岩体初始应力场的分析方法[J].岩土工程学报,1983,5(3):64-75.
GUO Huaizhi,MA Qichao,XUE Xicheng,et al.The analytical method of the initial stress field for rock masses[J].Chinese Journal of Geotechnical Engineering,1983,5(3):64-75.
[3] 朱伯芳.岩体初始地应力反分析[J].水利学报,1994(10):30-35.
ZHU Bofang.Back analysis of initial stresses in rock masses[J].Journal of Hydraulic Engineering,1994(10):30-35.
[4] 刘泉声,刘恺德.淮南矿区深部地应力场特征研究[J].岩土力学,2012,33(7):2089-2097.
LIU Quansheng,LIU Kaide.Characteristics of in-situ stress field for deep levels in Huainan coal mine[J].Rock and Soil Mechanics,2012,33(7):2089-2097.
[5] 付成华,汪卫明,陈胜宏.溪洛渡水电站坝区初始地应力场反演分析研究[J].岩石力学与工程学报,2006,25(11):2305-2312.
FU Chenghua,WANG Weiming,CHEN Shenghong.Back analysis study on initial geostress field of dam site for Xiluodu hydropower project[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(11):2305-2312.
[6] 岳晓蕾.大岗山地应力反演与工程应用研究[D].济南:山东大学,2006.
YUE Xiaolei.Research on geostress inversion and engineering application in Dagangshan Mountain[D].Jinan:Shandong University,2006.
[7] 胡斌,冯夏庭,黄小华,等.龙滩水电站左岸高边坡区初始地应力场反演回归分析[J].岩石力学与工程学报,2005,24(11):4055-4064.
HU Bin,FENG Xiating,HUANG Xiaohua,et al.Regression analysis of initial geostress field for left bank high slope region at Longtan hydropower station[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(11):4055-4064.
[8] 梅松华,盛谦,冯夏庭,等.龙滩水电站左岸地下厂房区三维地应力场反演分析[J].岩石力学与工程学报,2004,23(23):4006-4011.
MEI Songhua,SHENG Qian,FENG Xiating,et al.Back analysis of 3D in-situ stress field of underground powerhouse area of Longtan hydropower station[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(23):4006-4011.
[9] 张延新,宋常胜,蔡美峰,等.深孔水压致裂地应力测量及应力场反演分析[J].岩石力学与工程学报,2010,29(4):778-786.
ZHANG Yanxin,SONG Changsheng,CAI Meifeng,et al.Geostress measurements by hydraulic fracturing method at great depth of boreholes and numerical modelling predictions of stress field[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(4):778-786.
[10] 王成虎,张彦山,郭啟良,等.工程区地应力场的综合分析法研究[J].岩土工程学报,2011,32(10):1562-1568.
WANG Chenghu,ZHANG Yanshan,GUO Qiliang,et al.New integrated analysis method to analyze stress regime of engineering area[J].Chinese Journal of Geotechnical Engineering,2011,32(10):1562-1568.
[11] 谢红强,何江达,肖明砾.大型水电站厂区三维地应力场回归反演分析[J].岩土力学,2009,30(8):2471-2476.
XIE Hongqiang,HE Jiangda,XIAO Mingli.Regression analysis of 3D initial geostress in region of underground powerhouse for large hydropower station[J].Rock and Soil Mechanics,2009,30(8):2471-2476.
[12] 张建国,张强勇,杨文东,等.大岗山水电站坝区初始地应力场反演分析[J].岩土力学,2009,30(10):3071-3078.
ZHANG Jianguo,ZHANG Qiangyong,YANG Wendong,et al.Regression analysis of initial geostress field in dam zone of dagangshan hydropower station,rock and soil mechanics[J].Rock and Soil Mechanics,2009,30(10):3071-3078.
[13] 郭运华,朱维申,李新平,等.基于FLAC3D改进的初始地应力场回归方法[J].岩土工程学报,2014,36(5):892-898.
GUO Yunhua,ZHU Weishen,LI Xinping,et al.Improved regression method for initial geostress based on FLAC3D[J].Chinese Journal of Geotechnical Engineering,2014,36(5):892-898.
[14] 单鹏飞,崔峰,曹建涛,等.考虑区域地应力特征的裂隙煤岩流固耦合特性实验[J].煤炭学报,2018,43(1):105-117.
SHAN Pengfei,CUI Feng,CAO Jiantao,et al.Testing on fluid-solid coupling characteristics of fractured coal-rock mass considering regional geostress characteristics[J].Journal of China Coal Society,2018,43(1):105-117.
[15] 康红普,姜铁明,张晓,等.晋城矿区地应力场研究及应用[J].岩石力学与工程学报,2009,28(1):1-8.
KANG Hongpu,JIANG Tieming,ZHANG Xiao,et al.Research on in-situ stress field in Jincheng mining area and its application[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(1):1-8.
[16] 张延新,蔡美峰,王克忠.平顶山一矿地应力分布特征研究[J].岩石力学与工程学报,2004,23(23):4033-4037.
ZHANG Yanxin,CAI Meifeng,WANG Kezhong.Study on distribution characteristics of in situ stresses for Pingdingshan No.1 Mine[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(23):4033-4037.
[17] 彭华,马秀敏,姜景捷,等.赵楼煤矿1 000 m深孔水压致裂地应力测量及其应力场研究[J].岩石力学与工程学报,2011,30(8):1638-1645.
PENG Hua,MA Xiumin,JIANG Jingjie,et al.Research on stress field and hydraulic frac-turing in-situ stress measurement of 1 000 m deep hole in zhaolou coal mine[J].Chinese Journal of Rock Mechanics and Engineering,2011,30(8):1638-1645.
[18] 闫春岭,丁德馨,唐益群,等.硐室围岩力学参数分布特征与可靠性探讨[J].煤炭学报,2010,35(10):1609-1614.
YAN Chunling,DING Dexin,TANG Yiqun,et al.Probability distribution of mechanics parameters and reliability exploration of surrounding rock underground chamber[J].Journal of China Coal Society,2010,35(10):1609-1614.
[19] 陈宇龙,张宇宁.单轴压缩下横观各向同性岩石破裂过程的声发射特性离散元模拟[J].煤炭学报,2016,41(S1):88-92.
CHEN Yulong,ZHANG Yuning.Distinct element numerical simulation of acoustic emission characteristics during failure process of transversely isotropic rock subjected to uniaxial compression[J].Journal of China Coal Society,2016,41(S1):88-92.
[20] 张志增.横观各向同性岩体位移反分析的理论与应用研究[D].北京:清华大学,2010.
ZHANG Zhizeng.Theory and application research on displacement back analysis of transversely isotropic rock mass[D].Beijing:Tsinghua University,2010.
[21] 余大军.节理岩体特性的模型试验和特征单元体的研究[D].济南:山东大学,2012.
YU Dajun.Study on model test of jointed rock mass characteristics and representative elementary volume[D].Jinan:Shandong University,2012.
