目前对于冲击地压机制的研究主要集中于两大类:集中静载荷型冲击和集中动载荷型冲击,或称为高静载型冲击和强动载型冲击[1-2]。两类都是研究瞬时型冲击的发生机理和条件。然而,带时效特征的蠕变型冲击现象[3]也是不容忽视的,这类冲击隐蔽性较强,在工程中不易被重视,但其发生时同样威力巨大,给煤矿安全生产带来了严重隐患,因此对巷道围岩在常载地应力条件下因加速蠕变诱发冲击的现象进行深入研究是必要的。
对于蠕变引起的冲击机制学者们已开展过一定研究。LINKOV[4-5]指出应变软化与蠕变的相互作用,可用来解释从缓慢变形到瞬间失稳引发的与时间有关的冲击地压现象。王来贵等[6]对岩石试件的弱化失稳、流变失稳的过程之间的关系进行了初步分析,认为在应力超过长期强度后就有可能发生流变失稳;随着应力水平的不断增加,流变失稳的可能性增加,并提出了试件流变失稳的理论判据。窦林名等[7]提出了煤岩冲击破坏的弹塑脆性模型,描述了冲击地压发生的突发性和延时性。周晓军等[8]提出了以煤的黏弹性蠕变柔度系数来判别煤蠕变失稳的发生,同时给出了以此来划分冲击倾向度强弱的分级标准。上述研究都是对煤岩体蠕变冲击失稳所做的定性研究工作,与巷道围岩具体结构的联系不紧密。考虑具体工况条件,张晓春等[9]用黏弹性理论分析了具有层状(裂)结构特点的围岩延迟失稳特性。徐思朋等[10]建立了煤柱简单力学模型,从煤柱流变性的角度给出了其发生冲击的判别准则。尹万蕾等[11]针对孤立煤柱冲击地压发生具有时间滞后特性进行了深入研究。上述成果涉及的工况条件具有特殊性,未从巷道普遍存在的围岩结构(塑性区与弹性区)角度进行探讨。姜福兴等[3]通过三维蠕变方程,分析了高地应力特厚煤层巷道围岩塑性区加速蠕变破坏的过程,认为加速蠕变通过强度“腐蚀”减小阻抗和应力解除2方面实现冲击启动和显现,但其认为弹性区煤岩不发生加速蠕变,塑性区不扩展,冲击地压是塑性区煤岩蠕变的结果。姜鹏等[12]建立了基于应变能的岩石黏弹塑性损伤耦合蠕变本构模型,利用该模型数值分析了巷道围岩的蠕变破坏过程,用于解释煤矿中蠕变型冲击的力学机理,但其建立的模型不方便进行解析研究。
综上所述,目前巷道围岩加速蠕变诱发冲击地压的机制研究尚存在不足,需对此做进一步研究。笔者在分析巷道弹性区煤岩加速蠕变过程及其条件的基础上,利用煤岩蠕变破坏的时效力学参数,并考虑围岩塑性区强度的应变软化,探讨了蠕变冲击启动机制,并相应建立和分析了圆形断面巷道弹性区煤岩加速蠕变影响下的冲击启动临界条件。研究结果对深化认识巷道蠕变型冲击机制和制定针对性的防治措施提供了理论依据。
1 煤岩蠕变破坏的时效力学参数
GOODMAN[13]分析了岩石蠕变应变轨迹与岩石单轴全应力-应变曲线之间的关系,发现岩石蠕变破坏点与全应力-应变曲线的下降段(破坏段)具有很好的相关性,如图1所示,折线OCE为全应力-应变曲线的简化表示,即双线形模型,峰前弹性模量为E0,峰后降模量为λ,C点为瞬时加载峰值强度点(εc0,σc0);曲线OFT为σ>σ (σ
(σ 为长期强度)情况下任意时刻t时的等时应力-应变曲线。一般认为下降段CE上的强度点与蠕变曲线上加速蠕变破坏点相一致,即不同时刻t的等时应力-应变曲线与单轴全应力-应变曲线下降段CE的交点T为强度点。
为长期强度)情况下任意时刻t时的等时应力-应变曲线。一般认为下降段CE上的强度点与蠕变曲线上加速蠕变破坏点相一致,即不同时刻t的等时应力-应变曲线与单轴全应力-应变曲线下降段CE的交点T为强度点。

图1 全应力-应变曲线与等时应力-应变曲线的关系
Fig.1 Relationship between the complete stress-strain curve and isochronous stress-strain curve
基于短时蠕变试验,许宏发等[14]得到了强度点T的近似替代点P,T和P点相距较近,误差能满足工程要求。设直线FP的斜率表示F点的切线模量EtF(t),直线OF的斜率表示F点的割线模量EsF(t),则P点的位置,即不同时刻t的蠕变破坏强度[15]近似为
σc(t)=σc0Mt
(1)
其中,Mt为不同时刻的等时应力-应变曲线的割线模量比,仅是与时间有关的一个常数,其函数可由煤岩材料的短期蠕变试验数据拟合获得,一般随时间呈负指数关系单调衰减劣化,其值变化范围为1~σ /σc0。
/σc0。
全应力-应变曲线峰后下降段CE的方程为
σ=σc0-λ(ε-εc0)
(2)
由式(1),(2)可知,不同时刻蠕变破坏强度点P点对应的应变为
εc(t)=(σc0+λεc0-σc0Mt)/λ
(3)
得到煤岩材料的时效力学参数后,巷道围岩的蠕变问题可近似为考虑时效力学参数的弹塑性问题。
2 围岩加速蠕变的塑性区时效应力场
2.1 基本假设
(1)巷道围岩均质、各向同性。巷道断面为圆形,半径为a,长度无限长(平面应变问题),原岩应力为静水压力状态p0。巷道内表面受支护力pi作用,含巷道半径a处围岩自身及作业面提供的假想支护力p*和支护结构提供的支护反力ps。为方便对极坐标下应力应变进行转换、反映巷道围岩应力应变场的变化趋势和影响因素,且由于所研究对象属于大埋深条件,因此选用静水压力下圆形断面模型。
(2)采用M-C准则描述围岩塑性区的强度特征,其形式为
σθp=qσrp+σcp
(5)
式中,σθp,σrp分别为塑性区围岩的切向应力和径向应力;σcp为考虑塑性区应变软化的煤岩单轴抗压强度;q=(1+sin φ)/(1-sin φ),φ为煤岩内摩擦角。
2.2 巷道弹性区煤岩产生加速蠕变的条件
井下巷道围岩处于三向应力状态,研究其蠕变问题应明确围岩产生加速蠕变的阈值问题,即三轴长期强度σ3 ,而不是单轴长期强度σ
,而不是单轴长期强度σ 。当围岩的应力水平超过阈值时,就将产生加速蠕变效应;反之,如围岩的应力水平小于阈值,则只产生稳定蠕变。该阈值视围压情况可由试验具体确定。对于常规三轴蠕变,判断煤岩材料能否产生加速蠕变的应力条件为
。当围岩的应力水平超过阈值时,就将产生加速蠕变效应;反之,如围岩的应力水平小于阈值,则只产生稳定蠕变。该阈值视围压情况可由试验具体确定。对于常规三轴蠕变,判断煤岩材料能否产生加速蠕变的应力条件为
σ1>σ3
(6)
其中,σ1为轴向最大主应力;σ3 为常规三轴蠕变试验确定的长期强度。常规三轴蠕变试验下σ3
为常规三轴蠕变试验确定的长期强度。常规三轴蠕变试验下σ3 与σ3的关系[15]可表示为σ3
与σ3的关系[15]可表示为σ3 =Aσ3+σ
=Aσ3+σ ,其中,σ3为围压;A为大于0的拟合参数。
,其中,σ3为围压;A为大于0的拟合参数。
煤巷开挖后,现场规定须立即支护,支护必须紧跟作业面,此时假想支护力p*最大,pi= p*≈0.7p0。支护后,围岩已经处于蠕变变形状态。随着作业面的不断推进,围岩-支护之间开始发生相互作用,相互作用的过程和变化趋势为:虚拟支护力p*逐渐减小,至作业面后方2倍洞跨处,空间约束效应将基本消失,p*=0,支护反力ps由0逐渐增加到最大值psmax[16]。巷道内表面总支护力pi呈下降状态。
巷道自开挖起,随作业面的推进,其围岩状态是蠕变时间效应和作业面空间效应二者的耦合相互作用,取决于地应力p0、支护力pi、所选强度准则中的强度参数和三轴长期强度σ3∞。
(1)在作业面附近,由于强大的虚拟支护力p*作用,围岩内应力一般不会满足式(6),因此作业面往后一段距离内围岩只存在弹性区。弹性应力场中巷道围岩表面点的峰值应力为2p0-pi,若其在空间约束效应消失位置时仍不满足式(6),则围岩始终只存在弹性区,巷道始终呈稳定的黏弹性变形,产生加速蠕变的临界地应力判据依据式(6)为
p0=0.5(A+psmax)+0.5σ
(7)
由式(7)分析,在埋深相对较大条件下,巷道掘进过程中初始支护(即紧跟作业面的支护)若要使得空间约束效应消失时仍不具备加速蠕变的条件,可行的办法是加大支护力和提高煤的单轴长期强度σ∞,但鉴于目前大多数支护结构能提供的支护反力并不大(最大约1 MPa左右,锚网索支护最大支护反力小于1 MPa),注浆提高煤的单轴长期强度σ∞也有限,因此,特定的地应力条件和煤层强度下这些方法可能会取得较好的效果,但大埋深高地应力条件下往往支护困难,这也是深部岩石力学支护问题的难点之一[17]。
(2)若地应力高于式(7)中的临界地应力,则在空间约束效应影响范围内某位置起围岩表面点开始满足式(6)所示的加速蠕变条件,但由于其切向应力还远达不到相应围压下初始峰值强度σc0表达的峰值切向应力,因此围岩表面不会立即破坏,宏观表现为等速蠕变。假设此时保持作业面不推进,围岩表面因蠕变屈服导致煤岩强度的降低,最终会达到加速蠕变而破坏。一定深度范围内的围岩内部点变化过程与此类似,次一级应力的围岩内部某点将随时间的推移,其切向应力达到相应围压下时效强度σc(t)表达的峰值切向应力时进入加速蠕变而破坏,蠕变破坏区逐渐向围岩深处扩展,最终将使得围岩产生松动区并完全垮落,形成巷道破坏。
(3)随着作业面的往前推进,总支护力pi不断下降,围岩表面的切向应力将首先达到相应围压下的峰值切向应力,围岩表面点进入加速蠕变阶段立即破坏。然而,围岩内部达到加速蠕变破坏需要一定的时间间隔,远赶不上总支护力pi不断下降造成的围岩内弹塑性应力场分布的速度,或者可以认为总支护力pi不断下降造成了一定深度区域的煤岩几乎同时进入加速蠕变而破坏,这个区域即是相应应力状态下的塑性区分布范围。考虑到空间约束效应影响范围如此之短(井下煤巷宽度通常在4~6 m,空间约束效应影响范围一般在8~12 m),可以近似认为空间约束效应消失时初始的弹塑性应力场调整完毕,然后在此基础上弹性区煤岩(相当于次一级应力的煤岩)随时间的推移产生加速蠕变。
2.3 圆巷围岩加速蠕变塑性区分析
在初始弹塑性应力场下,部分弹性区的应力一定满足式(6),将产生加速蠕变,由此推动初始塑性区随时间向深部发展。塑性区扩展后应力场相应调整,调整的结果是围岩内部应力在原有基础上升高,紧连塑性区的弹性点由于应力相对较大,随时间延长达到相应条件时又进入加速蠕变阶段而破坏,形成新的塑性状态,因此,塑性区的扩大随时间增加连续发生,直至新塑性区半径处的应力不满足式(6)为止。在应力场调整使围岩内部应力升高的过程中,弹性区煤岩在之前蠕变的基础上继续发生应力增大后的蠕变变形,相当于对同一煤岩进行多级加载蠕变试验。围岩弹性区不同位置应力不同,不同位置煤岩处于的蠕变阶段也不同,这种蠕变变形和破坏方式非常复杂,直接采用复杂的围岩加速蠕变本构关系不方便进行弹塑性解析。如前所述,弹性区煤岩随塑性区的扩展承受着多级加载而最终加速蠕变破坏,多级加载过程中煤岩的强度特性随时间会产生变化,这种变化特性可采用多级加载蠕变试验获得的如图2所示的蠕变曲线簇转换成等时应力应变曲线结合瞬时应力应变曲线进行分析。因此,利用等时应力应变曲线和瞬时全应力应变曲线的关系得到的煤岩时效力学参数,近似进行巷道弹塑性分析是可能的。综上分析,围岩弹性区中某位置在应力作用下于某个时刻因加速蠕变而至蠕变破坏强度点,这个位置即是新的蠕变塑性区半径处,而在此处,围岩承受外力正好与其时效强度相等。基于这个思路,本文进行巷道围岩蠕变塑性区解析。
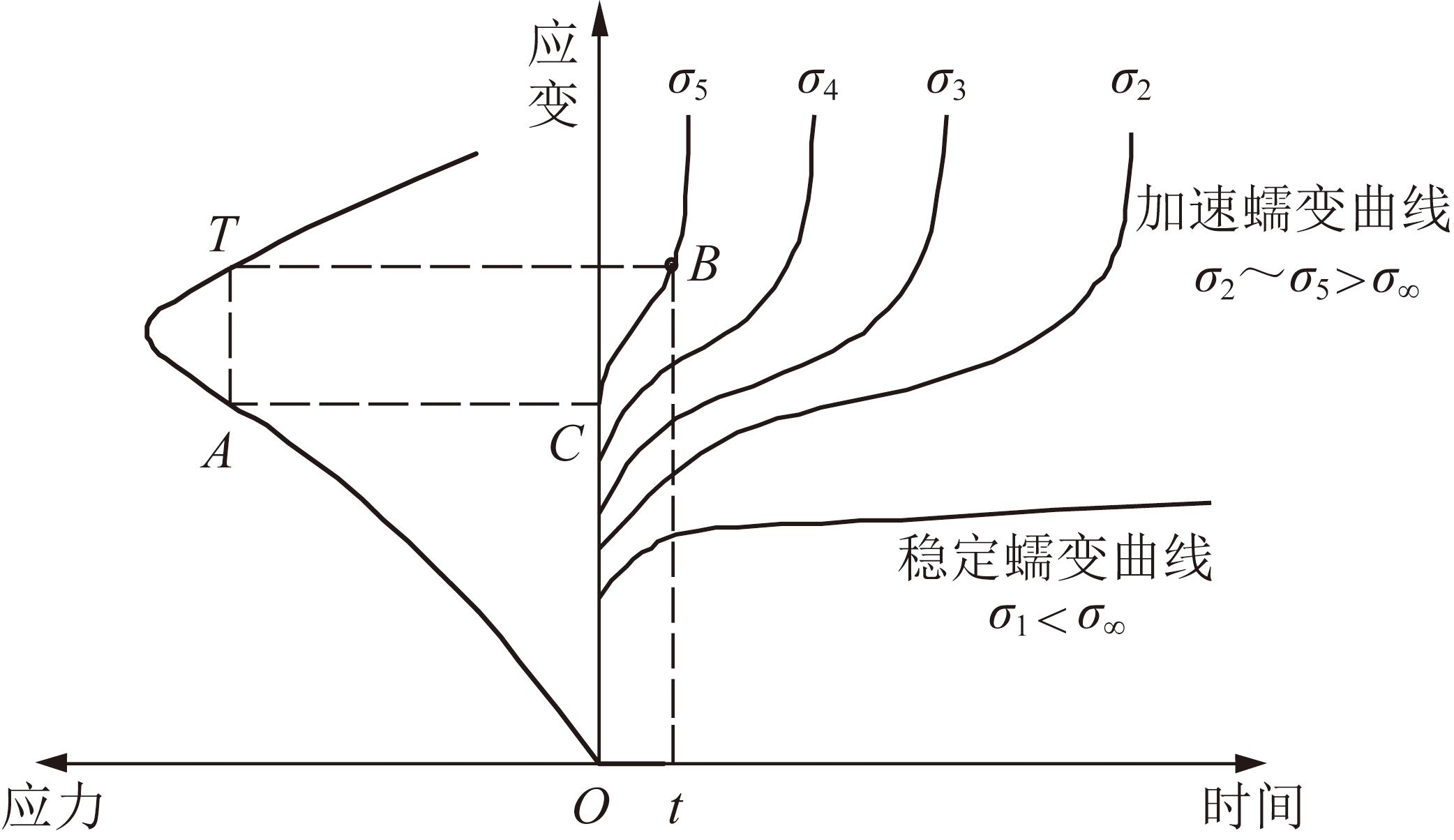
图2 蠕变曲线簇与全应力应变曲线的对应示意
Fig.2 Corresponding diagram of creep curve clusters and the complete stress-strain curves
塑性区应满足的方程有几何方程:
![]()
(8)
平衡方程:
![]()
(9)
假定塑性区煤岩材料不可压缩,即![]() 得
得
εθ=-εr=J/r2
(10)
式中,J为与时间有关的积分常数。
利用弹塑性交界处塑性区一侧煤岩材料等效应变εi刚好达到时效破坏强度所对应的应变的条件,即式(3),可得
![]()
(11)
式中,R为塑性区半径。
金俊超等[18]基于WONG[19]进行的一系列常规压缩试验及蠕变破坏试验结果认为,岩石加速蠕变变形至蠕变破坏强度时(图1中T点对应为图2中的B点),后续应力应变关系将由破坏点沿瞬时塑性应变软化的轨迹演化,即图1中由T点往TE的方向演化而进入塑性状态。OKUBO等[20]通过几种岩石的单轴蠕变实验,获得了岩石加速蠕变阶段的完整曲线,认为加速蠕变阶段上的点对应于瞬时全应力应变曲线的峰后段。因此,围岩时效蠕变强度峰后的本构关系仍有式(2)的表达。
根据式(2),(3),峰后的强度σcp可表示为
σcp=σc(t)-λ[εi-εc(t)]
(12)
将式(1),(3),(11)代入式(12),可得
σcp=σc0(1+λ/E0)-σc0(1+λ/E0-Mt)R2/r2
(13)
r=a时,σrp=psmax。由式(5),(13)并联立式(9)得
![]()
(14)
将式(13),(14)代入式(5)可得塑性区切向应力σθp,再由r=R处应力连续条件:σθp+σrp=2p0,可得
![]()
(15)
由式(15)可得巷道蠕变塑性区半径R。当t=t0=0时,Mt0=1,此时Rt=0即为初始的塑性区半径。
3 加速蠕变下巷道冲击的启动条件
冲击地压扰动响应判别准则理论[21]是根据李雅普诺夫关于受扰运动的有界性概念提出的,研究各种不可避免的干扰性因素(巷道的开挖、工作面的推进等)对系统冲击失稳的影响,本质与能量判别准则一致,但是其形式简单,便于进行解析分析。巷道围岩是由塑性区和弹性区组成的变形系统,在较小地应力条件或某支护约束条件下,弹性区围岩只发生稳定蠕变,围岩强度不会发生蠕变劣化,围岩塑性区半径不再调整。但在高地应力条件下或巷道支护稳定后因支护力的一定损失,使得弹性区一侧应力满足加速蠕变条件时,该区域煤岩最终将发生加速蠕变而破坏,并引起弹性区煤岩强度的劣化,应力场和塑性区半径不断调整。显然,此种情况下塑性区半径向围岩深处不断转移不是因外部静载地应力的变化或动载造成的,而是受弹性区煤岩强度劣化的影响。借鉴冲击地压扰动响应判别准则理论的思想,在塑性区半径调整过程中,若系统处于非稳定平衡状态,无论弹性区煤岩强度劣化的影响多么小,都会导致塑性区半径R的无限增长,相当于塑性区瞬间出现急剧、跳跃式扩展[22],围岩发生失稳,冲击开始启动,此时恰好对应于使塑性区无限扩展的临界塑性区半径或临界地应力。应当指出,启动条件是围岩弹性区能量释放的条件,不是冲击显现条件,冲击显现应视释放的能量是否大于弹性区煤体破坏消耗的能量和克服外围塑性阻抗能量消耗之和,即有剩余能量时冲击才显现。
启动条件根据式(15)可表示为
![]()
(16)
根据式(15),(16),冲击启动的临界塑性区半径Rcr为
![]()
(17)
将式(17)得到的临界塑性区半径Rcr代入式(15),可得临界地应力pcr。当t=t0=0时,Mt0=1,此时pcr,t=0即为初始的冲击启动条件,与文献[21]考虑支护力的结果一致。本文的解形式上虽然与时效强度下外载荷p0的微小扰动得到的临界地应力启动条件一致,但反映的外部载荷状态不同,本文的解是在外部静载地应力不变的情况下得到的。由式(15),(17)进一步可得到发生蠕变冲击的延期时间。
4 分析和讨论
某矿参数值如下:煤层巷道地应力p0=16.25 MPa,相当于650 m埋深。煤体的模量比为1.0,σc0=16 MPa,φ=30°。临界地应力pcr随psmax,Mt的变化规律、临界地应力pcr随λ/E0,Mt的变化规律分别如图3,4所示。

图3 临界地应力pcr随psmax,Mt的变化规律
Fig.3 Variation of critical geostress pcrwith psmax and Mt

图4 临界地应力pcr随λ/E0,Mt的变化规律
Fig.4 Variation of critical geostress pcr with λ/E0 and Mt
结合前述分析和图3,4,得到以下规律和认识:
(1)支护力的增大可明显提高巷道初始的冲击启动临界地应力,使得巷道在初始情况下不会冲击启动。但不论初次支护力大或小,一旦发生加速蠕变,巷道冲击启动的临界地应力皆随时间降低。随时间的推移,当临界地应力下降到与地应力p0相等时,冲击启动。
(2)弹性区煤岩加速蠕变影响下,增大支护力对抑制冲击发生有促进作用:支护力越高,弹性区煤岩需历经较大的强度劣化才可冲击启动,但启动时煤岩内应力较低且塑性区半径增大较大,阻抗变大,不易冲击显现;支护力低时弹性区煤岩只需历经较小的强度劣化,就可冲击启动,启动时煤岩内峰值应力更高,塑性区半径较小,更易冲击显现。
(3)巷道所处地应力越高,发生冲击启动时的Mt越大,说明弹性区煤岩只需历经较小的强度劣化,就可冲击启动,且启动时煤层内应力较高,易满足冲击显现的能量条件,这可解释高地应力下巷道更易发生蠕变冲击的现象。
(4)抑制巷道蠕变冲击的核心在于控制弹性区煤岩不满足产生加速蠕变的条件。由于初始支护通常为锚网索支护,能提供的支护反力最大在 1 MPa,这样量级的支护反力往往不能抑制巷道弹性区煤岩加速蠕变的产生,而且初支由于支护时机太早,很可能因巷道变形较大而损坏,因此,巷道须进行二次支护控制,并在支护时机上充分利用围岩蠕变变形的第II阶段。这对深部高地应力巷道优化巷道支护防冲具有一定的启迪意义。
(5)上述认识对于高地应力下采用某种支护方式控制住了弹性区煤岩强度的蠕变劣化而不易冲击启动的成巷同样适用。成巷期间因一些原因导致支护力下降或丧失过大,弹性区煤岩又恢复至高应力状态,巷道因加速蠕变效应易发生蠕变型冲击。
(6)在相同地应力作用下若发生蠕变冲击,λ/E0(煤岩冲击的重要参数之一[21])越小则需历经更大程度的Mt变化,但由于λ/E0与Mt的关系不明确,并不能得出λ/E0越大越易发生蠕变冲击的结论,这需要进一步研究。
5 结 论
(1)巷道弹性区煤岩产生加速蠕变与地应力、支护方式、煤岩强度参数和煤岩三轴长期强度密切相关。
(2)加速蠕变导致巷道冲击启动通过弹性区煤岩强度的时效劣化实现,当冲击临界地应力下降到与巷道所处的地应力相等时,冲击启动。
(3)加速蠕变影响下,高地应力、低支护力、高模量比属性均使得巷道弹性区煤岩只需历经较小的强度劣化,就可冲击启动。
(4)抑制巷道蠕变冲击的核心在于控制弹性区煤岩不满足产生加速蠕变的条件。
[1] 潘俊锋,宁宇,毛德兵,等.煤矿开采冲击地压启动理论[J].岩石力学与工程学报,2012,31(3):586-596.
PAN Junfeng,NING Yu,MAO Debing,et al.Theory of rockburst start-up during coal mining[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(3):586-596.
[2] 窦林名,何江,曹安业,等.煤矿冲击矿压动静载叠加原理及防治[J].煤炭学报,2015,40(7):1469-1476.
DOU Linming,HE Jiang,CAO Anye,et al.Rock burst prevention methods based on theory of dynamic and static combined load induced in coal mine[J].Journal of China Coal Society,2015,40(7):1469-1476.
[3] 姜福兴,冯宇,KOUAME K J A,等.高地应力特厚煤层“蠕变型”冲击机理研究[J].岩土工程学报,2015,37(10):1762-1768.
JIANG Fuxing,FENG Yu,KOUAME K J A,et al.Mechanism of creep-induced rock burst in extra-thick coal seam under high ground stress[J].Chinese Journal of Geotechnical Engineering,2015,37(10):1762-1768.
[4] LINKOV A M.Rockbursts and the instability of rock masses[J].International Journal of Rock Mechanics & Mining Science & Geomechanics Abstracts,1996,33(7):727-732.
[5] LINKOV A M.Instability,fracture acceleration and amplification[J].International Journal of Rock Mechanics & Mining Science & Geomechanics Abstracts,2000,37(1):31-37.
[6] 王来贵,王泳嘉,刘学,岩石试件的流变失稳理论及判据[J].阜新矿业学院学报,1994,13(3):93-97.
WANG Laigui,WANG Yongjia,LIU Xue.The rheological instability theory for rock sample and its criteria[J].Journal of Fuxin Mining Institute(Natural Science),1994,13(3):93-97.
[7] 周晓军,鲜学福.基于粘弹性模型的煤体冲击倾向指标的试验研究[J].西部探矿工程,1999,11(1):30-34.
ZHOU Xiaojun,XIAN Xuefu.Experimental study on coalburst proneness index via visco-elastic creep model[J].West-China Exploration Engineering,1999,11(1):30-34.
[8] 窦林名,何学秋.煤岩冲击破坏模型及声电前兆判据研究[J].中国矿业大学学报,2004,33(5):504-508.
DOU Linming,HE Xueqiu.Model for rock burst failure and its critical values of acoustic and electromagnetic emission[J].Journal of China University of Mining and Technology,2004,33(5):504-508.
[9] 张晓春,张东升,缪协兴.井巷围岩的延迟失稳机理分析[J].岩石力学与工程学报,2001,20(6):830-833.
ZHANG Xiaochun,ZHANG Dongsheng,MIAO Xiexing.Study of delay instability on surrounding rock masses of roadway[J].Chinese Journal of Rock Mechanics and Engineering,2001,20(6):830-833.
[10] 徐思朋,钟卫平,贾凤苏.煤柱冲击地压时间效应研究[J].矿山压力与顶板管理,2001(1):75-77.
XU Sipeng,ZHONG Weiping,JIA Fengsu.Study on the time effect of rock burst for a pillar[J].Ground Pressure and Strata Control,2001(1):75-77.
[11] 尹万蕾,潘一山,李忠华,等.孤立煤柱非线性蠕变失稳滞后时间的研究[J].应用力学学报,2016,33(6):1106-1113.
YIN Wanlei,PAN Yishan,LI Zhonghua,et al.Lag time study on nonlinear creep buckling of the isolated coal pillar[J].Chinese Journal of Applied Mechanics,2016,33(6):1106-1113.
[12] 姜鹏,潘鹏志,赵善坤,等.基于应变能的岩石黏弹塑性损伤耦合蠕变本构模型及应用[J].煤炭学报,2018,43(11):2967-2979.
JIANG Peng,PAN Pengzhi,ZHAO Shankun,et al.coupled elasto-viscoplastic damage model based on strain energy theory of rock and application[J].Journal of China Coal Society,2018,43(11):2967-2979.
[13] GOODMAN R E.Introduction to rock mechanics (2nd edition)[M].New York:John Wiley & Sons,1989.
[14] 许宏发,柏准,齐亮亮,等.基于全应力-应变曲线的软岩蠕变寿命估计[J].岩土力学,2018,39(6):1973-1980.
XU Hongfa,BAI Zhun,QI Liangliang,et al.Creep life estimation of soft rock based on the complete stress-strain curve[J].Rock and Soil Mechanics,2018,39(6):1973-1980.
[15] 董海龙,高全臣.考虑流变特性的两向不等压巷道围岩塑性区近似解[J].煤炭学报,2019,44(2):419-426.
DONG Hailong,GAO Quanchen.Approximate solution on plastic zone of roadway surrounding rock under unequal compression in two directions by considering rheology[J].Journal of China Coal Society,2019,44(2):419-426.
[16] 孙钧.岩石流变力学及其工程应用研究的若干进展[J].岩石力学与工程学报,2007,26(6):1081-1106.
SUN Jun.Rock rheological mechanics and its advance in engineering applications[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(6):1081-1106.
[17] 侯公羽.围岩-支护作用机制评述及其流变变形机制概念模型的建立与分析[J].岩石力学与工程学报,2008,27(S2):3618-3629.
HOU Gongyu.Review of interaction mechanism between surrounding rock and support and analysis of conceptual model of rheological deformation mechanism[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(S2):3618-3629.
[18] 金俊超,佘成学,尚朋阳.基于应变软化指标的岩石非线性蠕变模型[J].岩土力学,2019,40(6):1-9.
JIN Junchao,SHE Chengxue,SHANG Pengyang.A nonlinear creep model of rock based on the strain softening index[J].Rock and Soil Mechanics,2019,40(6):1-9.
[19] WONG T F.Effects of temperature and pressure on failure and post-failure behavior of westerly granite[J].Mechanics of Materials,1982,1(1):3-17.
[20] OKUBO S,NISHIMATSU Y,FUKUI K.Complete creep cures under uniaxial compression[J].International Journal of Rock Mechanics & Mining Science & Geomechanics Abstracts,1991,28:77-82.
[21] 潘一山.冲击地压发生和破坏过程研究[D].北京:清华大学,1999.
PAN Yishan.Study on rockburst initiation and failure propagation[D].Beijing:Qinghua University,1999.
[22] 马念杰,郭晓菲,赵志强,等.均质圆形巷道蝶型冲击地压发生机理及其判定准则[J].煤炭学报,2016,41(11):2679-2688.
MA Nianjie,GUO Xiaofei,ZHAO Zhiqiang,et al.Occurrence mechanisms and judging criterion on circular tunnel butterfly rock burst in hom-ogeneous medium[J].Journal of China Coal Society,2016,41(11):2679-2688.
