全国有113 000多个矿山,其中有8 457个矿山对矿区的整体环境影响比较大[1],而我国又是一个多露天矿的国家,露天矿主要的地质灾害问题中滑坡和泥石流是最突出的,这类地质灾害的发生往往会造成非常严重的损失[2-4]。滑坡和泥石流灾害会严重影响排土场排土作业安全,排土场的边坡的稳定性进而会影响露天矿安全生产作业与开采进度[5],所以排土场边坡稳定性的研究对于矿山的安全和经济效益来说都具有重要的意义[6]。
影响排土场边坡稳定性的因素总体可以分为4类:外力作用、基底的物理力学性质、排弃物的物理力学性质和水的影响[7-11]。排土场稳定性评价方法主要分为极限平衡分析法[12-13]、数值分析法[14-15]和可靠性分析法[16-17]。基于排土场稳定性评价的各种方法,国内外众多学者对排土场边坡失稳诱因开展大量的研究工作,并取得显著成果。例如,STEIAKAKIS等[18]采用极限平衡法分析希腊主要的露天矿“South Field”发生大规模排土场失稳破坏现象,最终确定高含水量黏性土排弃物较低的抗剪强度是诱发排土场破坏的主要因素。为能更好理解由碎石和松散颗粒组成的排土场在任何位置上应力、应变历史及位移和破坏信息,KONER和CHAKRAVARTY[19]采用离散元数值模拟方法,从颗粒性质的角度对具有节理的岩质边坡进行分析,以评估排堆场的稳定性。LÜ Xiangfeng等[20]建立渗流-损伤耦合数值模型对饱水排土场边坡进行稳定性分析,结果表明较高的孔隙压力可以降低滑动面上的正压力和摩擦力,使饱水岩体强度降低,进而导致边坡失稳。RADHAKANTA和DEBASHISH[21]使用二维的有限差分法,以5种不同土工材料为对象,评估不同排土场边坡倾角对平均降雨和强降雨的响应。WANG等[22]以边坡稳定系数为切入点研究地下水渗流对排土场边坡稳定性的影响,结果表明随着地下水位的升高,边坡稳定系数减小,且边坡稳定系数降低率随地下水位的升高而降低。
排土场的变形量远超普通岩质边坡的变形量,所以传统岩质边坡的监测系统无法在排土场边坡中广泛应用[23-24]。例如通过立桩和全站仪经纬仪等进行监测,排土场滚石会对监测设施造成破坏,难以实现长期监测;排土工作过程中地表位移无时无刻不随排土施工的进行而发生变化,会造成地表位移变形扫描监测法预警频繁。排土场大多由碎石颗粒组成,通过根管钻孔的方法来施工不现实,利用高压注浆的方法成本过高。目前使用最多的点状监测无法实现长距离大面积监测,存在监测盲区;增加监测点数虽然可靠性有所提高,但工作量倍增,况且监测点数的增加也会影响岩土体的整体性和结构安全。
为解决上述排土场稳定性监测中存在的问题,笔者以辽宁本溪南芬露天铁矿Ⅱ号全段高排土场为研究背景,采用数值模拟与物理模型实验相结合的方式对降雨和堆载影响下排土场边坡的稳定性进行研究,并采用光纤作为监测设备制定工程尺度上适用于南芬露天铁矿Ⅱ号全段高排土场大变形监测方案。
1 排土场区域地质及稳定性概况
Ⅱ号排土场位于采场西南的上盘,地貌为单斜构造,主要由变质岩系地层构成,属侵蚀构造中的高山地,其中排土场内部地基基础部分以泥灰岩为主。Ⅱ号排土场属沟谷型排土场,大气降水是地表和地下水的主要补给来源。
随着天气变暖,温度上升导致排土场内部冻土层开始融化,内部水压增大导致土场的稳定性降低。2014-04-10,Ⅱ号排土场发生泥石流,泥石流排泄区长100 m;排岩机工作区域出现多条长而宽的裂缝,局部区域出现大面积塌陷,长约350 m,宽160 m的范围。必须引起重视,加大排土场边坡的巡查力度,增强监测预警技术的研究和应用,提高排土场泥石流监测预警的自动化、智能化和信息化,加快土场监测系统的建设进度,通过科学的方法对土场变形进行监测。
2 排土场边坡相似物理模型
2.1 排土场边坡相似模型设计
本次实验以南芬露天铁矿Ⅱ号全段高排土场为原型,采用物理模拟的方法研究Ⅱ号全段高排土场边坡稳定性及监测方案,排土场相关参数见表1。排土场排渣的物理力学性质是决定边坡高度和边坡角的关键性因素,而边坡高度和边坡角的大小又是影响边坡稳定性的重要因素,所以排渣的物理力学性质对研究排土场边坡稳定性至关重要。根据Ⅱ号全段高排土场散体各粒级质量分数以及光纤监测排土场变形的特点,通过选取相应的物理指标进行模拟研究,排土场散体各粒级含量见表2。
表1 排土场边坡相关参数
Table 1 Relevant parameters of dump slope

序号参数取值1坡高/m2502排弃物粒径/mm1 0003排土场最大容积/m33 800×1044年降雨量/mm8475最大年降雨量/mm1 2126最小年降雨量/mm518
表2 排土场散体各粒级含量
Table 2 Content of each particle size of the dump
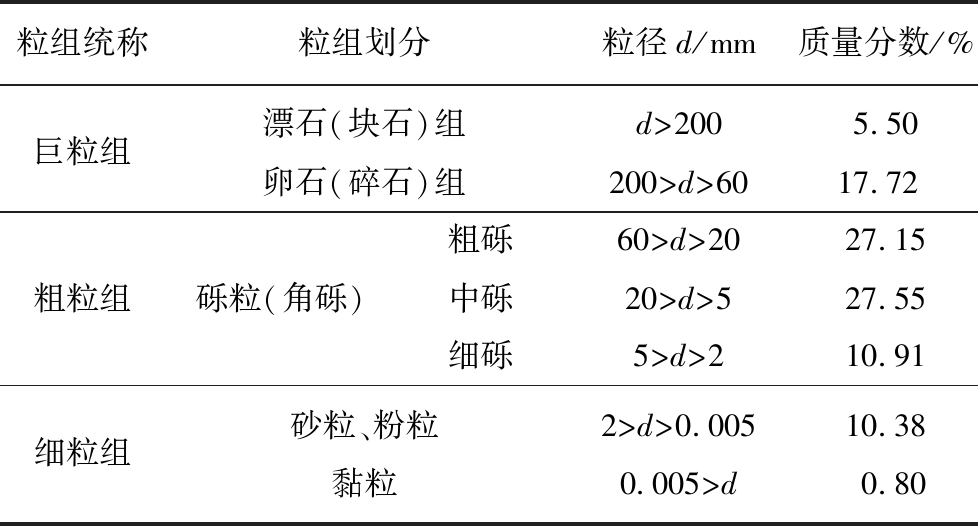
粒组统称粒组划分粒径d/mm质量分数/%巨粒组漂石(块石)组d>2005.50卵石(碎石)组200>d>6017.72粗砾60>d>2027.15粗粒组砾粒(角砾)中砾20>d>527.55细砾5>d>210.91细粒组砂粒、粉粒2>d>0.00510.38黏粒0.005>d0.80
根据相似三定理,相似比按照如下公式计算:
式中,Lp为排土场相关实际尺寸(冯家东沟);Lm为相似物理模型相关尺寸;CL为相似比。
设置排土场边坡相似模型高1 m,根据上式计算得相似比为1∶250,模型所用物料的最大粒径为4 mm。按照现场筛分散体各粒级质量分数(表1)及相似比将南芬露天矿潜在滑动面(带)上广泛分布的绿泥角闪岩取材破碎后进行室内实验配比。实验室级配表见表3。模型尺寸设定为2 m×2 m×1 m,其中坡顶尺寸2 m×0.5 m,坡角34°,如图1所示。
表3 室内试验各粒级质量分数
Table 3 Indoor test of the content of each particle size
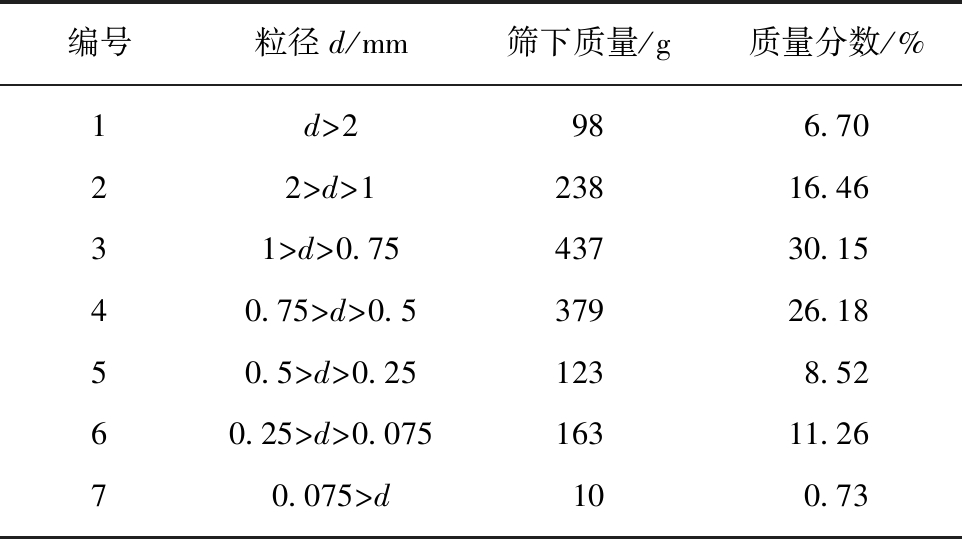
编号粒径d/mm筛下质量/g质量分数/%1d>2986.7022>d>123816.4631>d>0.7543730.1540.75>d>0.537926.1850.5>d>0.251238.5260.25>d>0.07516311.2670.075>d100.73
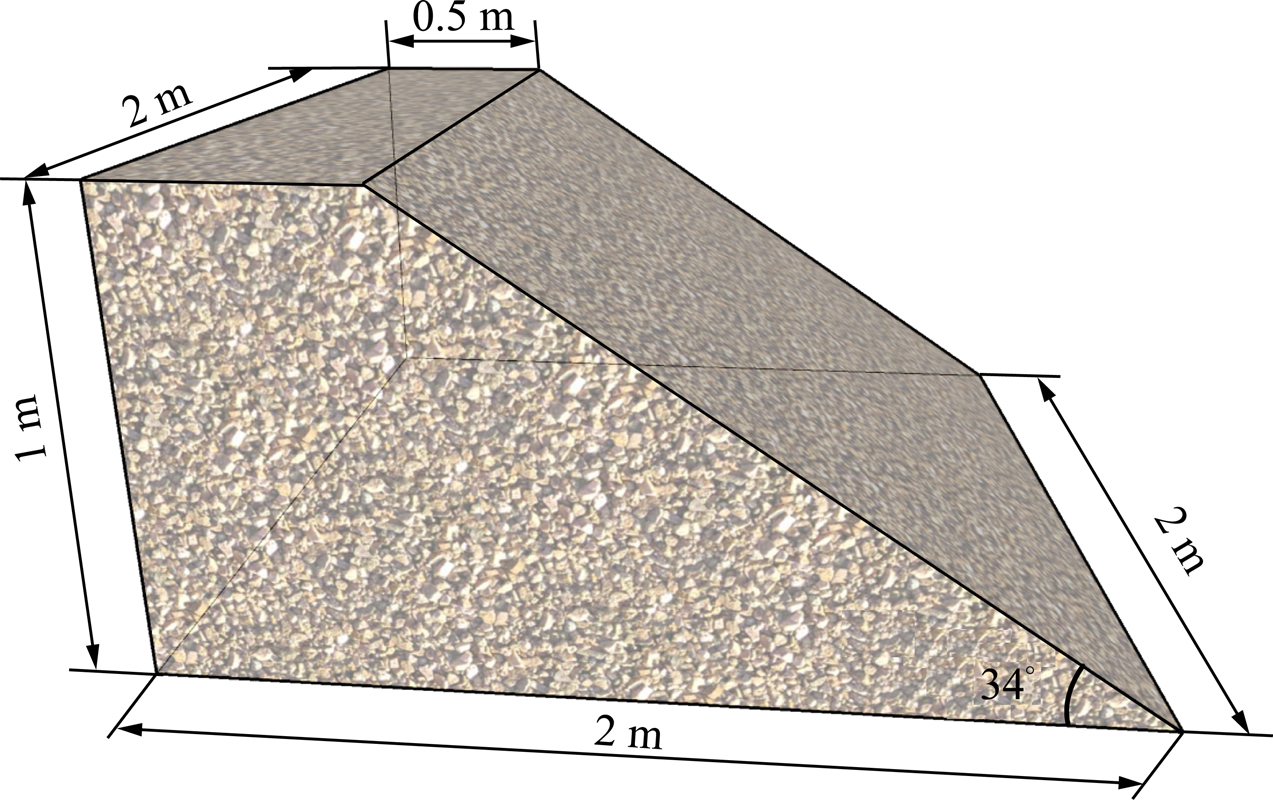
图1 排土场边坡相似模型尺寸
Fig.1 Dimensions of similar model of dump slope
2.2 排土场边坡相似模型变形监测设备
本实验基于分布式光纤监测原理和排土场边坡破坏机理,采用直径仅2 mm的光纤作为监测设备展开Ⅱ号全段高排土场室内物理模型实验研究。布里渊光时域分析仪(BOTDA)测量时主要是通过受激产生的布里渊散射光产生布里渊频率漂移实现,产生漂移的原因在于光纤轴向温度和应变发生变化。BOTDA需在光纤两端安置激光器,分别将连续光和脉冲光射入光纤,构成监测回路[25-26]。BOTDA各参数的设置见表4。
表4 光纤应变分析仪的参数设置
Table 4 Parameter settings for fiber strain analyzer

测量范围/m采样间隔/m脉冲宽度/ns平均次数起始频率/GHz扫描间隔/MHz终止频率/GHz1000.051021610.700512.195
光纤铺设示意图如图2所示(X方向为边坡倾向、Y方向为边坡走向、Z方向为边坡沉降方向),其中X方向布置2层,每层传感光纤布置6根,下层(X1层)编号为X11~X16,监测光纤线性长67 cm,上层(X2层)编号为X21~X26,监测光纤线性长108 cm;Y方向布置2层,每层布置2根,上层(Y1层)编号为Y11,Y12,下层(Y2层)编号为Y21,Y22,监测光纤线性长均为200 cm;Z方向布置2组共4根,编号分别为Z11,Z12,Z21,Z22监测光纤线性长度为170 cm。

图2 传感光纤布置
Fig.2 Sensing fiber arrangement
各传感光纤的铺设间距如图3所示,每层X方向光纤间距360 mm,最外侧光纤与模型边界之间距离100 mm,X向光纤层间距220 mm;Y向光纤间离110 mm,Y向光纤层间距220 mm;Z1组光纤距离坡脚670 mm,且位于模型Y方向3等分点处,Z向2组光纤间距离426 mm。

图3 光纤分布间距
Fig.3 Fiber distribution spacing
2.3 排土场边坡相似模型实验设置
根据《中国岩土工程勘察规范》(GB 50021—2001)和《中国土工试验规范》(SL237—99),中国科学院岩土力学研究所于2014年4月进行现场试验,确定影响Ⅱ号排土场边坡稳定性的主要因素是大气降水和排土荷载。所以,笔者选择模拟不同堆载和降雨对边坡变形的影响。堆载分为2阶段5级,第1阶段模拟汽车排土荷载,在坡顶3等分处设置2个排岩通道,分20,50,70 kg三级加载(JZ20,JZ50,JZ70);第2阶段模拟排岩机排土荷载,在坡顶5等分处设置4个排岩通道,分100,140 kg两级加载(JZ100,JZ140);分别测定堆载稳定后光纤的变形。
在堆载稳定的情况下模拟不同降雨条件对边坡变形的影响,基于相似三定理与南芬露天铁矿水文地质条件计算得每小时降雨量v为60 L,模型降雨面积S为4 m2,求得室内试验达到日最大降雨量时降雨时间t为
![]()
(1)
式中,t为降雨时间,h;p为日最大降雨量,83 mm。
计算得出达到日最大降雨量所需时间为5.5 h,故实验过程中根据当地降雨情况,分别进行3 d连续降雨5.5 h,对比分析各传感光纤的变形量。降雨及堆载设置如图4所示。

图4 降雨及堆载设置
Fig.4 Setting of rainfall and heap loading
3 排土场边坡模型实验结果分析
3.1 不同堆载条件下模型应变分析
3.1.1 X向光纤应变分析
X向光纤应变如图5所示,随着荷载的不断增大,光纤整体拉伸应变量逐渐增大,排土场不同位置的变形量也相应变大。X1层光纤变形规律:在荷载施加位置正下方应变量更加突出,其中X12,X13,X14号光纤的应变量达到3 000×10-6左右,从应变量最大处沿边坡倾向应变量逐渐减小并趋于稳定。X2层光纤整体变化趋势明显,不同位置光纤的应变量均随荷载的增加而增大;X2层光纤距坡顶位置较X1层稍深,受荷载施加位置的影响相对较小,并未出现明显应变突变。
3.1.2 Y向光纤应变分析
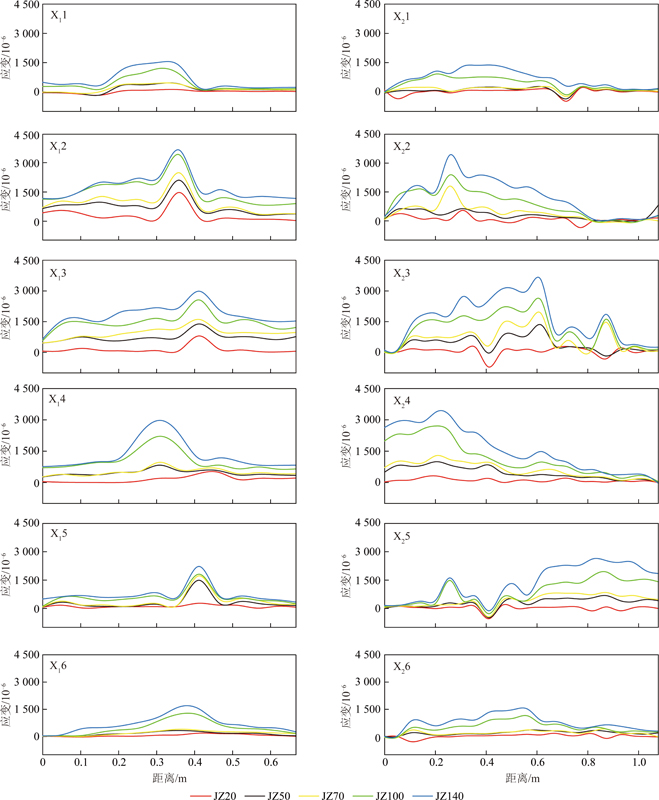
图5 不同加载条件下X向光纤应变
Fig.5 Strain of X-direction optical fiber under different loading conditions
Y向光纤应变如图6所示,光纤随排土场岩土体的变形产生同步应变,并且岩土体在施加荷载的位置发生不均匀沉降,光纤受拉,应变量为正;由于整个排土场岩土体可视为塑性体,在施加两荷载之间的位置,岩土体将会受到挤压的作用,光纤随着受压,应变量为负。在施加三级荷载时,Y11,Y12,Y21,Y22光纤的最大应变量分别为2 060×10-6,279×10-6,615×10-6,229×10-6,施加两级荷载时,Y11,Y12,Y21,Y22光纤的最大应变量分别为2 223×10-6,409×10-6,689×10-6,287×10-6。结果表明,边坡走向上岩土体变形量离施加荷载位置越近则越大,反之则反。
3.1.3 Z向光纤应变分析

图6 不同加载条件下Y向光纤应变
Fig.6 Strain of Y-direction optical fiber under different loading conditions
Z方向光纤应变如图7所示,在分别施加不同荷载的情况下测试光纤的应变量,更直观的反映排土场沉降量大小。图7表明,随着荷载的增大光纤的拉伸应变量增加,排土场边坡相似模型的沉降量也相应地增长。

图7 不同加载条件下Z向光纤应变
Fig.7 Strain of Z-direction optical fiber under different loading conditions
3.2 不同降雨条件下模型应变分析
3.2.1 X向光纤应变分析
X向光纤在第1天至第3天降雨工况下应变情况对比如图8所示,从X1层光纤的应变可得,传感光纤应变量关系为:降雨第1天>降雨第2天>降雨第3天。在降雨第1天时每根光纤不同位置均发生应变突变,且X11和X16,X12和X15,X13和X14号光纤的应变趋势和突变位置基本一致。X2层传感光纤应变量和X1层表现出相同的演化规律。由于X2层光纤距荷载施加位置较远,传感光纤整体应变量相对于X1层光纤较小。
3.2.2 Y向光纤应变分析
Y向光纤应变整体表现出与X向光纤相似的空间分布规律,由于Y向光纤与坡面位置平行,沿边坡走向出现2个应变突变点,突变位置沿光纤中点呈对称分布,但Y22号光纤整体变化趋势相对较平稳,并未出现明显的应变突变处。由于Y22号光纤远离岩土体滑动方向,靠近模型边界,其所在部位的岩土体变形存在较大阻力,故其应变量较小且平稳,Y向光纤降雨3天工况下应变如图9所示。
3.2.3 Z向光纤应变分析

图8 X向光纤降雨3 d综合应变
Fig.8 X fiber integrated strain in the rain for three days

图9 Y向光纤降雨3 d综合应变
Fig.9 Y fiber integrated strain in the rain for three days

图10 Z向光纤降雨3 d综合应变
Fig.10 Z fiber integrated strain in the rain for three days
从图10中Z向光纤应变可得Z11和Z12,Z21和Z22应变趋势相近,光纤应变突变处均出现在光纤余坡面的分界处,位置如图11所示,但整体应变量较小。

图11 Z向光纤应变突变位置
Fig.11 Strain mutation location diagram of Z Fiber
3.3 滑动面位置判断
图12为降雨前后物理模型同一位置处取样后经扫描电子显微镜(SEM)放大50倍得到颗粒间孔隙度的照片。由图12可知,降雨前的孔隙度明显小于降雨后。在降雨作用下,泥质胶结物冲刷流失,砂岩颗粒间胶结作用减弱。降雨过程中细颗粒在粗颗粒间的孔隙中移动,小裂缝在排土荷载作用下随着颗粒的移动逐渐形成,裂缝逐渐增多并最终贯通形成潜在的危险滑动面。但由于降雨量不足,并未形成滑坡。
表5为第1天降雨过程中各传感光纤应变突变情况汇总表,由表5可知第1天降雨中各光纤的应变量均出现不同程度的增加。各传感光纤关于Y向中轴对称分布,所以各光纤的应变量表现出对称增长的规律。光纤应变突变表明其所在位置的岩土体产生变形突变,综合分析各光纤应变,第1天降雨的时边坡处于不稳定状态,形成潜在危险滑动面。滑动面形成过程如图13所示,将各应变突变位置坐标在室内物理模型实验三维示意图中连接起来,可得最危险的滑动面位置如图14所示。

图12 降雨前后样品电镜扫描
Fig.12 Sample electron microscopy scanning pictures before and after the rain
表5 各光纤应变对应数据
Table 5 Corresponding data of each fiber strain
光纤编号应变长度/m突变位置至光纤起点距离/m突变处应变量/10-6应变增量/10-6X110.6670.591 624571X120.6670.432 028917X130.6670.362 5581 236X140.6670.322 7771 497X150.6670.442 3231 170X160.6670.611 708731X211.0780.921 042346X221.0780.691 675721X231.0780.631 991971X241.0780.641 969912X251.0780.671 910952X261.0780.871 292552Y112.0000.21/1.75∗2 066/2 195∗892/994∗Y122.0000.82/1.27∗1 772/1 698∗892/690∗Y212.0000.81/1.20∗1 541/1 321∗661/424∗Y212.000———Z111.6940.46695309Z121.6940.43709314Z211.6940.85885338Z221.6940.87896357
注:*表示沿光纤中点呈对称分布的突变位置至光纤起点距离、突变处应变量、应变增量。
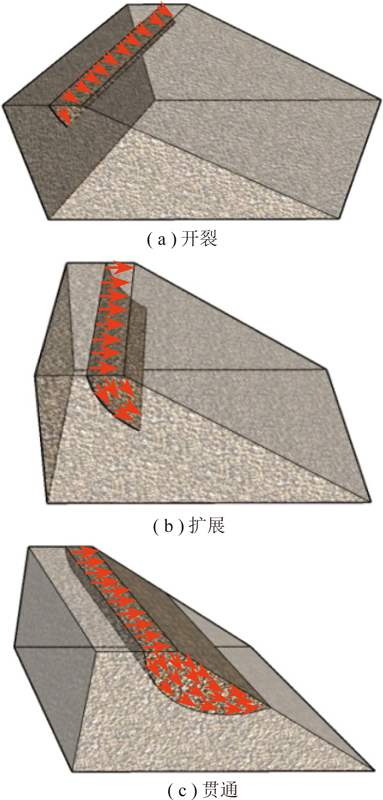
图13 边坡滑动面形成过程
Fig.13 Slope instability process
4 排土场边坡堆载变形数值模拟分析
4.1 数值模型的建立
如图15所示,为使数值模拟监测数据与室内试验监测数据在相似度上保持一致并进行相互验证,数值模型尺寸采用与物理模型相同的尺寸。本次模拟根据实验加载过程进行相似模拟,加载过程同样分为2个阶段5个工况,并根据室内物理模型相关参数设置数值参数进行弹性模型计算,生成符合实验现场的应力条件。弹性应力场计算结果如图16所示,数值参数见表6。
4.2 堆载变形数值模拟结果分析
4.2.1 坡体稳定阶段
20,50 kg加载计算结果如图17所示,计算稳定后竖向位移最大值分别为0.09,0.62 mm;模型中下部稳定区与上部应变区分界明显,但并未出现破坏现象。模型加载后在其剪切应力场中表现出潜在剪切应变贯通带,潜在贯通带通过加载点并呈圆弧状分布。
4.2.2 坡体内部开裂
70 kg加载计算结果如图18(a)所示,计算稳定后坡体竖向变形为1.2 mm(加载点的沉降不计入最大值),模型中下部稳定区与上部应变区分界明显,但并未出现明显破坏。模型加载后剪切应力场中剪切应变起始于顶部加载点位置,以加载点为中心产生的楔形变形向内部扩散,并且在2个加载点中右侧加载点下部已经形成弧形贯通面。说明该加载工况中,内部的弧形破坏面由顶端至下部形成。
4.2.3 坡体滑动面扩展
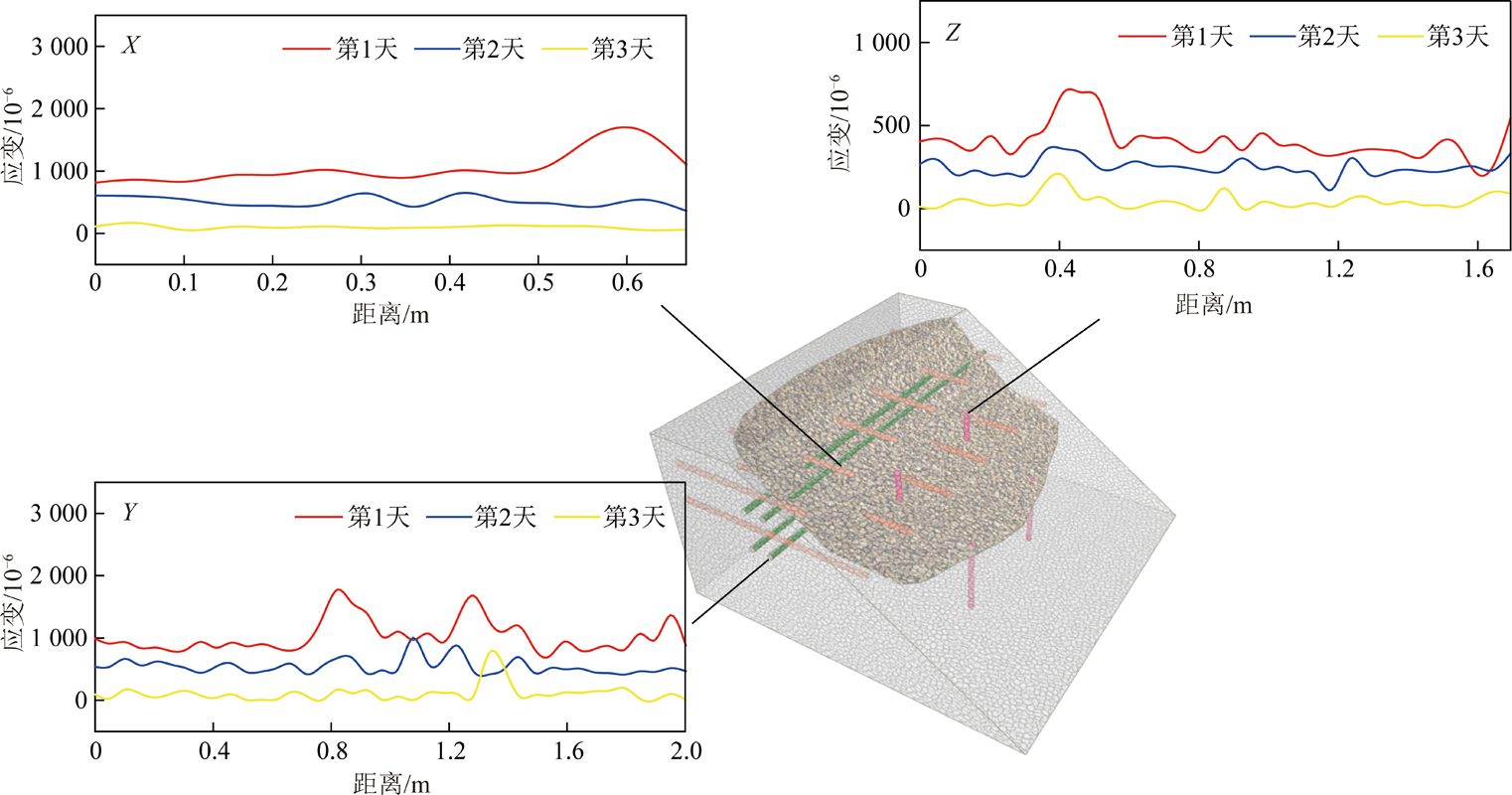
图14 滑动面
Fig.14 Sliding surface

图15 模型尺寸
Fig.15 Model size
图16 弹性计算应力场结果
Fig.16 Elasticity calculation of stress field results
100 kg加载计算结果如图18(b)所示,该工况4个加载点,加载点位置首先出现较大沉降与剪切应变,坡体竖向变形为1.2 mm。说明虽然本次加载总荷载较大,但荷载作用在坡体内部扩散,并未对边坡稳定性起到严重破坏作用。在剪切应变场中,中间2个加载点先出现剪切贯通带,并在顶部加载位置出现扩大的剪切区。
表6 绿泥角闪岩模型物理力学参数
Table 6 Physical and mechanical parameters of the green mud amphibolite model

密度/(kg·m-3)体积模量/MPa剪切模量/MPa黏聚力/Pa摩擦角/(°)抗拉强度/Pa2 5607041900210
4.2.4 坡体滑动面贯通
140 kg加载计算结果如图18(c)所示,同样为4个加载点,加载点位置首先出现较大沉降与剪切应变,坡体竖向变形为4 mm。本次加载后边坡变形较大,出现明显破坏现象,说明在该工况下边坡失稳。在模型剪切应变场中,中间2个加载点先出现剪切贯通带,且顶部加载位置出现扩大的剪切区,但并未扩展至模型表面。
5 工程尺度排土场边坡稳定性监测方法设计
以Ⅱ号全段高排土场光纤监测室内物理模型试验和数值模拟计算结果为依据,针对Ⅱ号全段高排土场排土现状进行大变形监测方法设计。在边坡坡顶平台位置开挖沟槽,将分布式感测光缆和光纤监测管埋设到边坡体内部。受排土荷载影响,若边坡产生向下滑动趋势,在边坡土体变形区域,光缆随边坡一起变形,从而产生拉伸变形。利用分布式光纤应变测试仪,可以测试出光缆变形大小,圈定出边坡体变形区域。如图19所示,在Ⅱ号全段高排土场的排岩机轨道外侧布置200 m测线进行监测。A,B测线开挖长度均为200 m,测线光缆两端需各冗余20 m。

图17 加载20,50 kg后竖向位移场及剪切应变场
Fig.17 Vertical displacement field and Shear strain field after loading of 20 kg and 50 kg
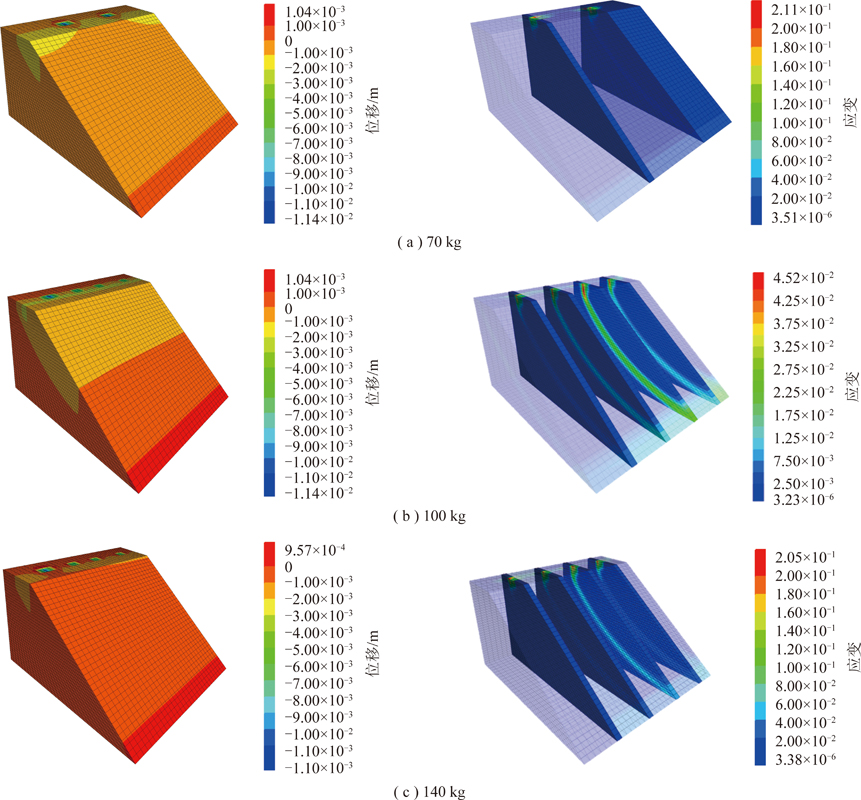
图18 加载70,100,140 kg后竖向位移场及剪切应变场
Fig.18 Vertical displacement and Shear strain field after loading of 70,100 and 140 kg

图19 边坡变形监测位置示意
Fig.19 Slope deformation monitoring location map
根据监测现场实际情况及监测要求,尽量选取与边坡顶部走向平行的监测线路,标明监测区带的端点,用生石灰粉进行定线标识出监测线路。沟槽开挖后,将沟槽底部整平或在沟底铺砂垫摊平压实;将平整放线且两端预留足够长度的光纤固定在沟底并加装保护套,待上述工序完成后即可进行回填并修筑监测站。
6 结 论
(1)对模型尺度Ⅱ号全段高排土场开展堆载和降雨模拟实验,并对不同工况下监测光纤得到的曲线进行分析得排土场变形量与堆载的空间演化规律:排土场的变形量与堆载增量呈正相关;但随深度增加,堆载对模型变形量的影响逐渐减小,说明深度的增加使边坡变形敏感度降低。排土场变形量与降雨量的时间演化规律:排土场在变形量与降雨时长呈负相关,与单位降雨时长(h)呈正相关,说明排土场在雨水持续冲刷下产生变形,但随着降雨的进行模型发生排水固结,变形量逐渐减小。
(2)排土场模型实验中堆载和降雨作用下排土场边坡对称分布监测光纤的应变量各具有相似的空间分布规律:X向中部产生突变且随着深度增加应变量波动加剧,靠近临空面与内部的应变趋于稳定,随着堆载增加模型内部也产生不均匀变形。Y向监测光纤应变突变位置与模拟排岩堆载位置一致,精准反映堆载在排土场内部应力扩散带来的影响。反映排土场模型沉降量的Z向监测光纤在加载后随即产生应变,加载完成后Z向应变达到稳定并维持在同一水平。加载完成后降雨条件下X,Y,Z三向监测光纤在早期降雨随即做出整体应变量突增的响应,排土场边坡吸水能力随着降雨的持续进行降低,长期降雨对边坡变形带来的影响逐渐降低。
(3)结合堆载及降雨作用下模型尺度排土场边坡稳定性监测实验、堆载作用下的数值模拟结果和降雨影响下材料的电镜结构扫描结果可知:降雨影响下排土场边坡泥质胶结材料冲刷流失,颗粒间接触力减小,排弃物间隙变大。堆载增加使降雨在边坡内部产生的潜在滑动面扩大最终形成贯通的滑动面。
(4)监测光纤组成排土场滑坡监控网络后,测得应变量的变化位置能精确反映排土场边坡内部变形量及沉降量变化过程,不仅为确定排土场边坡内部潜在滑动面提供科学的实验依据,也可供工程尺度排土场边坡失稳监测借鉴。
[1] 孙世国,杨宏,冉启发,等.典型排土场边坡稳定性控制技术[M].北京:冶金工业出版社,2011.
[2] United States Geological Survey.Landslide hazard[R].Reston,VA.2000.
[3] SCHUSTER R L.HIGHLAND L M.Socioeconomic impacts of landslides in the Western Hemisphere[R].Reston,VA.2001.
[4] KRISTO C,RAHARDJO H,SATYANAGA A.Effect of variations in rainfall intensity on slope stability in Singapore[J].International Soil and Water Conservation Research,2017,5(4):258-264.
[5] DAWSON R F,MORGENSTERN N R,STOKES A W.Liquefaction flowslides in Rocky Mountain coal mine waste dumps[J].Canadian Geotechnical Journal,1998,35(2):328-343.
[6] CHAULYA S K,SINGH R S,CHAKRABORTY M K,et al.Quantification of stability improvement of a dump through biological reclamation[J].Geotechnical & Geological Engineering,2000,18(3):193-207.
[7] 刘福明,才庆祥,周伟,等.露天矿排土场边坡降水入渗规律试验研究[J].煤炭学报,2015,40(7):1534-1540.
LIU Fuming,CAI Qingxiang,ZHOU Wei,et al.Experimental study on the rainfall in filtration rule in the dump slope of surface mines[J].Journal of China Coal Society,2015,40(7):1534-1540.
[8] 缪海宾,王建国,费晓欧,等.基于孔隙水压力消散的排土场边坡动态稳定性研究[J].煤炭学报,2017,42(9):2302-2306.
MIAO Haibin,WANG Jianguo,FEI Xiaoou,et al.Study on dynamic stability of dump slope based on the dissipation of pore pressure[J].Journal of China Coal Society,2017,42(9):2302-2306.
[9] LI Y,ZHANG S,ZHANG X.Classification and fractal characteristics of coal rock fragments under uniaxial cyclic loading conditions[J].Arabian Journal of Geosciences,2018,11(9):201.
[10] TAO Zhigang,LI Mengnan,ZHU Chun,et al.Analysis of the critical safety thickness for pretreatment of mined-out areas underlying the final slopes of open-pit mines and the effects of treatment[J].Shock and Vibration,2018,2018:1-8.
[11] SUN Guanhua,LIN Shan,JIANG Wei,et al.A simplified solution for calculating the phreatic line and slope stability during a sudden drawdown of the reservoir water level[J].Geofluids,2018,2018:1-14.
[12] ALAN W Bishop.The use of the slip circle in the stability analysis of slope[J].Geotechnique,1995,16(1):177-197.
[13] NILMAR Janbu.Earth pressure and bearing capacity by generalized procedure of slices[A].Proceedings of the 4th International conference of soil mechanics and foundation engineering[C].London:1997,(2):207-212.
[14] SRIKRISHNAN S,PORATHUR J L,AGARWAL H.Impact of ear-thquake on mining slopes-a numerical approach[J].Arabian Journal of Geosciences,2013,7(12):5193-5208.
[15] WANG J,CHEN C.Stability analysis of slope at a disused waste dump by two-wedge model[J].International Journal of Mining,Reclamation and Environment,2016,31(8):575-588.
[16] NGUYEN V U,CHOWDHURY R N.Probabilistic Analysis of Mining Spoil Piles-Two Techniques Compared[J].Internatlonal Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts,1984,21(6):303-312.
[17] NGUYEN V U,CHOWDHURY R N.Simulation for risk analysis with correlated variables[J].Geotechnique,1985,35(1):47-58.
[18] STEIAKAKIS E,KAVOURIDIS K,MONOPOLIS D.Large scale failure of the external waste dump at the “South Field” lignite mine,Northern Greece[J].Engineering Geology,2009,104(3-4):269-279.
[19] RADHAKANTA Koner,DEBASHISH Chakravarty.Discrete element approach for mine dump stability analysis[J].Mining Science and Technology,2010,20(6):809-813.
[20] LÜ Xiangfeng,WANG Zhenwei,WANG Jianguo.Seepage-damage coupling study of the stability of water-filled dump slope[J].Engineering Analysis with Boundary Elements,2014,42:77-83.
[21] RADHAKANTA Koner,DEBASHISH Chakravarty.Numerical ana-lysis of rainfall effects in external overburden dump[J].International Journal of Mining Science and Technology,2016,26(5):825-831.
[22] WANG Zhiliu,LIU Bo,HAN Yanhui,et al.Stability of inner dump slope and analytical solution based on circular failure:Illustrated with a case study[J].Computers and Geotechnics,2020,117103241.1-103241.10.
[23] CHO Y C,SONG Y S.Deformation measurements and a stability analysis of the slope at a coal mine waste dump[J].Ecological Engineering.2014,68(7):189-199.
[24] SUN Yijie,XU Hongzhong,GU Peng,et al.Application of FBG sensing technology in stability analysis of geogrid-reinforced slope[J].Sensors,2017,17(3):597.
[25] ZHANG Hao,WU Zhishen.Performance evaluation of PPP-BOTDA-Based distributed optical fiber sensors[J].International Journal of Distributed Sensor Networks,2012,8(12):1-12.
[26] XIAO Henglin,HUANG Jie.Experimental study of the applications of fiber optic distributed temperature sensors in detecting seepage in soils[J].Geotechnical Testing Journal,2013,36(3):360-368.
