岩爆是硬岩矿井、深埋隧道、地下水电站等深部岩体工程开挖过程中，围岩受到应力重分布的作用，其内部集聚的高弹性应变能猛烈释放，使岩体发生脆性破坏的一种常见地质灾害，常常表现为片状剥落、严重片帮，有的伴有声响、弹射甚至抛掷，直接威胁到施工人员、设备以及建筑安全。世界上最早有资料记载的岩爆发生于1738年英国的锡矿坑道，我国最早记录的岩爆发生于1933年抚顺胜利煤矿[1]。随着我国经济建设的不断发展，地下工程日益增多，岩爆灾害呈频发趋势，开展岩爆灾害预测研究已迫在眉睫[2-4]。

早期主要是从单一因素出发进行岩爆的预测研究，在强度、刚度、能量、稳定、断裂、损伤、分形和突变等方面提出各种假设和判据，如Russenes判据[5]、陆家佑判据[6]、王元汉判据[7]和Kidybinski判据[8]等。随着研究的不断深入，逐渐意识到岩爆是一种非常复杂的动力失稳现象，其涉及的影响因素众多，目前多采用多指标综合评价法对岩爆进行预测，如模糊数学综合评判法[7]、Bayes判别分析法[9]、距离判别分析法[10]、Fisher判别分析法[11]、集对分析法[12-13]、证据理论[14]、物元分析理论[15]、未确知测度理论[16]、云模型[17-18]、人工神经网络[19-20]、支持向量机[21]等，取得诸多研究成果。但由于岩爆问题的模糊性和复杂性，目前的研究中主要存在2方面的问题:① 迄今为止还没有一种理论或方法能非常准确地预测岩爆，需要多种方法和理论的结合，因此，引入新的有效预测方法是十分必要的；② 运用多指标综合评价法预测岩爆的一个关键问题是评价指标权重的确定，目前常用的权重确定方法有层次分析法、德尔菲法、熵权法等，但这些方法都存在一些不足，如层次分析法、德尔菲法主观性太强，熵权法对指标差异度敏感性较大，因此，探索新的赋权方法对于岩爆问题也是至关重要的。

为了较合理地确定岩爆烈度分级预测中各评价指标的权重，笔者提出一种新的组合赋权方法，并将属性区间识别模型[22]引入到岩爆问题中进行岩爆灾害预测。该模型采用反熵权法，克服了传统熵权法对指标差异度敏感性较大的问题，并基于离差平方和最大的原则将主、客观权重相结合得到组合权重，最后利用置信度准则进行岩爆等级判别。研究结果表明该模型的预测结果能客观地反映岩爆的真实状况，为岩爆预测提供了一种新的思路。

1 属性区间识别模型

设X为评价对象的全体，xi∈X(i=1,2,…,m)为评价对象，每个评价对象有n个评价指标I1,I2,…,In，xij为第i个评价对象的第j个评价指标的测量值。假定F为X上的某类属性空间，(C1,C2,…,Ck)为F的有序分割，根据已知的分级标准构造的分级标准矩阵为

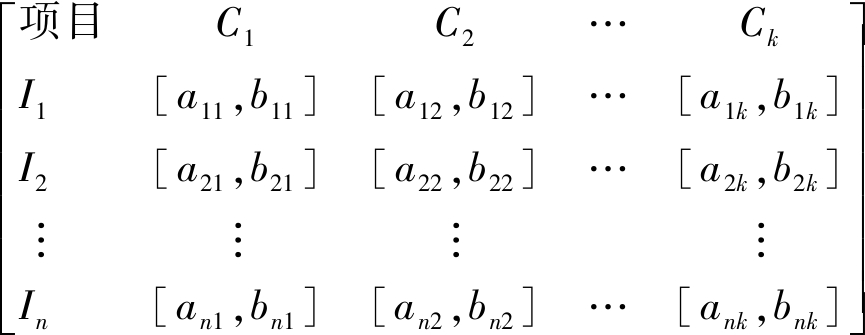
其中，ajp,bjp(1≤j≤n,1≤p≤k)分别为第j个评价指标在属性Cp上的左右端点值，且满足aj1<aj2<…<ajk，bj1<bj2<…<bjk或aj1>aj2>…>ajk，bj1>bj2>…>bjk。

1.1 属性测度区间的计算

将xij具有属性Cp(1≤p≤k)的属性测度区间记为则有

当xij≤aj1(xij≥aj1)时，

当xij≤bj1(xij≥bj1)时，

当xij≥ajk(xij≤ajk)时，

当xij≥bjk(xij≤bjk)时，

当ajl≤xij≤aj(l+1)(或aj(l+1)≤xij≤ajl)(1≤l≤k-1)时，

当bjl≤xij≤bj(l+1)(或bj(l+1)≤xij≤bjl)(1≤l≤k-1)时，

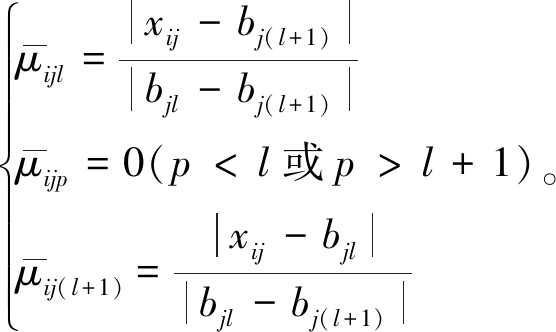
1.2 属性测度的计算

计算得到各评价指标测量值的属性测度区间后，通过引入均化系数[23]按下式计算各测量值的属性测度μijp:

(1)

式中，α为均化系数且α∈(0，1)。

1.3 评价对象等级识别

根据各测量值的属性测度，按式(2)计算第i个评价对象属于等级Cp的综合属性测度μip:

(2)

式中，wj为第j个评价指标的权重。

按照置信度准则，对置信度λ(0.5≤λ≤1.0)，计算

(3)

取p直到满足式(3)，则评价对象xi属于Cp级。

2 组合赋权

2.1 层次分析法

层次分析法[24](简称AHP)由美国著名的运筹学家Saaty于20世纪70年代提出，目前主要应用于确定模糊、复杂的决策问题中不同层次的指标权重。该方法简单、灵活、易于分析计算，但带有一定的主观性，不够客观全面。运用层次分析法确定权重的步骤如下:

(1)构造判断矩阵。判断矩阵中的元素表示的是同一层次指标之间的相对重要性。笔者引入适当的赋值标准来描述指标之间的相对重要性，将其以数字形式体现，赋值标准见表1。设判断矩阵为R，rij为第i个指标相比第j个指标的重要程度且满足rii=1和rij=1/rji，则判断矩阵的基本形式为

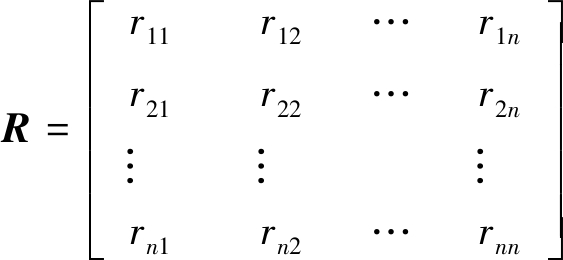
其中，n为指标的数目。

(2)求出判断矩阵R的最大特征值λmax所对应的特征向量，对该特征向量进行归一化处理，得到新的向量，该向量中的每个元素值即是相应指标的权重。

(3)一致性检验。判断矩阵是否满足一致性要求，用指标CR刻画。当CR<0.1时，判断矩阵满足一致性要求，标准化后的特征向量可以作为权向量。其相关计算公式为

CR=CI/RI

(4)

CI=(λmax-n)/(n-1)

(5)

式中，CI为一致性指标;RI为平均随机一致性指标，其取值标准见表2。

2.2 反熵权法

熵的概念来源于热力学，用来表征系统的无序程度。在信息论中，熵还可以用来度量数据本身所提供信息的有效性，并在多个领域均得到了广泛的应用。传统熵权法生成的权重对指标差异度敏感性较大，在权重分配时可能会出现个别权重过大或过小的极端情况，导致部分指标的信息被淹没。与传统熵权法相比，反熵权法[25]对指标差异度的敏感性较弱，可以有效地避免上述极端情况。所以笔者在确定客观权重时采用反熵权法，其主要步骤如下：

(1)建立原始数据矩阵。

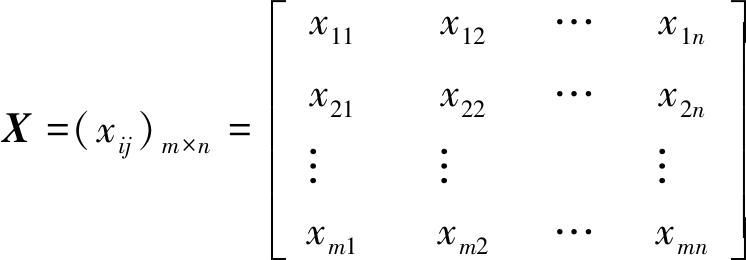
其中，m为评价对象的数目;n为评价指标的数目。

(2)对原始数据进行标准化处理。

对越大越优的指标有

(6)

对越小越优的指标有

(7)

则可得到标准化处理后的矩阵

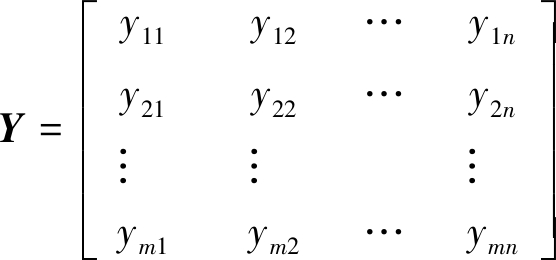
(3)计算第j个评价指标的反熵值Ej，公式为

(8)

式中，

(4)根据所求得的各个指标的反熵值，计算第j个评价指标的权重

(9)

2.3 基于离差平方和的最优组合赋权

层次分析法主要是根据评价者的主观经验来确定权重，而反熵权法则是依据评价对象的指标信息来确定权重，将主客观权重相结合可以得到组合权重，使属性赋权达到主观与客观的统一。笔者采用基于离差平方和最大的最优组合赋权方法[26]，确定主、客观权重在组合权重中的比重，使m个评价对象的总离差平方和达到最大。

设主观权向量为客观权向量为则组合权向量为

Wc=θ1W1+θ2W2

(10)

式中，θ1,θ2为组合系数。

定义第i1个评价对象和第i2个评价对象的离差为

(11)

则第i个评价对象和其他各评价对象的离差平方和为

(12)

根据前述基本思想，要使m个评价对象的总离差平方和达到最大，可构造如下目标函数:

(13)

若令矩阵Y1为

则目标函数J(Wc)可表示为

(14)

要求出组合权向量Wc，由式(10)知只要求出系数向量Θ即可。于是基于离差平方和的最优组合赋权即为如下最优化问题:

maxF(Θ)=ΘTWTY1WΘ

(15)

设λmax为矩阵WTY1W的最大特征值，Θ*为最大特征值所对应的单位特征向量，则F(Θ)的最大值可记为λmax，式(15)的最优解可记为Θ*。

求出Θ*后，代入式(10)可进一步求出组合权向量由于权向量一般都满足归一化条件，因此需要对进行归一化处理，即令

(16)

3 岩爆烈度分级预测模型

3.1 模型框架

本文建立的基于最优组合赋权岩爆烈度分级预测属性区间识别模型的基本框架如下:① 根据岩爆的发生机制选取评价指标并建立评价指标体系;② 统计近些年来国内外典型岩爆相关数据并对其进行预处理;③ 结合属性区间识别模型的基本原理，根据岩爆烈度分级标准确定各评价指标测量值的属性测度;④ 利用层次分析法和反熵权法分别确定各评价指标的主观权重和客观权重，提出一种基于离差平方和的最优组合赋权规则确定各评价指标的最终权重;⑤ 根据评价指标测量值的属性测度和对应评价指标的权重，计算样本隶属于各个岩爆等级的综合属性测度;⑥ 按照置信度准则确定样本所对应的岩爆等级。

具体流程如图1所示。

3.2 评价指标体系的确定

岩爆的影响因素众多，它的发生不仅取决于岩石的物理力学性质，还受岩体完整性和地应力大小的影响[27]。综合考虑岩爆发生的内外因条件，结合国内外的一些岩爆判据，选取围岩最大切向应力与岩石单轴抗压强度比σθ/σc、岩石单轴抗压强度与抗拉强度比σc/σt、弹性变形能指数Wet和岩体完整性系数Kv作为岩爆烈度分级预测的评价指标。其中，σc,σt和Wet反映了岩石的物理力学性质，Kv反映了岩体节理和裂隙的发育情况，σθ反映了地应力的大小。参照王元汉等[7]及张乐文等[28]的研究成果，将岩爆划分为无岩爆(Ⅰ级)、弱岩爆(Ⅱ级)、中等岩爆(Ⅲ级)和强烈岩爆(Ⅳ级)4个等级，并建立了岩爆等级与4个评价指标之间的关系。为了正确应用属性区间识别模型，根据Ⅱ级和Ⅲ级岩爆各评价指标分布的区间状况，应该为Ⅰ级和Ⅳ级岩爆的指标分布区间补充相应的上限值和下限值，经过补充修正之后的岩爆等级和各评价指标的关系见表3，对应的分级标准矩阵为

3.3 原始工程数据及预处理

为了检验本文所采用的最优组合赋权-属性区间识别模型的可行性和有效性，统计整理了近些年来国内外12个典型岩爆相关数据[29]，见表4。

为了消除评价指标的量纲影响，使各评价指标具有可比度和可公度性，便于利用反熵权法确定各评价指标的客观权重，需对原始工程数据进行标准化处理。由表3可知，σθ/σc,Wet和Kv越小时，岩爆等级越低，属于越小越优型指标，应采用式(7)进行标准化处理;σc/σt越大时，岩爆等级越低，属于越大越优型指标，应采用式(6)进行标准化处理。标准化后的数据见表4。

3.4 组合权重的确定

3.4.1 层次分析法主观权重计算

综合文献[24，30]和相关专家意见构建的判断矩阵(按照σθ/σc,σc/σt,Wet,Kv的顺序)为

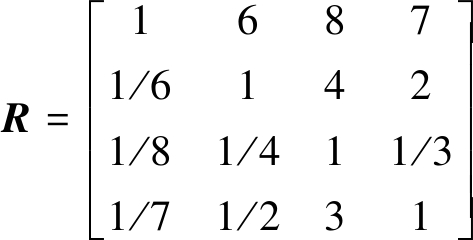
经过计算可得判断矩阵R的最大特征值λmax=4.165 2，最大特征值所对应的特征向量因此该判断矩阵满足一致性要求，归一化后的特征向量可以作为主观权向量。

3.4.2 反熵权法客观权重计算

将标准化后的岩爆数据代入式(8)，可以得到各个评价指标的反熵值为

再由式(9)可进一步求得各个评价指标的反熵权为

3.4.3 组合权重确定

根据Y1的定义式有

层次分析法得到的主观权向量反熵权法得到的客观权向量令W=(W1,W2)。

由W和Y1计算WTY1W得

其最大特征值为λmax=24.498 4，最大特征值所对应的单位特征向量为

最后结合式(10),(16)可求得组合权重

3.5 模型检验

笔者采用置信度准则对近些年来国内外12个典型岩爆工程实例进行等级识别，λ取0.5。

在确定评价指标测量值的属性测度时引入了均化系数α，α的取值对预测结果有一定的影响。为了选取最优的α值，使α在区间[0.05，0.95]内变化，步长为0.1。通过图2可以发现，当α取0.55,0.65,0.75,0.85和0.95时，正确预测的岩爆数量均为6个;当α取0.45时，正确预测的岩爆数量为7个;当α取0.35时，正确预测的岩爆数量为9个;当α取0.25时，正确预测的岩爆数量为10个;当α取0.05和0.15时，正确预测的岩爆数量为11个，此时预测精度达到最高。

表5给出了当α=0.15时本文模型的预测结果，并与模糊综合评判法、灰评估模型的预测结果以及实际岩爆等级进行了比较，发现除了样本9外，其他样本的预测结果与实际岩爆等级均相符，准确率达91.7%，且与模糊综合评判法和灰评估模型的预测结果基本一致。但将样本9的岩爆等级由中等岩爆误判为强烈岩爆，结果偏安全，从工程安全的角度来说是允许的。由此可见，基于最优组合赋权的属性区间识别模型用于岩爆烈度分级预测是可行且有效的。

4 结 论

(1)综合考虑岩爆的特点及成因，选取围岩最大切向应力与岩石单轴抗压强度比σθ/σc、岩石单轴抗压强度与抗拉强度比σc/σt、弹性变形能指数Wet和岩体完整性系数Kv作为岩爆烈度分级预测的评价指标。

(2)为了克服传统熵权法对指标差异度敏感性较大的问题，采用反熵权法确定客观权重，并利用一种基于离差平方和的最优组合赋权方法将反熵权法确定的客观权重与层次分析法确定的主观权重相结合，使得评价更加全面、客观合理。

(3)岩爆烈度分级预测是一个典型的多属性有序分割问题，属性区间识别模型在解决这类问题上具有显著的优越性。本文将属性区间识别模型引入到岩爆问题中，建立了岩爆烈度分级预测的最优组合赋权-属性区间识别模型，结合国内外12个岩爆实例表明:该模型计算方法简单，结果与实际情况较吻合，具有较高的准确性和可靠性。

(4)属性区间识别模型用于岩爆烈度分级预测虽具有一定的应用意义，但还只是初步尝试，在评价指标权重的确定、岩爆烈度分级标准的划分以及评价指标的选取等问题上需要更加深入的研究。

参考文献（References）:

[1] 裴启涛，李海波，刘亚群，等.基于组合赋权的岩爆倾向性预测灰评估模型及应用[J].岩土力学，2014，35(S1):49-56.

PEI Qitao,LI Haibo,LIU Yaqun,et al.A grey evaluation model for predicting rockburst proneness based on combination weight and its application[J].Rock and Soil Mechanics,2014,35(S1):49-56.

[2] 冯夏庭，陈炳瑞，张传庆，等.岩爆孕育过程的机制、预警与动态调控[M].北京:科学出版社，2013.

[3] DOU Linming,MU Zonglong,LI Zhenlei,et al.Research progress of monitoring,forecasting,and prevention of rockburst in underground coal mining in China[J].International Journal of Coal Science & Technology,2014,1(3):278-288.

[4] XUE Sheng,YUAN Liang,WANG Junfeng,et al.A coupled DEM and LBM model for simulation of outbursts of coal and gas[J].International Journal of Coal Science & Technology,2015,2(1):22-29.

[5] 张镜剑，傅冰骏.岩爆及其判据和防治[J].岩石力学与工程学报，2008，27(10):2034-2042.

ZHANG Jingjian,FU Bingjun.Rockburst and its criteria and control[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(10):2034-2042.

[6] PACK K H,LEE J G,ADISORN O.Seepage force in a drained circular tunnel:An analytical approach[J].Canadian Geotechnical Journal,2008,45(3):432-436.

[7] 王元汉，李卧东，李启光，等.岩爆预测的模糊数学综合评判方法[J].岩石力学与工程学报，1998，17(5):493-501.

WANG Yuanhan,LI Wodong,LI Qiguang,et al.Method of fuzzy comprehensive evalutions for rockburst prediction[J].Chinese Journal of Rock Mechanics and Engineering,1998,17(5):493-501.

[8] KIDYBINSKI A.Bursting liability indices of coal[J].Journal of Rock Mechanics and Mining Sciences,1981,18(4):295-304.

[9] 宫凤强，李夕兵，张伟.基于Bayes判别分析方法的地下工程岩爆发生及烈度分级预测[J].岩土力学，2010，31(S1):370-377,387.

GONG Fengqiang,LI Xibing,ZHANG Wei.Rockburst prediction of underground engineering based on Bayes discriminant analysis method[J].Rock and Soil Mechanics,2010,31(S1):370-377,387.

[10] 宫凤强，李夕兵.岩爆发生和烈度分级预测的距离判别方法及应用[J].岩石力学与工程学报，2007，26(5):1012-1018.

GONG Fengqiang,LI Xibing.A distance discriminant analysis method for prediction of possibility and classification of rockburst and its application[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(5):1012-1018.

[11] 白云飞，邓建，董陇军，等.深部硬岩岩爆预测的FDA模型及其应用[J].中南大学学报(自然科学版)，2009，40(5):1417-1422.

BAI Yunfei,DENG Jian,DONG Longjun,et al.Fisher discriminant analysis model of rock burst prediction and its application in deep hard rock engineering[J].Journal of Central South University(Science and Technology),2009,40(5):1417-1422.

[12] 陈红江，李夕兵，张毅.基于集对分析法的岩爆烈度分级预测研究[J].南华大学学报(自然科学版)，2008，22(4):10-14.

CHEN Hongjiang,LI Xibing,ZHANG Yi.Study on application of set pair analysis method to prediction of rockburst[J].Journal of University of South China(Natural Science Edition),2008,22(4):10-14.

[13] 汪明武，李丽，金菊良.岩爆预测的改进集对分析模型[J].岩土力学，2008，28(S1):511-514,518.

WANG Mingwu,LI Li,JIN Juliang.An improved set pair analysis model for the prediction of rockburst[J].Rock and Soil Mechanics,2008,28(S1):511-514,518.

[14] 贾义鹏，吕庆，尚岳全，等.基于证据理论的岩爆预测[J].岩土工程学报，2014，36(6):1079-1086.

JIA Yipeng,LÜ Qing,SHANG Yuequan,et al.Rockburst prediction based on evidence theory[J].Chinese Journal of Geotechnical Engineering,2014,36(6):1079-1086.

[15] 熊孝波，桂国庆，郑明新，等.基于可拓方法的深埋长大隧道岩爆预测研究[A].第10次全国岩石力学与工程学术大会论文集[C].北京:中国电力出版社，2008.

XIONG Xiaobo,GUI Guoqing,ZHENG Mingxin,et al.Study on application of extension method to prediction of rockburst in deep and over-length highway tunnel[A].Proceedings of 10th Learning Congress About Rock Mechanics and Engineering[C].Beijing:China Electric Power Press,2008.

[16] 史秀志，周健，董蕾，等.未确知测度模型在岩爆烈度分级预测中的应用[J].岩石力学与工程学报，2010，29(S1):2720-2726.

SHI Xiuzhi,ZHOU Jian,DONG Lei,et al.Application of unscertained measurement model to prediction of classification of rockburst intensity[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(S1):2720-2726.

[17] 王迎超，靖洪文，张强，等.基于正态云模型的深埋地下工程岩爆烈度分级预测研究[J].岩土力学，2015，36(4):1189-1194.

WANG Yingchao,JING Hongwen,ZHANG Qiang,et al.A normal cloud model-based study of grading prediction of rockburst intensity in deep underground engineering[J].Rock and Soil Mechanics,2015,36(4):1189-1194.

[18] 周科平，林允，胡建华，等.基于熵权-正态云模型的岩爆烈度分级预测研究[J].岩土力学，2016，37(S1):596-602.

ZHOU Keping,LIN Yun,HU Jianhua,et al.Grading prediction of rockburst intensity based on entropy and nomal cloud model[J].Rock and Soil Mechanics,2016,37(S1):596-602.

[19] 陈海军，郦能惠，聂德新，等.岩爆预测的人工神经网络模型[J].岩土工程学报，2002,24(2):229-232.

CHEN Haijun,LI Nenghui,NIE Dexin,et al.A model for prediction of rockburst by artificial neural network[J].Chinese Journal of Geotechnical Engineering,2002,24(2):229-232.

[20] FENG X T,WEBBER S,OZBAY M U,et al.Neural network assessment of rockburst risks for deep gold mines in South Africa[J].Transactions of Nonferrous Metals Society of China,1998,8(2):335-341.

[21] 赵洪波.岩爆分类的支持向量机方法[J].岩土力学，2005，26(4):642-644.

ZHAO Hongbo.Classication of rockburst using support vector machine[J].Rock and Soil Mechanics,2005,26(4):642-644.

[22] 李群，宁利.属性区间识别理论模型研究及其应用[J].数学的实践与认识，2002(1):50-54.

LI Qun,NING Li.Attribute interval recognition theoretical model with application[J].Mathematics in Practice and Theory,2002(1):50-54.

[23] 刘洋，叶义成，刘晓云，等.组合赋权-属性区间识别模型法优选采矿方法[J].金属矿山，2017(7):25-30.

LIU Yang,YE Yicheng,LIU Xiaoyun,et al.Optimal selection of mining method by attribute interval recognition model based on empowerment combination theory[J].Metal Mine,2017(7):25-30.

[24] 徐琛，刘晓丽，王恩志，等.基于组合权重-理想点法的应变型岩爆五因素预测分级[J].岩土工程学报，2017，39(12):2245-2252.

XU Chen,LIU Xiaoli,WANG Enzhi,et al.Prediction and classification of strain mode rockburst based on five-factor criterion and combined weight-ideal point method[J].Chinese Journal of Geotechnical Engineering,2017,39(12):2245-2252.

[25] 张海瑞，韩冬，刘玉娇，等.基于反熵权法的智能电网评价[J].电力系统保护与控制，2012，40(11):24-29.

ZHANG Hairui,HAN Dong,LIU Yujiao,et al.Smart grid evaluation based on anti-entropy weight method[J].Power System Protection and Control,2012,40(11):24-29.

[26] 陈伟，夏建华.综合主、客观权重信息的最优组合赋权方法[J].数学的实践与认识，2007(1):17-22.

CHEN Wei,XIA Jianhua.An optimal weights combination method considering both subjective and objective weight information[J].Mathematics in Practice and Theory,2007(1):17-22.

[27] MARK Christopher.Coal bursts in the deep longwall mines of the United States[J].International Journal of Coal Science & Technology,2016,3(1):1-9.

[28] 张乐文，张德永，李术才，等.基于粗糙集理论的遗传-RBF神经网络在岩爆预测中的应用[J].岩土力学，2012，33(S1):270-276.

ZHANG Lewen,ZHANG Deyong,LI Shucai,et al.Application of RBF neural network to rockburst prection based on rough set theory[J].Rock and Soil Mechanics,2012,33(S1):270-276.

[29] 宋艳艳.黄岛地下水封油库施工地质灾害危险性评价研究[D].北京:中国地质大学(北京)，2012.

SONG Yanyan.Risk evaluation on geological hazards under construction of Huangdao underground water-sealed oil storage caverns[D].Beijing:China University of Geosciences(Beijing),2012.

[30] 舒磊，王磊，彭金伟.秦岭铁路隧道岩爆预报的模糊综合评判研究[J].四川联合大学学报(工程科学版)，1998(4):55-60.

SHU Lei,WANG Lei,PENG Jinwei.The rockburst forecast based on fuzzy comprehensive evaluation of Qinling railway tunnel[J].Journal of Sichuan Union University(Engineering Science Edition),1998(4):55-60.

Prediction model of rockburst intensity classification based on combined weighting and attribute interval recognition theory

YIN Xin1,LIU Quansheng1,WANG Xinyu1,HUANG Xing2

(1.School of Civil Engineering and Architecture,Wuhan University,Wuhan 430072,China; 2.State Key Laboratory of Geotechnical Engineering,Institute of Rock and Soil Mechanics,Chinese Academy of Sciences,Wuhan 430071,China)

Abstract:Rockburst is a kind of dynamic instability phenomenon that easily occurs in the excavation process of deep underground engineering.It has the characteristics of suddenness,uncertainty and strong destructiveness.The research on the classification and prediction of rockburst intensity has become a worldwide problem that needs urgent solution.Due to the classification and prediction of rockburst intensity is a typical multi-attribute ordered segmentation problem,the prediction model is established by using attribute interval recognition theory.Considering the causes of rockburst and its characteristics,the ratio of the maximum tangential stress of surrounding rock to the uniaxial compressive strength of rock,the ratio of the uniaxial compressive strength to the tensile strength of rock,the elastic strain energy index,and the intactness index of rock mass are selected as the evaluation indexes from the aspects of physical and mechanical properties of rock,rock mass integrity and in-situ stress.The subjective weight and objective weight of these evaluation indexes are determined by the analytic hierarchy process (AHP) and anti-entropy weight method respectively,overcoming the problem that the traditional entropy weight method is sensitive to the index difference when determining the objective weight,and based on which,an optimal combined weighting rule on the basis of the sum of squares of deviations is proposed.Further,the optimal combined weighting-attribute interval recognition model for the classification and prediction of rockburst intensity is established.12 groups of typical rockburst engineering cases are chosen to test the proposed model.Since the averaging coefficient has a great influence on the prediction performance of the model,in order to select the optimal averaging coefficient,it is changed within the interval[0.05,0.95] and the step size is 0.1.After the analysis,it is found that when the averaging coefficient is 0.05 and 0.15,the prediction accuracy of the model is the highest,reaching 91.7%.Finally,the prediction result with averaging coefficient being 0.15 is showed and compared with the fuzzy comprehensive evaluation method,the grey evaluation model and the actual situations,which indicates that the proposed model in this paper is feasible and applicable.

Key words:rockburst;attribute interval recognition model;optimal combined weighting;analytic hierarchy process;anti-entropy weight method;averaging coefficient

中图分类号:TD313

文献标志码:A

文章编号:0253-9993(2020)11-3772-09

殷欣，刘泉声，王心语,等.基于组合赋权和属性区间识别理论的岩爆烈度分级预测模型[J].煤炭学报,2020,45(11):3772-3780.

YIN Xin,LIU Quansheng,WANG Xinyu,et al.Prediction model of rockburst intensity classification based on combined weighting and attribute interval recognition theory[J].Journal of China Coal Society,2020,45(11):3772-3780.

收稿日期:2019-09-07

修回日期:2019-11-19

责任编辑:陶 赛

DOI:10.13225/j.cnki.jccs.2019.1250

基金项目:国家重点基础研究发展计划资助项目(2015CB058102)

作者简介:殷 欣(1996—)，男，湖北孝感人，硕士研究生。E-mail:yinxin_engineering@163.com

通讯作者:刘泉声(1962—)，男，江苏溧阳人，教授，博士生导师。E-mail:liuqs@whu.edu.cn