工程岩体中的裂隙扩展规律和岩桥破断机理一直是工程界十分关注的问题。露天矿边坡工程在开挖扰动作用下使得岩体中原生裂隙等不连续面尖端产生高度应力集中,进而使裂隙起裂扩展并相互贯通,引发边坡局部或整体突发性滑坡灾害,这给周围作业人员生命及财产造成极大威胁。因此,揭示开挖卸荷下岩质边坡内部裂隙扩展机制和相互作用规律,对边坡工程开挖设计、施工及长期安全运行具有重要的指导意义。
关于岩体内部多裂隙之间的扩展演化机制及其相互作用规律研究,前人已经做了大量卓有成效的研究。XU等[1-3]通过在相似模拟材料中预制断续裂隙来模拟岩石材料的破坏特征和裂隙扩展模式。杨圣奇等[4]、付金伟等[5]通过在岩石试件中预制断续节理,系统地研究了断续单裂隙、双裂隙、三裂隙、多裂隙在岩体中不同的分布方式对岩体力学性质的影响和裂隙的扩展模式。宋彦琦等[6]通过双轴加卸荷实验分析了裂隙岩体的裂纹起裂、扩展及贯通模式。侯振坤等[7]通过在类岩石材料中预制两条裂隙,研究了其在单轴压缩下的裂隙试件破断机理。以上关于岩体内裂隙之间扩展演化过程及其相互作用规律的研究主要集中在加载力学方面的探讨。ZHOU等[8]用含裂纹试样研究加载速率对裂纹扩展速率和岩石断裂韧性的影响。在裂隙岩体卸荷方面,最早由哈秋舲[9]提出并研究。王瑞红等[10]、郑青松等[11]通过常规三轴卸荷和卸荷损伤后的岩体再次加载的方式对预制断续节理岩体的应力-应变特征、强度、变形特征、破坏规律以及岩体力学性质的影响进行了深入的探讨。陈国庆等[12]针对边坡中间锁固段类岩桥在岩体中的不同几何分布形式,利用真三轴试验系统研究了其在卸荷状态下的扩展模式和对岩体力学性质的影响。
综合目前研究成果发现,对于卸荷条件下岩体多裂隙问题的研究,主要是通过实验和数值模拟方法来定性分析裂隙不同几何分布对岩体力学特性的影响,在理论方面的定量研究鲜少,这主要是因为卸荷条件下岩体受力状态复杂,很难直接求得裂隙尖端的应力强度因子。因此,笔者基于经典Kachanov法和叠加原理,推导了卸荷条件下一对不等长共线裂隙尖端应力强度因子表达式。通过引入应力强度因子比作为评价指标,探讨了在卸荷条件下不同几何尺寸的双裂隙扩展演化过程及其相互作用规律。通过类岩石材料的双轴卸荷实验进一步分析验证了理论计算的正确性。进行该课题可为研究开挖诱发岩体失稳机制和设计边坡开挖方案提供重要参考。
1 卸荷条件下不等长共线裂隙应力强度因子求解
1.1 卸荷条件下不等长共线双裂隙断裂力学模型分析
露天矿边坡工程中,通常采用分级开挖的方式,每一级开挖过程都是开挖面的应力逐渐降低至0的一种动态过程,开挖过程可等效为在开挖面施加拉应力并逐渐减小至0的过程[13]。黄润秋[14]研究发现,边坡体在开挖后其内部岩体应力场重分布,如图1所示,出现的二次应力场会呈现应力降低区(破坏区)、应力增高区和原岩应力区的分布特点。露天矿边坡通常发生的局部滑坡就是破坏区岩体裂隙之间相互作用贯通的结果,因此本文选取破坏区岩体两条共线断续裂隙作为研究对象,探讨其内部裂隙的受力状态和裂隙之间的相互作用规律。由文献[12-14]可知,所选取的破坏区岩体在开挖前受到竖直方向地应力σ1和水平方向地应力σ3的作用(本文不考虑中间主应力的影响),岩体位于应力增高区,受力状态如图1(a)所示;开挖后,应力路径发生了改变,竖直方向仍受σ1的作用,而水平方向由之前的压应力转变成拉应力作用,岩体应力状态由压剪应力状态转变成拉剪应力状态,岩体位于应力降低区,受力状态如图1(b)所示。
由于卸荷条件下裂隙所处应力状态较为复杂,并不能直接通过断裂力学相关理论直接求得其裂隙尖端应力强度因子,因此,本文对边坡开挖卸荷岩体概化模型做二维断裂力学分析,采用一次叠加的方法分析卸荷条件下岩体的受力状态,分解为单轴拉伸应力状态C和单轴压缩应力状态B的相加,其分解原理如图2所示,其中α+β=90°,α,β为最大主应力σ1与水平方向的夹角,即裂隙倾角。根据分解原理,得出卸荷条件下共线裂隙岩体应力状态A的应力强度因子KA为
KA=KB+KC
(1)
其中,KA为卸荷状态下裂隙尖端应力强度因子;KB为单轴压缩作用下裂隙尖端应力强度因子;KC为单轴拉伸作用下裂隙尖端应力强度因子。Kachanov法对于多裂隙岩体应力强度因子求解较其他方法具有较好的优势,本文基于Kachanov法对单轴压缩作用下和单轴拉伸作用下裂隙尖端应力强度因子KB和KC进行求解。

图1 边坡开挖过程中不同部位应力分布及岩体受力状态力学模型
Fig.1 Mechanical model of stress distribution and stress state of rock mass in different parts of slope excavation process

图2 卸荷条件下双裂隙岩体应力状态二次叠加
Fig.2 Secondary superposition of stress state of double-crack rock mass under condition of unloading
1.2 单轴拉伸作用下裂隙尖端应力强度因子KC的求解
“经典Kachanov法”[15-16]将在远场应力作用下的无限大平板中的多裂隙问题等效为多个子问题,每个子问题只有一个裂隙且裂隙面上受到伪面力。伪面力等于其他裂隙对该裂隙引起的面力和该裂隙初始面力之和。该法认为伪面力由均匀部分和合力为0的非均匀部分组成。假定裂隙相互作用只由均匀部分产生,而忽略合力为0的非均匀部分的作用。
笔者基于以上原理,研究如图3所示的无限大平板中受压应力σ1作用的不等长共线裂隙相互作用。建立如图3所示的xoy坐标系,ξ1,ξ2为裂隙1和2的局部坐标轴,裂隙1长度为c-d,裂隙2长度为a-d,裂隙间距为2d,裂隙倾角为β。以仅含裂隙1为例,图4为仅含裂隙1 时裂隙面上伪面力分解图示,其中,初始面力![]() 为压应力σ1在裂隙1上的分量;Δp12为裂隙1在裂隙2上产生的面力;〈〉为取平均值。
为压应力σ1在裂隙1上的分量;Δp12为裂隙1在裂隙2上产生的面力;〈〉为取平均值。

图3 单轴拉伸不等长共线裂隙力学模型
Fig.3 Mechanical model of uniaxial compression unequal length collinear cracks
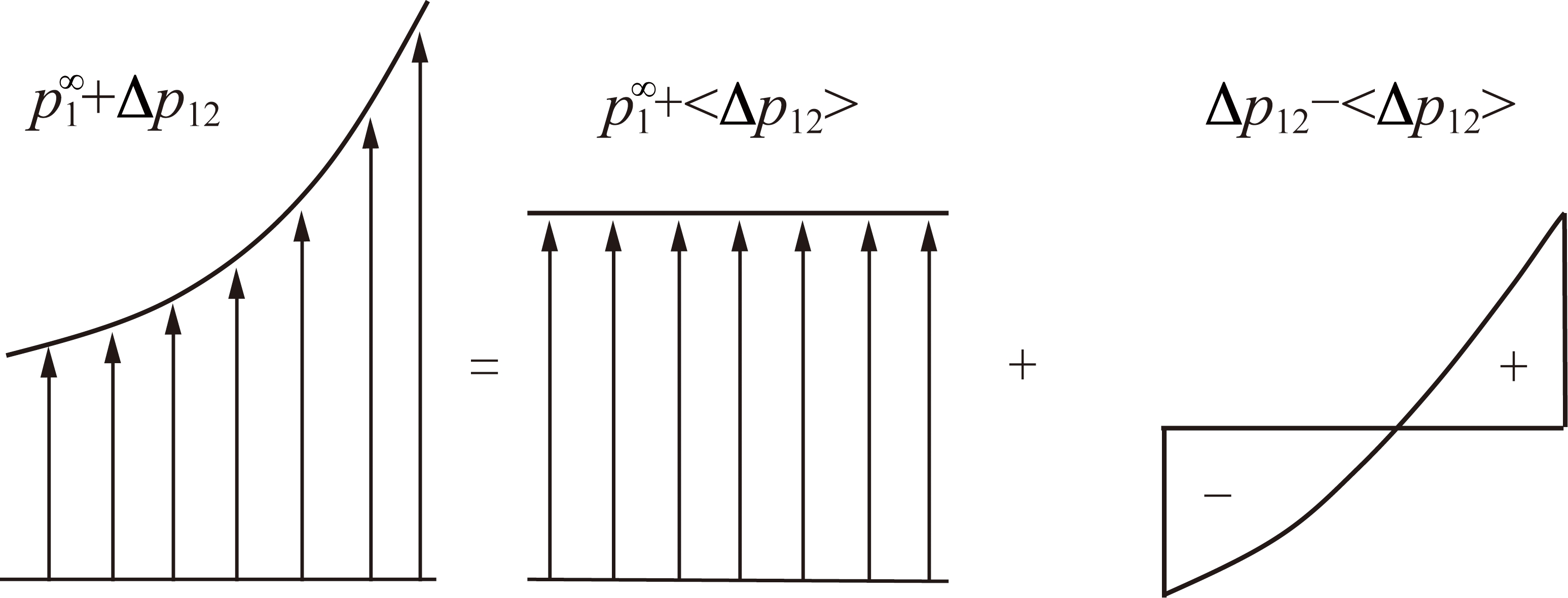
图4 仅含裂隙 1 时其上面力分解
Fig.4 Force decomposition which only crack 1
根据应力强度因子的定义,单轴拉伸作用下的不等长共线裂隙会发生I-II复合型破坏。裂隙i上的伪面力pi(ξi)[17-18]为
(i,j=1,2;i≠j,下同)
(2)
其中,σi(ξi)和τi(ξi)分别为裂隙i面上的法向和切向伪面力;![]() 为裂隙i面上的初始面力;Δpij(ξi)为裂隙j均布面力对裂隙i产生的附加面力。裂隙i初始面力
为裂隙i面上的初始面力;Δpij(ξi)为裂隙j均布面力对裂隙i产生的附加面力。裂隙i初始面力![]() 与附加面力Δpij(ξi)为
与附加面力Δpij(ξi)为
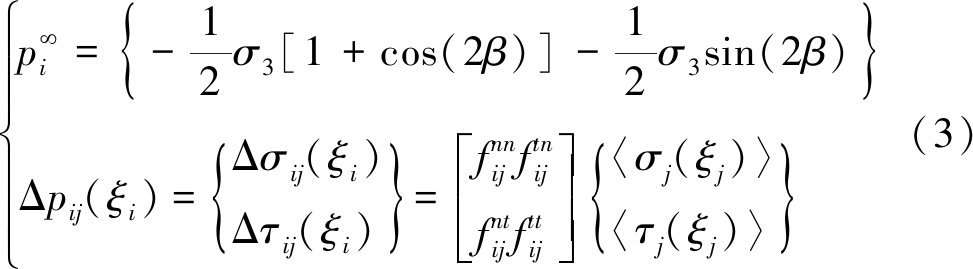
对于共线裂隙,![]() 则式(3)变为
则式(3)变为
![]()
(4)
对式(2)取平均得
![]()
(5)
其中,i≠j,i,j=1,2;Δσij(ξi)和Δτij(ξi)分别为裂隙i在裂隙j上产生的法向应力和切向伪面力,如Δσ21(ξ1)和Δτ21(ξ1)分别为裂纹1在裂纹2上产生的法向应力和切向应力;![]() 为相互作用系数,如
为相互作用系数,如![]() 为裂隙1单位均布法向力在裂隙2产生的切向附加应力;
为裂隙1单位均布法向力在裂隙2产生的切向附加应力;![]() 为相互作用因子,如
为相互作用因子,如![]() 为裂纹单位均布法向力在裂纹1产生的切向附加应力的平均值。其他公式含义以此类推。
为裂纹单位均布法向力在裂纹1产生的切向附加应力的平均值。其他公式含义以此类推。![]() 和
和![]() 表达式可以通过文献[15]附录部分求得。
表达式可以通过文献[15]附录部分求得。
根据文献[19]可知,单轴压缩作用下裂隙尖端的I,II型应力强度因子KC求解公式为
![]()
(6)
其中,![]() 分别为在模型C中裂隙尖端的I和II型应力强度因子;ai为裂隙i 半长;
分别为在模型C中裂隙尖端的I和II型应力强度因子;ai为裂隙i 半长;![]() 和
和![]() 分别为在模型C中裂隙i面上的法向和切向伪面力;ξi为裂隙i局部坐标轴。至此,可根据式(2)~(5)求得的裂隙面上的伪面力,将其代入式(6)可求得2条裂隙尖端内外的应力强度因子。
分别为在模型C中裂隙i面上的法向和切向伪面力;ξi为裂隙i局部坐标轴。至此,可根据式(2)~(5)求得的裂隙面上的伪面力,将其代入式(6)可求得2条裂隙尖端内外的应力强度因子。
1.3 单轴压缩作用下裂隙尖端应力强度因子KB的求解
在单轴压缩作用下,裂隙受到法向压应力而发生闭合,此时在裂隙尖端只存在II型应力强度因子。考虑如图5所示的压剪共线裂隙模型,裂隙1和2上的实际面力分别为![]() 取0<α<90°,假设裂隙在压剪应力作用下发生滑动,则根据摩尔-库仑定律得裂隙上的面力满足:
取0<α<90°,假设裂隙在压剪应力作用下发生滑动,则根据摩尔-库仑定律得裂隙上的面力满足:
![]() (i=1,2;下同)
(i=1,2;下同)
(7)
式中,τc和μ分别为黏聚力和摩擦因数。

图5 单轴压缩不等长共线裂隙力学模型
Fig.5 Mechanical model of uniaxial compression unequal length collinear fracture
该问题和图6所示的问题等效,裂隙面上受到![]() 的切向面力和
的切向面力和![]() 的法向面力作用,其中
的法向面力作用,其中![]() 和
和![]() 分别为远场应力σ1在裂隙面上产生的法向和切向应力分量:
分别为远场应力σ1在裂隙面上产生的法向和切向应力分量:

图6 裂隙面应力等效叠加
Fig.6 Equivalent superposition of stress on fracture surface
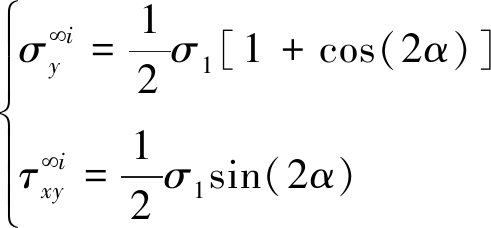
(8)
“经典Kachanov法”将该问题分解为2个子问题,每个子问题仅含一个受到未知伪面力![]() 和
和![]() 的裂隙,其表达式为
的裂隙,其表达式为
![]()
(9)
其中,![]() 为受面力
为受面力![]() 和
和![]() 作用的裂隙 j在裂隙i上产生的附加法向应力;
作用的裂隙 j在裂隙i上产生的附加法向应力;![]() 为相应的附加切向应力,i≠j,i,j=1,2。对于滑动闭合裂隙,
为相应的附加切向应力,i≠j,i,j=1,2。对于滑动闭合裂隙,![]() 则式(7)可表示为
则式(7)可表示为
![]()
(10)
利用Kachanov法求得附加应力项![]()
![]()
(11)
式中,![]() 和
和![]() 为裂隙j伪面力在法向和切向的平均值,把式(9),(10)联立得
为裂隙j伪面力在法向和切向的平均值,把式(9),(10)联立得
![]()
(12)
进一步对式(12)取平均得
![]()
(13)
通过式(13)求得![]() 和
和![]() 将其代入式(12)求得
将其代入式(12)求得![]() 和
和![]() 将其代入式(14)便求得两条裂隙内外尖端II型应力强度因子:
将其代入式(14)便求得两条裂隙内外尖端II型应力强度因子:
![]()
(14)
式中,![]() 为在模型B中裂隙尖端的II型应力强度因子;
为在模型B中裂隙尖端的II型应力强度因子;![]() 为裂隙i面上的伪面力。
为裂隙i面上的伪面力。
1.4 卸荷条件下双裂隙尖端应力强度因子KA的求解
在1.2节中求得了单轴拉伸作用下两裂隙内外尖端的应力强度因子KC,1.3节中求得了单轴压缩作用下两裂隙内外尖端的应力强度因子KB,联立式(1),(6)和(14)可求得卸荷条件下裂隙尖端应力强度因子:
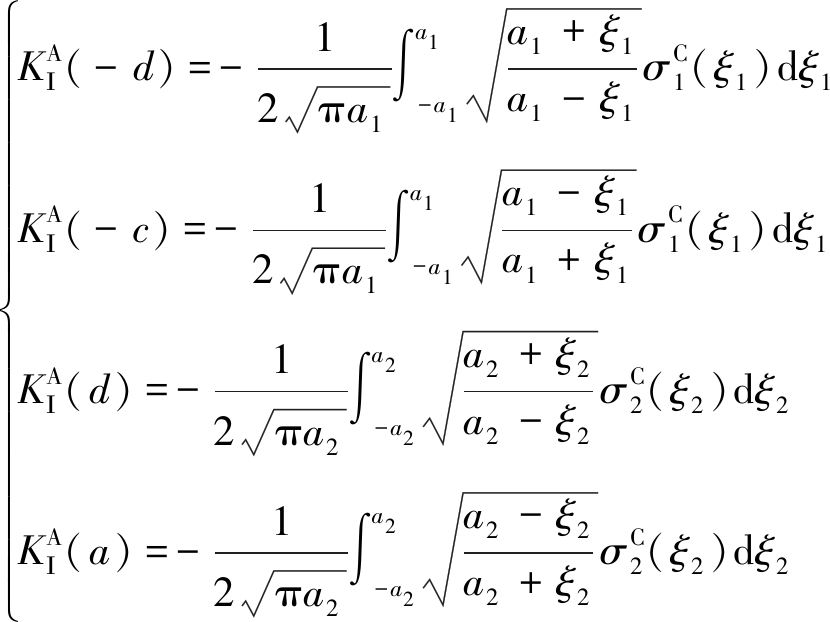
(15)

(16)
式中,![]() 分别为在卸荷条件下裂隙1和2内外尖端的I型应力强度因子;
分别为在卸荷条件下裂隙1和2内外尖端的I型应力强度因子;![]() 分别为在模型C中裂隙1和2面上的法向伪面力;
分别为在模型C中裂隙1和2面上的法向伪面力;![]() 分别为在卸荷条件下裂隙1和2内外尖端的II 型应力强度因子;
分别为在卸荷条件下裂隙1和2内外尖端的II 型应力强度因子;![]() 分别为在模型C中裂隙1和2面上的切向伪面力;
分别为在模型C中裂隙1和2面上的切向伪面力;![]() 分别为在模型B中裂隙1和2面上的伪面力;a1和a2为裂隙1和2的半长,a1=(c-d)/2,a2=(a-d)/2。
分别为在模型B中裂隙1和2面上的伪面力;a1和a2为裂隙1和2的半长,a1=(c-d)/2,a2=(a-d)/2。
1.5 卸荷条件下单裂隙尖端应力强度因子KD的求解
卸荷条件下单裂隙应力强度因子求解过程和双裂隙求解方法一样,将卸荷条件下单裂隙岩体的应力状态D分解为单轴压缩作用下的应力状态M和单轴拉伸作用下的应力状态N,如图7所示,其中β+α=90°。卸荷状态下单裂隙尖端应力强度因子KD为
KD=KM+KN
(17)
式中,KD为卸荷状态下裂隙尖端应力强度因子;KM为单轴压缩作用下裂隙尖端应力强度因子;KN为单轴拉伸作用下裂隙尖端应力强度因子。

图7 卸荷条件下单裂隙岩体应力等效叠加模型
Fig.7 Stress equivalent superposition model of single fractured rock mass under unloading conditions
在单轴压缩状态下,裂隙发生闭合,沿裂隙发生剪切滑动,此时只存在II型应力强度因子,则裂隙尖端应力强度因子![]() 为
为
![]()
(18)
式中,λ为裂隙半长度。
在单轴拉伸状态下,裂隙尖端应力强度因子KN为
![]()
(19)
因此,卸荷条件下单裂隙尖端应力强度因子KD为
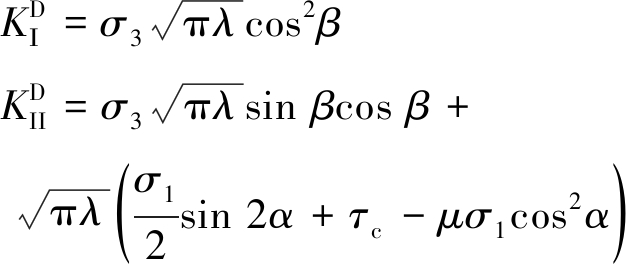
(20)
式中,![]() 分别为单轴拉伸作用下裂隙尖端的I和II型应力强度因子;
分别为单轴拉伸作用下裂隙尖端的I和II型应力强度因子;![]() 分别为在卸荷条件下裂隙尖端的I和II型应力强度因子。
分别为在卸荷条件下裂隙尖端的I和II型应力强度因子。
2 卸荷作用下不等长共线裂隙之间相互作用规律分析
裂隙间相互作用对应力强度因子的影响可分为增大、减小、无影响3种情况。![]() 和
和![]() 为在卸荷状态下一对不等长共线裂隙的应力强度因子,
为在卸荷状态下一对不等长共线裂隙的应力强度因子,![]() 和
和![]() 为卸荷状态下单裂隙的应力强度因子。定义F=KA/KD为应力强度因子比,表示一对不等长共线裂隙与单裂隙的应力强度因子比值,利用F的大小来表征两裂隙相互之间的影响程度。根据文献[21]可知,当两条裂隙等长且裂隙间距等于裂隙长度时,裂隙之间基本相互无影响,此时F=1.05。故本文认为当裂隙应力强度因子比F≤1.05时,就认为裂隙之间扩展不受相互作用的影响。由式(15)和(19)可知,裂隙内侧尖端I型和II型应力强度因子的比值相等,故只分析I型应力强度因子比值随裂隙间距及大小的变化规律。本文主要考虑裂隙倾角、间距和长度对裂隙间相互作用的影响规律,不考虑裂隙的充填,将在之后研究中在考虑裂隙是否充填的情况下组合考虑裂隙长度、倾角和间距对裂隙间相互作用的影响规律。
为卸荷状态下单裂隙的应力强度因子。定义F=KA/KD为应力强度因子比,表示一对不等长共线裂隙与单裂隙的应力强度因子比值,利用F的大小来表征两裂隙相互之间的影响程度。根据文献[21]可知,当两条裂隙等长且裂隙间距等于裂隙长度时,裂隙之间基本相互无影响,此时F=1.05。故本文认为当裂隙应力强度因子比F≤1.05时,就认为裂隙之间扩展不受相互作用的影响。由式(15)和(19)可知,裂隙内侧尖端I型和II型应力强度因子的比值相等,故只分析I型应力强度因子比值随裂隙间距及大小的变化规律。本文主要考虑裂隙倾角、间距和长度对裂隙间相互作用的影响规律,不考虑裂隙的充填,将在之后研究中在考虑裂隙是否充填的情况下组合考虑裂隙长度、倾角和间距对裂隙间相互作用的影响规律。
2.1 裂隙倾角的影响
根据卸荷条件下一对不等长共线裂隙尖端应力强度因子计算式(15),(16)与单裂隙应力强度因子计算式(20)的比值F发现,当裂隙其他几何因素不变时,应力强度因子比F与裂隙倾角无关,这表明共线裂隙的相互作用程度不受裂隙倾角的影响。各个裂隙尖端的I型奇异随着裂隙倾角的不断增大而逐渐减小,裂隙水平共线时的I型应力强度因子最大。II型奇异随裂隙倾角的增大先增大后减小,在裂隙倾角为45°时,II型应力强度因子最大。
2.2 裂隙间距的影响
保持裂隙长度恒定,改变裂隙间距,分析裂隙间距对裂隙相互作用的影响规律。图8为a1=2a2=0.8时裂隙尖端 I 型应力强度因子比F随裂隙间距2d的变化规律。由图8可知,两裂隙存在时其尖端的应力强度因子大于单裂隙,F 随裂隙间距的增加而减小,表明裂隙之间的相互作用随着裂隙间距的增大而不断减小。大裂隙外尖端 F 随裂隙间距变化最小,即受裂隙之间相互作用影响最小。小裂隙内侧 F 随裂隙间距变化最大,即受裂隙之间相互作用影响最大。当2d=0.8时,即裂隙间距等于小裂隙长度时,大裂隙 F≤1.05,表明大裂隙的扩展几乎不受小裂隙影响。当2d=1.6时,即裂隙间距等于大裂隙长度时,小裂隙F≤1.05,表明小裂隙扩展几乎不受大裂隙影响。

图8 应力强度因子比F随裂隙间距2d的变化关系
Fig.8 Relationship between the ratio F of SIF and the spacing 2d of crack
2.3 大裂隙长度的影响
保持小裂隙长度和裂隙间距恒定,改变大裂隙长度,分析大裂隙长度对裂隙相互作用的影响规律。如图9为2d=a2=0.4时裂隙尖端 I 型应力强度因子比F随大裂隙长度的变化规律。由图9可知,当裂隙间距等于小裂隙长度时,小裂隙的F 随大裂隙长度的增加几乎呈线性增长,裂隙内侧 F 稍大于外侧,而大裂隙的F 变化幅度不大,这表明大裂隙对小裂隙的影响程度随着大裂隙长度的增加而呈现线性增加,且内侧稍大于外侧。当2a1≥0.4时,即大裂隙长度开始大于裂隙间距时,小裂隙内侧 F 开始大于1.05,即大裂隙开始对小裂隙内侧扩展产生影响。当2a1≥0.6时,即大裂隙长度等于1.5倍裂隙间距时,小裂隙外侧 F 开始大于1.05,即大裂隙开始对小裂隙外侧扩展产生影响。在整个过程中大裂隙的 F 变化较小,表明大裂隙受小裂隙影响较小。

图9 应力强度因子比F随大裂隙长度2a1的变化关系
Fig.9 Relationship between the ratio F of SIF and the length 2a1 of large crack
2.4 小裂隙长度的影响
保持大裂隙长度和裂隙间距恒定,改变小裂隙长度,分析其对裂隙相互作用的影响规律。如图10为a1=2d=0.3时裂隙尖端 I 型应力强度因子比F随大裂隙长度的变化规律。由图10可知,当大裂隙长度等于2倍裂隙间距时,大裂隙的F 随着小裂隙长度的减小而减小,内侧减小幅度大于外侧,这表明随着小裂隙的减小,大裂隙的扩展受小裂隙的影响减小,但是内侧影响大于外侧。当小裂隙长度等于大裂隙长度时,两裂隙内外尖端 F 相等,即裂隙之间的影响程度相同。当2a2≤0.3时,即小裂隙长度等于裂隙间距时(大裂隙半长),大裂隙的 F 开始小于1.05,即大裂隙的扩展开始不受小裂隙影响。

图10 应力强度因子比F随小裂隙长度2a2的变化关系
Fig.10 Relationship between the ratio F of SIF and the length 2a2 of small crack
3 含不等长共线裂隙类岩石材料卸荷试验
3.1 试验条件
本次试验基于图1所示边坡破坏区岩体开挖前后的应力路径,从平面应变的角度(不考虑中间主应力的影响),通过双轴加卸载试验模拟边坡的开挖卸荷过程,分析卸荷岩体内部非贯通不等长共线断续裂隙的扩展演化情况。实验在中国矿业大学(北京)深部岩土力学与地下工程国家重点实验室的MS-500型三轴冲击岩爆试验系统上进行,其可实现6个面独立控制加卸载,并实时记录在实验过程中三向应力数据[22]。实验过程系统布置如图11所示,采用SA-5型高速摄影机对试件破坏全过程进行图像采集。

图11 真三轴卸载试验系统
Fig.11 Experimental system of true triaxial unloading
3.2 试验试样制备
本次研究采用水泥砂浆为模型配比材料,由425号普通硅酸盐水泥、标准砂、水按质量比=1∶2.35∶0.5配制而成,其完整试件力学参数见表1,由文献[20]可知,本文所用配比材料标准试件力学参数与砂岩相近(表1)。裂隙采用厚度为0.5 mm 的高强薄钢片制作。将材料按配比质量混合搅拌均匀后,倒入模具中浇筑预定配合比的实验试块,在材料初凝前抽出钢片,并于室温内静置养护12 h脱模,然后在养护室内养护28 d,脱模检查裂隙的平整度和贯穿性并打磨平整,试件制作完毕。试件尺寸为110 mm×110 mm×30 mm,如图12所示。实验方案及裂隙尺寸见表2。
表1 完整试件及砂岩力学参数
Table 1 Mechanical parameters of complete specimens
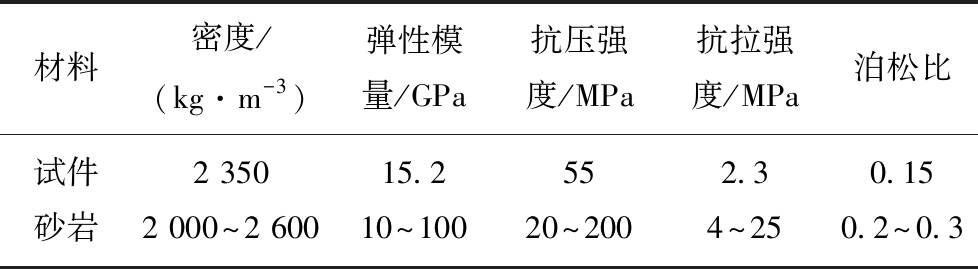
材料密度/(kg·m-3)弹性模量/GPa抗压强度/MPa抗拉强度/MPa泊松比试件2 35015.2552.30.15砂岩2 000~2 60010~10020~2004~250.2~0.3

图12 预制试验试件模具及试件尺寸
Fig.12 Prefabricated experimental specimen die and spe-cimen size
表2 试件中裂隙几何参数
Table 2 Crack geometric parameters in specimens
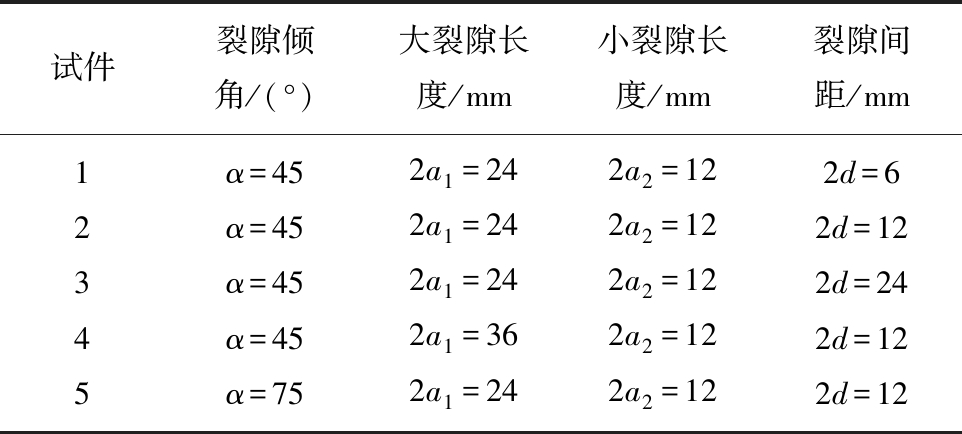
试件裂隙倾角/(°)大裂隙长度/mm小裂隙长度/mm裂隙间距/mm1α=452a1=242a2=122d=62α=452a1=242a2=122d=123α=452a1=242a2=122d=244α=452a1=362a2=122d=125α=752a1=242a2=122d=12
3.3 试验方案
为模拟边坡开挖过程,本次试验采用双轴卸荷,不考虑中间主应力的影响,实验中应力方向设置如图13(a)所示,具体应力路径如图13(b)所示。每组实验独立重复3次,以降低试验结果的离散性,实验具体操作步骤为
(1)首先以位移控制方式将轴向应力σ1和水平向应力σ3同时以0.004 mm/s的速率加载到σ1 =σ3=1 MPa,固定试件。
(2)继续以位移控制方式将轴向应力σ1和水平向应力σ3同时以0.004 mm/s的速率加载到σ1=σ3=15 MPa,水平向位移锁定。
(3)保持水平向位移恒定,轴向继续以位移控制的方式0.004 mm/s的速率加载到σ1=30 MPa,轴向位移锁定。
(4)以应力控制方式迅速卸载σ3到0,轴向继续以0.004 mm/s的速率加载,直到试件破坏,结束实验。

图13 实验应力设置及应力路径示意
Fig.13 Experimental stress setting and stress path diagram
3.4 裂隙扩展过程分析
在实验结束后观测试件裂隙破坏情况,若裂隙破裂面上有明显的摩擦痕迹,则认为是剪切裂隙。若有张拉破坏痕迹,没有明显摩擦痕迹,则认为是拉裂隙。拉裂隙与剪裂隙的形态区别如图14所示。

图14 裂隙扩展类型
Fig.14 Types of crack propagation
图15为不同试验方案试件裂隙扩展过程,图15(a)为试件1裂隙扩展过程,在卸荷过程中首先在小裂隙内外尖端和大裂隙内尖端产生翼形拉裂隙,大裂隙外尖端延后起裂。随着卸载持续进行,翼形拉裂隙沿着最大主应力方向扩展,在中间岩桥区域产生剪切裂隙,翼形拉裂隙与剪裂隙相互扩展造成岩桥拉剪贯通。进一步地在小裂隙外尖端随着翼形拉裂隙的扩展而产生次生拉裂隙。最后裂隙之间相互贯通而形成局部脱落区,造成试件破坏,靠近卸荷面附近集中产生次生拉裂隙。图15(b)为试件2裂隙扩展过程,在卸荷过程中首先在大裂隙内尖端和小裂隙内尖端产生翼形拉裂隙,且在中间岩桥区域产生剪切裂隙,小裂隙和大裂隙外尖端延后起裂。进一步地翼形拉裂隙沿着最大主应力方向扩展,卸荷面附近集中产生拉裂隙。最后小裂隙外尖端剪切裂隙与拉裂隙贯通而形成局部域脱落区,造成试件破坏。图15(c)为试件3裂隙扩展过程,在卸荷过程中首先在大裂隙内外尖端和小裂隙外尖端先后萌生翼形拉裂隙且均先沿最大主应力方向扩展,但是大裂隙两端产生的翼形拉裂隙均向上扩展。随着卸载持续进行,两裂隙外尖端继续沿着最大主应力方向扩展,中间岩桥区域并没有发生贯通。在大裂隙尖端随着翼形拉裂隙的扩展而产生次生拉裂隙。最终裂隙之间相互贯通形成局部脱落区,造成试件破坏。图15(d)为试件4裂隙扩展过程,在卸荷过程中首先在小裂隙内外尖端先后萌生翼形拉裂隙且均先沿最大主应力方向扩展。随着卸载持续进行,在大裂隙外尖端随着翼形拉裂隙的扩展而产生次生拉裂隙,岩桥区域发生剪破坏。最后拉裂隙之间的扩展贯通造成试件破坏。在靠近卸荷面附近萌生许多拉裂隙。图15(e)为试件5裂隙扩展过程,在卸荷过程中首先在大小裂隙内尖端萌生翼形拉裂隙且均先沿最大主应力方向扩展。随着卸载持续进行,在小裂隙中间部位产生次生裂隙,岩桥区域发生剪破坏。
3.4.1 裂隙倾角的影响

图15 实验各试件裂隙扩展过程
Fig.15 Experiments on crack propagation of specimens
对比试件2和5的试验现象可知,当裂隙其他参数不变,只改变裂隙倾角时,裂隙起裂顺序不发生改变,进一步验证了倾角对裂隙间相互作用无影响,这与2.1节中分析结果一致。
3.4.2 裂隙间距的影响
对比试件1~3的试验现象可知,当裂隙间距较小时,小于小裂隙长度,如图15(a)所示,此时大裂隙对小裂隙尤其是其内尖端的影响较为显著,导致小裂隙内外尖端在卸荷过程中最先起裂,而小裂隙对大裂隙的影响较弱,大裂隙外尖端所受影响最小,导致在卸荷过程中大裂隙内尖端先于外尖端起裂;随着裂隙间距的增大,如图15(b)所示,大裂隙对小裂隙的影响逐渐减弱,导致小裂隙外尖端延后起裂。小裂隙对大裂隙的影响减弱,导致大裂隙外尖端起裂相对延后;随着裂隙间距持续增大,如图15(c)所示,裂隙彼此无影响,这与2.2节中分析结果一致。
3.4.3 大裂隙长度的影响
对比试件2~4试验现象可知,当大裂隙长度等于裂隙间距时,如图15(c)所示,裂隙之间几乎没有影响,各自沿最大主应力方向扩展;当大裂隙长度等于2倍裂隙间距时,如图15(b)所示,大裂隙对小裂隙产生较大影响,导致在卸荷过程中,小裂隙内尖端首先起裂。小裂隙对大裂隙影响较小,导致大裂隙外尖端起裂相对延后;当大裂隙长度等于3倍裂隙间距时,如图15(d)所示,大裂隙对小裂隙的影响持续增强,导致在卸荷过程中,小裂隙内外尖端首先起裂。大裂隙受小裂隙影响较小。这与2.3节分析结果一致。
3.4.4 小裂隙长度的影响
根据试件1~3的试验现象可知:当小裂隙长度大于裂隙间距时,如图15(a)所示,裂隙之间作用明显,导致小裂隙内外尖端和大裂隙内尖端在卸荷过程中最先起裂。大裂隙外尖端的受影响最小;当小裂隙长度等于裂隙间距时,如图15(b)所示,小裂隙对大裂隙影响较小,导致大裂隙外尖端起裂相对延后;当小裂隙长度小于裂隙间距时,如图15(c)所示,裂隙相互之间几乎没有影响,各自沿最大主应力方向扩展。这与2.4节分析结果一致。
3.5 试样裂隙起裂及极限荷载分析
在岩质高边坡的设计中,经常需要对岩体强度进行评价,由于在现场破坏过程中难以获得节理岩体的起裂及极限荷载,而通过室内试验可以提供有效的参考。第3.4节介绍和分析了不同节理分布的岩体裂隙扩展和贯通特征,可以看出,不同裂隙分布形态对试件破坏具有复杂的影响。在本节中,着重讨论裂隙分布形态对试件起裂及极限强度的影响。
根据图16的试件应力应变曲线能够明显看出试件在完全破坏前发生两次突降,第1次为裂隙尖端翼裂隙起裂,第2次为翼裂隙搭接、贯通,次生裂隙发育、扩展,裂隙的起裂扩展过程能够与应力-应变曲线很好的对应。由图17可知,试件1~4的轴向峰值应力分别为55.1,57.8,60.2和50.3 MPa,轴向起裂应力分别为47.9,50.0,51.1和46.8 MPa,试件4的轴向峰值荷载与轴向起裂荷载均小于其他试件,主要是因为试件4大裂隙长度较大所致,这也进一步说明裂隙的间距、大小等几何尺寸对试件的破坏有着重要的影响。对比试件1~4可知,当裂隙大小一定时,随着裂隙间距的增加,试件的起裂应力和峰值应力在不断增加,这主要是因为随着裂隙之间的相互作用随着裂隙间距的增加而减小,裂隙尖端起裂较为困难。其他对比方案与前文研究规律一致,这里不再赘述。
根据最大周向应力理论[23],岩体裂隙尖端裂隙扩展起裂角θ0满足
KΙsin θ0+KII(3cos θ0-1)=0
(21)
解得裂隙尖端起裂角θ0为
![]()
(22)
式中,![]() 分别为卸荷条件下双裂隙岩体应力状态Ⅰ型和Ⅱ型应力强度因子,可通过式(15),(16)计算求得。
分别为卸荷条件下双裂隙岩体应力状态Ⅰ型和Ⅱ型应力强度因子,可通过式(15),(16)计算求得。
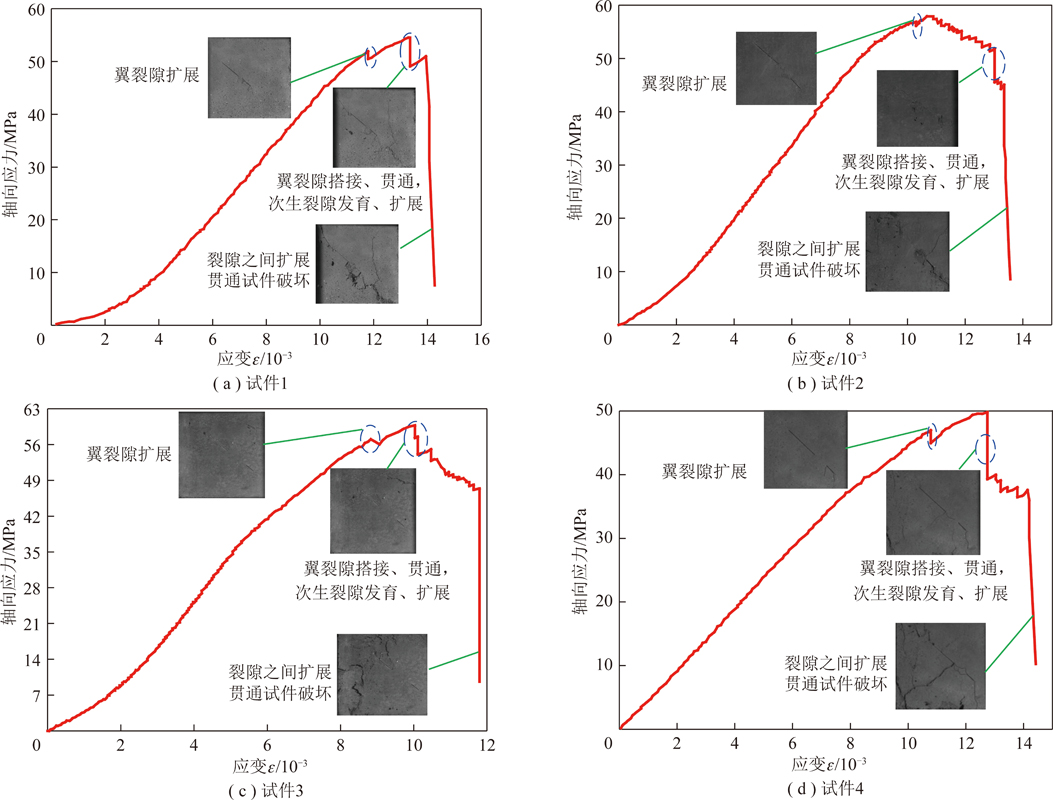
图16 实验各试件轴向应力应变曲线
Fig.16 Axial stress-strain curves of test specimens

图17 实验各试件轴向峰值应力和起裂应力随裂隙间距变化曲线
Fig.17 Curves of peak stress and initiation stress varying with crack spacing of test specimens
实验过程中,高速摄影拍摄与加卸载同步进行,通过高速摄影观察裂隙起裂并记录起裂时刻,此时刻与应力应变曲线对照近似地确定轴向起裂应力σ1的大小。
随着卸载的持续进行,水平向拉应力σ3在不断变化,可通过下式确定:
σ3=σ0-σ3t
(23)
式中,σ0为开始卸载时刻的水平应力值;σ3t为在试验过程中的高速摄影记录下裂隙起裂时刻所对应的水平应力值。
为定量验证理论推导的可靠性和合理性,将裂隙起裂时刻垂直应力σ1和水平向应力σ3代入式(15),(16)求得裂隙尖端应力强度因子,继续将计算结果代入式(22)求得裂隙起裂角θ0,并与实际裂隙起裂角进行比较(表3)。
表3 卸荷条件下裂隙起裂位置及起裂角的理论与实验值对比
Table 3 Comparison of theoretical and experimental values of crack initiation position and angle under unloading conditions

试件编号起裂位置起裂角/(°)实验实测理论计算试件1小裂隙外尖端4144.23试件2大裂隙内尖端3741.36试件3大裂隙外尖端3742.18试件4小裂隙内尖端4447.26试件5大裂隙内尖端4043.56
表3为卸荷条件下理论与实验起裂角对比结果,理论计算结果与实验结果在误差基允许范围内,这进一步验证了本文理论计算结果的可行性与合理性。
4 结 论
(1)共线裂隙的相互作用程度不受裂隙倾角的影响。各个裂隙尖端的I型奇异随着裂隙倾角的不断增大而逐渐减小,裂隙水平共线时的I型应力强度因子最大。II型奇异随裂隙倾角的增大先增大后减小,在裂隙倾角为45°时,II型应力强度因子最大。
(2)卸荷条件下裂隙间距对裂隙之间相互作用有重要影响。裂隙间距开始大于任一裂隙长度时,该裂隙几乎不影响另一裂隙扩展。
(3)卸荷条件下裂隙长度对裂隙之间相互作用规律有重要影响。裂隙长度大于裂隙间距时,该裂隙开始影响另一裂隙扩展。裂隙长度小于裂隙间距时,该裂隙几乎不影响另一裂隙扩展。
(4)试件轴向起裂和峰值荷载随着裂隙间距的增大而增大。理论计算和实验所得裂隙起裂角及起裂位置基本一致,验证了理论计算结果的可行性与合理性。
[1] XU Jun,LI Zhaoxia.Crack propagation and coalescence of step-path failure in rocks[J].Rock Mechanics and Rock Engineering,2019,52(4):965-979.
[2] WONG R H C,CHAU K T,TANG C A,et al.Analysis of crack coalescence in rock-like materials containing three flaws-Part I:Experimental approach[J].International Journal of Rock Mechanics and Mining Sciences,2001,38(7):909-924.
[3] LIU Zhina,XU Haoran,ZHAO Zhihong,et al.DEM modeling of interaction between the propagating fracture and multiple pre-existing cemented discontinuities in shale[J].Rock Mechanics and Rock Engineering,2019,52(6):1993-2001.
[4] 杨圣奇.断续三裂隙砂岩强度破坏和裂隙扩展特征研究[J].岩土力学,2013,34(1):31-39.
YANG Shengqi.Study of strength failure and crack coalescence behavior of sandstone containing three pre-existing fissures[J].Rock and Soil Mechanics,2013,34(1):31-39.
[5] 付金伟,朱维申,曹冠华,等.岩石中三维单裂隙扩展过程的试验研究和数值模拟[J].煤炭学报,2013,38(3):411-417.
FU Jinwei,ZHU Weishen,CAO Guanhua,et al.Experimental study and numerical simulation of propagation and coalescence process of a single three-dimensional flaw in rocks[J].Journal of China Coal Society,2013,38(3):411-417.
[6] 宋彦琦,李名,王晓,等.基于高速摄影的单预制裂纹大理岩加卸载试验[J].中国矿业大学学报,2014,43(5):773-781.
SONG Yanqi,LI Ming,WANG Xiao,et al.Observation of marble with single pre-existing crack using high-speed photography under loading and unloading conditions[J].Journal of China University of Mining and Technology,2014,43(5):773-781.
[7] 侯振坤,杨春和,孙书伟,等.板状页岩单轴压缩实验及断裂力学分析[J].煤炭学报,2017,42(5):1251-1257.
HOU Zhenkun,YANG Chunhe,SUN Shuwei,et al.Experiment and fracture mechanics analysis of plate shale under uniaxial compression[J].Journal of China Coal Society,2017,42(5):1251-1257.
[8] ZHOU Lei,ZHU Zheming,QIU Hao,et al.Study of the effect of loading rates on crack propagation velocity and rock fracture toughness using cracked tunnel specimens[J].International Journal of Rock Mechanics and Mining Sciences,2018,112:25-34.
[9] 哈秋舲.加载岩体力学与卸荷岩体力学[J].岩土工程学报,1998,20(1):114.
HA Qiuling.Loading and unloading rock masses mechanics[J].Chinese Journal of Geotechnical Engineering,1998,20(1):114.
[10] 王瑞红,李建林,蒋昱州,等.峰前卸荷对节理岩体力学特性影响试验研究[J].岩土力学,2014,35(4):972-976,985.
WANG Ruihong,LI Jianlin,JIANG Yuzhou,et al.Experimental research on mechanical property of jointed rock mass unloading before peak[J].Rock and Soil Mechanics,2014,35(4):972-976,985.
[11] 郑青松,刘恩龙,刘明星.三轴试验下结构面倾角对制备岩样力学特性的影响[J].岩土力学,2019,40(5):1-10.
ZHENG Qingsong,LIU Enlong,LIU Mingxing.Influence of dip angle of structural planes on mechanical properties of artificial rock samples under triaxial test conditions[J].Rock and Soil Mechanics,2019,40(5):1-10.
[12] 陈国庆,刘顶,徐鹏,等.节理岩桥真三轴开挖卸荷试验研究[J].岩石力学与工程学报,2018,37(2):325-338.
CHEN Guoqing,LIU Ding,XU Peng,et al.True-triaxial test on unloading failure of jointed rock bridge[J].Chinese Journal of Rock Mechanics and Engineering,2018,37(2):325-338.
[13] 黄达,黄润秋.卸荷条件下裂隙岩体变形破坏及裂纹扩展演化的物理模型试验[J].岩石力学与工程学报,2010,29(3):502-512.
HUANG Da,HUANG Runqiu.Physical model test on deformation failure and crack propagation evolvement of fissured rocks under unloading[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(3):502-512.
[14] 黄润秋.岩石高边坡发育的动力过程及其稳定性控制[J].岩石力学与工程学报,2008,27(8):1525-1544.
HUANG Runqiu.Geodynamical process and stability control of high rock slope development[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(8):1525-1544.
[15] KACHANOV M.A simple technique of stress analysis in elastic solids with many cracks[J].International Journal of Fracture,1985,28(1):11-19.
[16] KACHANOV M.Elastic solids with many cracks:A simple method of analysis[J].International Journal of Solids and Structures,1987,23(1):23-43.
[17] 朱帝杰,陈忠辉,席婧仪,等.岩石平行偏置裂纹相互作用规律分析[J].岩土工程学报,2017,39(2):235-243.
ZHU Dijie,CHEN Zhonghui,XI Jingyi,et al.Interaction between offset parallel cracks in rock[J].Chinese Journal of Geotechnical Engineering,2017,39(2):235-243.
[18] 席婧仪,陈忠辉,朱帝杰,等.岩石不等长裂纹应力强度因子及起裂规律研究[J].岩土工程学报,2015,37(4):727-733.
XI Jingyi,CHEN Zhonghui,ZHU Dijie,et al.Stress intensity factors and initiation of unequal collinear cracks in rock[J].Chinese Journal of Geotechnical Engineering,2015,37(4):727-733.
[19] LI Y P,THAM L G,WANG Y H.A modified Kachanov method for analysis of solids with multiple cracks[J].Engineering Fracture Mechanics,2003,70(9):1115-1129.
[20] 黎立云,许凤光,高峰,等.岩桥贯通机理的断裂力学分析[J].岩石力学与工程学报,2005,24(23):4328-4334.
LI Liyun,XU Fengguang,GAO Feng,et al.Fracture mechanics analysis of rock bridge failure mechanism[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(23):4328-4334.
[21] 中国航空研究院.应力强度因子手册[M].北京:科学出版社,1981.
[22] 何满潮,刘冬桥,宫伟力,等.冲击岩爆试验系统研发及试验[J].岩石力学与工程学报,2014,33(9):1729-1739.
HE Manchao,LIU Dongqiao,GONG Weili,et al.Developement of a testing system for impact rock bursts[J].Chinese Journal of Rock Mechanics and Engineering,2014,33(9):1729-1739.
[23] 李世愚,和泰名,尹祥础,等.岩石断裂力学导论[M].合肥:中国科学技术大学出版社,2010:1.
