井壁的作用是保证矿井的长期安全生产和运营，因此井壁应具有足够的强度、刚度和隔水性能。
我国现有的斜井井壁从结构上可视为双层井壁，外层为喷射混凝土等结构，用于抵抗施工临时荷载，防止井帮片帮等问题，内层井壁为钢筋混凝土结构等，用于抵抗永久地压和水压等荷载。因斜井井壁形状和受力特征均较为复杂，目前国内现行的规范[1]并没有给出斜井井壁的设计理论。斜井井壁的设计主要参考立井圆形井壁和施工经验等方法。
斜井井壁受力分析的两大关键点即为:形状不规则和受力不均匀。复变函数法可将不规则双连通域问题映射为规则的圆环，进而简化为规则形状受力问题。GERCEK[2]首次根据复变函数法给出了不规则形状隧洞的应力场计算公式。此后，EXADAKTYLOS[3-4]完整地给出了带缺口的圆形隧洞开挖问题的应力和位移近似解答。HUO等[5]研究了矩形隧洞在远场剪应力作用下的应力分布。国内，陈子荫[6]和吕爱钟等[7]系统地对不规则形状隧洞开挖问题进行了弹性解析分析，但是他们只研究了单连通域问题的解答(即只考虑隧洞开挖，未考虑支护结构)。对于圆形隧洞支护问题，EINSTEIN等[8-9]根据弹性力学给出了双向不等压作用下隧洞围岩和衬砌解析解。BOBET等[10-13]给出了深埋圆形衬砌压力隧洞应力和位移场解析解，并考虑了围岩为各向同性和横观各项异性介质两种情况。LI等[14-15]亦对深埋圆形衬砌压力隧洞结构进行了弹性分析，并考虑了隧洞开挖应力释放效应以及渗流影响。对于浅埋隧洞问题，FU[16]和VERRUIJT[17]利用复变函数方法给出了变形隧道在半平面内的解析解。
上述研究虽对非均匀荷载作用下，不规则轮廓隧洞问题进行了近似解答，但均局限于单连通域问题，而斜井井壁属于双连通域问题，增加了断面映射以及求解的难度。目前针对斜井井壁的研究尚处于数值模拟、物理实验和现场实测阶段[18-20]，杜子博[18]虽对斜井井壁进行了物理实验模拟，但只进行了水压作用下的井壁研究。张旭[19]根据相似理论，利用钢板模拟斜井井壁，对井壁的受力和变形进行了试验研究。笔者针对直墙半圆拱井壁形式，给出非均匀荷载作用下井壁的应力和位移近似解析解，并分析了不同影响因素对井壁的影响。
1 问题描述
1.1 力学模型
由于井壁周围岩体为孔隙型介质，故井壁受到的外载可分为孔隙水压力和围岩骨架压力。井壁与围岩之间的接触状态有3种情况:① 完全贴合，即围岩骨架通过与井壁接触部分传递荷载，孔隙水压力通过接触面孔隙作用于井壁上，井壁力学模型如图1所示;② 不完全贴合，即井壁与围岩之间存在剥离区，剥离区围岩骨架对井壁无作用，取而代之的是水压作用;③ 完全剥离;当井壁与围岩完全剥离时，井壁只受水压作用。
图1 土骨架有效应力与孔隙水压力共同作用下井壁力学模型
Fig.1 Mechanical model of shaft lining under the combined action of soil skeleton effective stresses and pore water pressure
本文采用复变函数方法对弹性状态下非圆形井壁的应力、位移场分布进行求解。不考虑钢筋对井壁的影响，假设井壁为线弹性均质材料，采用平面应变模型进行计算。
1.2 应力和位移复势表达
应力和位移分量可通过2个解析函数φ1(z),ψ1(z)表达[21]为
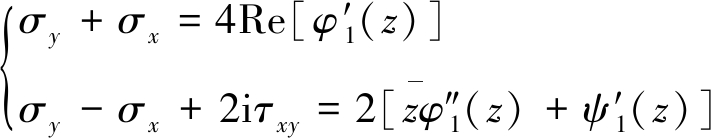
(1)
应力和位移边界条件可表示为
(2)
(3)
式中，G为剪切模量，2G=E/(1+μ);σx,σy分别为任一点水平、竖向应力;κ为系数，平面应变模型取κ=(3-4μ);τxy为任一点剪应力；Re为取复数的实部；i为虚数单位；φ1(z)，ψ1(z)为两个复势解析函数；φ′1(z)和φ″1(z)分别为φ1(z)的一阶和二阶导数；ψ′1(z)为ψ1(z)的一阶导数;z为复势坐标;
分别为边界水平和竖向面力。
为了便于根据各复变函数在弹性体边界上的已知条件来决定这些函数，采用保角变换z=ω(ζ)，把弹性体在z平面上(xy平面)所占的区域变换为ζ平面上的区域。现给出z平面和ζ平面中应力函数的换算关系:
(4)
式中，φ(ζ)，ψ(ζ)为ζ平面上两个复势解析函数。
曲线坐标中的应力分量与应力函数的关系:
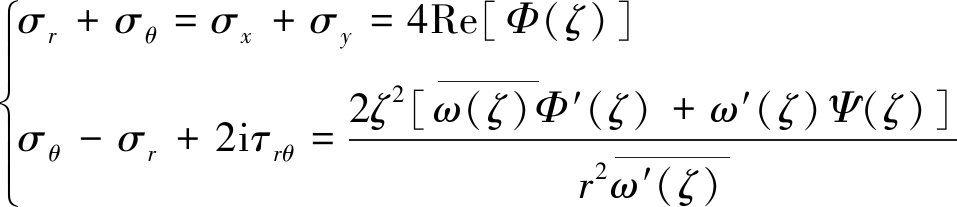
(5)
(6)
1.3 边界条件
据图1力学模型可知，沿井壁外内边界，应力边界条件分别满足式(7)和(8):
(7)
(8)
式中，φf(z)，ψf(z)为z平面中应力解析函数;
与
为z平面上井壁外边界上的面力分量;z0和z1分别表示z平面上井壁内外边界上的点。
井壁所受荷载由围岩骨架和孔隙水共同作用。故此情况下井壁外边界所受荷载可表示为
(9)
式中，np为井壁与围岩接触面孔隙率;fx和fy分别为不考虑孔隙率时，围岩传递给井壁的荷载;
和
分别为考虑接触面孔隙率后井壁外边界所受围岩骨架荷载;η为围岩卸载率，η=0表示围岩未卸载，η=1表示围岩完全卸载;p为静水压力;
为作用在井壁外边界上的孔隙水压。
对于完全弹性介质井壁，求解过程可分为两个部分，即井壁边界受力为骨架压力和孔隙水压力作用，井壁解析解等于骨架压力和孔隙水压力作用之和。由此可将式(7)分解为
土骨架应力边界
(10)
孔隙水压应力边界
(11)
1.4 参数无量纲化
文中井壁应力、外载和力学参数等可无量纲化为
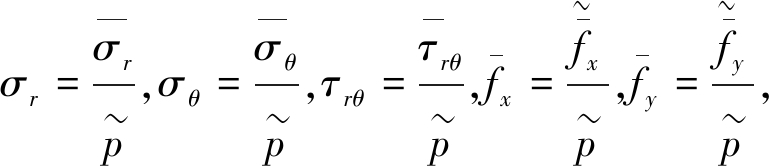
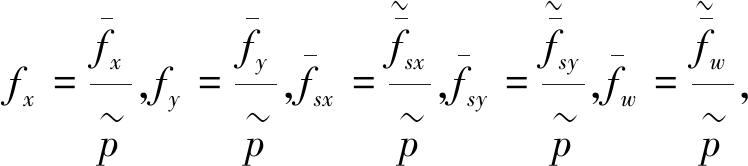
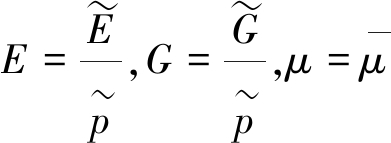
(12)
井壁几何参数可无量纲化为
(13)
式中，σr，σθ分别为极坐标下r，θ方向应力；τrθ为剪应力；ur，uθ分别为极坐标下r，θ方向位移；ri为井壁上半圆半径；rdi为井壁仰拱半径；hi为侧墙高度；h为井壁厚度。
各参量带“～”的表示原型值，不带“～”的表示无量纲化值;E，G和μ分别表示弹性模量、剪切模量和泊松比;下标i=0,1分别表示井壁内、外边界。
2 复应力函数的求解
假设复应力函数形式为
(14)
因模型关于x轴对称，故式中，ak,bk,ck,dk均为待定实数。
z平面映射到ζ平面上，面力F(z)可展开成傅里叶级数形式，故ζ平面上，映射后的井壁内外边界应力边界条件(7)～(8)可分别表示为
(15)
(16)
式中，ζ0和ζ1分别为ζ平面上井壁内外边界上的点。
井壁与围岩完全贴合和井壁与围岩完全剥离两种情况边界条件均可通过式(15)～(16)表达，只是式中的Ak和Bk取值不同。
令式(15)～(16)中左端第2项中
展开为
(17)
至此，将的内外边界值代入式(15)～(16)，令式(15)～(16)等式两端eikθ项系数相等，即可得出含待解系数的无穷方程组
(18)
由式(18)组成的无穷方程组可计算出应力函数系数ak,bk,ck,dk。
井壁受有效土骨架应力和孔隙水压力两种荷载作用均可通过式(18)求解应力函数系数ak,bk,ck,dk，只是式中的Am和Bn取值不同。
3 结果分析
3.1 映射函数求解
某斜井井壁断面为直墙半圆拱型，井壁设计参数见表1。
表1 斜井井壁设计参数
Table 1 Parameter values of inclined shaft lining
参数r0/mr1/mh0/mh1/mrd0/mrd1/mh/mp/MPaγ/(MPa·m-1)E/MPaμλ取值2.83.52.22.66.370.720.0236 0000.20.65
注:
分别为井壁拱顶部分内、外半径;
分别为井壁内、外侧墙高度;
分别为井壁底板内、外半径;
为井壁厚度;
为静水压力;
为围岩容重
取ρ=2 000 kg/m3)，用以计算作用与井壁上的边界荷载;
和
分别为井壁弹性模量和泊松比;λ为侧压系数。
井壁为带仰拱的直墙半圆拱形状，根据最优化设计思路，利用混合罚函数方法求解出映射函数见式(19)。映射后井壁内边界半径无量纲化后为r0=0.815 2。
z=ω(ζ)=1.044 6(ζ-0.058 4-0.004 6ζ-1+
0.040 5ζ-2-0.028 5ζ-3+0.002 83ζ-4)
(19)
由式(19)绘出的映射形状如图2所示。图2中实线代表井壁实际轮廓线，虚线代表井壁映射轮廓线。从图2可知，井壁内外边界的映射效果较好，尤其是上部半圆拱段;井壁外边界上半部分，映射结果与实际轮廓基本重合，只在侧墙拐角处有一定误差。
图2 井壁实际轮廓与映射轮廓
Fig.2 Actual shape and mapped shape of shaft liner
将映射函数式(19)代入式(18)即可求出井壁内各点的应力和位移解析值。
图3给出了通过解析分析获得的无量纲化井壁内径向位移和环向位移分布规律，图3中坐标以井壁上半圆拱圆心为坐标原点，水平坐标表示井壁宽度方向坐标，竖向坐标表示井壁仰拱至拱顶方向坐标。由图3(a)可知，井壁径向位移表现为:拱顶和底板向井内变形，侧墙向井外变形，由于井壁厚度小，弹性模量大，井壁内外侧变形值基本相同。由图3(b)可知，井壁内环向位移主要集中在半圆拱45°以及侧墙与底板连接处。
图3 井壁径向和环向位移值分布解析解(无量纲化)
Fig.3 Distribution of radial and tangential displacements in shaft liner
图4给出了井壁内径向、环向和剪切应力的解析分布规律。因井壁内缘无应力和位移约束，井壁内径向应力分布由外至内逐渐减至0，在侧墙与底板连接处存在较大的应力集中。井壁底板由内至外环向应力变化梯度明显，底板内侧受拉应力作用，外侧受压应力作用。井壁侧墙与底板连接处应力变化亦较为显著，内侧受压应力作用，外侧受拉应力作用。井壁内切向应力主要集中在半圆拱45°以及侧墙与底板连接处。由图4可知，井壁在底板内侧和侧墙拐角外侧易出现受拉区，由于常规井壁材料为钢筋混凝土，混凝土属于抗压不抗拉材料，因此在满足设计和施工条件下，应尽可能避免井壁出现拉应力区。
图4 井壁径向、环向和剪切应力值分布解析解(无量纲化)
Fig.4 Distribution of radial,hoop and shear stresses in shaft liner
3.2 理论与数值模拟对比
以表1中原型参数建立井壁有限元模型，按图1所示施加荷载，分别考虑井壁外侧与围岩完全剥离和完全贴合两种工况下井壁环向应力对比。
图5给出了井壁与围岩完全剥离和完全贴合两种工况下，井壁数值模拟与理论计算结果对比，可知，理论结果与数值模拟结果有较高的吻合度，仅在侧墙范围有一定误差(图中以拱顶为θ=0°，底板中心θ=180°，侧墙上部θ=90°，侧墙下部θ=120°，下同)。
图5 井壁内外缘环向应力和径向位移数值与理论值对比
Fig.5 Comparison of hoop stress and radial displacement between numerical and theoretical values around inner and outer boundaries of liner
图6 接触面孔隙率np对井壁内、外缘环向应力的影响
Fig.6 Effect of porosity of interface between liner and ground np on hoop stresses around inner and outer boundaries of liner
3.3 孔隙率np的影响
以围岩卸载率η=0.4为例，不同接触面孔隙率下井壁内外缘关键点环向应力变化规律如图6所示。np=0表示接触面无孔隙水压作用，np=1表示接触面无围岩骨架压力作用，井壁外边界作用全水压。
由图6可知，井壁与围岩接触面孔隙率对井壁应力的影响呈线性变化趋势。井壁拱顶和拱底应力变化受接触面孔隙率影响相似，随着孔隙率的增加，井壁拱顶和底拱内缘环向拉应力和外缘环向压应力均逐渐减小。与之相反，随着孔隙率的增加，侧墙内缘环向压应力逐渐减小，外缘环向压应力逐渐增加。井壁内缘拱顶处在np<0.4时处于受拉状态，np≥0.4后受压应力作用。当np≥0.8后，半圆拱与侧墙连接处内侧开始出现拉应力。
图7 接触面孔隙率np对井壁内缘径向位移的影响
Fig.7 Effect of porosity of interface between liner and ground np on radial displacements around inner boundary of liner
不同接触面孔隙率下井壁内缘关键点径向位移变化规律如图7所示。由图7可知，井壁与围岩接触面孔隙率对井壁位移的影响呈线性变化趋势。随着接触面孔隙率的增加，拱顶和拱底径向位移逐渐减小，侧墙处各点表现为由向井外变形逐步向井内变形。
3.4 卸载率η的影响
以围岩孔隙率np=0.2为例，不同卸载率下井壁内外缘环向应力变化规律如图8所示。η=0表示开挖围岩未卸载，即围岩压力全部作用于井壁上，η=1表示开挖围岩完全卸载，即围岩压力在井壁支护前已完全卸载，此时只有孔隙水压作用于井壁上。
图8 围岩卸载率η对井壁内、外缘环向应力的影响
Fig.8 Effect of ground relaxation η on hoop stresses around inner and outer boundaries of liner
不同卸载率下井壁内缘径向位移变化规律如图9所示。
图9 围岩卸载率η对井壁内缘径向位移的影响
Fig.9 Effect of ground relaxation η on radial displacements around inner boundary of liner
由图8可知，随着围岩卸载率增加，井壁内外缘环向应力线性减小。拱顶内缘和侧墙外缘对卸载率不敏感。由图9可知，随着围岩卸载率增加，井壁径向位移同样线性减小，且卸载率对各部位影响均显著。围压卸载率反映了井筒开挖后围岩作用于井壁上的荷载大小，在保证围岩稳定性的前提下，应尽可能增加围岩的卸载率，减小井壁的外载。
3.5 侧压系数λ的影响
以接触面孔隙率np=0.2，围岩卸载率η=0.4为例，不同侧压系数下井壁内外缘环向应力变化规律如图10所示。
图10 侧压系数λ对井壁内、外缘环向应力的影响
Fig.10 Effect of lateral pressure coefficient λ on hoop stresses around inner and outer boundaries of liner
由图10可知，随着侧压系数增加，井壁内缘拱顶和拱底环向拉应力线性减小并逐渐转为压应力，侧墙环向压应力线性减小并逐渐转为拉应力。当λ>0.8后拱顶内缘转为受压状态，半圆拱与侧墙连接处内缘转为受拉状态，当λ>1.5后，拱底内缘方才转为受压状态，拱顶外缘亦转为受拉状态。
不同侧压系数下井壁内缘径向位移变化规律如图11所示。
由图11可知，随着侧压系数的增加，井壁拱顶和拱底径向位移线性减小，当λ>1.5后，井壁拱顶和拱底开始由向内变形转为向外变形。当λ<0.8时，侧墙整体变现为向井外变形，λ>0.8后，侧墙开始向井内变形。
3.6 井壁厚径比ξ的影响
以接触面孔隙率np=0.2，围岩卸载率η=0.4为例，不同井壁厚径比ξ(厚度与内径比)情况下，井壁内外缘环向应力如图12所示，井壁内缘径向位移分布如图13所示。
由图12(a)可知，在相同外载下，随着井壁厚径比的增加，井壁拱顶和底板内外缘环向应力绝对值逐渐减小，但应力变化幅度逐渐减小，由图12(b)可知，侧墙下端(θ=120°)处内外缘环向应力受厚径比影响显著，侧墙上端(θ=90°)内外缘受厚径比影响较小，环向应力影响甚微。由图13可知，随着厚径比增加，井壁各关键点径向位移均显著减小，并趋于0。可见，井壁厚径比增加，可显著改善井壁的整体受力和变形环境，但厚径比增加并非无限制，当厚径比ξ>0.25后，影响可以忽略。
图11 侧压系数λ对井壁内缘径向位移的影响
Fig.11 Effect of lateral pressure coefficient λ on radial displacements around inner boundary of liner
图12 井壁厚径比ξ对井壁内外缘环向应力的影响
Fig.12 Effect of the ratio of liner thickness to radius on hoop stresses around inner and outer boundaries of liner
图13 井壁厚径比ξ对井壁内缘径向位移的影响
Fig.13 Effect of the ratio of liner thickness to radius ξ on radial displacements around inner boundary of liner
4 结 论
(1)采用混合罚函数法求解不规则双连通域的映射函数，结果表明，映射形状与实际形状较为接近。
(2)井壁与围岩接触面孔隙率np影响井壁的受力特征，井壁孔隙率较小时(np<0.4)，拱顶(θ=0°)内侧受拉，当np≥0.8时，拱顶转为受压，侧墙(θ=90°)附近开始进入受拉状态。
(3)井壁的支护应综合考虑围岩卸载率的影响，在合理安全的条件下，应待围岩变形趋于稳定后支护。侧压力系数的变化可改变井壁各关键点的拉压状态和变形形态。侧压力系数的增加可改善顶底板的受力，但对侧墙受力产生了恶化作用，故井壁的设计(侧墙高度)还应综合考虑侧压力系数的影响。
(4)井壁厚径比的增加可显著改善井壁的受力和变形大小，但当厚径比ξ>0.25后，影响可以忽略。井壁厚径比的增加并没有改变井壁各点的受力状态(拉压)和变形形态(向内或向外)。
[1] 中华人民共和国国家标准编写组.煤矿斜井井筒及硐室设计规范[J].北京:中国计划出版社,2007:5-10.
[2] GERÇEK H.An elastic solution for stresses around tunnels with conventional shapes[J].International Journal of Rock Mechanics and Mining Science,1997,34(3):96-110.
[3] EXADAKTYLOS G E,STAVROPOULOU M C.A closed-form elastic solution for stresses and displacements around tunnels[J].International Journal of Rock Mechanics and Mining Science,2002,39(7):905-916.
[4] EXADAKTYLOS G E,LIOLIOS P A,STAVROPOULOU M C.A semi-analytical elastic stress-displacement solution for notched circular openings in rocks[J].International Journal of Solids and Structure,2003,40(5):1165-1187.
[5] HUO H,BOBET A.FERNANDEZ G,RAM
REZ J.Analytical solution for deep rectangular structures subjected to far-field shear stresses[J].Tunnelling and Underground Space Technology,2006,21(6):613-625.
[6] 陈子荫.围岩力学分析中的解析方法[M].北京:煤炭工业出版社,1994:1-42.
[7] 吕爱钟.地下隧道力学分析的复变函数方法[M].北京:科学出版社,2007:1-61.
[8] EINSTEIN H H,SCHWARTZ C W.Simplified analysis for tunnel supports[J].Journal of Geotechnical and Geoenvironmental Engineering,1979,104(4):499-518.
[9] CARRANZA TORRES C,RYSDAHL B,KASIM M.On the elastic analysis of a circular lined tunnel considering the delayed installation of the support[J].International Journal of Rock Mechanics and Mining Science,2013,61:57-85.
[10] BOBET A.Effect of pore water pressure on tunnel support during static and seismic loading[J].Tunnelling and Underground Space Technology,2003,18(4):377-393.
[11] BOBET A.Lined circular tunnels in elastic transversely anisotropic rock at depth[J].Rock Mechanics and Rock Engineering,2011,44(2):149-167.
[12] BOBET A,YU H.Full stress and displacement fields for steel-lined deep pressure tunnels in transversely anisotropic rock[J].Tunnelling and Underground Space Technology,2016,56,125-135.
[13] BOBET A.Analytical solutions for shallow tunnels in saturated ground[J].ASCE Journal of Engineering Mechanics,2001,127(12):1258-1266.
[14] LI S,WANG M.Elastic analysis of stress-displacement field for a lined circular tunnel at great depth due to ground loads and internal pressure[J].Tunnelling and Underground Space Technology,2008,23(6):609-617.
[15] LI S.,WANG M.An elastic stress-displacement solution for a lined tunnel at great depth[J].International Journal of Rock Mechanics and Mining Science,2008,45(4):486-494.
[16] FU J,YANG J KLAPPERICH H,WANG S.Analytical prediction of ground movements due to a nonuniform deforming tunnel[J].ASCE International Journal of Geomechanics,2016(4):1-14.
[17] VERRUIJT A.A complex variable solution for a deforming circular tunnel in an elastic half-plane[J].International Journal for Numerical and Analytical Methods in Geomechanics,1997,21(2):77-89.
[18] 杜子博.斜井冻结井壁内壁力学特性与设计方法研究[D].徐州:中国矿业大学,2013.
DU Zibo.Study on the mechanical characteristics and design method of the freezing inclined shaft inside lining[D].Xuzhou:China University of Mining and Technology,2013.
[19] 张旭.孔隙含水基岩中斜井冻结井壁受力模拟试验系统研制与试验[D].徐州:中国矿业大学,2015.
ZHANG Xu.Development and test of mechanical simulation system for inclined shaft frozen wall in Pore-Water Bedrock[D].Xuzhou:China University of Mining and Technology,2015.
[20] 王千星.斜井冻结法凿井过程中冻结壁与井壁的受力与变形规律研究[D].徐州:中国矿业大学,2014.
WANG Qianxing.Study on the stress and deformation law of inclined shaft frozen wall and shaft lining during freezing sinking[D].Xuzhou:China University of Mining and Technology,2014.
[21] 徐芝纶.弹性力学(第四版)[M].北京:高等教育出版社,2006.
[22] 龚纯,王正林.精通MATLAB最优化计算[M].北京:电子工业出版社,2005:1-206.
