当前,随着矿井开采深度的增加,巷道围岩由于应力集中程度极高且分布极不均匀,变形异常显著,很大程度上增加了巷道坍塌、冒顶和冲击地压等动力灾害发生的可能性,为深部资源的安全开采带来了极大的困难[1-5]。巷道围岩应力状态和破坏区分布范围是研究巷道围岩稳定性的重要课题,对于指导深部矿井巷道维护和利用具有重要的科学意义。
巷道断面形成之后,随着原岩应力的重新分布,围岩周边依次分布破碎区、塑性区和弹性区[1]。针对巷道开掘之后的围岩屈服破坏范围,许多学者开展了大量研究。例如,范文等[6]采用三线性材料软化模型对有压隧洞围岩进行了弹塑性分析,得到了弹性区和塑性区的应力分布;蒋斌松等[7-8]针对圆形巷道,采用Mohr-Coulomb准则和Hoek-Brow准则对其围岩进行了非关联弹塑性分析,获得其应力和变形的封闭解析解;郭延华等[9]基于统一强度理论和塑性应变损伤模型,对高地应力下的圆形巷道的弹性和塑性应力场进行了分析;吴顺川等[10]采用Mohr-Coulomb准则研究了围岩位移、位移灵敏度和塑性区等随荷载的变化规律。姜福兴等[11]运用Druker-Prager准则推导出煤层扰动区长度、塑性区长度的解析公式。
但是,目前针对巷道围岩稳定性研究成果中仅仅区分了围岩的弹性和塑性区域及其范围,并未给出围岩塑性屈服后进一步发生的破碎区范围;而且,现有的松动圈理论是基于围岩处于轴对称均匀围压状态下得出的结论[13-14],而对非轴对称围压作用下的围岩变形特征鲜有报道。
因此,笔者将着重研究非轴对称的非静水压力作用下巷道围岩的弹塑性应力分布特征,确定破碎区和塑性区的分界。同时,以铁法集团大兴矿为工程背景,探究巷道埋深及侧压系数对其破碎区及塑性区范围的影响机制。
1 巷道围岩的弹塑性分析
1.1 巷道围岩力学模型的建立
弹性理论中针对圆形孔洞受双向均布荷载作用的应力给出了弹性阶段的齐尔西(G.Kirsch)解[12]。本文在该解的基础上,在均布压力q1和q2作用下,巷道断面形成后,由于卸压的作用,巷道周边将依次分布破碎区、塑性区和弹性区(图1)[1]。设破碎区半径为RD,塑性区半径为RP。

图1 巷道围岩应力计算模型
Fig.1 Theoretical model of the stress calculation
已知巷道围岩破坏时其应力平衡微分方程为
(σθ-σr)dr=rdσr
(1)
式中,σr和σθ为围岩径向和环向正应力。
采用摩尔库伦准则判断围岩是否达到屈服破坏,该准则的主应力形式为
![]()
(2)
式中,σ1和σ3为第1和第3主应力;c为材料黏聚力;φ为内摩擦角。
由于σ1=σθ,σ3=σr,则式(2)可变换为
![]()
(3)
令![]() 则式(3)为
则式(3)为
σθ=Nσr+S
(4)
联立式(1)和(4),可得围岩屈服后的径向应力和环向应力,即

(5)
1.2 围岩分区应力与变形
1.2.1 破碎区(R≤r≤RD)
已知当r=R时,σRD=0则
eA(N-1)=SD/RN-1
(6)
将式(6)代入式(5)可得破碎区应力表达式:

(7)
已知破碎区和塑性区的本构方程为
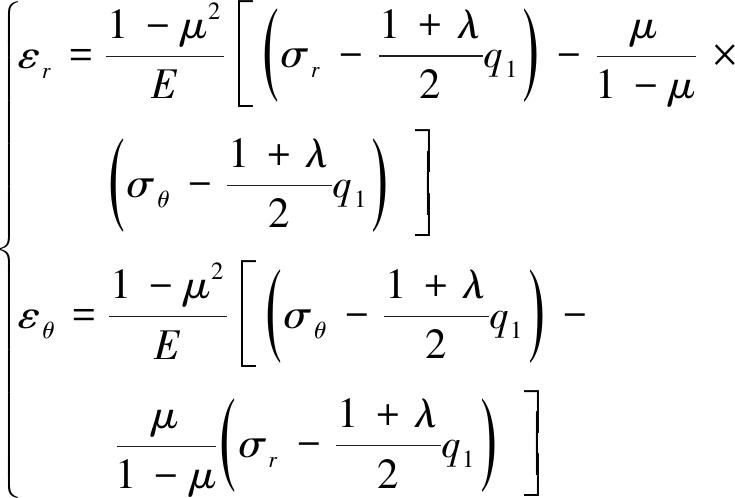
(8)
将式(7)代入本构方程和几何方程可得

(9)
式中,![]()
因此,破碎区范围沿径向的位移变化uD为
uD=εθDr
(10)
1.2.2 塑性区(RD≤r≤RP)
类似于破碎区的解法可得塑性区应力表达式

(11)
将式(11)代入本构方程和几何方程可得

(12)
因此,塑性区范围沿径向的位移变化uP为
uP=εθPr
(13)
1.2.3 弹性区(r≥RD)
由式(1)可知,

(14)
将式(14)代入本构方程和几何方程可得
![]()
(15)
因此,弹性区范围沿径向的位移变化u为
u=εθr
(16)
1.3 破碎区与塑性区范围的确定
利用不同分区边界位移连续的条件,可将式(10)与(13)在r=RD处联立起来,同样在r=RP处式(13)与(16)联立,即可得出R,RD和RP的关系式,如式(17)和(18)所示。
![]()
(17)

(18)
式中,Q和W为与围岩物理力学参数及受力状况有关的常量,即


图2 N2-902工作面采掘工程平面图
Fig.2 Integrated mining engineering plan of N2-902 mining panel
当岩石的物理力学参数确定时,式(17)和(18)可以解出RD和RP关于具体的岩石物理力学参数的表达式,从而可以确定圆形巷道围岩破碎区和塑性区的范围大小。
2 工程验证及参数影响分析
大兴煤矿位于辽宁省铁岭,隶属于铁法集团市。已知该矿北二采区902工作面运输巷位于9号煤层,埋深650 m,该煤巷横截面为圆形,直径为5.0 m,东侧为未采动区,西侧为北二903工作面采空区;南侧为保护煤柱;北侧为F15号井田边界断层,如图2所示。大兴矿地应力以水平压应力为主,根据大兴矿井下测量结果最大主应力为25 MPa,方向近东西,中间主应力为垂直应力16.78 MPa,最小主应力为10 MPa,该运输巷处于非轴对称的非静水压力状态,故选取该煤巷对围岩破碎区理论解进行验证。查其矿区内岩层物理力学参数可知,该煤巷围岩以粉砂岩为主,其物理力学参数见表1。
表1 大兴煤矿粉砂岩物理力学性质
Table 1 Physical and mechanical properties of siltstone in Daxing Coal Mine

参数数值密度ρ/(kg·m-3)2 410弹性模量 E/MPa9 700泊松比μ0.21黏聚力C/MPa1.06内摩擦角φ/(°)26
巷道埋深以及围岩侧压系数是巷道掘进过程中对巷道围岩破碎程度影响较大的2个因素。因此笔者主要探究了巷道埋深、侧压系数对围岩塑性区及其破碎区范围的影响机制。
2.1 围岩应力变化特征分析
2.1.1 分区应力分布特征
利用大兴矿的工程地质岩层的物理力学参数,并假设巷道埋深为1 000 m,巷道半径为1.5 m,则可通过式(7),(11)及(14)计算出不同侧压系数下巷道围岩不同区域内环向主应力及径向主应力逐渐远离巷道中心的变化特征,其计算结果如图3所示。由图3可知,巷道开挖后,围岩破碎区域内应力比塑性区域内的小,且围岩环向正应力的变化比径向正应力剧烈,说明围岩破坏的主要形式是沿纵向破坏;围岩应力在破碎区与塑性区边界处以及在弹塑性边界上都出现了应力不连续现象。

图3 围岩应力变化曲线
Fig.3 Curve of stress changes of surrounding rock
分析式(4)和(5)可以看出:巷道围岩环向正应力要大于其径向正应力,故随着围岩破坏变形的加剧,其环向正应力最先达到极限承载力从而使围岩主要发生环向破坏,并伴随部分纵向破坏;分析式(7),(11)及(14)可以看出:围岩物理力学参数的大小在围岩破碎区、塑性区以及弹性区内不尽相同,这将导致围岩应力在破碎区与塑性区边界处以及弹塑性边界处不连续;这与图3所得结论相一致,证明了该理论解的合理性。
2.1.2 分区边界应力不连续影响机制
由于围岩应力在不同分区边界上均出现的不连续现象,究其根本为黏聚力及内摩擦角等参数大小的变化对围岩应力的影响度及敏感度不同[15],进而导致不同分区的应力在边界上出现了不连续。本节以破碎区与塑性区边界的环向正应力差值随内摩擦角及黏聚力改变的变化特征为例验证该结论的正确性,如图4所示。由此可知,随着内摩擦角的不断增大,围岩应力在破碎区与塑性区边界处的应力差逐渐减小;随着黏聚力的不断增大,围岩应力在破碎区与塑性区边界处的应力差逐渐增大。

图4 环向应力差随内摩擦角及黏聚力变化曲线
Fig.4 Curves of hoop stress difference between internal friction angle and cohesion
黏聚力及内摩擦角等物理力学参数值的变化会导致围岩分区边界应力不连续,这和Lippmann的基本理论是一致的[16-17],其原因在于不同区域的岩石变形特征不同,各参数值大小不同,因而导致了分区边界上应力产生不连续的现象。
2.2 围岩塑性区范围的变化特征分析
根据理论计算中的数学模型,建立了长120 m、宽120 m、厚1 m的FLAC3D数值模型;模型上边界根据埋深h的不同而施加不同大小的载荷以模拟地应力,侧压系数为2.0,如图5所示,采用Mohr-Coulomb准则作为材料的破坏准则,模拟在非静水压力条件下巷道开挖围岩塑性区变化。
以大兴煤矿北二采区902工作面运输巷为工程背景,由于地下工程实际地质条件较为复杂,往往需要在不同深度的地层中开挖巷道,本文通过改变模型上覆岩层压力来模拟巷道所处的不同埋深,并通过观察巷道围岩的破碎区范围变化,分析埋深对巷道围岩破碎区半径的影响机制,如图6所示。

图5 数值模型
Fig.5 Diagram of numerical model

图6 不同埋深下围岩破碎区变化
Fig.6 Variation of excavation damaged zone under different depths
特别说明的是,根据文献[13]中对松动圈的研究可知,松动圈主要是由于围岩产生剪切破坏而产生的环状破裂带,故本文利用FLAC3D中的后处理使其显示单元状态为shear-n,shear-p(过去和现在都达到剪切破坏)状态的单元,即视为破碎区的分布特征。
由图6可知,巷道围岩破碎区范围随埋深的增加而逐渐往外扩散,且扩散幅度在一定范围内较为均匀。在巷道埋深较小时,巷道围岩破碎区较小,巷道处于相对稳定的状态;而在埋深较大时,巷道围岩破碎区中过去和现在都达到塑性状态的单元分布不均匀,巷道左右两帮处较巷道顶底板更易发生失稳破坏。在巷道埋深等于800 m时,巷道围岩破碎区中过去和现在都达到塑性状态的单元分布最为均匀,巷道处于相对稳定的状态;当埋深达到1 400 m时,巷道围岩破碎区中过去和现在都达到塑性状态的单元扩散幅度突增,围岩破坏严重。
将表1中围岩的物理力学参数代入第1节中巷道围岩塑性区和破碎区的解析解中求出其半径大小,并将其与数值模型中的计算结果进行对比,见表2。
表2 理论计算与数值模拟对比
Table 2 Comparison table between theoretical calculation and numerical simulation m
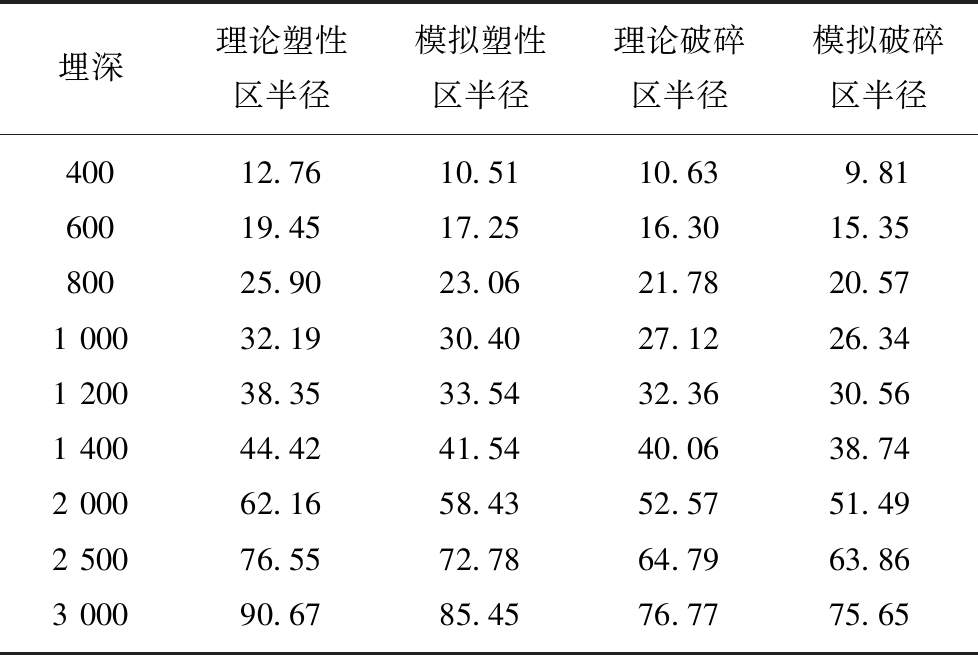
埋深理论塑性区半径模拟塑性区半径理论破碎区半径模拟破碎区半径40012.7610.5110.639.8160019.4517.2516.3015.3580025.9023.0621.7820.571 00032.1930.4027.1226.341 20038.3533.5432.3630.561 40044.4241.5440.0638.742 00062.1658.4352.5751.492 50076.5572.7864.7963.863 00090.6785.4576.7775.65
由表2可知,数值模拟计算所得的塑性区半径和破碎区小于理论计算结果,其原因在于数值模拟计算是在巷道开掘下模型内部单元应力不断迭代计算,达到平衡后计算的结果,其存在因巷道开掘产生的扰动影响,而该理论解则是在非静水压力下的简化计算结果,故其值要大于数值模拟计算的塑性区半径。
利用大兴矿的工程地质物理力学参数,可通过式(18)计算得到如图7所示的塑性区半径随埋深及侧压系数改变的变化特征。

图7 围岩塑性区半径随埋深变化曲线
Fig.7 Curves of radius of plastic zone with buried depth
观察图7可得:同一侧压系数下,在一定埋深范围内,巷道围岩塑性区半径随着埋深的增加呈线性增大;在埋深为1 500 m处曲线斜率突然增大,说明此时巷道围岩自承能力已达到极限破坏状态。这与文献[18]中所定义的极限深度为1 500 m基本吻合,证明了该理论解的正确性与合理性。
2.3 围岩破碎区范围的变化特征分析
利用大兴矿工程地质物理力学参数,通过式(17)计算得到如图8所示的破碎区半径随埋深及侧压系数改变的变化特征。

图8 围岩破碎区半径随埋深变化曲线
Fig.8 Curves of radius of damaged zone with buried depth
由图8可知,同一侧压系数下,在一定埋深范围内,巷道围岩破碎区半径随着埋深的增加呈线性增大;与塑性区半径类似,在埋深为1 500 m处巷道破坏严重,破碎区范围突然增大。
2.4 围岩破碎区与塑性区对比分析
图9为塑性区半径与破碎区半径随埋深的变化曲线。由图9可以看出,埋深及侧压系数对巷道围岩破碎区半径的影响机制与塑性区半径基本一致,其原因在于围岩发生破碎是其塑性变形的下一阶段过程,是其积聚过多能量而发生变形的最终结果。
其次,塑性区半径与破碎区半径的相对变化特征随埋深的变化如图10所示。随着埋深的增加,塑性区的范围在相对减小,而破碎区范围在相对增大;随着埋深逐渐增大,塑性区半径与破碎区半径比值的变化逐渐趋于平稳,深部巷道围岩进入塑性状态和破碎状态范围同比例增大。

图9 不同埋深下塑性区与破碎区半径对比
Fig.9 Comparison of the radius between plastic zone and damaged zone at different depths

图10 塑性区与破碎区半径比值随埋深变化曲线
Fig.10 Curves of radius ratio of plastic zone and damaged zone with buried depth

图11 塑性区与破碎区半径比值随侧压系数变化曲线
Fig.11 Curves of radius ratio of plastic zone and damaged zone with side pressure coefficient
图11为塑性区与破碎区半径比值随侧压系数增加的变化曲线示意。由图11可知,随着侧压系数的不断增加,塑性区与破碎区半径比值逐渐减小,即随着侧压系数的增加,塑性区的范围在相对减小,而破碎区范围在相对增大;随着埋深逐渐增大,塑性区与破碎区半径的比值随侧压系数增大的变化逐渐趋于平缓,深部巷道围岩塑性区和破碎区半径比值趋向稳定。
3 结 论
(1)在巷道断面形成后,随着向围岩深部延伸,其围岩环向正应力的变化比径向正应力剧烈,围岩以纵向破坏为主。不同区域的围岩变形特征不同,导致其黏聚力及内摩擦角等物理力学参数的大小存在差异,从而使围岩分区边界应力产生不连续现象。
(2)塑性区与破碎区范围均在一定埋深范围内随埋深的增加而增大。当埋深达到1 500 m时,2者半径增大显著,围岩自承能力达到了极限破坏状态,围岩破坏严重。
(3)巷道埋深的变化对塑性区与破碎区范围比例的变化影响较为剧烈;且随埋深的增大,侧压系数对其影响程度逐渐减弱,巷道围岩应力状态逐渐趋于静水压力状态。
[1] WANG Hongwei,JIANG Yaodong,XUE Sheng.Assessment of excavation damaged zone around roadways under dynamic pressure induced by an active mining process[J].International Journal of Rock Mechanics & Mining Sciences,2015,77(7):265-277.
[2] 何满潮,谢和平,彭苏萍,等.深部开采岩体力学及工程灾害控制研究[J].煤矿支护,2007(3):1-14.
HE Manchao,XIE Heping,PENG Suping,et al.Study on rock mechanics and engineering disaster control in deep mining[J].Mei Kuang Zhi Hu,2007(3):1-14.
[3] ZHU W C,BRUNHNS O T.Simulating excavation damaged zone around a circular opening under hydromechanical conditions[J].International Journal of Rock Mechanics & Mining Sciences,2008,45(5):815-830.
[4] 谢和平.矿山岩体力学及工程的研究进展与展望[J].中国工程科学,2003,5(3):31-38.
XIE Heping.Progress and prospect of research on rock mechanics and engineering[J].Engineering Science of China,2003,5(3):31-38.
[5] 何满潮,谢和平,彭苏萍,等.深部开采岩体力学研究[J].岩石力学与工程学报,2005,24(16):2803-2813.
HE Manchao,XIE Heping,PENG Suping,et al.Study on rock mechanics in deep mining engineering[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(16):2803-2813.
[6] 范文,俞茂宏,陈立伟.考虑材料剪胀及软化的有压隧洞弹塑性分析的解析解[J].工程力学,2004,21(5):16-24.
FAN Wen,YU Maohong,CHEN Liwei.An analytic solution of elastic-plastic pressure tunnel considering material softening and dilatancy[J].Engineering Mechanics,2004,21(5):16-24.
[7] 蒋斌松,张强,贺永年,等.深部圆形巷道破裂围岩的弹塑性分析[J].岩石力学与工程学报,2007,26(5):982-986.
JIANG Binsong,ZHANG Qiang,HE Yongnian,et al.Elastoplastic analysis of cracked surrounding rocks in deep circular openings[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(5):982-986.
[8] 蒋斌松,杨乐,时林坡.基于Hoek-Brown准则的破裂围岩应力分析[J].固体力学学报,2011,32:300-305.
JIANG Binsong,YANG Le,SHI Linpo.Stress analysis of cracked surrounding rock based on Hoek-Brown criterion[J].Chinese Journal of Solid Mechanics,2011,32:300-305.
[9] 郭延华,姜福兴,张常光.高地应力下圆形巷道临界冲击地压解析解[J].工程力学,2011,28(2):118-122.
GUO Yanhua,JIANG Fuxing,ZHANG Changguang.Analytical solution for critical rockburst of a circular chamber subjected to high in-situ stress[J].Engineering Mechanics,2011,28(2):118-122.
[10] 吴顺川,潘旦光,高永涛.深埋圆形巷道围岩和衬砌相互作用解析解[J].工程力学,2011,28(3):136-142.
WU Shunchuan,PAN Danguang,GAO Yongtao.Analytic solution for rock-liner interaction of deep circular tunnel[J].Engineering Mechanics,2011,28(3):136-142.
[11] 姜福兴,刘金海,王平.基于Druker-Prager准则的煤层冲击失稳模型[J].煤炭学报,2011,36(5):727-731.
JIANG Fuxing,LIU Jinhai,WANG Ping,et al.Model of coal burst and instability based on Druker-Prager yield criterion[J].Journal of China Coal Society,2011,36(5):727-731.
[12] 徐芝纶.弹性力学[M].北京:高等教育出版社,2006.
[13] 董方庭,宋宏伟,郭志伟,等.巷道围岩松动圈支护理论[J].煤炭学报,1994,19(1):21-32.
DONG Fangting,SONG Hongwei,GUO Zhiwei,et al.Support theory of loose rock of roadway surrounding rock[J].Journal of China Coal Society,1994,19(1):21-32.
[14] 董方庭等.巷道围岩松动圈支护理论及应用技术[M].北京:煤炭工业出版社,2001.
[15] 赵同彬,谭云亮,张玉明,等.巷道工程位移反分析的可反演性评价研究[J].采矿与安全工程学报,2006,23(2):224-227.
ZHAO Tongbin,TAN Yunliang,ZHANG Yuming,et al.Invertibility evaluation of back analysis of roadway displacement[J].Journal of Mining & Safety Engineering,2006,23(2):224-227.
[16] 姜耀东,赵毅鑫,刘文岗.深采煤层巷道平动式冲击失稳三维模型研究[J].岩石力学与工程学报,2005,24(16):2864-2869.
JIANG Yaodong,ZHAO Yixin,LIU Wengang,et al.Investigation on three-dimensional model of instability of translatory coal bumps in deep mining[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(16):2864-2869.
[17] 祝捷,姜耀东,赵毅鑫,等.改进的Lippmann煤层平动突出模型[J].煤炭学报,2007,32(4):353-357.
ZHU Jie,JIANG Yaodong,ZHAO Yixin,et al.The improved Lippmann’s translator model of coal bumps[J].Journal of China Coal Society,2007,32(4):353-357.
[18] 谢和平,周宏伟,薛东杰,等.煤炭深部开采与极限开采深度的研究与思[J].煤炭学报,2012,37(4):535-542.
XIE Heping,ZHOU Hongwei,XUE Dongjie,et al.Research and consideration on deep coal mining and critical mining depth[J].Journal of China Coal Society,2012,37(4):535-542.
