无煤柱切顶留巷开采核心工艺为超前工作面采用预裂爆破技术切断巷道顶板与采空区顶板力学联系,达到卸压效果[1]。预裂爆破期间巷道顶板不仅承受静载作用,同时还承受爆破动载作用,属动静耦合作用,相较于常规回采巷道其力学过程复杂。
国内外学者关于预裂爆破致裂岩体机理方面进行了大量研究,何满潮等[2]对岩体在爆破作用下裂纹发生、扩展原理上进行了描述,并采用凝聚炸药的C-J理论,给出了爆破冲击波峰值应力计算方法及基于爆破损伤叠加范围确定炮孔间距的方法;梁洪达等[3]认为爆破应力波的叠加及爆生气体在水平径向裂隙中膨胀挤压合力大于岩体抗拉强度而造成岩体开裂;高魁等[4-5]通过描述爆破应力波对岩体的作用过程,认为爆破应力波衍生的拉伸应力是造成岩体裂纹扩展,导致岩体破坏的根本原因,且聚能方向上产生的初始导向裂隙远大于其他细小裂纹,高压爆生气体进入初始导向裂隙使裂隙扩展发育、破裂岩体;左建平等[6]认为爆破应力波加大了裂隙发生、扩展的可能性,在爆破应力波强度恒定的条件下,改变爆破应力波入射角度,能够实现爆破应力波对裂隙扩展的最大扰动作用;高玉兵[7]采用裂纹尖端起裂强度因子论述了地应力与爆破应力共同作用下裂纹发生、发展过程;在聚能爆破模式下,爆破起始阶段主要为聚能流的侵彻作用,在此作用下形成了定向裂缝,认为应力波主要在定向裂隙的引导作用下继续扩展原有裂隙。通过上述研究成果可以发现,爆破应力波在岩体内产生了拉应力,拉应力的作用使岩体产生并扩展裂纹,爆生气体加剧了裂纹扩展,致使岩体成缝破裂。
无煤柱切顶留巷中,装药长度与炮孔间距会直接影响成缝效果与顶板稳定,国内外学者对成缝效果与顶板稳定和装药长度与炮孔间距之间的关系也进行了相关研究。高玉兵等[8-9]认为常规爆破模式下,炸药量过多会影响本工作面巷道的稳定性,炸药量过少则达不到理想的预裂效果,采用聚能爆破工艺技术可实现对巷道顶板的切开与保护;何满潮等[10-12]通过数值模拟方法分析爆破作用下岩体应力及裂缝分布规律,并采用单孔爆破应力致岩石损伤深度叠加方法确定合理的炮孔间距;马新根等[13]通过数值模拟方法确定最优装药不耦合系数,并通过现场实测导向孔裂隙率,确定最优炮孔间距;陈上元等[14]认为对聚能爆破效果影响较大的是炮孔装药量和炮孔间距,并通过现场实测及数值模拟方法确定合理的炮孔装药量及炮孔间距;孙晓明等[15]认为单孔聚能装置中的装药量不能过多,预裂爆破设计需要在考虑岩体强度的基础上,根据单孔装药量所产生的聚能爆破能量,通过现场试验确定预裂爆破钻孔间距;朱珍等[16]认为聚能爆破装药量、装药方式、炮孔封泥长度及爆破孔间距等参数与顶板岩性及岩层构造有关,需根据现场试验进行确定。有关装药长度和炮孔间距的研究多以数值模拟、现场试验方法为主,定性研究了装药长度与炮孔间距对成缝效果的影响,缺乏对保证巷道基本顶稳定方面的深入研究。
综上所述,爆破致裂岩体机理上,国内外学者普遍认为岩体在爆破应力波作用下,拉应力超过岩体抗拉强度时,使岩体产生并扩展裂纹,爆生气体加剧裂纹扩展,致使岩体破裂。无煤柱切顶留巷预裂爆破不仅要保证沿炮孔连线方向顶板成缝还要保证巷道顶板稳定。笔者以祁东煤矿7135工作面回风巷基本顶为研究对象,深入研究无煤柱切顶留巷预裂爆破期间基本顶成缝与稳定机理,并以此建立基本顶成缝与稳定判据。研究成果为无煤柱切顶留巷顶板预裂爆破技术工艺及巷道顶板稳定控制方面提供重要理论依据。
1 无煤柱切顶留巷基本顶受力特征
1.1 无煤柱切顶留巷工程概况
安徽祁东煤矿在7135工作面回风巷试验无煤柱切顶留巷。工作面开采参数:倾向长度为175 m,走向长度为1 688 m,采用走向长壁一次采全高开采方式,顶板全部垮落法管理。工作面煤层赋存条件:工作面平均埋深H=520 m,煤层厚度M=3 m,巷道宽度b=5.0 m,高度h=3.0 m,基本顶抗拉强度σt=4.2 MPa。工作面巷道布置及地质综合柱状如图1所示。为减小工作面采动对爆破期间顶板稳定性的影响,祁东煤矿7135回风巷超前50~60 m实施预裂爆破,爆破工艺为聚能爆破,采用反向装药,炮孔同时起爆,孔内反向起爆。采用三级煤矿许用水胶炸药,炸药药卷参数:直径φ=35 mm,长度l=400 mm,质量m=0.44 kg,本文计算过程中装药量等于装药长度乘以三级煤矿需用水胶炸药的药卷质量。

图1 工作面巷道布置及地质综合柱状
Fig.1 Working face roadway layout and geological compreh-ensive histogram
1.2 无煤柱切顶留巷基本顶预裂爆破受力特征
无煤柱切顶留巷预裂爆破使顶板沿炮孔连线方向产生贯通裂隙,如图2(a)所示,爆破作用期间基本顶不仅承受覆岩、支护体及采掘活动施加的静载作用[17-19],同时还承受爆破动载作用,如图2(b)所示。此时基本顶受覆岩支承应力简化为均布载荷,巷道范围内支护体对基本顶的支撑反力简化为均布载荷,实体煤采动应力影响范围内对基本顶的支撑反力可简化为线性载荷[20-22]。
爆破后,聚能方向的岩体受到爆破冲击波的压缩作用发生破坏,形成的粉碎区尽管范围小,却消耗了冲击波的大部分能量,此时冲击波衰减为应力波。应力波的作用使炮孔连线方向(径向)岩体受压、垂直炮孔连线方向(切向)岩体受拉。当切向拉应力超过岩体的抗拉强度时,产生径向裂缝,使炮孔连线方向的岩体发生破坏。非聚能方向,由于药卷外PVC管、套管与炮孔壁之间的不耦合介质(空气)对爆轰产物具有缓冲和抑制作用,极大的降低了冲击波对炮孔壁的破坏,因此,在非聚能方向,冲击压缩波急剧衰减为弹性压缩波作用于基本顶,弹性压缩波由于反射作用在基本顶内形成拉应力波,产生拉应力。当拉应力峰值大于基本顶抗拉强度时,基本顶产生裂缝,利用聚能爆破的聚能效应可实现无煤柱切顶留巷沿炮孔连线方向成缝。

图2 预裂爆破阶段基本顶受力分析
Fig.2 Analysis diagram of main roof stress in presplitting blasting stage
2 基本顶成缝机理
爆破应力波对顶板的拉伸效应远大于顶板所处的应力环境,爆破应力波是顶板产生贯通裂缝的关键因素。本文在研究成缝机理过程中忽略顶板所处的应力环境,将炮孔内爆破载荷简化为均布载荷。
爆破应力波向孔壁四周传播过程中不断衰减,聚能方向的作用能量远大于非聚能方向,以聚能方向为研究对象,根据应力波在岩体中随距离的衰减公式及波动理论,得到炮孔连线间切向最大拉应力,建立以岩石抗拉强度为标准的成缝条件[23],进而确定不同炮孔间距所需的最小装药长度。
2.1 成缝机理分析
对于普通爆破径向和轴向不耦合装药的炮孔,炮孔壁所受的爆破峰值荷载Prmax[24]可表示为
![]()
(1)
式中,ρ0为基本顶密度,kg/m3;D为爆轰速度,m/s;γ为炸药的等熵指数(一般取3.0);dc为装药直径,mm;db为炮孔直径,mm;dc/db为炮孔径向装药不耦合系数;lc为装药长度,m;lb为炮孔长度,m;lc/lb为炮孔轴向装药不耦合系数。
应力波在岩体中传播时会发生能量衰减,径向应力峰值将不断减小,径向应力峰值随着距离衰减的关系表达式可表示为
![]()
(2)
式中,![]() 为相对距离,
为相对距离,![]() 其中,r为距装药中心的距离,mm,rb为炮孔半径,mm;β为应力衰减指数,β=2±μ/(1-μ),其中,μ为基本顶泊松比,当冲击波作用时取“+”号,应力波作用时取“-”号。
其中,r为距装药中心的距离,mm,rb为炮孔半径,mm;β为应力衰减指数,β=2±μ/(1-μ),其中,μ为基本顶泊松比,当冲击波作用时取“+”号,应力波作用时取“-”号。
单孔起爆应力波在该岩体中产生的切向拉应力σθ可表示为
![]()
(3)
当相邻炮孔同时起爆时,爆破应力波在相邻炮孔连线中点发生叠加,爆破应力波在相邻炮孔连线中点叠加产生的切向拉应力为2σθ,如图3所示。若炮孔间距刚好满足成缝效果,则相邻炮孔同时起爆在连线中点产生最小切向拉应力需大于或等于基本顶抗拉强度,成缝条件可表示为
2σθ≥σt
(4)

图3 联孔聚能爆破力学模型
Fig.3 Mechanical model of double cumulative blasting holes
当爆破炮孔与岩层顶板存在夹角时,如图2(b)所示,则式(4)可表示为
2σθsin θ≥σt
(5)
工程实践中,θ一般取70°~80°,sin θ为0.94~0.98,本文计算过程中将sin θ≈1进行计算,因此将式(2),(3)代入式(4),成缝条件可表示为
![]()
(6)
式(8)为普通装药条件下相邻炮孔同时起爆时顶板形成切缝的条件。当采用聚能爆破时,圆柱形孔壁上聚能方向的峰值应力约为普通爆破时孔壁峰值应力的14倍,非聚能方向的峰值应力约为普通爆破峰值应力的0.062倍[25],因此聚能爆破时顶板的切缝条件可表示为
![]()
(7)
对比式(6),(7)可以看出:在同等爆破条件下,相较于普通爆破,聚能爆破沿聚能方向对岩体的致裂距离更长。
2.2 成缝与炮孔间距及装药长度量化关系
针对祁东煤矿7135工作面回风巷,基本顶泊松比μ为0.25、密度ρ0为2 500 kg/m3、爆轰速度D取3 800 m/s、炮孔半径rb为25 mm、炮孔直径db为50 mm、装药直径dc为35 mm及炮孔长度lb为9 m,均为固定值,因此式(7)中的拉应力仅与炮孔间距r及装药长度lc存在量化关系。根据式(7)可得到在炮孔连线间最大拉应力与炮孔间距及装药长度的量化关系,见表1,黑色加粗应力值表示已经超过基本顶抗拉强度。
表1 最大拉应力与装药长度及炮孔间距量化关系
Table 1 Quantitative relationship between maximum tensile stress and charge length and blasthole spacing MPa

装药长度/m炮孔间距/m0.40.50.60.70.80.91.00.80.070.050.030.030.020.020.011.20.230.160.120.090.070.060.051.60.550.380.280.220.170.140.122.01.070.740.540.420.340.280.232.41.851.270.940.730.580.480.402.82.932.021.491.150.920.760.643.24.373.022.231.721.381.130.953.66.234.293.172.451.961.611.354.08.545.894.353.362.692.211.864.411.377.845.794.483.582.942.474.814.7710.187.515.814.653.823.215.218.7712.949.557.395.914.864.085.623.4516.1611.939.237.396.075.096.028.8419.8814.6711.359.087.466.266.435.0024.1317.8113.7711.029.067.606.841.9828.9421.3616.5213.2210.879.127.249.8334.3625.3519.6115.7012.9010.82
相邻炮孔连线间的切向最大拉应力随着装药长度的增加而增大,当相邻炮孔连线中间的最大拉应力大于基本顶抗拉强度时,则认为在爆破作用下相邻炮孔间能产生径向贯通裂隙;当装药长度确定,切向最大拉应力随炮孔间距增加而降低。若要保证相邻炮孔间能够形成贯通裂隙,在装药长度一定时,则需减小炮孔间距,同理,若炮孔间距一定时,则需要增大装药长度。如炮孔间距达到600 mm时,为保证炮孔连线间岩层产生贯通裂隙,则最小装药长度为4.0 m。

图4 最大拉应力与炮孔间距及装药长度变化曲线
Fig.4 Variation curves of maximum tensile stress with SBH and LAL
根据基本顶切向最大拉应力与炮孔间距及装药长度变化关系,如图4所示,当炮孔间距一定时,最大拉应力随装药长度增大呈幂指数增加,当装药长度一定时,最大拉应力随炮孔间距增大而呈幂指数减小。
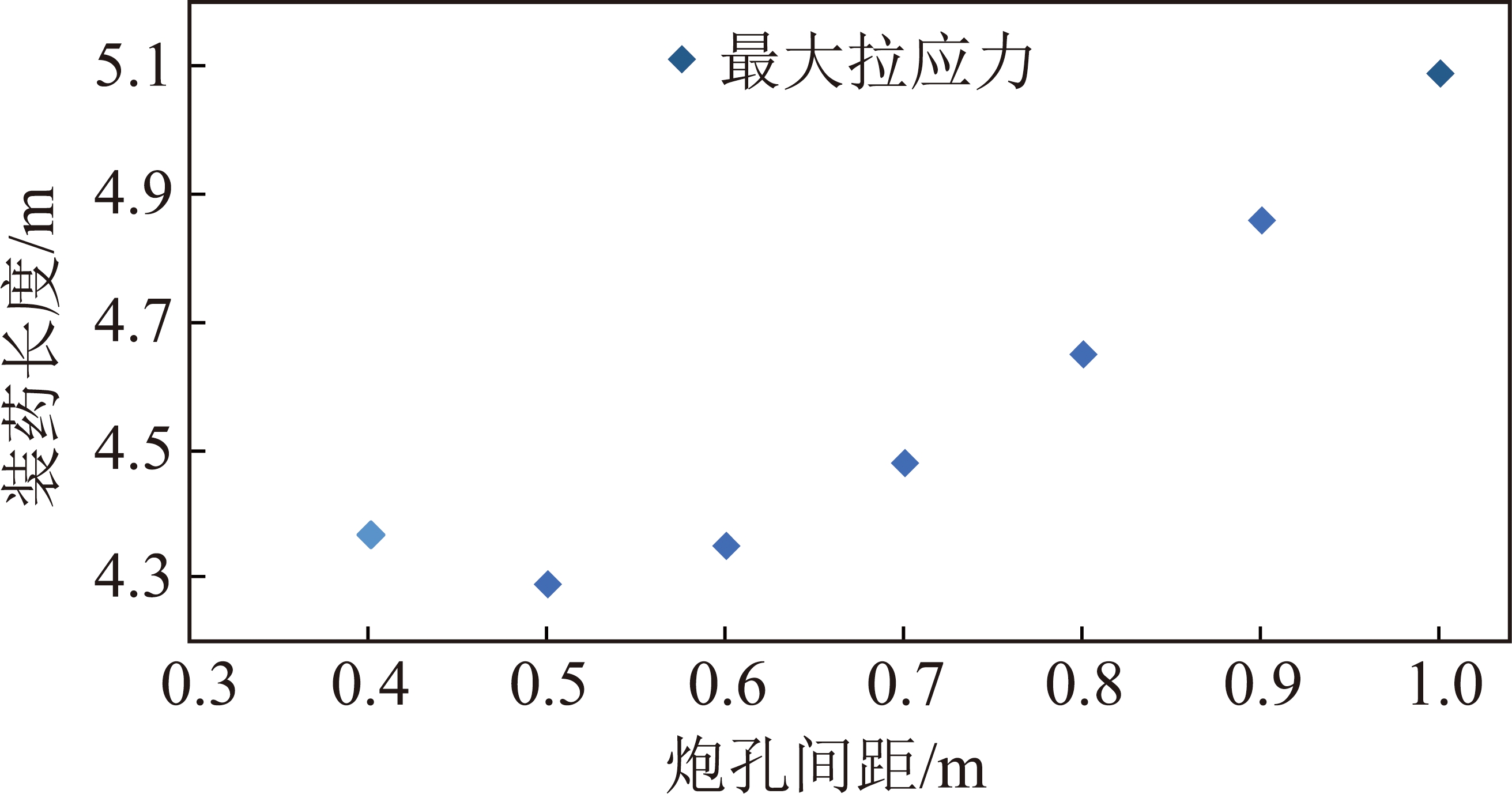
图5 最大拉应力与装药长度及炮孔间距变化关系
Fig.5 Relationship between critical tensile stress with SBH and LAL
将表1中表示大于基本顶抗拉强度的临界值作为考察基本顶成缝判据,如图5所示,随着装药长度及炮孔间距的增大,基本顶切向最大拉应力呈先降低后增大趋势,切向拉应力的增大能够保证基本顶沿炮孔连线间成缝,也可能使巷道基本顶产生裂缝,破坏基本顶稳定性。因此,炮孔间距与装药长度存在一个合理范围能够满足基本顶成缝且稳定的要求。
3 巷道基本顶稳定机理
根据图6(a)基本顶的力学分析,将爆炸动载简化为均布载荷垂直作用于切顶面;由于爆破动载持续时间极短,爆破动载作用后,岩体内应力波的作用过程为爆破动载的卸荷过程,忽略爆破对基本顶的瞬态受迫振动,仅研究基本顶在爆破动载作用后的稳态自由振动。
3.1 动载作用下基本顶应力分布
根据冲量原理,可将基本顶受瞬时动载的动力问题归结为在初始条件下的自由振动问题。为便于理论分析,对基本顶力学模型作以下假设:① 基本顶为弹性变形体,通过平面应变问题求解;② 基本顶覆岩重力的载荷集度为q1,满足均匀分布;③ 基本顶下方实体煤侧范围内直接顶对其作用力满足线性分布特征,该分布力系在巷帮处为q2,在极限平衡位置为λ2q2;④ 巷道范围内被动支护体对顶板的支护强度,满足均匀分布。
根据预裂爆破阶段基本顶受力分析,可将爆破动载简化为如图6所示的力学模型,模型左边界至实体煤极限平衡区边界,右边界至炮孔连线。根据叠加原理,可将基本顶力学模型分别表示为静载作用下力学模型与动载作用下力学模型,如图6所示,其中,h为基本顶岩梁的厚度。

图6 基本顶力学模型
Fig.6 Mechanical model of main roof
根据图6(a),基本顶纵向自由振动满足波动方程:
![]()
(8)
式中,u为基本顶某点的位移,m;t为时间,s;α为基本顶内纵波传播的速度,m/s;E为基本顶弹性模量。
波动方程一般解的形式为
u(x,t)=U(x)(Acos pt+Bsin pt)
(9)
式中,U(x)为振型函数;p为基本顶岩梁的固有频率;t为时间;A,B为待定常数。
将式(9)代入式(8),可得
![]()
(10)
式中,C,D为待定常数。
基本顶边界条件可表示为
![]()
(11)
将式(11)代入式(10),可确定得
![]()
(12)
式中,k为基本顶纵向振动的半波数。
因此,自由振动的解可表达为
![]()
(13)
式中,Ak,Bk为基本顶纵向振动位移解的待定常数。
基本顶的初始条件可表示为
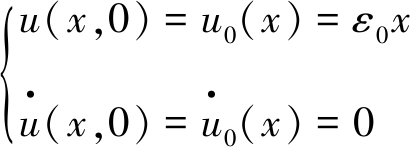
(14)
式中,u0(x)为基本顶在t=0时的初始位移;ε0为基本顶在t=0时刻的初始应变。
将式(12)代入式(14),可得
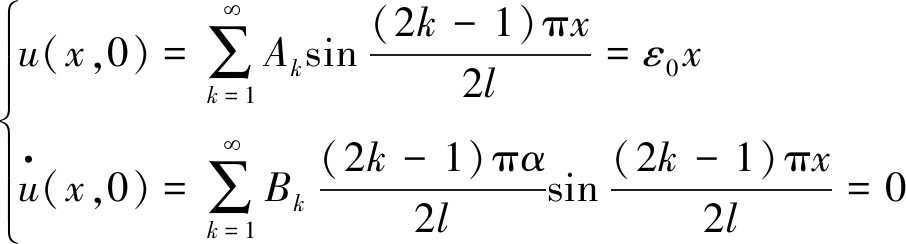
(15)
根据三角函数的正交性,可以确定:
![]()
(16)
将式(16)代入式(13)中,得出基本顶对爆破冲击的位移响应:
![]()
(17)
根据式(17)可求出巷道基本顶中任一点在任一时刻的应力σ(x,t)表达式为
![]()
(18)
式中,E为基本顶弹性模量,取8.12 GPa;由式(8)可得,应力波传播速度α=1 800 m/s,k为正整数。
式(18)给出了爆破应力波在基本顶内的传播规律,如图7所示:t=0时,拉伸力波作用在基本顶x=9 m的爆破端切平面上,随后由此位置向极限平衡位置传播,依次经过x=6,4,2 m位置。当t=0.005 s时,拉伸波到达极限平衡位置并发生反射,反射波和入射波相比,发生了π相位突变,也就是所谓的半波损失,但此时波的性质不变,即经过固定端反射后拉伸波仍为拉伸波;此后,拉伸波向自由端切平面传播并在t=0.01 s到达,拉伸波在自由端切平面发生反射,此时反射波和入射波相位相同,但应力波的性质发生了改变,经过自由端反射后拉伸波变为压缩波。可以看出,在同一位置,基本顶受到拉、压缩波的持续作用,若基本顶内的拉应力超过岩石的抗拉强度时,基本顶内产生裂纹,稳定性降低。

图7 不同时间基本顶应力分布规律
Fig.7 Distribution law of main jacking stress in different time
根据文献[25],由式(18)及式(7)可得不同装药长度条件下巷道基本顶应力分布,见表2。
表2 不同装药长度巷道基本顶拉应力分布
Table 2 Main roof dynamic stress distribution of different charge length MPa

距极限平衡处距离/m装药长度/m0.81.21.62.02.42.83.23.64.04.44.800.020.060.140.280.490.771.151.642.253.003.900.500.020.060.140.280.490.771.151.642.253.003.901.000.020.060.140.280.490.771.151.642.263.003.901.500.020.060.140.280.490.771.161.652.263.003.902.000.020.060.140.280.490.771.161.652.263.003.902.500.020.060.140.280.490.771.161.652.263.003.903.000.020.060.140.280.490.771.161.652.263.003.903.500.020.060.140.280.490.771.151.642.263.003.904.000.020.060.140.280.490.771.151.642.253.003.904.500.020.060.140.280.490.771.151.642.253.003.89
续 表

距极限平衡处距离/m装药长度/m0.81.21.62.02.42.83.23.64.04.44.85.000.020.060.140.280.490.771.151.642.253.003.905.500.020.060.140.280.490.771.151.642.263.003.906.000.020.060.140.280.490.771.161.652.263.003.906.500.020.060.140.280.490.771.161.652.263.013.907.000.020.060.140.280.490.781.161.652.263.013.907.500.020.060.140.280.490.771.161.652.263.013.908.000.020.060.140.280.490.771.151.642.253.003.908.500.020.060.140.280.480.771.151.642.242.993.88
随着装药长度的增加,巷道基本顶不同位置的最大拉应力随之增大,且同一装药长度下,巷道基本顶不同位置的拉应力值相同。结合表1,2,爆破应力波在非聚能方向(巷道基本顶)形成的切向最大拉应力远小于聚能方向(炮孔连线方向)最大拉应力;动载作用下,当装药长度增加到4.8 m时,非聚能方向基本顶不同位置的最大拉应力值为3.9 MPa,均未达到基本顶的抗拉强度;因此,装药长度在4.8 m范围内时,爆破产生的拉应力不会对巷道基本顶产生破坏作用。
爆破作用下巷道基本顶不同位置拉应力与装药长度变化关系,如图8所示,爆破动载作用下巷道基本顶最大拉应力随装药长度增加呈幂指数增大关系,装药长度在0.8~2.8 m增加时,巷道基本顶最大拉应力增大趋势平缓,装药长度在2.8~4.8 m增加时,巷道基本顶最大拉应力增大趋势明显。

图8 拉应力与装药长度变化关系
Fig.8 Dynamic stress and change curve of charge length
3.2 静载作用下巷道基本顶应力分布
根据基本顶力学模型的基本假设,由图6(c)可得基本顶任一截面处的弯矩M(x)为
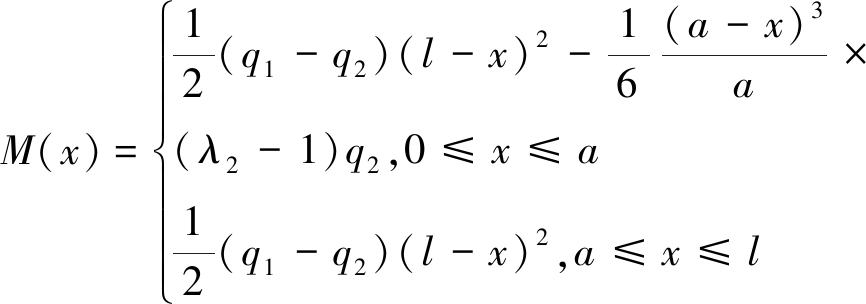
(19)
文中规定σ(x)以压为负,拉为正;根据材料力学中正应力与弯矩的关系,可将基本顶中的正应力分量表示为
![]()
(20)
式中,y为梁内任一点距离中性层的距离;I为巷道基本顶惯性矩,m4。
将式(19)代入式(20),可得
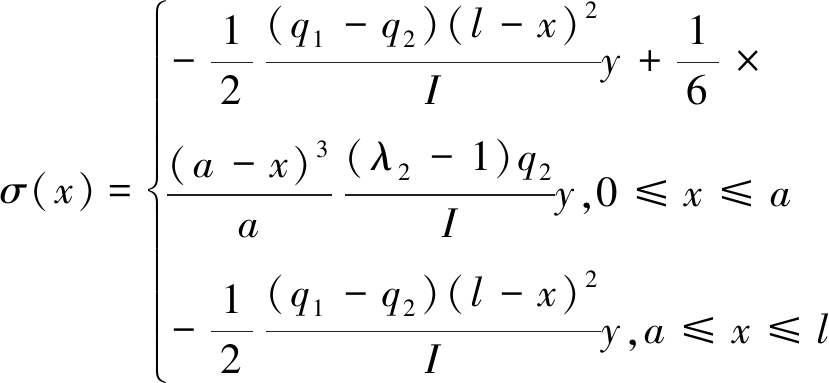
(21)
式中,q1为基本顶上部支承应力,MPa;q2为巷道被动支护体对巷道顶板的支护强度,MPa;a为巷帮距离极限平衡区位置长度,m;b为巷道的宽度,m;l为切顶侧巷帮距离极限平衡区位置长度,m;λ2为侧向应力集中系数;其中巷帮距离极限平衡区位置长度a可由式(22)[26]计算获得
![]()
(22)
其中,λ为侧压系数,取2.0;M为煤层厚度,M=3 m;c0,φ0 为煤层与顶板交界面处的黏聚力(2.2 MPa)与内摩擦角(36°);n为应力集中系数,取1.5;γ 为岩层平均容重,25 kN/m3;H为煤层埋深,520 m;px为巷帮支护阻力,0.1 MPa。计算可得a=4.0 m。
式(21)计算参数取值为:λ2=1.5,a=4.0 m,q1=0.44 MPa,q2=0.15 MPa,I=18,可得不同应力集中系数时顶板应力分布见表3。
表3 不同应力集中系数巷道基本顶拉应力分布规律
Table 3 Distribution of main jacking stress with different stress concentration factors MPa

距极限平衡处距离/m应力集中系数1.01.52.02.53.03.54.001.9581.9241.8911.8581.8241.7911.7580.51.7461.7241.7011.6791.6571.6341.6121.01.5471.5331.5191.5041.4901.4761.4621.51.3591.3511.3431.3351.3271.3191.3112.01.1841.1801.1761.1721.1681.1631.1592.51.0211.0191.0181.0161.0141.0121.0103.00.8700.8690.8690.8680.8680.8670.8673.50.7310.7310.7310.7310.7310.7310.7314.00.6040.6040.6040.6040.6040.6040.6044.50.4890.4890.4890.4890.4890.4890.4895.00.3870.3870.3870.3870.3870.3870.3875.50.2960.2960.2960.2960.2960.2960.2966.00.2180.2180.2180.2180.2180.2180.2186.50.1510.1510.1510.1510.1510.1510.1517.00.0970.0970.0970.0970.0970.0970.0977.50.0540.0540.0540.0540.0540.0540.0548.00.0240.0240.0240.0240.0240.0240.0248.50.0060.0060.0060.0060.0060.0060.006
静载作用下:巷道基本顶不同位置随着应力集中系数的增大而减小,当应力集中系数一定时,基本顶最大拉应力随着距离极限平衡位置增加而减小;巷道基本顶内最大拉应力与应力集中系数有关,随着应力集中系数增大,基本顶内的最大拉应力减小;当基本顶距离极限平衡区位置大于3 m时,随着应力集中系数变化巷道基本顶内不同位置的最大拉应力值不再发生变化,即应力集中系数仅对巷道基本顶局部拉应力分布有影响(0<x<3.0 m),而对远处基本顶拉应力分布无影响(x>3.0 m)。
3.3 稳定与炮孔间距及装药长度量化关系
预裂爆破时,基本顶受到动静载耦合作用,为避免爆破作用使巷道基本顶发生破坏,必须保证巷道基本顶内部最大拉应力小于其抗拉强度;因此,基本顶稳定机理可以表示为
[σ(x)+σ(x,t)]max<σt
(23)
当动静耦合作用产生的最大拉应力小于基本顶抗拉强度时,则基本顶保持稳定;当产生的最大拉应力超过基本顶抗拉强度时,则基本顶内产生裂纹,基本顶稳定性降低。因此,式(23)可作为预裂爆破期间巷道基本顶稳定判据。
预裂爆破期间,巷道极限平衡位置的应力集中系数λ2=1.5,因此将表3中λ2=1.5时基本顶不同位置的最大拉应力与表2中拉应力相叠加,得到不同装药长度条件下,动静载耦合作用时基本顶的应力分布如表4及图9所示。表4中黑色加粗为超过基本顶抗拉强度的拉应力值。在动静载耦合作用下,巷道基本顶在不同装药长度下最大拉应力均发生在极限平衡位置,可知巷道基本顶在极限平衡位置最易发生断裂;巷道基本顶同一位置最大拉应力随装药长度增加而增大,同一装药长度下巷道基本顶最大拉应力随距极限平衡位置距离增大而减小。当装药长度为4.8 m时,巷道基本顶0~5 m内最大拉应力均超过其抗拉强度(4.2 MPa),巷道基本顶在动静载耦合作用下产生裂缝的范围大,基本顶不稳定;当装药长度为4.4 m时,在巷道基本顶0~1.5 m内最大拉应力超过其抗拉强度,不利于基本顶完整性;当装药长度小于4.4 m时,巷道基本顶不同位置最大拉应力均未超过其抗拉强度。因此,为确保基本顶在预裂爆破期间的稳定性,最大装药长度必须小于4.4 m,当选择装药长度为4 m时,对照表1可得:最大炮孔间距为600 mm。
表4 动静载作用下基本顶最大拉应力分布规律
Table 4 Distribution rule of maximum tensile stress of main roof under dynamic and static load MPa

距极限平衡距离/m装药长度/m0.81.21.62.02.42.83.23.64.04.44.801.941.992.072.212.412.703.083.574.184.925.820.51.741.781.872.012.212.502.883.373.984.725.621.01.551.591.681.812.022.312.693.183.794.535.431.51.371.411.501.631.842.132.513.003.614.355.252.01.201.241.321.461.671.952.342.833.444.185.082.51.041.081.161.301.511.792.182.663.284.024.923.00.890.931.011.151.361.642.022.513.133.874.773.50.750.790.881.011.221.501.892.382.993.734.634.00.620.670.750.891.091.381.762.252.863.604.504.50.510.550.630.770.981.261.642.132.743.494.385.00.400.450.530.670.871.161.542.032.643.394.285.50.310.360.440.580.781.071.451.942.553.304.196.00.240.280.360.500.710.991.371.862.473.224.126.50.170.210.300.430.640.931.311.802.413.164.057.00.110.160.240.380.580.871.251.742.363.104.007.50.070.120.200.340.540.831.211.702.313.063.968.00.040.090.170.310.510.801.181.672.283.023.928.50.020.070.150.290.490.781.151.642.252.993.88

图9 动静载作用下顶板拉应力与装药长度变化关系
Fig.9 Relation curves between tensile stress of roof and charging length under the coupling action of dynamic and static loads
4 工程验证
上述计算公式较复杂,为增加公式的适用性,利用VB计算程序编制了相应的计算平台,通过输入相应参数,可直接得到预裂爆破切顶效果评价,如图10所示。为保证祁东煤矿7135工作面回风巷预裂爆破时,沿炮孔连线方向成缝且巷道基本顶稳定;将工程参数代入后,得到装药长度为4 m,炮孔间距为600 mm。

图10 无煤柱切顶留巷装药长度及炮孔间距计算程序
Fig.10 Calculation program of SBH and LAL in non-pillar gob-side entry retaining by roof cutting
其他切顶参数为:切顶角度10°、炮孔深度9 m、封孔深度2 m、装药结构为“4+4+2”,如图11所示。

图11 切顶参数
Fig.11 Cutting parameter diagram

图12 炮孔内裂隙分布
Fig.12 Crack distribution in blast-hole

图13 巷道顶底板变形及变形速率
Fig.13 Deformation and deformation rate curves of roadway roof and floor
爆破后,采用炮孔钻孔窥视法实测基本顶裂隙分布如图12所示,炮孔装药段切缝明显,且切缝呈对称分布,符合聚能爆破成缝特征,将成缝段与爆破深度对比可得,成缝率达到了90%,爆破成缝效果好。
实测巷道顶板在工作面回采期间顶底板变形量如图13所示,工作面前方0~60 m,该阶段为预裂爆破阶段,顶板变形及底臌均呈增加趋势,最大底臌量明显大于顶板下沉量,底臌变形速率呈先增加后降低变化,较顶板变形速率大,顶板变形速率呈整体增加趋势,顶底板变形在该阶段增加明显,顶板最大变形量为61 mm,底臌最大量为106 mm,顶底板最大移近量为167 mm,由该阶段顶板变形量可知基本顶没有发生结构性破坏,处于稳定状态,能够满足工作面安全生产的要求。
由图12,13可知,基于岩体抗拉强度建立的基本顶成缝与稳定判据,以此计算得到的装药长度与炮孔间距,用于工程实践中能够取得良好的应用效果。
5 结 论
(1)基于岩层中应力波衰减公式,分析了基本顶爆破预裂成缝机理,并建立基于抗拉强度的基本顶成缝判据,以祁东煤矿7135工作面为工程背景,获得基本顶成缝时装药长度及炮孔间距之间的最小量化关系。
(2)根据预裂爆破期间基本顶受力特征,构建了基本顶动静耦合作用下力学模型,获得巷道基本顶稳定机理,并以此建立基于抗拉强度的巷道基本顶稳定判据,获得巷道基本顶稳定时装药长度及炮孔间距之间的最大量化关系,并揭示爆破应力波在基本顶内呈拉压交替变换且巷道基本顶同一位置持续受到拉、压应力脉冲作用的传播规律。
(3)基于静载力学模型,得到基本顶最大拉应力与极限平衡区应力集中系数的量化关系,揭示极限平衡区应力集中系数仅对巷道基本顶局部拉应力分布有影响(0<x<3.0 m),而对远处的巷道基本顶应力分布无影响(x>3.0 m)的规律。
(4)基于基本顶成缝与稳定判据,通过VB计算平台获得祁东煤矿7135工作面回风巷切顶爆破装药长度4 m,炮孔间距600 mm,实测考察炮孔装药段成缝率达到了90%,爆破效果好,开采期间超前工作面0~60 m顶板变形量较小,巷道顶板未出现结构性失稳显现,验证了计算模型的合理性。
[1] 王炯,朱道勇,宫伟力,等.切顶卸压自动成巷岩层运动规律物理模拟实验[J].岩石力学与工程学报,2018,37(11):2536-2547.
WANG Jiong,ZHU Daoyong,GONG Weili,et al.Physical simulation experiment on the movement of rock strata upon automatic roadway forming by roof cutting and pressure releasing[J].Chinese Journal of Rock Mechanics and Engineering,2018,37(11):2536-2547.
[2] 何满潮,高玉兵,杨军,等.无煤柱自成巷聚能切缝技术及其对围岩应力演化的影响研究[J].岩石力学与工程学报,2017,36(6):1314-1325.
HE Manchao,GAO Yubing,YANG Jun,et al.An energy-gathered roof cutting technique in no-pillar mining and its impact on stress variation in surrounding rocks[J].Chinese Journal of Rock Mechanics and Engineering,2017,36(6):1314-1325.
[3] 梁洪达,郭鹏飞,孙鼎杰,等.不同聚能爆破模式应力波传播及裂纹扩展规律研究[J].振动与冲击,2020,39(4):157-164,184.
LIANG Hongda,GUO Pengfei,SUN Dingjie,et al.A study on crack propagation and stress wave propagation in different blasting modes of shaped energy blasting[J].Journal of Vibration and Shock,2020,39(4):157-164,184.
[4] 高魁,刘泽功,刘健,等.爆破扰动松软煤层对巷道围岩稳定性的影响[J].振动与冲击,2018,37(15):136-142.
GAO Kui,LIU Zegong,LIU Jian,et al.Effects of blast disturbing soft coal seam on stability of roadway surrounding rock[J].Journal of Vibration and Shock,2018,37(15):136-142.
[5] 高魁,刘泽功,刘健,等.定向聚能爆破弱化综掘工作面逆断层应用研究[J].岩石力学与工程学报,2019,38(7):1408-1419.
GAO Kui,LIU Zegong,LIU Jian,et al.Application research of directional cumulative blasting for weakening reverse faults in fully mechanized excavation face[J].Chinese Journal of Rock Mechanics and Engineering,2019,38(7):1408-1419.
[6] 左建平,孙运江,刘文岗,等.浅埋大采高工作面顶板初次断裂爆破机理与力学分析[J].煤炭学报,2016,41(9):2165-2172.
ZUO Jianping,SUN Yunjiang,LIU Wengang,et al.Mechanical analysis and blasting mechanism of main roof initial fracturing in shallow depth mining face with large cutting height[J].Journal of China Coal Society,2016,41(9):2165-2172.
[7] 高玉兵.柠条塔煤矿厚煤层110工法关键问题研究[D].北京:中国矿业大学(北京),2018.
GAO Yubing.Study on key issues of 110 mining method used in a thick coal seam—a case study in Ningtiaota coal mine[D].Beijing:China University of Mining and Technology(Beijing),2018.
[8] 高玉兵,杨军,张星宇,等.深井高应力巷道定向拉张爆破切顶卸压围岩控制技术研究[J].岩石力学与工程学报,2019,38(10):2045-2056.
GAO Yubing,YANG Jun,ZHANG Xingyu,et al.Study on surrounding rock control of roadways in deep coal mines based on roof cutting and pressure release technology by directional tensile blasting[J].Chinese Journal of Rock Mechanics and Engineering,2019,38(10):2045-2056.
[9] 高玉兵,杨军,王琦,等.无煤柱自成巷预裂切顶机理及其对矿压显现的影响[J].煤炭学报,2019,44(11):3349-3359.
GAO Yubing,YANG Jun,WANG Qi,et al.Mechanism of roof presplitting in a nonpillar mining method with entry automatically retained and its influence on the strata behaviors[J].Journal of China Coal Society,2019,44(11):3349-3359.
[10] 何满潮,郭鹏飞,张晓虎,等.基于双向聚能拉张爆破理论的巷道顶板定向预裂[J].爆炸与冲击,2018,38(4):795-803.
HE Manchao,GUO Pengfei,ZHANG Xiaohu,et al.Directional pre-splitting of roadway roof based on the theory of bilateral cumulative tensile explosion[J].Journal of Vibration and Shock,2018,38(4):795-803.
[11] 何满潮,马资敏,郭志飚,等.深部中厚煤层切顶留巷关键技术参数研究[J].中国矿业大学学报,2018,47(3):468-477.
HE Manchao,MA Zimin,GUO Zhibiao,et al.Key parameters of the gob-side entry retaining formed by roof cutting and pressure release in deep medium-thickness coal seams[J].Chinese Journal of Rock Mechanics and Engineering,2018,47(3):468-477.
[12] 高玉兵,郭志飚,杨军,等.沿空切顶巷道围岩结构稳态分析及恒压让位协调控制[J].煤炭学报,2017,42(7):1672-1681.
GAO Yubing,GUO Zhibiao,YANG Jun,et al.Steady analysis of gob-side entry retaining formed by roof fracturing and control techniques by optimizing mine pressure[J].Journal of China Coal Society,2017,42(7):1672-1681.
[13] 马新根,何满潮,李钊,等.复合顶板无煤柱自成巷切顶爆破设计关键参数研究[J].中国矿业大学学报,2019,48(2):236-246,277.
MA Xingen,HE Manchao,LI Zhao,et al.Key parameters of gob-side entry retaining automatically formed by roof cutting and blasting in compound roof condition[J].Journal of China University of Mining & Technology,2019,48(2):236-246,277.
[14] 陈上元,赵菲,王洪建,等.深部切顶沿空成巷关键参数研究及工程应用[J].岩土力学,2019,40(1):332-342,350.
CHEN Shangyuan,ZHAO Fei,WANG Hongjian,et al.Determination of key parameters of gob-side entry retaining by cutting roof and its application to a deep mine[J].Rock and Soil Mechanics,2019,40(1):332-342,350.
[15] 孙晓明,刘鑫,梁广峰,等.薄煤层切顶卸压沿空留巷关键参数研究[J].岩石力学与工程学报,2014,33(7):1449-1456.
SUN Xiaoming,LIU Xin,LIANG Guangfeng,et al.Key parameters of gob-side entry retaining formed by roof cut and pressure releasing in thin coal seams[J].Chinese Journal of Rock Mechanics and Engineering,2014,33(7):1449-1456.
[16] 朱珍,张科学,何满潮,等.无煤柱无掘巷开采自成巷道围岩结构控制及工程应用[J].煤炭学报,2018,43(S1):52-60.
ZHU Zhen,ZHANG Kexue,HE Manchao,et al.Surrounding rocks control technology and application of automatically formed roadway in mining without coal pillar and gateroad excavation[J].Journal of China Coal Society,2018,43(S1):52-60.
[17] 钱鸣高,许家林.煤炭开采与岩层运动[J].煤炭学报,2019,44(4):973-984.
QIAN Minggao,XU Jialin.Behaviors of strata movement in coal mining[J].Journal of China Coal Society,2019,44(4):973-984.
[18] 于远祥,洪兴,陈方方.回采巷道煤体荷载传递机理及其极限平衡区的研究[J].煤炭学报,2012,37(10):1630-1636.
YU Yuanxiang,HONG Xing,CHEN Fangfang.Study on load transmission mechanism and limit equilibrium zone of coal-wall in extraction opening[J].Journal of China Coal Society,2012,37(10):1630-1636.
[19] 韩昌良.沿空留巷围岩应力优化与结构稳定控制[D].徐州:中国矿业大学,2013.
HAN Changliang.Stress optimization and structure stability control for the surrounding rock of gob-side entry retaining[D].Xuzhou:China University of Mining and Technology,2013.
[20] 何满潮,陈上元,郭志飚,等.切顶卸压沿空留巷围岩结构控制及其工程应用[J].中国矿业大学学报,2017,46(5):959-969.
HE Manchao,CHEN Shangyuan,GUO Zhibiao,et al.Control of surrounding rock structure for gob-side entry retaining by cutting roof to release pressure and its engineering application[J].Journal of China University of Mining and Technology,2017,46(5):959-969.
[21] ZUO Jianping,WANG Jintao,JIANG Yunqian.Macro/meso failure behavior of surrounding rock in deep roadway and its control technology[J].International Journal of Coal Science & Technology,2019,6(3):301-319.
[22] 张劳恩.某煤矿采空区安全廊道稳定性分析[J].铁道勘察,2020,46(2):10-14.
ZHANG Laoen.Stability analysis of safety corridor in goafs of a coal mine[J].Railway Investigation and Surveying,2020,46(2):10-14.
[23] 李新平,陈俊桦,李友华,等.溪洛渡电站地下厂房爆破损伤范围及判据研究[J].岩石力学与工程学报,2010,29(10):2042-2049.
LI Xinping,CHEN Junhua,LI Youhua,et al.Study of criterion and damage zone induced by excavation blasting of underground power-house of Xiluodu hydropower station[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(10):2042-2049.
[24] 王文龙.钻孔爆破[M].北京:煤炭工业出版社,1984:53-58.
[25] 李必红.椭圆双极线型聚能药柱爆炸理论及预裂爆破技术研究[D].长沙:中南大学,2013.
LI Bihong.Research on theory and application technology of Elliptic Bipolar Linear Shaped Charge’s Presplit blasting[D].Changsha:Central South University,2013.
[26] 陈上元,何满潮,郭志飚,等.深部沿空切顶成巷围岩稳定性控制对策[J].工程科学与技术,2019,51(5):107-116.
CHEN Shangyuan,HE Manchao,GUO Zhibiao,et al.Control countermeasures of surrounding rock in deep gob-side entry retaining by cutting roof[J].Advanced Engineering Sciences,2019,51(5):107-116.
