大倾角煤层在我国分布广泛,经过近年来开采技术与配套设备的共同发展,已在多个煤矿试验成功,并进行大规模开采。随着大倾角煤层的开采强度的不断增加,如何能够安全高效的开采大倾角煤层也得到广泛关注[1]。大倾角煤层的工作面系统稳定性较低,大倾角状态下煤(岩)块滑滚形成飞矸,极易伤人和损坏设备。目前由于大倾角工作面的安全防护技术缺乏,使得飞矸防护装置效率偏低,安全事故屡有发生,这严重制约了大倾角煤层的开采能力[2-3]。工作面飞矸现场实测发现产生煤(岩)块的形式有多种,主要包括煤壁片帮、架间矸石漏冒。煤壁片帮是大倾角工作面飞矸的主要形成形式,实测期内仅工作面煤壁片帮衍生的飞矸灾害伤人毁物事故就多达12起[4]。且飞矸灾害发生位置具有很强的随机性。
国内学者分别针对具体的大倾角煤层长壁工作面出现“飞矸”现象进行了一系列的研究与实践,曾先后设计提出了多种挡矸设备和飞矸防护技术,并取得了一定的效果。罗生虎等[5]提出了“两封闭、两隔离”技术。采用这一技术,不仅充分发挥了生产设备的作用,而且提高了工作面生产效率,降低了回采期间“飞矸”伤人事故发生的机率。吕晓等[6]在研究大倾角煤层的工况特点后,研制了3款液压挡矸装置,布置在架间、机道和架前。该装置占地面积小,防矸效率比传统装置高。随着对飞矸综合治理能力的不断提升,邓柱林[7]、何贵荣等[8]均提出改进型的“挡煤帘”“易片帮处设置网状护帘”“柔性防矸(煤)设施”等。李守滨等[9]结合实际工况特点,在易发生飞矸伤害地点专门增加防护设施,减少飞矸对人员及设备的损害。虽然目前对飞矸的研究已经取得了一定的成果[10-14],但是对于飞矸威胁等级评估很少有人研究。准确的评估飞矸对人、设备造成的威胁是大倾角煤层安全防护的基础。由于飞矸的运动具有一定的不确定性,其间伴随着速度、角速度等一系列变量随时间不断变化。
为了探寻飞矸这类不确定性的运动对人或设备的威胁,笔者以飞矸沿工作面滑滚运动为例,采用动态贝叶斯网络建立工作面飞矸威胁评估模型[15-19],由于贝叶斯网络作为一种概率网络模型,能够运用概率论表达飞矸威胁等级评估中的不确定知识,并且由于知识之间的推理是运用可视化的网络方法来表达,因而能够很好地结合工作面飞矸的历史数据及专家经验应对不完备的知识,有效解决飞矸威胁等级评估中的关键问题。
1 动态贝叶斯网络
动态贝叶斯网络(DBN),是定义在每一个时间片的静态贝叶斯网路结构和参数都一致的基础上,是1个由不同时间点的变化的概率结果所组成的网络模型。动态贝叶斯网络表现为1个静态的初始网络以及1个转移网络。一个任意长度的动态贝叶斯网络都可由二者表示,如图1所示。

图1 动态贝叶斯网络
Fig.1 Dynamic bayesian networks
对于一个从启动至与人员或设备碰撞的飞矸事故,可以看作是由T个时间片组成的离散动态贝叶斯网络,假定每个时间片有n个隐藏节点和m个观测节点,分别为(X1,X2,…,Xn)和(Y1,Y2,…,Ym),则离散动态贝叶斯网络推理的目的是计算在观测值下隐藏变量的分布
p(x11,…,xTn|y11,…,yTm)
(1)
式中,xij(yij)为第i个时间片的第j个隐藏节点(观测节点)Xij(Yij)的取值;i∈[1,T],j∈[1,m]。
任何贝叶斯网络推理的基础都是贝叶斯公式(式(2))和贝叶斯网络的条件独立假设(式(3))。

(2)
式中,p(x|y)为条件概率。
![]()
(3)
式中,pa(xi)为节点xi的父节点。
由式(2),(3),可以得到
p(x11,…,xTn|y11,…,yTm)=

(4)
由于离散贝叶斯网络本身也符合条件独立性假设,因此有
p(x11,…,xTn,y11…,yTm)=
![]()
(5)
因此有
p(x11,…,xTn|y11,…,yTm)=
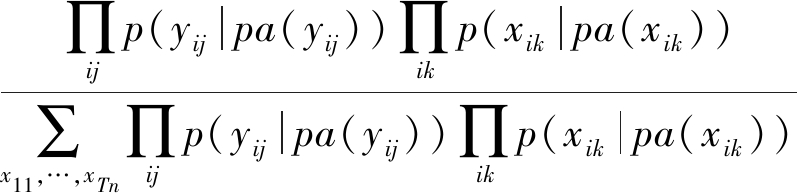
(6)
其中,k∈[1,n]。
2 基于贝叶斯网络的飞矸威胁估计
2.1 贝叶斯网络特征变量的选取
飞矸在工作面内的运动过程是一个多源不确定性耦合的复杂动态过程。在一定时间范围内由不确定性信息和数据对飞矸的威胁做出准确的判断和评估,为之后获得最佳的飞矸防护效果具有重要的意义。飞矸对人或设备的伤损程度取决于飞矸的能级,因此将飞矸具有的总动能作为飞矸威胁的评判依据,飞矸的总动能为
![]()
(7)
式中,Ek为飞矸总动能;m为飞矸质量;v为飞矸运动速度;J为飞矸的转动惯量;ω为飞矸运动角速度。
由式(7)可知飞矸的总动能与飞矸的质量、飞矸的运动速度和角速度有关。为了探究飞矸运动特征量对飞矸动能的影响,笔者以新疆乌鲁木齐市艾维儿沟2130煤矿25221工作面为例[13],工作面倾向长度100 m,平均倾角44°,考虑到工作面底板的不平整性,工作面底板坐标设置随机且有起伏,工作面底板岩性为砂岩,基本参数见表1。
表1 模型参数
Table 1 Model parameters
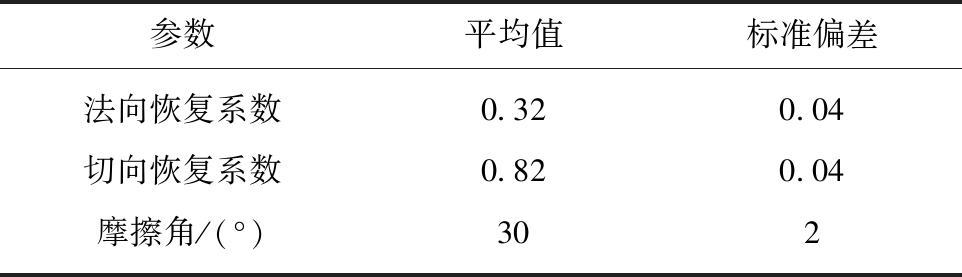
参数平均值标准偏差法向恢复系数0.320.04切向恢复系数0.820.04摩擦角/(°)302
采用RocFall软件模拟50次,得到飞矸沿工作面底板滑滚的轨迹如图2所示。在工作面环境不变的条件下,得到飞矸运动特征量分别取不同值时飞矸的动能变化规律如图3所示。

图2 飞矸滑落轨迹
Fig.2 Slip trajectory of flying gangue

图3 不同飞矸运动特征量取值的飞矸动能变化
Fig.3 Change of kinetic energy of flying gangue with different motion charaoteristic values
由图3可以看出,飞矸质量、速度、角速度对飞矸运动动能均有不同程度的影响,由于飞矸的质量属于确定性因素,在飞矸运动过程中无论是否破裂其总质量是不变的,在飞矸威胁估计中只需考虑随时间变化的特征变量。此外,飞矸运动距离越大,则距离工作面下端头人或设备越近,其伤人损物的威胁等级也越高。因此,本文选取飞矸的速度、角速度和距工作面下端头人和设备的距离3个特征量变量,建立动态贝叶斯网络模型,这样更能准确的反映出各个变量在威胁等级评估中所产生的影响。
2.2 贝叶斯网络基础模型的建立
由于国内外对于飞矸事故的统计数据较少,很难通过大量样本数据来学习网络结构和参数,因此本文主要采用专家知识来构建贝叶斯网络模型。以威胁等级作为隐藏节点,速度、角速度和距工作面下端头人或设备的距离作为观测节点,确定该贝叶斯模型如图4所示。

图4 贝叶斯模型
Fig.4 Bayesian model
其中,TL为飞矸对人或设备的威胁等级,变量状态分别采用高(H)、中(M)、低(L)表示;v为飞矸运动速度;ω为飞矸运动角速度;l为飞矸距工作面下端头人或设备的距离。各节点的状态集合见表2。
在飞矸运动过程中,特征变量会随时间片的变化而变化,形成一个随时间片变动的动态值。因此,需要建立关于飞矸运动过程的动态贝叶斯模型,实现飞矸对人或设备的威胁等级的评估。将图4建立的静态贝叶斯网络模型系统作为动态贝叶斯网络的先验模型,再建立转移网络,得到动态贝叶斯网络模型如图5所示。
表2 模型中变量的定义
Table 2 Definition of variables in the model

节点状态空间状态记号TL高、中、低{H,M,L}v快、中、慢{F,M,S}ω大、中、小{B,M,L}l远、中、近{F,M,N}

图5 动态贝叶斯网络模型系统
Fig.5 Dynamic bayesian network model system
2.3 威胁等级评估流程
(1)脱离母体的煤(岩)块形成飞矸,在外界的扰动下开始运动,观测飞矸运动过程中的特征变量,收集数据信息并导入分析层;
(2)数据信息进入分析层,建立的动态贝叶斯数学模型开始运行,通过转移概率运算,分别导出3个特征变量的数据信息;
(3)特征变量数据信息处理后作出威胁等级评评估;
(4)导出危险等级评估信息,并根据信息判断是否发出危险预警。
具体流程如图6所示。

图6 威胁等级评估流程
Fig.6 Assessment process of threat level
3 动态贝叶斯网络模型参数设定
3.1 动态贝叶斯网络的条件概率
飞矸滑滚运动威胁等级中的先验概率表示在事件还未发生之前,此事件发生的可能性的大小。条件概率为模型中由因至果运算过程中的载体,在得知先验概率的情况下,通过中间的条件概率从而计算得出相关后验概率分布。针对飞矸运动的动态贝叶斯模型先验概率和条件概率以及时间片间的条件概率,以质量4 kg、初速度为0的飞矸从工作面上端头处沿底板滑滚运动为例。依据大倾角煤层开采领域专家经验知识得到先验概率见表3。
表3 先验概率
Table 3 Prior probability

威胁等级先验概率H0.4M0.4L0.2
当在各级威胁等级发生的情况,估算其各个特征变量所能引发威胁等级的条件概率见表4~6。
表4 速度的威胁条件概率
Table 4 Threat conditional probability of velocity

威胁等级FMSH0.70.20.1M0.50.30.2L0.20.30.5
表5 角速度的威胁条件概率
Table 5 Threat conditional probability of angular velocity
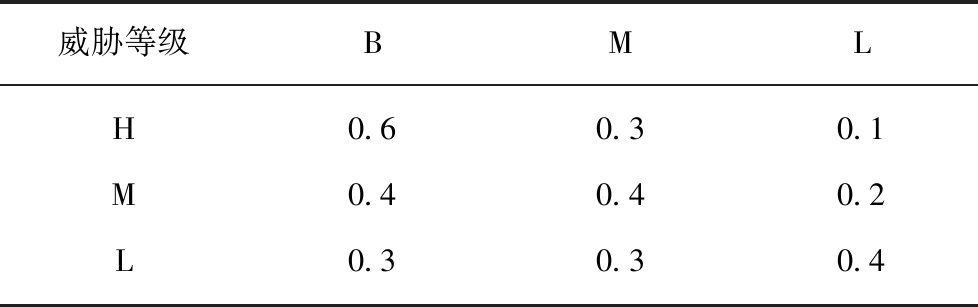
威胁等级BMLH0.60.30.1M0.40.40.2L0.30.30.4
表6 距工作面下端头距离威胁条件概率
Table 6 Threat conditional probability of the distance from the lower ends of working face
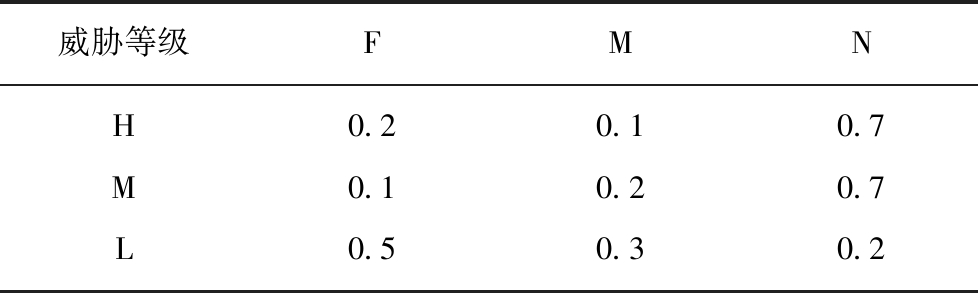
威胁等级FMNH0.20.10.7M0.10.20.7L0.50.30.2
条件概率是由专家经验知识得到的,必然会存在一定的主观性,可通过对样本数据进行适度调整,以提高评估结果的可信度与可靠性。
由表4~6可以看出:① 速度威胁等级中,速度由快到慢的过程中,其高威胁等级所发生的概率逐渐降低,而低威胁等级反之,中级威胁等级并未出现增大或者减小的明显趋势,即飞矸的运动速度与其威胁等级成正比;② 角速度威胁等级中,与速度威胁等级近乎处于同一个增减趋势内,即飞矸的角速度大小仍然与其威胁等级成正比;③ 距工作面下端头人或设备距离威胁等级中,由于实际现场中工作面下端头处常有人员来往和作业设备,所以,飞矸距离工作面下端头的距离越近,其威胁等级也就越高。
3.2 动态贝叶斯网络的后验概率
由上述飞矸威胁等级的动态贝叶斯网络模型、先验概率和条件概率计算得到后验概率结果见表7。
表7 后验概率
Table 7 Posterior probability

威胁等级时刻1时刻2时刻3高0.158 40.353 40.486 6中0.185 20.445 20.454 2低0.656 40.201 40.059 2
3.3 联合概率分布
在动态贝叶斯网络模型计算中,由各个条件概率所得的联合概率分布是动态贝叶斯网络模型运算中必不可少的数据来源,本模型联合概率分布由各个特征变量的条件概率代入贝叶斯公式,所得计算结果见表8。
4 基于维特比动态规划算法仿真分析
4.1 飞矸运动观测节点的选取
维特比算法实际是用动态规划解马尔科夫模型预测问题,即用动态规划求概率最大路径,此路径对应一个序列状态[20]。
依据动态规划原理,从时刻t=1时开始计算一个完整序列中到达各个节点的最大概率,直至计算至序列最末端停止,最末端的点即为终结节点,然后由终结节点反向计算各个节点,从而得到该序列的最优路径,此即为维特比算法。
笔者依据维特比算法寻找动态贝叶斯网络模型中的观测节点,为保证模型仿真模拟的可靠性,选取多个观测节点来描述飞矸沿工作面运动的全过程直至停止。本模型中观测序列的节点选取见表9。
表8 联合概率分布
Table 8 Joint probability distribution

组合节点HML组合节点HMLFBF0.057 70.012 50.007 8MMN0.068 70.075 00.008 9FBM0.028 80.025 00.007 8MLF0.020 60.018 80.062 5FBN0.144 20.037 50.002 2MLM0.010 30.037 50.062 5FMF0.038 50.016 70.015 6MLN0.051 50.056 30.017 9FMM0.019 20.033 30.015 6SBF0.016 50.018 80.039 1FMN0.096 20.050 00.004 5SBM0.008 20.037 50.039 1FLF0.028 80.012 50.031 3SBN0.041 20.056 30.011 2FLM0.014 40.025 00.031 3SMF0.011 00.025 00.078 1FLN0.072 10.037 50.008 9SMM0.005 50.050 00.078 1MBF0.041 20.018 80.015 6SMN0.027 50.075 00.022 3MBM0.020 60.037 50.015 6SLF0.008 20.018 70.156 3MBN0.103 00.056 30.004 5SLM0.004 10.037 50.156 3MMF0.027 50.025 00.031 3SLN0.020 60.056 20.044 6MMM0.013 70.050 00.031 3
表9 动态节点取值
Table 9 Dynamic node selection

时刻1234567891011节点SLFMLFMMFMMMFMMFBMFBNMMNMLNSLNSLN
由上述所选取观测节点,得到节点的篱笆网络如图7所示。

图7 观测节点的篱笆网络
Fig.7 Fence network of observation nodes
4.2 飞矸的威胁等级分析
选取上述飞矸运动的各个观测节点后,依据各个时间片的顺序将上述所选各个观测节点排序,即工作面飞矸所处的初始位置为第一观测节点,随着飞矸的运动,其自身速度逐步增大:S→M→F;角速度逐渐增大:L→M→B;而距工作面下端头人或设备的距离随着时间片的推移而越来越近:F→M→N。由此过程为依据运行系统,得到飞矸沿工作面运动全过程的威胁等级评估结果见表10。飞矸威胁等级变化曲线如图8所示。
表10 仿真结果
Table 10 Simulation results

威胁等级节点1234567H0.060.200.360.430.290.520.82M0.120.180.340.380.620.440.17L0.820.620.300.190.090.040.01

图8 飞矸威胁等级变化曲线
Fig.8 Changing curves of threat level of flying gangue
从图8可以看出,飞矸由工作面上端头开始运动时,初始阶段飞矸的速度与角速度相对较慢,且距工作面下端头距离最远,所以出现高危的概率处于0.1以下,中危概率也在0.15以下,而低危概率处于0.8以上,而后由于其开始加速向下运动,随着速度与角速度的提高,距工作面下端头人或设备的距离越近,高危与中危的发生概率逐渐增加,两者几乎处于同一趋势,而低危概率则大幅下降,直至达到第3个时间片处,3者概率接近。
第3时间片后,由于飞矸的特征变量一直向威胁等级增大的趋势变化,所以其低危概率一直呈现下降的趋势。从第4时间片开始,观测变量变为MMM,飞矸的速度、角速度和距工作面下端头人或设备的距离全都变为中等水平,随时间的推移,飞矸的中危概率逐渐增大,高危概率也呈现减小趋势。直至第5时间片,观测变量转为FMM,从此时开始,高危因素进入观测节点内,高危概率立即呈现大幅增长趋势,同时,中危概率呈现下降趋势。进入第6时间片后,观测变量再次变为FBM,此时速度与角速度2个特征变量已转变为高危因素。随着飞矸沿大倾角工作面的运动,速度与角速度已经增大到可产生高危等级的程度,此时高危概率陡增,由于速度大、角速度大且距工作面下端头距离越来越近,低危概率几乎下降接近于0,中危概率也大幅下降。直至第7时间片时,高危概率已经达到最高程度,此时飞矸已运动至工作面下端头,其特征变量已全部达到高危程度。本文的理论方法与工作面现场实测下部区域设备破坏程度更加剧烈的情况相符合,进一步印证了本文所提供方法用于飞矸威胁等级评估的可行性。
5 结 论
(1)通过动态贝叶斯网络模拟方法,以飞矸的速度、角速度和距离工作面下端头人或设备的距离作为模型的特征变量和观测变量,建立随时间片转移的动态贝叶斯网络。在维特比算法的基础上,选取了多个飞矸运动过程中的动态观测节点,以观测节点为基础观测出多个不同时间片间的运动状态,得到飞矸沿工作面底板运动全过程的威胁等级评估结果。仿真结果表明该方法可准确的给出飞矸威胁等级,且符合客观实际,具有合理性和科学性。可为飞矸防护装置的设置提供一定的理论依据。
(2)飞矸在工作面内运动过程中,随着时间片的递增,飞矸的变量数值也随之变化,飞矸各变量所共同影响的威胁等级也由低到高的变化。随着其威胁等级的不断变化,为避免发生飞矸损害事故,可在飞矸威胁等级较高的位置处设置分级防护装置。
(3)动态贝叶斯网络推理是一种定性的推理工具,能实现连续观测值的推理,如能获得更多的工作面现场飞矸灾害的历史数据,结合专家经验知识,将使得飞矸威胁等级的评估与工程实际的结合更加紧密。
[1] 伍永平,胡博胜,解盘石,等.大倾角长壁工作面飞矸灾害区域治理技术[J].煤炭科学技术,2017,45(2):1-5.
WU Yongping,HU Bosheng,XIE Panshi,et al.Flying gangue regional control technology in longwall mining face of steeply dipping seam[J].Coal Science and Technology,2017,45(2):1-5.
[2] 伍永平,胡博胜,王红伟,等.大倾角煤层飞矸运移能量演化特征仿真与实验研究[J].西安科技大学学报,2018,38(1):37-42.
WU Yongping,HU Bosheng,WANG Hongwei,et al.Simulation and experiment research on the evolution characteristics of flying gangue energy in steeply dipping coal seam[J].Journal of Xi’an University of Science and Technology,2018,38(1):37-42.
[3] 伍永平,刘孔智,贠东风,等.大倾角煤层安全高效开采技术研究进展[J].煤炭学报,2014,39(8):1611-1618.
WU Yongping,LIU Kongzhi,YUN Dongfeng,et al.Research progress on the safe and efficient mining technology of steeply dipping seam[J].Journal of China Coal Society,2014,39(8):1611-1618.
[4] 张浩,伍永平.大倾角煤层长壁大采高采场煤壁片帮机制[J].采矿与安全工程学报,2019,36(2):331-337.
ZHANG Hao,WU Yongping.Coal wall caving mechanism of longwall large mining height stope in steeply dipping coal seams[J].Journal of Mining & Safety Engineering,2019,36(2):331-337.
[5] 罗生虎,伍永平,刘孔智,等.大倾角大采高综采工作面煤壁非对称受载失稳特征[J].煤炭学报,2018,43(7):1829-1836.
LUO Shenghu,WU Yongping,LIU Kongzhi,et al.Asymmetric load and instability characteristics of coal wall at large mining height fully-mechanized face in steeply dipping seam[J].Journal of China Coal Society,2018,43(7):1829-1836.
[6] 吕晓,庄建平.大倾角薄煤层液压支架挡矸装置的设计及应用[J].煤矿机械,2011,32(12):178-180.
LÜ Xiao,ZHUANG Jianping.Design and application of flying gangue prevention devices at high dip and thin seam working face[J].Coal Mine Machinery,2011,32(12):178-180.
[7] 邓柱林.大倾角综采工作面滚矸事故的研究与防治[J].科技信息,2009,(17):386-387.
DENG Zhulin.Research and prevention of gangue rolling accident in fully mechanized coal face with large inclination angle[J].Science & Technology Information,2009(17):386-387.
[8] 何贵荣,张正鹏,梁吉国.大倾角综放工作面飞矸防治措施与实践[J].山东煤炭科技,2014(12):67-68.
HE Guirong,ZHANG Zhengpeng,LIANG Jiguo.Flying waste prevention measures and practice of fully mechanized top coal caving (mining) face with large dip angle[J].Shandong Coal Science and Technology,2014(12):67-68.
[9] 李守滨,申兢,魏利朋,等.泉店煤矿11采区运输巷防飞矸技术[J].煤矿机械,2015,36(3):121-122.
LI Shoubin,SHEN Jing,WEI Lipeng,et al.Fly bottles prevention technique of 11 quandian coal mine belt conveyor lane[J].Coal Mine Machinery,2015,36(3):121-122.
[10] 李冬,常聚才,史文豹,等.大倾角坚硬顶板冒落撞击摩擦试验研究[J].煤炭科学技术,2019,47(2):41-46.
LI Dong,CHANG Jucai,SHI Wenbao,et al.Experimental study on collision and friction of falling hard roof with large dip angle[J].Coal Science and Technology,2019,47(2):41-46.
[11] 景玲玲,屈钧利,刘明,等.大倾角煤层飞矸运动估计的非概率区间分析法[J].煤炭技术,2019,38(5):105-108.
JING Lingling,QU Junli,LIU Ming,et al.Non-probabilistic interval analysis method for estimation of flying gangue movement in steeply dipping seam[J].Coal Technology,2019,38(5):105-108.
[12] 刘明,伍永平,徐刚.大倾角煤层开采飞矸运动规律研究[J].煤炭技术,2016,35(7):17-18.
LIU Ming,WU Yongping,XU Gang.Research on rule of flying gangue in steeply dipping seam mining[J].Coal Technology,2016,35(7):17-18.
[13] 伍永平,胡博胜,王红伟,等.大倾角煤层长壁开采工作面飞矸致灾机理研究[J].煤炭学报,2017,42(9):2226-2234.
WU Yongping,HU Bosheng,WANG Hongwei,et al.Mechanism of flying gangue-caused disasters in longwall mining of steeply dipping seam[J].Journal of China Coal Society,2017,42(9):2226-2234.
[14] 伍永平,胡博胜,解盘石,等.大倾角工作面飞矸冲击损害及其控制[J].煤炭学报,2018,43(10):2694-2702.
WU Yongping,HU Bosheng,XIE Panshi,et al.Impact damage of flying gangue in steeply dipping seams and its control[J].Journal of China Coal Society,2018,43(10):2694-2702.
[15] 史建国,高晓光.离散动态贝叶斯网络的直接计算推理算法[J].系统工程与电子技术,2005,27(9):1626-1630.
SHI Jianguo,GAO Xiaoguang.Direct calculation inference algorithm for discrete dynamic bayesian network[J].Systems Engineering and Electronics,2005,27(9):1626-1630.
[16] 晏师励,李德华.基于动态贝叶斯网络的空战目标威胁等级评估[J].计算机与数字工程,2015,43(12):2150-2154.
YAN Shili,LI Dehua.Threat level assessment of the air combat target based on DBN[J].Computer & Digital Engineering,2015,43(12):2150-2154.
[17] MURPHY K P.Dynamic bayesian networks:Representation,inference and learning[M].Berkeley:University of California,2002.
[18] 胡汇洋.基于动态贝叶斯网络的目标毁伤等级评估[D].南京:南京理工大学,2009.
HU Huiyang.Target damage rating evaluation based on dynamic bayesian network[D].Nanjing:Nanjing University of Science and Technology,2009.
[19] ENRIGHT C G,MADDEN M G,MADDEN N.Bayesian networks for mathematical models:Techniques for automatic construction and efficient inference[J].International Journal of Approximate Reasoning,2013,54(2):323-342.
[20] 肖扬.序列挖掘算法研究及其在用户行为分析中的应用[D].北京:北京邮电大学,2014.
XIAO Yang.Research on the sequence mining algorithm and its application in user behavior analysis[D].Beijing:Beijing University of Post and Telecommunications,2014.
