在煤矿生产中,从原煤中分拣煤矸石是煤炭洗选的首要环节,原煤入选率是评价煤矿生产效益的重要指标[1]。矸石是影响煤矿煤炭生产质量的重要因素[2],拣矸率则是评价煤矿分选效果的重要参数。传统的干选[3-4]和湿选[5-7]方法在一定程度上提高了煤炭入选率,但是其所带来的资源浪费、环境污染和成本高等问题已不能满足绿色开采要求[8]。特别是大粒度(100~300 mm)的矸石依然依靠人工分拣来完成,存在人员需求多、拣矸效率低、劳动强度大、工作环境劣等问题[9]。随着机器人、煤矸石识别[10]等技术的不断发展和成熟,利用机器人进行煤矸石分拣已经成为一种新的研究方向,国内相关研究工作者在该方向做了大量的研究工作,也取得了一定的研究成果[11-12]。特别是在煤矸石视觉识别的基础上,多机械臂协同分拣煤矸石技术的提出[13-14],打开了机器人迈向煤矿煤矸石分拣领域的大门,也为这一研究方向提供了新的思路。
煤矿生产中,煤和矸石通过带式输送机进行运输,其运行速度高,分布随机,并且矸石质量和体积较大,和传统工业领域传送带分拣相比,由于分拣对象的特殊性,对机器人在负载、速度等参数的要求较高。在分拣领域最核心的问题便是动态目标快速跟踪问题,在这方面,大量研究人员在高速分拣领域做了充分的实验研究,并且取得了显著的成果。目前常用的方法主要有PTP(Point-To-Point)[15]、比例导引法[16]、金字塔寻优[17]、PID跟踪[18]等。这些方法通过视觉获取目标实时位置,然后通过算法控制机器人末端对目标进行动态抓取,具有较高的响应,分拣速度可高达110次/min[19]。由于在工业高速分拣中,其分拣对象属于小体积、小质量目标,在对机器人末端控制时,只需要机器人末端与目标在位置上相遇便可完成分拣;同时,分拣机器人为轻量化设计,机械系统本身惯量负载小,这2个因素决定了其具有较高的响应速度和分拣速度。
但是对于煤矸石分拣来讲,由于分拣粒度在100~300 mm,分拣质量在5~20 kg,这就决定了分拣机器人机械本体系统具有较大惯量负载,也在一定程度上影响了系统的响应。在前期试验中,利用以上算法对煤矸石进行动态抓取实验时发现,机器人在动态跟踪过程中出现动作延迟和抖动,并且在跟踪到目标后进行抓取时有较大的冲击载荷,甚至对机械手造成损坏。分析其原因主要有以下几个方面:① 由于煤矸石分拣机器人机械本体惯量负载较大,同时算法较为复杂,导致系统响应时间过长,进而出现机械臂在运动过程中出现抖动现象;② 由于煤矸石质量过大,并且其运动速度较高,在对其进行抓取时若只采用拦截的方式进行位置匹配,而不考虑其速度和加速度的匹配,则会因为煤矸石具有较大的惯性力而出现抓取时较大的冲击;③ 以上算法在控制机器人末端逼近目标时虽然有较高的位置精度,但是应用在煤矸石分拣机器人上时会出现跟踪时间过长而出现目标超出机器人工作空间现象,最终导致抓取失败。再者,不同的煤矿其含矸量不同,以含矸量15%的煤矿为例,通过计算,要求分拣机器人分拣速度要达到30次/min以上,对机器人性能提出了很高的要求。因此,研究适用于煤矿分拣机器人的动态目标快速、准确、稳定的抓取算法对于提高煤矸石分拣机器人分拣技术水平具有重要意义。
综合以上分析,笔者结合以上算法的优点,提出了基于余弦定理-PID的机器人动态目标抓取算法。该方法通过余弦定理计算出煤矸石理论抓取点,然后控制机器人末端到达理论抓取点后转为PID跟踪,最后使得机器人末端与煤矸石同步,有效解决了其他算法因迭代次数过多而产生的机械臂响应时间长、运行抖动问题,同时确保机器人以最优的时间实现对煤矸石同步跟踪,实现机器人对大质量、动态煤矸石的快速、准确和稳定抓取。
1 煤矸石分拣机器人原理
煤矸石分拣机器人如图1所示。多机械臂煤矸石分拣机器人系统由煤矸石识别系统、机械臂、上位机、机器人控制器、视觉伺服系统等组成。该系统通过煤矸石识别系统对矸石进行识别并获取其位置和姿态。然后将所获取的矸石信息进行数据打包发送给上位机。上位机在获取煤矸石信息后,根据煤矸石位置进行排序工作,并通过多目标任务分配策略将抓取任务下达给相应机械臂控制器。机械臂根据获得的任务对目标进行监测,当目标进入机械臂工作空间后机器人控制器对机械臂进行轨迹规划完成煤矸石分拣。

图1 多机械臂煤矸石分拣机器人系统原理
Fig.1 Structure of multi-manipulator coal and gangue
sorting robot system based on machine vision
在上述过程中,矸石经过视觉传感器采集信息之后,随传送带向前运动,因此需要对工件进行动态追踪抓取。传统的高速分拣机器人中所使用的跟踪方法虽然可以快速对运动目标进行拦截式抓取,而对于煤矸石分拣来讲,由于煤矸石存在质量大、运动速度快的特点,这种方法在应用过程中会产生较大的冲击和振动。因此,为了避免这种现象发生,要使机器人末端与煤矸石快速相遇并同步。首先通过余弦定理获得最小时间下机器人与煤矸石理论抓取点,并在机器人末端到达理论抓取点后转为位置-速度双环PID控制,使得机器人末端和煤矸石在位置、速度和加速度上同步,然后进行稳定抓取。
2 煤矿分拣机器人轨迹规划
在实际生产中,人工分拣区域的带式输送机为平皮带,并且通过张紧装置,确保了皮带在运输过程中始终保持水平,不会出现下坠现象,这也为机器人分拣提供了很好的分拣条件,即机器人抓取高度相同。机器人在进行分拣任务时一般分为“上升—追踪—下降—抓取”4个环节,而通常采用的轨迹为门子型轨迹,如图2中P1P3P6P8的轨迹,其中,S1~S5为机器人轨迹长度。而P1P3P6P8轨迹中上升和追踪初始阶段为直角过渡,这种过渡方式很容易造成振动和冲击,对于机器人的高速运行造成严重影响。因此,在对机器人轨迹进行设计时,将直角过渡区域进行圆弧过渡处理,如P1P2P4P5P7P8。
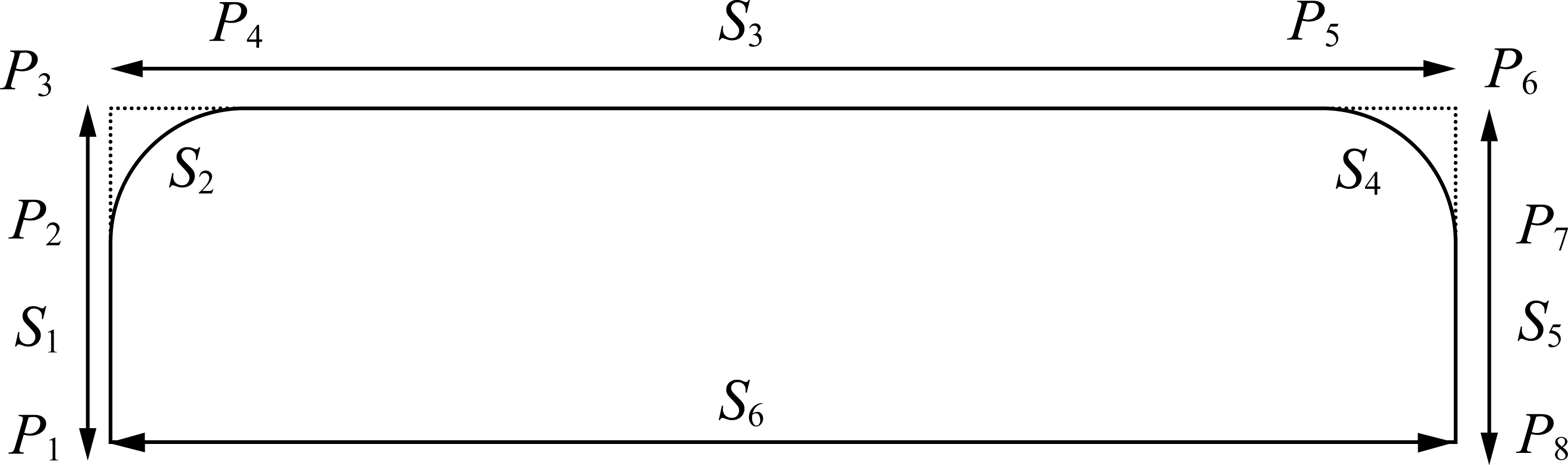
图2 点对点门字形轨迹
Fig.2 Point-to-point gate glyph trajectory
根据机器人特性,同时保证机器人在运动过程中运动性能的稳定、连续和不突变,采用梯形速度轨迹规划,机器人加速度为a,由加速度公式可得速度和位移表达式。
速度v(t)表达式为
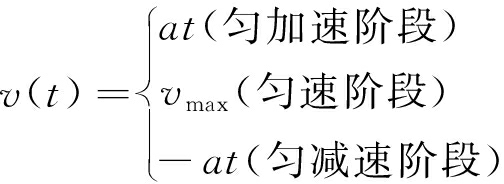
(1)
式中,vmax为机械臂末端最大速度;a为机械臂末端加速度;t为时间。
位移s(t)表达式为

(2)
在门字型轨迹中,S1,S2,S4,S5为已知,可根据实际工况设置机器人末端高度和圆弧过渡半径,各段的运行时间可根据各段位移和边界条件求出。而S3则由煤矸石抓取位置和机器人末端位置关系决定。
3 动态目标稳准抓取算法
为了提高煤矸石分拣机器人分拣效率,避免过长的跟踪时间,首先通过余弦定理计算出机器人理论抓取点,使得机器人末端与煤矸石快速逼近,然后通过PID算法控制机器人末端与煤矸石同步。具体控制流程如图3所示。
为使机器人完成动态目标快速跟踪,系统采用分层控制的思想,将机器人的轨迹跟踪控制分为两层:轨迹跟踪控制器和速度PID控制器。在初始阶段,引入余弦定理,计算出机器人抓取目标的理论抓取点,由轨迹规划器控制机器人末端到达理论抓取点。然后转入位置与速度双环PID跟踪阶段,图3中Pg,vg为煤矸石实时位置与速度,通过编码器实时获取,P为机器人理论抓取点坐标,Pi,vi为机器人末端位置和速度输出。该算法具体计算过程如下。

图3 动态目标跟踪原理
Fig.3 Schematic diagram of dynamic target tracking
3.1 动态目标理论抓取点计算方法
要实现机器人对煤矸石的准确抓取,最重要的是煤矸石的定位精度。系统采用基于位置的视觉控制,根据计算机视觉系统提供的煤矸石位置等信息来计算煤矸石的抓取位置[20-21]。当监测到煤矸石进入机器人工作空间,则将矸石坐标发送至机器人轨迹规划器,由轨迹规划器计算煤矸石理论抓取点坐标,动态目标理论抓取点计算示意如图4所示。

图4 理论抓取点计算示意
Fig.4 Schematic diagram of theoretical point grab calculation
在计算理论抓取点时,设传送带匀速运动,当机器人完成上一煤矸石的分拣或处于初始状态,分拣机器人末端位于放置点R,此时分拣机器人分拣目标为A处的矸石,假设机器人在B点便可与矸石位置重合。A点坐标和放置点R坐标均已知,设A点坐标为A(xg,yg),该坐标由煤矸石识别系统获取,R点坐标为R(xr,yr),传送带速度为vd,则有LAB=Δtvd,Δt为从点A运动到点B的时间,因此点B坐标为(xg+Δtvd,yg),AR的距离LAR为
![]()
(3)
机器人末端在B点和煤矸石相遇,则煤矸石从A点运动到B点所花费的时间与机器人末端从R点运动到B点所用的时间相等,并且通过煤矸石和机器人末端初始位置可获得∠BAR。那么在ΔABR中通过余弦定理可建立关于时间t的关系式。
![]()
(4)
![]()
(5)
LAB=Δtvd,Δt=T1+T2+T3+T4+T5,其中T1为S1段位移时间,T2为S2段位移时间,T3为S3段位移时间,T1=T5,T2=T4。T1,T2,T4,T5可根据式(1),(2)求出。门字型轨迹投影到水平面上BR的距离为
LBR=S6=S′2+S′4+S3
(6)
S′2,S′4分别为S2和S4在水平面上的投影,其值可根据具体工况来设定,为已知量。通过设定S1,S2数值,令机器人末端运动到S3阶段时,机器人末端处于匀速运动阶段,则
S3=T3vRmax
(7)
其中,T3为未知量;vRmax为机器人末端最大速度。联立式(3)~(7)可得关于T3的方程:
(S′2+S′4)vRmax-LARvdcos θ]T3-2vdLAR×
![]()
(8)
式中,θ为∠ABR角度;vd为带式输送机带速。
f(T3)为无匀速段下机器人动态跟踪煤矸石的数学模型。对方程f(T3)进行求解,如果方程无解,则选择放弃跟踪,若方程有正负解,则选择绝对值最小的解。在计算出S3段的时间T3后,将其代入B点坐标中可获取机器人与煤矸石理论抓取点。
3.2 基于位置-速度双环PID同步跟踪方法
机器人分拣煤矸石不同于工业应用的高速分拣机器人,其分拣目标质量大、运动速度快,采用传统的拦截方式对目标进行直接抓取会对机械手造成较大的冲击和振动导致抓取失败,甚至造成机械手损坏。因此,机器人末端在到达理论抓取点时,并不能直接执行抓取动作,要保证机器人末端与煤矸石在位置和速度上同步后,再进行抓取动作,这样才能确保机械手在抓取时以最小的冲击将煤矸石抓取。PID 控制算法是工业控制应用方面主要技术之一,它以数学结构简单、稳定性好、性能可靠、调制方便等优点在机器人控制方面广泛应用[22]。因此,当机器人末端到达理论抓取点后,转入位置-速度PID跟踪,实现同步后稳定抓取。PID时域控制表达式为
![]()
(9)
式中,m(t)为PID控制输出;Kpε(t)为比例控制项;Kp为比例系数;![]() 为积分控制项;Ti为积分时间常数;
为积分控制项;Ti为积分时间常数;![]() 为微分控制项;Td为微分时间常数;ε(t)为输入值与实际值的差值。
为微分控制项;Td为微分时间常数;ε(t)为输入值与实际值的差值。
系统通过视觉系统定位后,开始读取带式输送机编码器获取煤矸石实时位置与速度,并发送至机器人控制器,机器人控制根据煤矸石坐标变化实时调整机械臂末端,逐步使机器人末端与煤矸石保持位置一致[23-24]。机器人控制器通过PID算法不断获取机器人末端与煤矸石之间的位置和速度差,并生成机器人控制量使机器人末端在位置和速度保持一致进行抓取。动态目标抓取过程示意如图5所示。

图5 动态目标抓取示意
Fig.5 Schematic diagram of dynamic target capture
当机器人末端到达第1阶段的理论抓取点后,马上切入双环PID控制阶段,系统通过视觉实时获取待抓取矸石坐标(xg,yg,zg)和速度(vxg,vyg,vzg),同时读取机器人末端坐标(xr,yr,zr)与速度(vxr,vyr,vzr)。则目标在3个方向的位置误差与速度误差εx(t),εy(t),εz(t)表示为
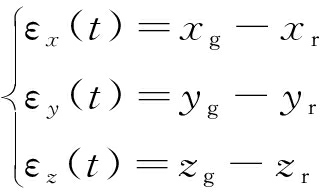
(10)

(11)
根据式(10)可得出机械臂在t时刻的位置调整量m(t)和速度调整量mv(t)分别表示为
![]()
(12)
![]()
(13)
式中,KPv为速度比例控制系数;Tdv为速度微分常数;εv(t)为速度输入值与实际值得差值。
对于带式输送机运输来讲,煤矸石在胶带上只有沿运输方向拥有速度,即只有vx。Y方向和Z方向速度可认为是0。因此在对机器人控制时,其位置和速度分量可以表示为
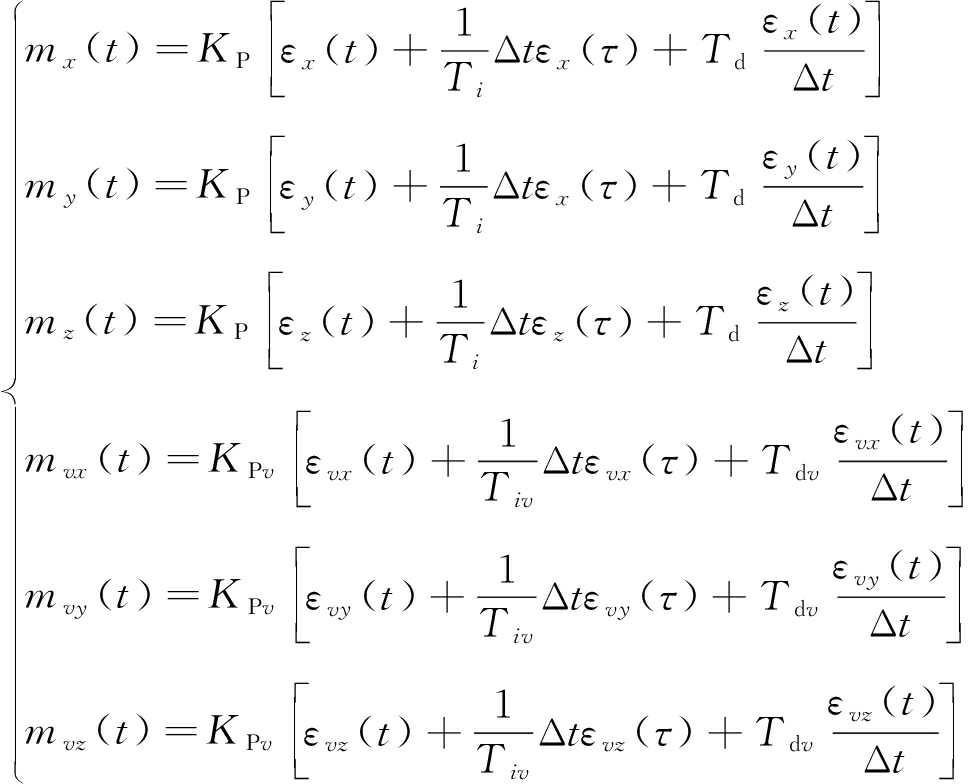
(14)
式中,Tiv为速度积分时间常数。
通过位置-速度双环PID控制实现机械臂末端与煤矸石进行同步,在执行抓取动作时,两者保持相对静止,可以有效的防止由于煤矸石质量大引起的惯性量以及由于速度不匹配而产生的冲击,通过实验,验证了机械臂在抓取过程中的平稳性。
4 煤矸石动态抓取算法实验验证
实验采用 Windows 10 操作系统,用Matlab将本算法与比例导引法、金字塔寻优法进行测试对比,测试条件根据机器人实际运行参数和带式输送机运行速度,目标初始位置为(1,1),机器人末端初始位置为(0,0.5),机器人最大速度为4 m/s,最大加速度为10 m/s2,带式输送机速度为0.7 m/s,测试结果如图6所示。
从图6可以看出,本算法在时间上明显优于其他算法,图中点1为本算法抓取点,点2为金字塔寻优算法抓取点,点3为比例导引法抓取点。在计算过程中比例导引法迭代次数过多,算法运行时间最长,金字塔寻优算法比比例导引法运算时间短,本算法的运行时间最小。

图6 不同算法追踪效果仿真结果
Fig.6 Simulation results of tracking effects of different
algorithms
为了进一步验证本算法的高效性与可行性,以实验室双机械臂煤矸石分拣系统为基础,用以上几种算法分别在不同带速下进行跟踪抓取实验并记录实验结果,同时观察实验过程中机器人是否发生冲击、振动等现象。实验统计结果见表1。
表1 动态目标抓取算法及对比算法测试结果
Table 1 Dynamic target capture algorithm and comparison of algorithm test results

vd/(mm·s-1)xryrxr-xgyr-ygtP/mstJ/mstB/ms300150150300200259.32284.26276.89500200150200300265.16302.15289.41600200150500200304.58334.85326.58700200150400200354.23386.47379.84
实验中运行参数与仿真参数相同。表1中tP为本算法抓取时间;tB为比例导引法的抓取时间;tJ为金字塔寻优的抓取时间。由表1可得,在同等条件下,比例导引算法和金字塔寻优算法同步时间都大于本文算法,并且,比例导引与金字塔寻优算法在抓取过程中多次出现冲击、抖动现象。
图7为煤矸石机器人实验样机。煤矸石分拣机器人采用直角坐标结构,可以在空间拥有4个自由度,并配备了视觉传感器。用实验室样机进行实际抓取实验,测试在不同传送带速度下算法的准确性与稳定性。

图7 煤矸石分拣机器人实验样机
Fig.7 Experimental prototype of coal gangue sorting robot
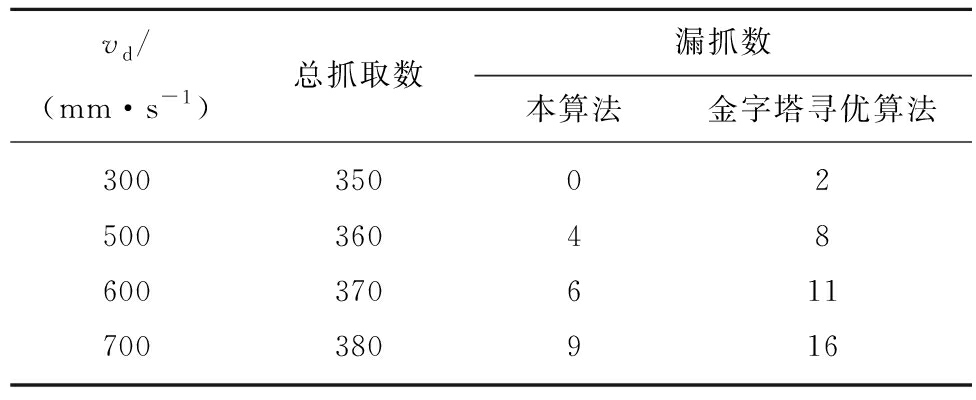
样机实验结果见表2。实验中漏抓率<0.3%,实验对比了基于金字塔寻优的分拣效果,结果表明本文算法具有更高的准确性、稳定性和高效性。在实验室条件下,单机器人分拣速度最高可达25次/min,拣矸率可达40%。而本课题组所设计的双机械臂煤矸石分拣机器人分拣速度最高可达50次/min,通过统计,最高拣矸率可达63%。
表2 样机实验结果
Table 2 Experimental results of prototype
vd/(mm·s-1)总抓取数漏抓数本算法金字塔寻优算法3003500250036048600370611700380916
5 结 论
(1)提出的算法通过余弦定理求解出机械臂预抓取点,并结合 PID 算法控制机械臂末端与煤矸石同步。2者的结合在很大程度上减少了同步跟踪时间,提高了分拣效率。
(2)结合实际工况,通过仿真与实验的方法对提出的算法进行验证,对比不同算法测试结果,本文所提出的算法计算精准、速度快,满足实时性要求。
(3)样机对比实验结果表明:利用本文算法能使煤矸石分拣机器人最高以 25 次/min 的速度进行分拣操作,并且在分拣过程中系统有较高的稳定性,使得分拣速度和拣矸率最大化。在后期的研究中,将着力于多机械臂协同分拣,以提高煤矸石分拣机器人拣矸率。
[1] MA Dan,DUAN Hongyu,LIU Jiangfeng.The role of gangue on the mitigation of mining-induced hazards and environmental pollution:An experimental investigation[J].Science of the Total Environment,2019,664:436-448.
[2] 《中国煤炭工业改革发展年度报告》(2016)[J].中国煤炭,2017,43(2):10.
Annual report on the reform and development of China’s coal industry(2016)[J].China Coal,2017,43(2):10.
[2] ZHAO Yuemin,YANG Xuliang,LUO Zhenfu,et al.Progress in development of dry coal beneficiation[J].International Journal of Coal Science & Technology,2014,1(1):103-112.
[4] SAIKIA Binoy K,KHOUND Kakoli,SAHU Om P,et al.Feasibility studies on cleaning of high sulfur coals by using ionic liquids[J].International Journal of Coal Science & Technology,2015,2(3):202-210.
[5] VENUGOPAL R,PATEL J P,BHAR C.Coal washing scenario in India and future prospects[J].International Journal of Coal Science & Technology,2016,3(2):191-197.
[6] VASUMATHI N,KUMAR T V Vijaya,RATCHAMBIGAI S,et al.Beneficiation of an Indian non-coking coal by column flotation[J].International Journal of Coal Science & Technology,2016,3(2):206-214.
[7] 张秀梅,郭德,王露,等.煤泥自载体浮选[J].煤炭学报,2018,43(4):1127-1133.
ZHANG Xiumei,GUO De,WANG Lu,et al.Autogenous carrierflotation of coal slime[J].Journal of China Coal Society,2018,43(4):1127-1133.
[8] 樊晓光.煤矿绿色开采技术的应用[J].资源节约与环保,2019(9):39-40.
FAN Xiaoguang.Application of green mining technology in coal mine[J].Resource Conservation and Environmental Protection,2019(9):39-40.
[9] 洪惠超.基于机器视觉的煤矸石分选算法的研究[D].泉州:华侨大学,2018.
HONG Huichao.Study on gangue sorting algorithm based on machine vision[D].Quanzhou:Huaqiao University,2018.
[10] 钟志平,孔力.煤矸石在线自动分选系统的识别原理[J].煤炭科学技术,2000,28(11):27-29.
ZHONG Zhiping,KONG Li.Identification principle of online automatic sorting system for coal gangue[J].Coal Science and Technology,2000,28(11):27-29.
[11] 曹现刚,费佳浩,王鹏,等.基于多机械臂协同的煤矸分拣方法研究[J].煤炭科学技术,2019,47(4):7-12.
CAO Xiangang,FEI Jiahao,WANG Peng,et al.Study on coal-gangue sorting method based on multi-manipulator Collaboration[J].Coal Science and Technology,2019,47(4):7-12.
[12] 王鹏,曹现刚,夏晶,等.基于机器视觉的多机械臂煤矸石分拣机器人系统研究[J].工矿自动化,2019,45(9):47-53.
WANG Peng,CAO Xiangang,XIA Jing,et al.Research on multi-manipular coal and gangue sorting robot system based on machine vision[J].Industry and Mine Automation,2019,45(9):47-53.
[13] 曹现刚,吴旭东,王鹏,等.面向煤矸分拣机器人的多机械臂协同策略[J].煤炭学报,2019,44(S2):763-774.
CAO Xiangang,WU Xudong,WANG Peng,et al.Collaborative strategy of multi-manipulator for coal-gangue sorting robot[J].Journal of China Coal Society,2019,44(S2):763-774.
[14] 李宁.煤矸分拣机器人控制系统研究[D].西安:西安科技大学,2019,6.
LI Ning.Study on robot control system of coal waste sorting[D].Xi’an:Xi’an University of Science and Technology,2019,6.
[15] 蔡菲,郭倩.基于动态抓取算法的机器人分拣研究[J].自动化与仪器仪表,2018,8:10-13.
CAI Fei,GUO Qian.Research on robot sorting based on dynamic grasping algorithm[J].Automation and Instrumentation,2018,8:10-13.
[16] 张朝阳,周惠兴,曹荣敏,等.基于金字塔形寻优的传送带动态抓取研究[J].制造业自动化,2015,37(5):92-95.
ZHANG Chaoyang,ZHOU Huixing,CAO Rongmin,et al.Dynamic grab of conveyor belt based on pyramid shape optimization[J].Manufacturing Automation,2015,37(5):92-95.
[17] 张朝阳.基于视觉的机器人废金属分拣系统研究[D].北京:中国农业大学,2015.
ZHANG Chaoyang.Research on robot scrap metal sorting system based on vision[D].Beijing:China Agricultural University,2015.
[18] 苏婷婷,张好剑,王云宽,等.基于费拉里法的 Delta 机器人动态目标抓取算法[J].华中科技大学学报(自然科学版),2018,46(6):128-132.
SU Tingting,ZHANG Haojian,WANG Yunkuan,et al.Delta robot dynamic target grasping algoritm based on ferrari method[J].Journal of Huazhong University of Science and Technology (Natural Science Edition),2018,46(6):128-132.
[19] 倪鹤鹏,刘亚男,张承瑞,等.基于机器视觉的Delta机器人分拣系统算法[J].机器人,2016(1):49-55.
NI Hepeng,LIU Yanan,ZHANG Chengrui,et al.Delta robot sorting system algorithm based on machine vision[J].Robotics,2016(1):49-55.
[20] 蔡菲,郭倩.基于动态抓取算法的机器人分拣研究[J].自动化与仪器仪表,2018,8:10-13.
CAI Fei,GUO Qian.Research on robot sorting based on dynamic grasping algorithm[J].Automation and Instrumentation,2008,8:10-13.
[21] 梅江平,臧家炜,乔正宇,等.三自由度Delta并联机械手轨迹规划方法[J].机械工程学报,2016,52(19):9-17.
MEI Jiangping,ZANG Jiawei,QIAO Zhengyu,et al.Trajectory planning method of three-degree-of-freedom Delta parallel manipulator[J].Chinese Journal of Mechanical Engineering,2016,52(19):9-17.
[22] 董鹏飞.基于位置的工业机器人视觉伺服控制系统研究[D].广州:华南理工大学,2015.
DONG Pengfei.Research on visual servo control system of industrial robot based on position[D].Guangzhou:South China University of Technology,2015.
[23] RAMALINGAM S,STURM P,LODHA S K.Towards complete generic camera calibration[A].IEEE Computer Society Conference on Computer Vision and Pattern Recognition[C].IEEE,2005,1:1093-1098.
[24] LARI,ZAHRA,HABIB,et al.Multi-camera system calibration with builtin relative orientation constraints (Part 1) theoretical principle[J].Journal of the Korean Society of Surveying Geodesy Photogrammetry & Cartography,2014,32(3):191-204.
